A&A 384, 689-701 (2002)
DOI: 10.1051/0004-6361:20020029

Accurate spin axes and solar system dynamics: Climatic variations for the Earth and Mars

S. Edvardsson - K. G. Karlsson - M. Engholm

Department of physics, Mid Sweden University, 851 70 Sundsvall, Sweden

Received 10 April 2001 / Accepted 4 January 2002

Abstract
Celestial mechanical simulations from a purely classical point of view of the solar system, including our Moon and the Mars moons - Phobos and Deimos - are carried out for 2 millions of years before present. Within the classical approximation, the results are derived at a very high level of accuracy. Effects from general relativity for a number of variables are investigated and found to be small. For climatic studies of about 1 Myr, general relativity can safely be ignored. Three different and independent integration schemes are used in order to exclude numerical anomalies. The converged results from all methods are found to be in complete agreement. For verification, a number of properties such as spin axis precession, nutation, and orbit inclination for Earth and Mars have been calculated. Times and positions of equinoxes and solstices are continously monitored. As also observed earlier, the obliquity of the Earth is stabilized by the Moon. On the other hand, the obliquity of Mars shows dramatic variations. Climatic influences due to celestial variables for the Earth and Mars are studied. Instead of using mean insolation as in the usual applications of Milankovitch theory, the present approach focuses on the instantaneous solar radiation power (insolation) at each summer solstice. Solar radiation power is compared to the derivative of the icevolume and these quantities are found to be in excellent agreement. Orbital precessions for the inner planets are studied as well. In the case of Mercury, it is investigated in detail.

Key words: solar system: general - planets and satellites: general - methods: N-body simulations - celestial mechanics: spin axes - relativity - Earth - Mars


1 Introduction

During the last decade a large number of simulations of the planetary system have been reported. Most of these papers have been concerned with the influence of variations in the Earth's orbit on climate (Berger & Loutre 1991, 1992, 1997; Berger et al. 1993; Quinn et al. 1991), while others (Laskar & Robutel 1993; Laskar et al. 1993a; Néron de Surgy & Laskar 1997; Sussman & Wisdom 1992) have, at least in part, concentrated on other effects. Some authors have had their main focus on Mars (Bouquillon & Souchay 1999; Touma & Wisdom 1993). As for climate it is generally agreed that changes in the Earth's orbital parameters play an important role in climate forcing, an idea originally brought forward by Milutin Milankovitch. The climatic history of the Earth shows clear evidence of the precession periods (about 19000 and 23000 years) and changes in the obliquity (period of about 41000 years). The main period in glacial data (around 100000 years) is, however, hard to explain in terms of orbital variations. Instead, other mechanisms have been suggested responsible for this period, e.g. changes in the Earth's orbital plane (Muller & MacDonald 1995). A problem with former studies is that comparisons have been made between insolation and ice volume of the Earth. In this study we instead compare the instantaneous summer radiation power at high northern latitudes with the differentiated ice volume. We find our results convincing. Simulations of Mars are not as common as those of the Earth. One reason is that reliable observational results to confirm the theoretical calculations have not been available until quite recently. Accurate determinations of e.g. the precession of the planet were achieved in the late 1990's through the Mars Pathfinder mission (Folkner et al. 1997).

1.1 Introductory comments on accuracy

We shall now provide a brief introduction to the accuracy of our theoretical approach that will be presented in detail below. It is often desired to answer the question: which solution in the literature is the "best''? Unfortunately this is not easily answered. What can be said about the present solution, is that within the idealistic models our solutions are exact. However, the real world is often more complicated and our and others claimed accuracy can easily be rendered obsolete due to various uncertainties that might be discovered in the future. Be it as it may, our approach is believed to be good because: 
- interactions from all the planets, from the Moon (in the case of Earth) or from Phobos and Deimos (in the case of Mars) and that from the Sun shall be accounted for at every time step in the simulation. To our knowledge, no other simulations have integrated the Moon orbit for this extended time period. All the intricate many-particle-effects in our simulations are therefore properly accounted for;  
- we shall use numerical integration techniques that of course are equivalent to taking standard perturbation theory to all orders. We are always testing several time steps in order to verify that complete convergence is fulfilled. We have also tested several different numerical algorithms to ensure consistency; 
- we will derive an exact numerical treatment of the instantaneous spin axis. This property will also be computed at every time step. This has the advantage that we obtain all oscillations from hours up to millions of years. It will be shown that this approach is very stable; 
- in the calculation of the total torque acting on the planet under study, we take into account torques from all the other bodies in the system at each time step; 
- we shall apply the latest and most accurate ephemeris data (DE-406); 
- we will also verify that general relativity, tides and solar mass loss in practise are negligible for time periods of at least 1 Myr which also is a relevant period for climatic studies. 
 
In Appendix we discuss some of the approximations in the chosen model and also give a pointer for obtaining some of the resulting data files.

2 Theoretical considerations

2.1 Definition of units

In all calculations below we use the following units. The unit of time is one Julian day (1 d), where 1 d is exactly 86400 s. The sidereal day is given by 86164.09054 s (JPL). The unit of length is 1 astronomical unit (1 AU = $1.49597870691 \times 10^{11} $ m). Moreover the gravitational constant is chosen as G=1. In this system of units, 1 Solar mass is = $2.9591221 \times 10^{-4} $.

2.2 Initial conditions and input data

Although the number of figures in numerical input data below is sometimes greater than the estimated accuracy, those are the input parameters used in our program. We present them here simply for reproducibility reasons.

All planetary masses are derived from the mass ratios listed at the JPL database (JPL). However, the Earth and the Moon are integrated separately. Their individual masses are therefore computed using the mass ratios of Sun/(Earth+Moon) and Moon/Earth. The mass ratios are listed in Table 1.


 
Table 1: IAU estimates of the mass ratios used in present work, see (JPL).
Sun/Mercury 6023600
Sun/Venus 408523.71
Sun/(Earth+Moon) 328900.56
Sun/(Mars system) 3098708
Sun/(Jupiter system) 1047.3486
Sun/(Saturn system) 3497.898
Sun/(Uranus system) 22902.98
Sun/(Neptune system) 19412.24
Sun/(Pluto system) $1.35 \times 10^{8} $
Moon/Earth 0.012300034
Phobos/Mars $1.683 \times 10^{-8} $
Deimos/Mars $2.804 \times 10^{-9} $


Relative masses for Phobos and Deimos as well as the positions and velocities for all the bodies are obtained from "Horizons On-Line Ephemeris System'' (DE-406) (JPL). The reference frame is ICRF/J2000.0. All our simulations start at MJD 51600.5 (2000-Feb.-26 00:00).

The moments of inertia for the Earth are based on the JPL data (Jz-Jy)/Jz =0.0032737634, Jz/mR2 =0.3307007, R=6378.136 km, $m=8.8877456\times 10^{-10} $(JPL). This gives that $ J_{z} =5.3427328\times 10^{-19} $ and $ J_{x} = J_{y} =5.3252420 \times 10^{-19} $. For Mars, the moments of inertia are: $ J_{z} =1.8034092 \times 10^{-20} $ corresponding to Jz/mR2 =0.3662, $m=9.5495922 \times 10^{-11} $ (JPL) and R=3397.2 km (Bouquillon & Souchay 1999); $ J_{x} =1.7931150 \times 10^{-20} $ and $ J_{y} =1.7943585 \times 10^{-20} $ from Jz/Jx =1.005741and Jz/Jy =1.005044 (Bouquillon & Souchay 1999).

The obliquity of the Earth is given by $ \epsilon =23.4393$ degrees at MJD 51600.5 (JPL). The present obliquity of Mars is $ \epsilon =25.189417$ degrees (Folkner et al. 1997). Finally, the spin angular velocities (denoted $ \omega $) for Earth or Mars are listed in Sects. 2.4 and 2.7.

2.3 Treatment of the N-body problem

The N-body problem is here treated in a purely classical way. In order to keep the model simple we will not include relativistic effects, solar mass-loss or tides. These effects are studied and discussed in Appendix. Two independent engines to integrate the equations of motion are applied. First, we use the SWIFT library (Levison & Duncan 2000) which contains both the Mixed Variable Symplectic method (MVS) and the Bulirsch-Stoer method. Secondly, we have implemented a simple, but general algorithm for repeated Richardson extrapolation of Euler's method. The time step in this method is cut in half an arbitrary number of times (usually five) for each time interval $ \triangle t $ and then extrapolations are repeatedly carried out in order to obtain very good positions and velocities (analogous to Romberg's method). This method is applied for the tests in the Appendix.

We have written an ANSI C program where all the above numerical methods can be used. The stability of the numerical results are tested using all methods. For appropriate time steps they all yield identical results (e.g. $ \sim $15 figures in the positions are the same after thousands of years of simulation). For the final simulations, we decided to apply the MVS method because of its high speed and high stability properties (e.g. stability of the total angular momentum).

The program tests that the total mechanical energy and angular momentum are conserved at every time step. If conservation is violated the particle system is moved back to the previous time step. The integration is then attempted using half the previous time step. This procedure may then be repeated until conservation is fulfilled. The simulation then continues a certain number of steps (user defined) using the smaller time step before restoring the original time step. Another check of the accuracy is to study rapid oscillations (such as moon orbits) for peculiarities, since those are most sensitive to numerical errors. Standard modifications in order to gain numerical stability are also applied in the code, e.g. summation order. Trivial checks such as that compiler optimizations do not alter the results are also done. For every computed output quantity $ \chi $, we check that for two distinct simulations the numerical truncation error $ \varepsilon $is negligible: $ \varepsilon =\left\vert \chi (\triangle t)-\chi (\frac{\triangle t}{2})\right\vert $. We have also investigated the sensitivity in obliquity (output) to variation in some input parameters by computing the condition number C = (relative change in output)/(relative change in input). Variations in solar mass, Earth mass, Moon mass, moments of inertia and spin angular velocity typically result in C= 10-4-10-2. This indicates that the problem is well conditioned. In present computations, we use the time step $ \triangle t =0.182625$ d or lower (as low as 0.0036525 d in extreme cases). Finally, the consistency of our results is also checked by comparisons with measurements and findings of other authors, whenever possible.

2.4 The instantaneous behavior of the spin axis of a rigid body - rotation of the Earth

Instantaneous studies of spin axis precession, nutation and obliquity require a method for treating the momentary dynamics of a rotating rigid body. The approach below is general for rigid bodies and in principle exact; it can be used to study oscillations at any time scale and is still convenient for numerical simulations. We use a center of mass reference system S(x,y,z), i.e. a system that always follows the center of mass G of the body and has its axes fixed in inertial space. These axes are parallel with the external heliocentric system. $ S^{\prime }(x^{\prime },y^{\prime },z^{\prime }) $ is also a reference system with the origin at the center of mass, but its axes are instead fixed in the precessing body. These axes coincide with the body's principal axes so the inertia tensor $ \overline{\overline{J}}_{_{\rm G}}(S^{\prime }) $ is always diagonal. Furthermore, the body is considered to be a rigid (not necessarily homogeneous) oblate ellipsoid with principal moments of inertia $ J_{x}\neq J_{y}\neq J_{z} $in the general case. The actual numerical values are taken from satellite measurements (see Sect. 2.2). We shall thus ignore the phenomenon of variation of latitude and assume that the spin axis is rigidly fixed along the z'-axis of S'. In the S-system, the total external torque ( $ \overline{M}_{_{\rm G}} $) acting on the body w.r.t. the center of mass G is related to the angular momentum ( $ \overline{L}_{_{\rm G}} $) according to:

 \begin{displaymath} \overline{M}_{_{\rm G}}=\frac{\rm d}{{\rm d}t}\overline{L}_{... ...J}}_{_{\rm G}}(S)\frac{\rm d\overline{\omega }}{{\rm d}t}\cdot \end{displaymath} (1)

The similarity transformation between the S- and S'-system is given by:

 \begin{displaymath} \overline{\overline{J}}_{_{\rm G}}(S)=\overline{\overline{R}... ...\prime })\overline{\overline{R}}\equiv \overline{\overline{A}} \end{displaymath} (2)

where $ \overline{\overline{J}}_{_{\rm G}}(S^{\prime }) $ remains diagonal at all times and $ \overline{\overline{R}} $ is the Eulerian rotation matrix in the x-convention (Goldstein 1980):

 \begin{displaymath}\overline{\overline{R}}= \left[\! \begin{array}{ccc} \cos \p... ... \theta \cos \phi & \cos \theta \end{array}\!\right]\!\!\cdot \end{displaymath} (3)

If we define $ {\rm d}\overline{\overline{J}}_{_{\rm G}}(S)/{\rm d}t\equiv \overline{\overline{B}} $, the matrix elements of $ \overline{\overline{B}} $ then depend on time according to:

 \begin{displaymath}B_{ij}=\frac{\rm d}{{\rm d}t}A_{ij}(\phi ,\theta ,\psi )= \le... ...partial }{\partial \psi }\right] A_{ij} (\phi ,\theta ,\psi ). \end{displaymath} (4)

We thus obtain the following first order nonhomogeneous differential equation:


 \begin{displaymath} \overline{M}_{_{\rm G}}=\overline{\overline{B}}\, \overline{... ...ine{\omega }(t+{\rm d}t)-\overline{\omega }(t)}{{\rm d}t}\cdot \end{displaymath} (5)

By replacing dt with $ \triangle t $, we end up with the numerical expression:

 \begin{displaymath}\overline{\omega }(t+\triangle t)= \left[ \overline{\overline... ...\overline{\omega }(t)\right] \triangle t+\overline{\omega }(t) \end{displaymath} (6)

which subsequently can be improved using a few Richardson extrapolations. The explicit expression within the brackets is too long and complicated to be given here; it is fully implemented in our C-program. Initial conditions for Earth are given for simulations forward in time as follows: $ \overline{\omega }(0)=\omega \sin \epsilon \overline{e}_{y}+\omega \cos \epsilon \overline{e}_{z} $, where $ \omega =2\pi \times 1.00273791 $ radians/d. The second factor is the ratio between a Julian day and a sidereal day (JPL). The obliquity at MJD 51600.5 is $ \epsilon =23.4393$ degrees (JPL). $ \overline{\omega }(t) $will certainly at a later stage precess away from this direction but never away from the z'-axis. $ \overline{\overline{A}}\, ^{^{-1}}(0) $ is determined by $ \phi (0)=\pi ,\theta (0)=\epsilon ,\psi (0)=0 $. In the case of $ \overline{\overline{B}}(0) $, we set $ \frac{\rm d\phi }{{\rm d}t}(0)=\frac{\rm d\theta }{{\rm d}t}(0)=0 $ and $ \frac{\rm d\psi }{{\rm d}t}(0)=\omega $. For simulations backward in time, the initial conditions that change are: $ \overline{\omega }(0)\rightarrow -\overline{\omega }(0) $, $ \frac{\rm d\psi }{{\rm d}t}(0)\rightarrow -\omega $ and $ \phi (0)=0,\theta (0)=\pi -\epsilon $. $ \overline{M}_{_{\rm G}}(0) $ also needs to be calculated at the start of the simulation (and also of course at every other time step). Note that an arbitrary vector must obey the transformation $ \overline{u}=\overline{\overline{R}}\, ^{^{-1}}\overline{u}' $between the S and $ S^{\prime } $-system. In  $ S^{\prime } $, the basis vector $ \overline{e}_{\omega } $ is always given by (0,0,1)while in S, $ \overline{e}_{\omega }=(x,y,z) $. We therefore have the specific relation:

 \begin{displaymath} \overline{e}_{\omega }(t)=\left[ \begin{array}{c} x(t)\\ y(... ...a (t)\cos \phi (t)\\ \cos \theta (t) \end{array}\right] \cdot \end{displaymath} (7)

This means that given $ \overline{e}_{\omega }(t) $ in S, we also obtain $ \theta (t) $ and $ \phi (t) $. The last angle is simply given by $ \psi (t)=\omega t $ in the case Jx=Jy, otherwise $ \psi (t+\triangle t)=\psi (t)+\omega \triangle t $. Finally, the angular velocities in Eq. (4) needed to determine $ \overline{\overline{B}}(t) $ are approximated with $ \triangle \phi /\triangle t $and $ \triangle \theta /\triangle t $, while $ \frac{{\rm d}\psi }{{\rm d}t}=\omega (t) $.

2.5 External torques acting on the planet

The exact expression for external torques from particles j acting on an ellipsoid at time t may in the body fixed system $ S^{\prime } $be written:

 \begin{displaymath} \overline{M}^{\prime }_{_{\rm G}}(t)=-G\sum _{j}m_{j}\int _{... ...^{\prime }+\overline{r}^{\prime }_{j}\right\vert ^{3}}{\rm d}m \end{displaymath} (8)

where $ \overline{r}^{\prime } $ is pointing at an arbitrary mass element dm in the ellipsoid and $ \overline{r}^{\prime }_{j}=(x^{\prime }_{j},y^{\prime }_{j},z^{\prime }_{j}) $is the radius vector to the particle j. However, this expression becomes far too complicated to compute, even for a spheroid. An extremely good approximation is due to MacCullagh (see Goldstein 1980, p. 228). In this approximation the potential energy of an oblate ellipsoid of mass m and a particle j is:

 \begin{displaymath} W(i,j)=-\frac{Gmm_{j}}{r_{j}}-\frac{Gm_{j}}{2r_{j}^{3}}\left( J_{x}+J_{y}+J_{z}-3I\right) \end{displaymath} (9)

where $ I=(J_{x}x^{\prime 2}_{j}+J_{y}y^{\prime 2}_{j}+J_{z}z^{\prime 2}_{j})/r_{j}^{2} $is the moment of inertia about the direction of $ \overline{r}^{\prime }_{j} $. Jx, Jy and Jz are of course the moments of inertia w.r.t. the principal axes. The torque about the center of mass G of body i exerted by all particles j may now be written as:

 \begin{displaymath}\overline{M}^{\prime }_{_{\rm G}}(t)= 3G\sum _{j}\frac{m_{j}}... ...}z^{\prime }_{j},(J_{y}-J_{x})x^{\prime }_{j}y^{\prime }_{j}). \end{displaymath} (10)

The instantaneous torques from all the other planets, the Moon and the Sun are included in the summation at every time step. In the case of Mars we are also including the moons Phobos and Deimos (see Sect. 2.10). Since $ \overline{M}^{\prime }_{_{\rm G}}(t) $is computed in $ S^{\prime } $, it is subsequently transformed back to S ( $ \overline{M}_{_{\rm G}}(t)=\overline{\overline{R}}\, ^{^{-1}}\overline{M}'_{_{\rm G}}(t) $) so it can be used in Eq. (6).

2.6 The summer solstice for the northern hemisphere

Suppose $ \overline{r} $ is the radius vector from the center of the Sun pointing at the Earth-Moon system's center of mass and $ \overline{v} $ is its velocity. The normal vector to the ecliptic plane is then given by $ \overline{n}=\overline{r}\times \overline{v}/\left\vert \overline{r}\times \overline{v}\right\vert $. Let $ \overline{\omega } $ be the spin angular velocity of Earth. If $ \left( \overline{r}\times \overline{\omega }\right) \cdot \overline{n}=0 $is fulfilled we have either summer or winter solstice. It may then be checked if the angle $ \varphi =\arccos \left( \overline{\omega }\cdot \overline{r}/\left\vert \overline{\omega }\right\vert \left\vert \overline{r}\right\vert \right) >90^{\circ } $in which case we have summer solstice. However, for simulations backward in time the condition for summer solstice instead becomes $ \varphi <90^{\circ } $since $ \overline{\omega } $ is then replaced by $ -\overline{\omega } $. An analogous calculation can also be performed to find the northern summer solstices in the case of Mars.

2.7 Rotation of Mars

One day at Mars is slightly longer than the day for Earth, namely 24.622962 h compared to 23.93419 h (JPL). The angular velocity for Mars is therefore given by $ \omega (0) =6.1241471$ radians/d. The obliquity (the angle between the Mars equator and its instantaneous orbital plane) of Mars is given by $ \epsilon =25.189417$degrees (Mars pathfinder mission, Folkner et al. 1997). Currently, the summer solstice of the northern hemisphere of Mars occurs at Dec. 16, 2000, 04h UT. Given that $ \overline{n},\, \overline{r} $ and $ \epsilon $ are known, the equations

 
           $\displaystyle \overline{n}\cdot \overline{\omega }$ = $\displaystyle n\omega \cos (\epsilon )$ (11)
$\displaystyle \overline{r}\cdot \overline{\omega }$ = $\displaystyle r\omega \cos (\epsilon +\frac{\pi }{2})$ (12)
$\displaystyle \omega ^{2}$ = $\displaystyle \omega ^{2}_{x}+\omega ^{2}_{y}+\omega ^{2}_{z}$ (13)

completely determine the components of $ \overline{\omega } $. Here, $ \overline{n} $( $ \overline{n}=\overline{r}\times \overline{v} $) is the normal vector to the orbital plane of Mars and $ \overline{r} $ is the heliocentric position of Mars at its summer solstice. The obtained results in radians/d are:
 
$\displaystyle \omega _{x}(0)=$2.7318578   (14)
$\displaystyle \omega _{y}(0)=$-0.3438322   (15)
$\displaystyle \omega _{z}(0)=$5.4702752.   (16)

The initial conditions for the Mars fixed system ( $ S^{\prime } $) is $ \phi (0)= 82.826460 ^{\circ } $. The Euler angle $ \theta (0) $ is no longer directly related to the obliquity because the Mars orbital plane has an inclination of about $ i=1.8504^{\circ } $relative to the ecliptic. This gives that the angle between $ \overline{\omega } $(z'-axis) and the ecliptic normal (z-axis) becomes $ \theta (0) =26.717957 ^{\circ } $. The last Eulerian angle is arbitrarily given by $ \psi (0)=0 $. The time derivatives are set analogously to what we did in Sect. 2.4. For simulations backwards in time the changes become as follows: $ \overline{\omega }(0)\rightarrow -\overline{\omega }(0) $, $ \frac{\rm d\psi }{{\rm d}t}(0)\rightarrow -\omega $ and $ \phi (0)\rightarrow (\phi (0)-\pi ),\theta (0)\rightarrow (\pi -\theta (0)) $.

2.8 The length of the summer half year

Given the semi major axis a, eccentricity e and the distance r at summer solstice for a specific year, we get from the definition of eccentric anomaly (E) that at summer solstice: $ E_{\rm s}=\arccos ((a-r)/ae) $. The general relation between E and the true anomaly v is:

 \begin{displaymath} \tan \frac{E}{2}=\sqrt{\frac{1-e}{1+e}}\tan \frac{v}{2}\cdot \end{displaymath} (17)

The specific true anomaly $ \varphi $ from perihelion to the planet at summer solstice then becomes:

 \begin{displaymath} \varphi =2\arctan \left( \sqrt{\frac{1+e}{1-e}}\tan \left( \frac{E_{\rm s}}{2}\right) \right) \cdot \end{displaymath} (18)

The angle from perihelion to the vernal equinox is given by $ v_{\rm v}=\varphi -\pi /2 $and for the autumnal equinox, $ v_{\rm a}=\varphi +\pi /2 $. The change in time dt is directly related to the change in eccentric anomaly dE through (Danby 1964):

 \begin{displaymath} n{\rm d}t={\rm d}E(1-e\cos E) \end{displaymath} (19)

where n is the mean motion. Integrating between the equinoxes then gives that

 \begin{displaymath} nt=E_{\rm a}-e\sin E_{\rm a}-E_{\rm v}+e\sin E_{\rm v} \end{displaymath} (20)

where $ E_{\rm a} $ and $ E_{\rm v} $ are the eccentric anomalies at autumnal and vernal equinoxes respectively. According to Eq. (17) we have:
 
                        $\displaystyle E_{\rm a}$ = $\displaystyle 2\arctan \left( \sqrt{\frac{1-e}{1+e}}\tan \left( \frac{\varphi }{2}+\frac{\pi }{4}\right) \right)$ (21)
$\displaystyle E_{\rm v}$ = $\displaystyle 2\arctan \left( \sqrt{\frac{1-e}{1+e}}\tan \left( \frac{\varphi }{2}-\frac{\pi }{4}\right) \right)\cdot$ (22)

The length of the summer half year relative to a full year is finally given by $ nt/2\pi $. For more discussions regarding variations of the astronomical seasons, see e.g. Berger & Loutre (1994).

2.9 Spin axis precession and orbital precession

The precession angle of the spin axis ( $ \phi _{\rm p} $) is calculated by

 \begin{displaymath} \phi _{\rm p}={\rm arccos}\left( \frac{(\overline{n}\times \... ...rline{n}_{0}\times \overline{\omega }_{0}\right\vert }\right) \end{displaymath} (23)

where $ \overline{n} $ and $ \overline{n}_{0} $ are normal vectors to the instantaneous and present orbital plane, respectively, and analogously for $ \overline{\omega } $ and $ \overline{\omega }_{0} $.

The orbital precession is studied by calculating the Laplace-Runge-Lenz vector which is conserved for the two-particle problem. It is directed along the radius vector $ \overline{r} $ to the perihelion point. In the solar system, many particle interactions (as well as the smaller general relativistic effect) cause the orbit of a planet of mass m to precess. The orbital precession can easily be studied by observing the rotating Laplace-Runge-Lenz vector which is given by:

 \begin{displaymath} \overline{A}=\overline{p}\times \overline{L}-\frac{GM_{\rm s}m^{2}}{r}\overline{r} \end{displaymath} (24)

where $ \overline{p} $ and $ \overline{L} $ (of the planet) are the linear and angular momentum, respectively. An alternative method would be to compute the combined changes in the orbital parameters: the longitude of the ascending node $ \Omega $, the argument of perihelion $ \omega $and the inclination i: d $\omega /{\rm d}t+\cos (i){\rm d}\Omega /{\rm d}t $.

2.10 Torques due to Phobos and Deimos

Since Phobos and Deimos are so close to Mars (for Phobos the distance is less than 3 Mars radii), their motions are incredibly rapid compared to all other bodies in our simulation. For the time periods of interest, it is impossible to integrate these moons in the same manner as our own Moon. The objective here is therefore instead to obtain an average formula for the torque on Mars due to its moons. First a full integration will be carried out including Phobos and Deimos for a time span that is long enough to contain all relevant oscillations. The torques acting on Mars are calculated instantaneously, i.e. at every time step. We then choose circular moon orbits in the orbital plane of Mars (virtual moons) that yield exactly the same average torques as those obtained from the full integration. This treatment is similar to that given by Goldstein (1980, p. 229). Account will also be taken to the triaxiality of Mars, i.e., $ J_{x}\neq J_{y}\neq J_{z} $. The expression for I in Eq. (9) may be rewritten as:

 \begin{displaymath} I=J_{x}\cos ^{2}\alpha +J_{y}\cos ^{2}\beta +J_{z}\cos ^{2}\gamma \end{displaymath} (25)

where the angles $ (\alpha ,\beta ,\gamma ) $ to a moon-position $ \overline{r}' $are measured relative to the body fixed system $ S^{\prime } $. Let us now use a coordinate system xyz for which the effective mean orbit of a virtual moon is in the xy-plane and the spin axis of Mars ( $ \overline{\omega } $) is in the xz-plane. The xy-plane is chosen as the instantaneous Mars orbit plane with the origin at the Mars center. The transformation between $ S^{\prime } $ and this new xyz-system obeys: $ \overline{r}'=\overline{\overline{R}}\, \overline{r} $, i.e. with $ (\phi ,\theta ,\psi )=(\frac{\pi }{2},\theta ,\psi ) $ one obtains:

 \begin{displaymath} \left[ \begin{array}{c} x^{\prime }\\ y^{\prime }\\ z^{\pr... ...ight] \left[ \begin{array}{c} x\\ y\\ 0 \end{array}\right] . \end{displaymath} (26)

We treat a mean virtual moon orbit as a simple circular orbit which in polar coordinates becomes: $ (x,y)=r(\cos \eta ,\sin \eta ) $. We thus obtain:

 \begin{displaymath}\cos^{2}\alpha \equiv \left( \frac{x^{\prime }}{r}\right) ^{2... ...si \cos^{2}\eta\! -\!\frac{1}{2}\cos\theta \sin2\psi\sin2\eta. \end{displaymath} (27)

As usual, the moon revolution ($ \eta $) and the rotation of Mars ($ \psi $) are extremely rapid compared to the change in $ \theta $ allowing a time average over an integer number of periods to be performed (the symbol $ \left\langle \, \, \right\rangle $refers to a time average, e.g. for a function f(t) this is given by $ \left\langle f\right\rangle =\frac{1}{T}\int _{0}^{T}f(t){\rm d}t $):

\begin{displaymath}\left\langle \cos^{2}\alpha \right\rangle =\left\langle \cos^... ...{2}\theta \left\langle \sin^{2}\psi \cos^{2}\eta \right\rangle \end{displaymath}


 \begin{displaymath} -\frac{1}{2}\cos\theta \left\langle \sin2\psi \sin2\eta \right\rangle =(\cos^{2}\theta +1)/4. \end{displaymath} (28)

In the same way one obtains that $ \left\langle \cos^{2}\beta \right\rangle =(\cos^{2}\theta +1)/4 $and $ \left\langle \cos^{2}\gamma \right\rangle =\frac{1}{2}\sin^{2}\theta $. The average moment of inertia can now be written:

 \begin{displaymath} \left\langle I\right\rangle \!=\!J_{x} (\cos^{2}\theta \!+\!... ...y} (\cos^{2}\theta +1)/4\!+\!J_{z}\frac{1}{2}\sin^{2}\theta . \end{displaymath} (29)

The part of the averaged potential energy that has an orientational dependence is (see Eq. (9)):
 
                   $\displaystyle \left\langle W\right\rangle$ = $\displaystyle \frac{Gm}{2r^{3}}\left( 3\left\langle I\right\rangle -(J_{x}+J_{y}+J_{z})\right)$  
  = $\displaystyle \frac{Gm}{2r^{3}}(J_{z}-\frac{J_{x}+J_{y}}{2})\left( \frac{1}{2}-\frac{3}{2}\cos^{2}\theta \right) \cdot$ (30)

Finally the average torque acting on Mars due to a moon becomes:

 \begin{displaymath} \left\langle \overline{M}_{_{\rm G}}\right\rangle =\frac{3Gm... ...-\frac{J_{x}+J_{y}}{2}\right)\sin2\theta \overline{e}_{\xi } . \end{displaymath} (31)

The torque is in the direction of $ \overline{e}_{\xi }=\overline{n}\times \overline{\omega }/\left\vert \overline{n}\times \overline{\omega }\right\vert $, where $ \overline{n} $ is the normal vector to the instantaneous Mars orbit and $ \overline{\omega } $ is the spin axis of Mars. In order to apply this average formula at every time step we need to know the best possible value of r. Fortunately, we already have access to the accurate instantaneous Eq. (10). We therefore first start a simulation performing an exact integration of the Mars moons ( $ \triangle t=1.82625 \times 10^{-3} $ d). We then divide the resulting instantaneous torques by the instantaneous $ \sin2\theta $. By forming the average (k)

 \begin{displaymath} k=\sqrt{\left\langle \frac{M_{x}}{\sin2\theta }\right\rangle... ...{2}+\left\langle \frac{M_{z}}{\sin2\theta }\right\rangle ^{2}} \end{displaymath} (32)

r can be computed from $ k=\frac{3Gm}{4r^{3}}(J_{z}-\frac{J_{x}+J_{y}}{2}) $. In order to get an accurate value of r, one has to be very careful in selecting the period over which the average is taken. During the simulation we found that the angle between the Mars equator and the orbital planes of Phobos and Deimos have periods of 6050 and 6050/4 years, respectively (see Figs. 1 and 2). Averages must be taken over the full periods. The resulting averages of r for Phobos and Deimos are $7.222214 \times 10^{-5} $ and $1.804138 \times 10^{-4} $AU, respectively. Note that this results in much greater average torques acting on Mars than do averages taken over shorter periods. A 10 year mean treatment would instead result in $r=1.7251 \times 10^{-4} $ and $4.485 \times 10^{-4} $AU for Phobos and Deimos, respectively. For long simulations, it is important to use the first set of values for r.

3 Results and discussion

3.1 Tests of the model

Our spin axis model includes all instantaneous effects, e.g. precession and nutation. This is demonstrated by a number of tests. Figure 3 displays the nutational wobble of the Earth. The curve shows the familiar 18.6 year period with an 9.2 arcsec amplitude (as measured w.r.t present ecliptic), in agreement with observation. Faster and smaller oscillations, with periods of one half year and one half sidereal month are also seen in the inset figure.

In Fig. 4 we plot the instantaneous spin precession rate (see Sect. 2.9). A short period corresponding to one half of a sidereal month is easily seen, as is a half year period. A longer period corresponding to the nutation period (18.6 years) is also present (not seen in Fig. 4 due to the limited time span). Averaging over an integer number of nutation periods (93 years) yields an annual average precession rate of 50.42 arcsec/yr, again in agreement with observation.

Figure 5 shows the variation of the Earth's precession cycle over the last 2 million years. The cycle is rather stable with a maximum difference of only about 800 years, or 3%. The mean precession cycle length is 25709 yr. This corresponds to a mean annual precession of 50.41 arcsec/yr, in excellent agreement with the aforementioned result of 50.42. These results are a confirmation of the stability of the model.


  \begin{figure} \par\resizebox*{8.8cm}{5cm}{\includegraphics{H2799F1.eps}}\end{figure} Figure 1: Instantaneous torques (divided by $ \sin2\theta $) on Mars from Phobos in x-, y- and z-direction. The bottom subfigure displays the orbit inclination of Phobos w.r.t. the Mars equator.
Open with DEXTER


  \begin{figure} \par\resizebox*{8.8cm}{5cm}{\includegraphics{H2799F2.eps}}\end{figure} Figure 2: Instantaneous torques (divided by $ \sin2\theta $) on Mars from Deimos in x-, y- and z-direction. The bottom subfigure displays the orbit inclination of Deimos w.r.t. the Mars equator.
Open with DEXTER


  \begin{figure} \par\resizebox*{12cm}{8cm}{\includegraphics{H2799F3.eps}}\end{figure} Figure 3: Nutation of the Earth. The main figure shows the 18.6 yr period caused by the precessing nodes of the lunar orbit. Inset displays the fine structure.
Open with DEXTER


  \begin{figure} {\par % \par\resizebox*{8.8cm}{5cm}{\includegraphics{H2799F4.eps}}\par } \end{figure} Figure 4: Instantaneous spin precession rate of the Earth over one yr.
Open with DEXTER


  \begin{figure} {\par % \par\resizebox*{8.8cm}{5cm}{\includegraphics{H2799F5.eps}}\par } \end{figure} Figure 5: Length of the precession cycles of Earth's spin axis during the last 2 Myr. The dashed line shows the mean value of 25 709 yr.
Open with DEXTER

Figure 6 gives the inclination of the instantaneous ecliptic relative to the present ecliptic for the time interval -1 Myr to +1 Myr. The result is in good agreement with that of Muller & MacDonald (1997). From the above tests we conclude that the model yields trustable results to a high degree of accuracy.


  \begin{figure} \par\includegraphics[width=8.8cm,height=5cm,clip]{H2799F6.eps}\end{figure} Figure 6: Inclination of the Earth orbit w.r.t. the present ecliptic.
Open with DEXTER

3.2 Earth

Figure 7 shows the variations of the Earth's obliquity, i.e. the angle between the Earth's spin axis and the normal of the instantaneous ecliptic, for the last 2 million years. The main period is around 41000 years, which is close to the expected value (cf. Berger & Loutre 1991). The maximum amplitude is around $ \pm $1.3 degrees. We have compared our results with the classical findings of Berger & Loutre (1991) and Berger (1992). The curve centered on 22 degrees shows the differences between Berger's and our results. The differences increase considerably for times earlier than 1 Myr before present. A closer analysis reveals that the differences are mainly caused by a temporal phase shift between the two sets of results, while the amplitudes remain quite similar. In a comparison with Fig. 7 of Quinn et al. (1991) the above mentioned discrepancy is much smaller despite the fact that Quinn et al. also included relativistic effects and tides. The curve centered at 21 degrees is the difference between the La93 program of Laskar et al. (1993c) and our findings. In this case relativity is included but not tides (nominal solution). The agreement with our data is also here better than the agreement with


  \begin{figure} \par\includegraphics[width=12.7cm,height=8cm]{H2799F7.eps}\end{figure} Figure 7: (Top) Obliquity of the Earth over the last 2 Myr. The curve centered at 22 degrees shows the difference between the results of Berger & Loutre (1991) and ours while the curve centered at 21 degrees shows the difference between the relativistic results of Laskar et al. (1993c) and ours. (Bottom) Obliquity of the Earth with and without the Moon.
Open with DEXTER

Berger & Loutre. The differences between our data and those of Laskar et al. are due to relativity and differences in model intricacies and input parameters. The curves indicate that over at least a 1 Myr time-span, the influence of relativity and tides on obliquity can in practise be disregarded. For a more detailed discussion, see Appendix. The bottom part of Fig. 7 shows the variations of obliquity with and without the Moon. As has been pointed out by others (e.g. Laskar et al. 1993a) the Moon is very important in stabilizing the Earth. Without the Moon, the amplitude shows a tenfold increase compared to the case where the Moon is present. Without the Moon, however, the obliquity variations are much slower.

3.3 Mars

We have computed the spin precession rate of Mars, and the results for the last 10 years are presented in Fig. 8. This integration included both Mars moons and was carried out at the extreme time step $ \triangle t =3.6525 \times 10^{-3} $ d. The mean precession rate over this period of time is 7.57 arcsec/yr, in excellent agreement with the results given by Folkner et al. (1997) based on the Mars Pathfinder mission.

  \begin{figure} \par\resizebox*{8.8cm}{5cm}{\includegraphics{H2799F8.eps}}\end{figure} Figure 8: Instantaneous Mars spin precession rate. A period of 1 marsian year is clearly seen. Variations in amplitude are due to the large eccentricity of the Mars orbit.
Open with DEXTER

As is seen in Fig. 9, however, the precession rate of Mars is not very stable. The precession cycle has varied with around 26000 years, corresponding to about 16%, during the last 1.6 million years. The mean precession cycle length is 167000 yr, corresponding to 7.76 arcsec/yr.


  \begin{figure} \par\resizebox*{8.8cm}{5cm}{\includegraphics{H2799F9.eps}}\end{figure} Figure 9: Length of the precession cycles of Mars during the last 1.6 Myr. The dashed line shows the mean value of 167 000 yr.
Open with DEXTER

The inclination of the Mars orbit from 2 Myr before present up to 1 Myr after present is plotted in Fig. 10. There are two main periods - one shorter of around 65000 years and one longer of about 1.3 Myr.


  \begin{figure} \par\resizebox*{8.8cm}{5cm}{\includegraphics{H2799F10.eps}}\end{figure} Figure 10: Inclination of the Mars orbit w.r.t. the present orbital plane.
Open with DEXTER

Figure 11 displays the length of successive summer half years of Mars 500 kyr before present (Sect. 2.8). The oscillations show a period of about 50 kyr and the variation of amplitudes is $ \pm $15%; since the eccentricity of the Earth orbit is small, this effect for Earth is less significant. The lengths of summers is further discussed in the climate section below.


  \begin{figure} \par\resizebox*{8.8cm}{5cm}{\includegraphics{H2799F11.eps}}\end{figure} Figure 11: Length of summers in the northern hemisphere of Mars.
Open with DEXTER

The obliquity variations of Mars are much greater than those for the Earth. The small moons cannot stabilize the spin axis as the Moon does for the Earth. The influence of Phobos and Deimos are still important, however, as can be seen in Fig. 12, which gives the obliquity for the last 500 kyr with and without the moons.

  \begin{figure} \par\resizebox*{8.8cm}{5cm}{\includegraphics{H2799F12.eps}}\end{figure} Figure 12: Mars obliquity with and without its moons.
Open with DEXTER

When the moons are included, the obliquity is stretched to the left and the difference between the two curves is seen to become significant. Our curve without the moons is very similar to the curve given by Bouquillon & Souchay (1999, Fig. 5). It is interesting to note that their computation included the moons. One would therefore expect that their curve should match our curve with the moons better. The reason for this discrepancy is that our mean torques are taken over a considerably longer period resulting in much greater mean torques, see Sect. 2.10. This is also demonstrated in Fig. 13. Here we show the tiny difference between the curves with and without the moons for the case where the mean torques are based on a too short time period (10 years). This short period gives an underestimate of the influence of the moons due to the fact that they are at present very close to the equatorial plane of Mars thus giving very small torques. For long simulations it is therefore important to treat the influence of the moons appropriately.

  \begin{figure} \par\resizebox*{8.8cm}{5cm}{\includegraphics{H2799F13.eps}}\end{figure} Figure 13: Obliquity difference for Mars. The underestimated mean treatment (10 yr) - isolated Mars. This difference is clearly very small; the correct treatment yields a difference that is 10-15 times larger cf. Fig. 12.
Open with DEXTER

3.4 A climatic application

The usual way for computing astronomical influence on climate is to use the eccentricity, the obliquity, and the longitude of the perihelion to compute the climatic precession parameter $ e\sin (\omega ) $ and then to compute the mean insolation for various latitudes. Although similar, we have adopted a slightly different approach. The overall climate of Earth is assumed to mainly be governed by events at high northern latitudes. The present land mass distribution dictates that it is for northern latitudes that the continental ice sheets develop. Due to the ocean, the size of Antarctica is assumed to be rather inert in comparison. Below it shall also be argued for the vital role that is played by the summer radiation. Since the planet's spin axis is computed at each time step, the instants for millions of northern summer solstices can easily be identified (see Sect. 2.6). When the time of summer solstice is identified, the obliquity $ \epsilon $ and sun-planet distance r are simultaneously recorded. The quantity $ P=\sin\epsilon /r^{2} $ is proportional to the summer radiation power received at high northern latitudes. We shall now argue for a model where


  \begin{figure} \par\resizebox*{12.8cm}{8cm}{\includegraphics{H2799F14.eps}}\end{figure} Figure 14: (Top) Mean summer solar radiation power (insolation) and differentiated ice volume ( $ \left\langle P\right\rangle \propto {\rm d}V_{\rm ice}/{\rm d}t $). (Bottom) Ice volume (Imbrie et al. 1990).
Open with DEXTER

the knowledge of this radiation power (P) will be very useful. According to thermodynamics, the energy dQ flowing into the glacial system causes melting of ice into water of mass dm:

 \begin{displaymath} {\rm d}Q=L_{\rm f} {\rm d}m \end{displaymath} (33)

where the proportionality constant $ L_{\rm f} $ is the heat of fusion. The power is the incoming energy per unit of time:

 \begin{displaymath} {\rm power}=\frac{{\rm d}Q}{{\rm d}t}=L_{\rm f}\frac{{\rm d}m}{{\rm d}t}=L_{\rm f}\rho \frac{{\rm d}V}{{\rm d}t} \end{displaymath} (34)

where $ \rho $ is the density for water and dV is the increase in water volume during a particular interval dt. There are certainly many effects that can melt ice such as the incoming solar radiation power, the oceans and various weather phenomena etc. Suppose that the solar radiation power plays an important role for the heating of the oceans, creation of the weather systems and (after absorption in the atmosphere) directly causing ice melting to take place. Our hypothesis here is that in average for long periods, the various complications smear out and the most important remaining effect that really changes is the solar radiation power. These changes are mainly caused by changes in the Earth's orbit and spin axis. As mentioned above, the value for the solar radiation power P is calculated at each summer solstice. This gives an indication how warm or cold a particular summer was. It is very interesting to look for proportionality by replacing "power'' above with the radiation power P so that $ P=\sin(\varepsilon )/r^{2}\propto {\rm d}V/{\rm d}t $. Since dV was taken to be the amount of melted water it is replaced by $ -(\rho _{\rm ice}/\rho _{\rm water}){\rm d}V_{\rm ice} $. When the water volume increases the ice volume decreases, thus the negative sign. The interesting proportionality to look for thus becomes: $ P\propto {\rm d}V_{\rm ice}/{\rm d}t $. It could, of course, be argued that this is not the radiation power near the surface of the ice sheets. However, it is likely that a relative increase in power above the atmosphere in average leads to a corresponding relative increase in power near the ice sheets. The SPECMAP data (Imbrie et al. 1990) are based on sea sediment measurements in the Northern Atlantic. The resolution in these ice volume data is 1000 yrs. We assume that melting mostly takes place during the summer half years. In Sect. 2.8, it is shown how the length of each summer half year is computed. The total melting period dt is then obtained by summing all these 1000 summer half years. The power P is also averaged for 1000 summer solstices resulting in the appropriate $ \left\langle P\right\rangle $. The lower part of Fig. 14 shows the ice volume as a function of time for the last 782000 years. The upper part of the figure shows a comparison between mean summer radiation power $ \left\langle P\right\rangle $ and the differentiated ice volume. Here, the curves were brought together and "zoomed'' until they match each other. This simple procedure is presented in Fig. 15 (i.e. to move the curves together and determine the proportionality constant). If the proportionality assumption is perfect the match would be perfect. The top part of Fig. 14 indeed shows that the match is very good and that the proportionality hypothesis is sound. What needs to be further addressed is the perhaps surprising fact that also ice growth is very well predicted. It is evident that during one year we have two competing effects: namely ice growth during the winter half year and melting during the summer half year. If the summer radiation power is high the melting will be high. The corresponding winter (the complement) for that year is probably quite cold and dry meaning that the ice growth should be low. The net result for that year is high melting. On the other hand, if summer radiation power is low the melting should also be low. The corresponding winter will in this case be unusually warm and humid with a high probability of snowfall thus causing an increase in ice growth. The net for this year is ice growth. The true weather conditions are of course much more complicated. However, the resolution for the ice volume data is 1000 years. No matter how complicated a given year actually was, the average melting and growth for 1000 year intervals follows the proposed mechanism very well. One interesting interpretation is worthwhile to mention. If one takes the average of the whole power curve in Fig. 14 (top), one gets a line crossing through the whole power curve. All the crossing points between the power curve and this average power line correspond almost exactly to maxima or minima of the ice volume (bottom curve). In other words, the average summer radiation power corresponds to status quo. Ice melting equals ice growth during a complete year [or rather 1000 years since this is the resolution in ice volume] so the total change in ice volume becomes zero.


  \begin{figure} \par\resizebox*{8.8cm}{5cm}{\includegraphics{H2799F15.eps}}\end{figure} Figure 15: This least square fit of summer radiation power and differentiated ice volume determines the proportionality constant between the curves. r=0.76 is the correlation coefficient.
Open with DEXTER


  \begin{figure} \par\resizebox*{8.8cm}{5cm}{\includegraphics{H2799F16.eps}}\end{figure} Figure 16: Fine structure of the mean summer radiation power (solid curve) and differentiated ice volume (dotted curve). No $ \sim $5 kyr time lag is observed.
Open with DEXTER


  \begin{figure} \par\resizebox*{8.8cm}{5cm}{\includegraphics{H2799F17.eps}}\end{figure} Figure 17: Comparison of relative summer radiation power for Mars (top) and Earth (bottom) for their northern latitudes.
Open with DEXTER

Positions of peaks in the top two curves of Fig. 14 are seen to coincide almost perfectly over the entire time interval. The only major deviations are occurring at 10, 130, 340, 430, and 620 kyr before present. A comparison with the ice volume curve shows that these deviations always correspond to extremely rapid terminations of the ice ages. Perhaps this indicates an accelerated absorption of heat due to a reduction in continental ice cover. It is also possible that the initial melting is much more rapid for a fully developed continental ice sheet compared to a later stage when the ice-covered area is smaller. Other complicated reasons involve feedback mechanisms such as greenhouse gases (water vapor, carbon dioxide etc.). This calls for further investigations. It is interesting to observe that the usual frequency problem with the 100000 year period in the ice volume data disappears in our comparison. Neither are there any time lag problems between summer radiation power and $ {\rm d}V_{\rm ice}/{\rm d}t $. This problem occurs only when comparing summer radiation power (or insolation) with ice volume ( $ V_{\rm ice} $). Figure 16 displays the fine-structure of our Fig. 14. It is evident that there exists no time lag of about 4-5 kyr as reported e.g. by Berger et al. (1993).

Finally, we compare the variations in summer radiation power for Mars and the Earth. The results are displayed in Fig. 17. The huge variations ($ \pm $50%) for Mars are obvious for the northern parts of Mars. The causes involve both large variations in obliquity and, due to the comparatively large eccentricity of the Mars orbit, large variations in sun-planet distance at summer solstice. The northern polar regions of the ancient Mars were probably subject to similarly large climatic variations that may have had a tremendous impact on glaciers, atmospheric pressure and the planet's ability to sustain life.

4 Conclusion

We have developed a numerical model of the solar system where the integration of the planets and spin axes are performed simultaneously. This approach gives reliable results for integration periods 1-2 Myr and it also permits detailed studies of dynamical variables on very short time scales. If GR is included the simulation could in principle be taken further although there may be uncertainties with regard to tidal effects. Our approach has also interesting applications for climatic studies. We find very good agreement between radiation power and differentiated ice volume of the Earth. Both build-up and melting of ice are found to fit nicely with the theoretical model predictions.

5 Appendix - Good or bad approximations?

Several simplifications were done in the above calculations. It is thus important to confirm that they are justified.

5.1 Solar mass loss

Including both electromagnetic radiation and particle radiation the relative solar mass loss is: $ ({\rm d}M_{\rm s}/{\rm d}t)/M_{\rm s}=-9.13\times 10^{-14}~\rm yr^{-1} $ (Noerdlinger 2001). In our mass units, the mass of the Sun is $2.9591221 \times 10^{-4} $. The total mass loss in 1 Myr is then about $ 2.7\times 10^{-11} $ while the estimated accuracy of the solar mass is of the same order. It is thus unlikely that solar mass loss would give any significant change in the results of present work (cf. Quinn et al. 1991).

5.2 Tides

Present tides result in an expansion of the Moon orbit of 3.82 cm/yr (Dickey et al. 1994) or 38.2 km/Myr or 0.01 percent of the Earth-Moon distance which is very small compared to other variations in the Moon orbit. There is also an expected decrease of Earth's spin angular velocity for the future.

Laskar et al. (1993b) performed simulations both with and without tides [(CMAR, FGAM) = (1, 1) and (0, 1) respectively, see program La93 of Laskar et al. (1993c)]. It can there be observed that the maximum difference in obliquity up to 1 Myr before present is less than 0.04$ ^{\circ } $. By comparing the solutions it is obvious that the inclusion of tides results in a small phase difference only (it is less than a few 100 years). For simulations longer than a few Myr, it is necessary to include tides. Fortunate for present work, the tidal effects are so tiny for 1-2 Myr simulations that they can hardly be detected by the eye and can thus be disregarded. Moreover, Laskar et al. (1993b) argued that Earth's moments of inertia (and tidal dissipation) may change considerably during glaciation giving quite different solutions for simulations earlier than about 2-3 Myr (see their Fig. 10). If these uncertainties are real, it is actually questionable if realistic long simulations are at all possible.

5.3 Effects of general relativity

General relativity (GR) effects can be studied by adding a correction to the usual equation of motion in a heliocentric system. The correction for particle i may be found in the DE102 ephemeris article of Newhall et al. (1983) or Quinn et al. (1991):

 \begin{displaymath}\frac{GM_{\rm s}}{r^{3}_{i}}\overline{r}_{i}\left( 2\left( \b... ...ine{v}_{i}\left( \overline{r}_{i}\cdot \overline{v}_{i}\right) \end{displaymath} (35)

where GR corresponds to the PPN parameters $ \beta _{\rm ppn}=\gamma _{\rm ppn}=1 $. Relativistic effects are quite important for Mercury. The well known relativistic contribution to the orbital precession rate is about 43 $^{\prime\prime}$/century as compared to the classical value of about 532 $^{\prime\prime}$/century from many particle interactions. However, Mercury is affecting Earth's spin axis very little due to the distance and low mass of Mercury. This effect is therefore expected to be negligible. It is nevertheless very interesting to study this further. Figure 18 shows the evolution of the mean precession rates 100 kyr back in time for both the GR and classical approach. These precession rates are derived from angles sampled at 1 kyr intervals (see Sect. 2.9). It is interesting to note that the variations are quite large. The figure indicates that the present 1 kyr means are around 532 (classical) and 575 (GR) arcsec/cy in agreement with the generally accepted values. The difference between the curves results in the inset figure. Although the present isolated GR effect is 43 arcsec/cy, it is quite interesting to realise that the values vary quite considerably. About 100000 years ago the correct value was instead 33 arcsec/cy.


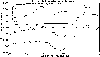  \begin{figure} \par\resizebox*{8.8cm}{5cm}{\includegraphics{H2799F18.eps}}\end{figure} Figure 18: Orbital precession rates of Mercury displayed as 1 kyr means during the last 100 kyr. The x-curve is due to a pure classical simulation while the o-curve corresponds to corrections from GR. The inset figure displays the isolated GR effect (i.e. the difference between o- and x-curve).
Open with DEXTER

For Mercury, Venus, Earth, Mars and Jupiter the 1000 yr mean perihelion advancements due to general relativity are found to be 42.91, 8.36, 4.08, 1.35 and 0.054 $^{\prime\prime}$/century, respectively. This was also computed by first performing a classical 1000 yr long simulation and then compare it with a similar simulation with the GR-correction included. Although the influence is quite small, it is even less important since the orbits of Venus and Earth are nearly circular (the velocity term becomes negligible). Experimentally it is certainly also extremely difficult to measure. Further, for the acceleration of the Earth-Moon system it is according to Quinn et al. [p. 2287] about an order of magnitude more important to consider the quadrupole moment of the Earth-Moon system correctly than to include general relativity effects. This quadrupole moment is fully accounted for in present approach. For the time span we are primarily interested in ($ \sim $1 Myr), relativistic effects should be comparatively small. Nevertheless, it is interesting to perform a few simulations with GR included to verify that the above assumption is correct.


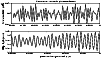  \begin{figure} \par\resizebox*{8.8cm}{5cm}{\includegraphics{H2799F19.eps}}\end{figure} Figure 19: Earth summer radiation and obliquity using our classical and GR treatment. The differences are clearly small and can hardly be detected.
Open with DEXTER

Summer radiation and obliquity are important climatic variables for this purpose. Figure 19 displays these quantities for both the classical and the GR simulations. In practise they are very similar. In the case for the summer radiation power, there are actually some slight deviations starting to develop at 350 kyr before present, but they are so tiny that it is difficult to detect by the eye. We can thus conclude that the approximations are reasonably good up to about 1 Myr or so for climatic purposes of the Earth. In the case of the Mars calculations, GR is much less important and the effect is negligible for simulations of several Myr. Interested parties may investigate these intricate differences further by obtaining our converged files of the 2 Myr simulations for both cases: the classical and the GR approach [http://www.fmi.mh.se/celmech].

References

 

Copyright ESO 2002