A&A 384, 513-520 (2002)
DOI: 10.1051/0004-6361:20020068
E. Poretti1 - C. Koen2 - M. Bossi1 - E. Rodríguez3 - S. Martín3,1 - K. Krisciunas4 - M. C. Akan5 - R. Crowe6 - M. Wilcox6 - C. Ibanoglu5 - S. Evren5
1 - Osservatorio Astronomico di Brera, Via Bianchi 46,
23807 Merate, Italy
2 - South African Astronomical Observatory, PO Box 9, Observatory 7935, Cape Town,
South Africa
3 - Instituto de Astrofisica de Andalucia, C.S.I.C., Apdo. 3004, 18080 Granada, Spain
4 - Cerro Tololo Inter-American Observatory, Casilla 603, La Serena, Chile
5 - Ege University, Science Faculty, Dept. of Astronomy and Space Sciences,
Bornova 35100 Izmir, Turkey
6 - Department of Physics and Astronomy, University of Hawaii - Hilo, 200 West Kawili Street,
Hilo, Hawaii, 96720-4091, USA
Received 11 September 2001 / Accepted 9 January 2002
Abstract
We discuss new photometric data collected on the ![]() Dor
variables HD 224945 and HD 224638. Multiperiodicity was detected
in both stars, thanks to the clear spectral window of a multisite campaign
that involved five observatories. HD 224945 shows the shortest period among
the
Dor
variables HD 224945 and HD 224638. Multiperiodicity was detected
in both stars, thanks to the clear spectral window of a multisite campaign
that involved five observatories. HD 224945 shows the shortest period among
the ![]() Dor stars, i.e., 0.3330 d. The
pulsation behaviour is very different: HD 224945 displays a set of
frequencies spread over an interval much larger than that of HD 224638.
We clearly found evidence for amplitude variations in the excited modes by
comparing data from different years. HD 224945 and HD 224638 are among the
best examples of
Dor stars, i.e., 0.3330 d. The
pulsation behaviour is very different: HD 224945 displays a set of
frequencies spread over an interval much larger than that of HD 224638.
We clearly found evidence for amplitude variations in the excited modes by
comparing data from different years. HD 224945 and HD 224638 are among the
best examples of ![]() Dor stars that show multimode pulsations, which make
them very interesting from an asteroseismological point of view.
Dor stars that show multimode pulsations, which make
them very interesting from an asteroseismological point of view.
Key words: methods: data analysis - stars: oscillations - stars: variables: general - techniques: photometric
The variability of
![]() Psc (V=7.5, F1 V) and
Psc (V=7.5, F1 V) and
![]() Psc (V=6.93, F0 V)
was announced by Mantegazza & Poretti
(1991), as a by-product of the monitoring of the
Psc (V=6.93, F0 V)
was announced by Mantegazza & Poretti
(1991), as a by-product of the monitoring of the ![]() Sct star
Sct star
![]() Psc. Both stars had been used as comparison stars in the
first observing run devoted to BH Psc. They increased the number of known
F-type
stars located close to the low-temperature edge of the Cepheid instability strip
which exhibit small amplitude variability on time scales of several hours, usually
longer than the length of a night of observation
and therefore easily detectable only when used as comparison stars for short-period
variables.
At that time, the debate on the nature of these variations was divided between
spot activity (observed periods as rotational periods) and pulsation
(nonradial g-modes).
Mantegazza et al. (1994, hereinafter Paper I)
tried to explain the complicated light behaviour of HD 224639 and HD 224945 in the
simplest way possible, by means of periodicities shaped as double- or triple-wave
curves. Balona et al. (1994) reported on
the multiperiodicity of
Psc. Both stars had been used as comparison stars in the
first observing run devoted to BH Psc. They increased the number of known
F-type
stars located close to the low-temperature edge of the Cepheid instability strip
which exhibit small amplitude variability on time scales of several hours, usually
longer than the length of a night of observation
and therefore easily detectable only when used as comparison stars for short-period
variables.
At that time, the debate on the nature of these variations was divided between
spot activity (observed periods as rotational periods) and pulsation
(nonradial g-modes).
Mantegazza et al. (1994, hereinafter Paper I)
tried to explain the complicated light behaviour of HD 224639 and HD 224945 in the
simplest way possible, by means of periodicities shaped as double- or triple-wave
curves. Balona et al. (1994) reported on
the multiperiodicity of ![]() Dor, giving decisive evidence in favour of
pulsation. Also, as a result of combined photometry and line profile variations
for 9 Aurigae (Krisciunas et al. 1995) and
Dor, giving decisive evidence in favour of
pulsation. Also, as a result of combined photometry and line profile variations
for 9 Aurigae (Krisciunas et al. 1995) and ![]() Dor (Balona et al. 1996), plus
the preliminary results on HD 224945 (Poretti et al. 1996), the hypothesis of variability caused by g-modes achieved
a wide consensus. The properties of this new class of variable stars were
delineated step-by-step through observational efforts and have been summarized by
Kaye et al. (1999),
while the problem of the driving mechanism and the excitation of g-modes
constitutes the target of continuing theoretical investigations.
As a result,
Dor (Balona et al. 1996), plus
the preliminary results on HD 224945 (Poretti et al. 1996), the hypothesis of variability caused by g-modes achieved
a wide consensus. The properties of this new class of variable stars were
delineated step-by-step through observational efforts and have been summarized by
Kaye et al. (1999),
while the problem of the driving mechanism and the excitation of g-modes
constitutes the target of continuing theoretical investigations.
As a result,
![]() Dor variables are now considered intermediate between A-F pulsators and
solar-type stars, finding a special place in the main programmes of
asteroseismologic missions such as COROT and MONS.
Dor variables are now considered intermediate between A-F pulsators and
solar-type stars, finding a special place in the main programmes of
asteroseismologic missions such as COROT and MONS.
On the basis of this progress, it is worth investigating in more detail the pulsational behaviour of HD 224639 and HD 224945. Here we present the results of a multisite campaign carried out in October 1995.
HD 224945 and HD 224638 are located very close to the celestial equator and therefore can be monitored from both the northern and southern hemispheres. As comparison stars we used the same two stars as in the 1991 campaign (HD 225086 and HD 200), since they proved to be stable within a few mmag. Five telescopes were used for this multisite campaign:
The original measurements were provisionally reduced by the observers themselves to check the data quality and for comparison purposes. The original raw data were then re-reduced by means of the same algorithm; this homogenous procedure allowed us to avoid the introduction of local drifts caused by routines using different interpolation formulae and/or different methods of applying extinction corrections. Since the weather was not particularly favourable during the campaign, the rejection of some parts of nights characterized by unfavourable weather conditions was decided on the basis of a uniform criterion. We also decided to use the code which allows us to calculate instantaneous values of the extinction coefficients (Poretti & Zerbi 1993) since in some cases changes were expected to occur.
Table 1 lists some details regarding observing runs at each site. As can be noted, the mean values of the magnitude differences between the two comparison stars show the presence of systematic shifts (up to 0.03 mag). This is not surprising, taking into account that different photomultipliers and filters were used. The systematic shifts between HD 225086 and HD 200 cannot be used to correct magnitude differences between HD 225086 and the two program stars since they have different colours from HD 200; uncertainties of the colour transformations are larger than the precision we need. Hence, to apply this correction we exploited the very useful circumstance that the spread in longitude between different observing sites is not larger than the length of the night. There were always some overlapping segments of the light curve, which allowed us to determine the amounts of the corrections in a straightforward way.
It should also be noted that the Turkish measurements show a scatter larger
than all the others. At first, all the Turkish data were considered, but
in the last step of the analysis (once it was established that rapid variations are
not present in the light curves) those measurements were averaged in groups of
4-5. Thus, the final set of data contains the original measurements from
all the observatories except for the averaged values from Turkey.
The standard deviations of the ![]() and
and ![]() values
between the comparison stars are 3.7 and 3.8 mmag, respectively.
values
between the comparison stars are 3.7 and 3.8 mmag, respectively.
| Site | Check star (HD 200) | HD 224945 | HD 224638 | |||||||||||
| N | s.d. | t1 | tN | n | N | t1 | tN | n | N | |||||
| ESO | 0.1472 | 198 | 0.0029 | 4.605 | 14.597 | 10 | 205 | 4.512 | 14.572 | 10 | 219 | |||
| Ege Obs. | 0.1180 | 117 | 0.0102 | 3.250 | 12.317 | 5 | 36 | 3.252 | 12.311 | 5 | 33 | |||
| SAAO | 0.1294 | 41 | 0.0055 | 1.427 | 14.479 | 6 | 36 | 1.432 | 14.482 | 6 | 44 | |||
| Mauna Kea | 0.1371 | 39 | 0.0051 | 7.824 | 14.003 | 6 | 37 | 7.840 | 14.023 | 6 | 38 | |||
| OSN | 0.1304 | 126 | 0.0032 | 7.364 | 19.524 | 9 | 128 | 7.362 | 19.527 | 9 | 133 | |||
| N | s.d. | t1 | tN | n | N | t1 | tN | n | N | |||||
| ESO | 0.2569 | 198 | 0.0029 | 4.604 | 14.597 | 10 | 203 | 4.512 | 14.572 | 10 | 217 | |||
| Ege Obs. | 0.2672 | 125 | 0.0091 | 3.264 | 12.312 | 5 | 32 | 3.251 | 12.322 | 5 | 29 | |||
| SAAO | 0.2458 | 41 | 0.0060 | 1.436 | 14.479 | 6 | 32 | 1.432 | 14.482 | 6 | 44 | |||
| Mauna Kea | 0.2554 | 20 | 0.0041 | 10.751 | 14.002 | 3 | 21 | 10.743 | 14.021 | 3 | 21 | |||
| OSN | 0.2449 | 126 | 0.0029 | 7.364 | 19.524 | 9 | 129 | 7.362 | 19.527 | 9 | 133 | |||
Figure 1 shows a part of the B light curves of HD 224945 and HD 224638. The fits
derived in the next sections are also shown. The original measurements can be
requested from the authors.
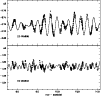 |
Figure 1: Light curves (B light) of HD 224945 and HD 224638 obtained during the 1995 multisite campaign; measurements from JD 2450005 to 2450014 are shown. Note the different timescales and amplitudes between the two curves. |
| Open with DEXTER | |
Since data in the final form circulated amongst all the participants, several co-authors analysed the time series independently and by different period search algorithms (least-squares, CLEAN, DFT, ...) and it was particularly satisfying to see that they detected the same terms, even if, owing to the complexity of the light variations, the terms did not always stand out in a clear way.
We present here the analysis carried out by
using the least-squares method (Vanicek 1971) used by the Merate group
in the analysis of ![]() Sct star light curves. This method has the
advantage of not using any data prewhitening since only the frequency values
previously found are considered as input values (known constituents; k.c.'s);
their amplitude and phase values are recalculated as unknowns in the new searches.
That means that after the detection of the f1 term, only the frequency value
f1was considered as established (i.e. a k.c.) and in the second search the
unknowns were
Sct star light curves. This method has the
advantage of not using any data prewhitening since only the frequency values
previously found are considered as input values (known constituents; k.c.'s);
their amplitude and phase values are recalculated as unknowns in the new searches.
That means that after the detection of the f1 term, only the frequency value
f1was considered as established (i.e. a k.c.) and in the second search the
unknowns were
![]() .
The ordinates of the
power spectra show the reduction factor
.
The ordinates of the
power spectra show the reduction factor
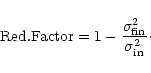 |
(1) |
Moreover, we can present the term detection step-by-step. The
frequency values were refined after each new detection.
We can also obtain useful evidence concerning the amplitude by applying a
least-squares
fit to the datasets. The interpolating formula we used is
![\begin{displaymath}%
\Delta m(t)= \Delta m_{\rm o} + \sum_i^N {A_i \cos [2\pi f_i (t-T_{\rm o}) +\phi_i ]}.
\end{displaymath}](/articles/aa/full/2002/11/aa1903/img11.gif) |
(2) |
We collected 442 V and 417 B measurements of HD 224945, considering
the Turkish measurements as binned points. The results
of the frequency analysis of the B data are shown in Fig. 2.
In each panel the horizontal line indicates the level for
S/N=4.0, i.e., the limit usually accepted for significance
(Kuschnig et al. 1997).
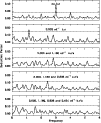 |
Figure 2: Power spectra of the B measurements of HD 224945 obtained during the 1995 multisite campaign. Note the different scale of the top panel. |
| Open with DEXTER | |
The top panel shows the spectrum obtained without any k.c.: the peak at 3.00 cd-1 stands out clearly, and the alias structure mimics very well the spectral window (see also Fig. 1 in Poretti et al. 1996). In the discussion of the 1991 data (Paper I), the alias at 2.00 cd-1was erroneously preferred. The reality of this term close to a multiple of 1 cd-1was discussed in Paper I. We note that it is also detected in the new campaign data for HD 224945, but in neither the HD 224638, nor the HD 200, time series; its physical presence in the HD 224945 data is therefore certain. When introducing the 3.00 cd-1frequency as k.c., the power spectrum shows an almost flat pattern, indicating that the amplitude of the remaining terms is smaller. However, two peaks reach the acceptance level: the first is located at 1.16 cd-1(second panel), the second at 2.84 cd-1(third panel). After introducing these three terms as k.c.'s, the detection of further terms becomes delicate. The highest peak in the fourth panel is at 2.42 cd-1and after that the power spectrum does not show a really dominant peak (bottom panel).
The analysis of the V measurements yields the same results, except with a slight difference in the frequency of the 2.84 cd-1term. A value close to 2.77 cd-1is preferred. Since the peak at 2.84 cd-1is broad (see third panel of Fig. 2), the presence of another undetectable term combined with the noise distribution could be responsible for the difference between the two values. In the least-squares solution we will consider the 2.84 cd-1term as the only well-established term.
These independent terms describe a different scenario from that
in Paper I. In that case the single-site
observations make the power spectrum very complicated, with a great
uncertainty between a peak and its ![]() 1 cd-1aliases. This
uncertainty led us to propose a solution based on two periodicities
each having a triple-wave shape, as it was considered the
simplest. Thanks to the multisite observations,
we now know that many pulsational modes are simultaneously excited.
1 cd-1aliases. This
uncertainty led us to propose a solution based on two periodicities
each having a triple-wave shape, as it was considered the
simplest. Thanks to the multisite observations,
we now know that many pulsational modes are simultaneously excited.
The frequency analysis of the B data collected in the 1994 season is much more complicated than that of the multisite campaign. In spite of that, we could detect the 3.00 and the 2.84 cd-1terms. When introducing these two terms as k.c.'s, the highest peak is at 2.27 cd-1. This peak is significantly different than the 2.42 cd-1detected in the 1995 multisite campaign. The search for a fourth component is not easy since we get numerous peaks: however, we could recognize the 1.16 cd-1term and its aliases. We considered it as a real mode on the basis of the results of the 1995 campaign. After that, the new search showed evidence of a complicated structure centered at 1.66 cd-1. We have no way of selecting in a reliable way the true term amongst this peak and the aliased ones. Moreover, the S/N of this term is less than 3.0. The V data allowed us to identify the same terms, supporting the presence of the new term at 2.27 cd-1. In the 1991 dataset the detection order of the terms is 3.00, 2.84 and 2.31 cd-1: the only difference with respect to the previous least-squares search (see the beginning of Sect. 3.2 in Paper I) is the identification of the first term as 3.00 cd-1instead of 2.00 cd-1. No other term can be detected after considering this triplet as k.c.'s; in particular there is no evidence of the presence of the 1.16 cd-1term.
It should be emphasized that it would be very difficult to solve the 1994 and 1991 light curves without having the way shown by the results of the 1995 campaign. In turn, the similar structures observed in the three independent datasets corroborate the proposed identification of the excited frequencies, even if some of them are at the limit of the acceptance level.
The much longer time interval covered by the 1991 data (the two runs span 14 and 10 days, respectively, and they are separated by a gap of 10 days) allowed us to use these data to refine the frequency values. First, we calculated the best solution using all the 1991 data. Then we calculated the amplitudes for each 1991 subset keeping fixed frequencies and phases.
Before applying these frequency values to other datasets, we verified the correspondence between some terms. We considered the 2.27 cd-1term detected in the 1994 data as the same detected at 2.31 cd-1in the 1991 campaign. However, we note that the least-squares solution yields a better fit when considering different values for different seasons. On the other hand, we cannot consider the 2.42 cd-1term detected in 1995 as coincident with the 2.31 cd-1term. We suggest that there are many terms excited (simultaneously or not) in the narrow range 2.2-2.5 cd-1and their detection is not an easy task. We considered the following five terms as independent modes detected in the three campaigns: 3.003, 2.836, 2.313, 2.424 and 1.160 cd-1. We also note the almost 2:1 ratio between the 2.313 and 1.160 cd-1terms: the similar amplitude does not support a monoperiodic contribution to the light curve as it should be very asymmetric. The resonance effect is more plausible, even if it should be noted that the 1.160 cd-1term was not observed in the 1991 dataset.
Using the four frequencies above, we calculated the amplitudes from the 1994
and 1995 datasets.
Table 2 summarizes the
results. The formal errors of the amplitudes are about 0.4 mmag.
Looking at the differences between the amplitudes of the two 1991 subsets
we can see that they are marginally significant, being in the interval 0.7-0.9
mmag. This very close similarity demonstrates that solutions
obtained from short runs are self-consistent.
The dense time coverage in each dataset ensures the reliability of
the amplitude determination. Therefore, we can
look at the differences in the amplitudes between the 1991, 1994 and
1995 datasets with greater confidence.
| Amplitude B [mmag] | Amplitude V [mmag] | |||||||||||
| Freq. | 1991 | 1991 | 1991 | 1994 | 1995 | 1994 | 1995 | |||||
| [cd-1] | All | I | II | |||||||||
|
|
4.3 | 4.5 | 3.8 | 5.4 | 6.1 | 4.0 | 5.1 | |||||
|
|
4.9 | 5.2 | 4.3 | 4.0 | 2.5 | 3.4 | 1.5 | |||||
|
|
4.3 | 4.5 | 3.8 | 2.5 | - | 2.3 | - | |||||
|
|
- | - | - | - | 2.3 | - | 1.9 | |||||
|
|
- | - | - | 2.5 | 3.0 | 2.2 | 2.4 | |||||
| Res. rms [mmag] | 5.4 | 5.3 | 5.4 | 5.1 | 4.2 | 5.0 | 4.2 | |||||
We also analyzed in frequency the data obtained by merging
the 1991, 1994 and 1995 datasets. For each detected term, it is
not possible to select the true value owing to the numerous aliases separated
by integer values of ![]() 1 cy-1; therefore, in the case of
HD 224945 we cannot
propose a full, comprehensive solution and evaluate in a reliable way the
phase coherence of the pulsation. The amplitude variability is a
further complication.
It should be noted that an attempt at such an analysis
detected two peaks at 2.27 and 2.31 cd-1, suggesting that these two peaks
are related to two independent terms (see the above comparison of the 1994 and
1991 results).
1 cy-1; therefore, in the case of
HD 224945 we cannot
propose a full, comprehensive solution and evaluate in a reliable way the
phase coherence of the pulsation. The amplitude variability is a
further complication.
It should be noted that an attempt at such an analysis
detected two peaks at 2.27 and 2.31 cd-1, suggesting that these two peaks
are related to two independent terms (see the above comparison of the 1994 and
1991 results).
The sum of the squared amplitudes
are the same in 1991 and 1994 (61 and 58 mmag2, respectively),
while it is lower in 1995 (50 mmag2). However, the amplitude of a mode
can change dramatically: the 2.836 cd-1term halved its B amplitude from
1991 to 1995 while the 2.313 cd-1term disappeared.
As a matter of fact, in the 1991 dataset there are three terms having
the same amplitude, while in the 1995 ones the 3.003 cd-1term is
dominating. The amplitude variability looks like a
well-established fact for this ![]() Dor star.
Dor star.
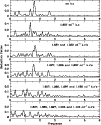 |
Figure 3: Power spectra of the B measurements of HD 224638 obtained during the 1995 multisite campaign. Note the different scales of the panels. |
| Open with DEXTER | |
| Amplitude B [mmag] | Amplitude V [mmag] | |||||||||||
| Freq. | 1991 | 1991 | 1991 | 1994 | 1995 | 1994 | 1995 | |||||
| [cd-1] | All | I | II | |||||||||
|
|
9.1 | 9.0 | 8.9 | 7.1 | 10.8 | 6.2 | 9.2 | |||||
|
|
9.0 | 8.4 | 8.7 | 7.3 | 10.2 | 6.0 | 7.4 | |||||
|
|
8.0 | 7.1 | 9.4 | 7.7 | 7.4 | 6.6 | 6.3 | |||||
|
|
4.7 | 5.0 | 6.0 | 9.1 | 5.2 | 7.0 | 4.0 | |||||
|
|
2.1 | 2.6 | 4.5 | 2.1 | 3.0 | 1.7 | 2.1 | |||||
| Res. rms [mmag] | 6.4 | 4.9 | 7.1 | 5.6 | 4.7 | 5.1 | 4.3 | |||||
The power spectrum obtained by introducing the five frequencies as k.c.'s is not homogenously flat (bottom panel). The noise in the region 0.0-2.0 cd-1 is 1.34 mmag, while in the region 4.0-6.0 cd-1it is only 0.65 mmag. However, it should be noted that the general patterns of the residual B and V power spectra are slightly different. This fact suggests that noise dominates over pulsation and the latter is really undetectable owing to the very small amplitude of the involved terms.
Once again, the light curves of the 1991 and 1994 seasons can only be understood if extra alias-free frequency information is available. The frequency analysis of the 1991 B data provided evidence for the terms 1.697, 1.627, 1.368 and 1.565 cd-1. The first three terms were already reported in Paper I, where two periodicities having each the shape of a double-wave were proposed. The 1.565 cd-1(detected also in the 1995 dataset) is a new term obtained by pushing one further step in the analysis. As a result, we also detect here the close triplet observed in the 1995 campaign. Since the frequency resolution in the 1991 dataset is much better than in the 1995 one, this confirmation strengthens our confidence in the reality of the triplet. The peak at 1.145 cd-1does not appear very clearly in the power spectrum, but it has been considered for the least-squares solution.
The first four terms are also detected in the 1994 B and V datasets, but residual signal is left, especially in the region 0.5-1.0 cd-1. The 1.145 cd-1term shows an amplitude much smaller than the other four terms. As a matter of fact, in this season it seems that many terms having amplitudes at the mmag level are excited.
We followed the same procedure used for HD 224945, refining the frequency values by means of the 1991 dataset and then calculating the amplitudes for the two 1991 subsets and the other datasets. The frequency analysis already gave some hint about the amplitude variability of some terms, since for example the 1.145 cd-1peak was not clearly detected in all datasets.
This is confirmed by the large amplitude variability, which can be discerned from Table 3. Considering the 1991 subsets we can see differences of up to 2.3 mmag, but note the +3.7, +2.9 and -3.9 mmag differences between the amplitudes of the 1.627, 1.368 and 1.565 cd-1terms in 1995 and 1994 datasets, which look extremely large. The term ranking is also largely changing. Note that the largest amplitude of the 1.565 cd-1term was in 1994, whereas usually this term was below the first three in 1991 and 1995. The amplitude is also greatly changing. The sum of the squared amplitudes is higher in the 1995 data (311 mmag2) and lower in the 1994 dataset (250 mmag2), with a variation of 25%. This difference supports the intrinsic variability of the mode amplitudes. Note for example that in the 1991 data there are three terms having a large amplitude, in 1994 data there are four and in 1995 data two of them clearly have the largest amplitude, considerably greater than the others. Hence, the amplitude changes look more conspicuous in HD 224638 than in HD 224945.
In the case of HD 224638 we can merge the 1991, 1994 and 1995 datasets knowing that all the datasets show the same frequency content. Indeed, the frequency analysis of the whole set yields the same frequencies listed in Table 3. The detection of the three terms at 1.565, 1.627 and 1.697 cd-1supports the identification as three independent modes proposed in Sect. 5.1. Unfortunately, we cannot give refined values for the frequencies, owing to the cy-1 aliases. However, we performed some tests assuming a constant value for the frequency and then calculated the amplitudes and phases of each term for each observing season. Besides the verification of the amplitude variability, we found that the same frequency displays similar phase values from one season to the next. This fact supports an intrinsic variability of the mode amplitudes, rather than a beating phenomenon between two very close terms.
The properties of ![]() Dor stars have been reviewed by Zerbi (2000);
driving mechanisms have been proposed by Guzik et al. (2000), Wu (2002) and
Löffler (2002), but the origin of the pulsation in
Dor stars have been reviewed by Zerbi (2000);
driving mechanisms have been proposed by Guzik et al. (2000), Wu (2002) and
Löffler (2002), but the origin of the pulsation in ![]() Dor stars still remains
an open problem.
Dor stars still remains
an open problem.
HD 224945 and HD 224638 have very similar physical properties
(Zerbi 2000):
MV=2.98,
![]() ,
,
![]() K,
K,
![]() and
and
![]() for HD 224638, MV=3.07,
for HD 224638, MV=3.07,
![]() ,
,
![]() K,
K,
![]() and
and
![]() for HD 224945. Also the difference in metallicity is
not significant,
for HD 224945. Also the difference in metallicity is
not significant,
![]() vs. -0.30, respectively. The two stars occupy very
similar positions also in the colour-magnitude diagram, being located on the ZAMS,
in the middle of the domain of
vs. -0.30, respectively. The two stars occupy very
similar positions also in the colour-magnitude diagram, being located on the ZAMS,
in the middle of the domain of ![]() Dor stars and on the low temperature edge of
the
Dor stars and on the low temperature edge of
the ![]() Sct region (Handler 1999).
Therefore, two very similar
stars display different pulsational modes, since HD 224945 is characterized
by four frequencies spread over a large interval, while HD 224638 displays a much
more closely spaced set (it is similar to HR 2740; see Poretti et al. 1997).
Moreover, the residual
power spectrum of HD 224638 has a very low noise level above 4.0 cd-1,
while that of HD 224945 has a higher level, suggesting some
signal contribution.
Sct region (Handler 1999).
Therefore, two very similar
stars display different pulsational modes, since HD 224945 is characterized
by four frequencies spread over a large interval, while HD 224638 displays a much
more closely spaced set (it is similar to HR 2740; see Poretti et al. 1997).
Moreover, the residual
power spectrum of HD 224638 has a very low noise level above 4.0 cd-1,
while that of HD 224945 has a higher level, suggesting some
signal contribution.
The large spread in the frequency values observed for HD 224945 is another piece of evidence that the cause of light variability in these stars is pulsation and not stellar activity. Differential rotation is not able to match a spread in frequencies as large as 0.7 cd-1(considering the three terms always observed, i.e., not considering the even more distant frequency at 1.16 cd-1).
We note that multiperiodicity is not observed in all
![]() Dor stars. Some display only a single photometric
period (i.e., a single low-order mode).
A relevant example is
Dor stars. Some display only a single photometric
period (i.e., a single low-order mode).
A relevant example is
![]() (Aerts & Kaye 2001), which is also monoperiodic
from a spectroscopic point of view (i.e. it does not show any high-order modes).
Another example is HD 164615 (Zerbi et al. 1997), one of the first known
(Aerts & Kaye 2001), which is also monoperiodic
from a spectroscopic point of view (i.e. it does not show any high-order modes).
Another example is HD 164615 (Zerbi et al. 1997), one of the first known
![]() Dor stars. It is probably a monoperiodic variable which shows amplitude
modulation.
Dor stars. It is probably a monoperiodic variable which shows amplitude
modulation.
Finally, we note that HD 224945 exhibits the shortest known period (i.e.
0.3330 d) of the ![]() Dor stars. Guzik et al. (2000) considered 0.48 d as
the lower limit (probably the old value of the same term, i.e. 2.00 cd-1,
Paper I).
Therefore, the period value cannot be used to separate p- and
g-modes, as
Dor stars. Guzik et al. (2000) considered 0.48 d as
the lower limit (probably the old value of the same term, i.e. 2.00 cd-1,
Paper I).
Therefore, the period value cannot be used to separate p- and
g-modes, as ![]() Sct stars can display such "long-period'' p-modes.
A careful evaluation of the physical parameters is necessary. Indeed,
in HD 224638 and HD 224945 the fundamental radial mode is shorter than 0.07 d,
confirming that p- and g-modes are well separated in
Sct stars can display such "long-period'' p-modes.
A careful evaluation of the physical parameters is necessary. Indeed,
in HD 224638 and HD 224945 the fundamental radial mode is shorter than 0.07 d,
confirming that p- and g-modes are well separated in ![]() Dor stars.
Dor stars.
The solution of the light curves of HD 224638 and HD 224945 has been deduced only on
the basis of a multisite campaign, since the true peaks could not be recognized if a
![]() cd-1effect is present in the spectral window.
We did our best to identify the correct excited
modes, but the more important characteristic of these two stars is the
strong multiperiodicity itself, independent of the exact frequency values.
In our opinion, HD 224638 and HD 224945
provide two of the best examples of features typical of multiperiodicity
among
cd-1effect is present in the spectral window.
We did our best to identify the correct excited
modes, but the more important characteristic of these two stars is the
strong multiperiodicity itself, independent of the exact frequency values.
In our opinion, HD 224638 and HD 224945
provide two of the best examples of features typical of multiperiodicity
among ![]() Dor variables:
different sets of frequency content, amplitude variations, disappearing terms, close
doublets of frequencies. Also, after detecting five or six terms,
the rms scatter is larger than the observational error. Therefore,
residual signal is hidden in the noise.
Such extreme multiperiodicity can be clearly ascribed to
pulsation, as stellar activity is not able to generate it.
Dor variables:
different sets of frequency content, amplitude variations, disappearing terms, close
doublets of frequencies. Also, after detecting five or six terms,
the rms scatter is larger than the observational error. Therefore,
residual signal is hidden in the noise.
Such extreme multiperiodicity can be clearly ascribed to
pulsation, as stellar activity is not able to generate it.
The differences in the frequency and amplitude
ranges of HD 224638 and HD 224945 (clearly visible in Fig. 1)
remind us of the
unpredictable frequency content of ![]() Sct stars,
where the selection mechanism among all the possible modes seems to be different
from one star to the next (Poretti 2000).
The amplitude variability of the excited modes is another point of similarity
between
Sct stars,
where the selection mechanism among all the possible modes seems to be different
from one star to the next (Poretti 2000).
The amplitude variability of the excited modes is another point of similarity
between ![]() Dor and
Dor and ![]() Sct stars. Other than multiperiodicity,
HD 224945 and HD 224638 provide the best
examples of amplitude variability among
Sct stars. Other than multiperiodicity,
HD 224945 and HD 224638 provide the best
examples of amplitude variability among ![]() Dor stars, following the
three campaigns
carried out on these stars. This observational evidence suggests
strategies for asteroseismological space missions: a long observing run (or
two separate runs) may be very helpful in detecting more terms
(excited at different levels
at different times) or in studying damping effects.
Dor stars, following the
three campaigns
carried out on these stars. This observational evidence suggests
strategies for asteroseismological space missions: a long observing run (or
two separate runs) may be very helpful in detecting more terms
(excited at different levels
at different times) or in studying damping effects.
Acknowledgements
ER and SM acknowledge the partial support by the Junta de Andalucia and by the Direccion General de Investigacion (DGI) under project AYA2000-1559. SM also acknowledges the financial support by the Osservatorio Astronomico di Brera and by the Agenzia Spaziale Italiana (ASI Contract I/R/037/01). Thanks are due to an anonymous referee and to M. Breger for useful comments and suggestions on the first version of the manuscript.