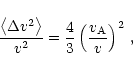A&A 384, 299-302 (2002)
DOI: 10.1051/0004-6361:20011825

Different solar wind types reflected in pick-up ion spectral signatures

S. V. Chalov 1 - H. J. Fahr2

1 - Institute for Problems in Mechanics of the Russian Academy of Sciences, Prospect Vernadskogo 101-1,
117526 Moscow, Russia
2 - Institut für Astrophysik und Extraterrestrische Forschung der Universität Bonn, Auf dem Hügel 71,
53121 Bonn, Germany

Received 6 November 2001 / Accepted 20 December 2001

Abstract
In the more recent years several papers have been published which presented theoretical results concerning the phase-space behaviour of pick-up ions (PUIs) after their injection into the supersonic solar wind. PUI spectra thereby were obtained which revealed detailed spectral properties that could well be compared with observational data. Effects of convection, adiabatic deceleration, pitch-angle diffusion, and even of energy diffusion could clearly be identified. It was, however, becoming evident in the data that specific spectral differences between pick-up spectra in slow solar wind streams and in fast solar wind streams can be found. For instance, the high-energy shoulders of pick-up spectra beyond the injection energy were less pronounced in fast compared to slow solar wind streams. In order to come up with a more quantitative theoretical representation of this phenomenon we shall study in this paper the specifically different conditions for PUI phase-space transports in fast and in slow solar wind streams taking into account the type-specific main quantities governing pick-up ion phase-space motions like the injection velocities, the turbulence levels, and the exposure times.

Key words: acceleration of particles - solar wind - interplanetary medium


1 Introduction

Most interesting as an observational basis of this study here are pick-up ion (PUI) spectral observations obtained at moderate solar distances, i.e. inside 5 AU. In this heliospheric region many high-quality spectral observations have been carried out with plasma analysers on board of AMPTE, ULYSSES, SOHO, and ACE. The PUI spectra presented by Möbius et al. (1988, 1998, 1999), Gloeckler et al. (1994, 2000), or Gloeckler & Geiss (1998) are of very high quality with high statistical significance levels of the spectral fluxes up to energies of 10 keV. These observational data can really serve as a basis to control on the quality and physical correctness of transport theories which have been applied to calculate PUI spectra. In a recent paper by Chalov & Fahr (2000) specifically He+ PUI spectra obtained by Möbius et al. (1999) were taken as a basis for comparisons with corresponding theoretical results.

As was shown in this paper the claim made by Möbius et al. (1999) that they can detect a signature of the actual injection velocity of He+PUIs in their data could in fact be supported by theoretical results even though the complicated PUI phase-space transport under disfavourable solar wind conditions may hide this effect somehow (see Chalov & Fahr 2000). Especially interesting in this respect was the predicted fact that typically different He+ PUI spectra should result under conditions of fast or slow solar winds, respectively. At high solar wind velocities higher degrees of pitch-angle anisotropies and less pronounced high-energy shoulders of the spectra should occur according to theoretical predictions. The latter prediction in fact was observed in many PUI measurements as clearly stated by Gloeckler (1999) and Gloeckler et al. (2000). A first qualitative explanation for why these features can occur was given by Chalov & Fahr (2000) by pointing out that under fast solar wind conditions the so-called exposure times are reduced for which injected PUIs are subject to stochastic diffusion processes while they are convected to the place of measurement. It is, however, not yet clear as to what extent these phenomena are due to reduced exposure times alone, or whether perhaps other action mechanisms are even more important for these phenomenological occurences.

In the present paper we emphasize some effects different from that of the exposure time which yield a higher efficiency of stochastic acceleration of PUIs in slow solar wind as compared to fast solar wind under identical solar wind turbulence conditions.

2 The role of the exposure times and PUI injection velocities

Interstellar PUIs immediately after their creation have velocities in the solar wind frame which are close to the solar wind bulk velocity. Hence the velocities of PUIs in fast solar wind streams are larger than those in slow streams. Interaction of PUIs with solar wind turbulence leads to their pitch-angle scattering and stochastic acceleration. Hereby the mean value of the squared change of the PUI velocity v due to scattering in the case of Alfvénic turbulence is given by

 \begin{displaymath}\frac{\left\langle \Delta v^{2}\right\rangle }{v^{2}}=\frac{4}{3}\left( \frac{v_{{\rm A}}}{v}\right) ^{2}\,, \end{displaymath} (1)

where $v_{{\rm A}}$ is the Alfvén velocity. It is clear from Eq.  (1) that the larger the ratio $v_{{\rm A}}/v$ the larger is this relative change of the velocity. Since the velocity of PUIs in fast solar wind is larger than that in slow wind one can expect that the process of stochastic acceleration in slow wind is more efficient under the assumption of equal conditions of solar wind turbulence and equal values of $v_{{\rm A}}$.

To demonstrate this effect we consider stochastic acceleration of pick-up helium in near-equatorial solar wind. We again start our studies from the phase-space transport equation for the pitch-angle anisotropic PUI velocity distribution function $f(r,\varphi,v,\mu)$ which we have already used at earlier occasions (see e.g. Chalov & Fahr 1998, 1999, 2000) and which is given in the following form:

 
$\displaystyle {\frac{\partial f}{\partial t}}$ + $\displaystyle \left( U_{{\rm SW}}+v\mu \chi \right) {\frac{\partial f}{\partial... ...U_{{\rm SW}} {\frac{1-\chi ^{2}}{r}} \right] {\frac{\partial f}{\partial \mu }}$  
    $\displaystyle {} = \hat{S} f + Q(r,\varphi ,v,\mu ) \,,$ (2)

where $U_{{\rm SW}}$ is the solar wind velocity, v and $\mu$ are the velocity magnitude and the cosine of the ion pitch-angle in the solar wind frame, $\chi$ is the cosine of the angle between the radial direction and Parker's interplanetary magnetic field, $\varphi$ is the off-upwind angle of the position, Q is the local production rate of PUIs, and $\hat{S}f$ is the Fokker-Planck diffusion operator describing the quasilinear interaction of PUIs with the ambient hydromagnetic wave turbulences. As is well known this operator consists of first and second order partial derivatives of f with respect to the velocity space coordinates v and $\mu$ connected with the relevant diffusion coefficients $D_{{\rm vv}}$, $D_{{\rm v\mu}}$, and $D_{{\rm\mu\mu}}$. We are interestedhere in the velocity diffusion coefficient which can be given in the following form (Schlickeiser 1989):
 
$\displaystyle D_{{\rm vv}} = v_{{\rm A}}^{2}D_{0}\left( 1-\mu^{2}\right) \left[... ...^{q-1} + \varepsilon\left\vert 1+\mu v/v_{{\rm A}}\right\vert ^{q-1}\right] \,,$     (3)

where the diffusion factor D0 turns out to be given by:

 \begin{displaymath}D_{0}=\frac{\pi}{2}\Omega_{{\rm c}}\frac{q-1}{1+\varepsilon}\... ...-1} \frac{\left\langle \delta B^{2}\right\rangle }{B^{2}}\cdot \end{displaymath} (4)

On the right-hand side of Eqs. (3) and (4) B, $\left\langle \delta B^{2}\right\rangle $, $\Omega_{{\rm c}}$, q, $k_{\min}$, and $\varepsilon$ denote the magnitude of the interplanetary magnetic field, the mean-squared amplitude of Alfvénic fluctuations, the ion gyrofrequency, the spectral index of turbulence, the scale of the large energy containing fluctuations, and the ratio of intensities of inward and outward moving waves, respectively. For present purposes it is convenient to rewrite Eq. (4) in the following form:

 \begin{displaymath}D_{0}\propto v_{{\rm A}}n_{{\rm e}}^{1-q/2}\frac{\left\langle \delta B^{2}\right\rangle }{B^{2}}\,, \end{displaymath} (5)

where $n_{{\rm e}}$ is the electron number density.
  \begin{figure} \par\includegraphics[width=6.8cm,clip]{h3365f1.eps} \end{figure} Figure 1: The velocity distribution functions $F_{\rm v}$ of pick-up helium at 1 AU in the case of fast solar wind with $U_{{\rm SW}}=700$ kms-1 (curve 1) and slow solar wind with $U_{{\rm SW}}=300$ kms-1 (curve 2). Curve 3 is the velocity distribution in slow solar wind with artificially increased injection velocity of PUIs from 300 kms-1 to 700 kms-1.
Open with DEXTER

Figure 1 shows calculated pitch-angle integrated velocity distribution functions $F_{\rm v}$ at r=1 AU and $\varphi=90^{\circ}$ (the cross-wind direction) which are defined as

 \begin{displaymath}F_{{\rm v}}={\frac{2\pi U_{{\rm SW}}v^{2}f_{{\rm v}}}{n_{\inf... ...quad f_{{\rm v}}(r,\varphi,v)=\int^{1}_{-1} f\,{{\rm d}}\mu\,, \end{displaymath} (6)

where

 \begin{displaymath}\int_{0}^{\infty}F_{{\rm v}}\,{{\rm d}}\left( v/U_{{\rm SW}}\right) =n_{{\rm PU}}/n_{\infty}({{\rm He}})\,, \end{displaymath} (7)

The quantities $n_{{\rm PU}}$ and $n_{\infty}({{\rm He}})$ are the local number density of pick-up helium and number density of neutral helium in the local interstellar medium. Curves 1 and 2 correspond to the cases when the solar wind velocity equals 700 kms-1 and 300 km s-1, respectively. All other relevant parameters of the solar wind are taken as identical in both cases. Namely, $B_{{\rm E}}=5$nT, $n_{{\rm eE}}=5$ cm-3, $\left\langle \delta B_{{\rm E}}^{2}\right\rangle /B_{{\rm E}}^{2}% =0.01$, $\varepsilon=0.2$, and q=5/3, where the suffix "${\rm E}$'' denotes reference quantities taken at the orbit of the earth. Differences in the magnitudes of B and  $n_{{\rm e}}$ in fast and slow solar wind streams and possible influence of these differences on the spectral shape of PUIs are shortly discussed at the end of Sect. 2. As one can clearly see the high-velocity tail is almost absent in the high-velocity wind and comparatively much more pronounced in the low-velocity wind. Two reasons for such a behaviour are possible: 1) acceleration time (exposure time which PUIs spend after injection while they are convected with the solar wind till they are appearing at 1 AU) is larger in slow wind; 2) initial or injection velocities of PUIs are smaller in slow wind and, therefore, acceleration efficiency is higher according to Eq. (1).
  \begin{figure} \par\includegraphics[width=6.8cm,clip]{h3365f2.eps} \end{figure} Figure 2: Same as Fig. 1, but for increased level of Alfvénic turbulence.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=6.8cm,clip]{h3365f3.eps} \end{figure} Figure 3: The velocity distribution functions of pick-up helium with negative (solid curves) and positive (dashed curves) values of the pitch-angle cosine. I - $U_{{\rm SW}}=700$ kms-1, II - $U_{{\rm SW}}=300$ kms-1.
Open with DEXTER

In order to clear up the role of these two factors in formation of high-velocity tails we calculated the velocity distribution of PUIs in slow wind artificially increasing the injection velocity from 300 km s-1 to 700 km s-1 (curve 3 in Fig. 1). One can see that the slopes of the distributions given by curves 1 and 3 in the region above the injection velocities then are almost identical in both cases. This fact reveals that the different exposure times of PUIs in slow and fast solar wind flows essentially are not responsible for the observationally confirmed fact that under fast solar wind conditions the high-velocity shoulders of PUI spectra are only weakly pronounced. The role of the exposure time can, however, increase with increasing the level of solar wind turbulence as it can be seen in Fig. 2 which shows the same as Fig. 1 but for $\left\langle \delta B_{{\rm E}}^{2}\right\rangle /B_{{\rm E}}^{2}=0.05$ (instead of =0.01). The velocity distribution above the injection velocity in fast solar wind (curve 1) is slightly harder than that in slow wind with the artificially increased injection velocity (curve 3). The small shift of maxima of the velocity distributions given by curves 1 and 2 in Figs. 1 and 2 above the value $v/U_{{\rm SW}}=1$ which is different for fast and slow solar winds is due to taking into account the bulk velocities of neutral helium atoms (for more details see Chalov & Fahr 2000).

Figure 3 shows similar distributions as in Fig. 1 (curves 1 and 2) but this time separately for PUIs with negative $\mu$-values (solid curves) and with positive $\mu$-values (dashed curves). One can see that the velocity distribution of PUIs in fast solar wind (curves I) is more anisotropic than in slow wind (curves II). The main reason of larger anisotropy in fast solar wind as compared with slow one most likely is the difference in the exposure times and the more radial configuration of the magnetic field in the fast wind. Another interesting feature which can be seen in Fig. 3 is the fact that the high-velocity tail in the slow wind distribution is mainly composed of particles with positive $\mu$. In addition, the maximum of the velocity distribution of PUIs with $\mu>0$ in the fast solar wind is shifted towards lower velocities due to the effect of adiabatic deceleration, while in the slow wind the adiabatic deceleration of PUIs with $\mu>0$ close to the maximum of the velocity distribution is compensated by stochastic acceleration.

We have considered here acceleration efficiencies of PUIs in fast and slow solar wind flows taking into account only the differences in the wind velocities and keeping all other relevant quantities unvaried and have shown that then acceleration in slow flows is more effective mainly because of lower injection velocities of PUIs. The MHD properties of fast and slow solar wind plasmas differ, however, not only in the values of the wind velocity. Besides of that also properties of solar wind turbulence and of the velocity diffusion coefficient $D_{{\rm vv}}$ are likely to be different. The latter depends on $v_{{\rm A}}$ and $n_{{\rm e}}$ (see Eq. (5)) which can be different in fast and slow flows.

The Ulysses spacecraft during the near-ecliptic mission in 1992 and 1993 detected a large number of interplanetary shocks associated with corotating interaction regions. Claßen et al. (1998) presented parameters of the solar wind in front of reverse and forward shocks, i.e. in unperturbed fast and slow flows. Although the values of the magnetic field and of the electron number densities are different in these flows, the values of the Alfvén velocity $v_{{\rm A}}$ are not correlated with the solar wind velocity. Since the dependence of D0 on  $n_{{\rm e}}$ is very weak in the case when $v_{{\rm A}}$ remains unchanged, any differences in  $D_{{\rm vv}}$ in fast and slow flows thus are apparently determined by different solar wind turbulence properties.

3 Discussion

It has been demonstrated in Sect. 2 that slow solar wind flows constitute preferential conditions for an acceleration of PUIs to the region above their injection velocities. This preference as compared to acceleration under fast flow conditions is evident at least if identical parameters are applied to describe the solar wind turbulence. Furthermore, it also seems that turbulences convected in slow flows, in some respects at least, are more favourable to accelerate ions than those in fast flows. This follows from observations that magnetic fluctuations in the solar wind can be considered as composed of a combination of a dominant two-dimensional component (wave vectors are perpendicular to the mean magnetic field) and a minor slab component (Matthaeus et al. 1990; Zank & Matthaeus 1992; Bieber et al. 1996). Since the two-dimensional component can hardly be involved in resonant wave-particle interactions with PUIs, it is the slab component which makes the major contributions to the velocity diffusion coefficient. Recently Saur & Bieber (1999) analysing magnetic field data from the National Space Science Data Center have shown that magnetic fluctuations in slow solar winds are on average more slab-like and energetic than fluctuations in fast winds. In addition, the Helios spacecraft measurements between 0.3 and 1 AU have shown strong correlation between the magnitude of the solar wind velocity and the ratio $\varepsilon$ of intensities of outward and of inward propagating waves (Tu et al. 1990). In fast solar wind flows essentially outward propagating waves have been observed. In this respect acceleration in slow winds also is more effective since stochastic acceleration can only operate if both outward and inward propagating waves are present. This brings us to the final conclusion that with the above considerations we could reliably pin-point the reasons why one observes more pronounced high energy shoulders in the PUI spectra in slow winds as compared to what is found in fast winds.

Acknowledgements
This work was partially carried out while S. V. Chalov during his stay in 2001 was a guest at the Institute for Astrophysics and Extraterrestrial Research of the University of Bonn. The authors are grateful to the Deutsche Forschungsgemeinschaft (DFG) for the financial support of this stay in the frame of a bi-national cooperation project with grant number: 436 RUS 113/110/6-2 and in the frame of the DFG project with number Fa-97/24/2. S. V. Chalov was also partially supported by the Russian Foundation for Basic Research (RFBR) Grants 99-02-04025, 01-01-00759, and by Avard No. RPI-2248 U.S. Civilian Research and Development Foundation.

References

 
Copyright ESO 2002