Scattering and absorption of light by a homogeneous distribution of intergalactic large dust grains has been proposed as an alternative, non-cosmological explanation for the faintness of type Ia supernovae at
A&A 384, 1-10 (2002)
DOI: 10.1051/0004-6361:20020002
A. Goobar - L. Bergström - E. Mörtsell
Department of Physics, Stockholm University, SCFAB, 106 91 Stockholm, Sweden
Received 10 August 2001 / Accepted 2 January 2002
Abstract
Scattering and absorption of light
by a homogeneous distribution of intergalactic large dust grains has been
proposed as an alternative, non-cosmological explanation for the faintness of type Ia supernovae at ![]() .
We investigate the differential extinction for high-redshift
sources caused by extragalactic dust along the line of sight.
Future observations of type Ia supernovae up to
.
We investigate the differential extinction for high-redshift
sources caused by extragalactic dust along the line of sight.
Future observations of type Ia supernovae up to ![]() ,
e.g. by
the proposed SNAP satellite, will allow the measurement of the properties of dust
over cosmological distances. We show that 1% relative spectrophotometric accuracy
(or broadband photometry) in
the wavelength interval 0.7-1.5
,
e.g. by
the proposed SNAP satellite, will allow the measurement of the properties of dust
over cosmological distances. We show that 1% relative spectrophotometric accuracy
(or broadband photometry) in
the wavelength interval 0.7-1.5 ![]() m is required to measure the
extinction caused by "grey'' dust down to
m is required to measure the
extinction caused by "grey'' dust down to
![]() mag.
We also argue that the presence of grey dust is not necessarily inconsistent with
the recent measurement of the brightness of a supernova at z=1.7 (SN 1997ff),
in the absence of accurate spectrophotometric information of the supernova.
mag.
We also argue that the presence of grey dust is not necessarily inconsistent with
the recent measurement of the brightness of a supernova at z=1.7 (SN 1997ff),
in the absence of accurate spectrophotometric information of the supernova.
Key words: cosmological parameters; dust, extinction; supernovae: general
There is observational evidence (Perlmutter et al. 1999; Riess et al. 1998)
that type Ia supernovae, when used as calibrated
standard candles, are dimmer at high redshift than can be explained
in models without a cosmological constant. At least there seems
to be a need for a
non-clustered "dark energy''
component with a negative coefficient in the equation
of state, such as obtained in models with an evolving scalar
field ("quintessence'') (Steinhardt 2000). Since there are potential systematic
effects affecting this interpretation, it is
important to investigate alternative explanations.
In this note, we investigate dimming due to absorption and scattering
on intergalactic dust, as has been proposed by Aguirre (1999a,1999b) to be a viable
explanation for the supernova results. The recent measurements of
the CMB small angle anisotropies showing that the universe is most likely flat
(de Bernardis et al. 2000; Balbi et al. 2000; Pryke et al. 2001), combined with measurements of
![]() from large scale structure (Peacock et al. 2001)
and galaxy cluster evolution (Bahcall & Fan 1998) makes Aguirre's idea for the origin of the
type Ia supernovae faintness at
from large scale structure (Peacock et al. 2001)
and galaxy cluster evolution (Bahcall & Fan 1998) makes Aguirre's idea for the origin of the
type Ia supernovae faintness at ![]() unlikely.
unlikely.
Moreover, Aguirre & Haiman (2000) have shown
that the amount of dust required to make the supernova results compatible with
a flat universe, as indicated by the CMB results, but without a cosmological constant, is
already disfavored by the far-infrared background measured by the DIRBE/FIRAS instruments.
However, a sizable grey dust
column density capable of biasing the results cannot be excluded with
the present knowledge. Precision measurements of "Dark Energy'' and "Dark Matter'' with high-z supernovae have
been proposed see e.g. (Goliath et al. 2001; Mörtsell et al. 2001). The assumption in those studies is that the systematic uncertainties
do not exceed
![]() mag. Thus, in this work we concentrate on the needed relative
spectrophotometric accuracy to meet this requirement.
mag. Thus, in this work we concentrate on the needed relative
spectrophotometric accuracy to meet this requirement.
Extinction must be considered for at least four different dust environments:
Properties such as the extinction scale-length and the wavelength dependence can be different for each case.
The main emphasis of this work is on the calculation of the possible effects from
intergalactic dust (1). To avoid
observational constraints on reddening, such a component must
mainly consist of
large dust grains as
described in (Aguirre 1999a,1999b). However, even large-grain
dust will
cause some reddening, and going to higher redshift should enable
to distinguish between extinction or a cosmological origin for the
faintness of type Ia supernovae at ![]() .
The future data sample
we have in mind here is the one expected from the SNAP satellite
(Perlmutter et al. 2000), which will provide several thousand type Ia supernovae
out to
.
The future data sample
we have in mind here is the one expected from the SNAP satellite
(Perlmutter et al. 2000), which will provide several thousand type Ia supernovae
out to ![]() .
.
In this note we also discuss the light extinction by "normal'' dust in either
the SN host galaxy (2) or galaxies along the line of sight (3). As
we will see, the latter
only affects sizably about 1% of the supernovae at ![]() .
.
Type Ia supernovae form a remarkably homogeneous class of astronomical
objects and are therefore well suited for studying the dust properties
over cosmological distances. Figure 1 shows the average
brightness at maximum light in V, R, I and J-band for type Ia
supernovae along with the filter transmission functions
used![]() .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3090F1_a.eps}\\ [4mm]
\includegraphics[width=8.8cm,clip]{H3090F1_b.eps} \end{figure}](/articles/aa/full/2002/10/aah3090/Timg22.gif) |
Figure 1:
Top: mean VRIJ magnitudes for type Ia supernovae vs. redshift for
(
|
| Open with DEXTER | |
Other potential sources for spectrophotometric studies of dust are
quasars and core collapse supernovae. The SDSS and 2DF
collaborations are preparing templates that will eventually include
about 105 QSOs up to redshift ![]() .
A recent study
performed by the SDSS group of a sample of 2200
QSO spectra in the redshift range
0.044<z<4.789 showed a
spectrum-to-spectrum 1
.
A recent study
performed by the SDSS group of a sample of 2200
QSO spectra in the redshift range
0.044<z<4.789 showed a
spectrum-to-spectrum 1![]() difference of approximately 20% in
the rest system wavelength range 0.1 to 0.85
difference of approximately 20% in
the rest system wavelength range 0.1 to 0.85 ![]() m (Vanden Berk et al. 2001). By averaging over
some 400 QSOs in redshift bins of
m (Vanden Berk et al. 2001). By averaging over
some 400 QSOs in redshift bins of
![]() ,
one could thus
possibly achieve a 1% spectrophotometric measurement, if the scatter
is of stochastic nature, i.e. not related to evolutionary effects.
Type II supernovae exhibit an approximate black body spectrum and are
used for distance estimations through the "Expanding Photosphere
Method''. Although fainter than type Ia and thus harder to observe at
high-z, they could potentially be used for probing dust, especially if
observed with NGST.
,
one could thus
possibly achieve a 1% spectrophotometric measurement, if the scatter
is of stochastic nature, i.e. not related to evolutionary effects.
Type II supernovae exhibit an approximate black body spectrum and are
used for distance estimations through the "Expanding Photosphere
Method''. Although fainter than type Ia and thus harder to observe at
high-z, they could potentially be used for probing dust, especially if
observed with NGST.
Following the idea of Aguirre (1999a,1999b), we assume that the intergalactic dust population can be described by a Draine & Lee model (Draine & Lee 1984) where the smaller grains have been destroyed by some unspecified process, plausibly connected to the expulsion of the dust from the star-forming galaxies where the dust originated.
The reddening parameter RV is defined by
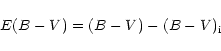
The presence of small dust grains enhances the wavelength dependence
of extinction. In the adopted parameterization this corresponds to lower
values of RV. Measurements of the restframe E(B-V)for
![]() supernovae have been used to set a lower limit
supernovae have been used to set a lower limit
![]() (Perlmutter et al. 1999),
see also caveats with regards to this limit in (Aguirre 1999b).
(Perlmutter et al. 1999),
see also caveats with regards to this limit in (Aguirre 1999b).
A population of large grains may have an RV parameter as large as 5 to 10, thus giving a rather achromatic ("grey'') absorption.
Typically, the most important types of intergalactic grains are silicates
and graphite. The optical properties, of which RV is the most
important for our applications, depend to some extent on the actual
value chosen for the small-size cutoff
![]() in the Draine-Lee power-law
size distribution. To make contact with Aguirre's calculations, we will
use
in the Draine-Lee power-law
size distribution. To make contact with Aguirre's calculations, we will
use
![]() between 0.08 and 0.12
between 0.08 and 0.12 ![]() m, corresponding
roughly to RV between 5.5 and 9.5.
In the numerical calculations, we use the convenient parameterization
of the extinction versus wavelength given by Cardelli et al. (1989).
The existence of small dust grains would make the differential extinction effects
larger than the ones described here, i.e. easier to identify observationally.
m, corresponding
roughly to RV between 5.5 and 9.5.
In the numerical calculations, we use the convenient parameterization
of the extinction versus wavelength given by Cardelli et al. (1989).
The existence of small dust grains would make the differential extinction effects
larger than the ones described here, i.e. easier to identify observationally.
For a given emission redshift ![]() ,
the attenuation
,
the attenuation
![]() at observed
wavelength
at observed
wavelength
![]() due to dust can be written
due to dust can be written
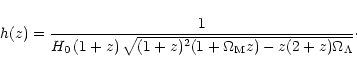 |
(2) |
The Monte-Carlo simulation program SNOC (Goobar et al. 2002)
was used to perform the integral in Eq. (1)
numerically by following individual light paths through a large
number of cells containing galaxies and intergalactic dust. Through
each cell the background cosmology, the wavelength of the photon and the
dust density were updated, and the contributions from each cell added. Note that the model is
approximately valid also for a patchy dust distribution,
as long as the scale of
inhomogeneities is small enough, i.e.,
![]() where N is the
number of
dust clouds intersected by the light-ray.
where N is the
number of
dust clouds intersected by the light-ray.
First we summarize the situation concerning the dependence of
the observed magnitudes on the cosmological background model, in
the absence of dust. Figure 2 shows the magnitude difference
for three cosmologies,
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3090F2.eps} \end{figure}](/articles/aa/full/2002/10/aah3090/Timg40.gif) |
Figure 2:
Differential magnitude for three cosmologies,
|
| Open with DEXTER | |
Turning now to extinction due to a homogeneous component of dust, we consider in this work the following scenarios:
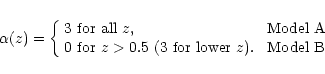
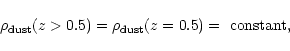
A more detailed
calculation would make use of an explicit model for the past star formation
rate. However, the predicted evolution of the comoving density between, say,
![]() and
and ![]() corresponds
to less than around a factor of 2 (Madau 2000).
corresponds
to less than around a factor of 2 (Madau 2000).
In Fig. 3,
![\begin{figure}
\par\includegraphics[width=8cm,clip]{H3090F3_a}\\ [4mm]
\includegraphics[width=8cm,clip]{H3090F3_b} \end{figure}](/articles/aa/full/2002/10/aah3090/Timg50.gif) |
Figure 3:
Differential magnitude for three cosmologies,
|
| Open with DEXTER | |
Clearly, accurate spectrophotometric data from a statistical sample of supernovae at this redshift are needed to settle the issue, as described below.
In order to quantify the induced differential spectral shift due to large dust grains
we introduce two quantities: R1 and R2.
R1 is the magnitude difference
in extinction between
![]() and 1.0
and 1.0 ![]() m.
R2 measures the differential extinction between
m.
R2 measures the differential extinction between
![]() and 1.5
and 1.5 ![]() m,
as shown in Fig. 4 for a source at z=1.
m,
as shown in Fig. 4 for a source at z=1.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{H3090F4.eps} \end{figure}](/articles/aa/full/2002/10/aah3090/Timg53.gif) |
Figure 4:
Monte-Carlo simulation of the differential extinction between
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=10.7cm,width=4.2cm,clip]{H3090F5_a.ep...
...mm}
\includegraphics[height=10.7cm,width=4.2cm,clip]{H3090F5_b.eps} \end{figure}](/articles/aa/full/2002/10/aah3090/Timg54.gif) |
Figure 5:
Dust extinction in model B for RV=5.5 (left side) and RV=9.5 (right side)
in a flat (
|
| Open with DEXTER | |
The rationale for introducing R1 and R2 is twofold: 1) the color dependence
is almost linear in the range between
![]() and 1.5
and 1.5 ![]() m. 2) R1 and R2can be measured within the sensitive range of an infrared (HgCdTe) detector. R1 can
also be measured with a CCD detector.
m. 2) R1 and R2can be measured within the sensitive range of an infrared (HgCdTe) detector. R1 can
also be measured with a CCD detector.
The idea of Aguirre (1999a,1999b) was to explain the faintness of high-z type Ia supernovae without invoking a "Dark Energy'' component. In such a scenario, an extinction of 0.2-0.5 mag is required to reconcile the supernova data with either an open or flat universe without a cosmological constant. Although perfectly grey dust (i.e., with wavelength-independent absorption) with a fine-tuned redshift distribution possibly can mimick the effects of a cosmological constant, we want to investigate here whether a more natural dust model can do the same. The point to make is that realistic dust firstly has to be related to astrophysical sources, such as star formation, and secondly that it always implies some wavelength-dependence in the absorption and scattering properties.
Figure 5 shows the magnitude and differential
extinction as a function of source redshift for model B and RV=5.5and 9.5 in a flat universe without cosmological constant.
The color
terms for the highest redshifts are
![]() and
and
![]() ,
i.e., clearly measurable with a population of SNe as expected
for the proposed SNAP
satellite. Figure 6 shows the color
extinction (at maximum intensity) in V-J,
,
i.e., clearly measurable with a population of SNe as expected
for the proposed SNAP
satellite. Figure 6 shows the color
extinction (at maximum intensity) in V-J,
![\begin{figure}
\par\includegraphics[height=10.7cm,width=4.2cm,clip]{H3090F6_a.ep...
...{4mm}\includegraphics[height=10.7cm,width=4.2cm,clip]{H3090F6_b.eps}\end{figure}](/articles/aa/full/2002/10/aah3090/Timg57.gif) |
Figure 6:
Color extinctions E(V-J), E(R-J) and E(I-J) for type Ia supernovae in dust model B
for RV=5.5 (left side) and RV=9.5 (right side)
in a flat (
|
| Open with DEXTER | |
Figure 7 shows the effects of dust extinction in an open universe
for RV=5.5 and 9.5 where the dust density has been adjusted to fit the
observational constraints at ![]() .
.
![\begin{figure}
\par\includegraphics[height=11.4cm,width=4.2cm,clip]{H3090F7_a.ep...
...mm}
\includegraphics[height=11.4cm,width=4.2cm,clip]{H3090F7_b.eps} \end{figure}](/articles/aa/full/2002/10/aah3090/Timg58.gif) |
Figure 7:
Dust extinction in model A for RV=5.5 (left side) and RV=9.5 (right side)
in an open (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=10.6cm,width=4.2cm,clip]{H3090F8_a.ep...
...mm}
\includegraphics[height=10.6cm,width=4.2cm,clip]{H3090F8_b.eps}\end{figure}](/articles/aa/full/2002/10/aah3090/Timg60.gif) |
Figure 8:
Color extinctions E(V-J), E(R-J) and E(I-J) for type Ia supernovae in dust model A
for RV=5.5 (left side) and RV=9.5 (right side)
in an open (
|
| Open with DEXTER | |
Figures 9 and 10 show the effect of
extinction in an open universe with dust model B.
![\begin{figure}
\par\includegraphics[height=10.4cm,width=4.2cm,clip]{H3090F9_a.ep...
...4mm}\includegraphics[height=10.4cm,width=4.2cm,clip]{H3090F9_b.eps} \end{figure}](/articles/aa/full/2002/10/aah3090/Timg61.gif) |
Figure 9:
Dust extinction in model B for RV=5.5 (left side) and RV=9.5 (right side)
in an open (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=10.4cm,width=4.2cm,clip]{H3090F10_a.e...
...mm}
\includegraphics[height=10.4cm,width=4.2cm,clip]{H3090F10_b.eps}\end{figure}](/articles/aa/full/2002/10/aah3090/Timg62.gif) |
Figure 10:
Color extinctions E(V-J), E(R-J) and E(I-J) for type Ia supernovae in dust model B
for RV=5.5 (left side) and RV=9.5 (right side)
in an open (
|
| Open with DEXTER | |
Next, we consider the scenario where the extinction due to dust is negligible at
![]() but that it may introduce a bias in the Hubble diagram in excess of
but that it may introduce a bias in the Hubble diagram in excess of
![]() for
for ![]() .
Thus, we consider a universe where
.
Thus, we consider a universe where
![]() and
and
![]() ,
e.g.
Figs. 11 and 12 show a case in dust model A.
,
e.g.
Figs. 11 and 12 show a case in dust model A.
![\begin{figure}
\par\includegraphics[height=10.6cm,width=4.2cm,clip]{H3090F11_a.e...
...m}
\includegraphics[height=10.6cm,width=4.2cm,clip]{H3090F11_b.eps} \end{figure}](/articles/aa/full/2002/10/aah3090/Timg67.gif) |
Figure 11:
Dust extinction in model A for RV=5.5 (left side) and RV=9.5 (right side)
in a flat |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=10.6cm,width=4.2cm,clip]{H3090F12_a.e...
...mm}
\includegraphics[height=10.6cm,width=4.2cm,clip]{H3090F12_b.eps}\end{figure}](/articles/aa/full/2002/10/aah3090/Timg68.gif) |
Figure 12:
Color extinctions E(V-J), E(R-J) and E(I-J) for type Ia supernovae in dust model A
for RV=5.5 (left side) and RV=9.5 (right side)
in a flat |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=9.8cm,width=4.2cm,clip]{H3090F13_a.ep...
...mm}
\includegraphics[height=9.8cm,width=4.2cm,clip]{H3090F13_b.eps} \end{figure}](/articles/aa/full/2002/10/aah3090/Timg70.gif) |
Figure 13:
Dust extinction in model B for RV=5.5 (left side) and RV=9.5 (right side)
in a flat |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=9.8cm,width=4.2cm,clip]{H3090F14_a.ep...
...{4mm}\includegraphics[height=9.8cm,width=4.2cm,clip]{H3090F14_b.eps}\end{figure}](/articles/aa/full/2002/10/aah3090/Timg71.gif) |
Figure 14:
Color extinctions E(V-J), E(R-J) and E(I-J) for type Ia supernovae in dust model B
for RV=5.5 (left side) and RV=9.5 (right side)
in a flat |
| Open with DEXTER | |
The "greyness'' of r>100 nm dust grains make them completely undetectable with colors bluer than R-band in the restframe system. However, for longer wavelengths the extinction leaves a measurable signature in the observed V-J, R-J and I-J. This indicates that the average V-J, R-J and I-J colors of normal type Ia supernovae are significantly different with and without the extinction due to large dust grains.
As dust in galaxies is generally known to cause more reddening than the hypothetical extragalactic "grey'' component, intervening galaxies along the line of sight cause less potential danger. Still, it may be of interest to estimate the frequency and size of such encounters. In order to estimate the effects from dust due to intervening galaxies, we have thus performed a number of ray-tracing Monte-Carlo simulations. We follow a light-ray between the source and the observer by sending the ray through a series of spherical cells. Each cell encompasses a galaxy at the center and the size of the cell is computed to accurately represent the number density of galaxies, see (Goobar et al. 2002) for a more detailed description of the Monte-Carlo method.
In Fig. 15 we have plotted the smallest galaxy impact parameters for
10000 light-rays originating at redshifts
z=0.5, z=1 and
z=1.5 in a ![]() -dominated universe, (
-dominated universe, (
![]() ,
,
![]() ,
0.7).
,
0.7).
| |
Figure 15:
The distribution of smallest galaxy impact parameters for 10000 sources at
redshifts z=0.5 (dotted line), z=1 (dashed line) and z=1.5 (full line) in a |
| Open with DEXTER | |
In order to estimate the magnitude of the effect, we model
the dust distribution in spiral galaxies by a double exponential disk with random
inclination,
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{H3090F16.eps} \end{figure}](/articles/aa/full/2002/10/aah3090/Timg79.gif) |
Figure 16: The correlation of the demagnification due to dust and the magnification due to gravitational lensing for the 33 out of 10000 sources at z=1 which are demagnified more than 0.02 mag by intervening galactic dust for an extinction scale-length at the galaxy centers of 1 kpc. To obtain the demagnification for an arbitrary scale-length, divide the numbers on the x-axis with the scale-length expressed in kpc. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{H3090F17.eps} \end{figure}](/articles/aa/full/2002/10/aah3090/Timg80.gif) |
Figure 17:
The demagnification due to dust in the host galaxy.
For an extinction scale-length of 1 kpc, |
| Open with DEXTER | |
Type Ia supernovae occur in both late and early type galaxies. In the case of
late type hosts, we need to take obscuration due to dust in the host galaxy
into account. We model the distribution of dust in late type host according to
Eq. (3), and the generation of type Ia SNe as two different components,
following (Hatano et al. 1998).
In the disk component, the generation of type Ia SNe follows the dust distribution
only that the scale-length in the ![]() -direction is increased to 0.35 kpc. There
is also a bulge component where the SNe are spherically distributed as
(R3+0.73)-1, where the distance from galactic center, R,
is expressed in kpc and the bulge is truncated
at 3 kpc. We assume that the probability
for a SNe to occur in the bulge is 1/8 of the probability in the disk.
Following (Matteucci & Recchi 2001), we estimate the probability for a type Ia SNe to occur in an
early type galaxy to be
-direction is increased to 0.35 kpc. There
is also a bulge component where the SNe are spherically distributed as
(R3+0.73)-1, where the distance from galactic center, R,
is expressed in kpc and the bulge is truncated
at 3 kpc. We assume that the probability
for a SNe to occur in the bulge is 1/8 of the probability in the disk.
Following (Matteucci & Recchi 2001), we estimate the probability for a type Ia SNe to occur in an
early type galaxy to be
The effects of grey dust extinction capable of biasing the results of experiments such as
the proposed SNAP satellite can be diagnosed through accurate relative spectrophotometry or
broadband photometry at the 1%
level in the 0.7-1.5 ![]() m wavelength range, as shown in e.g.
Figs. 13 and 14. This would allow tests
for intergalactic dust obscuration
affecting the measurement of high-z supernovae up to
m wavelength range, as shown in e.g.
Figs. 13 and 14. This would allow tests
for intergalactic dust obscuration
affecting the measurement of high-z supernovae up to
![]() ,
the target for
systematic uncertainties for SNAP.
,
the target for
systematic uncertainties for SNAP.
Achieving 1-2% relative spectrophotometric accuracy in the optical and
NIR for 22-29 mag objects is rather challenging. As the
measurements will rely on a large number of homogeneous high-redshift
sources, it is not required to get S/N=50-100 for individual
objects. On the other hand, the instrument calibration must be within
1% over the course of at least one year for the case of SNAP. This
can be accomplished e.g. through repeated observations of hot galactic
white dwarfs (Bohlin 1996; Finley et al. 1997).
In the Rayleigh-Jeans limit,
![]() K, the color of the calibrators
become independent of temperature and are therefore ideal for relative
calibration.
K, the color of the calibrators
become independent of temperature and are therefore ideal for relative
calibration.
Significant progress in examining the possible bias due to grey dust in the
published type Ia supernova Hubble diagram can already be made with existing NIR
instruments.
If the faintness of type Ia SNe at high-z is to be
attributed to grey dust obscuration as opposed to the cosmological
explanation a color extinction
![]() mag is
to be expected for sources at
mag is
to be expected for sources at
![]() .
Testing this possibility is within reach with ground based
facilities.
.
Testing this possibility is within reach with ground based
facilities.
We have also examined the possibility of extinction as the beam of high redshift passes through foreground galaxies. This was found to be a relatively small effect, only causing >0.02 mag dimming for less than 1% of the sources at z=1, whereas extinction in the host galaxy potentially is a more serious problem.
However, in general we expect dust in galaxies along the line of sight and
in host galaxies to have ![]() ,
causing considerably more reddening than an
intergalactic "grey" dust component. Thus, with high accuracy spectrophotometry,
it should be possible to control the effects from extinction in galaxies.
,
causing considerably more reddening than an
intergalactic "grey" dust component. Thus, with high accuracy spectrophotometry,
it should be possible to control the effects from extinction in galaxies.
Acknowledgements
The authors would like to thank Anthony Aguirre, Alex Kim, and Peter Nugent for useful discussions and Serena Nobili for a careful reading of the manuscript. AG is a Royal Swedish Academy Research Fellow supported by a grant from the Knut and Alice Wallenberg Foundation. LB would like to thank the Swedish Research Council for financial support.