Retrograde waves with frequencies much lower than the rotation frequency become trapped in the solar radiative interior. The eigenfunctions of the compressible, nonadiabatic (
A&A 384, 282-298 (2002)
DOI: 10.1051/0004-6361:20011836
N. S. Dzhalilov1,2 - J. Staude2 - V. N. Oraevsky1
1 - Institute of Terrestrial Magnetism,
Ionosphere and Radio Wave Propagation of the Russian Academy of Sciences,
Troitsk City, Moscow Region 142190, Russia
2 - Astrophysikalisches Institut Potsdam, Sonnenobservatorium Einsteinturm,
14473 Potsdam, Germany
Received 27 June 2001 / Accepted 20 December 2001
Abstract
Retrograde waves with frequencies much lower than the rotation frequency
become trapped in the solar radiative interior. The eigenfunctions of the
compressible, nonadiabatic (![]() -mechanism and radiative losses taken
into account) Rossby-like modes are obtained by an asymptotic method assuming
a very small latitudinal gradient of the rotation rate. An integral
dispersion relation for the complex eigenfrequencies is derived as a
solution of the boundary value problem. The discovered resonant cavity modes
(called R-modes) are fundamentally different from the known r-modes:
their frequencies are functions of the solar interior structure, and the
reason for their existence is not related to geometrical effects. The most
unstable R-modes are those with periods of
-mechanism and radiative losses taken
into account) Rossby-like modes are obtained by an asymptotic method assuming
a very small latitudinal gradient of the rotation rate. An integral
dispersion relation for the complex eigenfrequencies is derived as a
solution of the boundary value problem. The discovered resonant cavity modes
(called R-modes) are fundamentally different from the known r-modes:
their frequencies are functions of the solar interior structure, and the
reason for their existence is not related to geometrical effects. The most
unstable R-modes are those with periods of ![]() 1-3yr, 18-30yr,
and 1500-20000yr; these three separate period ranges are known from
solar and geophysical data. The growing times of those modes which are
unstable with respect to the
1-3yr, 18-30yr,
and 1500-20000yr; these three separate period ranges are known from
solar and geophysical data. The growing times of those modes which are
unstable with respect to the ![]() -mechanism are
-mechanism are ![]() 102, 103,and 105 years, respectively. The amplitudes of the R-modes are growing
towards the center of the Sun. We discuss some prospects to develop the
theory of R-modes as a driver of the dynamics in the convective zone which
could explain, e.g., observed short-term fluctuations of rotation, a control
of the solar magnetic cycle, and abrupt changes of terrestrial climate in the
past.
102, 103,and 105 years, respectively. The amplitudes of the R-modes are growing
towards the center of the Sun. We discuss some prospects to develop the
theory of R-modes as a driver of the dynamics in the convective zone which
could explain, e.g., observed short-term fluctuations of rotation, a control
of the solar magnetic cycle, and abrupt changes of terrestrial climate in the
past.
Key words: hydrodynamics - Sun: activity - Sun: interior - Sun: oscillations - Sun: rotation
The 22-year magnetic cycle of solar activity is the most prominent
phenomenon of several large-scale dynamic events that occur in the Sun.
(Really, the magnetic half cycles or sunspot number cycles vary in length
between 9-13 years, and 11 yr is an average of the ![]() 20 half-cycles
available.) An explanation of the basic mechanism underlying this fameous
phenomenon is the fundamental challenge of solar physics. The achievements of
the theory of the
20 half-cycles
available.) An explanation of the basic mechanism underlying this fameous
phenomenon is the fundamental challenge of solar physics. The achievements of
the theory of the ![]() -
-![]() dynamo turned out to be a great success.
However, neither all observations of magnetic and flow fields nor the
radiation fluxes which are related to this phenomenon and which are measured
at the surface of the Sun or indirectly, by helioseismology, in its interior,
can be explained unambigously in this way. Although our present work is not
directly related to the dynamo theory, we will outline here those
difficulties which have common points with our results.
dynamo turned out to be a great success.
However, neither all observations of magnetic and flow fields nor the
radiation fluxes which are related to this phenomenon and which are measured
at the surface of the Sun or indirectly, by helioseismology, in its interior,
can be explained unambigously in this way. Although our present work is not
directly related to the dynamo theory, we will outline here those
difficulties which have common points with our results.
As a consequence of our imperfect knowledge of basic characteristics of turbulent convection as well as meridional circulation and details of the rotation of the Sun's interior, the solutions of the dynamo equations become functions of many free, unknown parameters (e.g. Stix 1976). For instance, by clever combinations of these parameters it is possible to get from kinematic theory an oscillatory magnetic field with a 22-year period and a growing amplitude. However, another choice of these parameters leads to waves of growing amplitude for other periods. So one could draw a butterfly diagram not only with an 11-year periodicity. It remains still an open question which of the clever combinations resulting in a solar-like 22-year activity cycle is realized in the Sun. We could not find a work on the dynamo wave problem, showing that just the 22-year period is preferred among others with a maximum growth rate and with the spatial scales required for solar activity. Instead, many authors pointed out that the cycle period of 22 years is hard to explain (Stix 1991; Gilman 1992; Levy 1992; Schmitt 1993; Brandenburg 1994; Weiss 1994; Rüdiger & Arlt 2000).
From the solution of the inverse problem of helioseismology (e.g. Tomczyk et al. 1995)
it is known that the convective envelope of the Sun is rotating
with a latitude dependence of the angular velocity similar to that of the
surface but almost rigid in radial direction. A stronger radial gradient
which is required for the ![]() -
-![]() dynamo mechanism is located in a
shallow layer (thickness
dynamo mechanism is located in a
shallow layer (thickness ![]()
![]() (Kosovichev 1996), where
(Kosovichev 1996), where
![]() is the solar radius) immediately below the convective zone -
the tachocline (Spiegel & Zahn 1992). Below the tachocline up to a depth of
at least
is the solar radius) immediately below the convective zone -
the tachocline (Spiegel & Zahn 1992). Below the tachocline up to a depth of
at least
![]() the radiative interior is rotating with an angular
velocity law similar to that of a solid-body. The question arises: what
compels the Sun to rotate in such a strange manner, which is different from
the generally accepted, theoretically predicted stable rotation law? How to
handle a dynamo theory for which the "
the radiative interior is rotating with an angular
velocity law similar to that of a solid-body. The question arises: what
compels the Sun to rotate in such a strange manner, which is different from
the generally accepted, theoretically predicted stable rotation law? How to
handle a dynamo theory for which the "![]() " area is separated from the
"
" area is separated from the
"![]() " area over a large part of the extent of the convective zone? In
order to solve this problem Parker (1993) has put forward the idea of an
interface dynamo, the basic features of which existed already in earlier
dynamo models (Steenbeck et al. 1966). To close the cycle of such a stretched
dynamo it is necessary to have some mechanism delivering toroidal magnetic
flux, arising by the shear of differential axisymmetric rotation (Cowling 1953)
in the tachocline, to the "
" area over a large part of the extent of the convective zone? In
order to solve this problem Parker (1993) has put forward the idea of an
interface dynamo, the basic features of which existed already in earlier
dynamo models (Steenbeck et al. 1966). To close the cycle of such a stretched
dynamo it is necessary to have some mechanism delivering toroidal magnetic
flux, arising by the shear of differential axisymmetric rotation (Cowling 1953)
in the tachocline, to the "![]() " dynamo area (e.g. Moffatt 1978; Krause &
Rädler 1980). To get a solar-like magnetic activity it is necessary to
suppose the existence of a huge (
" dynamo area (e.g. Moffatt 1978; Krause &
Rädler 1980). To get a solar-like magnetic activity it is necessary to
suppose the existence of a huge (![]() 105G) toroidal magnetic field
to create enough magnetic buouancy for the leakage of magnetic flux and to
solve the tilt problem of lifting loops (e.g. Caligari et al. 1998).
Moreover, a high magnetic diffusivity contrast between the convective
envelope and the underlying radiative core should be assumed to solve the
quenching problem of the
105G) toroidal magnetic field
to create enough magnetic buouancy for the leakage of magnetic flux and to
solve the tilt problem of lifting loops (e.g. Caligari et al. 1998).
Moreover, a high magnetic diffusivity contrast between the convective
envelope and the underlying radiative core should be assumed to solve the
quenching problem of the ![]() effect (see, e.g., Fan et al. 1993;
Cattaneo & Hughes 1996). However, it is a major challenge for any dynamo
model to produce such strong fields.
effect (see, e.g., Fan et al. 1993;
Cattaneo & Hughes 1996). However, it is a major challenge for any dynamo
model to produce such strong fields.
The idea of the interface dynamo was further developed, e.g. by Charbonneau & MacGregor (1997). Later, a fit to the real solar rotation profile with its latitudinal and radial dependencies has been included by Markiel & Thomas (1999), but so far no satisfactory solar-like oscillatory solutions for the interface dynamo have been found. Growing wave solutions are suppressed by the latitudinal shear.
Mechanisms for braking the solar internal rotation are also under discussion. The character of the core rotation is not clear because here the accuracy of helioseismic inversions gets worse (Chaplin et al. 1999) and the results seem to be in contradiction with the oblateness measurements (Paterno et al. 1996). There are some suggestions that a deceleration of the radiative interior depends on the transport of angular momentum between this region and the convective zone. For instance, Mestel & Weiss (1987) supposed that even a weak large-scale magnetic field would be sufficient to couple very efficiently the interior and the convective zone, leading essentially to solid body rotation. In this way the magnetic torques can also extract angular momentum from the radiative interior (e.g. Charbonneau & MacGregor 1993).
The wave mechanism for the solution of this problem is more popular.
Schatzman (1993), Zahn et al. (1997), and Kumar & Quataert (1997) have
concluded that the solid rotation of the radiative interior is a direct
consequence of the effect of internal gravity waves. Gravity waves generated
near the interface between the convective and radiative regions transport
retrograde angular momentum into the interior, thereby spinning it down. Here
the main idea is that the isotropically generated gravity waves become
anisotropic due to Doppler shifts of frequencies in the differentially
rotating Sun. In that way for anisotropic retrograde and prograde waves the
radiative damping is different, and the residual negative angular wave
momentum may compel the solar radiative interior to co-rotate with the
convective zone. This idea has been further developed by Kumar et al. (1999)
including a toroidal magnetic field to explain the existence of the unstable
shear layer "tachocline". However, Ringot (1998) has shown that a quasi-solid
rotation of the radiative interior cannot be a direct consequence of the
action of internal gravity waves produced in the convective zone. Gough
(1997) questioned this idea emphasizing that the mechanism can work only if
the waves are generated with strong amplitudes to transport the required
angular momentum. This means, resonance waves are required, but such waves
may penetrate only to distances less than
![]() beneath the
convective zone due to the strong radiative damping. These waves must deposit
their angular momentum before returning to the convective zone, but not
before penetrating far into the radiative interior.
beneath the
convective zone due to the strong radiative damping. These waves must deposit
their angular momentum before returning to the convective zone, but not
before penetrating far into the radiative interior.
For the wave mechanism the question of an anisotropic propagation relative to the azimuthal rotation is a key moment. Fritts et al. (1998) have shown that convection, penetrating into the stratified and strongly sheared tachocline, can produce preferentially propagating gravity waves.
There have also been speculations that the rotation of the core may be variable, perhaps with a time scale of the solar cycle (e.g. Gough 1985). The present paper is along these lines.
From our short discussion we conclude that the convective envelope and the radiative interior are coupled to each other through a certain global agent, resulting in almost co-rotation. To advance the solution of the problem the dynamo theory should take into account the presence of this global agent. We suppose that really this agent is provided by waves with the following properties:
Waves should represent large-scale global eigenoscillations of the Sun. Their origin must be related to rotation, they must be strongly anisotropic with respect to the azimuthal angle. Looking at the characteristics of the solar cycle we immediately see the high coherency of these global motions (the constant periods, phase shifts, amplitudes, the latitude appearence, etc.). Activity grows in the first phase with a timescale which is considerably shorter than the decay time in the second phase; this fact and the quick eruptive release of energy by the reconnection mechanism indicate that the waves must be unstable.
It is noteworthy that the inner gravity waves do not fulfill these requirements. The quesion is whether the r-modes do?
In a non-rotating sphere (![]() ,
where
,
where ![]() is the angular frequency
of solar rotation) the wave motion is subdivided into two non-coupling
components: spheroidal p-, f- and g-modes (for which the main restoring
forces are pressure gradient and buouancy) and toroidal modes (e.g. Unno
et al. 1989). Toroidal modes are degenerated horizontal eddy motions confined
to a spherical surface with a radius r for which
is the angular frequency
of solar rotation) the wave motion is subdivided into two non-coupling
components: spheroidal p-, f- and g-modes (for which the main restoring
forces are pressure gradient and buouancy) and toroidal modes (e.g. Unno
et al. 1989). Toroidal modes are degenerated horizontal eddy motions confined
to a spherical surface with a radius r for which ![]() ,
,
![]() ,
and
,
and
![]() .
Here
Yml is the spherical harmonic with a degree l and order m,
.
Here
Yml is the spherical harmonic with a degree l and order m, ![]() is the colatitude,
is the colatitude, ![]() is the azimuthal angle in the spherical polar
coordinates,
is the azimuthal angle in the spherical polar
coordinates, ![]() is the fluid velocity field,
is the fluid velocity field, ![]() is the angular
frequency of the fluid motion, and Qml(r) is an arbitrary amplitude
function. Toroidal modes have zero radial velocity but have non-zero radial
vorticity,
is the angular
frequency of the fluid motion, and Qml(r) is an arbitrary amplitude
function. Toroidal modes have zero radial velocity but have non-zero radial
vorticity,
![]() (for the spheroidal modes it is vice
versa). These modes do not alter the equilibrium configuration.
(for the spheroidal modes it is vice
versa). These modes do not alter the equilibrium configuration.
When a slow rotation (
![]() )
is included the spheroidal
modes are slightly modified but they keep their main properties. Degeneracy
of toroidal modes is removed only partially by the rotation, and
quasi-toroidal waves - known as r-modes - appear with a non-zero
frequency of
)
is included the spheroidal
modes are slightly modified but they keep their main properties. Degeneracy
of toroidal modes is removed only partially by the rotation, and
quasi-toroidal waves - known as r-modes - appear with a non-zero
frequency of
![]() in the rotating frame
(Papaloizou & Pringle 1978; Brayn 1889). Usually the governing equations of
the r-modes are obtained by expanding the initial physical variables of the
equations in the rotating system into power series with respect to the small
parameter
in the rotating frame
(Papaloizou & Pringle 1978; Brayn 1889). Usually the governing equations of
the r-modes are obtained by expanding the initial physical variables of the
equations in the rotating system into power series with respect to the small
parameter
![]() (
(![]() 10-4.7 for the Sun, e.g.
Papaloizou & Pringle 1978; Provost et al. 1981; Smeyers et al. 1981; Saio
1982). These power series practically describe the deviation of the
surface of the star from its initial spherical state, resulting from rotation
through Coriolis and centrifugal forces. As a result of the deformation of
the spherical surface with a radius r the radial vorticity of the toroidal
modes cause a surface pressure perturbation through the Coriolis force.
However, the r-modes practically keep the main properties of toroidal
flows:
10-4.7 for the Sun, e.g.
Papaloizou & Pringle 1978; Provost et al. 1981; Smeyers et al. 1981; Saio
1982). These power series practically describe the deviation of the
surface of the star from its initial spherical state, resulting from rotation
through Coriolis and centrifugal forces. As a result of the deformation of
the spherical surface with a radius r the radial vorticity of the toroidal
modes cause a surface pressure perturbation through the Coriolis force.
However, the r-modes practically keep the main properties of toroidal
flows:
![]() ,
,
![]() .
The degeneracy of the r-modes is that their frequencies hardly depend
on Qml(r), i.e. they are independent from the inner structure of the
star. For the l=1 modes the frequency in the inertial system is again close
to zero,
.
The degeneracy of the r-modes is that their frequencies hardly depend
on Qml(r), i.e. they are independent from the inner structure of the
star. For the l=1 modes the frequency in the inertial system is again close
to zero,
![]() (Papaloizou & Pringle 1978). The r-mode
equations define the amplitudes Qml(r), and taking into account the next
terms with small
(Papaloizou & Pringle 1978). The r-mode
equations define the amplitudes Qml(r), and taking into account the next
terms with small
![]() in the series practically does not
change the frequencies.
in the series practically does not
change the frequencies.
Due to the fact that the r-modes are practically surface deformation waves,
some similarity of these waves to the surface gravity waves or to the
f-modes is apparent. For high l the f-modes are an analogy to surface
gravity waves in a plane-parallel fluid with
![]() .
In the
Cowling approximation f-modes with l=1 have zero frequency too,
.
In the
Cowling approximation f-modes with l=1 have zero frequency too,
![]() (Unno et al. 1989). This corresponds to a parallel
displacement of the whole star. For high l the f-mode frequencies are
also independent of the inner structure, with
(Unno et al. 1989). This corresponds to a parallel
displacement of the whole star. For high l the f-mode frequencies are
also independent of the inner structure, with
![]() (Gough 1980). So, r-modes are also fundamental rotating modes with an
inertial frequency,
(Gough 1980). So, r-modes are also fundamental rotating modes with an
inertial frequency,
![]() .
.
For the Sun the properties of r-modes have been investigated in great detail by Wolff et al. (1986) and Wolff (1998, 2000; and Refs. therein).
Some properties of the r-modes are also similar to those of the Rossby
waves in geophysics (Pedlosky 1982). Similar to the Rossby waves and unlike
the g-modes the r-modes are strongly anisotropic. They propagate only in
azimuthal direction, opposite to rotation (i.e. they are retrograde waves in
the co-rotating frame). Because we are interested in length scales
corresponding to those of large sunspots, we have to
consider r-modes with
![]() .
To get oscillations with periods of
years (
.
To get oscillations with periods of
years (
![]() )
we must choose
)
we must choose
![]() ,
just
such r-modes are physically more interesting (Lockitch & Friedman 1999).
However, in the case of high l the amplitudes of the r-modes will be
concentrated near the surface of the Sun (Provost et al. 1981; Wolff 2000),
and so they can actively interact with convective motions (Wolff 1997, 2000).
Because for these modes
,
just
such r-modes are physically more interesting (Lockitch & Friedman 1999).
However, in the case of high l the amplitudes of the r-modes will be
concentrated near the surface of the Sun (Provost et al. 1981; Wolff 2000),
and so they can actively interact with convective motions (Wolff 1997, 2000).
Because for these modes
![]() and
and
![]() ,
their chance to take part in the redistribution of angular rotation momentum
in the radiative interior is low. Note that the slow solar differential rotation does
not change the behavior of such r-modes with
,
their chance to take part in the redistribution of angular rotation momentum
in the radiative interior is low. Note that the slow solar differential rotation does
not change the behavior of such r-modes with ![]() (Wolff 1998).
(Wolff 1998).
Looking for further analogies between waves connected with gravity and with
rotation, we remember that beside the surface gravity waves there exist
internal gravity waves with
![]() ,
the
frequencies of which depend on the inner structure (N is the
Brunt-Väisälä frequency). Similar to these waves there exist "true"
Rossby (not deformation) waves, the frequency of which depends also on
the internal structure.
,
the
frequencies of which depend on the inner structure (N is the
Brunt-Väisälä frequency). Similar to these waves there exist "true"
Rossby (not deformation) waves, the frequency of which depends also on
the internal structure.
We include here a short review on the main features of Rossby waves; they have
been investigated in great detail in geophysics (e.g. Pedlosky 1982; Gill 1982).
In the simplest case, that is in a plane-parallel, homogeneous, rotating
layer, the dispersion relation for the Rossby waves is
![]() .
Here kx is the wave number
perpendicular to the rotation axis, kz is expressed by the internal
deformation radius of Rossby which depends on the Brunt-Väisälä
frequency,
.
Here kx is the wave number
perpendicular to the rotation axis, kz is expressed by the internal
deformation radius of Rossby which depends on the Brunt-Väisälä
frequency, ![]() is the transverse gradient (in y direction) of the
Coriolis parameter: a vertical component of the "planetary" vorticity
is the transverse gradient (in y direction) of the
Coriolis parameter: a vertical component of the "planetary" vorticity
![]() in the given local point. Unlike the r-modes the Rossby wave
frequencies are functions of the internal structure and have maximum
dependence on the gradient
in the given local point. Unlike the r-modes the Rossby wave
frequencies are functions of the internal structure and have maximum
dependence on the gradient ![]() :
:
![]() if
if ![]() and if
and if
![]() .
.
Any disturbance of the local flow in a rotating frame may generate waves of
the Rossby type. These waves exist only if there is a gradient of the
potential vorticity
![]() .
Here an absolute vorticity is the sum of the relative and the planetary
vorticities,
.
Here an absolute vorticity is the sum of the relative and the planetary
vorticities,
![]() ,
,
![]() is any
conserved scalar quantity,
is any
conserved scalar quantity,
![]() (for instance, for adiabatic
motion that could be the entropy or the density in the case of
incompressible plasma). The Rossby wave motion is a solution of the
nonlinear equation for transport of
(for instance, for adiabatic
motion that could be the entropy or the density in the case of
incompressible plasma). The Rossby wave motion is a solution of the
nonlinear equation for transport of ![]() .
The potential vorticity is
conserved if the medium is barotropic (
.
The potential vorticity is
conserved if the medium is barotropic (
![]() )
and if
there are no torques. The rotation of the frame is added to any vorticity in
the velocity field. Any motion within a rotating fluid serves as a potential
source for vorticity.
)
and if
there are no torques. The rotation of the frame is added to any vorticity in
the velocity field. Any motion within a rotating fluid serves as a potential
source for vorticity.
The relative vorticity may be evoked by the geometrical surface as well as by
internal gradients. It depends on the choice of the function
![]() and on
and on
![]() .
For example, an
unevenness of the ocean bottom causes the topographic Rossby waves, or a
dependence of the Coriolis parameter on the earth latitude
(
.
For example, an
unevenness of the ocean bottom causes the topographic Rossby waves, or a
dependence of the Coriolis parameter on the earth latitude
(
![]() ,
where
,
where ![]() is the geographic latitude)
is the main cause of atmospheric Rossby waves.
is the geographic latitude)
is the main cause of atmospheric Rossby waves.
In the solar dynamo context the ability of Rossby waves to induce solar-like magnetic fields has been considered by Gilman (1969). Here the mechanism for sustaining the Rossby waves is a latitudinal temperature gradient in a thin, rotating, incompressible convective zone. To interpret the dynamical features of large-scale magnetic fields the Rossby vorticies excited within a thin layer beneath the convective zone are considered by Tikhomolov & Mordvinov (1996) as the result of a deformation of the lower boundary of the convective zone.
From the discussion in Sect. 1.4 we conclude that just Rossby-like waves
could be suitable for our requirements. As the main driving mechanism we
choose a latitudinal (or horizontal) differential rotation,
![]() .
Baker & Kippenhahn (1959) have pointed out
that the uniform rotation of a star is not a typical case. Low frequencies
(periods of years) could easily be obtained searching for the
eigenoscillations of the Sun's radiative interior, where the gradient of the
rotation speed is close to zero (in accordance with the helioseismology
results). Large scales such as those associated with sunspots
(
.
Baker & Kippenhahn (1959) have pointed out
that the uniform rotation of a star is not a typical case. Low frequencies
(periods of years) could easily be obtained searching for the
eigenoscillations of the Sun's radiative interior, where the gradient of the
rotation speed is close to zero (in accordance with the helioseismology
results). Large scales such as those associated with sunspots
(
![]() )
decrease the frequencies too. Similar to the
r-modes the Rossby waves are strongly anisotropic (retrograde waves), but
unlike the r-modes these waves are concentrated close to the solar center.
These results have already been obtained by Oraevsky & Dzhalilov (1997), who
investigated the trapping of adiabatic, incompressible Rossby-like waves in
the solar interior. In the present work we take into account compressibility
for the nonadiabatic waves. We look for unstable waves. It is clear that the
necessary condition for the Kelvin-Helmholtz shear instability,
)
decrease the frequencies too. Similar to the
r-modes the Rossby waves are strongly anisotropic (retrograde waves), but
unlike the r-modes these waves are concentrated close to the solar center.
These results have already been obtained by Oraevsky & Dzhalilov (1997), who
investigated the trapping of adiabatic, incompressible Rossby-like waves in
the solar interior. In the present work we take into account compressibility
for the nonadiabatic waves. We look for unstable waves. It is clear that the
necessary condition for the Kelvin-Helmholtz shear instability,
![]() (Ando 1985), is not fulfilled in the
radiative interior. Then we decided to include the thermal
(Ando 1985), is not fulfilled in the
radiative interior. Then we decided to include the thermal
![]() -mechanism of
instability which is favoured at low frequencies (Unno et al. 1989). To
balance the
-mechanism of
instability which is favoured at low frequencies (Unno et al. 1989). To
balance the
![]() -mechanism the radiative losses in the diffusion regime are
included. To exclude all geometrical effects we ignore the influence of the
spherical surface at the given radius. The dispersion relation in the limit
of adiabatic incompressiblity and at very low frequencies is the same as that
for Rossby waves in geophysics. In order to distinguish these rotational body
waves from the r-modes we call them R-modes (Rossby rotation).
-mechanism the radiative losses in the diffusion regime are
included. To exclude all geometrical effects we ignore the influence of the
spherical surface at the given radius. The dispersion relation in the limit
of adiabatic incompressiblity and at very low frequencies is the same as that
for Rossby waves in geophysics. In order to distinguish these rotational body
waves from the r-modes we call them R-modes (Rossby rotation).
The governing fourth order equation is obtained from the basic equations in Sect.2. Some qualitative analysis of the wave cavity trapping is done for the simpler adiabatic case in Sect.3. Using the asymptotic solutions obtained in Sect.4 the complex boundary value problem is solved in Sect.5. The calculation of the eigenfrequencies and the instability analysis are done in Sect.6. The obtained unstable modes are shortly discussed in Sect.7.
Let us investigate global motions with large timescales such that the Rossby
number is small,
![]() .
Before the appearence of any
disturbances the basic stationary state of the rotating star is defined
mainly by the balance of pressure gradient, gravity force, and forces
exerted by the noninertiality of the motion (Coriolis and centrifugal forces).
In the case of an incompressible fluid with a homogeneous rotation rate
usually this state is called "geostrophic balance". A star disturbed by an
external force tends to return to this basic state. Our aim is to study for
the Sun the dynamics of small deviations from the steady geostrophic balance.
For this purpose it is natural to write the dynamic equations in a frame
rotating together with the Sun. The magnetic field will be ignored. For
arbitrary
.
Before the appearence of any
disturbances the basic stationary state of the rotating star is defined
mainly by the balance of pressure gradient, gravity force, and forces
exerted by the noninertiality of the motion (Coriolis and centrifugal forces).
In the case of an incompressible fluid with a homogeneous rotation rate
usually this state is called "geostrophic balance". A star disturbed by an
external force tends to return to this basic state. Our aim is to study for
the Sun the dynamics of small deviations from the steady geostrophic balance.
For this purpose it is natural to write the dynamic equations in a frame
rotating together with the Sun. The magnetic field will be ignored. For
arbitrary
![]() the equation of momentum in conventional
definitions is given by
the equation of momentum in conventional
definitions is given by
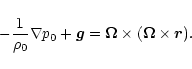
The next simplification of Eq. (2) is connected with the quasi-rigid
rotation of the inner part of the Sun below the convective zone, which
is known from the solution of the inverse problem of helioseismology. In this
case we can omit the third term of the l.h.s of Eq. (2). Such a
restriction of the gradients of
![]() requires to obey the
conditions:
requires to obey the
conditions:
The next equations are the mass and energy conservation equations in the
standard form:
In the limit of incompressible fluid,
![]() or
or
![]() ,
it follows from Eq. (6) that the condition
,
it follows from Eq. (6) that the condition
![]() is not needed to satisfy
is not needed to satisfy
![]() .
Hence, in a
dissipative (
.
Hence, in a
dissipative (
![]() ), incompressible fluid sound cannot propagate
instantaneously. It means,we cannot use the condition of
), incompressible fluid sound cannot propagate
instantaneously. It means,we cannot use the condition of
![]() to
get the incompressible limit for nonadiabatic waves.
to
get the incompressible limit for nonadiabatic waves.
Now we will try to simplify the energy loss function ![]() assuming
reasonable approximations for the Sun's interior. We use the formula for the
heat conductivity of a fully ionized gas to show that in the Sun radiative
transport of energy is more important than that by particle heat
conductivity:
assuming
reasonable approximations for the Sun's interior. We use the formula for the
heat conductivity of a fully ionized gas to show that in the Sun radiative
transport of energy is more important than that by particle heat
conductivity:
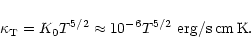
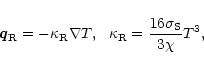 |
(7) |
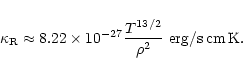
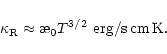
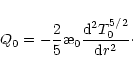 |
(9) |
Let us take an arbitrary point at the surface of the rotating sphere. The
position of this point is defined by its radius r, its co-latitude
![]() ,
and its azimuth angle. We assign to this point a local,
left-handed Cartesian system of coordinates
,
and its azimuth angle. We assign to this point a local,
left-handed Cartesian system of coordinates ![]() ,
where the
,
where the ![]() -axis is directed along the radius (local vertical), the direction of the
-axis is directed along the radius (local vertical), the direction of the
![]() -axis is meridional (towards the pole), and that of the
-axis is meridional (towards the pole), and that of the ![]() -axis
azimuthal. In this frame of reference
-axis
azimuthal. In this frame of reference
![]() .
Strictly speaking, the
.
Strictly speaking, the
![]() -axis coincides with the rotation axis only at the pole
(
-axis coincides with the rotation axis only at the pole
(
![]() ). In the case of a homogeneous fluid
). In the case of a homogeneous fluid ![]() is included into
the wave equation only in the term
is included into
the wave equation only in the term
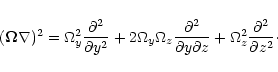
In order to construct the "![]() -plane" limit we expand
-plane" limit we expand ![]() around
a fixed
around
a fixed
![]() (
(
![]() ):
):
![]() .
Here
.
Here
![]() ,
,
![]() ,
and
,
and
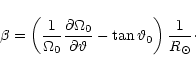
Note that such a "![]() "-limit is applicable also around the equator plane,
where the traditional approximation does not fit. The advantage of this limit
is the possibility to include
"-limit is applicable also around the equator plane,
where the traditional approximation does not fit. The advantage of this limit
is the possibility to include ![]() as a parameter in the Cartesian
system. In this way we use here an inertial Cartesian system of coordinates
(x,y,z) in a frame rotating with an angular frequency
as a parameter in the Cartesian
system. In this way we use here an inertial Cartesian system of coordinates
(x,y,z) in a frame rotating with an angular frequency
![]() .
All
non-perturbed model variables are functions of z only, and for the gravity
acceleration we have
.
All
non-perturbed model variables are functions of z only, and for the gravity
acceleration we have
![]() .
For the observer from the non-rotating frame
the elements of fluid are moving due to rotation with a velocity
.
For the observer from the non-rotating frame
the elements of fluid are moving due to rotation with a velocity
![]() ,
where in the frame of
our approximation
,
where in the frame of
our approximation
![]() .
V0x<0 means that the
x-axis is directed opposite to the rotation.
.
V0x<0 means that the
x-axis is directed opposite to the rotation.
For linearization each physical variable f=f0+f' is decomposed into a mean
term f0 and a small fluctuating term f'. Neglecting terms of higher
order than the first one we get our oscillation equations
We define
| = | 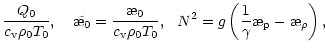 |
||
| = | 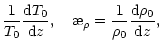 |
||
| = | 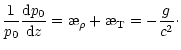 |
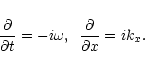 |
(14) |
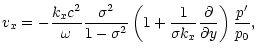 |
(22) | ||
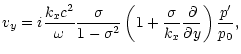 |
(23) | ||
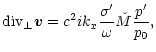 |
(24) |
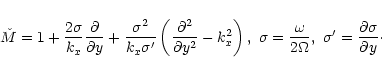
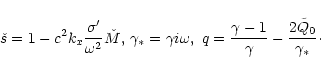 |
(28) |
Our next step is to separate the z and y dependence of the variables in
the governing equations to have finally one ordinary differential equation.
In the general case such a separation is not possible, and we consider here
the very simple case when the function
![]() is
independent of y. Only in this case it is possible to separate the
equations with respect to the variables y and z and we can write
is
independent of y. Only in this case it is possible to separate the
equations with respect to the variables y and z and we can write
![]() .
Here ky should be determined
from the boundary conditions, and a complex ky is not excluded. In this
way the system of partial differential equations in the plane-parallel
approximation is reduced to ordinary differential equations. Now we assume
the following formula for the rotation profile
.
Here ky should be determined
from the boundary conditions, and a complex ky is not excluded. In this
way the system of partial differential equations in the plane-parallel
approximation is reduced to ordinary differential equations. Now we assume
the following formula for the rotation profile
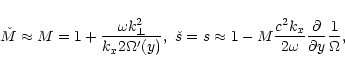 |
(32) |
Our next step is to derive one differential equation for the temperature
perturbations. The variable vz is easily excluded from
Eqs. (25)-(27). Then we get for the pressure perturbations
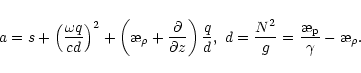 |
(34) |
Introducing a new dependent variable
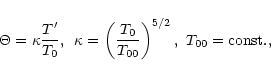 |
(35) |
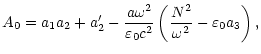 |
(36') | ||
| A1=a1a3+a2+a3', | |||
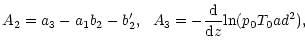 |
|||
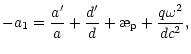 |
|||
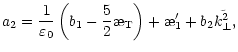 |
|||
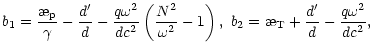 |
|||
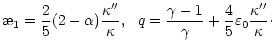 |
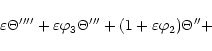
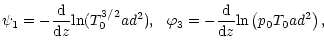 |
|||
| (37') | |||
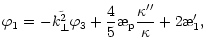 |
|||
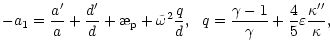 |
|||
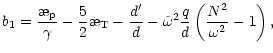 |
|||
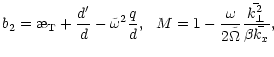 |
|||
 |
|||
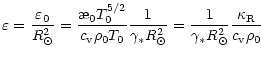 |
|||
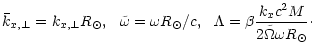 |
Because we are interested in very low frequency oscillations with periods of
1-20 years, we take
![]() s-1,
s-1,
![]() ,
and we have a small parameter for our task
,
and we have a small parameter for our task
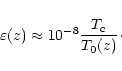 |
(38) |
For idealized adiabatic waves (
![]() )
we have a second order equation,
)
we have a second order equation,
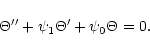 |
(39) |
As we consider adiabatic waves, the transition to the incompressible
case can be done by
![]() .
In this case
.
In this case
![]() and instead of Eq. (41) we
obtain
and instead of Eq. (41) we
obtain
For waves running in opposite direction to rotation in the azimuth
(
![]() ), the cavities (trapped wave area) can form
between the bottom of the convective zone and almost the center of the Sun
as well as in the outer part of the Sun where N2>0.
), the cavities (trapped wave area) can form
between the bottom of the convective zone and almost the center of the Sun
as well as in the outer part of the Sun where N2>0.
Waves propagating parallel to rotation may be trapped only in the convective zone (N2<0). To the outer and inner sides from the convective zone the amplitude of these waves decrease exponentially.
For the incompressible case it is easy to solve the eigenvalue problem of the
cavity oscillations, because Eq. (42) has no singularity. Such a task
has been solved by Oraevsky & Dzhalilov (1997). However, in the nonadiabatic
case we cannot apply
the limit
![]() .
Therefore we have to investigate the more complicated compressible case.
.
Therefore we have to investigate the more complicated compressible case.
To investigate the function I(z) given by Eq. (41) in a
compressible plasma we need the orders of the quantities entering
the function I(z). To estimate these values let us consider a linear profile
of temperature,
![]() ,
where the gradient
,
where the gradient
![]() ,
,
![]() is the effective
temperature. Then we
have a limit for the parameter
is the effective
temperature. Then we
have a limit for the parameter
![]() from the center (z=0) up to the
surface (z=1):
from the center (z=0) up to the
surface (z=1):
![]() .
The other parameters have the same
order,
.
The other parameters have the same
order,
![]() .
Then
we get also:
.
Then
we get also:
![]() .
Now we can estimate the sign
behavior of I(z). We shall consider more characteristic places of the Sun.
In the following the condition
.
Now we can estimate the sign
behavior of I(z). We shall consider more characteristic places of the Sun.
In the following the condition
![]() will be supposed.
will be supposed.
At the center, where
![]() kms-1, if
kms-1, if ![]() we have
we have
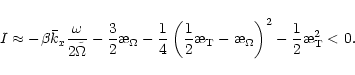
The area around the convective zone is more complicated.
The function I(z) has singularities at the points where d=0 and a=0;
d is connected with the Brunt-Väisälä frequency and
a is defined mainly by the rotation gradient, Eqs. (37').
The two points of d=0 correspond to the bottom and the upper boundary
of the convective zone. The function a(z) is defined mainly by two terms
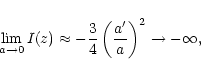
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig01.ps}\end{figure}](/articles/aa/full/2002/10/aah2966/Timg307.gif) |
Figure 1: Scheme of the dependence of the wave potential I(z) defined by Eq. (41) on the distance normalized to the solar radius. Zeros of this function I(z)=0 (turning points) divide the wave zone into transparent (cavity) and opaque (tunnel) parts. In the upper part of the Sun there are singular points of the function I(z) which are located between the turning points: the circles correspond to a(z)=0 and the boxes correspond to N2(z)=0 (boundaries of the convective zone). The narrow area at the bottom of the convective zone between circles and boxes is the tachocline. The main internal cavity comprises the whole radiative interior as the convective zone becomes opaque for the waves. |
| Open with DEXTER | |
Thus if we approach the convective zone from below there exists a sequence
of special points: four times the function I(z) crosses zero (turning
points), and between these zeros the singular points are placed (see Fig. 1).
The turning points are determined practically by the condition of
![]() and the singularities by the conditions a=0 (circles in
Fig. 1) and N2=0 (boxes in Fig. 1). Due to the very low frequency and the
sharp decrease of N2(z) the turning point of the main inner cavity
and the singularities by the conditions a=0 (circles in
Fig. 1) and N2=0 (boxes in Fig. 1). Due to the very low frequency and the
sharp decrease of N2(z) the turning point of the main inner cavity ![]() is
very close to the first singular point where a=0.
is
very close to the first singular point where a=0.
In this way for waves with kx>0 a main large internal cavity is placed practically between the center and the bottom of the tachocline. The solar atmosphere is a wave-propagating zone. Between the inner cavity and the solar surface a dark convective tunnel is placed; a very narrow wave-trapping zone around the bottom of convective zone is also possible. It is clear that a tunneling of waves across the magnetized and turbulent convective area to the surface is probably possible. For waves with kx<0 the convective zone becomes a cavity. In this case the waves cannot be propagating at the solar surface.
Not all singularities of the wave potential I(z) are singular levels of the
physical variables. Around the point ![]() where
where
![]() we can write
we can write
![]() .
Then we have the equation
x2Y'' +2 Y=0, where
.
Then we have the equation
x2Y'' +2 Y=0, where
![]() .
The solutions of this equation are
.
The solutions of this equation are
![]() .
As
.
As
![]() we get from
Eqs. (33) + (40) that
we get from
Eqs. (33) + (40) that
![]() if
if
![]() .
It means, that the boundaries of the convective zone are not
singular levels for the initial physical variables.
.
It means, that the boundaries of the convective zone are not
singular levels for the initial physical variables.
Another situation exists at the point
![]() where a=0. If we denote now
x as
where a=0. If we denote now
x as
![]() ,
our Eq. (40) around the point
,
our Eq. (40) around the point
![]() is
x2Y''-Y3/4=0, the solutions of which are
is
x2Y''-Y3/4=0, the solutions of which are
![]() .
Hence, for these solutions
we have
.
Hence, for these solutions
we have
![]() const. Then we get from
Eq. (33) that the second solution in p'/p0 diverges at a=0.
const. Then we get from
Eq. (33) that the second solution in p'/p0 diverges at a=0.
There exist methods to construct asymptotic solutions of differential
equations of second order with a singular turning point. However, we are now
returning to our fourth order Eq. (37) for two reasons: our intent is
to consider the instability problem of the eigenmodes, and consequently in the
complex ![]() plane the singularity at
plane the singularity at
![]() is removed from
the real z-axis.
is removed from
the real z-axis.
The existence of the small parameter
![]() in Eq. (37) allows us to
apply asymptotic methods to solve this equation. Here we shall construct
the inner cavity solutions only. As it has been discussed above the
coefficients of Eq. (37) vary over a wide range. Very crudely, we have
the following estimates from the center of the Sun to the bottom of the
convective zone:
in Eq. (37) allows us to
apply asymptotic methods to solve this equation. Here we shall construct
the inner cavity solutions only. As it has been discussed above the
coefficients of Eq. (37) vary over a wide range. Very crudely, we have
the following estimates from the center of the Sun to the bottom of the
convective zone:
![]() -
-
![]() -
-
![]() and
and
![]() .
Assuming that
.
Assuming that
![]() -10) we can separate the
variable part of
-10) we can separate the
variable part of
![]() as
as
![]() and rewrite Eq. (37) in a convenient form:
and rewrite Eq. (37) in a convenient form:
The solutions corresponding to the dissipative modes are searched for in the
form:
| S2 | = | (47) | |
| B1 | = | 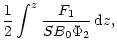 |
(48) |
| F0 | = | 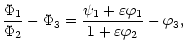 |
(49) |
| F1 | = | S(2SB0''+3S'B0'+S''B0)+3[S(SB0)']' | |
| (50) |
Thus we have a radiation boundary condition for the dissipative modes: from the
point
![]() (turning point of adiabatic waves) the dissipative waves
are radiated. In all directions the amplitudes of these modes
must decrease, and while setting
(turning point of adiabatic waves) the dissipative waves
are radiated. In all directions the amplitudes of these modes
must decrease, and while setting
![]() these modes must disappear.
The following solution obeys these conditions:
these modes must disappear.
The following solution obeys these conditions:
Now we will search for "slow" quasi-adiabatic wave solutions in the form
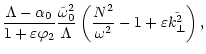 |
(61) |
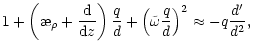 |
(62) |
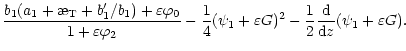 |
(63) |
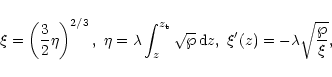 |
(65) |
Now we have to determine from the boundary conditions one of the unknown
constants C1,2. Here we assume the next simplification. In the real solar
situation we should include the tunneling of waves through the opaque
convective zone to the transparent solar surface. However, in this work we do
not complicate the situation by including this important effect. Here we are
interested in the eigenoscillation spectrum of the main interior cavity. So our
solutions must be finite in the whole domain of integration:
![]() .
In the limit of
.
In the limit of
![]() we have the asymptotics
we have the asymptotics
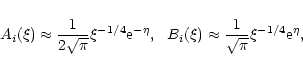 |
(67) |
In this section we impose physically reasonable boundary conditions to the general solution of (69) to determine the spectrum of the eigenoscillations of the inner cavity.
At the solar center (z=0) where
![]() ,
and
,
and
![]() we apply a rigid boundary condition: vz(0)=0. As the function
we apply a rigid boundary condition: vz(0)=0. As the function ![]() is
finite at the center Eq. (25) reads as
is
finite at the center Eq. (25) reads as
![]() .
Using Eqs. (27) + (21) with dimensionless parameters we have
.
Using Eqs. (27) + (21) with dimensionless parameters we have
Let us consider the location of the upper turning point (
![]() ): there the
equation
): there the
equation
![]() is fulfilled, from which we may define the
parameter d,
is fulfilled, from which we may define the
parameter d,
![]() .
Here we can apply a free boundary condition, because at the bottom of the
convective zone the Brunt-Väisälä frequency and the rotation rate
.
Here we can apply a free boundary condition, because at the bottom of the
convective zone the Brunt-Väisälä frequency and the rotation rate
![]() change very sharp. (A more realistic approach would be to
include the tunneling of the waves.) At the free surface the Lagrangian
pressure must be constant,
change very sharp. (A more realistic approach would be to
include the tunneling of the waves.) At the free surface the Lagrangian
pressure must be constant,
![]() ,
where p=p0 +p' is the total
pressure. From here we have
,
where p=p0 +p' is the total
pressure. From here we have
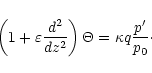 |
(76) |
From Eqs. (72) + (78) we get the general dispersion
relation
Now we can determine the complex eigenfrequencies
![]() from the integral dispersion relation
Eq. (86) for the given
from the integral dispersion relation
Eq. (86) for the given
![]() s-1.
Recall that
s-1.
Recall that ![]() is the latitudinal gradient of the rotation rate,
is the latitudinal gradient of the rotation rate,
![]() is the temperature exponent of the nuclear reaction power,
is the temperature exponent of the nuclear reaction power,
![]() ,
and
,
and ![]() determines the
power exponent of the temperature of the nuclear reactions,
determines the
power exponent of the temperature of the nuclear reactions,
![]() (Eq. (5)). For the p-p reactions we will use
(Eq. (5)). For the p-p reactions we will use ![]() .
The
dependence of this equation on the free parameter ky is a drawback of this
equation. In real situations the waves cannot be progressive across the shear
in y-direction. In the general case the complex
.
The
dependence of this equation on the free parameter ky is a drawback of this
equation. In real situations the waves cannot be progressive across the shear
in y-direction. In the general case the complex
![]() is a solution of the two-dimensional eigenvalue problem. To simplify our task
for a very small latitudinal gradient of rotation
is a solution of the two-dimensional eigenvalue problem. To simplify our task
for a very small latitudinal gradient of rotation ![]() we have introduced
the free parameter ky. To simulate the decay of the wave amplitudes
towards the pole, in y direction, we shall consider only the case with real
ky2<0 . A negative spectral parameter ky2 could also be confirmed by
the tidal equation of Laplace (e.g. Lee & Saio 1997) for very low
frequencies. This equation includes the influence of sphericity on the
angular dependence of the eigenfunctions, if simple rigid rotation is
considered in the frame of the traditional geophysical approximation (which
fails near the equator).
we have introduced
the free parameter ky. To simulate the decay of the wave amplitudes
towards the pole, in y direction, we shall consider only the case with real
ky2<0 . A negative spectral parameter ky2 could also be confirmed by
the tidal equation of Laplace (e.g. Lee & Saio 1997) for very low
frequencies. This equation includes the influence of sphericity on the
angular dependence of the eigenfunctions, if simple rigid rotation is
considered in the frame of the traditional geophysical approximation (which
fails near the equator).
Ando (1985) has derived a local dispersion relation for waves around the
stellar equator. Solving his Eq. (15) with respect to k (that is our
ky) for low frequencies
![]() we get two solutions:
k2 = -m2 and
we get two solutions:
k2 = -m2 and
![]() ,
where m is the azimuthal wave
number. As
,
where m is the azimuthal wave
number. As
![]() ,
the second solution is strongly damped in
y-direction. Our case corresponds to the first solution,
k2 = -m2.
,
the second solution is strongly damped in
y-direction. Our case corresponds to the first solution,
k2 = -m2.
From geophysical applications (Pedlosky 1982; Gill 1982) we infer that
![]() is obeyed for the ageostrophic wave propagation
across the shear flow. Really, it is seen from Fig. 2, that the mode
separation with respect to n is essential for the solar situation if the
condition
is obeyed for the ageostrophic wave propagation
across the shear flow. Really, it is seen from Fig. 2, that the mode
separation with respect to n is essential for the solar situation if the
condition
![]() is fulfilled. In Fig. 2 the Re
is fulfilled. In Fig. 2 the Re
![]() dependence is shown for the case
dependence is shown for the case
![]() and
and
![]() for
example. Here, a very small imaginary part of the frequency is supposed,
for
example. Here, a very small imaginary part of the frequency is supposed,
![]() ,
where
,
where
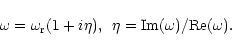 |
(87) |
![\begin{figure}
\par\includegraphics[width=8.4cm,height=7.1cm,clip]{fig02.ps}\end{figure}](/articles/aa/full/2002/10/aah2966/Timg455.gif) |
Figure 2:
Mode separation region versus
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,height=7.1cm,clip]{fig03.ps}\end{figure}](/articles/aa/full/2002/10/aah2966/Timg456.gif) |
Figure 3:
The harmonic numbers (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,height=14.3cm,clip]{fig04.ps}\end{figure}](/articles/aa/full/2002/10/aah2966/Timg457.gif) |
Figure 4:
Real (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.6cm,height=7.1cm,clip]{fig05.ps}\end{figure}](/articles/aa/full/2002/10/aah2966/Timg460.gif) |
Figure 5:
Growth rate of the instabilities of the eigenmodes of the
differentially rotating Sun. Three modes with periods of |
| Open with DEXTER | |
It follows from Eq. (86) that for a given ![]() the
frequencies
the
frequencies ![]() decrease with increasing harmonic number n(
decrease with increasing harmonic number n(
![]() )
in the adiabatic case (
)
in the adiabatic case (
![]() ). At very high
). At very high
![]() we have almost steady motions with a frequency
we have almost steady motions with a frequency
![]() .
Howewer, the situation is changed if dissipation is taken into account,
.
Howewer, the situation is changed if dissipation is taken into account,
![]() .
In this case small-scale motions are quickly damped, very low
frequency oscillations with high n could not become trapped and cannot
manifest themselves as eigenmodes. Really, as the nonadiabatic parameter
.
In this case small-scale motions are quickly damped, very low
frequency oscillations with high n could not become trapped and cannot
manifest themselves as eigenmodes. Really, as the nonadiabatic parameter
![]() ,
at very low frequencies the solutions of the initial
equations must have a dissipative character. An investigation of the initial
equations for a steady flow with
,
at very low frequencies the solutions of the initial
equations must have a dissipative character. An investigation of the initial
equations for a steady flow with
![]() is a separate task. Here we
restrict ourselves only to our dispersion relation Eq. (86) with
increasing n. We can rewrite this equation as
is a separate task. Here we
restrict ourselves only to our dispersion relation Eq. (86) with
increasing n. We can rewrite this equation as
![]() .
With decreasing
.
With decreasing ![]() the right-hand part
the right-hand part
![]() decreases, and then
it becomes independent from
decreases, and then
it becomes independent from ![]() .
It means, that n is limited:
.
It means, that n is limited:
![]() .
Hence, it is a results of the dissipative effects, that only
limited modes become trapped. The value of
.
Hence, it is a results of the dissipative effects, that only
limited modes become trapped. The value of
![]() depends on kx and
depends on kx and
![]() .
In Fig. 3 the
.
In Fig. 3 the
![]() dependence is presented. It
follows from this figure that for a given kx the number
dependence is presented. It
follows from this figure that for a given kx the number
![]() increases strongly by increasing the rotation gradient
increases strongly by increasing the rotation gradient ![]() .
So, if the
solar interior is rotating similar to a solid-body, very long-period
oscillations (almost steady flows) should be suppressed. As the values of
.
So, if the
solar interior is rotating similar to a solid-body, very long-period
oscillations (almost steady flows) should be suppressed. As the values of
![]() are sufficiently high, the accuracy of the asymptotic solutions
is high.
are sufficiently high, the accuracy of the asymptotic solutions
is high.
Now we consider which spectrum of trapped waves with
![]() is
possible. To calculate the wave spectrum from Eq. (86) we use the
standard model of Stix (private communication; Stix & Slaley 1990) for the
solar interior. For the special case
is
possible. To calculate the wave spectrum from Eq. (86) we use the
standard model of Stix (private communication; Stix & Slaley 1990) for the
solar interior. For the special case
![]() (i.e.
(i.e.
![]() km) the
n-dependence of the real and imaginary parts of the eigenfrequencies are
shown in Figs. 4a,b. The calculations were done for different small values of
the rotation rate gradient
km) the
n-dependence of the real and imaginary parts of the eigenfrequencies are
shown in Figs. 4a,b. The calculations were done for different small values of
the rotation rate gradient ![]() ,
covering a wide range:
,
covering a wide range:
![]() -10-4. This is done because we know from helioseismology
only that the
-10-4. This is done because we know from helioseismology
only that the ![]() parameter is small, but the exact value is not yet
known. In Figs. 4a,b
parameter is small, but the exact value is not yet
known. In Figs. 4a,b
![]() and
and
![]() are
normalized to the cycle frequency of the 22-year oscillations:
are
normalized to the cycle frequency of the 22-year oscillations:
![]() s
s
![]() nHz). As expected the
frequencies decrease with n and increase with
nHz). As expected the
frequencies decrease with n and increase with ![]() or kx. The
imaginary parts
or kx. The
imaginary parts ![]() oscillate around the zero value: if
oscillate around the zero value: if
![]() ,
the waves are unstable and their amplitudes increase with time; in the
opposite case, if
,
the waves are unstable and their amplitudes increase with time; in the
opposite case, if
![]() ,
we have stable/damped waves. In Fig. 4b we
have two positive maxima: the first corresponds to short-period oscillations
of 1-3 yr ("quasi-biennial modes") and the second one to medium-period
oscillations of 18-30-yr ("22-yr modes"). The position of the
quasi-biennial modes versus n is stable and is
,
we have stable/damped waves. In Fig. 4b we
have two positive maxima: the first corresponds to short-period oscillations
of 1-3 yr ("quasi-biennial modes") and the second one to medium-period
oscillations of 18-30-yr ("22-yr modes"). The position of the
quasi-biennial modes versus n is stable and is ![]() 15. For the 22-yr
modes n22 is slightly increased with an increase of
15. For the 22-yr
modes n22 is slightly increased with an increase of ![]() .
It is seen
from Fig. 4a that n must increase to keep the same frequency with increasing
.
It is seen
from Fig. 4a that n must increase to keep the same frequency with increasing
![]() .
For smaller frequencies this shift is stronger. Figure 4b shows that
the instability gets stronger if
.
For smaller frequencies this shift is stronger. Figure 4b shows that
the instability gets stronger if ![]() increases: unstable waves become
more unstable and damped waves are stronger damped. Waves with high n>200
at very low frequencies also show instability which cannot be shown in Fig. 4b
due to the scaling.
increases: unstable waves become
more unstable and damped waves are stronger damped. Waves with high n>200
at very low frequencies also show instability which cannot be shown in Fig. 4b
due to the scaling.
Of course, ![]() will change with the radius in the real solar radiative
interior. Hence, those places, where
will change with the radius in the real solar radiative
interior. Hence, those places, where ![]() becomes relatively large, may
become sources of unstable waves. Our calculations can easily be generalized
for any kx as Eq. (86) is a function of
becomes relatively large, may
become sources of unstable waves. Our calculations can easily be generalized
for any kx as Eq. (86) is a function of ![]() only.
only.
To characterize the mode instability, the behavior of the parameter ![]() is
more important.
is
more important. ![]() is the growth rate (increment) of the instability of
the modes if
is the growth rate (increment) of the instability of
the modes if ![]() and the damping rate (decrement) if
and the damping rate (decrement) if ![]() .
In Fig. 5
we present the
.
In Fig. 5
we present the
![]() dependence for the whole range of frequencies
(
dependence for the whole range of frequencies
(
![]() )
for which our asymptotic theory is valid. We
have three distinguished global maxima for the growth rate
)
for which our asymptotic theory is valid. We
have three distinguished global maxima for the growth rate ![]() which
correspond to period ranges of
which
correspond to period ranges of ![]() 1-3yr, 18-30yr with a small
additional peak at 100 yr, and 1500-20000yr ("4000-yr modes") of the
eigenmodes. These modes have radial node numbers near n=850, 60, and 15,
respectively. It was already mentioned, that for the unstable modes the value
of n is slightly changed with a change of
1-3yr, 18-30yr with a small
additional peak at 100 yr, and 1500-20000yr ("4000-yr modes") of the
eigenmodes. These modes have radial node numbers near n=850, 60, and 15,
respectively. It was already mentioned, that for the unstable modes the value
of n is slightly changed with a change of ![]() .
So for the unstable
modes n is high and the asymptotic results are reliable. The growth rates
of the 22-yr oscillations are always greater than those of the quasi-biennial
modes. The characteristic growing time for the 22-year modes is
.
So for the unstable
modes n is high and the asymptotic results are reliable. The growth rates
of the 22-yr oscillations are always greater than those of the quasi-biennial
modes. The characteristic growing time for the 22-year modes is ![]() 1000yr as
1000yr as
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.6cm,height=14.3cm,clip]{fig06.ps}\end{figure}](/articles/aa/full/2002/10/aah2966/Timg485.gif) |
Figure 6:
The existence area of the 22-yr (solid lines) and 2-yr (dashed
lines) eigenmodes versus the parameters
|
| Open with DEXTER | |
Now we consider in which range of n and
![]() the unstable modes
are located. For this aim we fix the frequency as
the unstable modes
are located. For this aim we fix the frequency as
![]() s-1, and for a given
s-1, and for a given
![]() we find
the complex root of the dispersion relation Eq. (86). The parameters
we find
the complex root of the dispersion relation Eq. (86). The parameters
![]() and
and ![]() correspond to this root. The same calculations
were done for the 2-yr oscillations. The results are shown in Fig. 6. Here the
solid lines correspond to the 22-yr and the dashed lines to the
quasi-biennial modes. A sharp increase of n to
correspond to this root. The same calculations
were done for the 2-yr oscillations. The results are shown in Fig. 6. Here the
solid lines correspond to the 22-yr and the dashed lines to the
quasi-biennial modes. A sharp increase of n to
![]() with
with
![]() in Fig. 6a indicates some upper limit for the parameter
in Fig. 6a indicates some upper limit for the parameter
![]() .
For the 22-yr and 2-yr modes these limits are approximately
.
For the 22-yr and 2-yr modes these limits are approximately
![]() and
and
![]() ,
respectively. Figure 6b (where the
increment/decrement is presented) shows for which values of
,
respectively. Figure 6b (where the
increment/decrement is presented) shows for which values of
![]() and n the 22-yr and 2-yr modes become unstable. Two maxima for each mode
appear in
and n the 22-yr and 2-yr modes become unstable. Two maxima for each mode
appear in ![]() .
These are for the 22-year modes:
.
These are for the 22-year modes:
![]() and
and
![]() ;
;
for the 2-yr modes:
![]() and
and
![]() .
These estimates could be used to define a possible value of
.
These estimates could be used to define a possible value of ![]() inside of the Sun. This will be possible if we can identify these modes
from observations. For instance, at
inside of the Sun. This will be possible if we can identify these modes
from observations. For instance, at
![]() (sunspot scale)
a gradient of the rotation rate with
(sunspot scale)
a gradient of the rotation rate with
![]() or
or
![]() is needed to excite the 22-yr modes. Here the
possibility of an excitation of both the n=15 and the n=55 modes is not
excluded if
is needed to excite the 22-yr modes. Here the
possibility of an excitation of both the n=15 and the n=55 modes is not
excluded if ![]() is changed with the radius.
A better way to define
is changed with the radius.
A better way to define ![]() would be to identify both the 22-yr and the
quasi-biennial modes, with different kx at the surface of the Sun.
would be to identify both the 22-yr and the
quasi-biennial modes, with different kx at the surface of the Sun.
In the present paper we have shown that toroidal eddy flows which are
degenerated in a non-rotating fluid can become a reservoir of various branches
of oscillatory modes when the degeneracy is removed by rotation. The mechanism
depends on the condition for the existence and alteration of the relative
vorticity as well as on the stellar rotation rate and its gradient.
Apparently at least for slowly rotating stars (
![]() )
the
rotation waves could be divided into two types: r-modes with high frequencies
(
)
the
rotation waves could be divided into two types: r-modes with high frequencies
(
![]() )
which are independent from the inner structure and mainly
caused by geometrical effects, and the R-modes with low frequencies
(
)
which are independent from the inner structure and mainly
caused by geometrical effects, and the R-modes with low frequencies
(
![]() )
which depend on the inner structure and are considered
in the present paper. This classification is similar to that of f- and
g- modes or to that of surface and body tube modes of magnetic cylinders.
Note that the properties of Coriolis forces and ponderomotive forces in MHD
are very similar to each other. Both rotation modes are prototypes of the
geophysical Rossby waves.
)
which depend on the inner structure and are considered
in the present paper. This classification is similar to that of f- and
g- modes or to that of surface and body tube modes of magnetic cylinders.
Note that the properties of Coriolis forces and ponderomotive forces in MHD
are very similar to each other. Both rotation modes are prototypes of the
geophysical Rossby waves.
We investigated the instability problem of the R-modes sustained by a
very small latitudinal gradient ![]() of the rotation rate in the solar
radiative interior. The problem has been solved for a realistic solar model
without an arbitrary choice of free parameters except
of the rotation rate in the solar
radiative interior. The problem has been solved for a realistic solar model
without an arbitrary choice of free parameters except ![]() ,
the
product of
,
the
product of ![]() and the horizontal wave number. Among the
eigenoscillations three modes with periods of
and the horizontal wave number. Among the
eigenoscillations three modes with periods of ![]() 1-3yr,
18-30yr, and 1500-20000yr turn out to be maximum unstable to the
1-3yr,
18-30yr, and 1500-20000yr turn out to be maximum unstable to the
![]() -mechanism. Here the smoothing effect is the radiative damping. All of
these instabilities are in the range of high radial node numbers n which
indicates that the applicability of the asymptotic solution is satisfied.
-mechanism. Here the smoothing effect is the radiative damping. All of
these instabilities are in the range of high radial node numbers n which
indicates that the applicability of the asymptotic solution is satisfied.
The 22-yr modes with a growing time of ![]() 1000 yr are of particular
interest with respect to the solar activity cycle problem. In the simpler
case when adiabatic R-modes are considered in an incompressible fluid,
1000 yr are of particular
interest with respect to the solar activity cycle problem. In the simpler
case when adiabatic R-modes are considered in an incompressible fluid,
![]() in Eq. (86) is independent of the wave number and of the
frequency for very low frequencies. Then in the azimuthal direction the phase
and group velocities are
in Eq. (86) is independent of the wave number and of the
frequency for very low frequencies. Then in the azimuthal direction the phase
and group velocities are
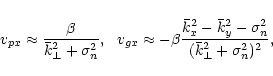 |
(88) |
A nice property of the Rossby waves is that every monochromatic mode is a
solution of the full nonlinear hydrodynamic equations. It means, that
we should expect the development of nonlinear R-modes with large amplitudes.
We could also expect that just in this nonlinear regime the toroidal magnetic
flux will be lifted from the upper boundary of the cavity (the tachocline) to
the surface. The energy release of the nonlinear waves could be accomplished
by magnetic reconnection. Here it is possible that toroidal currents are
generated via a twist of toroidal magnetic field lines by the cyclonic flows
of regular R-modes with fixed characteristics. Parker (1955) as well as
Steenbeck et al. (1966; see also Krause & Rädler 1980) have suggested for
the dynamo process that such a mechanism, the ![]() effect, is working by
turbulent motions under the influence of Coriolis forces.
effect, is working by
turbulent motions under the influence of Coriolis forces.
Our present model points out the possibility of forced oscillations instead of a self-excited dynamo to solve the solar cycle problem, and this with the correct period of 22 yr. Similar ideas are due to Tikhomolov (2001) who has recently suggested a hydrodynamic driving of the 11-yr sunspot cycle. There is still a smaller peak of the growth rate (Fig. 5) at 100 years; such a period is observed as a modulation of the 11/22 yr cycles.
We expect that in a non-linear stage of our model a huge toroidal
magnetic field of ![]() 105G will no longer be required to cause a
buoyant rise of magnetic flux tubes, because the external nonzero upflow
produced by the regular vortical R-modes could trigger the eruption of
stable magnetic flux tubes stored in the overshoot region. However, we did
not yet calculate the details of the rise of the flux tubes, thus the problem
of their appearance at the surface with small tilt angles and at low
latitudes remains still unresolved.
105G will no longer be required to cause a
buoyant rise of magnetic flux tubes, because the external nonzero upflow
produced by the regular vortical R-modes could trigger the eruption of
stable magnetic flux tubes stored in the overshoot region. However, we did
not yet calculate the details of the rise of the flux tubes, thus the problem
of their appearance at the surface with small tilt angles and at low
latitudes remains still unresolved.
There is observational evidence for the short-period oscillations as well: from helioseismic sounding Howe et al. (2000, 2001) have recently discovered variations of solar rotation with a period of 1.3 yr in the lower convective zone. Quasi-two year modes are very likely seen regularly in various solar data (e.g. Waldmeier 1973; Akioka et al. 1987; Rivin & Obridko 1992). The existence of two magnetic cycles (the main 22-yr and the quasi-biennial period) on the Sun has been reported by Benevolenskaya (1996, 1998). So far the origin of these modes was not yet clear. Terrestrial quasi-biennial oscillations have been clearly seen in tropical meteorological radiosonde data, and a possible solar origin by related phenomena in the solar interior, Rossby waves in particular, has been discussed as well (McIntire 1994).
The long-period oscillations in the broad range
![]() -
-
![]() yr, with a maximum growth rate around 4500 yr,
could be the cause of abrupt changes of the global terrestrial climate in the
past: Dansgaard-Oeschger events, these are abrupt onsets of warm periods
during the last ice age, had mean distances of 4500 yr, but they were
distributed over a larger period range, similar to that in our model, with
shortest distances often around 1500 years (see, e.g., Ganopolski &
Rahmstorf 2001). These events were caused by changes of the thermohaline
circulation of the ocean, which in its turn were probably triggered by
changes in the solar energy output.
yr, with a maximum growth rate around 4500 yr,
could be the cause of abrupt changes of the global terrestrial climate in the
past: Dansgaard-Oeschger events, these are abrupt onsets of warm periods
during the last ice age, had mean distances of 4500 yr, but they were
distributed over a larger period range, similar to that in our model, with
shortest distances often around 1500 years (see, e.g., Ganopolski &
Rahmstorf 2001). These events were caused by changes of the thermohaline
circulation of the ocean, which in its turn were probably triggered by
changes in the solar energy output.
Acknowledgements
Michael Stix kindly provided detailed tables from his internal solar model calculations. The critical comments and suggestions by Kris Murawski, Karl-Heinz Rädler, and the referee J. Andrew Markiel helped to improve earlier versions of the paper. The authors gratefully acknowledge financial support of the present work by the German Science Foundation (DFG) under grant No. 436 RUS 113/560/1-1 and -3, by the German Federal Ministry of Education and Research through the German Space Research Center (DLR) under grant No. 50QL96019, and by the Russian Foundation for Basic Research (RFBR) under grant No. 00-02-16271.