A&A 384, 33-47 (2002)
DOI: 10.1051/0004-6361:20011747
A. Boselli 1 - J. Lequeux 2 - G. Gavazzi 3
1 -
Laboratoire d'Astrophysique de Marseille, BP 8,
Traverse du Siphon, 13376 Marseille Cedex 12, France
2 - DEMIRM and URA 336 du CNRS, Observatoire de Paris, 61 Av. de
l'Observatoire, 75014 Paris, France
3 - Università degli Studi di Milano-Bicocca, Dipartimento di Fisica,
Piazza dell'Ateneo Nuovo 1,
20126 Milano, Italy
Received 7 September 2001 / Accepted 28 November 2001
Abstract
We present 12CO(J=1-0) line observations of 22 low-luminosity spiral galaxies
in the Virgo cluster. These data, together with 244 others
available in the literature,
allow us to build a large sample that we use to study the molecular gas
properties of galaxies spanning a large range of morphological types
and luminosities and belonging to different environments (clusters - field).
The molecular gas content of the target galaxies is estimated using
a luminosity-dependent X = N(H2)/I(CO) conversion factor that has
been calibrated on a sample of nearby galaxies.
X spans from ![]() 1020 mol cm-2 (K km s-1)-1 in giant
spirals to
1020 mol cm-2 (K km s-1)-1 in giant
spirals to ![]() 1021 mol cm-2 (K km s-1)-1 in dwarf irregulars.
The value of the X conversion factor is found consistent with a value derived
independently from dust masses estimated from FIR fluxes, with a metallicity-dependent
dust to gas ratio.
The relationships between X and the UV radiation field
(as traced by the H
1021 mol cm-2 (K km s-1)-1 in dwarf irregulars.
The value of the X conversion factor is found consistent with a value derived
independently from dust masses estimated from FIR fluxes, with a metallicity-dependent
dust to gas ratio.
The relationships between X and the UV radiation field
(as traced by the H![]() NII]EW), the metallicity and the H band
luminosity are analysed.
We show that the molecular gas contained in molecular clouds or complexes
is of the order of 15% of the total gas on average whatever the luminosity
or the Hubble type of the galaxies. We discuss the relation between the star formation
rate and the molecular gas content and estimate the average star formation efficiency
of late-type galaxies.
NII]EW), the metallicity and the H band
luminosity are analysed.
We show that the molecular gas contained in molecular clouds or complexes
is of the order of 15% of the total gas on average whatever the luminosity
or the Hubble type of the galaxies. We discuss the relation between the star formation
rate and the molecular gas content and estimate the average star formation efficiency
of late-type galaxies.
Key words: galaxies: general, spiral - ISM - galaxies: intergalactic medium - radio lines: galaxies
Our understanding of galaxy evolution is still limited by the poor knowledge of the physical mechanisms behind the process of star formation, i.e. the condensation of the primordial gaseous material (HI) into molecular clouds (H2), then their collapse into stars. Also poorly understood are the feed-back processes induced by the newly born stars on the interstellar medium (ISM). The UV radiation field associated with massive star formation produces the ionization of the surrounding gas and causes the photo-dissociation of the hydrogen molecules. Meanwhile supernova winds inject kinetic energy (and metals) into the ISM with the effect of triggering new star formation on the shock fronts.
The first and last stages of this complex chain of transformations
are constrained observationally:
the atomic hydrogen is directly and easily observable through
the 21 cm line, and the star formation rate (SFR) can be estimated
from H![]() and UV luminosities, once corrected for extinction,
using stellar population synthesis models (Kennicutt 1998).
and UV luminosities, once corrected for extinction,
using stellar population synthesis models (Kennicutt 1998).
Kennicutt (1989) suggested the existence of a
universal relationship between gas surface density at disc scales and
star formation activity, known as the Schmidt law (Schmidt 1959),
modulated by differential rotation.
Even if the total amount of gas in late-type galaxies is dominated by
atomic hydrogen (Boselli et al. 1997b), which commonly spans
a diameter ![]() 1.8 times the optical disc (Cayatte et al. 1994),
the molecular phase might dominate the gas column density inside
the optical disc (Young & Scoville 1991).
An accurate determination of the content and distribution of
the molecular gas is thus crucial for studying the interplay between
gas and star formation over galactic discs.
1.8 times the optical disc (Cayatte et al. 1994),
the molecular phase might dominate the gas column density inside
the optical disc (Young & Scoville 1991).
An accurate determination of the content and distribution of
the molecular gas is thus crucial for studying the interplay between
gas and star formation over galactic discs.
The amount of molecular hydrogen, can only be estimated by indirect methods.
The most common method starts from the 12CO(1-0) line emission
at 115 GHz using a standard X conversion factor
between the intensity of the CO line (I(CO)) and the
column density of H2 (N(H2)) calibrated
in the solar neighborhood, X=N(H2)/I(CO) (Young & Scoville 1991).
Detailed analyses of giant molecular clouds (GMC) in nearby galaxies
have however questioned the validity of
this method. X can vary by up to a factor of ![]() 10
as observed in giant molecular clouds in the SMC (Rubio et al. 1993)
or in M 31 (Allen & Lequeux 1993).
Higher values of X are generally observed at
low metallicities and strong UV radiation fields.
10
as observed in giant molecular clouds in the SMC (Rubio et al. 1993)
or in M 31 (Allen & Lequeux 1993).
Higher values of X are generally observed at
low metallicities and strong UV radiation fields.
Using the few local galaxies for which X has been determined with
independent methods, it might be possible to calibrate some
empirical relationships between X and other parameters characterizing
the ISM, such as metallicity,
intensity of the UV radiation field and cosmic ray density.
This approach is however not easy since the determination of
X relies on molecular gas mass estimates based on different techniques:
from the virial equilibrium of GMCs (Young & Scoville 1991), from the
line ratios of different CO isotopes (Wild et al. 1992), assuming
a metallicity-dependent gas to dust ratio (Guélin et al. 1993, 1995),
or relying on ![]() -ray data (Hunter et al. 1997).
Furthermore the relation between the CO emission properties and
the physical parameters of the ISM (UV radiation field, cosmic ray density,
metallicity, gas density) are still poorly known, even though some
success in modeling the ISM has recently been reported (Lequeux et al. 1994;
Kaufman et al. 1999; Bolatto et al. 1999).
-ray data (Hunter et al. 1997).
Furthermore the relation between the CO emission properties and
the physical parameters of the ISM (UV radiation field, cosmic ray density,
metallicity, gas density) are still poorly known, even though some
success in modeling the ISM has recently been reported (Lequeux et al. 1994;
Kaufman et al. 1999; Bolatto et al. 1999).
An ideal approach in determining X would be to use a consistent method on a sample of galaxies spanning a large range in luminosity and morphological type. The technique applied by Guélin and collaborators to a few nearby galaxies (Guélin et al. 1993, 1995; Neininger et al. 1996; see also Israel 1997) seems very promising. It consists of determining the amount of dust from millimetric/submillimetric observations and correlating it with CO and HI. Provided that the gas to dust ratio is constant or metallicity-dependent in a known way, the molecular gas mass can be determined assuming that the difference between the expected total gas to dust ratio and the observed HI to dust ratio is due to molecular gas. This technique could be profitably applied to larger galaxy samples provided that the necessary multifrequency data are available.
For the last few years we have been gathering spectrophotometric data
from the UV to the radio centimetric domain for
a large sample of ![]() 2500 galaxies in the nearby Universe.
The database created so far is ideal for this purpose since it includes
the data necessary for the determination of X (HI, CO and far-IR fluxes)
as well as those needed to characterize the physical properties of
the ISM (H
2500 galaxies in the nearby Universe.
The database created so far is ideal for this purpose since it includes
the data necessary for the determination of X (HI, CO and far-IR fluxes)
as well as those needed to characterize the physical properties of
the ISM (H![]() fluxes as tracers of the UV radiation field
and metallicity measurements).
The present dataset is however still limited
to the bright end of the luminosity function. In particular we are
lacking CO and metallicity measurements for galaxies with
MB > -18.
fluxes as tracers of the UV radiation field
and metallicity measurements).
The present dataset is however still limited
to the bright end of the luminosity function. In particular we are
lacking CO and metallicity measurements for galaxies with
MB > -18.
In order to extend the available CO data to lower luminosities, we observed 22 galaxies with -19< MB < -16 in the Virgo cluster. The new observations are described in Sects. 2-4. These new data are combined in Sect. 5 with the many data points already available for the galaxies included in our database in order to derive X and then their molecular content. The results of our analysis are discussed and compared with those obtained for a sample of 14 nearby galaxies with independent measurements of X (Sect. 6). The agreement in the determination of X allows us to calibrate a luminosity-dependent X conversion factor which is later used to re-analyse the molecular gas statistical properties of late-type galaxies (Sect. 7). After correcting for the systematic trend of X with luminosity, we estimate the molecular gas fraction and the star formation efficiency of galaxies spanning a large range in luminosity and morphological type and belonging to different environments (Sect. 7).
We report on new observations of the 12CO(1-0) line emission of 22 galaxies belonging to the Virgo Cluster. These are mostly low luminosity late-type galaxies.
The target galaxies are listed in Table 1, arranged as follows:
| VCC | NGC/IC | UGC | RA(1950) | dec(1950) | type | agg | vel | dist | a | b |
|
|
|
| h m s | |
km s-1 | Mpc | ' | ' | km s-1 | |||||||
| 58 | IC769 | 7209 | 120959.20 | 122407.0 | Sb | M | 2207 | 32.0 | 2.54 | 1.75 | 13.17 | 252 | 10.51 |
| 87 | - | - | 121108.20 | 154354.0 | Sm | N | -134 | 17.0 | 1.45 | 0.72 | 15.00 | 109 | 13.64 |
| 92 | 4192 | 7231 | 121115.50 | 151042.0 | Sb | N | -135 | 17.0 | 9.78 | 2.60 | 10.92 | 469 | 7.07 |
| 97 | 4193 | 7234 | 121120.80 | 132703.0 | Sc | M | 2476 | 32.0 | 1.96 | 0.97 | 13.20 | 367 | 9.61 |
| 199 | 4224 | 7292 | 121400.50 | 074424.0 | Sa | W | 2594 | 32.0 | 2.92 | 1.00 | 12.95 | 554 | 8.87 |
| 318 | IC776 | 7352 | 121630.50 | 090802.0 | Scd | W | 2469 | 32.0 | 1.71 | 1.00 | 14.01 | 178 | 12.95 |
| 459 | - | - | 121839.60 | 175457.0 | BCD | A | 2108 | 17.0 | 0.84 | 0.36 | 14.95 | 127 | 12.70 |
| 792 | 4380 | 7503 | 122249.60 | 101738.0 | Sab | B | 971 | 23.0 | 3.52 | 1.75 | 12.36 | 290 | 8.55 |
| 874 | 4405 | 7529 | 122335.50 | 162728.0 | Sc | A | 1738 | 17.0 | 1.89 | 1.11 | 12.99 | 169 | 9.61 |
| 939 | - | 7546 | 122414.70 | 090940.0 | Sc | B | 1271 | 23.0 | 3.45 | 3.45 | 12.92 | 91 | 10.53 |
| 957 | 4420 | 7549 | 122425.20 | 024618.0 | Sc | S | 1695 | 17.0 | 2.01 | 0.85 | 12.67 | 214 | 9.87 |
| 1205 | 4470 | 7627 | 122705.30 | 080559.0 | Sc | S | 2339 | 17.0 | 1.84 | 1.15 | 13.04 | 147 | 10.22 |
| 1290 | 4480 | 7647 | 122753.40 | 043127.0 | Sb | S | 2438 | 17.0 | 2.01 | 1.07 | 13.09 | 319 | 9.80 |
| 1375 | - | 7668 | 122906.20 | 041256.0 | Sc | S | 1732 | 17.0 | 4.76 | 3.77 | 12.00 | 173 | 11.17 |
| 1412 | 4503 | 7680 | 122934.20 | 112708.0 | Sa | A | 1342 | 17.0 | 4.33 | 1.71 | 12.12 | - | 8.28 |
| 1508 | 4519 | 7709 | 123057.90 | 085549.0 | Sc | S | 1212 | 17.0 | 3.60 | 2.60 | 12.34 | 187 | 9.69 |
| 1554 | 4532 | 7726 | 123146.70 | 064439.0 | Sm | S | 2021 | 17.0 | 2.60 | 1.00 | 12.30 | 185 | 9.76 |
| 1686 | IC3583 | 7784 | 123412.30 | 133202.0 | Sm | A | 1122 | 17.0 | 2.79 | 1.71 | 13.95 | 116 | 11.19 |
| 1929 | 4633 | 7874 | 124006.50 | 143748.0 | Scd | E | 291 | 17.0 | 2.48 | 1.07 | 13.77 | 190 | 10.75 |
| 1943 | 4639 | 7884 | 124021.50 | 133152.0 | Sb | E | 1048 | 17.0 | 3.20 | 2.01 | 12.19 | 295 | 8.90 |
| 2023 | IC3742 | 7932 | 124300.90 | 133615.0 | Sc | E | 958 | 17.0 | 2.01 | 1.00 | 13.86 | 186 | 11.57 |
| - | 4866 | 8102 | 125657.70 | 142626.0 | Sa | E | 1986 | 17.0 | 6.00 | 1.44 | 11.90 | 537 | 8.19 |
The observations were carried out during a remote-observing run (120 hours) from
the Laboratoire d'Astrophysique de Marseille in June 2000
using the NRAO Kitt Peak 12 m telescope![]() .
At 115 GHz [12CO(1-0)], the telescope
half-power beam width (HPBW) is 55'' which corresponds to 4.5 kpc
at the assumed distance of 17 Mpc for the Virgo cluster.
Weather conditions were fairly good, with typical
zenith opacities of 0.30-0.45.
The pointing accuracy was checked every
night by broad band continuum observations of Saturn and/or 3C 273, with an
average error of 7'' rms. We used a dual-polarization SIS mixer, with a
receiver temperature for each polarisation of about
.
At 115 GHz [12CO(1-0)], the telescope
half-power beam width (HPBW) is 55'' which corresponds to 4.5 kpc
at the assumed distance of 17 Mpc for the Virgo cluster.
Weather conditions were fairly good, with typical
zenith opacities of 0.30-0.45.
The pointing accuracy was checked every
night by broad band continuum observations of Saturn and/or 3C 273, with an
average error of 7'' rms. We used a dual-polarization SIS mixer, with a
receiver temperature for each polarisation of about
![]() -600 K
(in
-600 K
(in
![]() scale) at the elevation of the sources. We used a dual beam-switching
procedure, with two symmetric reference positions offset by 4' in
azimuth. The backend was a 256 channel filter bank spectrometer with channel
width of 2 MHz. Each 6-min scan began by a chopper wheel
calibration on a load at ambient temperature, with a chopper wheel
calibration on a cold load every two scans. Galaxies were observed
at their nominal coordinates listed in Table 1, with one position per
galaxy. The total integration time was on average 120 min on+off (i.e. 60 min on the source), yielding rms noise levels of about 3 mK (in the
scale) at the elevation of the sources. We used a dual beam-switching
procedure, with two symmetric reference positions offset by 4' in
azimuth. The backend was a 256 channel filter bank spectrometer with channel
width of 2 MHz. Each 6-min scan began by a chopper wheel
calibration on a load at ambient temperature, with a chopper wheel
calibration on a cold load every two scans. Galaxies were observed
at their nominal coordinates listed in Table 1, with one position per
galaxy. The total integration time was on average 120 min on+off (i.e. 60 min on the source), yielding rms noise levels of about 3 mK (in the
![]() scale) after velocity smoothing to 21 km s-1. The baselines
were flat owing to the use of beam-switching, thereby requiring that only
linear baselines be subtracted.
The antenna temperature
scale) after velocity smoothing to 21 km s-1. The baselines
were flat owing to the use of beam-switching, thereby requiring that only
linear baselines be subtracted.
The antenna temperature
![]() was corrected for telescope and
atmospheric losses. In the following analysis we use the main-beam
brightness temperature scale,
was corrected for telescope and
atmospheric losses. In the following analysis we use the main-beam
brightness temperature scale,
![]() ,
with
,
with
![]() /0.84
(where the main beam efficiency is
/0.84
(where the main beam efficiency is ![]()
![]() and the forward
scattering and spillover efficiency
and the forward
scattering and spillover efficiency ![]()
![]() ).
This scale is
appropriate for sources with sizes comparable to, or smaller than, the
beam size. These main-beam temperatures can be converted into
flux densities using 29 Jy/K.
).
This scale is
appropriate for sources with sizes comparable to, or smaller than, the
beam size. These main-beam temperatures can be converted into
flux densities using 29 Jy/K.
The 12CO(1-0) spectra of all the detected galaxies, reduced with the CLASS package (Forveille et al. 1990), are shown in Fig. 1: the observational results are listed in Table 2. Of the 22 observed galaxies 11 were not detected. Table 2 is arranged as follows:
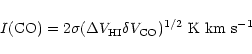 |
(1) |
where ![]() is the rms noise of the spectrum,
is the rms noise of the spectrum,
![]() is the HI
line width, and
is the HI
line width, and
![]() is the spectral resolution (for galaxies with
is the spectral resolution (for galaxies with
![]() not available, the
HI width has been determined assuming a standard
not available, the
HI width has been determined assuming a standard
![]() km s-1, where i is the galaxy inclination or
km s-1, where i is the galaxy inclination or
![]() km s-1 if i = 0).
km s-1 if i = 0).
![]() km s-1.
km s-1.
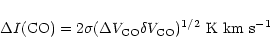 |
(2) |
where ![]() is the rms noise of the spectrum,
is the rms noise of the spectrum,
![]() is the CO linewidth
(given in Col. 7), and
is the CO linewidth
(given in Col. 7), and
![]() is the spectral
resolution. Spectra were
smoothed to
is the spectral
resolution. Spectra were
smoothed to
![]() km s-1.
km s-1.
![\begin{figure}
\par {
\includegraphics[width=5.5cm,angle=-90,viewport=1 120 500 ...
...[width=5.5cm,angle=-90,viewport=1 120 500 700,clip]{MS1894f1m.ps} }
\end{figure}](/articles/aa/full/2002/10/aa1894/Timg40.gif) |
Figure 1:
12CO(1-0) line spectra (smoothed to
|
| Open with DEXTER | |
| name | int-time | rms | I(CO) | V(CO) |
|
FF | |||
| min(on+off) | mK | K km s-1 | K km s-1 | km s-1 | km s-1 | ||||
| 58 | 162 | 3 | <0.44 | - | - | - | <8.04 | 0.19 | <8.10 |
| 87 | 156 | 4 | <0.38 | - | - | - | <7.43 | 0.80 | <8.15 |
| 92 | 30 | 9 | 7.66 | 1.56 | -102 | 360 | 8.74 | 0.04 | 8.49 |
| 97 | 96 | 3 | 3.89 | 0.55 | 2442 | 400 | 8.99 | 0.44 | 8.91 |
| 199 | 240 | 3 | <0.86 | - | - | - | <8.21 | 0.29 | <8.01 |
| 318 | 132 | 3 | <0.37 | - | - | - | <7.96 | 0.49 | <8.37 |
| 459 | 204 | 2 | <0.21 | - | - | - | <7.17 | 2.78 | <7.75 |
| 792 | 192 | 2 | 1.86 | 0.27 | 934 | 210 | 8.38 | 0.14 | 8.25 |
| 874 | 120 | 4 | 2.53 | 0.40 | 1736 | 120 | 8.25 | 0.40 | 8.37 |
| 939 | 240 | 3 | 0.52 | 0.13 | 1265 | 20 | 7.83 | 0.07 | 8.00 |
| 957 | 174 | 4 | 2.30 | 0.37 | 1669 | 100 | 8.21 | 0.49 | 8.36 |
| 1205 | 120 | 4 | 1.72 | 0.23 | 2312 | 40 | 8.09 | 0.40 | 8.30 |
| 1290 | 198 | 3 | 1.23 | 0.17 | 2336* | 40 | 7.94 | 0.39 | 8.09 |
| 1375 | 270 | 2 | 0.93 | 0.21 | 1720 | 130 | 7.81 | 0.05 | 8.17 |
| 1412 | 114 | 7 | <1.07 | - | - | - | <7.88 | 0.11 | <7.81 |
| 1508 | 408 | 3 | 1.08 | 0.29 | 1226 | 110 | 7.88 | 0.09 | 8.02 |
| 1554 | 222 | 2 | 1.17 | 0.24 | 2006 | 170 | 7.92 | 0.32 | 8.08 |
| 1686 | 168 | 4 | <0.39 | - | - | - | <7.45 | 0.18 | <7.81 |
| 1929 | 228 | 3 | <0.38 | - | - | - | <7.43 | 0.32 | <7.72 |
| 1943 | 78 | 10 | <1.57 | - | - | - | <8.05 | 0.13 | <7.70 |
| 2023 | 282 | 4 | <0.50 | - | - | - | <7.55 | 0.42 | <7.96 |
| N4866 | 168 | 4 | <0.85 | - | - | - | <7.78 | 0.10 | <7.67 |
CO measurements are often used to estimate the molecular hydrogen
content of galaxies adopting a standard conversion factor from CO
intensities to H2 column densities (X). In order to allow a comparison with
previous works we convert the CO line fluxes into H2 masses
using the conventional Galactic conversion factor
![]() mol cm-2 (K km s-1)-1
of Strong et al. (1988) where I(CO) from Col. 4 of Table 2 is converted into the
mol cm-2 (K km s-1)-1
of Strong et al. (1988) where I(CO) from Col. 4 of Table 2 is converted into the
![]() scale (see Sect. 3).
The molecular gas mass (M(H
scale (see Sect. 3).
The molecular gas mass (M(H
![]() ,
in solar units) as determined from CO measurements, is given by:
,
in solar units) as determined from CO measurements, is given by:
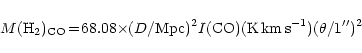 |
(3) |
Since the galaxies were
observed only at the central position, our mass determinations should be
considered as lower limits of the total M(H
![]() .
However since the optical angular
sizes of the observed galaxies do not generally exceed the adopted beam
by more than a factor of two, and since the CO emission in spiral
galaxies is centrally peaked, with an exponential distribution
with a scale length
.
However since the optical angular
sizes of the observed galaxies do not generally exceed the adopted beam
by more than a factor of two, and since the CO emission in spiral
galaxies is centrally peaked, with an exponential distribution
with a scale length ![]() 1.5 smaller than the optical one
(Young et al. 1995), the present data should
give reliable estimates of the total CO emission.
1.5 smaller than the optical one
(Young et al. 1995), the present data should
give reliable estimates of the total CO emission.
Seven target galaxies were previously observed using the 13.7 m FCRAO radiotelescope,
which, at this frequency, has a beam size of 45 arcsec, thus comparable
to the NRAO 12 m.
We compare in Table 3 the different
sets of data. The intensities given in Table 3 are transformed to the main beam scale
adopting a main beam efficiency ![]()
![]() for the FCRAO.
Masses are estimated adopting the same CO to H2 standard conversion factor
for the FCRAO.
Masses are estimated adopting the same CO to H2 standard conversion factor
![]() mol cm-2 (K km s-1)-1and distance
(as given in Table 1). For galaxies observed at several positions, we compare
the central beam observations.
mol cm-2 (K km s-1)-1and distance
(as given in Table 1). For galaxies observed at several positions, we compare
the central beam observations.
| name | rms | I(CO) |
|
reference | ||
| mK | K km s-1 | km s-1 | ||||
| 92 | 13 | 9.29 | 12 | 8.74 | 8.57 | KY |
| 792 | 15 | <1.65 | 12 | 8.38 | <8.08 | KY |
| 1412 | 20 | <2.63 | 15 | <7.88 | <8.02 | Y |
| 1508 | 20 | <1.90 | 12 | 7.88 | <7.88 | K |
| 1554 | 14 | <1.32 | 12 | 7.92 | <7.72 | KY |
| 1943 | 10 | <1.20 | 12 | <8.05 | <7.68 | KY |
| N4866 | 12 | <1.95 | 12 | <7.78 | <7.89 | KY |
In spite of the different beam sizes of the telescopes, the two sets of CO intensity determinations are consistent within a factor of 2. Our observations are generally more sensitive than the published ones, except for VCC 92 (NGC 4192), which was observed as a cross check, and VCC 1943 (NGC 4639), which was interrupted because of incoming bad weather.
The molecular gas properties of late-type galaxies are analysed in this section using the presently reported data jointly with those available in the literature for a large sample of optically selected galaxies in the Coma/A1367 supercluster and in the Virgo cluster (Boselli et al. 1997b, 1995a and references therein) extracted respectively from the Zwicky catalogue (CGCG) and from the Virgo cluster catalogue of Binggeli et al. (1985, VCC). The sample, which is not complete in any sense, includes 266 normal galaxies with 12CO(1-0) data spanning a large range in morphological type (Sa to Im and BCD) and luminosity ( -16 > MB > -22).
The accuracy of the morphological classification is excellent for the
Virgo galaxies (Binggeli et al. 1985, 1993).
Because of the higher distance, the morphology of galaxies belonging
to the other surveyed regions suffers from an uncertainty
of about ![]() 0.75 Hubble type bins.
0.75 Hubble type bins.
We assume a distance of 17 Mpc for the members (and possible members)
of Virgo cluster A, 22 Mpc for
Virgo cluster B, 32 Mpc for
objects in the M and W clouds (see Gavazzi et al. 1999b).
Members of the Coma and A1367 clusters are assumed to be at
distances of 86.6 and 92 Mpc respectively.
Isolated galaxies in the Coma supercluster are assumed to be
at their redshift distance adopting
H0 = 75 km s-1 Mpc-1.
Three different subsamples can be extracted from the Coma/A1367 supercluster and Virgo cluster galaxies:
i) the
unperturbed sample is composed of 153 late-type galaxies, both isolated or
cluster members, whose HI-deficiency
(defined as the logarithm of the ratio of the HI mass to the
average HI mass of isolated objects
of similar morphological type and linear size, Haynes & Giovanelli 1984) is
![]() .
.
ii) the isolated sample is composed of 47 strictly isolated galaxies in the bridge between Coma and A1367 (see Gavazzi et al. 1999a).
iii) the ISOPHOT sample consists of 18 galaxies in Coma and A1367 observed by ISOPHOT (see next section; Contursi et al. 2001).
A small sample of 14 nearby galaxies with an independent measure of the X conversion factor is described in Table 4.
Multifrequency spectrophotometric data are available for most of the analysed galaxies.
The CO data (266 sources) are taken from
Boselli et al. (1995a, 1997b), Kenney & Young (1988a), Young et al. (1995)
and references therein. For mapped galaxies (most of the bright Virgo spirals),
the total CO emission is estimated as the sum of the emission in each single
pointing. The error on the CO line intensity is approximately ![]() 10%.
10%.
211 of the sample galaxies have been observed in H![]() .
H
.
H![]() +[NII] fluxes obtained from imaging,
aperture photometry or integrated spectra
are taken from Kennicutt & Kent (1983), Kennicutt et al. (1984),
Gavazzi et al. (1991) Gavazzi et al. (1998), Moss et al. (1998),
and references therein. Additional observations of several galaxies have been
recently obtained by us
during several runs at the Observatoire de Haute Provence (France), at San Pedro
Martir (Mexico) and at Calar Alto (Boselli & Gavazzi 2002; Gavazzi et al. 2002).
H
+[NII] fluxes obtained from imaging,
aperture photometry or integrated spectra
are taken from Kennicutt & Kent (1983), Kennicutt et al. (1984),
Gavazzi et al. (1991) Gavazzi et al. (1998), Moss et al. (1998),
and references therein. Additional observations of several galaxies have been
recently obtained by us
during several runs at the Observatoire de Haute Provence (France), at San Pedro
Martir (Mexico) and at Calar Alto (Boselli & Gavazzi 2002; Gavazzi et al. 2002).
H![]() NII]EW (equivalent widths) from Kennicutt & Kent (1983),
have been multiplied by
1.16, as suggested by Kennicutt et al. (1994), in order to account
for the continuum flux overestimate due to inclusion of the telluric
absorption band near 6900 Å in the comparison filter.
The estimated error on the H
NII]EW (equivalent widths) from Kennicutt & Kent (1983),
have been multiplied by
1.16, as suggested by Kennicutt et al. (1994), in order to account
for the continuum flux overestimate due to inclusion of the telluric
absorption band near 6900 Å in the comparison filter.
The estimated error on the H![]() NII]EW is
NII]EW is ![]()
![]() 7%.
7%.
HI fluxes are available for 263 galaxies.
HI data are taken from Scodeggio & Gavazzi (1993) and
Hoffman et al. (1996) and references therein.
HI fluxes are transformed into neutral hydrogen masses
with an uncertainty of ![]()
![]() 5%.
5%.
NIR data for 255 galaxies, mostly from Nicmos3 observations, are taken from
Gavazzi et al. (1996a,b, 2000a), Boselli et al. (1997a, 2000).
From these data we derive total (extrapolated to infinity)
magnitudes ![]() ,
as described in Gavazzi et al. (2000b)
with typical uncertainties of
,
as described in Gavazzi et al. (2000b)
with typical uncertainties of ![]()
![]() 5%. These are
converted into total luminosities
using:
5%. These are
converted into total luminosities
using:
![]() (in solar units),
where D is the distance to the source (in Mpc). For a few objects we
derive the H luminosity
from K' band measurements assuming an average H-K' colour of
0.25 mag (independent of type; see Gavazzi et al. 2000a).
A minority of the objects in our sample have an H band magnitude
obtained from aperture photometry, thus with no asymptotic extrapolation.
For these we use the magnitude H25 determined as in Gavazzi & Boselli
(1996) at the optical radius
(the radius at which the B surface brightness is 25 mag arcsec-2)
which is on average 0.1 mag fainter than
(in solar units),
where D is the distance to the source (in Mpc). For a few objects we
derive the H luminosity
from K' band measurements assuming an average H-K' colour of
0.25 mag (independent of type; see Gavazzi et al. 2000a).
A minority of the objects in our sample have an H band magnitude
obtained from aperture photometry, thus with no asymptotic extrapolation.
For these we use the magnitude H25 determined as in Gavazzi & Boselli
(1996) at the optical radius
(the radius at which the B surface brightness is 25 mag arcsec-2)
which is on average 0.1 mag fainter than ![]() (Gavazzi et al. 2000a,b).
The total H magnitudes are corrected
for internal extinction according to Gavazzi & Boselli (1996).
No such correction has been applied to galaxies of type >Scd.
(Gavazzi et al. 2000a,b).
The total H magnitudes are corrected
for internal extinction according to Gavazzi & Boselli (1996).
No such correction has been applied to galaxies of type >Scd.
Metallicity measurements
![]() O/H) are available for a small fraction of the sample (46 galaxies).
These are either determined at
O/H) are available for a small fraction of the sample (46 galaxies).
These are either determined at
![]() for galaxies
from individual HII region measurements
(Zaritsky et al. 1994), or average estimates
if obtained from integrated spectra (Kennicutt 1992; Gavazzi et al. in
preparation).
for galaxies
from individual HII region measurements
(Zaritsky et al. 1994), or average estimates
if obtained from integrated spectra (Kennicutt 1992; Gavazzi et al. in
preparation).
Far-IR fluxes at 100 ![]() m from IRAS for 262 galaxies are taken from several compilations
such as Bicay & Giovanelli (1987), Thuan & Sauvage (1992) and references therein.
For 18 galaxies ISOPHOT data in the wavelength range 100-200
m from IRAS for 262 galaxies are taken from several compilations
such as Bicay & Giovanelli (1987), Thuan & Sauvage (1992) and references therein.
For 18 galaxies ISOPHOT data in the wavelength range 100-200 ![]() m are also available
(Contursi et al. 2001).
m are also available
(Contursi et al. 2001).
The corresponding multifrequency spectrophotometric data for the reference
sample of nearby galaxies are listed in Table 4.
Giant molecular complexes of angular dimensions larger than 100 pc might
be in non-equilibrium. Furthermore the contribution of the atomic hydrogen
inside these complexes to their total mass can be important.
An accurate estimate of the molecular gas mass using the virial theorem can be
obtained only for the dense cores in virial equilibrium of giant molecular
clouds, where the contribution of HI is negligible. These cores have
linear dimensions of ![]() 10 pc. We thus decided to include in Table 4
only those galaxies with interferometric CO observations where the high
resolution (
10 pc. We thus decided to include in Table 4
only those galaxies with interferometric CO observations where the high
resolution (![]() 100 pc) allowed the determination of X from CO line
widths and intensities measurements of the resolved cores of molecular clouds.
100 pc) allowed the determination of X from CO line
widths and intensities measurements of the resolved cores of molecular clouds.
| name | type | dist | MBa | est.
|
ref. | H |
ref. | X | methode | ref. | |
| Mpc | mag | solar units | Å | 1020 | |||||||
| MW | 0 | -20.40 | 10.76c | 8.90 |
1 | - | - | 1.56 |
gamma | 15 | |
| SMC | SB(s)m | 0.061 | -16.30 | 8.81c | 8.04 |
1 | 24 |
5 | 10.0 | virial | 16 |
| LMC | SB(s)m | 0.055 | -18.40 | 9.81c | 8.37 |
1 | 36 |
5 | 8.0 | virial | 17 |
| M31 | SA(s)b | 0.77 | -20.67 | 11.07 | 9.01 |
1 | 3.7 |
6 | 2.4 |
virial | 1 |
| M33 | SA(s)cd | 0.84 | -18.31 | 9.90 | 8.78 |
2 | 20 |
7 | 5.0 |
virial | 1 |
| M51 | SA(s)bc | 9.6 | -20.75 | 11.08 | 9.23 |
2 | 19 |
8 | 0.6 | mm | 16 |
| M81 | SA(s)ab | 3.8 | -20.51 | 10.90 | 9.00 |
2 | 10 |
8 | 0.7f | virial | 18,19 |
| M82 | I0sbrst | 3.63 | -18.94 | 10.69 | 9.00 |
3 | 42 |
8 | 1 | mm | 20 |
| IC10 | IBm | 0.66 | -15.90 | 8.62c | 8.31 |
1 | - | - | 6.6 |
virial | 1 |
| N891 | SA(s)b?Sp | 9.5 | -20.52 | 10.78 | - | - | 7.5 |
10,11,12,13 | 1.5 | mm | 16,22 |
| N1569 | IBm | 2.2 | -16.90 | 8.79 | 8.19 |
4 | 149 |
9, 14 | 15f | virial | 10 |
| N4565 | SA(s)b?Sp | 9.4 | -21.77 | 11.13 | - | - | 2.7 |
12 | 1.0 | mm | 16 |
| N6822 | IB(s)m | 0.5 | -15.10 | 8.15 | 8.16 |
1 | - | - | 6.6 |
virial | 1 |
| N6946 | SAB(rs)cd | 5.5 | -20.92 | 10.60 | 9.06 |
2 | 29 |
14 | 1.8 | mm | 21 |
b H band magnitudes, corrected for extinction as in Gavazzi & Boselli (1996), are extracted from
the 2MASS survey and/or from aperture photometry (Gezari et al. 1993), or form recent observations taken at the 3.5 TNG
telescope (Gavazzi et al., in preparation). The estimated error on the H luminosity is <![]() 10% (photometric accuracy plus the
extrapolation to a total value),
10% (photometric accuracy plus the
extrapolation to a total value), ![]() 0.12 mag (in log) when determined from the LH vs. MB relation given in c),
and
0.12 mag (in log) when determined from the LH vs. MB relation given in c),
and ![]() 0.15 mag for the Milky Way (MW).
c For galaxies not observed in the H band (5), the H luminosity
is determined from
0.15 mag for the Milky Way (MW).
c For galaxies not observed in the H band (5), the H luminosity
is determined from ![]() (
(
![]() (
(![]() 0.22) - 0.48 (
0.22) - 0.48 (![]() 0.01
0.01
![]() (R2=0.84, where R is the regression coefficient)
has been determined from 246 galaxies in our sample.
(R2=0.84, where R is the regression coefficient)
has been determined from 246 galaxies in our sample.
d For M 31 and NGC 4565 H![]() NII]EW have been estimated using published H
NII]EW have been estimated using published H![]() fluxes
and red continuum as determined from the R band photometry assuming 0.0 mag in R equivalent to
fluxes
and red continuum as determined from the R band photometry assuming 0.0 mag in R equivalent to
![]() erg cm-2 s-1. Given its high inclination, we corrected the H
erg cm-2 s-1. Given its high inclination, we corrected the H![]() flux of NGC 4565 for 2 mag.
flux of NGC 4565 for 2 mag.
e Gamma: from high-energy gamma-ray emission from EGRET observations; virial: from CO observations of resolved molecular clouds assuming virial equilibrium; mm: from millimetric observations assuming a metallicity-dependent dust to gas ratio.
f Uncertain values
References:
1: Arimoto et al. (1996), average of the disc;
2: Zaritsky et al. (1994);
3: Gavazzi et al., in preparation;
4: Kobulnicky & Skillman (1997);
5: Kennicutt et al. (1995);
6: H![]() flux from Devereux et al. (1994), and R magnitude from Walterbos & Kennicutt (1987);
7: Devereux et al. (1997), and private communication;
8: Boselli & Gavazzi (2002);
9: Hunter et al. (1993);
10: Taylor et al. (1999);
11: Hoopes, private communication;
12: Rand et al. (1992);
13: Hoopes et al. (1999);
14: Kennicutt & Kent (1983);
15: Hunter et al. (1997), average over the whole Milky Way;
16: Boselli et al. (1997b), scale of 10 pc for SMC;
17: Rubio (1999), scale 10 pc;
18: Taylor & Wilson (1998);
19: Allen et al. (1997);
20: Wild et al. (1992), central 1 kpc;
21: Bianchi et al. (2000);
22: Alton et al. (2000).
flux from Devereux et al. (1994), and R magnitude from Walterbos & Kennicutt (1987);
7: Devereux et al. (1997), and private communication;
8: Boselli & Gavazzi (2002);
9: Hunter et al. (1993);
10: Taylor et al. (1999);
11: Hoopes, private communication;
12: Rand et al. (1992);
13: Hoopes et al. (1999);
14: Kennicutt & Kent (1983);
15: Hunter et al. (1997), average over the whole Milky Way;
16: Boselli et al. (1997b), scale of 10 pc for SMC;
17: Rubio (1999), scale 10 pc;
18: Taylor & Wilson (1998);
19: Allen et al. (1997);
20: Wild et al. (1992), central 1 kpc;
21: Bianchi et al. (2000);
22: Alton et al. (2000).
| This work | ||||
| Variable | slope | constant | n. of objects | R2a |
|
|
0.51 |
19.76 |
11 | 0.29 |
| -1.01 |
29.28 |
12 | 0.83 | |
|
|
-0.38 |
24.23 |
14 | 0.75 |
| MB | 0.18 |
23.77 |
14 | 0.67 |
| Literature | ||||
| Variable | slope | constant | reference | |
| -1.00 | 29.30 | 1 | ||
| -0.67 |
26.43 |
2 | ||
| MB | 0.20 | 24.44 | 1 |

Table 4 contains the best-estimated values of X for a sample of 14 well-studied
nearby galaxies.
Table 4 shows that X spans the range
![]() mol cm-2 (K km s-1)-1for galaxies of different morphological type.
mol cm-2 (K km s-1)-1for galaxies of different morphological type.
The ratio between 12CO(1-0) line emission and the molecular hydrogen column density strongly depends on several physical properties of the ISM such as the UV radiation field, the metallicity and the cosmic ray density (Lequeux et al. 1994; Kaufman et al. 1999), which are known to vary from galaxy to galaxy.
We empirically quantify these dependences by plotting in Fig. 2.
(left panels) the relationship between X, the
H![]() NII]EW and the metallicity (
NII]EW and the metallicity (![]() O/H)) for the 14
nearby galaxies.
O/H)) for the 14
nearby galaxies.
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{MS1894f2.ps}\end{figure}](/articles/aa/full/2002/10/aa1894/Timg67.gif) |
Figure 2:
The relationship for the template sample of nearby galaxies
between the X conversion factor from CO line intensity to H2 column density and a) the H |
| Open with DEXTER | |
The relationship with the H![]() NII]EW (taken as a SFR tracer),
if any, is ill-defined and that with metallicity is quite clear.
In galaxies with a low metallicity
and a strong UV radiation field (high H
NII]EW (taken as a SFR tracer),
if any, is ill-defined and that with metallicity is quite clear.
In galaxies with a low metallicity
and a strong UV radiation field (high H![]() NII]EW) (both go together in general)
the X conversion factor is
a factor of
NII]EW) (both go together in general)
the X conversion factor is
a factor of ![]() 20 higher than in quiescent, high metallicity galaxies such as
the Milky Way. These two relationships can be used in principle to determine
a more accurate value of the X conversion factor once the metallicity and/or
the H
20 higher than in quiescent, high metallicity galaxies such as
the Milky Way. These two relationships can be used in principle to determine
a more accurate value of the X conversion factor once the metallicity and/or
the H![]() NII]EW is known. Metallicity measurements
are available for only a minority of galaxies, while H
NII]EW is known. Metallicity measurements
are available for only a minority of galaxies, while H![]() NII]EW
exist for a few hundred.
However there is a well-known anticorrelation (correlation) between
H
NII]EW
exist for a few hundred.
However there is a well-known anticorrelation (correlation) between
H![]() NII]EW (metallicity) and luminosity (Gavazzi et al. 1998; Zaritsky et al. 1994)
in normal galaxies. It is reflected here by a strong relation between
X and the H luminosity (Fig. 2c) or the B absolute magnitude (Fig. 2d).
The best fits to the data are given in Table 5.
The slope of the fits are consistent with those found by Arimoto et al. (1996), but significantely
steeper than that found by Wilson (1995) for the X vs.
NII]EW (metallicity) and luminosity (Gavazzi et al. 1998; Zaritsky et al. 1994)
in normal galaxies. It is reflected here by a strong relation between
X and the H luminosity (Fig. 2c) or the B absolute magnitude (Fig. 2d).
The best fits to the data are given in Table 5.
The slope of the fits are consistent with those found by Arimoto et al. (1996), but significantely
steeper than that found by Wilson (1995) for the X vs.
![]() O/H) relation
(see Table 5). This difference in slope with Wilson is probably due to the fact that our
sample includes many metal rich spiral galaxies with low values of X
(
O/H) relation
(see Table 5). This difference in slope with Wilson is probably due to the fact that our
sample includes many metal rich spiral galaxies with low values of X
(
![]() mol cm-2 (K km s-1)-1)
not present in the Wilson's sample.
Our intercept for the X vs.
mol cm-2 (K km s-1)-1)
not present in the Wilson's sample.
Our intercept for the X vs.
![]() O/H) relation is consistent
with that of Arimoto et al. (1996).
Our intercept in the X vs. MB relation is lower since
Arimoto et al. (1996) includes all the objects rejected here whose Xvalue is probably overestimated due to the low spatial resolution of the
CO observations (>100 pc).
O/H) relation is consistent
with that of Arimoto et al. (1996).
Our intercept in the X vs. MB relation is lower since
Arimoto et al. (1996) includes all the objects rejected here whose Xvalue is probably overestimated due to the low spatial resolution of the
CO observations (>100 pc).
The relationships given in Table 5
between X and LH and/or MB are de facto empirical calibrations
for a luminosity-dependent X conversion factor.
Given the large uncertainty in the determination of X in the nearby
sample of galaxies, it is difficult to quantify the resulting accuracy in
the molecular gas mass estimated using the relationships given in Table 5.
We should also remind that even inside a given object X might change by
a factor of ![]() 10 from the diffuse medium to the core of GMCs (Polk et al. 1988);
it is thus difficult to estimate a single value of X representing the entire galaxy.
We can however conclude that the adoption of the relations given in Table 5
should remove the first-order systematic effect with luminosity
in the estimate of the molecular hydrogen content of galaxies using CO data.
The use of a standard X conversion factor as those generally used in the literature
(X=2.3-
10 from the diffuse medium to the core of GMCs (Polk et al. 1988);
it is thus difficult to estimate a single value of X representing the entire galaxy.
We can however conclude that the adoption of the relations given in Table 5
should remove the first-order systematic effect with luminosity
in the estimate of the molecular hydrogen content of galaxies using CO data.
The use of a standard X conversion factor as those generally used in the literature
(X=2.3-
![]() mol cm-2 (K km s-1)-1)
overestimates the molecular gas mass by a factor of
mol cm-2 (K km s-1)-1)
overestimates the molecular gas mass by a factor of ![]() 2-3
in massive galaxies of
2-3
in massive galaxies of
![]() ,
or
,
or
![]() mag,
while underestimates M(H2) in low mass objects of
mag,
while underestimates M(H2) in low mass objects of
![]() ,
or
,
or
![]() mag as those observed in this work by a factor of
mag as those observed in this work by a factor of ![]() 2.
The relationship between X and
2.
The relationship between X and
![]() O/H) might
be used to estimate the radial distribution of molecular hydrogen in
galaxies mapped in CO with available measurements of the metallicity gradient.
O/H) might
be used to estimate the radial distribution of molecular hydrogen in
galaxies mapped in CO with available measurements of the metallicity gradient.
An alternative technique for determining the molecular gas content can be pursued by assuming a metallicity-dependent dust to gas ratio and determining the dust mass using far-IR or submillimetric continuum data. The dust to gas ratio is then determined in regions with no CO emission, hence supposed to be strongly dominated by HI. In regions with CO emission, the excess dust emission with respect to this ratio indicates the mass of H2. This technique has been succesfully applied to M 51, NGC 891, NGC 4565 and to some nearby irregular galaxies such as the Magellanic Clouds (Guélin et al. 1995; Guélin et al. 1993; Neininger et al. 1996; Israel 1997).
In normal galaxies such as those in our sample the dust mass is dominated
by the cold dust emitting in the far-IR with a peak at ![]() 200
200 ![]() m.
The determination of the total dust mass can be achieved provided that the
100-1000
m.
The determination of the total dust mass can be achieved provided that the
100-1000 ![]() m far-IR flux and the cold dust
temperature are known. Recent observations aimed at determining the
spectral energy distribution in the far-IR of normal, quiescent
galaxies indicate that their SED can be fitted
by a modified Planck law
m far-IR flux and the cold dust
temperature are known. Recent observations aimed at determining the
spectral energy distribution in the far-IR of normal, quiescent
galaxies indicate that their SED can be fitted
by a modified Planck law ![]()
![]()
![]() ,
with
,
with ![]() (Alton et al. 2000).
The total dust mass can be thus determined from the relation (Devereux & Young 1990):
(Alton et al. 2000).
The total dust mass can be thus determined from the relation (Devereux & Young 1990):
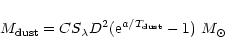 |
(4) |
The determination of the dust to gas ratio in a way consistent with that
obtained in the solar neighbourhood, requires the estimate of the gas and dust surface densities,
thus of the spatial distribution of dust and gas over the discs.
Unfortunately only integrated HI and dust masses are available for our spatially
unresolved galaxies. It is however reasonable to assume that the cold dust
is as extended as the optical disc (Alton et al. 1998).
The HI gas surface density is available only for a few galaxies in our sample
from VLA observations (Cayatte et al. 1994). For these objects we
observe a good relationship between the HI surface density ![]() HI and
the HI-deficiency parameter (
HI and
the HI-deficiency parameter (
![]() ), (defined as in Sect. 5.1) (Fig. 3):
), (defined as in Sect. 5.1) (Fig. 3):
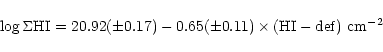 |
(5) |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{MS1894f3.ps}\end{figure}](/articles/aa/full/2002/10/aa1894/Timg88.gif) |
Figure 3: The relationship between the HI surface density and the HI-deficiency parameter for the galaxies in common with Cayatte et al. (1994). The dashed line gives the best fit to the data. |
| Open with DEXTER | |
The gas to dust ratio should depend on metallicity since
the dust content is expected to be proportional to the metal content.
A gas to dust vs. metallicity relation can be calibrated using the
data available for the MW (Sodroski et al. 1994), the LMC (4 times
solar; Koornneef 1982) and the SMC (10 times solar; Bouchet et al. 1985).
This gives the relation:
| = | |||
| (6) |
where the gas to dust ratio is given relative to the solar neighborhood,
estimated by Sodroski et al. (1994) at (gas/dust)
![]() .
The metallicity can be predicted using the metallicity vs. H band luminosity relation shown in Fig. 4:
.
The metallicity can be predicted using the metallicity vs. H band luminosity relation shown in Fig. 4:
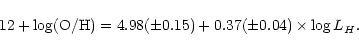 |
(7) |
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{MS1894f4.ps}\end{figure}](/articles/aa/full/2002/10/aa1894/Timg94.gif) |
Figure 4:
The relationship between the metallicity (
|
| Open with DEXTER | |
Using Eqs. (6) and (7) we can predict the gas to dust ratio for a galaxy
of any H luminosity.
The molecular gas mass comes directly if we assume that the H2 is
homogeneously distributed over the optical disc and
X is given by X=M(H
![]() /I(CO). The assumption of a homogeneous,
flat distribution for the molecular hydrogen component over the disc of galaxies,
which is in contradiction with the observational evidence that the CO emission
is generally centrally peaked (see Sect. 4.1), might introduce a systematic error in the
determination of X. We remark however that the expected H2 distribution is
flatter than that of the CO emitting gas because of the observed decrease of the metallicity
in the outer parts of galaxy discs.
/I(CO). The assumption of a homogeneous,
flat distribution for the molecular hydrogen component over the disc of galaxies,
which is in contradiction with the observational evidence that the CO emission
is generally centrally peaked (see Sect. 4.1), might introduce a systematic error in the
determination of X. We remark however that the expected H2 distribution is
flatter than that of the CO emitting gas because of the observed decrease of the metallicity
in the outer parts of galaxy discs.
![\begin{figure}
\par\includegraphics[width=17.6cm,clip]{MS1894f5.ps}\end{figure}](/articles/aa/full/2002/10/aa1894/Timg96.gif) |
Figure 5:
Same as Fig. 2 but including values of X determined using
the alternative method described in Sect. 6.2 for the
unperturbed sample (small symbols).
Small open dots are for galaxies detected at 100 |
| Open with DEXTER | |
The values of X obtained for the sample galaxies are compared with those of the template galaxies in Fig. 5 (small symbols). In spite of the larger scatter, it is encouraging to see that the new values of X, at any given luminosity, metallicity and UV radiation field, are in rough agreement with those obtained for the template. The large uncertainty and systematic effects are not unexpected given the number of assumptions underlying the method. From Fig. 5 we conclude that the luminosity-dependent X conversion factor given in Table 5 is appropriate for estimating the molecular gas content of late-type galaxies from 12CO(1-0) line intensity measurements. From now on, the molecular gas content of the 266 sample galaxies, M(H2), is estimated using the H band luminosity-dependent X value given in Table 5.
The molecular gas content of our sample galaxies, normalized to the total mass of galaxies,
is plotted in Figs. 6a and b as a function of the H luminosity and the morphological type.
To avoid any systematic environmental effect, only unperturbed
galaxies with an HI-deficiency ![]() 0.3 (defined as in Sect. 5.1)
are considered.
0.3 (defined as in Sect. 5.1)
are considered.
![\begin{figure}
\par\includegraphics[width=12.3cm,clip]{MS1894f6.ps}\end{figure}](/articles/aa/full/2002/10/aa1894/Timg97.gif) |
Figure 6:
The relationship between the normalised molecular gas mass of unperturbed
galaxies (HI-deficiency |
| Open with DEXTER | |
Figure 6 shows a strong anticorrelation between the normalized molecular gas mass and the total mass of galaxies, as traced by the H luminosity. The relationship with the morphological type is significantely weaker, even though it seems that early spirals have a lower normalized amount of molecular gas than late-type ones. Figures 6c and d show that the molecular to atomic hydrogen ratio is roughly constant in galaxies spanning a large range in luminosity and morphological type. The average value is M(H2)/M(HI)=0.14 (with upper limits treated as detections).
The weak trends of the molecular gas content (per unit mass) with the morphological type and with the H luminosity as well as the constant molecular to atomic gas fraction observed by Boselli et al. (1997b) on a small, optically selected sample of Sa-Sc galaxies in the Coma supercluster is confirmed here with higher statistical significance and extended to lower luminosities, including Im and BCDs. The decrease of the molecular hydrogen to dynamical mass ratio or to the atomic hydrogen ratio claimed by Casoli et al. (1998), Sage (1993), Young & Knezek (1989) and Kenney & Young (1988b) for Scd-Sm-Im galaxies is probably due to a systematic underestimate of the total M(H2) in low mass galaxies when derived assuming a constant X conversion factor.
The available data can be used to analyse the effects of environment on the
molecular gas content of normal galaxies. Following Boselli et al.
(1997b) an H2 deficiency parameter can be defined once the relationship
between the molecular gas content and the H luminosity is calibrated
on the unperturbed sample:
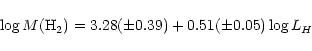 |
(8) |
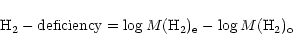 |
(9) |
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{MS1894f7.ps}\end{figure}](/articles/aa/full/2002/10/aa1894/Timg102.gif) |
Figure 7:
The relationship between the H2 and the HI-deficiency parameter;
filled dots are for the isolated galaxies sample. Triangles indicate lower
limits to the H2 ( |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.2cm,clip]{MS1894f8.ps}\end{figure}](/articles/aa/full/2002/10/aa1894/Timg103.gif) |
Figure 8:
The relationship between the normalized star formation
index H |
| Open with DEXTER | |
The present work confirms the lack of molecular-gas deficient galaxies in clusters such as Coma (Boselli et al. 1997b; Casoli et al. 1991) or Virgo (Kenney & Young 1989; Boselli 1994), extending previous results to lower luminosities. This analysis suggests that the low luminosity, CO deficient spiral galaxies observed in Virgo by Kenney & Young (1988b) are not necessarily deficient in molecular hydrogen.
The atomic gas has to condense into molecular clouds to form new stars. A strong relationship between any tracer of star formation and the molecular gas content of late-type galaxies is thus expected.
| Whole sample | |||
|
slope | constant | scatter |
| 0.797 | 2.184 | 0.603 | |
| 1.005 | 3.042 | 0.723 | |
|
|
0.938 | 2.214 | 0.554 |
| Unperturbed sample (
|
|||
|
slope | constant | scatter |
| 1.078 | 2.300 | 0.902 | |
| 0.896 | 2.944 | 0.741 | |
|
|
1.116 | 2.251 | 0.792 |
The relationship between the normalized star formation index H![]() NII]EW
NII]EW![]() and the molecular gas content (per unit mass) observed in bright galaxies
by Boselli et al. (1995b, 1997b) extends to low luminosity galaxies
(
and the molecular gas content (per unit mass) observed in bright galaxies
by Boselli et al. (1995b, 1997b) extends to low luminosity galaxies
(
![]() )
(see Fig. 8a)
once their molecular gas mass is estimated using a luminosity-dependent
X conversion factor. The best fits to the data along with the scatter
from the linear fit are given in Table 6
for the whole sample and for the unperturbed sample (
)
(see Fig. 8a)
once their molecular gas mass is estimated using a luminosity-dependent
X conversion factor. The best fits to the data along with the scatter
from the linear fit are given in Table 6
for the whole sample and for the unperturbed sample (
![]() ).
This observational evidence confirms that the
lack of a strong relationship between any star formation tracer and
the molecular gas mass when determined assuming a constant value of Xis due to a systematic underestimate of the total molecular gas mass
of low luminosity galaxies. Figure 8 shows that the relationship
between the star formation activity and the total
gas (HI + H2) content of galaxies is stronger and less dispersed than for the
individual gas components. This relationship is shared by normal and gas deficient
galaxies, even though unperturbed galaxies have on average higher values of
H
).
This observational evidence confirms that the
lack of a strong relationship between any star formation tracer and
the molecular gas mass when determined assuming a constant value of Xis due to a systematic underestimate of the total molecular gas mass
of low luminosity galaxies. Figure 8 shows that the relationship
between the star formation activity and the total
gas (HI + H2) content of galaxies is stronger and less dispersed than for the
individual gas components. This relationship is shared by normal and gas deficient
galaxies, even though unperturbed galaxies have on average higher values of
H![]() NII]EW.
NII]EW.
The efficiency in transforming gas into stars can be estimated using
the star formation rate (SFR) according to Boselli et al. (2001), i.e.
using H![]() +[NII] fluxes corrected for the contribution
of the [NII] line, for extinction, and transformed into SFR (in solar masses per year)
assuming a IMF of slope
+[NII] fluxes corrected for the contribution
of the [NII] line, for extinction, and transformed into SFR (in solar masses per year)
assuming a IMF of slope
![]() in the mass range
in the mass range
![]() and
and
![]() .
.
![\begin{figure}
\par\includegraphics[width=13.7cm,clip]{MS1894f9.ps}\end{figure}](/articles/aa/full/2002/10/aa1894/Timg109.gif) |
Figure 9:
The relationship between the present star formation efficiency SFE and a) the H luminosity and b)
the morphological type. Filled symbols are for
the unperturbed sample (
|
| Open with DEXTER | |
Figure 9 shows the relationship between the present SFE, defined as:
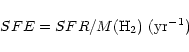 |
(10) |
Using spectro-photometric data available in the literature for a small
sample of nearby galaxies we have analysed the relationships between the
X = N(H2)/I(CO) conversion factor and various parameters
characterizing the physical properties of the ISM.
The behaviour of the nearby galaxies, whose value of X has been
measured by independent techniques,
is compared to that of a sample of 266 late-type galaxies with available
multifrequency data. For these 266 galaxies X is estimated
by assuming a metallicity-dependent dust to gas ratio, where the
dust masses have been determined using ISOPHOT and IRAS
100-200 ![]() m data.
Both samples show an anticorrelation (correlation) between X and the
metallicity (or the UV radiation field), with
higher values of X in metal-poor, star forming galaxies.
These observational results can be explained if the diffuse
carbon monoxide in the outskirts of the giant molecular clouds is dissociated by
UV photons at a rate higher than the molecular hydrogen which, given
its higher density, is more efficiently self-shielded.
The ratio between N(H2) and I(CO) is thus expected to increase
when the UV radiation field increases, as in star forming
regions or in regions where the extinction, therefore the dust
content and the metallicity, are low.
m data.
Both samples show an anticorrelation (correlation) between X and the
metallicity (or the UV radiation field), with
higher values of X in metal-poor, star forming galaxies.
These observational results can be explained if the diffuse
carbon monoxide in the outskirts of the giant molecular clouds is dissociated by
UV photons at a rate higher than the molecular hydrogen which, given
its higher density, is more efficiently self-shielded.
The ratio between N(H2) and I(CO) is thus expected to increase
when the UV radiation field increases, as in star forming
regions or in regions where the extinction, therefore the dust
content and the metallicity, are low.
Given the strong relationship between metallicity, star formation
activity and luminosity, the sample of nearby galaxies is used to
calibrate a luminosity-dependent X conversion factor.
Using this new calibration, we re-analyse the molecular
gas properties of galaxies spanning a large range in morphological
type and luminosity.
Low-mass, dwarf galaxies have higher molecular gas masses (per
unit galaxy mass) than early-type, massive spirals. The molecular gas
fraction in clouds or complexes is ![]() 15% of the total HI reservoir for all
late-type galaxies.
15% of the total HI reservoir for all
late-type galaxies.
Galaxies strongly interacting with the cluster environment have, on average, a molecular gas content comparable to isolated, unperturbed objects.
The star formation rate of late-type galaxies is strongly related to their molecular gas content. This relationship is valid for galaxies spanning a large range in luminosity.
The efficiency in transforming gas into stars is roughly constant in galaxies of different type and luminosity and belonging to different environments.
Acknowledgements
We want to thank the 12 m telescope operators for their invaluable help during the remote observations. We thank J. Kenney for providing us with some unpublished CO data, and C. Hoopes and N. Devereux for the H
NII]EW of NGC 891 and M 33. We thank C. Bonfanti for providing us with some metallicity measurements, V. Buat, A. Contursi and J. M. Deharveng for interesting discussions, and S. Zibetti for providing us with fitting routines. We thank the anonymous referee for comments and suggestions which helped improving the quality of the manuscript. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center, funded by the National Aeronautics and Space Administration and the National Science Foundation.