A&A 384, 329-342 (2002)
DOI: 10.1051/0004-6361:20011726
B. F. Vitorino - V. Jatenco-Pereira - R. Opher
Instituto Astronômico e Geofísico, Universidade de São Paulo,
Av. Miguel Stéfano 4200,
04301-904 São Paulo, Brazil
Received 29 November 2000 / Accepted 26 November 2001
Abstract
We study the outflows from randomly perturbed Keplerian accretion disks. In the velocity field of the gas at the surface of the disk, we introduce a random perturbation proportional to ra, where
r is the radial distance and a is a fixed parameter in the simulation (with values of
-3/2, -1, -1/2, 0, 1/2 or 1). In the simulations, the disk is a fixed boundary
from which the gas is ejected with continuous and random velocities added together. The
continuous ejection velocity is taken to be a thousandth of that of the local Keplerian disk;
the maximum value of the random velocity is 10 times the continuous velocity. We observe the
formation of periodic structures along the outflow axis. The distance of the axial separation
between the structures is found to be about 11 times the innermost radius of the accretion
disk. For a negative radial slope a, the structures are well defined and situated near the
jet axis, whereas for a positive slope, decollimation of the jet occurs.
Key words: ISM: jets and outflows - galaxies: jets - accretion, accretion disks - magnetohydrodynamics (MHD)
Episodic outbursts and knots have been observed in astrophysical jets. Recent theories and models try to provide a natural explanation for these features, common to all astrophysical jets.
There are two approaches in making the numerical simulations of axisymmetric magnetized flows from accrection disks. One approach attempts to follow the internal dynamics of the disk (Shibata & Uchida 1986; Stone & Norman 1994). The second approach does not follow the internal dynamics of the disk, but treats it as aboundary condition in Keplerian equilibrium at the base of the wind (Bell & Lucek 1995; Ustyugova et al. 1995).
Adopting the latter aproach, Ouyed & Pudritz (1997a,b, 1999) made 2.5-dimensional, high-resolution numerical MHD simulations of the onset and collimation of outflows from the surface of a Keplerian accretion disk around a central object. They obtained steady or episodic jets, depending upon the assumed values of the constant (in time) ejection velocity from the disk to the corona. For the smallest values of the ejection velocity, their results showed the episodic production of knots near the surface of the disk, which propagate along the jet axis. These knots are produced by MHD shocks.
We made 2.5-dimensional time-dependent simulations with the ZEUS-3D code (Stone & Norman
1992a,b) in the axisymmetry option, introducing a random velocity perturbation in the accretion
disk. We know that accretion disks are subject to instabilities, such as the
Balbus-Hawley instability. However, the origin of instabilities, in general, is unknown.
We investigate here the behaviour of the produced jets when the perturbations have a radial
dependence in the disk. The perturbation was random in time and its
amplitude, proportional to ra, where r is the radial distance and a defines the radial
dependence of the amplitude of the perturbation. For each time interval, the velocity amplitude
was chosen by a random generator at all radial positions. The time interval is defined by the
time step controled by the code which satisfies the Courant-Friedrichs-Lewy (CFL) stability
condition (this condition guaranties causality). In our simulations, the time step was
![]()
![]() periods of rotation at the innermost radius of the accretion disk
periods of rotation at the innermost radius of the accretion disk
![]() .
The radial position, where the perturbation is introduced, is defined by the radial
resolution used. A minimum interval of
.
The radial position, where the perturbation is introduced, is defined by the radial
resolution used. A minimum interval of
![]() was used at the radial position
was used at the radial position ![]() ,
while
a maximum interval of
,
while
a maximum interval of ![]() 1.16
1.16 ![]() was used at
was used at
![]() .
.
A random component was added to the continuous component with a maximum value at ![]() chosen
to be 10 times the continuous ejection velocity. The simulations were run with different
radial dependencies for the perturbation. We simulated the region 1-
chosen
to be 10 times the continuous ejection velocity. The simulations were run with different
radial dependencies for the perturbation. We simulated the region 1-
![]() of the accretion
disk.
of the accretion
disk.
Introducing the random perturbation with different radial slopes (i.e., values of a), we
observed the fomation of periodic structures along the outflow axis. The distance of the axial
separation of the structures was found to be about
![]() .
For a negative radial slope for
the perturbation (i.e., negative values of a), the density structures are well defined near
the jet axis. For a positive slope, decollimation of the jet occurs. As the slope from zero
to positive values is increased, the region near the jet axis is found to be less and less
well-defined.
.
For a negative radial slope for
the perturbation (i.e., negative values of a), the density structures are well defined near
the jet axis. For a positive slope, decollimation of the jet occurs. As the slope from zero
to positive values is increased, the region near the jet axis is found to be less and less
well-defined.
In Sect. 2 the basic equations that were solved are presented. The model is described in Sect. 3. In Sect. 4, the numerical results are presented and discussed. Finally, in Sect. 5, we present a summary and the final conclusions.
Cylindrical coordinates (r, ![]() ,
z) were adopted, with the central object at the origin.
The z-axis is perpendicular to the disk, such that the surface of the disk lies in the
z=0 plane.
,
z) were adopted, with the central object at the origin.
The z-axis is perpendicular to the disk, such that the surface of the disk lies in the
z=0 plane.
The equations that describe the conservation of mass, momentum, energy and
magnetic flux are:
We assumed a polytropic gas
![]() with the polytropic index
with the polytropic index
![]() .
Thus,
ignoring radiative transfer effects, the energy Eq. (3) need not be solved.
It was also assumed that an Alfvénic turbulent pressure
.
Thus,
ignoring radiative transfer effects, the energy Eq. (3) need not be solved.
It was also assumed that an Alfvénic turbulent pressure ![]() provides, together with
the thermal pressure, the main support against gravity for the cold corona. Here
provides, together with
the thermal pressure, the main support against gravity for the cold corona. Here
![]() ,
where
,
where
![]() is the ratio of the gas pressure to the Alfvénic turbulent pressure,
assumed to be constant (OP97a).
is the ratio of the gas pressure to the Alfvénic turbulent pressure,
assumed to be constant (OP97a).
All parameters are given in units of their values at the innermost radius of the accretion
disk ![]() .
Thus, the normalized equation of motion (Eq. (2)) is
.
Thus, the normalized equation of motion (Eq. (2)) is
We study a model in which the disk is a fixed boundary condition in pressure equilibrium with the corona. There is a point mass at the center of the disk that represents a star (or a black hole, a neutron star or a white dwarf). An initial potential (zero current) poloidal field threads the disk and the corona.
In the numerical simulations, the computational domain defines the spatial region where the MHD equations are time evolved. ZEUS-3D, a grid code, divides the computational domain into cells, called "active" zones. Finite differencing the evolution near the boundaries of the grid requires that values for the dependent variables be specified beyond the computational domain. Therefore, at each boundary, "ghost" zones are added. Values for the dependent variables in the ghost zones are specified, using boundary conditions appropriate to the geometry and the physics of the problem being solved. Thus, the evolution equations are not solved for the ghost zones.
Inflow and outflow are used to specify the boundary conditions which mean that a physical quantity is flowing inside or outside of the computational domain, respectively. We use the expression injection velocity to have the same meaning as the term inflow.
The values of all the variables in the ghost zones in the inflow boundary condition are held equal to a set of predetermined values (which may not be allowed to vary in time). Outflow is not permited. In the outflow boundary condition, the values of the variables in the ghost zones are equal to those in the corresponding active zones (extrapolating the flow beyond the boundary).
In the reflecting boundary condition, zone-centered variables (scalars), as well as the tangential components of the velocity and the magnetic field in the ghost zones are set equal to the corresponding values of their images in the active zones. The normal component of the velocity and the magnetic field are set equal to zero on the boundary and reflected into the adjacent zone.
We use inflow boundary conditions at the disk surface![]() and open outflow conditions on the remaining boundaries. Reflecting boundaries
are used along the axis of symmetry, coinciding with the disk axis. The initial setup and
boundaries are shown in Fig. 1.
and open outflow conditions on the remaining boundaries. Reflecting boundaries
are used along the axis of symmetry, coinciding with the disk axis. The initial setup and
boundaries are shown in Fig. 1.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{MS10516f1.eps}}\end{figure}](/articles/aa/full/2002/10/aa10516/Timg74.gif) |
Figure 1: The adopted model. The central object is placed at the origin of the coordinate system. The ghost zones (z<0) define the surface of the Keplerian disk, while the active zones (which evolve in time) define the corona. The poloidal magnetic field continues smoothly into the disk surface (Fig. 2 of OP97a). |
| Open with DEXTER | |
Initially, the corona has no toroidal magnetic field. In order to assure that an outflow can
only arise due to the magnetocentrifugal mechanism, magnetostatic equilibrium is numerically
maintained. Resolving Eq. (6) for magnetostatic equilibrium, we obtain the
expression for the coronal density distribution,
Assuming the surface of the accretion disk to be a fixed boundary condition, there is no back
reaction by the jet. Time evolution occurs only in the coronal region (![]() )
where the
jet exists. However, we fix the density at the base of the corona (first column of cells),
assuming that the disk is a suitable dynamic source of matter. The density distribution of
the disk surface has the form
)
where the
jet exists. However, we fix the density at the base of the corona (first column of cells),
assuming that the disk is a suitable dynamic source of matter. The density distribution of
the disk surface has the form
A poloidal magnetic field in a potential configuration (
![]() )
threads the corona and
the disk. This field is described by the stream function,
)
threads the corona and
the disk. This field is described by the stream function,
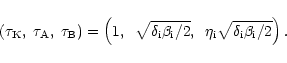 |
(13) |
The gas is continuously injected from the disk into the corona at a velocity
![]() ,
where
,
where
![]() is the local
Keplerian velocity at the disk surface,
is the local
Keplerian velocity at the disk surface,
![]() the local poloidal magnetic field that
threads the disk and
the local poloidal magnetic field that
threads the disk and
![]() is the injection velocity, an input parameter. For each time
interval, a random perturbation was introduced in the velocity field at each point of the
disk surface. The random perturbation was constructed, assuming a normal distribution for
each component of the velocity field. This was done using the function GASDEV which appears
in Numerical Recipes, 1st edition for FORTRAN, page 203. The function GASDEV gives a normally
distributed deviation D with a zero mean and a unit variance. The normal distribution for
the z-component of the velocity is given by
is the injection velocity, an input parameter. For each time
interval, a random perturbation was introduced in the velocity field at each point of the
disk surface. The random perturbation was constructed, assuming a normal distribution for
each component of the velocity field. This was done using the function GASDEV which appears
in Numerical Recipes, 1st edition for FORTRAN, page 203. The function GASDEV gives a normally
distributed deviation D with a zero mean and a unit variance. The normal distribution for
the z-component of the velocity is given by
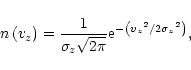 |
(15) |
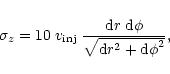 |
(16) |
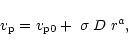 |
(17) |
| (18) |
We used the following parameters to investigate the time evolution of a jet from a randomly
perturbed Keplerian disk:
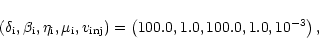 |
(19) |
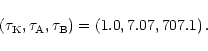 |
(20) |
Figure 2 shows the maximum poloidal velocity ![]() (perturbed plus continuous
velocities) for each simulation, using different values of the parameter a.
(perturbed plus continuous
velocities) for each simulation, using different values of the parameter a.
![\begin{figure}
\par\resizebox{\hsize}{!}{\includegraphics[clip]{MS10516f2.eps}}\end{figure}](/articles/aa/full/2002/10/aa10516/Timg118.gif) |
Figure 2:
Radial profile of the poloidal velocity |
| Open with DEXTER | |
| |
Figure 3:
Radial profile of the toroidal velocity, in units of
|
| Open with DEXTER | |
Simulations were made in the domain
![]() with a
resolution of
with a
resolution of
![]() for 500 time units
for 500 time units
![]() .
Along the z-axis, 30 zones span a distance of
.
Along the z-axis, 30 zones span a distance of
![]() outwards from the disk
surface. An additional 90 ratioed zones span an additional distance of
outwards from the disk
surface. An additional 90 ratioed zones span an additional distance of
![]() ,
with each
subsequent zone increasing in size by a factor of 1.017. Twenty uniform zones span an initial
distance of five disk radius in the radial direction. Outside of these uniform grid zones,
there are another 25 zones, with each subsequent zone increasing in size by a factor 1.065.
,
with each
subsequent zone increasing in size by a factor of 1.017. Twenty uniform zones span an initial
distance of five disk radius in the radial direction. Outside of these uniform grid zones,
there are another 25 zones, with each subsequent zone increasing in size by a factor 1.065.
Initial conditions in the atmosphere are shown in Fig. 4.
| |
Figure 4:
The initial conditions in the atmosphere. At the top:
density distribution in units of
|
| Open with DEXTER | |
The figures described below show the results of the simulations. Figures 5-7 show the distributions of the density, the poloidal and toroidal velocities,
and the poloidal and toroidal magnetic fields at 500 time units for simulations
A, B and G, our extrene cases. Contour lines are isocontours in the r-z plane.
![\begin{figure}
\par\resizebox{\hsize}{!}{\includegraphics[clip]{MS10516f5.eps}}\end{figure}](/articles/aa/full/2002/10/aa10516/Timg129.gif) |
Figure 5:
Simulation A (without perturbation). From top to bottom: the distributions of
density, poloidal velocity and magnetic field, and toroidal magnetic field and velocity
for |
| Open with DEXTER | |
When no perturbation was introduced in the disk (simulation A: Fig. 5), we
obtained at ![]() ,
the formation of a highly collimated steady state jet along
the z-axis (see the density distribution at the top of the figure). The strong radial
pinch of a dominant toroidal field (fourth panel from top) propagates into the corona
and collimates the outflow. The maximum value for the poloidal velocity (second panel
from top) is on the order of the Keplerian velocity at
,
the formation of a highly collimated steady state jet along
the z-axis (see the density distribution at the top of the figure). The strong radial
pinch of a dominant toroidal field (fourth panel from top) propagates into the corona
and collimates the outflow. The maximum value for the poloidal velocity (second panel
from top) is on the order of the Keplerian velocity at ![]() .
.
In simulations B (Fig. 6) - E , where a is negative or null, we observe
the formation of regularly spaced structures along the z-axis with a mean separation
distance of about
![]() (see the density distribution at the top panel of the Fig. 6).
(see the density distribution at the top panel of the Fig. 6).
![\begin{figure}
\par\resizebox{\hsize}{!}{\includegraphics[clip]{MS10516f6.eps}}\end{figure}](/articles/aa/full/2002/10/aa10516/Timg134.gif) |
Figure 6:
Simulation B (a=-3/2). From top to bottom: the distributions of
density, poloidal velocity and magnetic field, and toroidal magnetic field and velocity
for |
| Open with DEXTER | |
When we use a positive slope, a=1/2 for simulation F and a=1 for simulation G (Fig. 7), the formation of the regularly spaced structures occurs, but with an
ensuing decollimation of the jet.
![\begin{figure}
\par\resizebox{\hsize}{!}{\includegraphics[clip]{MS10516f7.eps}}\end{figure}](/articles/aa/full/2002/10/aa10516/Timg136.gif) |
Figure 7:
Simulation G (a=1). From top to bottom: the distributions of
density, poloidal velocity and magnetic field, and toroidal magnetic field and velocity
for |
| Open with DEXTER | |
In Fig. 8, the axial distributions of the density, axial and toroidal velocities
and the toroidal magnetic field along a cut at
![]() at 500 time units is shown for all
the simulations.
at 500 time units is shown for all
the simulations.
![\begin{figure}
\par\resizebox{13cm}{!}{\includegraphics[clip]{MS10516f8.eps}}\end{figure}](/articles/aa/full/2002/10/aa10516/Timg138.gif) |
Figure 8:
Simulations A - G.
The density (solid line), axial velocity (dotted line), toroidal
velocity (dashed line) and toroidal magnetic field (dashed-dotted line) along
the z-axis at
|
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{\hsize}{!}{\includegraphics[clip]{MS10516f9.eps}}\end{figure}](/articles/aa/full/2002/10/aa10516/Timg139.gif) |
Figure 9:
The density (thicker solid line), pressure (thinner solid line), axial
velocity (dotted line), toroidal velocity (dot-dashed line), axial magnetic field (dashed
line) and toroidal magnetic field (dot-dot-dashed line) along the r-axis at a z=40.5are shown for simulation A. The following quantities are scaled: |
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{\hsize}{!}{\includegraphics[clip]{MS10516f10.eps}}\end{figure}](/articles/aa/full/2002/10/aa10516/Timg140.gif) |
Figure 10:
The density (thicker solid line), the pressure (thinner solid line),
axial velocity (dotted line), toroidal velocity (dot-dashed line), axial magnetic field
(dashed line) and toroidal magnetic field (dot-dot-dashed line) along the r-axis at a
z=40.5 are shown for simulation B. The scaled quantities are: |
| Open with DEXTER | |
Figures 9 to 11 show the radial distributions of some physical quantities
in a cut at
![]() for simulations A, B and G.
for simulations A, B and G.
![\begin{figure}
\par\resizebox{\hsize}{!}{\includegraphics[clip]{MS10516f11.eps}}\end{figure}](/articles/aa/full/2002/10/aa10516/Timg144.gif) |
Figure 11:
The density (thicker solid line), pressure (thinner solid line), axial
velocity (dotted line), toroidal velocity (dot-dashed line), axial magnetic field (dashed
line) and toroidal magnetic field (dot-dot-dashed line) along the r-axis at a z=40.5are shown for simulation G. Scaled quantities:
|
| Open with DEXTER | |
Figure 12 shows the axial and radial mass fluxes for simulations A to G at
![]() .
.
![\begin{figure}
\par\resizebox{12.2cm}{!}{\includegraphics[clip]{MS10516f12.eps}}\end{figure}](/articles/aa/full/2002/10/aa10516/Timg146.gif) |
Figure 12:
Simulations A - G: axial and radial mass fluxes (Eq. (21)).
Axial (solid line) and radial (dotted line) mass fluxes at |
| Open with DEXTER | |
When we use a positive slope for the perturbation in simulations F (a=1/2) and
G (a=1), the axial mass fluxes decrease and the radial mass fluxes increase along the jet,
indicating decollimation of the jet. In simulation G, the radial mass flux at the
outer axial boundary (
![]() )
is roughly the same as the value of the axial mass flux at the
inner boundary (
)
is roughly the same as the value of the axial mass flux at the
inner boundary (![]() ). In these simulations, the axial mass fluxes are also modified by
the density structures.
). In these simulations, the axial mass fluxes are also modified by
the density structures.
Figure 13 shows the sonic (dotted lines), Alfvénic (dashed-dotted lines)
and magnetosonic Mach numbers (solid lines) for
simulations A - D at ![]() in a cut at
in a cut at
![]() .
Figure 14
shows these Mach numbers for simulations E - G. The sonic Mach numbers
are computed, using the thermal pressure p in the sound speed.
.
Figure 14
shows these Mach numbers for simulations E - G. The sonic Mach numbers
are computed, using the thermal pressure p in the sound speed.
![\begin{figure}
\par\resizebox{11.7cm}{!}{\includegraphics[clip]{MS10516f13.eps}}\end{figure}](/articles/aa/full/2002/10/aa10516/Timg150.gif) |
Figure 13:
Simulations A - D: the sonic Mach numbers
(dotted lines), Alfvénic Mach numbers (dashed-dotted lines) and magnetosonic Mach
numbers (solid lines) along the z-axis at |
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{12.5cm}{!}{\includegraphics[clip]{MS10516f14.eps}}\end{figure}](/articles/aa/full/2002/10/aa10516/Timg151.gif) |
Figure 14:
Simulations E - G: the sonic Mach numbers
(dotted lines), Alfvénic Mach numbers (dashed-dotted lines) and magnetosonic Mach numbers
(solid lines) along the z-axis at |
| Open with DEXTER | |
Beyond the Alfvén surface, where the Alfvénic Mach number is greater than unity, the
toroidal field dominates the poloidal field. The dynamical importance of the magnetic
field is evaluated using the quantity ![]() ,
which is the ratio of the magnetic
to the kinetic energy
,
which is the ratio of the magnetic
to the kinetic energy
After some manipulation of Eqs. (23) and (22), we can evaluate the
value of ![]() in the asymtotic limit
in the asymtotic limit
![]() on any field line of radius
on any field line of radius
![]() :
:
We plot in Fig. 15 the dependence of
![]() (Eq. (25))
as a function of r and the radial dependence of
(Eq. (25))
as a function of r and the radial dependence of ![]() (Eq. (22)), extracted
from simulation A (with no perturbation) at 500 time units in a cut at
(Eq. (22)), extracted
from simulation A (with no perturbation) at 500 time units in a cut at
![]() .
.
![\begin{figure}
\par\resizebox{\hsize}{!}{\includegraphics[clip]{MS10516f15.eps}}\end{figure}](/articles/aa/full/2002/10/aa10516/Timg166.gif) |
Figure 15:
The quantity |
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{\hsize}{!}{\includegraphics[clip]{MS10516f16.eps}}\end{figure}](/articles/aa/full/2002/10/aa10516/Timg170.gif) |
Figure 16:
The quantity |
| Open with DEXTER | |
Our results showed that episodic jets arise when perturbations are present.
In order to understand the origin of the structures, we analyzed the individual terms
of the radial component of the momentum equation (Eq. (6)). In the steady state,
the momentum equation is
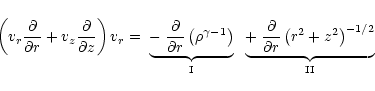
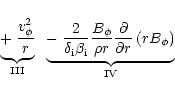
![\begin{figure}
\par\resizebox{\hsize}{!}{\includegraphics[clip]{MS10516f17.eps}}\end{figure}](/articles/aa/full/2002/10/aa10516/Timg175.gif) |
Figure 17:
A cut at
|
| Open with DEXTER | |
Chan & Henriksen (1980) studied the dynamical behaviour of axisymmetric jets in
a "transverse self-similar model". They considered the cases in which the flow is confined
and collimated by an external pressure or by pinching due to a toroidal magnetic field. In this
"transverse self-similar model" the variables are separated in the r and z components,
e.g.,
![]() ,
where br,
,
where br, ![]() ,
bz and R are functions only of z (R is the scaling radius and is taken to be the
radius of the jet boundary at z). The quantities br and
,
bz and R are functions only of z (R is the scaling radius and is taken to be the
radius of the jet boundary at z). The quantities br and ![]() are the values of Brand
are the values of Brand ![]() on the jet boundary. Studying the magnetic pinching case in which the magnetic
field is dynamically important (
on the jet boundary. Studying the magnetic pinching case in which the magnetic
field is dynamically important (
![]() ,
i.e., our case), with different
parameters, they obtained jets which undergo quasi-periodic oscillations caused by
the pinch instability due to the toroidal magnetic field. As explained by Chan & Henriksen (1980), the
calculations showed that the pinch by the toroidal magnetic field is stopped by thermal and
magnetic pressure and that the beam oscillates quasi-periodically. Moreover, they showed that
when only magnetic piching occurs,
,
i.e., our case), with different
parameters, they obtained jets which undergo quasi-periodic oscillations caused by
the pinch instability due to the toroidal magnetic field. As explained by Chan & Henriksen (1980), the
calculations showed that the pinch by the toroidal magnetic field is stopped by thermal and
magnetic pressure and that the beam oscillates quasi-periodically. Moreover, they showed that
when only magnetic piching occurs,
In an interesting analytic work, Bogoyavlenskij (2000) reported some new exact solutions of the plasma equilibrium equations that model astrophysical jets in the comoving reference frame. The equilibrium solutions depend on arbitrary parameters which can be adjusted so that the topology of the magnetic field becomes complex. The fields (e.g., Fig. 1 in Bogoyavlenskij 2000) are a combination of nested cylindrical magnetic surfaces and nested toroidal surfaces. The innermost tori are circular magnetic axes that are linked to the neighboring closed magnetic field lines. Certain solutions are quasiperiodic in z, i.e., the magnetic field shows structures with similar, but not equal, periods. This implies that the magnetic field never repeats in the z direction, but can have a structure arbitrarily close to the initial data. Their "winding pattern" changes continuously with z and does not repeat itself.
We made numerical 2.5-dimensional simulations of astrophysical jets from Keplerian disks,
subject to a random perturbation in the velocity field.
The simulations were made using different values for the parameter a, which defines the
radial dependence of the perturbation (
![]() ). In simulation A, no
perturbation was introduced, while in simulations B - G, we used a=-3/2, -1, -1/2,
0, 1/2, 1, respectively.
). In simulation A, no
perturbation was introduced, while in simulations B - G, we used a=-3/2, -1, -1/2,
0, 1/2, 1, respectively.
For simulation A, where there is no perturbation, we obtained a steady state, highly
collimated jet along the disk axis after a time ![]() .
The maximum axial velocity
was of the order of the Keplerian velocity at the innermost radius of the accretion disk
.
The maximum axial velocity
was of the order of the Keplerian velocity at the innermost radius of the accretion disk
![]() .
In a cut at
.
In a cut at
![]() ,
the jet is already supersonic and super-Alfvénic near the
base of the corona and super-magnetosonic at
,
the jet is already supersonic and super-Alfvénic near the
base of the corona and super-magnetosonic at
![]() .
.
The results common to simulations B - G are as follows:
a. The highest axial velocities are localized near the jet axis at about
![]() ;
;
b. The axial mass fluxes at
![]() are comparable to the axial fluxes at
are comparable to the axial fluxes at ![]() ,
their average values remaining roughly the same, as compared with the
case for no perturbation (simulation A); and
,
their average values remaining roughly the same, as compared with the
case for no perturbation (simulation A); and
c. The radial mass fluxes are similar to those of simulation A (where there was no perturbation).
The decollimation of the jet occurs when we use a positive radial power dependence (a > 0) for the perturbation. Simulations E and G show this effect where we observed that
a. The axial velocity increases in the regions far from the jet axis and decreases near the axis;
b. Decollimation modifies the sonic Mach number distributions with decreasing average values in the regions near the jet axis;
c. The region near the jet axis becomes less and less well-defined;
d. The axial mass flux decreases, while the radial mass flux increases along the jet axis
(in simulation G with a=1, the radial mass flux at the outer axial boundary (
![]() )
assumes the value of the axial mass flux at the inner boundary (
)
assumes the value of the axial mass flux at the inner boundary (![]() )).
)).
These simulations, introducing random perturbations in the accretion disk, produced a jet
in which regularly spaced structures are present with periods of about
![]() .
Using this
same numerical approuch, Ouyed & Pudritz (1999) obtained episodic jets introducing continuously the
gas from the disk with velocities smaller than the
.
Using this
same numerical approuch, Ouyed & Pudritz (1999) obtained episodic jets introducing continuously the
gas from the disk with velocities smaller than the
![]() which we used. For
injection velocities equal to this value, they obtained a highly collimated steady state
jet
which we used. For
injection velocities equal to this value, they obtained a highly collimated steady state
jet![]() with features similar to
our jet, with no perturbation in the velocity field of the disk. When we introduced
perturbations with specific features in our steady state jet, our results showed regular
structures with separation distances (
with features similar to
our jet, with no perturbation in the velocity field of the disk. When we introduced
perturbations with specific features in our steady state jet, our results showed regular
structures with separation distances (![]() 11
11 ![]() )
similar to the case when OP99 used
a smaller velocity of
)
similar to the case when OP99 used
a smaller velocity of
![]() .
Therefore, introducing the perturbations we
obtained the formation of strutuctures for the case in which that autors obtained a steady
state jet.
.
Therefore, introducing the perturbations we
obtained the formation of strutuctures for the case in which that autors obtained a steady
state jet.
We simulated a region very near the central object (
![]() ). It is
interesting to evaluate the spatial dimensions involved in our simulations. For a protostar
of mass
). It is
interesting to evaluate the spatial dimensions involved in our simulations. For a protostar
of mass
![]() ,
assuming that
,
assuming that
![]() AU for the inner radius of the disk,
AU for the inner radius of the disk,
![]() is equivalent to
is equivalent to ![]() 10-5 pc. For a black hole of
10-5 pc. For a black hole of
![]() (the
Schwartzschild radius is
(the
Schwartzschild radius is ![]() 1 AU), assuming
1 AU), assuming
![]() AU,
AU,
![]() is
equivalent to
is
equivalent to ![]() 10-2 pc. A distance of separation of
10-2 pc. A distance of separation of ![]() 11
11 ![]() for the structures
corresponds, for the protostar case, to
for the structures
corresponds, for the protostar case, to ![]() 10-6 pc and for the black hole case, to
10-6 pc and for the black hole case, to
![]() 10-3 pc. These scales are much smaller than the distances between the Herbig-Haro
objects observed in the protostellar jets (about 10-2 pc). They are also smaller than the
distances observed between the emission knots, frequently found in AGN jets. We are, therefore,
obtaining structures very near the formation region of the jets, involving scales not yet
resolved by current instruments.
10-3 pc. These scales are much smaller than the distances between the Herbig-Haro
objects observed in the protostellar jets (about 10-2 pc). They are also smaller than the
distances observed between the emission knots, frequently found in AGN jets. We are, therefore,
obtaining structures very near the formation region of the jets, involving scales not yet
resolved by current instruments.
Acknowledgements
B.F.V. acknowledges the financial support of the Brazilian agency FAPESP under grant 95/99122. V.J.P. and R.O. would like to thank the Brazilian agencies CNPq and FAPESP for partial support. We would like to thank LCCA-USP for granting the use of the CRAY J-90 computer in our simulations and especially the staff for their invaluable help. R. Ouyed and especially C. Fendt contributed to this paper with encouraging and valuable discussions, for which we are grateful. The authors also would like to thank the project PRONEX (No. 41.96.0908.00) for partial support.