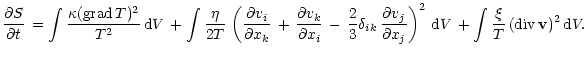 |
(A.1) |
General equation for the entropy production rate is given by
(Landau & Lifshits 1987):
The terms included in this equation account for only hydro- and thermodynamic processes since we assume the ionization balance in each point of the region which means that the radiative heating and cooling do not contribute to the entropy production. The second viscosity equals zero for dilute monoatomic gases (Chapman & Cowling 1970) so we omit it from further consideration.
We also assume that heat conductivity ![]() and viscosity
and viscosity ![]() are dominated by turbulence, and hence the
Prandtl number is about unity (Monin & Yaglom 1975):
are dominated by turbulence, and hence the
Prandtl number is about unity (Monin & Yaglom 1975):
From observations, only one component vx (along the sightline)
of the velocity vector v is known.
Therefore we are compelled
to neglect in (A.1) all terms including derivatives
other than
![]() .
The second right hand term in (A.1) can be re-written in the form:
.
The second right hand term in (A.1) can be re-written in the form:
For a monatomic ideal gas
![]() (n is the number of gram-moles and R is the universal gas constant),
and if the gas is fully ionized then
(n is the number of gram-moles and R is the universal gas constant),
and if the gas is fully ionized then
![]() (e.g. Lang 1999).
(e.g. Lang 1999).
Given the values of ![]() ,
Pr, T0,
,
Pr, T0, ![]() ,
and
,
and
![]() ,
we can rearrange the computational points
,
we can rearrange the computational points
![]() and
and
![]() in such a manner,
that minimum of (A.4) will be achieved.
Minimization of (A.4) was carried out by means of combinatorial
simulated annealing technique (Press et al. 1992).
The obtained configuration of the density and velocity distributions
should have the least dissipation
and therefore will exist longer than all others.
in such a manner,
that minimum of (A.4) will be achieved.
Minimization of (A.4) was carried out by means of combinatorial
simulated annealing technique (Press et al. 1992).
The obtained configuration of the density and velocity distributions
should have the least dissipation
and therefore will exist longer than all others.
Copyright ESO 2002