We present a newly measured X-ray temperature function of galaxy clusters using a complete flux-limited sample of 61 clusters. The sample is constructed with the total survey area of 8.14 steradians and the flux limit of
A&A 383, 773-790 (2002)
DOI: 10.1051/0004-6361:20011769
Y. Ikebe1 - T. H. Reiprich2 - H. Böhringer1 - Y. Tanaka1,3 - T. Kitayama4
1 - Max-Planck-Institut für extraterrestrische Physik,
Postfach 1312, 85741 Garching, Germany
2 -
Department of Astronomy, University of Virginia,
PO Box 3818, 530 McCormick Road, Charlottesville,
VA 22903-0818, USA
3 -
Institute of Space and Astronautical Science,
Yoshinodai 3-1-1, Sagamihara, Kanagawa 229-8510, Japan
4 -
Department of Physics, Toho University,
Miyama, Funabashi, Chiba 274-8510, Japan
Received 7 June 2001 / Accepted 11 December 2001
Abstract
We present a newly measured X-ray temperature function of galaxy clusters
using a complete flux-limited sample of 61 clusters.
The sample is constructed with the total survey area of 8.14 steradians
and the flux limit of
![]() ergs s-1 cm-2in the 0.1-2.4 keV band.
X-ray temperatures and fluxes of the sample clusters
were accurately measured with ASCA and ROSAT data.
The derived temperature function covers an unprecedentedly wide temperature
range of 1.4-11 keV.
By fitting these data with theoretically predicted temperature functions
given by the Press-Schechter formalism together with a recent formation
approximation and the CDM power spectrum,
we obtained tight and individual constraints on
ergs s-1 cm-2in the 0.1-2.4 keV band.
X-ray temperatures and fluxes of the sample clusters
were accurately measured with ASCA and ROSAT data.
The derived temperature function covers an unprecedentedly wide temperature
range of 1.4-11 keV.
By fitting these data with theoretically predicted temperature functions
given by the Press-Schechter formalism together with a recent formation
approximation and the CDM power spectrum,
we obtained tight and individual constraints on
![]() and
and ![]() .
We also employed the Formation-Epoch model
in which the distribution in the formation epoch of clusters
as well as the temperature evolution are taken into account,
showing significantly different results.
Systematics caused by the uncertainty in the mass-temperature relation are studied
and found to be as large as the statistical errors.
.
We also employed the Formation-Epoch model
in which the distribution in the formation epoch of clusters
as well as the temperature evolution are taken into account,
showing significantly different results.
Systematics caused by the uncertainty in the mass-temperature relation are studied
and found to be as large as the statistical errors.
Key words: cosmology: observations - cosmological: parameters - X-rays: galaxies: clusters
The mass function of clusters of galaxies (MF),
the number density of the most massive virialized systems,
contains information on the structure formation history of the universe.
A theoretical framework, e.g. the Press-Schechter formalism
(Press & Schechter 1974) together with the Cold Dark Matter model,
has been established to predict the MF.
This allows us to constrain cosmological parameters
using an observationally determined MF for the present epoch
(as well as its time evolution for even tighter constraints).
In particular, ![]() ,
the amplitude of mass density fluctuations
on a scale of 8h-1 Mpc where h is the Hubble constant in
unit of 100 km/s/Mpc,
and
,
the amplitude of mass density fluctuations
on a scale of 8h-1 Mpc where h is the Hubble constant in
unit of 100 km/s/Mpc,
and
![]() ,
the mean matter density,
are most sensitively determined by the cluster abundance measurements
(e.g. Henry & Arnaud 1991;
White et al. 1993;
Eke et al. 1996; Kitayama & Suto 1996;
Viana & Liddle 1996; Oukbir & Blanchard 1997;
Pen 1998; Eke et al. 1998).
,
the mean matter density,
are most sensitively determined by the cluster abundance measurements
(e.g. Henry & Arnaud 1991;
White et al. 1993;
Eke et al. 1996; Kitayama & Suto 1996;
Viana & Liddle 1996; Oukbir & Blanchard 1997;
Pen 1998; Eke et al. 1998).
Observationally the local MF has been derived from measuring masses of individual clusters from galaxy velocity dispersions or other optical properties by Bahcall & Cen (1993), Biviano et al. (1993), and Girardi et al. (1998). The estimated virial masses for individual clusters depend rather strongly on model assumptions, however. As argued by Evrard et al. (1997) on the basis of hydrodynamical N-body simulations, cluster masses may be presently more accurately determined from a temperature measurement and a mass-temperature relation determined from detailed observations or numerical modeling. Thus alternatively, as a well-defined observational quantity, the X-ray temperature function (XTF) has been measured, which can be converted to the MF by means of the mass-temperature relation.
The first measurements of the XTF were reported
by Edge et al. (1990) and Henry & Arnaud (1991),
using an X-ray flux-limited sample of 45 clusters and 25 clusters,
respectively.
Recent observational improvement on the XTF was made
by Markevitch (1998), Henry (2000),
Blanchard et al. (2000), and Pierpaoli et al. (2001),
using more accurate temperature-measurement results
for each cluster with ASCA data (Tanaka et al. 1994).
However, the narrow temperature ranges (3-10 keV) in which
the XTF is defined so far do not allow
an investigation of a more detailed shape of the XTF
other than just fitting a single power-law.
Without better information on the actual shape of the XTF,
no independent constraints on ![]() and
and
![]() can be derived, and a wide range of combinations is still allowed.
Recently, a number of new X-ray-cluster surveys were performed,
which provide a high completeness for the brightest clusters.
This motivated us to revisit the measurement of the local XTF
and to improve its accuracy in order to derive narrower constraints
on the cosmological parameters.
can be derived, and a wide range of combinations is still allowed.
Recently, a number of new X-ray-cluster surveys were performed,
which provide a high completeness for the brightest clusters.
This motivated us to revisit the measurement of the local XTF
and to improve its accuracy in order to derive narrower constraints
on the cosmological parameters.
Reiprich & Böhringer (2002) have compiled
a new X-ray flux-limited cluster sample
![]() with a flux limit of
with a flux limit of
![]() ergs s-1 cm-2 (0.1-2.4 keV).
Compared with previous samples with similar flux limits,
their catalog covers the largest volume and is the most complete.
Based on this cluster sample, Reiprich & Böhringer have measured
total masses for individual clusters and derived the X-ray mass function
for the first time.
In this paper we, using this cluster sample,
report the construction of a new measurement of the XTF.
The larger number of clusters in the sample
together with accurate temperature measurements with ASCA data
leads to a significant improvement of the XTF,
which covers 1.4-11 keV temperature range.
The X-ray flux-limited sample and the new temperature measurements
with ASCA data are presented in Sect. 2.
The derivation of the XTF is described in Sect. 3.
In Sect. 4, the XTF is used to obtain constraints on cosmological parameters,
and the results are compared with other work in Sect. 5.
Throughout the paper, the Hubble constant is given as
ergs s-1 cm-2 (0.1-2.4 keV).
Compared with previous samples with similar flux limits,
their catalog covers the largest volume and is the most complete.
Based on this cluster sample, Reiprich & Böhringer have measured
total masses for individual clusters and derived the X-ray mass function
for the first time.
In this paper we, using this cluster sample,
report the construction of a new measurement of the XTF.
The larger number of clusters in the sample
together with accurate temperature measurements with ASCA data
leads to a significant improvement of the XTF,
which covers 1.4-11 keV temperature range.
The X-ray flux-limited sample and the new temperature measurements
with ASCA data are presented in Sect. 2.
The derivation of the XTF is described in Sect. 3.
In Sect. 4, the XTF is used to obtain constraints on cosmological parameters,
and the results are compared with other work in Sect. 5.
Throughout the paper, the Hubble constant is given as ![]() km/s/Mpc,
and
km/s/Mpc,
and ![]() and
and ![]() denotes a decimal and natural logarithm, respectively.
denotes a decimal and natural logarithm, respectively.
For this study we use a sample of 106 galaxy clusters compiled by
Reiprich & Böhringer (2002),
which is used to construct a flux-limited complete sample
![]() with the flux-limit
of
with the flux-limit
of
![]() ergs s-1 cm-2 (0.1-2.4 keV).
The 106 clusters have been derived from combining previous X-ray cluster
or elliptical galaxy catalogs
that include Böhringer et al. (2000, 2001),
Böhringer (1999),
Retzlaff et al. in preparation,
Ebeling et al. (1996, 1998), de Grandi et al. (1999),
Beuing et al. (1999), Lahav et al. (1989),
and Edge et al. (1990).
Most of them are based on the ROSAT All Sky Survey
(Trümper 1993; Voges et al. 1999).
From these catalogs, all objects satisfying certain criteria,
mainly that the measured flux given in any of these catalogs
is above
ergs s-1 cm-2 (0.1-2.4 keV).
The 106 clusters have been derived from combining previous X-ray cluster
or elliptical galaxy catalogs
that include Böhringer et al. (2000, 2001),
Böhringer (1999),
Retzlaff et al. in preparation,
Ebeling et al. (1996, 1998), de Grandi et al. (1999),
Beuing et al. (1999), Lahav et al. (1989),
and Edge et al. (1990).
Most of them are based on the ROSAT All Sky Survey
(Trümper 1993; Voges et al. 1999).
From these catalogs, all objects satisfying certain criteria,
mainly that the measured flux given in any of these catalogs
is above
![]() ergs s-1 cm-2 (0.1-2.4 keV),
have been sampled.
A defined region around the center of M 87 is not included
in the survey area,
because of the large scale emission of the Virgo cluster
that compromises cluster detection and characterization in the region.
This excludes the Virgo cluster and M 86 from the master catalog.
The count rate of the PSPC (Pfeffermann et al. 1987)
in the 0.1-2.4 keV band for each object was redetermined
from the ROSAT All Sky Survey data or PSPC pointing observations
whenever available
by integrating all X-ray flux within a maximum radius where
the cluster emission is significantly detected.
See Reiprich & Böhringer (2002) for detailed descriptions
of the sample construction and data analysis.
The names and the redshifts compiled from the recent literature
of all the 106 clusters are listed in Table 1.
ergs s-1 cm-2 (0.1-2.4 keV),
have been sampled.
A defined region around the center of M 87 is not included
in the survey area,
because of the large scale emission of the Virgo cluster
that compromises cluster detection and characterization in the region.
This excludes the Virgo cluster and M 86 from the master catalog.
The count rate of the PSPC (Pfeffermann et al. 1987)
in the 0.1-2.4 keV band for each object was redetermined
from the ROSAT All Sky Survey data or PSPC pointing observations
whenever available
by integrating all X-ray flux within a maximum radius where
the cluster emission is significantly detected.
See Reiprich & Böhringer (2002) for detailed descriptions
of the sample construction and data analysis.
The names and the redshifts compiled from the recent literature
of all the 106 clusters are listed in Table 1.
As described below, we newly determine the X-ray temperature as well as the X-ray flux
for each of the 106 clusters.
ASCA data are available for 88 of the 106 clusters,
and the X-ray temperatures are measured by analyzing the ASCA data
(Sect. 2.2).
Using the ASCA results,
the correlation between the X-ray luminosity and the temperature,
L-T relation, is established (Sect. 2.3).
Among the other clusters for which no ASCA data exist
(18 clusters), temperatures of 4 clusters have been measured with
Einstein, EXOSAT, or XMM-Newton in previous works
and were used in our analysis. For the remaining 14 clusters,
the temperatures are estimated from the observed ROSAT PSPC
count rate by means of the L-T relation.
By setting a flux-limit of
![]() ergs s-1 cm-2 (0.1-2.4 keV),
a complete flux-limited sample comprising 63 clusters
is then constructed (Sect. 2.4).
ergs s-1 cm-2 (0.1-2.4 keV),
a complete flux-limited sample comprising 63 clusters
is then constructed (Sect. 2.4).
| NAME | redshift |
|
Flux(0.1-2.4 keV) | |||
| (1021 cm-2) | (keV) | (10-11 ergs s-1 cm-2) | Open | Flat | ||
| *PERSEUS | 0.0183 | 1.569 | 6.42+ 0.06-0.06 | 114.33 |
(4.12 |
(4.19 |
| *OPHIUCHUS | 0.0280 | 2.014 | 10.25+ 0.30-0.36 | 36.25 |
(3.07 |
(3.14 |
| COMA | 0.0232 | 0.089 | 8.07+ 0.29-0.27 | 35.13 |
(2.04 |
(2.08 |
| *A3627 | 0.0163 | 2.083 | 5.62+ 0.12-0.11 | 31.60 |
(9.04 |
(9.16 |
| A3526 | 0.0103 | 0.825 | 3.69+ 0.05-0.04 | 26.20 |
(2.99 |
(3.02 |
| *AWM7 | 0.0172 | 0.921 | 3.70+ 0.08-0.05 | 16.60 |
(5.30 |
(5.37 |
| *A2319 | 0.0564 | 0.877 | 8.84+ 0.29-0.24 | 12.15 |
(4.20 |
(4.39 |
| A3571 | 0.0397 | 0.393 | 6.80+ 0.21-0.18 | 12.00 |
(2.05 |
(2.12 |
| *TRIANGUL | 0.0510 | 1.229 | 9.06+ 0.33-0.31 | 11.26 |
(3.18 |
(3.31 |
| A2199 | 0.0302 | 0.084 | 4.28+ 0.10-0.10 | 10.73 |
(1.06 |
(1.09 |
| *3C129 | 0.0223 | 6.789 | 5.57+ 0.16-0.15 | 10.65 |
(5.72 |
(5.82 |
| A1060 | 0.0114 | 0.492 | 3.15+ 0.05-0.05 | 10.04 |
(1.41 |
(1.42 |
| 2A0335 | 0.0349 | 1.864 | 3.64+ 0.09-0.08 | 8.87 |
(1.17 |
(1.21 |
| A0262 | 0.0161 | 0.552 | 2.25+ 0.06-0.06 | 8.78 |
(2.46 |
(2.49 |
| FORNAX | 0.0046 | 0.145 | 1.56+ 0.05-0.07 | 8.68 |
(1.97 |
(1.98 |
| A0496 | 0.0328 | 0.568 | 4.59+ 0.10-0.10 | 8.20 |
(9.56 |
(9.81 |
| A0085 | 0.0556 | 0.358 | 6.51+ 0.16-0.23 | 7.37 |
(2.48 |
(2.59 |
| A3667 | 0.0560 | 0.459 | 6.28+ 0.27-0.26 | 7.12 |
(2.44 |
(2.54 |
| A2029 | 0.0767 | 0.307 | 7.93+ 0.39-0.36 | 6.88 |
(4.43 |
(4.70 |
| A3558 | 0.0480 | 0.363 | 5.37+ 0.17-0.15 | 6.68 |
(1.68 |
(1.74 |
| *S636 | 0.0116 | 0.642 | 2.06+ 0.07-0.06 | 6.65 |
(9.65 |
(9.75 |
| A2142 | 0.0899 | 0.405 | 8.46+ 0.53-0.49 | 6.21 |
(5.52 |
(5.90 |
| A1795 | 0.0616 | 0.120 | 6.17+ 0.26-0.25 | 6.21 |
(2.58 |
(2.70 |
| *PKS0745 | 0.1028 | 4.349 | 6.37+ 0.21-0.20 | 6.13 |
(7.18 |
(7.74 |
| A2256 | 0.0601 | 0.402 | 6.83+ 0.23-0.21 | 6.03 |
(2.38 |
(2.49 |
| A1367 | 0.0216 | 0.255 | 3.55+ 0.08-0.08 | 5.98 |
(3.02 |
(3.07 |
| A3266 | 0.0594 | 0.148 | 7.72+ 0.35-0.28 | 5.77 |
(2.22 |
(2.32 |
| A4038 | 0.0283 | 0.155 | 3.22+ 0.10-0.10 | 5.61 |
(4.86 |
(4.97 |
| A2147 | 0.0351 | 0.329 | 4.34+ 0.12-0.13 | 5.45 |
(7.28 |
(7.49 |
| A0401 | 0.0748 | 1.019 | 7.19+ 0.28-0.24 | 5.26 |
(3.23 |
(3.41 |
| N5044 | 0.0090 | 0.491 | 1.22+ 0.04-0.04 | 5.20 |
(4.54 |
(4.58 |
| A0478 | 0.0900 | 1.527 | 6.91+ 0.40-0.36 | 5.12 |
(4.58 |
(4.89 |
| HYDRA-A | 0.0538 | 0.486 | 3.82+ 0.20-0.17 | 4.71 |
(1.49 |
(1.56 |
| A2052 | 0.0348 | 0.290 | 3.12+ 0.10-0.09 | 4.57 |
(6.01 |
(6.18 |
| N1550 | 0.0123 | 1.159 | 1.44+ 0.03-0.02 | 4.24 |
(6.93 |
(7.00 |
| A2063 | 0.0354 | 0.292 | 3.56+ 0.16-0.12 | 4.23 |
(5.74 |
(5.90 |
| A1644 | 0.0474 | 0.533 |
|
4.09 |
(1.00 |
(1.04 |
| A0119 | 0.0440 | 0.310 | 5.69+ 0.24-0.28 | 4.05 |
(8.53 |
(8.82 |
| *A0644 | 0.0704 | 0.514 | 6.54+ 0.27-0.26 | 3.97 |
(2.16 |
(2.28 |
| N4636 | 0.0037 | 0.175 | 0.66+ 0.03-0.01 | 3.97 |
(5.84 |
(5.86 |
| A3158 | 0.0590 | 0.106 | 5.41+ 0.26-0.24 | 3.79 |
(1.44 |
(1.51 |
| A1736 | 0.0461 | 0.536 | 3.68+ 0.22-0.17 | 3.54 |
(8.21 |
(8.51 |
| A0754 | 0.0528 | 0.459 | 9.00+ 0.35-0.34 | 3.34 |
(1.01 |
(1.06 |
| A0399 | 0.0715 | 1.058 | 6.46+ 0.38-0.36 | 3.30 |
(1.85 |
(1.95 |
| MKW3S | 0.0450 | 0.315 | 3.45+ 0.13-0.10 | 3.22 |
(7.13 |
(7.38 |
| *A0539 | 0.0288 | 1.206 | 3.04+ 0.11-0.10 | 3.12 |
(2.80 |
(2.87 |
| EXO0422 | 0.0390 | 0.640 |
|
3.12 |
(5.16 |
(5.32 |
| A4059 | 0.0460 | 0.110 | 3.94+ 0.15-0.15 | 3.10 |
(7.16 |
(7.42 |
| A3581 | 0.0214 | 0.426 | 1.83+ 0.04-0.02 | 3.08 |
(1.53 |
(1.55 |
| A3112 | 0.0750 | 0.253 | 4.72+ 0.37-0.25 | 3.07 |
(1.90 |
(2.01 |
| A0576 | 0.0381 | 0.569 | 3.83+ 0.16-0.15 | 2.99 |
(4.73 |
(4.88 |
| A3562 | 0.0499 | 0.391 | 4.47+ 0.23-0.21 | 2.89 |
(7.87 |
(8.18 |
| A2204 | 0.1523 | 0.594 | 6.38+ 0.23-0.23 | 2.73 |
(7.13 |
(7.92 |
| A0400 | 0.0240 | 0.938 | 2.43+ 0.13-0.12 | 2.64 |
(1.65 |
(1.68 |
| A2065 | 0.0721 | 0.284 | 5.37+ 0.34-0.30 | 2.55 |
(1.46 |
(1.54 |
| A1651 | 0.0860 | 0.171 | 6.22+ 0.45-0.41 | 2.52 |
(2.06 |
(2.19 |
| A2589 | 0.0416 | 0.439 | 3.38+ 0.13-0.13 | 2.52 |
(4.75 |
(4.91 |
| MKW8 | 0.0270 | 0.260 | 3.29+ 0.23-0.22 | 2.51 |
(1.99 |
(2.03 |
| A2657 | 0.0404 | 0.527 | 3.53+ 0.12-0.12 | 2.49 |
(4.44 |
(4.58 |
| A3376 | 0.0455 | 0.501 | 4.43+ 0.39-0.38 | 2.44 |
(5.52 |
(5.72 |
| S1101 | 0.0580 | 0.185 |
|
2.44 |
(9.05 |
(9.46 |
| A1650 | 0.0845 | 0.154 | 5.68+ 0.30-0.27 | 2.43 |
(1.92 |
(2.04 |
| A2634 | 0.0312 | 0.517 | 3.45+ 0.16-0.16 | 2.38 |
(2.51 |
(2.58 |
| A3391 | 0.0531 | 0.542 | 5.89+ 0.45-0.33 | 2.20 |
(6.78 |
(7.06 |
| A2597 | 0.0852 | 0.250 | 4.20+ 0.49-0.41 | 2.20 |
(1.77 |
(1.88 |
| ZwCl1215 | 0.0750 | 0.164 |
|
2.17 |
(1.34 |
(1.42 |
|
|
||||||
| A2244 | 0.0970 | 0.207 | 5.77+ 0.61-0.44 | 2.10 |
(2.19 |
(2.35 |
| A0133 | 0.0569 | 0.160 | 3.97+ 0.28-0.27 | 2.06 |
(7.33 |
(7.66 |
| A2163 | 0.2010 | 1.227 | 10.55+ 1.01-0.68 | 2.04 |
(9.28 |
(10.59 |
| A2255 | 0.0800 | 0.251 | 5.92+ 0.40-0.26 | 2.02 |
(1.42 |
(1.51 |
| IIIZw54 | 0.0311 | 1.668 |
|
2.01 |
(2.11 |
(2.16 |
|
|
||||||
| A3395s | 0.0498 | 0.849 | 5.55+ 0.89-0.65 | 2.01 |
(5.42 |
(5.63 |
| N507 | 0.0165 | 0.525 | 1.40+ 0.04-0.07 | 2.00 |
(5.88 |
(5.96 |
| MKW4 | 0.0200 | 0.186 | 1.84+ 0.05-0.03 | 2.00 |
(8.65 |
(8.79 |
| UGC03957 | 0.0340 | 0.459 |
|
1.98 |
(2.49 |
(2.56 |
|
|
||||||
| A3827 | 0.0980 | 0.284 |
|
1.98 |
(2.10 |
(2.25 |
|
|
||||||
| A3822 | 0.0760 | 0.212 | 5.12+ 0.43-0.31 | 1.98 |
(1.26 |
(1.33 |
| IIZw108 | 0.0494 | 0.663 |
|
1.90 |
(5.06 |
(5.26 |
|
|
||||||
| M49 | 0.0044 | 0.159 | 1.33+ 0.03-0.03 | 1.89 |
(3.93 |
(3.94 |
| ZwCl1742 | 0.0757 | 0.356 |
|
1.87 |
(1.18 |
(1.25 |
|
|
||||||
| S405 | 0.0613 | 0.765 |
|
1.82 |
(7.48 |
(7.84 |
|
|
||||||
| A3532 | 0.0539 | 0.596 | 4.41+ 0.19-0.18 | 1.78 |
(5.65 |
(5.88 |
| A3695 | 0.0890 | 0.356 |
|
1.76 |
(1.54 |
(1.65 |
|
|
||||||
| HCG94 | 0.0417 | 0.455 | 3.30+ 0.17-0.16 | 1.72 |
(3.25 |
(3.36 |
| A3528s | 0.0551 | 0.610 | 4.60+ 0.49-0.27 | 1.70 |
(5.65 |
(5.89 |
| S540 | 0.0358 | 0.353 |
|
1.62 |
(2.26 |
(2.32 |
|
|
||||||
| A2877 | 0.0241 | 0.210 |
|
1.61 |
(1.01 |
(1.03 |
| A3395n | 0.0498 | 0.542 | 5.11+ 0.47-0.43 | 1.54 |
(4.16 |
(4.33 |
| A2151w | 0.0369 | 0.336 | 2.58+ 0.19-0.20 | 1.53 |
(2.26 |
(2.33 |
| A3560 | 0.0495 | 0.392 |
|
1.50 |
(4.02 |
(4.17 |
|
|
||||||
| A2734 | 0.0620 | 0.184 | 5.07+ 0.36-0.42 | 1.47 |
(6.19 |
(6.49 |
| A0548e | 0.0410 | 0.188 | 2.93+ 0.17-0.15 | 1.46 |
(2.68 |
(2.77 |
| A1689 | 0.1840 | 0.180 | 8.58+ 0.84-0.40 | 1.45 |
(5.53 |
(6.25 |
| A1914 | 0.1712 | 0.097 | 8.41+ 0.60-0.58 | 1.45 |
(4.77 |
(5.36 |
| RXJ2344 | 0.0786 | 0.354 |
|
1.37 |
(9.34 |
(9.91 |
|
|
||||||
| A3921 | 0.0936 | 0.280 | 5.39+ 0.38-0.35 | 1.31 |
(1.27 |
(1.36 |
| A1413 | 0.1427 | 0.162 | 6.56+ 0.65-0.44 | 1.28 |
(2.92 |
(3.23 |
| N5813 | 0.0064 | 0.419 | 0.76+ 0.19-0.19 | 1.27 |
(5.62 |
(5.66 |
| A1775 | 0.0757 | 0.100 | 3.66+ 0.34-0.20 | 1.26 |
(8.02 |
(8.49 |
| A3528n | 0.0540 | 0.610 | 4.79+ 0.50-0.44 | 1.26 |
(4.00 |
(4.17 |
| A1800 | 0.0748 | 0.118 |
|
1.20 |
(7.39 |
(7.82 |
|
|
||||||
| A3888 | 0.1510 | 0.120 |
|
1.09 |
(2.77 |
(3.08 |
|
|
||||||
| A3530 | 0.0544 | 0.600 | 4.05+ 0.32-0.30 | 0.96 |
(3.11 |
(3.25 |
| N5846 | 0.0061 | 0.425 | 0.64+ 0.04-0.03 | 0.83 |
(3.35 |
(3.36 |
| N499 | 0.0147 | 0.525 | 0.66+ 0.02-0.03 | 0.45 |
(1.07 |
(1.08 |
| A0548w | 0.0424 | 0.179 |
|
0.25 |
(4.84 |
(5.03 |
|
|
||||||
| *):
The Galactic latitude is lower than 20 (Edge & Stewart 1991), and XMM-Newton EPIC for S1101 (Kaastra et al. 2001). |
For our study we need to determine an average temperature for each cluster that closely reflects the mass of the cluster, i.e. a virial temperature. In many clusters, the X-ray emitting hot gas is not isothermal but a cooler gas component is often observed in the central region. The cool component, which is due to either a cooling flow (e.g. Fabian 1994) or the ISM of cD galaxies (e.g. Makishima et al. 2001), often exhibits a significant fraction of the luminosity and has to be separated from the rest of the X-ray emission to determine the cluster average temperature (see also Markevitch 1998; Arnaud & Evrard 1999).
Therefore, in the ASCA data analysis, we employed a two-temperature (2T) model, in which isothermal plasma is filling the entire cluster region, while, in the central region, another cooler isothermal gas component is allowed to coexist with the hotter plasma forming a multi-phase intra-cluster medium (ICM). This 2T picture was established for the Centaurus cluster (Fukazawa et al. 1994; Ikebe et al. 1999) and also gave a good account of the ASCA data of Virgo/M 87 (Matsumoto et al. 1996), Hydra-A (Ikebe et al. 1997), Abell 1795 (Xu et al. 1998), and other nearby clusters (Fukazawa 1997; Fukazawa et al. 1998, 2000). The hot component extends over the major part of cluster volume as far as is measurable (e.g. Fukazawa 1997; White 2000). The temperature of this hot component derived from the 2T model therefore represents the best estimation of the virial temperature of the cluster. Although a cooling flow spectral model also gives generally a good description of the ASCA spectra (e.g. Fabian et al. 1994; White 2000; Allen et al. 2001), the estimated temperatures from where gas starts to cool vary considerably from author to author and are sometimes spuriously high. More importantly, recent XMM-Newton data clearly show that the conventional cooling flow spectral model is not adequate (Peterson et al. 2001; Tamura et al. 2001; Kaastra et al. 2001). The 2T model, on the other hand, is valid to the XMM-Newton data and the hot component temperature well represents the temperature of the outer main component (see Ikebe 2001).
It is known that, apart from the central cool component, many clusters show deviations from isothermality such as an asymmetric temperature distribution due to merging (e.g. Briel & Henry 1994) or a global temperature decrement towards the outside (Markevitch et al. 1998). For such clusters, the 2T model fit gives insignificant flux to the cool component and works practically as an isothermal model. Thus the hot component temperature gives the average temperature, which also can be a good measure of the virial temperature.
Among the 106 sample clusters, 88 clusters have been observed with ASCA, and all the data sets have become publicly available by now. We retrieved the ASCA data from the ASCA archival data base provided by NASA Goddard Space Flight Center and by Leicester University. Here we will give a brief explanation of the analysis method of the ASCA data.
ASCA has four focal plane instruments,
two SIS (Solid-state Imaging Spectrometer)
and two GIS (Gas Imaging Spectrometer; Ohashi et al. 1996),
which were usually used simultaneously to observe an astronomical object.
In all the observations, the GIS were operated in the normal PH mode
and the SIS were operated in FAINT mode or BRIGHT mode.
The number of active CCD chips of each SIS used was 4, 2, or 1,
corresponding to the field of view of
![]() ,
,
![]() ,
or
,
or
![]() ,
respectively.
,
respectively.
We discarded the GIS and SIS data that were taken when
the elevation angle of the X-Ray Telescope (XRT) from the local horizon
was less than ![]() .
An additional screening requirement, that the elevation angle from
the sunlit earth be greater than
.
An additional screening requirement, that the elevation angle from
the sunlit earth be greater than
![]() and
and
![]() ,
was applied to the SIS-0 and SIS-1 data, respectively.
In order to ensure a low and stable particle background,
we also discarded GIS and SIS data acquired under a geomagnetic
cutoff rigidity smaller than 6 GV.
,
was applied to the SIS-0 and SIS-1 data, respectively.
In order to ensure a low and stable particle background,
we also discarded GIS and SIS data acquired under a geomagnetic
cutoff rigidity smaller than 6 GV.
The background is composed of cosmic X-ray background and non-X-ray background, which were estimated for each cluster observation from the data of blank-sky observations as well as the data taken when the X-Ray Telescope was pointing at the dark (night) earth.
In order to maximize the detection efficiency of the central cool component,
we accumulated spectra over two regions, a central region of 2' radius
and an outer region from 2' to
![]() ,
from each cluster data set.
,
from each cluster data set.
![]() ,
the maximum radius, is defined as the radius
within which at least 95% of all detected source X-ray counts,
within the field of view of the GIS, are included.
The data from the two GIS sensors and two SIS sensors were combined.
Thus for each cluster, four spectra: two central and two outer spectra
for GIS and SIS, were derived.
,
the maximum radius, is defined as the radius
within which at least 95% of all detected source X-ray counts,
within the field of view of the GIS, are included.
The data from the two GIS sensors and two SIS sensors were combined.
Thus for each cluster, four spectra: two central and two outer spectra
for GIS and SIS, were derived.
An effective area as a function of X-ray energy was calculated for each spectrum with an ASCA simulator (SimARF). The point-spread-function of the ASCA XRT is so largely extended that the X-ray flux from the central brightest region may contribute to the outer region spectrum (Serlemitsos et al. 1995; Takahashi et al. 1995). We therefore, simultaneously fitted the four spectra with the 2T model, taking into account the flux-contamination effect. As a plasma code, we used the MEKAL model (Mewe et al. 1985, 1986; Kaastra 1992; Liedahl et al. 1995), that is implemented in XSPEC version 10.0 (Arnaud 1996).
A best-fit model was derived by a chi-square minimization method.
The cool and hot component temperatures are separate free parameters.
Many clusters do not require an additional cool component to fit
the spectra, and the cool component temperatures cannot be constrained.
For each cluster we investigated the significance of adding
a cool component by comparison with a fit of a hot isothermal model
and performing an F-test.
For a cluster showing a low significance for the additional cool component
in the 2T model,
we fixed the temperature of the cool component at
![]() ,
where
,
where
![]() is the temperature derived with the isothermal model fitting.
The choice of the fixed cool-component temperature is based on
a clear correlation found in the 2T model fitting
that, for clusters showing a high significance for the cool component,
the cool-component temperature is always very close to half of
the hot component temperature (see Ikebe 2001).
The hot component temperatures thus derived are summarized in Table 1.
A more detailed analysis procedure description and
results on the cool components will be presented in a following publication.
is the temperature derived with the isothermal model fitting.
The choice of the fixed cool-component temperature is based on
a clear correlation found in the 2T model fitting
that, for clusters showing a high significance for the cool component,
the cool-component temperature is always very close to half of
the hot component temperature (see Ikebe 2001).
The hot component temperatures thus derived are summarized in Table 1.
A more detailed analysis procedure description and
results on the cool components will be presented in a following publication.
We compared the temperatures derived here with those of previous workers.
The temperatures agree with results of Fukazawa (1997)
within 1.5% on average (Fig. 1a),
who performed a similar analysis
on a smaller number of clusters with ASCA data,
accumulating spectra from a central region of 2-3 arcmin radius
and an outer region, and fitting them with the 2T model.
On the other hand,
temperatures given by Markevitch et al. (1998)
and White (2000),
who used different (cooling flow) models to fit the ASCA spectra,
are higher than our values respectively by a factor of 1.09 and 1.25 on average
for clusters hotter than 6 keV (Figs. 1b,c).
This difference causes a significant difference in the resulting XTFs
(see Sect. 3.2).
![\begin{figure}
\par\includegraphics[angle=-90,width=5cm,clip]{h2920f1a.ps}\par\i...
...20f1b.ps}\par\includegraphics[angle=-90,width=5cm,clip]{h2920f1c.ps}\end{figure}](/articles/aa/full/2002/09/aah2920/Timg72.gif) |
Figure 1: Comparison between the cluster temperatures derived here and those by Fukazawa (1997) a), by Markevitch et al. (1998) b), and by White (2000) c). |
| Open with DEXTER | |
For the 88 clusters observed with ASCA,
X-ray fluxes and luminosities were calculated
from the spectral-analysis results described above
and the ROSAT PSPC count rates in 50-201 PI channel
given by Reiprich & Böhringer (2002).
Assuming isothermality in each cluster at the hot-component temperature
and the Galactic column density given in Table 1,
we determined the 0.1-2.4 keV fluxes and luminosities that reproduce
the PSPC count rates.
As summarized in Table 1, the luminosities were calculated
for two different cosmological models
with an open (
![]() )
and a flat (
)
and a flat (
![]() )
universe.
)
universe.
We then established a correlation between the luminosity
in the 0.1-2.4 keV band,
![]() ,
and the temperature of the hot component,
,
and the temperature of the hot component, ![]() ,
as illustrated in Fig. 2.
The
,
as illustrated in Fig. 2.
The
![]() -
-![]() relations for
the open and flat universe were fitted individually
with power-law functions by a linear regression method.
For the fit we did not use clusters with a hot component temperature
cooler than 1.4 keV,
because it is known that
a single power-law function is not a good representation
of the L-T relation over a wide temperature range.
In particular, including clusters, groups, and elliptical galaxies,
the L-T relation becomes steeper below
relations for
the open and flat universe were fitted individually
with power-law functions by a linear regression method.
For the fit we did not use clusters with a hot component temperature
cooler than 1.4 keV,
because it is known that
a single power-law function is not a good representation
of the L-T relation over a wide temperature range.
In particular, including clusters, groups, and elliptical galaxies,
the L-T relation becomes steeper below ![]() 1 keV
(e.g. Xue & Wu 2000).
Moreover, the theoretically predicted XTFs as given in Sect. 4 may not be
directly compared with an observed XTF (see Sect. 4.3 for more explanation).
Therefore, in the power-law fitting, we exclude 6 sample clusters
cooler than 1.4 keV and use only 82 clusters.
For the linear regression fit,
we employed the BCES(X2|X1) estimator
given by Akritas & Bershady (1996).
(In this case, the luminosity and
temperature are assigned as X2 and X1, respectively.)
The choice of the estimator is based on an argument by
Isobe et al. (1990).
The best-fit functions are
1 keV
(e.g. Xue & Wu 2000).
Moreover, the theoretically predicted XTFs as given in Sect. 4 may not be
directly compared with an observed XTF (see Sect. 4.3 for more explanation).
Therefore, in the power-law fitting, we exclude 6 sample clusters
cooler than 1.4 keV and use only 82 clusters.
For the linear regression fit,
we employed the BCES(X2|X1) estimator
given by Akritas & Bershady (1996).
(In this case, the luminosity and
temperature are assigned as X2 and X1, respectively.)
The choice of the estimator is based on an argument by
Isobe et al. (1990).
The best-fit functions are
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{h2920f2.ps}\end{figure}](/articles/aa/full/2002/09/aah2920/Timg79.gif) |
Figure 2:
The luminosities in the energy range of 0.1-2.4 keV in the cluster
rest frame in a flat universe
(
|
| Open with DEXTER | |
We have made a correction
to the derived
![]() relation.
Since the less luminous clusters are less likely to be sampled,
the apparent mean luminosity at a given temperature,
which is estimated by the simple regression fit,
is biased towards higher values than the true mean value.
As will be shown in Sect. 4,
we studied this effect and corrected the normalization
to derive the "true''
relation.
Since the less luminous clusters are less likely to be sampled,
the apparent mean luminosity at a given temperature,
which is estimated by the simple regression fit,
is biased towards higher values than the true mean value.
As will be shown in Sect. 4,
we studied this effect and corrected the normalization
to derive the "true''
![]() relation,
as
relation,
as
Using the corrected
![]() relations,
we estimated the temperatures of 14 clusters for
which no ASCA data nor other spectroscopic measurement are available.
An
relations,
we estimated the temperatures of 14 clusters for
which no ASCA data nor other spectroscopic measurement are available.
An
![]() and
and ![]() combination was chosen
from the
combination was chosen
from the
![]() relation
such that the predicted PSPC count rate equals the observed value.
Scatter around the best-fit power-law in the L-T relation
was assigned as error.
The estimated temperatures and luminosities for the open and flat universe
cases as well as the corresponding 0.1-2.4 keV fluxes which are the same
for the open and flat universe cases are summarized in Table 1.
relation
such that the predicted PSPC count rate equals the observed value.
Scatter around the best-fit power-law in the L-T relation
was assigned as error.
The estimated temperatures and luminosities for the open and flat universe
cases as well as the corresponding 0.1-2.4 keV fluxes which are the same
for the open and flat universe cases are summarized in Table 1.
We set a flux-limit of
![]() ergs s-1 cm-2in 0.1-2.4 keV band to construct a flux-limited complete sample
from the master catalog of 106 clusters.
As in Reiprich & Böhringer (2002) for
ergs s-1 cm-2in 0.1-2.4 keV band to construct a flux-limited complete sample
from the master catalog of 106 clusters.
As in Reiprich & Böhringer (2002) for
![]() ,
additional selection criteria applied are that
the absolute Galactic latitude is greater than
,
additional selection criteria applied are that
the absolute Galactic latitude is greater than
![]() ,
and the cluster is located neither in the Magellanic Clouds
nor in the Virgo cluster region.
The total number of clusters thus selected is 63,
whose temperatures and redshifts are shown in Fig. 3.
Since the temperatures of the individual clusters were newly determined
in this paper,
the fluxes estimated from the PSPC count rate
are slightly revised from the value in Reiprich & Böhringer (2002)
where the temperatures are compiled from literature.
All of the 63 clusters selected here, however, still correspond with
the 63
,
and the cluster is located neither in the Magellanic Clouds
nor in the Virgo cluster region.
The total number of clusters thus selected is 63,
whose temperatures and redshifts are shown in Fig. 3.
Since the temperatures of the individual clusters were newly determined
in this paper,
the fluxes estimated from the PSPC count rate
are slightly revised from the value in Reiprich & Böhringer (2002)
where the temperatures are compiled from literature.
All of the 63 clusters selected here, however, still correspond with
the 63
![]() clusters.
Tests performed in Reiprich & Böhringer (2002)
showed no indication of incompleteness of the sample.
clusters.
Tests performed in Reiprich & Böhringer (2002)
showed no indication of incompleteness of the sample.
In the following analysis, we exclude 2 clusters cooler than 1.4 keV (see Sects. 2.3 and 4.3) from the flux-limited complete sample, and use 61 clusters to study the XTF and make constraints on cosmological parameters. This is the largest complete sample of clusters up to now with temperature measurements or reliable temperature estimates. We also stress the accuracy of the temperature measurements for the sample clusters: Among the 61 clusters used for constructing the XTF, the temperatures of 56 clusters (90% of the sample) were measured with ASCA data with 90% errors of 6-10%, other spectroscopic measurements were used for 3 clusters, and there are only two clusters for which the temperature is estimated with the L-T relation.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{h2920f3.ps}\end{figure}](/articles/aa/full/2002/09/aah2920/Timg85.gif) |
Figure 3: X-ray temperature vs. redshift for the clusters of the flux-limited sample. |
| Open with DEXTER | |
| NAME |
|
|
|
| Open | Flat | ||
| A2163 | 2.39e+08 | 2.65e+08 | |
| A0754 | 1.40e+08 | 1.52e+08 | |
| A2142 | 1.14e+08 | 1.23e+08 | |
| COMA | 9.69e+07 | 1.04e+08 | |
| A2029 | 9.12e+07 | 9.78e+07 | |
| A3266 | 8.30e+07 | 8.89e+07 | |
| A0401 | 6.50e+07 | 6.91e+07 | |
| A0478 | 5.66e+07 | 6.00e+07 | |
| A2256 | 5.45e+07 | 5.77e+07 | |
| A3571 | 5.36e+07 | 5.67e+07 | |
| A0085 | 4.60e+07 | 4.87e+07 | |
| A0399 | 4.46e+07 | 4.72e+07 | |
| A2204 | 4.28e+07 | 4.52e+07 | |
| ZwCl1215 | 4.09e+07 | 4.49e+07 | |
| A3667 | 4.05e+07 | 4.28e+07 | |
| A1651 | 3.92e+07 | 4.14e+07 | |
| A1795 | 3.81e+07 | 4.02e+07 | |
| A2255 | 3.29e+07 | 3.46e+07 | |
| A3391 | 3.23e+07 | 3.40e+07 | |
| A2244 | 3.01e+07 | 3.17e+07 | |
| A0119 | 2.86e+07 | 3.00e+07 | |
| A1650 | 2.85e+07 | 2.99e+07 | |
| A3395s | 2.64e+07 | 2.76e+07 | |
| A3158 | 2.40e+07 | 2.50e+07 | |
| A2065 | 2.34e+07 | 2.44e+07 | |
| A3558 | 2.35e+07 | 2.45e+07 | |
| A3112 | 1.48e+07 | 1.53e+07 | |
| A1644 |
|
1.46e+07 | 1.51e+07 |
| A0496 | 1.34e+07 | 1.39e+07 | |
| A3562 | 1.22e+07 | 1.27e+07 | |
| A3376 | 1.18e+07 | 1.22e+07 | |
| A2147 | 1.10e+07 | 1.13e+07 | |
| A2199 | 1.04e+07 | 1.08e+07 | |
| A2597 | 9.75e+06 | 1.01e+07 | |
| A0133 | 8.02e+06 | 8.25e+06 | |
| A4059 | 7.76e+06 | 7.98e+06 | |
| A0576 | 7.07e+06 | 7.26e+06 | |
| HYDRA-A | 6.98e+06 | 7.16e+06 | |
| A3526 | 6.15e+06 | 6.30e+06 | |
| A1736 | 6.11e+06 | 6.26e+06 | |
| 2A0335 | 5.87e+06 | 6.00e+06 | |
| A2063 | 5.41e+06 | 5.53e+06 | |
| A1367 | 5.36e+06 | 5.48e+06 | |
| A2657 | 5.25e+06 | 5.36e+06 | |
| A2634 | 4.84e+06 | 4.94e+06 | |
| MKW3S | 4.87e+06 | 4.97e+06 | |
| A2589 | 4.48e+06 | 4.57e+06 | |
| MKW8 | 4.08e+06 | 4.16e+06 | |
| A4038 | 3.78e+06 | 3.85e+06 | |
| A1060 | 3.50e+06 | 3.56e+06 | |
| A2052 | 3.37e+06 | 3.43e+06 | |
| IIIZw54 | 2.87e+06 | 2.99e+06 | |
| EXO0422 |
|
2.60e+06 | 2.63e+06 |
| S1101 |
|
1.76e+06 | 1.77e+06 |
| A0400 | 1.37e+06 | 1.38e+06 | |
| A0262 | 1.04e+06 | 1.04e+06 | |
| MKW4 | 5.00e+05 | 4.96e+05 | |
| A3581 | 4.88e+05 | 4.84e+05 | |
| FORNAX | 2.72e+05 | 2.68e+05 | |
| N1550 | 2.05e+05 | 2.02e+05 | |
| N507 | 1.83e+05 | 1.79e+05 | |
| N5044 | 1.10e+05 | 1.08e+05 | |
| N4636 | 1.16e+04 | 1.10e+04 | |
The improvement of the new result over previous work is mainly characterized by a significant broadening of the temperature range towards lower temperature systems down to 1.4 keV. A single power law is no longer a good description to the observationally measured XTF and an exponential cut off towards the higher temperature is clearly seen, as a theoretical model predicts. The detection of such a curvature brings tight constraints on cosmological parameters as will be shown in the next section.
Conventionally,
![]() in Eq. (5)
is often simply replaced by
in Eq. (5)
is often simply replaced by
![]() to evaluate the XTF (e.g. Henry 2000).
For comparison, the XTF evaluated with
to evaluate the XTF (e.g. Henry 2000).
For comparison, the XTF evaluated with
![]() is also overlayed in Fig. 4,
which overall shows good agreement
with the one with
is also overlayed in Fig. 4,
which overall shows good agreement
with the one with
![]() ,
but exhibits larger variance
due to the intrinsic scatter in the L-T relation.
,
but exhibits larger variance
due to the intrinsic scatter in the L-T relation.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{h2920f4.ps}\end{figure}](/articles/aa/full/2002/09/aah2920/Timg107.gif) |
Figure 4:
The X-ray temperature function derived with
the flux-limited complete sample of 61 clusters
for the case of a flat universe
(
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{h2920f5.ps}\end{figure}](/articles/aa/full/2002/09/aah2920/Timg108.gif) |
Figure 5:
The X-ray temperature function derived with
the flux-limited complete sample of 61 clusters
for the case of a flat universe
(
|
| Open with DEXTER | |
We have derived a cumulative XTF, which is the number density
of clusters that are hotter than a certain temperature, by
Blanchard et al. (2000), using a sample and temperatures mainly from the XBACS (Ebeling et al. 1996) and the ASCA measurement by Markevitch et al. (1998), respectively, obtained the XTF, which virtually perfectly agrees with that by Markevitch (1998) above 4 keV, and has larger abundance below 4 keV. Pierpaoli et al. (2001), who have made another attempt to derive the XTF, used the same sample as Markevitch (1998) but the temperatures given by White (2000). The Pierpaoli cumulative XTF has the highest amplitude among other works. This is because of the systematically higher temperatures by White (2000) (see Fig. 1).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{h2920f6NEW.ps}\end{figure}](/articles/aa/full/2002/09/aah2920/Timg111.gif) |
Figure 6:
The cumulative temperature function for the case of a flat universe
(
|
| Open with DEXTER | |
In the following, using the flux-limited complete sample of 61 clusters
(
![]() )
and theoretical XTF models,
we obtain constraints on cosmological parameters.
The XTF at the present epoch is most sensitive to the amplitude of
density fluctuations on a scale of 8 h-1 Mpc,
)
and theoretical XTF models,
we obtain constraints on cosmological parameters.
The XTF at the present epoch is most sensitive to the amplitude of
density fluctuations on a scale of 8 h-1 Mpc, ![]() ,
and least sensitive to the cosmological constant,
,
and least sensitive to the cosmological constant, ![]() .
We therefore concentrate on two different
.
We therefore concentrate on two different
![]() model
families including open (
model
families including open (
![]() ,
,
![]() )
and flat (
)
and flat (
![]() )
universes.
Recent measurements of high-redshift SN Ia indicate a positive cosmological
constant (Perlmutter et al. 1999; Riess et al. 1998).
Moreover, the cosmic microwave background (CMB) temperature-fluctuation
map recently derived with the Boomerang experiment strongly supports
a flat universe model (de Bernardis et al. 2000).
Therefore, a flat universe model with a positive cosmological constant
is currently the most plausible description of our universe.
For the purpose of comparison with previous works,
we also consider the case of an open universe.
)
universes.
Recent measurements of high-redshift SN Ia indicate a positive cosmological
constant (Perlmutter et al. 1999; Riess et al. 1998).
Moreover, the cosmic microwave background (CMB) temperature-fluctuation
map recently derived with the Boomerang experiment strongly supports
a flat universe model (de Bernardis et al. 2000).
Therefore, a flat universe model with a positive cosmological constant
is currently the most plausible description of our universe.
For the purpose of comparison with previous works,
we also consider the case of an open universe.
For the theoretical prediction of the XTF, we employ two different models, a conventional Press-Schechter mass function (Sect. 4.1) and the Formation-Epoch model by Kitayama & Suto (1996) that is a modification of the former theory (Sect. 4.2). The model XTF depends also on the Hubble constant, which is here assumed to be 71 km/s/Mpc (i.e. h=0.71) based on the latest results of the HST Hubble constant project (see Mould et al. 2000 and references therein).
According to the Press-Schechter formalism,
the number density of clusters with a mass in the range of M to
![]() that have collapsed before a redshift z is given as
that have collapsed before a redshift z is given as
The mass function given above is converted to the XTF by means of
a mass-temperature relation.
We assume that the ICM in a cluster is described by an isothermal
![]() model (e.g. Forman & Jones 1982),
in which the density profile is given as
model (e.g. Forman & Jones 1982),
in which the density profile is given as
![]() ,
and that hydrostatic equilibrium is achieved.
The virial mass is defined as
,
and that hydrostatic equilibrium is achieved.
The virial mass is defined as
We further assume that a cluster collapsed just before it is observed.
This recent formation approximation, which has been extensively
applied in previous conventional modelings, is relaxed
in the Formation-Epoch model described in the next section.
Combining all the formulae given above,
the model XTF at a given redshift is given by
In the model XTF given in the previous section, the formation redshift, zf, of an observed cluster is assumed to be the same as the observed redshift (i.e. recent formation approximation). However, this assumption is not reasonable in particular in a low density universe. Kitayama & Suto (1996) constructed a model XTF taking into account the distribution of the dark-matter-halo formation epoch as well as the evolution of temperature (hereafter FE model). They showed that the XTF predicted by the FE model can be significantly different from the PS model described in Sect. 4.1, in particular when the temperature evolves after the collapse.
The FE model is given as,
| Model XTF |
|
A |
|
||
| PS(Open) | 0.18 -0.05+0.08 | 0.96 -0.09+0.11 | 42.15 -0.20+0.17 | 2.47 -0.24+0.26 | 0.24 -0.04+0.04 |
| PS(Open, T>3 keV) | 0.25 -0.09+0.12 | 0.89 -0.11+0.13 | 42.19 -0.28+0.27 | 2.42 -0.37+0.38 | 0.22 -0.03+0.05 |
| FE(Open, s=0) | 0.15 -0.05+0.07 | 0.98 -0.07+0.08 | 42.14 -0.20+0.17 | 2.49 -0.25+0.26 | 0.24 -0.04+0.04 |
| FE(Open, s=1) | 0.11 -0.05+0.07 | 0.68 -0.03+0.04 | 42.12 -0.20+0.18 | 2.51 -0.25+0.27 | 0.24 -0.04+0.04 |
| PS(Flat) | 0.19 -0.05+0.08 | 1.02 -0.11+0.12 | 42.15 -0.20+0.17 | 2.49 -0.25+0.26 | 0.24 -0.03+0.04 |
| PS(Flat, T>3 keV) | 0.26 -0.09+0.12 | 0.94 -0.13+0.14 | 42.19 -0.29+0.27 | 2.44 -0.38+0.39 | 0.23 -0.04+0.04 |
| FE(Flat, s=0) | 0.18 -0.05+0.07 | 1.14 -0.11+0.13 | 42.15 -0.20+0.17 | 2.49 -0.25+0.26 | 0.24 -0.03+0.04 |
| FE(Flat, s=1) | 0.14 -0.05+0.06 | 0.89 -0.08+0.08 | 42.14 -0.21+0.17 | 2.51 -0.25+0.26 | 0.24 -0.03+0.04 |
Instead of fitting the model XTF to the XTF derived in Sect. 3,
we use the predicted XTF and the L-T relation
to calculate the expected luminosity and temperature distribution
for the given survey selection function which is given
in a form of
![]() ,
and perform a fit to the observed luminosity-temperature distribution
of the 61 clusters selected in Sect. 2.4.
In this analysis,
the intrinsic luminosity distribution for a given temperature,
which in other words is the conditional luminosity function
at a given temperature,
is assumed to follow a Gaussian function in logarithmic scale
with a constant standard deviation
and a mean luminosity given by a power-law function of the temperature.
This assumption can be justified by observational results as shown
in Sect. 3.1.
In order to simplify a model calculation,
we assume that the XTF does not change within the search volume
of our flux limit
and use a model XTF at the median redshift of our cluster sample
at z=0.046 as a representative value.
Systematic errors on the final results caused from this assumption
are found to be negligibly small compared with statistical errors.
Incorporated by another Gaussian that represents temperature
measurement errors,
the expected cluster number density
in a unit logarithmic temperature and a unit logarithmic luminosity
is given as
,
and perform a fit to the observed luminosity-temperature distribution
of the 61 clusters selected in Sect. 2.4.
In this analysis,
the intrinsic luminosity distribution for a given temperature,
which in other words is the conditional luminosity function
at a given temperature,
is assumed to follow a Gaussian function in logarithmic scale
with a constant standard deviation
and a mean luminosity given by a power-law function of the temperature.
This assumption can be justified by observational results as shown
in Sect. 3.1.
In order to simplify a model calculation,
we assume that the XTF does not change within the search volume
of our flux limit
and use a model XTF at the median redshift of our cluster sample
at z=0.046 as a representative value.
Systematic errors on the final results caused from this assumption
are found to be negligibly small compared with statistical errors.
Incorporated by another Gaussian that represents temperature
measurement errors,
the expected cluster number density
in a unit logarithmic temperature and a unit logarithmic luminosity
is given as
There are two reasons for setting the low temperature cut-off at 1.4 keV.
First, as discussed in Sect. 2.3,
the L-T relation breaks down for elliptical galaxies which have
a lower gas mass fraction, and actually gets steeper below ![]() 1 keV
as shown by e.g. Xue & Wu (2000).
Thus the simple power-law modeling for the L-T relation is not appropriate
for the whole temperature range.
The second reason is based on the more essential problem concerned
with the comparison between the theoretical XTFs and the observation.
The systems at the low temperature end are mostly single elliptical galaxies
and some of them may not be isolated but surrounded by larger scale dark
matter halos.
As has been shown by e.g. Matsushita (1998),
X-ray brightness profiles of elliptical galaxies have large variety
suggesting a significant variation in total mass for a given temperature,
i.e. a considerable scatter in the M-T relation would be expected.
Therefore, a cluster abundance at the low temperature end probably
does not directly correspond to an abundance of dark matter halos
at a certain mass scale.
1 keV
as shown by e.g. Xue & Wu (2000).
Thus the simple power-law modeling for the L-T relation is not appropriate
for the whole temperature range.
The second reason is based on the more essential problem concerned
with the comparison between the theoretical XTFs and the observation.
The systems at the low temperature end are mostly single elliptical galaxies
and some of them may not be isolated but surrounded by larger scale dark
matter halos.
As has been shown by e.g. Matsushita (1998),
X-ray brightness profiles of elliptical galaxies have large variety
suggesting a significant variation in total mass for a given temperature,
i.e. a considerable scatter in the M-T relation would be expected.
Therefore, a cluster abundance at the low temperature end probably
does not directly correspond to an abundance of dark matter halos
at a certain mass scale.
We first present the results from the PS model fitting.
The best-fit values and errors of the fitting parameters
are summarized in Table 3.
The best-fit distribution function in the
![]() space
in the flat universe case is illustrated in Fig. 7.
The corresponding model XTF is also illustrated in Fig. 4.
The constraint in
space
in the flat universe case is illustrated in Fig. 7.
The corresponding model XTF is also illustrated in Fig. 4.
The constraint in
![]() space is shown in
Fig. 8 for each open and flat universe case.
The contours represent the 90% confidence range for two parameters
of interest, and the constraint is notably tight.
space is shown in
Fig. 8 for each open and flat universe case.
The contours represent the 90% confidence range for two parameters
of interest, and the constraint is notably tight.
In order to demonstrate an improvement on the constraint
by the widest temperature range and the largest sample ever achieved,
we also performed the fitting with the PS model
only using 51 sample clusters above 3 keV.
As shown in Fig. 8, the improvement is significant,
in particular, for
![]() .
Since
.
Since
![]() is tightly related to the overall shape of
the mass variance, i.e. the power spectrum,
a larger mass range to measure the mass fluctuation amplitude
is essential.
is tightly related to the overall shape of
the mass variance, i.e. the power spectrum,
a larger mass range to measure the mass fluctuation amplitude
is essential.
The "true'' L-T relation employed in Sects. 2.3 and 3.1
was estimated by this fitting.
Fixing the ![]() value as obtained in Sect. 2.3,
to 2.47 and 2.50 for the open and flat universe case, respectively,
we performed the PS model fitting and derived
value as obtained in Sect. 2.3,
to 2.47 and 2.50 for the open and flat universe case, respectively,
we performed the PS model fitting and derived
![]() ,
,
![]() for the open universe case,
and
for the open universe case,
and
![]() ,
,
![]() for the flat universe case,
which are given in Eqs. (3) and (4)
and are applied in Eq. (6).
for the flat universe case,
which are given in Eqs. (3) and (4)
and are applied in Eq. (6).
![\begin{figure}
\par\includegraphics[width=7cm,clip]{h2920f7.ps}\end{figure}](/articles/aa/full/2002/09/aah2920/Timg167.gif) |
Figure 7: The best-fit model function in the luminosity-temperature space for the case of the flat universe is shown with contours. The 63 clusters from the flux-limited complete sample are overlayed with open circles. The vertical dotted lines indicate the temperature range used for the fitting. Therefore, 61 clusters are used to make constraints. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=6cm,clip]{h2920f8a.ps}\par\includegraphics[angle=-90,width=6cm,clip]{h2920f8b.ps}\end{figure}](/articles/aa/full/2002/09/aah2920/Timg168.gif) |
Figure 8:
Constraints on
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=6cm,clip]{h2920f9a.ps}\par\includegraphics[angle=-90,width=6cm,clip]{h2920f9b.ps}\end{figure}](/articles/aa/full/2002/09/aah2920/Timg169.gif) |
Figure 9:
Constraints on
|
| Open with DEXTER | |
The FE model gives somewhat different results.
In addition to
![]() and
and ![]() ,
the FE model introduces another parameter, s, that models
a temperature evolution, which can be a free parameter in a fit.
However, following Kitayama & Suto (1996), in the following analysis,
we rather fixed s at s=0 and s=1 such that they represent no evolution
and a maximum possible positive evolution of the temperature, respectively.
Since there is no observational evidence for the evolution of the temperature,
e.g. no redshift dependency in the L-T relation is found
(Mushotzky & Scharf 1997;
Donahue et al. 1999; Della Ceca et al. 2000),
the no evolution model may be more plausible.
However,
the effect of the temperature evolution is still interesting to study here.
The fitting results are summarized in Table 3,
and the constraints on
,
the FE model introduces another parameter, s, that models
a temperature evolution, which can be a free parameter in a fit.
However, following Kitayama & Suto (1996), in the following analysis,
we rather fixed s at s=0 and s=1 such that they represent no evolution
and a maximum possible positive evolution of the temperature, respectively.
Since there is no observational evidence for the evolution of the temperature,
e.g. no redshift dependency in the L-T relation is found
(Mushotzky & Scharf 1997;
Donahue et al. 1999; Della Ceca et al. 2000),
the no evolution model may be more plausible.
However,
the effect of the temperature evolution is still interesting to study here.
The fitting results are summarized in Table 3,
and the constraints on
![]() and
and ![]() are illustrated
in Fig. 9.
The FE model in the no temperature evolution case (s=0)
shows similar results with those of the PS model,
since the XTF predicted by the s=0 FE model
is very close to that of the PS model
(see Fig. 8 in Kitayama & Suto 1996).
On the other hand,
in the maximum temperature evolution cases (s=1),
the FE model gives significantly smaller
are illustrated
in Fig. 9.
The FE model in the no temperature evolution case (s=0)
shows similar results with those of the PS model,
since the XTF predicted by the s=0 FE model
is very close to that of the PS model
(see Fig. 8 in Kitayama & Suto 1996).
On the other hand,
in the maximum temperature evolution cases (s=1),
the FE model gives significantly smaller ![]() values
than those with the PS model.
values
than those with the PS model.
The M-T relation used in our analysis may be subject to uncertainties
introducing a significant systematic error in the final results
on the cosmological parameters.
Theoretical arguments yield a scaling law, that is
![]() (e.g. Kaiser 1986).
A number of numerical simulations support this scaling law,
but different normalizations are derived from different simulations.
Henry (2000) summarized such differences in the normalization
of the M-T relation derived from different hydrodynamical simulations.
A cluster mass may vary from 62% to 119% of the mean value.
(e.g. Kaiser 1986).
A number of numerical simulations support this scaling law,
but different normalizations are derived from different simulations.
Henry (2000) summarized such differences in the normalization
of the M-T relation derived from different hydrodynamical simulations.
A cluster mass may vary from 62% to 119% of the mean value.
| Source | |
| Hydrodynamic simulation (mean) |
|
| Hydrodynamic simulation (maximum) |
|
| Hydrodynamic simulation (minimum) |
|
| Horner et al. | 0.496 T-0.133 |
| Nevalainen et al. | 0.437 T0.193 |
| Finoguenov et al. | 0.415 T0.187 |
| Model XTF |
|
|
| PS(Open) | 0.09-0.37 | 0.55-1.13 |
| FE(Open, s= 0) | 0.07-0.32 | 0.61-1.15 |
| FE(Open, s= 1) | 0.03-0.23 | 0.52-0.80 |
| PS(Flat) | 0.10-0.38 | 0.57-1.19 |
| FE(Flat, s= 0) | 0.10-0.35 | 0.65-1.33 |
| FE(Flat, s= 1) | 0.06-0.18 | 0.66-0.97 |
The M-T relations derived observationally from X-ray mass measurements give somewhat different results. Horner et al. (1999) derived an M-T relation which has a similar exponent as the scaling law but a lower normalization than the numerical simulations. On the other hand, Nevalainen et al. (2000) and Finoguenov et al. (2001) obtained steeper relations of T1.79 and T1.78, respectively, and lower normalizations.
In order to investigate the effects of the different M-T relations,
we repeated the fitting performed in Sect. 4 with the PS model
for the flat universe case.
The six M-T relations we have examined are summarized in Table 4.
Each M-T relation can be expressed with Eq. (12),
replacing the ![]() value with the formula given in Table 4.
In Fig. 10, the best-fit parameters derived with the different
M-T relations are compared with the result presented in Sect. 4.4.
The effect of using different M-T relations is significant
and the systematic errors introduced are comparable to, or even larger than,
the current statistical errors.
As seen in Fig. 10, a change in the index of the M-T relation
moves the best-fit point along the elongation direction
of the confidence contour, while an amplitude change moves the best-fit
point along the perpendicular direction.
Taking into account these systematics from the different M-T relations,
the constraints on
value with the formula given in Table 4.
In Fig. 10, the best-fit parameters derived with the different
M-T relations are compared with the result presented in Sect. 4.4.
The effect of using different M-T relations is significant
and the systematic errors introduced are comparable to, or even larger than,
the current statistical errors.
As seen in Fig. 10, a change in the index of the M-T relation
moves the best-fit point along the elongation direction
of the confidence contour, while an amplitude change moves the best-fit
point along the perpendicular direction.
Taking into account these systematics from the different M-T relations,
the constraints on
![]() and
and ![]() are revised
and summarized in Table 5.
are revised
and summarized in Table 5.
With the FE model, where the recent formation approximation is not valid, it is not appropriate to use the empirical M-T relation obtained based on the observations of nearby clusters. This is because the current M-T relation should be a result of accumulation of different M-T relations from different formation redshifts which depend on the cluster masses. Therefore, the M-T relations obtained from the Hydrodynamic simulations may be more appropriately applied with the FE model.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{h2920f10.ps}\end{figure}](/articles/aa/full/2002/09/aah2920/Timg174.gif) |
Figure 10:
The best-fit values of
|
| Open with DEXTER | |
We compared our constraints on the cosmological parameters
with previous works.
Bahcall (2000) summarized the cluster constraints
on
![]() and
and ![]() as 0.2
as 0.2 ![]() 0.1 and
1.2
0.1 and
1.2 ![]() 0.2 (68% confidence level), respectively.
These values are consistent with our results.
0.2 (68% confidence level), respectively.
These values are consistent with our results.
The power spectrum of matter distribution in the present universe
has been measured from the spatial distribution of galaxies
and galaxy clusters,
and found to be generally well reproduced by the CDM power spectrum
(Peacock & West 1992; Einasto et al. 1993;
Jing & Valadarnini 1993; Einasto et al. 1997;
Retzlaff et al. 1998;
Tadros et al. 1998; Miller & Batuski 2001).
An important feature of the power spectra is a turnover,
where the scale is closely linked to the horizon scale at matter-radiation
equality.
Most recently Schuecker et al. (2001),
using a sample of 452 X-ray selected clusters of galaxies,
determined the location of the maximum of the power spectrum
in the range of
![]() h Mpc-1.
According to the CDM power spectrum,
h Mpc-1.
According to the CDM power spectrum,
![]() is well approximated by
is well approximated by
A measurement of the matter density fluctuation at the largest
spatial scale was performed using the COBE DMR experiment
(e.g. Bennett et al. 1996).
Bunn & White (1997), using the CDM power spectrum model,
extrapolated the COBE results to cluster scales
and gave constraints in
![]() -
-![]() space,
which are shown in Fig. 9.
In the case of the open universe,
our results with any of the model XTFs
do not overlap the COBE constraints,
even if the effects of the uncertainty in the M-T relation
are taken into account.
On the other hand, in the case of the flat universe,
our results with the effects of the uncertainty in the M-T relation,
are consistent with the COBE constraints
regardless of the choice of the model XTF.
space,
which are shown in Fig. 9.
In the case of the open universe,
our results with any of the model XTFs
do not overlap the COBE constraints,
even if the effects of the uncertainty in the M-T relation
are taken into account.
On the other hand, in the case of the flat universe,
our results with the effects of the uncertainty in the M-T relation,
are consistent with the COBE constraints
regardless of the choice of the model XTF.
The most important result concerning the XTF derived here
is that it covers a large enough range of temperatures
to reveal the shape of the function beyond a simple power law
representation.
As expected from theoretical considerations,
there should be a very sharp cut-off at the high mass end
and the function should turn into a shallower slope
at the low mass end as shown by our observations.
We have demonstrated that these constraints on the actual slope
of the XTF allow us to derive independent constraints on the two parameters
which are most important in cosmic structure formation models:
![]() and
and ![]() .
Leaving out only 16% of the sample clusters from the low temperature end
almost doubles the uncertainty for these independent constraints.
Therefore, while these independent constraints are an important achievement
of the present work on one hand,
this demonstration also shows that
these constraints are sensitive to any systematic error
introduced into the XTF.
.
Leaving out only 16% of the sample clusters from the low temperature end
almost doubles the uncertainty for these independent constraints.
Therefore, while these independent constraints are an important achievement
of the present work on one hand,
this demonstration also shows that
these constraints are sensitive to any systematic error
introduced into the XTF.
For this reason we have studied the stability of our results to
variations introduced to the observed data and also variations
of the theoretical modeling.
We have fully incorporated the measurement errors
in fluxes and temperatures of the sample clusters.
With the typical errors of 5% for the flux and 6-10% for the temperature,
the biases were found to be relatively small and not to cause a drastic change
on the final results in our analysis.
On the other hand,
we have shown that there are considerable variations
and uncertainties in the theoretical modeling of the XTF,
which introduce significant systematic errors in the final constraints
on
![]() and
and ![]() .
Various M-T relations that are employed to model the XTF
have resulted in considerably different values of
.
Various M-T relations that are employed to model the XTF
have resulted in considerably different values of
![]() and
and ![]() .
Another source of variation in the theoretical modeling
that we have studied is
a recent formation approximation which is employed with
the Press-Schechter formalism to build the PS model here.
Using the FE model,
in which the distribution of cluster formation redshifts
and the evolution of the mass as well as temperature of a cluster after
the collapse are analytically formulated,
we have shown that a considerable difference could be introduced
in the derived cosmological parameters, in particular in
.
Another source of variation in the theoretical modeling
that we have studied is
a recent formation approximation which is employed with
the Press-Schechter formalism to build the PS model here.
Using the FE model,
in which the distribution of cluster formation redshifts
and the evolution of the mass as well as temperature of a cluster after
the collapse are analytically formulated,
we have shown that a considerable difference could be introduced
in the derived cosmological parameters, in particular in ![]() .
This further motivates us to establish a more sophisticated model
to the XTF incorporating new X-ray observations
of the high redshift clusters with Chandra and XMM-Newton.
.
This further motivates us to establish a more sophisticated model
to the XTF incorporating new X-ray observations
of the high redshift clusters with Chandra and XMM-Newton.
Finally, taking into account all the uncertainties,
we put our general constraints on
![]() and
and ![]() as
as
![]() 0.03-0.37,
0.03-0.37, ![]() 0.52-1.15 in an open universe
and
0.52-1.15 in an open universe
and
![]() 0.06-0.38,
0.06-0.38, ![]() 0.57-1.33 in a flat universe,
respectively.
From the comparison with the COBE constraints,
a flat universe is more preferable than an open universe.
0.57-1.33 in a flat universe,
respectively.
From the comparison with the COBE constraints,
a flat universe is more preferable than an open universe.
Acknowledgements
We thank Peter Schuecker, Makoto Hattori, Patrick Henry, and Paul Lynam for valuable discussions and comments. We have made use of the ASCA archival database at Goddard Space Flight Center/NASA, U.S.A. and the Leicester Database and Archive Service at the Department of Physics and Astronomy, Leicester University, UK. We acknowledge FTOOLS.
Here we present our method, used in Sect. 3,
to evaluate the X-ray temperature function in more detail.
A flux limited sample has been extensively used for constructing
the X-ray luminosity function (XLF) by many authors
(e.g. Piccinotti et al. 1982;
Edge et al. 1990; Gioia et al. 1990;
Henry et al. 1992; Ebeling et al. 1997;
Rosati et al. 1998; de Grandi et al. 1999;
Ledlow et al. 1999).
Here we present the first description of how to construct
this function in the presence of measurement
uncertainties, correlation scatter and selection biases.
For a sample with a finite number of objects,
the differential XLF, i.e. the number density of clusters
having the rest frame luminosity in a range of
![]() to
to
![]() defined in a comoving space, can be evaluated as
defined in a comoving space, can be evaluated as
Using
![]() ,
the differential XTF can be given as
,
the differential XTF can be given as
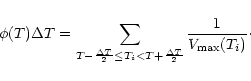 |
(A.7) |
When we apply this analysis method to our cluster sample, we further consider the following two points: our first concern is that the flux measurement may have a redshift bias such that for clusters with the same true luminosity, different luminosities are derived for different redshifts. In order to study this effect we produced a sample of cluster images at various redshifts as observed by the ROSAT PSPC and determined their fluxes with the growth curve analysis method (Böhringer et al. 2000) as performed for the actual observed data of the present sample by Reiprich & Böhringer (2002). The simulations show that the resulting luminosities are kept constant regardless of the redshift - at least in a range that we are considering here, i.e. z<0.2, despite the overall signal to noise ratio worsening with a dimming of the surface brightness that follows (1+z)-4.
Secondly, the effect from the measurement errors on X-ray fluxes
is considered.
If there are considerable measurement errors in the flux measurements,
a cluster that should be in the flux-limited sample
could be found to be fainter than the flux limit
and to be missed from the sample, and vice-versa.
If the measured flux distribution is assumed to be following
a Gaussian function with the sigma value of
![]() ,
the probability that a cluster of the luminosity Lat the redshift of z is found to be brighter
than the flux limit
,
the probability that a cluster of the luminosity Lat the redshift of z is found to be brighter
than the flux limit
![]() is given as
is given as
Although the correction is still insignificant with respect to
the Poisson error
that each temperature bin would have, we use the Eq. (A.9)
in the derivation of the XTF in Sect. 3.
Our sample selection criteria specify several parameters
in Eqs. (A.5), (A.6), (A.8) and (A.9)
as ![]() 8.139 str,
8.139 str,
![]() =
=
![]() ergs s-1 cm-2in 0.1-2.4 keV band in the observed frame,
and then
ergs s-1 cm-2in 0.1-2.4 keV band in the observed frame,
and then
![]() should be the 0.1-2.4 keV band luminosity
in the observed frame, which corresponds to a cluster rest frame luminosity
in the energy range from (
should be the 0.1-2.4 keV band luminosity
in the observed frame, which corresponds to a cluster rest frame luminosity
in the energy range from (
![]() to (
to (
![]() ) 2.4 keV.
Also, from the L-T relation studied in Sects. 2.3 and 4,
we estimated the following parameters as
) 2.4 keV.
Also, from the L-T relation studied in Sects. 2.3 and 4,
we estimated the following parameters as
![]() ,
,
![]() ,
and
,
and
![]() for an open universe case, and
for an open universe case, and
![]() ,
,
![]() ,
and
,
and
![]() for a flat universe case.
The XTF thus derived is shown in Fig. 4.
for a flat universe case.
The XTF thus derived is shown in Fig. 4.
Finally, we should note that Ti in Eq. (A.5)
is the measured cluster temperature rather than the "true'' temperature.
The derived XTF should have been smeared due to
the temperature measurement error,
which brings another systematic error into the resulting XTF.
In order to investigate the possible systematic errors due to
the temperature measurement errors and to confirm our analysis method,
we performed a Monte-Carlo simulation.
With an adopted XTF of
![]() ,
a number of cluster observations are simulated taking into account
the scatter in the L-T relation as well as the flux and temperature
measurement errors, and the XTF was constructed as performed
with the real data using Eqs. (A.5), (A.6),
(A.8) and (A.9).
The input XTF and the rederived XTF from the simulations show complete
agreement except a minor systematic increase - at most 2% at 10 keV,
which is due to the temperature measurement error for very hot clusters.
These systematics (Eddington bias; Eddington 1944)
remain in the XTF derived in Sect. 3 (Fig. 4),
while, for the model fitting in Sect. 4,
the temperature measurement error is taken into account (Eq. (15)).
,
a number of cluster observations are simulated taking into account
the scatter in the L-T relation as well as the flux and temperature
measurement errors, and the XTF was constructed as performed
with the real data using Eqs. (A.5), (A.6),
(A.8) and (A.9).
The input XTF and the rederived XTF from the simulations show complete
agreement except a minor systematic increase - at most 2% at 10 keV,
which is due to the temperature measurement error for very hot clusters.
These systematics (Eddington bias; Eddington 1944)
remain in the XTF derived in Sect. 3 (Fig. 4),
while, for the model fitting in Sect. 4,
the temperature measurement error is taken into account (Eq. (15)).