A&A 383, L23-L26 (2002)
DOI: 10.1051/0004-6361:20020089

On the origin of the broad, relativistic iron line of MCG-6-30-15 observed by XMM-Newton

A. Martocchia1 - G. Matt1 - V. Karas2


1 - Dipartimento di Fisica, Università degli Studi "ROMA TRE'', Via della Vasca Navale 84, 00146 Roma, Italy
2 - Astronomical Institute of the Charles University, Faculty of Mathematics and Physics, V Holesovickách 2, 18000 Praha, Czech Republic

Received 12 December 2001 / Accepted 10 January 2002

Abstract
The relativistic iron line profile recently observed by XMM-Newton in the spectrum of the Seyfert 1 galaxy MCG-6-30-15 (Wilms et al. 2001) is discussed in the framework of the lamp-post model. It is shown that the steep disc emissivity, the large line equivalent width and the amount of Compton reflection can be self-consistently reproduced in this scenario.

Key words: relativity - line: profiles; black hole physics - accretion, accretion discs - X-rays: galaxies - galaxies: individual: MCG-6-30-15


1 Introduction

Wilms et al. (2001; cited as W01 hereafter) recently presented and discussed an extremely broad and red-shifted iron K$\alpha $ feature detected in the 06/11-12/2000 100 ksec XMM-Newton observation of MCG-6-30-15. This Seyfert 1 galaxy is well known for possessing one of the best studied broad iron lines, whose profile is explained by relativistic effects (Tanaka et al. 1995; Guainazzi et al. 1998; see Fabian et al. 2000, for a review). The Fe K$\alpha $ profile observed by XMM-Newton's EPIC-pn camera is similar to the one observed by Iwasawa et al. (1996) using ASCA data during a short ($\sim$15.2 ksec) period of low X-ray flux. W01 may have caught the source in a similar "deep minimum state", i.e. a state in which the primary flux is lower ( $F_{\rm 2-10~keV}=2.3 \times 10^{-11}$ erg s-1 cm-2) and the line Equivalent Width (EW) higher (up to $300\div400$ eV) than the time-averaged values.

The line profile indicates that a large fraction of the emission comes from $r<6r_{\rm {g}}$ ( $r_{\rm {g}}=m={GM \over c^2}$). This implies either that the central Black Hole (BH) is rotating - thus the radius of the disc innermost stable orbit, $r_{\rm {ms}}$, lies between $6r_{\rm {g}}$ (= $r_{\rm {ms}}$ for a static BH) and $1.23r_{\rm {g}}$ ( $r_{\rm {ms}}$ of a canonically spinning BH: Thorne 1974) - or that the fluorescent line emission originates from matter falling freely below $r_{\rm {ms}}$ (Reynolds & Begelman 1997). Sako et al. (2001) proposed that also some spectral features observed at lower energies in this source, as well as in Mkn 766, are Ly$\alpha $ lines of carbon, nitrogen, and oxygen, affected by relativistic broadening in the spacetime of a rotating BH.

In most works on the subject, a simple power law parameterization of the disc emissivity $\epsilon(r) \propto r^{-\beta}$ is usually adopted. This is done also in the analysis of W01: letting $\beta$ be a free fitting parameter, they find $\beta \sim 4$, a value much larger than usually found in Seyfert galaxies (Nandra et al. 1997).

In order to provide a physical picture of a so steep emissivity, W01 invoke strong magnetic stresses acting in the innermost part of the system, which dissipate a considerable amount of energy in the disc at very small radii. If the magnetic field lines thread the BH horizon, this would imply magnetic extraction of the BH rotational energy - the so called Blandford-Znajek effect (Blandford & Znajek 1977; cited as BZ hereafter). However, the efficiency of the BZ effect has been questioned in recent years by e.g. Ghosh & Abramowicz (1997) and Livio et al. (1999). These works argue that the electromagnetic output from the inner disc regions should in general dominate over that due to the BH. Thus the BH spin would probably be irrelevant to the expected electromagnetic power output from the system.

Krolik (1999), Agol & Krolik (2000) and Li (2000) proposed that MHD processes play a dominant role if magnetic field lines connect downfalling plasma near the hole with more distant regions: high efficiency of energy extraction can be achieved in this way even if the magnetic field does not thread the horizon itself. This magnetized accretion offers an alternative to the original BZ process and to its follow-up generalizations (e.g., Phinney 1983); however, the mechanism is violently non-stationary and such situations have not been quantitatively modelled yet (cf. Koide et al. 2000 and Tomimatsu & Takahashi 2001, for the first attempts of such modelling).

In this paper we show that the required steep emissivity law, as well as the line EW and the amount of Compton reflection, may be reproduced with a phenomenological model in which a X-ray illuminating source is located on the BH symmetry axis (lamp-post model: Martocchia & Matt 1996; Petrucci & Henri 1997; Bao et al. 1998; Reynolds et al. 1999; Dabrowski & Lasenby 2001). This can be considered as a simplified scheme, appropriate for various physical scenarios, including the mentioned MHD energy extraction. Indeed, Agol & Krolik (2000) state that magnetized accretion may also lead to enhanced coronal activity immediately above the plunging region. "If so, this would provide a physical realization for models (...) which call for a source of hard X-rays on the system axis a few gravitational radii above the disc plane''. Alternatively, shock waves in an aborted jet close to the BH axis have been proposed as a source of the central irradiation by Henri & Petrucci (1997). This model assumes that a point source of relativistic leptons (e+,e-) illuminates the accretion disk by Inverse Compton process; the resulting angular and spectral distribution of soft and hard radiation has been derived.

2 A centrally illuminated disc in Kerr metric

The primary source is schematically supposed to be pointlike and located at a height h on the system symmetry axis. This allows to estimate the main effects resulting from various degrees of anisotropy of the illumination just by varying h.

If the primary source, assumed to be isotropic in its own reference frame, is very close to the BH, a fraction of photons emitted towards infinity are deflected by the BH gravitational field and illuminate the accretion disc, at the same time increasing the number of X-rays able to produce line emission and reducing the primary radiation observed at infinity (Fig. 1; see Martocchia & Matt 1996, Martocchia 2000, for details). For static BHs this effect is counterbalanced by the loss of solid angle subtended by the matter to the source when the latter is very close to the BH (because $r_{\rm {ms}}=6r_{\rm {g}}$). Martocchia & Matt (1996) showed that in the case of a spinning BH the increase in the line intensity can be up to a few times the value for a static BH, and that the increase in the equivalent width can be even more dramatic. Due to the high (relativistic) orbital speed of the disc medium at very low radii, the impinging photons as seen in the matter's frame arrive with high incident angles, which further increases the local emissivity of fluorescence and reflection. The local emissivity of fluorescence is further increased by the blue-shift of these photons.

  \begin{figure} \par\includegraphics[width=8.7cm,clip]{Dl101_f1.eps}\end{figure} Figure 1: $\Omega $ is the ratio between the solid angle of the radiation which reaches the equatorial plane and the same solid angle as it would come out in a flat spacetime ( $\Omega =\Omega _{\rm {disc}}/\Omega _{\rm {cl}}$), in the assumption that the disc extends up to $r_{\rm out}=1000r_{\rm {g}}$, and for three values of the BH spin (solid line: a/m=1.; dot-dashed: a/m=0.5; dashed: static BH). The photon deflection towards the disc, i.e. the anisotropy of the illuminating radiation field, strongly increases with decreasing primary source height.
Open with DEXTER

Using the lamp-post framework, iron line profiles with the underlying Compton-reflected continuum have been presented in Martocchia et al. (2000). Monte Carlo simulations have been used to calculate the photon transfer within disc matter on the base of Compton scattering, self-consistently taking into account GR effects such as those on the illuminating photons' impinging angle.

2.1 Emissivity law

In the lamp-post as well as in more realistic models, the actual profile of the disc emissivity - which depends on the geometry of the illuminating matter and is affected by many factors, including general-relativistic (GR) effects - is more complex than a simple power-law. Appropriate emissivity laws $\epsilon(r)$ have been presented in Martocchia (2000) and Martocchia et al. (2000).


  \begin{figure} \par\includegraphics[angle=0,width=8.8cm,clip]{Dl101_f2.eps}\end{figure} Figure 2: Disc emissivity (in arbitrary units) vs. radius (in units of $r_{\rm {g}}$), for a source located at $h = 3r_{\rm {g}}$ (solid line) and $h = 4r_{\rm {g}}$ (dashed line) in the metric of a maximally spinning BH ( $a\simeq 0.9981m$). Lower, a straight dotted line corresponds to a power law with $\beta =-4$. More plots, for different values of h, have been presented in Martocchia et al. (2000).
Open with DEXTER

In particular, $\epsilon(r)$steepens when h decreases, because of the enhanced anisotropy of the primary emission (see Fig. 2). It can be approximated by functions of the form $\epsilon(r) = A r^{-B} + C r^{-D}$. The best-fit coefficients for this formula, obtained by least square approximation, have been presented in Martocchia et al. (2000).

With decreasing h, the effect of light bending is enhanced (Martocchia & Matt 1996) and the fraction of (primary) photons impinging onto the innermost regions of the disc increases. It is easy to recognize (cf. Fig. 2) that an emissivity law with $\beta \sim 4$, i.e. the one derived by W01, may be produced in our model with a small height of the primary source ( $h \sim 3\div4r_{\rm {g}}$). For an emissivity law of this kind, the line profile comes out to be very broad and red-shifted (cf. Fig. 3; see Martocchia et al. 2000, for details). The differences between this profile and that obtained by a powerlaw emissivity with $\beta \sim 4$ are clearly too small to be measurable by XMM.

2.2 Line EW and reflection continuum

In the previous section we have shown that an emissivity law similar to the one derived by W01 in the XMM-Newton spectrum of MCG-6-30-15 may be obtained in the framework of the simple lamp-post model. Here we would like to stress that the large observed EW and R may be also self-consistently reproduced.

Martocchia & Matt (1996) showed that the model predicts an anti-correlation between the intensity of the reflected features (line and continuum) and the intensity of the primary flux, assuming that the latter is due to a change in the average height of the emitting matter. Indeed, for a low primary source ( $h \sim 3r_{\rm {g}}$) values of $EW\sim 250$ eV or more may be easily obtained (e.g. Martocchia et al. 2000). When allowing the source to be located off the axis of rotation, an even stronger enhancement can be obtained (Dabrowski & Lasenby 2001).


  \begin{figure} \par\includegraphics[angle=-90,width=8.4cm,clip]{Dl101_f3.ps}\end{figure} Figure 3: Fe K$\alpha $ profiles computed through the XSPEC routine KERRSPEC (Martocchia 2000), using respectively a power-law emissivity with $\beta = 4$ (solid line) and a lamp-post emissivity with $h = 3r_{\rm {g}}$ (dashed line). All other parameters have been fixed equal to the best-fit values reported by W01. Differences between the two models are clearly too subtle to be detectable with XMM.
Open with DEXTER

The lamp-post picture predicts that the intensity of the Compton-reflected continuum correlates with the intensity of the fluorescent emission line. The best-fit value for R found by W01 is not well constrained, but may be as high as $\sim$7.6. In our model (see Fig. 1), a primary source located at $h \sim 3r_{\rm {g}}$ produces an anisotropy ratio $\sim$1.6 (thus $\Omega_{\rm disc} \sim 3.2\pi$), i.e. we find

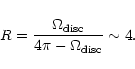
\begin{displaymath}R=\frac{\Omega_{\rm disc}}{4\pi-\Omega_{\rm disc}} \sim 4. \end{displaymath}

Let us finally determine the order of magnitude of the intrinsic luminosity of the point source in these assumptions. From the observed flux we can estimate the intrinsic (rest frame) value of the illumination in the 2-10 keV band by use of the anisotropy and gravitational redshift factors (the latter given by $g_{h=3m}\simeq0.63$, cp. Martocchia & Matt 1996), and assuming an energy index $\alpha=1.3$, $H_0\simeq 70$ kms-1 Mpc-1 and $z \simeq 0.008$, we get the following primary source luminosity:

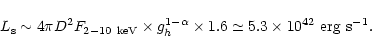
\begin{displaymath}L_{\rm {s}} \sim 4\pi D^2 F_{\rm {2-10~keV}} \times g_h^{1-\alpha} \times 1.6 \simeq 5.3 \times 10^{42} \rm {~erg~s}^{-1}. \end{displaymath}

In conclusion, we have shown that a simple lamp-post model is able to describe the results presented by W01 equally well and in a consistent way. It reproduces the observed emissivity and explains the large amount of line flux and reflection at the same time, providing that the primary X-ray source is located at $h \sim 3r_{\rm {g}}$.

Acknowledgements
AM and GM acknowledge financial support from MURST under grant COFIN-00-02-36, GM also from ASI, VK from GACR 205/00/1685. We thank the referee, J. Wilms, for his useful suggestions.

References

 

Copyright ESO 2002