A&A 383, 801-812 (2002)
DOI: 10.1051/0004-6361:20011832

Star formation and dust extinction in nearby star-forming and starburst galaxies

V. Buat1 - A. Boselli1 - G. Gavazzi2 - C. Bonfanti2


1 - Laboratoire d'Astrophysique de Marseille, BP 8, 13376 Marseille Cedex 12, France
2 - Universita degli studi di Milano-Bicocca, Dipatimento di Fisica, Piazza dell'Ateneo Nuovo 1, 20126 Milano, Italy

Received 28 August 2001 / Accepted 18 December 2001

Abstract
We study the star formation rate and dust extinction properties of a sample of nearby star-forming galaxies as derived from H$\alpha $ and UV ($\sim$2000 Å) observations and we compare them to those of a sample of starburst galaxies. The dust extinction in H$\alpha $ is estimated from the Balmer decrement and the extinction in UV using the FIR to UV flux ratio or the attenuation law for starburst galaxies of Calzetti et al. (2000). The H$\alpha $ and UV emissions are strongly correlated with a very low scatter for the star-forming objects and with a much higher scatter for the starburst galaxies. The H$\alpha $ to UV flux ratio is found to be larger by a factor $\sim$2 for the starburst galaxies. We compare both samples with a purely UV selected sample of galaxies and we conclude that the mean H$\alpha $ and UV properties of nearby star-forming galaxies are more representative of UV-selected galaxies than starburst galaxies. We emphasize that the H$\alpha $ to UV flux ratio is strongly dependent on the dust extinction: the positive correlation found between $F_{\rm H\alpha }/F_{\rm UV}$ and $F_{\rm FIR}/F_{\rm UV}$ vanishes when the H$\alpha $ and UV flux are corrected for dust extinction. The H$\alpha $ to UV flux ratios converted into star formation rate and combined with the Balmer decrement measurements are tentatively used to estimate the dust extinction in UV.

Key words: galaxies: starburst - ISM: dust extinction - galaxies: stellar content


1 Introduction

The Star Formation Rate (SFR) is a crucial ingredient to understand the star formation history of galaxies at all redshifts, as well as the global evolution of the Universe. This SFR is currently derived from the $\rm H\alpha$ line and the far-UV continuum luminosities since both are directly linked to the young stars and trace the SFR over a timescale shorter than $\sim$108 years (e.g. Buat et al. 1987; Kennicutt 1998a; Madau et al. 1998).

Since the pioneering work of Kennicutt (1983) for the H$\alpha $ line emission and of Donas & Deharveng (1984) for the UV continuum, various studies have taken advantage of these tracers. The comparison of the H$\alpha $ and UV emissions as tracers of recent star formation has also been studied on limited samples in the nearby universe (Buat et al. 1987; Bell & Kennicutt 2001; Boselli et al. 2001). A strong correlation is always found between these two tracers. In a UV-selected sample of galaxies at $ <z>\,\sim 0.2$, Sullivan et al. (2000) also found a good correlation between these luminosities but with a larger SFR deduced from the UV than from the H$\alpha $ especially for low luminosity galaxies, a trend not found in the sample of nearby galaxies analysed by Bell & Kennicutt (2001). Conversely at almost the same redshift (z< 0.3) Tresse & Maddox (1998) derived a global SFR from H$\alpha $ a factor of two higher than the one derived from UV measurements for a sample of I-band selected galaxies.

At z=1 Glazebrook et al. (1999) found a SFR from H$\alpha $ measurements three times as high as those inferred from UV fluxes for intrinsically bright galaxies and explained this result as due to recent bursts of star formation. At higher z, thanks to the redshifting, the SFR is often measured in the UV rest-frame and in the near future we will also have access to the rest frame H$\alpha $ of distant galaxies. Recently, Pettini et al. (2001) have measured H$\beta$ emission in few Lyman-break galaxies using NIR ground based spectroscopy.

Obviously, the main difficulty in estimating the SFR from the Balmer lines and the UV continuum is the uncertainty on the dust extinction (e.g. Buat 1992; Bell & Kennicutt 2001). Calzetti and collaborators made an important step in the comprehension of the extinction by using the IUE database to extract UV spectroscopic data on starburst galaxies. They used the shape of the UV continuum as a quantitative tracer of the dust extinction and studied it in relation to the Balmer decrement in order to derive an attenuation curve and a recipe which has been widely used especially for high redshift studies (Calzetti 1997). One limitation of their approach is that the IUE aperture covers only the central parts of the galaxies which are often quite extended (several arcmins). Therefore only the central starburst is studied.

The availability of the FIR emission is of great help in estimating the extinction. Indeed this emission is mainly due to the dust heated by the hot stars; therefore from the comparison of the UV and FIR emission one can estimate both the extinction and the total star formation rate in a robust way (e.g. Buat & Xu 1996; Buat et al. 1999; Flores et al. 1998) at least in actively star-forming galaxies. Using the FIR to UV flux ratio Meurer et al. (1995, 1999) and Calzetti et al. (2000) have quantified the UV extinction for starburst galaxies directly on the slope $\beta$ of the UV continuum. Since the dust is heated by all the stars contributing to the general interstellar radiation field the interpretation of the FIR emission in terms of star formation and its physical link to the UV stellar radiation may be complicated in galaxies containing a substantial old stellar population (e.g. Lonsdale Persson & Helou 1987; Thuan & Sauvage 1990). However this effect is likely to be negligible in galaxies with active star formation (Buat & Xu 1996; Kennicutt 1998b).

Recent studies have criticized the universality of the link between the slope $\beta$ and the dust extinction. Theoretical studies explain the close link between the extinction and the slope $\beta$ for starburst galaxies only under restrictive conditions (Granato et al. 2000; Witt et al. 2000 but see also Charlot & Fall 2000). Counter examples of the $\beta$- $F_{\rm FIR}/F_{\rm UV}$ relation of starburst galaxies have been observed both at low and high redshift (Meurer & Seibert 2001; Bell & Kennicutt 2001; Chapman et al. 2000; van der Werf et al. 2000; Baker et al. 2001).

Before using the UV and H$\alpha $ luminosities as SFR tracers at higher distance it is crucial to understand the properties of these tracers in nearby well-studied galaxies. In particular we must determine if the dust extinction properties of the IUE galaxies apply to any star-forming galaxy in the universe by comparing samples of galaxies taken with different selection criteria. However UV spectroscopic data are scarce. Only the STIS instrument onboard HST allows such observations thus making it unlikely that large samples of galaxies will shortly be made available. The situation will improve dramatically when the GALEX satellite will conduct its large spectroscopic UV survey.

As part of a large program of gathering multiwavelength data on nearby galaxies we have constructed a sub-sample of galaxies observed photometrically in UV (2000 Å), H$\alpha $ and spectroscopically in the optical. FIR data are available from the IRAS database. Although UV spectroscopy is not available we have the UV and H$\alpha $ total emissions as well as the Balmer decrement. Therefore we can compare the properties of our sample in terms of star formation rate and dust extinction with the IUE sample built and studied by Calzetti and collaborators.

2 The samples

2.1 The SFG sample (sample of nearby star-forming galaxies)

The sample consists of 47 spiral and irregular galaxies located in clusters (Coma, Abell 1367, Cancer and Virgo). The optical spectra obtained with the drift-scan technique will be published in a forthcoming paper (Gavazzi et al. 2001, in preparation). The galaxies have also been observed photometrically in H$\alpha $+[NII]. H$\alpha $ fluxes have been corrected for the contamination of [NII]. In most cases, thanks to the high resolution of the spectra, the [NII]6584 & 6548 Å/H$\alpha $ ratio has been directly measured. For few galaxies only the $\rm [NII]6584~\AA$ line has been measured and a standard ratio between the two [NII] lines has been adopted. The Balmer decrement is measured for all the galaxies (lower limits for 3 cases); details for this measurement will be given in Sect. 3. We have selected only galaxies with an equivalent width in H$\alpha $ $EW({\rm H\alpha}) > 6$ Å: it minimizes the error measurements both on the H$\alpha $ and H$\beta$ fluxes. Seyfert galaxies have been excluded as well as galaxies with $\rm [NII]6584/H\alpha > 1$. The UV fluxes at 2000 $\rm\AA$ come from a compilation from SCAP, FOCA or FAUST experiments (see Boselli et al. 2001 and references therein). All fluxes have been corrected for Galactic extinction using the Galactic B extinction (LEDA database, http://leda.univ-lyon1.fr) and a standard extinction curve (Pei 1992). FIR data are available from the IRAS database. Hereafter the FIR fluxes will be calculated in the range 40-120 $\mu $m as the combination of the fluxes at 60 and 100 $\mu $m (Helou et al. 1988).

Because it represents a template of nearby starburst galaxies, especially in FIR, M 82 has been added to our sample. The data for this galaxy have been obtained in the same way as for the SFG sample.

 

 
Table 1: The SFG sample. VCC is for the Virgo Cluster Name (Binggeli et al. 1985) and CGCG for the Zwicky name. All the data are corrected for the Galactic extinction. The UV fluxes are taken at 2000 $\rm\AA$. The H$\alpha $ fluxes are corrected for the [NII] contamination. The FIR fluxes are the 40-120 $\mu $m. The extinction in the H$\alpha $ line is calculated with the Balmer decrement. See text for details.
Name dist diam $\log(F_{\rm UV})$ $\log(F_{\rm FIR})$ $\log(F_{\rm H\alpha})$ A(H$\alpha $)
VCC/CGCG Mpc arcmin $\rm erg ~cm^{-2}~s^{-1}~\AA^{-1}$ $\rm erg ~cm^{-2}~s^{-1}$ $\rm erg ~cm^{-2}~s^{-1}$ mag
VCC 25 32.00 2.54 -13.14 -9.61 -11.99 0.70
VCC 66 17.00 5.34 -13.17 -9.77 -11.80 0.89
VCC 89 32.00 2.25 -13.19 -9.63 -12.15 0.95
VCC 92 17.00 9.77 -12.81 -9.26 -11.73 1.52
VCC 131 17.00 2.60 -13.54 -10.35 -12.98 0.58
VCC 307 17.00 6.15 -12.63 -8.64 -11.09 0.99
VCC 318 32.00 1.71 -13.78 -10.82 -12.74 0.39
VCC 459 17.00 0.83 -13.74 -10.85 -12.55 0.37
VCC 483 17.00 3.60 -13.39 -9.27 -11.94 >2.50
VCC 596 17.00 9.11 -12.54 -8.77 -11.11 >3.69
VCC 664 17.00 2.60 -13.61 -10.53 -12.30 -0.01
VCC 692 17.00 2.91 -13.64 -10.32 -12.55 0.30
VCC 801 17.00 2.60 -13.16 -9.36 -11.61 0.52
VCC 827 23.00 3.60 -13.75 -9.83 -12.55 0.65
VCC 836 17.00 5.00 -13.43 -9.26 -11.85 0.93
VCC 873 17.00 3.95 -13.90 -9.40 -12.12 2.53
VCC 912 17.00 2.91 -13.76 -10.15 -12.30 1.40
VCC 938 17.00 2.18 -13.58 -10.17 -12.38 0.84
VCC 1189 17.00 1.84 -13.74 -10.78 -12.76 0.56
VCC 1205 17.00 1.84 -13.32 -9.96 -12.66 1.47
VCC 1379 17.00 2.85 -13.28 -10.07 -12.13 -0.03
VCC 1450 17.00 2.60 -13.35 -10.00 -12.16 -0.04
VCC 1554 17.00 2.60 -12.93 -9.31 -11.39 0.49
VCC 1555 17.00 8.33 -12.63 -9.11 -11.33 4.02
VCC 1575 17.00 2.00 -13.91 -10.21 -12.86 0.86
VCC 1678 17.00 2.16 -13.70 -10.88 -12.60 0.47
VCC 2058 17.00 5.86 -13.43 -9.62 -12.00 2.24
CGCG 97079 91.20 0.75 -14.03 -10.68 -12.72 0.15
CGCG 97087 91.20 2.00 -13.43 -10.03 -12.29 0.88
CGCG 100004 17.00 3.80 -12.97 -9.42 -11.71 0.89
CGCG 119029 51.20 2.00 -14.00 -10.10 -12.57 1.06
CGCG 119041 66.40 1.33 -14.97 -10.39 -13.62 1.97
CGCG 119043 66.40 0.77 -14.56 -10.82 -13.34 1.56
CGCG 119046 51.20 1.85 -13.82 -10.47 -12.66 1.23
CGCG 119047 66.40 1.00 -14.18 -10.18 -13.08 0.96
CGCG 119054 66.40 0.94 -14.46 -10.79 -13.34 -0.03
CGCG 119059 66.40 0.71 -14.63 -10.77 -13.09 -0.04
CGCG 119080E 66.40 1.30 -14.05 -10.04 -12.61 0.90
CGCG 119080W 66.40 0.75 -13.91 -10.03 -12.66 0.91
CGCG 160020 96.00 0.45 -14.40 -10.46 -13.08 0.94
CGCG 160026 96.00 0.84 -14.56 -10.85 -13.21 >2.84
CGCG 160055 96.00 1.51 -13.95 -10.11 -12.71 0.49
CGCG 160067 96.00 0.56 -14.29 -10.60 -12.96 1.20
CGCG 160073 96.00 0.79 -14.44 -10.73 -13.29 2.12
CGCG 160128 96.00 0.63 -14.08 -10.90 -12.91 0.18
CGCG 160139 96.00 1.22 -14.03 -10.73 -12.79 0.26
CGCG 160252 96.00 0.84 -14.35 -10.11 -13.12 1.65


2.2 The IUE sample of starburst galaxies

The starburst galaxies have been extracted from the sample of 39 objects of Calzetti et al. (1994); 3 Seyfert galaxies have been excluded. Complementary data such as FIR, H$\alpha $ fluxes and Balmer decrements come from Calzetti et al. (1995). The Balmer lines emission was measured by the authors within the same aperture as the IUE observations. The UV fluxes are taken in the bin 1863-1963 $\rm\AA$ (Kinney et al. 1993) for consistency with the UV data for the SFG sample.

32 out of the 39 galaxies have been observed by IRAS at 60 and 100 $\mu $m. Given the limited size of the IUE aperture ( $10''\times 20''$) the FIR-UV flux comparison must be done cautiously. Only galaxies for which the IUE aperture includes a large part of the UV flux have been selected. Meurer et al. (1999) have also encountered this problem and they selected only galaxies with a diameter smaller than 4 arcmins. For a few galaxies observed in UV we have measured the fraction of the UV flux included in different circular apertures with diameters equal to fractions of d25,the isophotal diameter at 25 mag arcsec-2. In the case of spiral galaxies like M 51 or M 100 the effect is dramatic since less than 50$\%$ of the flux is comprised in d25/3. The case of irregular galaxies like NGC 4214 or NGC 4449 is more favorable with $\rm {\simeq} 50\%$ of the flux found within d25/5. In order not to loose statistical power and since starburst galaxies are very active in star formation in their central parts, we have selected galaxies for which d25 is less than 1.5 arcmin. This sub-sample contains 19 galaxies and will be used in the following when the FIR to UV flux ratio is involved.

 

 
Table 2: The IUE sample: the fluxes are corrected for the Galactic extinction following Calzetti et al. (1994). The UV fluxes are taken in the bin 1863-1963 $\rm\AA$ from Kinney et al. (1993). Other data come from Calzetti et al. (1994, 1995). The galaxies are sorted according to their diameter. The first part of the table consists of the 19 galaxies with a diameter lower than 1.5 arcmin. See text for details.

Name		 dist diam $\log(F_{\rm UV})$ $\log(F_{\rm FIR})$ $\log(F_{\rm H\alpha})$ A(H$\alpha $)
  Mpc arcmin $\rm erg ~cm^{-2}~s^{-1}~\AA^{-1}$ $\rm erg ~cm^{-2}~s^{-1}$ $\rm erg ~cm^{-2}~s^{-1}$ mag

MRK 499		 98.60 0.20 -14.14 -10.13 -12.85 1.10
MRK 357 200.40 0.23 -13.87 -10.37 -12.48 0.29
IC 1586 81.27 0.31 -14.26 -10.28 -12.58 1.42
MRK 66 81.27 0.35 -14.21 -10.56 -12.89 0.00
NGC 5860 73.47 0.54 -14.27 -10.04 -12.47 1.69
UGC 9560 17.00 0.55 -13.75 -10.41 -12.26 0.37
NGC 6090 106.67 0.58 -14.06 -9.48 -12.15 1.47
IC 214 125.27 0.59 -14.26 -9.56 -12.74 1.30
Tol1924-416 38.73 0.63 -13.43 -10.17 -11.84 0.05
Haro 15 86.67 0.77 -13.82 -10.16 -12.48 0.00
NGC 6052 58.60 0.85 -13.87 -9.48 -12.24 0.51
NGC 3125 12.13 0.92 -13.50 -9.64 -11.79 0.32
NGC 1510 11.07 1.05 -13.80 -10.36 -12.51 0.20
NGC 1614 73.07 1.20 -14.21 -8.83 -11.97 2.28
NGC 7673 45.07 1.25 -13.69 -9.61 -12.16 1.03
NGC 7250 16.60 1.33 -13.58 -9.77 -12.15 0.22
NGC 1140 20.07 1.37 -13.46 -9.77 -11.81 0.25
NGC 5996 30.20 1.37 -13.90 -9.64 -12.26 1.15
NGC 4194 37.00 1.48 -13.46 -8.96 -11.72 1.96
NGC 1800 8.13 1.62 -14.03 -10.30 -12.93 0.17
NGC 1705 5.93 1.67 -12.94 -10.32 -12.28 0.00
NGC 7714 26.07 1.67 -13.46 -9.30 -11.52 0.96
NGC 3049 20.60 1.85 -13.94 -9.83 -12.28 0.76
NGC 4385 33.13 1.85 -13.90 -9.64 -12.04 1.42
NGC 6217 19.07 2.77 -13.68 -9.20 -13.15 1.30
NGC 1569 3.13 2.83 -12.46 -8.61 -11.25 0.17
NGC 7552 24.87 3.07 -13.72 -8.42 -11.67 1.71
NGC 3256 37.67 3.08 -13.47 -8.33 -11.48 1.47
NGC 5253 2.80 3.78 -12.82 -8.84 -11.07 0.00
NGC 7793 3.00 7.95 -14.05 -8.87 -12.65 1.08
NGC 1313 3.47 8.07 -14.22 -8.63 -12.78 1.49
NGC 5236 4.40 12.22 -12.67 -7.84 -11.34 0.71


2.3 Comparison of the samples

Some systematic differences exist between the SFG and IUE samples. While the range of metallicities covered by both samples is almost similar, from $\sim$$Z_\odot/4$ to $\sim$$2~Z_\odot$ the mean metallicity of the IUE sample is lower: $\rm <12+\log(O/H)>~ = ~8.6 \pm 0.3$ against $\rm <12+\log(O/H)>= 8.8 \pm 0.2$ for the SFG sample, where the solar abundance is $Z_{\odot} = 8.93$. Almost all the IUE galaxies have sub-solar metallicities ( $Z_{\odot}/2$ on average) whereas the mean metallicity of the SFG sample is only slightly sub-solar.

We have compared the strength of the star-forming activity of both samples with the ratio of the FIR fluxes at 60 and 100 $\mu $m. The galaxies of both samples appear to be active in star formation with a F60/F100 almost systematically larger than usually found in quiescent discs ( $F_{60}/F_{100}\simeq 0.3$, e.g. Rowan-Robinson & Crawford 1989). With $<F_{60}/F_{100}>= 0.77\pm 0.33$ the galaxies of the IUE sample have a significantly higher ratio than the galaxies of the SFG sample ( $< F_{60}/F_{100}>= 0.45\pm 0.13$).

We have also compared the samples in terms of equivalent widths of H$\alpha $ and H$\beta$. The equivalent widths for the IUE sample have been estimated from the data of Storchi-Bergmann et al. (1995) and Mc. Quade et al. (1995). The galaxies of this sample have very high equivalent widths of both emission lines with average values of EW(H $\alpha) = 117$ Å and EW(H $\beta) = 17$ Å as compared to the average values found for the SFG sample: EW(H $\alpha) = 39$ Å and EW(H $\beta) = 7.5$ Å. Large Balmer equivalent widths are the signature of a high current star-forming activity compared to the past average. As for the analysis of F60/F100, it is found consistent with the IUE galaxies having a higher current star-forming activity for the IUE galaxies than for those of the SFG sample.

3 The dust extinction

3.1 The extinction in the H$\alpha $ emission line

The extinction in the Balmer lines H$\alpha $ and H$\beta$ can be deduced from the comparison of the observed ratio $F_{\rm H\alpha}/F_{\rm H\beta}$ with the theoretical value of 2.87 obtained for the case of B recombination. For 36 galaxies out of the 49 in the SFG sample the underlying stellar H$\beta$ absorption is clearly detected and the H$\beta$ emission line is measured by fitting both the absorption and emission lines. For the remaining 13 objects a stellar absorption of 2 Å is assumed which corresponds to the mean value found when the underlying stellar absorption is detected. We follow the classical approach by adopting a dust screen geometry and a Milky Way extinction curve (e.g. Kennicutt 1983; Calzetti et al. 1994). Whereas varying the extinction curves has negligible effects in the visible, the dust screen assumption seems to under-estimate the extinction by $\sim$0.2 mag in comparison with the amount deduced from the measurements of the thermal radio continuum (Caplan & Deharveng 1986; Bell & Kennicutt 2001). Nevertheless in the absence of thermal radio measurements we will rely on the Balmer decrement values.

We have computed the extinctions in the H$\alpha $ line for the SFG sample and used the values published by Calzetti et al. (1994) for the IUE sample. The extinctions are plotted in Fig. 1 against the FIR luminosity of the galaxies. The mean values are given in Table 3. We have assumed that the errors on A(H$\alpha $) are due to the uncertainty on the H$\beta$ flux (since only objects with $EW({\rm H\alpha}) > 6$ Å are selected, the estimate of the total H$\alpha $ flux is robust). These errors represent in fact lower limits because we do not account for the uncertainty introduced by the fitting of the lines. They range from 0.01 to 0.43 mag and are found strongly anti-correlated with EW(H$\beta$).

The mean values of A(H$\alpha $) are found similar for both samples and these values are consistent with previous studies (e.g. Kennicutt 1983; Kennicutt 1992; Thuan & Sauvage 1990). The slightly higher average A(H$\alpha $) found for the SFG sample may be explained by a loose correlation found in the SFG and the IUE samples between A(H$\alpha $) and O/H, the IUE sample exhibiting a lower average metallicity than the SFG one (Sect. 2.3).

Three galaxies (M 100, NGC 4298 and IC 3913) with a large H$\alpha $ equivalent width (>10 Å) have no detected H$\beta$ emission line. For each of them the underlying stellar absorption is clearly detected and we can put reliable upper limits on the H$\beta$ flux in emission. They translate into lower limits for A(H$\alpha $) which are rather high (Fig. 1). For example Messier 100 (VCC 596) has $ A({\rm H\alpha})>3.7$ mag. Such a high value might reflect the extinction in the nucleus of the galaxy which has a very high surface brightness and may dominate the integrated spectrum whereas the disk is likely to be less extincted. Such an effect cannot be excluded for other galaxies of our sample and might be at the origin of the high values of A(H$\alpha $) found in a few cases. Only spatially resolved studies would allow us to remove this uncertainty.

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{MS1861f1.eps}\par\end{figure} Figure 1: The extinction in the H$\alpha $ line, $A({\rm H\alpha })$, as measured with the Balmer decrement versus the FIR luminosity. The SFG sample is plotted with filled circles, the 3 lower limits in A(H$\alpha $) are plotted with triangles. The errors on $A({\rm H\alpha })$ are also plotted. The IUE sample is plotted with empty symbols: circles for the galaxies with d25<1.5 arcmin and squares for the larger ones. M 82 is plotted as a cross.
Open with DEXTER

Hopkins et al. (2001) and Sullivan et al. (2001) report a positive correlation between the dust extinction traced by the Balmer decrement and the star formation rate of the galaxies traced by their total FIR or H$\alpha $ luminosities. In Fig. 1 we have done the same comparison as Hopkins et al. between the extinction in the H$\alpha $ line and the FIR luminosity (two independant variables). A very dispersed correlation is found between these quantities, for the SFG sample (R=0.30) whereas the correlation is better for the IUE galaxies alone (R=0.63). The situation is worse when other observed luminosities like the B, H$\alpha $ or UV are considered instead of the FIR. A dispersed correlation between the dust extinction and the luminosity of the galaxies has already been reported (e.g. Wang & Heckman 1996; Buat et al. 1999) and can probably explain the present results without invoking an extra link between the extinction and the star formation rate as suggested by Hopkins et al. (2001).

3.2 The extinction in the UV continuum

Two methods are commonly used to estimate the dust extinction in the far ultraviolet range: using the slope $\beta$ of the UV continuum (1250-2500 Å) defined as $F_{\lambda} \propto \lambda^{\beta}$ (Calzetti et al. 1994) or the $F_{\rm FIR}/F_{\rm UV}$ ratio (Buat & Xu 1996, Gordon et al. 2000) with $F_{\rm FIR}$ in the range 40-120 $\mu $m and $F_{\rm UV}$ defined as $F_{\lambda}\cdot\lambda$ at 2000 Å. Meurer et al. (1999) have shown that for their sample of starburst galaxies the methods are consistent although the agreement is not perfect (Calzetti et al. 2000). Nevertheless, the method based on the UV slope may well not apply to all types of galaxies, even for those forming stars actively. Witt et al. (2000) and Granato et al. (2000) have modeled the dust extinction and shown that the slope of the UV continuum is related to the extinction only under restrictive conditions on the dust/stars geometry and the dust properties. Charlot & Fall (2000) developped a model for starburst galaxies which reproduces quite well the correlation between $\beta$ and $F_{\rm FIR}/F_{\rm UV}$by varying the amount of extinction in the diffuse interstellar medium. The $F_{\rm FIR}/F_{\rm UV}$ ratio appears to be much more robust and universal to trace the dust extinction: the calibration of this ratio as a quantitative dust extinction estimator is found almost independent on the dust/stars geometry and on the dust properties provided that the galaxies are forming stars actively (Buat & Xu 1996; Buat et al. 1999; Gordon et al. 2000).

 

 
Table 3: Mean H$\alpha $ and UV extinctions for the two samples using the various methods. The IUE sample contains 19 galaxies since the FIR fluxes are involved in the calculations (cf. Sect. 2.2). For the SFG sample we have only considered galaxies for which the extinction in H$\alpha $ is measured, the sample is reduced to 44 galaxies. f is the fraction of ionizing flux absorbed by the gas (defined in Sect. 4). M 82 is excluded from the calculations.
Extinction IUE SFG method
mag sample sample  
$A_{{\rm H\alpha}}$ $0.82 \pm 0.72$ $0.93 \pm 0.79$ Balmer decrement
AUV $1.59\pm 1.04$  $0.87\pm 0.52$  $F_{\rm FIR}/F_{\rm UV}$, Buat et al. (1999)
$A_{\rm UV}$ $1.95\pm 1.17$  $1.22\pm 0.62$  $F_{\rm FIR}/F_{\rm UV}$, Calzetti et al. (2000)
$A_{\rm UV}$ $1.31\pm 1.14$ $1.48\pm 1.25$ attenuation law Calzetti et al. (2000)
$A_{\rm UV}$ $1.34\pm 1.30~$ $0.54\pm 1.04~$ $F_{\rm H\alpha }/F_{\rm UV}$, f=1
  $1.72\pm 1.30$ $0.92\pm 1.04$ $F_{\rm H\alpha }/F_{\rm UV}$, f=0.7


3.2.1 The extinction deduced from the $\mathsfsl{F}_{\mathsf{FIR}}/\mathsfsl{F}_{\mathsf{UV}}$ ratio
In the following we will use both the calibration of Calzetti et al. (2000) suited for the sample of IUE starbursting galaxies and based on few ISOPHOT data and the calibration of Buat et al. (1999) built for a sample of star-forming galaxies not necessarily starbursting and from which the SFG sample is drawn.

The extinction derived by Calzetti et al. (2000) is at 1600 Å. Therefore, for the need of this calculation we have taken the flux at 1600 Å F1600 from the IUE atlas of star forming galaxies (Kinney et al. 1993) by interpolating the fluxes in the bins 1431-1532 Å and 1863-1963 Å. The extinction at 1600 Å is then translated to 2000 Å by using the attenuation curve also re-calibrated by Calzetti et al. (2000). Practically we multiply by 0.9 the extinction at 1600 Å. Thus we apply the following formula to estimate the extinction at 2000 Å for the starburst galaxies:

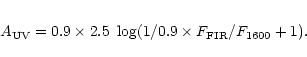
\begin{eqnarray*}A_{\rm UV} = 0.9\times 2.5~\log(1/0.9 \times F_{\rm FIR}/F_{1600}+1). \end{eqnarray*}


The mean value of $A_{\rm UV}$ is listed in Table 3.

The extinctions measured with the FIR to UV flux ratio using these empirical relations are found almost consistent with the theoretical ones of Gordon et al. (2000) (Buat 2000): while the agreement is perfect for the starburst galaxies, the extinction deduced by Buat et al. are slightly lower than the predicted values of Gordon et al. Here we use the model of Buat et al. for the SFG sample since it is suited to this sample. In Table 3 we also give the mean values of the extinction obtained by using the calibration of Calzetti et al. for the SFG sample (neglecting the difference in the flux at 1600 and 2000 Å) as well as the result of the model of Buat et al. applied to the IUE sample.

The extinction deduced from $F_{\rm FIR}/F_{\rm UV}$ correlates with the FIR and B luminosity of the galaxies, this result has already been found in previous studies (Buat & Burgarella 1998; Buat et al. 1999) and is not reproduced here but may be related to the correlation found in Fig. 1 between A(H$\alpha $) and $L_{\rm FIR}$.

3.2.2 The extinction deduced from the attenuation law for starburst galaxies

Since the Balmer decrement is measured for all the galaxies of our sample we can also follow the recipe first proposed by Calzetti (1997) and originaly based on the UV spectral slope of galaxies. We use the new absolute calibration of the attenuation law based on a comparison with the FIR emission of few galaxies measured with ISOPHOT (Calzetti et al. 2000). It leads to extinctions $\sim$0.2 mag lower than the previous law (Calzetti 1997).

The color excess of the stellar continuum is related to the color excess $E(B-V)_{\rm g}$ of the gas:

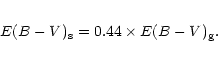
\begin{eqnarray*}E(B-V)_{\rm s} = 0.44 \times E(B-V)_{\rm g}. \end{eqnarray*}


Then the Galactic extinction curve (Pei 1992) is used to relate $E(B-V)_{\rm g}$ to A(H$\alpha $)

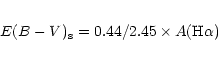
\begin{eqnarray*}E(B-V)_{\rm s} = 0.44/2.45\times A({\rm H\alpha}) \end{eqnarray*}


and the extinction at 2000 Å is given by:

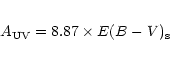
\begin{eqnarray*}A_{\rm UV} = 8.87\times E(B-V)_{\rm s} \end{eqnarray*}


or equivalently

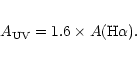
\begin{eqnarray*}A_{\rm UV} = 1.6\times A({\rm H\alpha}). \end{eqnarray*}


Therefore the extinction computed in this way is simply proportional to that in H$\alpha $.

3.3 Comparison of the extinctions


  \begin{figure} \par\includegraphics[width=8cm,clip]{MS1861f2.eps}\end{figure} Figure 2: The UV extinction $A_{\rm UV}$ derived from the attenuation law for starburst galaxies against the extinction derived from $F_{\rm FIR}/F_{\rm UV}$, the scale in A(H$\alpha $) is indicated on the right vertical axis. The SFG sample is plotted with filled symbols: circles for the galaxies with an error on A(H$\alpha $) lower than 0.3 mag and squares for those with an error larger than 0.3 mag, the 3 lower limits in A(H$\alpha $) are plotted with triangles. The IUE sample is plotted with empty symbols: circles for the galaxies with d25<1.5 arcmin and squares for the larger ones. M 82 is plotted as a cross. The dashed line corresponds to equal UV extinctions on both axes.
Open with DEXTER

In Fig. 2 the extinctions derived from the attenuation law of starburst galaxies are compared with the extinctions deduced from $F_{\rm FIR}/F_{\rm UV}$. The two samples have a different behavior. The extinctions computed with the attenuation law are found larger than those computed with $F_{\rm FIR}/F_{\rm UV}$ for the SFG sample with a mean difference of $\sim$0.6 mag whereas the situation is inverse for the IUE sample with a larger extinction traced by the FIR to UV flux ratio of $\sim$0.6 mag on average. Calzetti et al. (2000) also noted that the extinction based on the Balmer decrement of the gas under-estimates the extinction for the IUE sample. It is mandatory to observe spectroscopically star-forming galaxies without extreme properties in the far-ultraviolet in order to compare their $F_{\rm FIR}/F_{\rm UV}$to the slope of their UV continuum and to perform a direct comparison with the starburst galaxies.

If $F_{\rm FIR}/F_{\rm UV}$ is used to estimate the extinction, a $\sim$1 mag higher UV extinction is found in starburst galaxies as compared to more "normal" star-forming objects (Table 3). With the attenuation curve of starburst galaxies similar extinctions are found for both samples: the extinctions in H$\alpha $ are similar and in this case the UV extinction is proportional to that in H$\alpha $.

The H$\alpha $ and the UV extinctions estimated with $F_{\rm FIR}/F_{\rm UV}$ can also be compared using Fig. 2 since $A_{\rm UV} = 1.6\times A({\rm H\alpha})$. Within each sample both extinctions are correlated although the scatter is large for the SFG sample. The results for the SFG sample are consistent with a similar mean extinction at both wavelengths (Table 3), a result expected from the correlation found between the observed H$\alpha $ and UV luminosities (cf. next section). For the IUE sample the extinction in UV is larger than that in H$\alpha $ by $\sim$1 mag also in agreement with the large values of observed $L_{\rm H\alpha}/L_{\rm UV}$ for these galaxies (cf. next section).

4 H$\mathsf{\alpha}$ and UV emissions


  \begin{figure} \par\includegraphics[width=7.2cm,clip]{MS1861f3.eps} \end{figure} Figure 3: The observed H$\alpha $ and UV luminosities for the SFG sample (filled circles), the data of Bell & Kennicutt (empty circles) and the UV-selected sample of Sullivan et al. (+). M 82 is plotted with a cross. The dahed line is the expected relation between the luminosities for a constant star formation rate and a Salpeter IMF (baseline scenario presented in Sect. 4.1).
Open with DEXTER

4.1 The calibration of the H$\alpha $ and UV luminosities in Star Formation Rates

The conversion into SFR uses stellar population synthesis models assuming an history of star formation and an initial mass function. We adopt the following definitions:

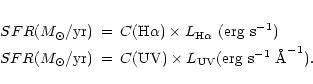
\begin{eqnarray*}SFR (M_\odot/{\rm yr}) &=& C({\rm H}\alpha)\times L_{\rm H\alph... ...}) &=& C({\rm UV})\times L_{\rm UV} ({\rm erg~s^{-1}~\AA}^{-1}). \end{eqnarray*}


To derive the calibration of the H$\alpha $ luminosity in terms of star formation rate, one must transform the number of Lyman continuum photons given by the synthesis models into H$\alpha $ photons. We assume that 0.45 H$\alpha $ photon is produced per ionising photon absorbed by the HI gas (case B recombination). It is necessary to estimate the number of Lyman continuum photons effectively absorbed by the gas and contributing to the recombination lines. Most authors (e.g. Kennicutt 1983; Glazebrook et al. 1999) adopt a conversion factor, hereafter called f, equal to 1 i.e. all the Lyman continuum photons are absorbed by the HI gas. Indeed the escape fraction of the Lyman continuum photons from nearby galaxies is likely to be very low and near 0 (Leitherer et al. 1995; Deharveng et al. 2001). Conversely the fraction of Lyman continuum photons escaping H II regions can be substantial (Shields & Kennicutt 1995; Inoue et al. 2001) but provided that the integrated H$\alpha $ flux is considered the contribution of the diffuse emission is accounted for and the fraction of Lyman continuum photons effectively absorbed by the interstellar gas increases (Kennicutt 1998a). A very low value of the conversion factor f is also ruled out by the agreement between the SFRs determined from H$\alpha $ and UV data. Nevertheless it is difficult to exclude that a moderate fraction of the Lyman continuum photons does not ionize the gas. A factor f lower than 1 directly affects the conversion of the H$\alpha $ flux in SFR.

We have accounted for realistic variations of the main parameters which affect $C({\rm H\alpha})$ and $C({\rm UV})$: the initial mass function, the star formation history and the metallicity. Some values of $C({\rm H\alpha})$ and $C({\rm UV})$for different scenarios are reported in Table 4. The model used is Starburst 99 (Leitherer et al. 1999). All the values are computed with f=1. For f < 1 one must subtract $-\log(f)$ from the values of $\log (C({\rm H\alpha})/C({\rm UV}))$ listed in Table 4. We have also compiled a few values from the literature. We define a baseline scenario with a Salpeter IMF ( $1{-}100~M_\odot$), a solar abundance, a constant SFR over 100 Myr and the assumption that all the Lyman continuum photons are absorbed by the gas (i.e. f=1), this scenario corresponds to $\log (C({\rm H\alpha})/C({\rm UV})) = -1.4$. The impact of the variations of the main parameters on the value of $\log (C({\rm H\alpha})/C({\rm UV}))$ are of the order of some tenths.

 

 
Table 4: Conversion of the H$\alpha $ to UV flux ratio in star formation rate ratio. The baseline scenario is reported in the first line. The lines 2-5 are dedicated to the variation of the IMF respectively to the standard scenario: a Salpeter IMF (Salp. IMF) with different low and high mass end and an IMF with an exponent -2.7 in mass unit (Scalo 1998). The lines 6-7 and 8-9 are dedicated to time variations and metallicity variations. All the calculations of lines 1-9 are made with Starburst 99 (Leitherer et al. 1999). Comparisons with other values taken in the literature are gathered at the end of the table. The values of Sullivan et al. are those calculated with the PEGASE synthesis model (Fioc & Rocca-Volmerange 1997). All the data are for f=1. See text for comments.

Source

 $\log (C({\rm H\alpha}))$ $\log (C({\rm UV}))$ $\log (C({\rm H\alpha})/C({\rm UV}))$ Specifications
  $M_\odot~{\rm yr}^{-1}/{\rm erg~s}^{-1}$ $M_\odot~{\rm yr}^{-1}/{\rm erg~s}^{-1}~{\rm\AA}^{-1}$    
SB99 Z=0.02 41.48 40.11 -1.37 Salpeter IMF, 1/ $100~M_\odot$ CSFR 100 Myr
SB99 Z=0.02 41.11 39.92 -1.19 IMF -2.7, 1/ $100~M_\odot$ CSFR 100 Myr
SB99 Z=0.02 41.06 39.70 -1.36 Salp. IMF, 0.1/ $100~M_\odot$ CSFR 100 Myr
SB99 Z=0.02 41.52 40.11 -1.41 Salp. IMF, 1/ $120~M_\odot$ CSFR 100 Myr
SB99 Z=0.02 41.38 40.10 -1.28 Salp. IMF, 1/ $80~M_\odot$ CSFR 100 Myr
SB99 Z=0.02 41.47 39.92 -1.55 Salp. IMF, 1/ $100~M_\odot$ CSRF 10 Myr
SB99 Z=0.02 41.48 40.17 -1.31 Salp. IMF, 1/ $100~M_\odot$ CSRF 900 Myr
SB99 Z=0.004 41.58 40.14 -1.44 Salp. IMF, 1/ $100~M_\odot$ CSFR 100 Myr
SB99 Z=0.04 41.40 40.08 -1.32 Salp. IMF, 1/ $100~M_\odot$ CSFR 100 Myr
Kennicutt (1998) 41.10 39.73 -1.37 Salp. IMF 0.1/ $100~M_\odot$ CSFR 100 Myr
Sullivan et al. (2000) 41.06 39.77 -1.29 Salp. IMF, 0.1/120 $M_\odot$ CSFR 100 Myr


4.2 The comparison of the H $\mathsf{\alpha}$ and UV luminosities

In Fig. 3 we compare the SFG sample with that of Bell & Kennicutt (2001) which is also composed of nearby star-forming galaxies. The expected relation for the baseline scenario and no extinction (or the same extinction at both wavelengths) is overplotted. We find a very good agreement with a slightly more dispersed relation for the sample of Bell & Kennicutt. The data appear globally consistent with a constant SFR over 100 Myr with a slight shift of the Bell and Kennicutt data toward a higher $L_{\rm H\alpha}/L_{\rm UV}$. Indeed the mean value of $L_{\rm H\alpha}/L_{\rm UV}$ corresponds to a ratio of SFR equal to $1.4\pm 0.8$ for the sample of Bell & Kennicutt against $0.8 \pm 0.4$ for the SFG sample again with our baseline scenario. Thus within the error bars both values are consistent. Nevertheless from the analysis of the SFG sample we do not conclude as Bell & Kennicutt that the extinction in UV is higher than that in H$\alpha $.

We have also overplotted the H$\alpha $ and UV luminosities of a purely UV selected sample of galaxies (Sullivan et al. 2000). These galaxies have a similar mean $L_{\rm H\alpha}/L_{\rm UV}$ as the SFG sample although with a much larger dispersion (corresponding to a SFR ratio of $0.8 \pm 1.2$). At low luminosities ( $L_{\rm UV} < 10^{40}~{\rm erg~s^{-1}~\AA}^{-1}$), an important fraction of the galaxies of the UV selected sample have a very low $L_{\rm H\alpha}/L_{\rm UV}$ (corresponding to a SFR ratio of $\sim$0.1). However this population is not well represented in the SFG sample with only two galaxies.

The comparison with the starburst galaxies observed by IUE is illustrated in Fig. 4 by plotting the observed ratio $L_{\rm H\alpha}/L_{\rm UV}$ as a function of the FIR luminosity for the SFG and IUE samples. The range of values (mean $\pm 1 \sigma$) found for the UV selected sample of Sullivan et al. is also indicated.

  \begin{figure} \par\includegraphics[width=7.2cm,clip]{MS1861f4.eps} \end{figure} Figure 4: Variation of the ratio of the observed H$\alpha $ and UV luminosities as a function of the FIR luminosity. The symbols are the same as in Fig. 2 except for the SFG sample which is plotted only with filled circles. The dotted and dashed horizontal lines indicate the mean $\pm 1~ \sigma$ of $\log(L_{\rm H\alpha}/L_{\rm UV})$ for the UV selected sample of Sullivan et al. (2000).
Open with DEXTER

The values of $L_{\rm H\alpha}/L_{\rm UV}$ are higher for the IUE sample than for the SFG and the UV selected samples. Their mean value of $L_{\rm H\alpha}/L_{\rm UV}$ corresponds to a ratio of SFRs of $\sim$2. M 82 is located within the IUE sample as expected for a starbursting galaxy.

We find a loose correlation between $L_{\rm H\alpha}/L_{\rm UV}$ and $L_{\rm FIR}$ (R=0.5 for both samples). Bell & Kennicutt (2001) and Sullivan et al. (2001) also reported a trend of a lower $F_{\rm H\alpha }/F_{\rm UV}$ for low luminosity galaxies. Such a correlation as well as that found in Fig. 1 between A(H$\alpha $) or $A_{\rm UV}$ and $L_{\rm FIR}$ can be related to the general tendency of bright galaxies undergo more extinction (Wang & Heckman 1996; Buat & Burgarella 1998).

The differences in H$\alpha $ to UV flux ratio found between the IUE and the UV selected samples must be considered. In particular the use of IUE templates might introduce systematic errors in the estimate of the extinction in high-z galaxies generally selected from optical surveys, UV selected in the rest frame. As far as their global tendencies, the SFG sample appears more representative of UV selected galaxies. Nevertheless extreme cases of low H$\alpha $ to UV ratios are not well represented in the SFG samples with only two galaxies which exhibit an observed SFR(H$\alpha $)/SFR(UV) of $\sim$0.15. The H$\alpha $ equivalent widths of the SFG sample and UV selected samples are also comparable: a mean $EW({\rm H\alpha})= 39$ Å for the former and $\sim$50 Å for the latter (Sullivan et al. 2000; Zapelli 2001) to be compared to 119 Å for the IUE sample (cf. Sect. 2.3).

4.3 The variation of SFR(H $\mathsf{\alpha}$)/SFR(UV)


  \begin{figure} \par\includegraphics[width=6.6cm,clip]{MS1861f5.eps}\end{figure} Figure 5: Variation of the ratio of the SFR deduced from H$\alpha $ and UV emissions as a function of the $F_{\rm FIR}/F_{\rm UV}$ and the corresponding extinction in UV. Top: SFR(H$\alpha $)/ SFR(UV) is deduced from the observed fluxes; bottom: SFR(H$\alpha $)/ SFR(UV) is deduced from fluxes corrected for dust extinction as described in the text. The symbols are the same as in Fig. 2 except for the top figure where all the SFG sample is plotted with filled circles. The axis indicating the UV extinctions are calibrated using the formula of Buat et al. 1999 (lower line) and Calzetti et al. 2000 (upper line).
Open with DEXTER

The ratio of the two SFRs as a function of $F_{\rm FIR}/F_{\rm UV}$ is plotted in Fig. 5a. We have also traced the UV extinction calculated with the FIR to UV flux ratio for starburst and star-forming galaxies. A strong correlation is found between these quantities for both samples (linear correlation coefficient R=0.8).

To test if the trend found in Fig. 5a can be attributed to the extinction we correct both SFRs for the dust extinction. The SFRs deduced from the H$\alpha $ fluxes are corrected with the extinction measured with the Balmer decrement (Sect. 3.1) and the SFRs deduced from the UV continuum are corrected with the attenuation factor measured with the FIR to UV flux ratio (Sect. 3.2.1). The dust corrected SFR ratios are plotted in Fig. 5b: the trend with $F_{\rm FIR}/F_{\rm UV}$ has vanished confirming the role of the dust in the observed variation of the H$\alpha $ to UV flux ratio.

The mean value of $SFR({\rm H\alpha})/SFR({\rm UV})$ after correction for dust extinction is found slightly lower than 1 for both samples: $0.79 \pm 0.60$ for the SFG sample considering only galaxies with and error on A(H$\alpha $) lower than 0.3 mag and $0.66 \pm 0.36$ for the IUE sample (Fig. 5b). An uncertainty of about 0.2 dex for the calibration in SFRs is reasonable (cf. Appendix) and there is probably no need to invoke complex scenarii of star formation to explain the mean $SFR({\rm H\alpha})/SFR({\rm UV})$. The dispersion on the ratio of the SFRs is similar with and without extinction when the SFG sample is restricted to objects for which the error on A(H$\alpha $) does not exceed 0.3 mag. This dispersion is rather high (a factor $\sim$3 in $SFR({\rm H\alpha})/SFR({\rm UV})$). It can probably be attributed to variations of the star formation history or of the IMF and almost certainly also to the uncertainties on the estimate of the extinction at both H$\alpha $ and UV wavelengths.

The UV selected sample of Sullivan et al. (2000) contains some cases of very low H$\alpha $ to UV flux ratios which correspond to SFR(H$\alpha $)/SFR(UV) as low as 0.1. Such low values probably imply the introduction of post starbursts as proposed by Sullivan et al. but what we find here is that the extinction is likely to also contribute to the variation of this ratio: a UV selection is probably biased toward galaxies with a low extinction and therefore a low H$\alpha $ to UV flux ratio whatever the star formation history might be. The fact that the lowest H$\alpha $ to UV flux ratios are found by Sullivan et al. in low luminosity galaxies (cf. Fig. 3) is consistent with a role of the extinction since intrinsically faint galaxies are known to be less extincted than larger ones (e.g. Wang & Heckman 1996).

4.4 Can we derive a UV extinction from the F $_{H\alpha }/$FUV ratio?


  \begin{figure} \par\includegraphics[width=6.8cm,clip]{MS1861f6.eps} \end{figure} Figure 6: The UV extinction $A_{\rm UV}$ deduced from the $F_{\rm H\alpha }/F_{\rm UV}$ ratio against the extinction calculated with $F_{\rm FIR}/F_{\rm UV}$. The symbols are the same as in Fig. 2. The line corresponds to equal extinctions on both axis.
Open with DEXTER

In the absence of FIR measurements it would be useful to estimate the UV extinction by comparing the H$\alpha $ and UV emissions of the galaxies. The direct use of this ratio to quantitatively estimate the dust extinction is not frequent although it has been proposed as a qualitative argument to compare the extinction at both wavelengths (Moy et al. 2001). Meurer et al. (1999) noticed a positive correlation between $F_{\rm H\alpha }/F_{\rm UV}$ and the extinction traced by $\beta$. The method developped by Calzetti and collaborators implies that the dust corrected $F_{\rm H\alpha }/F_{\rm UV}$ is almost constant for starburst galaxies (Calzetti 1997).

Practically, both emissions must be calibrated in SFR. The extinction in the H$\alpha $ line is measured with the Balmer decrement and the extinction in UV is obtained by matching the SFRs measured at these two wavelengths. This approach is motivated by the correlation found between $F_{\rm H\alpha }/F_{\rm UV}$ and $F_{\rm FIR}/F_{\rm UV}$ which has been successfully explained by the effect of the extinction in the previous section.

The UV extinction is related to the H$\alpha $ one via the relation:

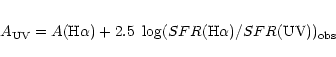
\begin{eqnarray*}A_{\rm UV} = A({\rm H\alpha})+2.5~\log(SFR({\rm H\alpha})/SFR({\rm UV}))_{\rm obs} \end{eqnarray*}


with

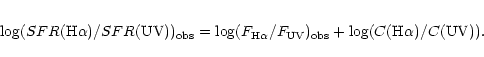
\begin{eqnarray*}\log(SFR({\rm H\alpha})/SFR({\rm UV}))_{\rm obs} = \log(F_{\rm... ...lpha}/F_{\rm UV})_{\rm obs}+\log (C({\rm H\alpha})/C({\rm UV})). \end{eqnarray*}


In Fig. 6 the values of $A_{\rm UV}$ are compared with the results of the models based on $F_{\rm FIR}/F_{\rm UV}$, the mean values are reported in Table 3. Both extinctions appear correlated but the extinctions calculated with the H$\alpha $ to UV flux ratio are lower than those estimated with the FIR to UV flux ratio by 0.3-0.6 mag with a rather large fraction of galaxies in the SFG sample (15/47) with $A_{\rm UV} < 0$ calculated with $F_{\rm H\alpha }/F_{\rm UV}$. Modifying the calibration of $F_{\rm H\alpha }/F_{\rm UV}$ in SFR ratio by increasing $\log (C({\rm H\alpha})/C({\rm UV}))$ would improve the situation. A slight increase would also be consistent with the mean $SFR({\rm H\alpha})/SFR({\rm UV})$corrected for dust extinction lower than 1 found in Sect. 4.1. If for example we adopt a value of $\log (C({\rm H\alpha})/C({\rm UV}))$ of -1.25 which corresponds to a fraction of ionizing flux absorbed by the gas f=0.7 instead of f=1 for the baseline scenario, the agreement between the estimates of the mean UV extinction woul improve (cf. Table 3).

The case of IR bright galaxies is particularly interesting. Unfortunately very few galaxies of our samples have a FIR luminosity larger than $10^{11}~L_\odot$: the most FIR luminous galaxy of the SFG sample reaches $2.45\times 10^{10}~L_\odot$ and only 3 galaxies out of the 19 of the IUE sample with reliable $F_{\rm FIR}/F_{\rm UV}$ have $L_{\rm FIR}> 10^{11}~L_\odot$: NGC 1614, IC 214 and NGC 6090. For NGC 1614 and NGC 6090 there is a good agreement between the estimates of the UV extinction with $F_{\rm FIR}/F_{\rm UV}$ and $F_{\rm H\alpha }/F_{\rm UV}$ with only a slightly higher extinction when $F_{\rm FIR}/F_{\rm UV}$ is used (4.8 mag against 4.4 mag for NGC 1614 and 2.8 mag against 3.1 mag for NGC 6090). In contrast, for IC 214, the extinction deduced from $F_{\rm FIR}/F_{\rm UV}$ is twice that estimated with $F_{\rm H\alpha }/F_{\rm UV}$ (1.6 mag against 3.2 mag). In the case of M82 ( $L_{\rm FIR} = 5\times 10^{10}~L_\odot$), both estimates are similar ($\sim$3.5 mag). Recent studies have found that for very luminous IR galaxies ( $L_{\rm FIR}> 3\times 10^{11}~L_\odot$) the extinction corrected SFR(H$\alpha $) is much lower than the SFR calculated with the FIR luminosity (Poggianti & Wu 2000; Elbaz, private communication).

Therefore, while there is a global correlation for our samples between the extinction calculated with $F_{\rm H\alpha }/F_{\rm UV}$ and $F_{\rm FIR}/F_{\rm UV}$, the derivation of an absolute value of the dust extinction using $F_{\rm H\alpha }/F_{\rm UV}$ is subject to uncertainties due to the measure of A(H$\alpha $) as well as to the calibration of H$\alpha $ and UV emissions in star formation rate.

5 Conclusions

We have compared the properties of two samples of nearby galaxies with UV, H$\alpha $ FIR and Balmer decrement data. The first sample is composed of normal star-forming galaxies (SFG sample) and the second of starburst galaxies extracted from the IUE database (IUE sample).

The extinction in the H$\alpha $ line deduced from Balmer decrement measurements is found similar on average for both samples with a mean value of $\sim$0.8-0.9 mag.

Two methods to estimate the UV extinction have been used and compared on both samples: the attenuation law derived for starburst galaxies and the calibration of the FIR to UV flux ratio in dust extinction.

The use of the attenuation law for starburst galaxies leads to a higher extinction by $\sim$0.6 mag than measuring the extinction with $F_{\rm FIR}/F_{\rm UV}$ for the star-forming galaxies. The situation is inverse for the starburst galaxies with a higher extinction measured by $F_{\rm FIR}/F_{\rm UV}$ of $\sim$0.6 mag.

Based on the measurements made with $F_{\rm FIR}/F_{\rm UV}$, the average UV extinction in starburst galaxies is higher than in star-forming objects by $\sim$1 mag ( $A_{\rm UV} \sim 2$ mag on average for the starburst galaxies against $A_{\rm UV} \sim 1$ mag for the star-forming galaxies).

A very tight correlation is found between the UV and H$\alpha $ luminosities for the SFG sample. The correlation is much more dispersed for the IUE galaxies with the H$\alpha $ to UV flux ratio systematically higher for the latter. The mean properties of the sample of star-forming galaxies are similar to those of the UV selected sample of Sullivan et al. whereas it is not the case for the starburst galaxies. However low luminosity galaxies with a very low $F_{\rm H\alpha }/F_{\rm UV}$ as found in the UV selected sample are almost absent in the star-forming galaxy sample. Applying the attenuation law derived for starburst galaxies to UV selected samples would lead to a systematic over estimate of the SFR by a factor $\sim$1.7 if the extinction calculated with $F_{\rm FIR}/F_{\rm UV}$ is taken as a reference.

$F_{\rm H\alpha }/F_{\rm UV}$ strongly correlates with $F_{\rm FIR}/F_{\rm UV}$. This trend can be explained by the effects of the dust extinction. Therefore this dust extinction is likely to play an important role in the variation of the observed $F_{\rm H\alpha }/F_{\rm UV}$. It is shown that using $F_{\rm H\alpha }/F_{\rm UV}$ to estimate a dust extinction in UV is subject to rather large uncertainties even when the Balmer decrement is measured.

Acknowledgements
We thank M. Sullivan for providing us the H$\alpha $ and UV luminosities of his galaxy sample. We acknowledge useful discussions with D. Calzetti and S. Charlot about some aspects of this work.

References

 

Copyright ESO 2002