Converting
![]() and
and
![]() to the corresponding
to the corresponding
![]() and T0 depends on many uncertain parameters, such as
the UV background and the reionization history.
If the UV background is dominated by QSOs without any extra heating,
T0 decreases and
and T0 depends on many uncertain parameters, such as
the UV background and the reionization history.
If the UV background is dominated by QSOs without any extra heating,
T0 decreases and
![]() increases as z decreases, until they approach
asymptotic values. The
increases as z decreases, until they approach
asymptotic values. The
![]() value, however, still
increases with decreasing z, until it approaches an asymptotic
value and finally decreases again at z < 2 (Schaye et al. 1999).
value, however, still
increases with decreasing z, until it approaches an asymptotic
value and finally decreases again at z < 2 (Schaye et al. 1999).
Instead of converting
to T0, we compare our
![]() with Figs. 3 and 4 of Schaye et al. (2000) from their
simulations assuming the QSO-dominated Haardt-Madau UV background,
with Figs. 3 and 4 of Schaye et al. (2000) from their
simulations assuming the QSO-dominated Haardt-Madau UV background,
![]() (Haardt
& Madau 1996)
(Haardt
& Madau 1996)![]() .
Our
.
Our
![]() is in agreement with their simulated
is in agreement with their simulated
![]() values without extra He II heating,
although the difference increases as zdecreases (ours being a factor of 1.1 lower at
values without extra He II heating,
although the difference increases as zdecreases (ours being a factor of 1.1 lower at ![]() ).
It is not clear what causes their numerical simulations without
the He II reionization produce their
).
It is not clear what causes their numerical simulations without
the He II reionization produce their
![]() similar to ours which suggest the extra heating.
One of the explanations could be a weaker effect on the forest
from the He II reionization than their simulations suggest.
When
similar to ours which suggest the extra heating.
One of the explanations could be a weaker effect on the forest
from the He II reionization than their simulations suggest.
When ![]() is converted from the same simulations (their Fig. 2),
is converted from the same simulations (their Fig. 2),
![]() decrease as z decreases.
decrease as z decreases.
For
![]() ,
we assume the conversion law between
,
we assume the conversion law between
![]() and
and ![]() by
Schaye (2001) assuming
by
Schaye (2001) assuming
![]() and
and
![]() for
thermally broadened lines.
The conversion law is defined by
for
thermally broadened lines.
The conversion law is defined by
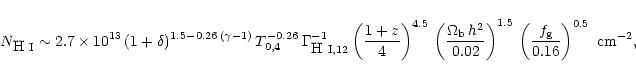 | (2) |
where
![]() K,
the H I photoionization rate
K,
the H I photoionization rate
![]() s-1,
s-1,
![]() is the baryon density, h is the Hubble constant divided by 100,
and
is the baryon density, h is the Hubble constant divided by 100,
and ![]() is the fraction of the mass in gas (Schaye
2001). We read
is the fraction of the mass in gas (Schaye
2001). We read ![]() from Fig. 3 of
Schaye et al. (2000) and
from Fig. 3 of
Schaye et al. (2000) and
![]() from
Fig. 8 of Haardt
& Madau (1996), while we assume
from
Fig. 8 of Haardt
& Madau (1996), while we assume
![]() and
and
![]() .
At
.
At
![]() ,
3.3 and 3.8,
,
3.3 and 3.8,
![]() ,
0.386 and 0.441. Assuming
,
0.386 and 0.441. Assuming
![]() ,
there is no clear z-evolution of
,
there is no clear z-evolution of
![]() within large
uncertainties. Our values and Schaye et al.'s
(
within large
uncertainties. Our values and Schaye et al.'s
(
![]() 0.4, 0.35 and 0.25 at
0.4, 0.35 and 0.25 at
![]() ,
3.3 and 3.8
assuming
,
3.3 and 3.8
assuming
![]() )
agree at
)
agree at ![]() 2.1, 3.3, while
our value is a factor of 1.8 larger than theirs at <z> = 3.8.
Our
2.1, 3.3, while
our value is a factor of 1.8 larger than theirs at <z> = 3.8.
Our
![]() values agree with those of McDonald et al.
at the similar z ranges within uncertainties, although their
simulations do not assume
values agree with those of McDonald et al.
at the similar z ranges within uncertainties, although their
simulations do not assume
![]() .
.
Copyright ESO 2002