![\begin{table}
\par\par\includegraphics[width=17.5cm,clip]{tab3.eps}\par\end{table}](/articles/aa/full/2002/09/aa1576/img31.gif) |
![\begin{table}
\par\par\includegraphics[width=17.5cm,clip]{tab3.eps}\par\end{table}](/articles/aa/full/2002/09/aa1576/img31.gif) |
| Names | J2000 Coords | X-Op | IR-Op | X-IR | Optical | X-ray | mid-IR | ||||||||||||||
|
|
|
|
|
|
V | V-I | R | R-Ks | SX | HX | LW2 | LW3 |
|
z | C | T | |||||
| (1) | (2) | (3) | (4) (5) | (6) (7) | (8) (9) | (10) | (11) | (12) | (13) | (14) | (15) | (16) | (17) | (18) | (19) | (20) | (21) | (22) | |||
| 144 PM3_6 | 36:36.64 | 13:46.9 | 0.4 | 0 | 1.5 | 5 | 1.9 | 1 | 22.1 | 1.3 | 20.8 | 2.7 | 4.43 | * 5.53 | - | 0.35 +0.04-0.07 | 0.9570 |
|
1 | ||
| 171 PM3_20 | 36:46.35 | 14:04.8 | 0.3 | 0 | 1.2 | 3 | 1.4 | 3 | 22.9 | 2.1 | 21.7 | 3.9 | 2.80 | *20.10 | 0.19 +0.04-0.09 | 0.11 +0.09-0.02 | 0.9612 | - | 1 | ||
| 163 PS3_10 | 36:42.22 | 15:45.8 | 0.2 | 0 | 1.1 | 3 | 1.2 | 0 | 23.3 | 2.4 | 21.6 | 4.3 | 0.84 | * 2.48 | - | 0.46 +0.05-0.09 | 0.8575 |
|
- | ||
| 198 PS3_24 | 36:55.46 | 13:11.4 | 0.4 | 1 | 0.9 | 4 | 0.6 | 1 | 24.5 | 2.8 | 22.9 | 4.7 | 0.40 | * 0.89 | <0.4 | 0.02 +0.01-0.01 | 1.3153 |
|
- | ||
| 190 PM3_29 | 36:51.75 | 12:21.4 | 1.3 | 5 | 1.9 | 10 | 1.4 | 5 | 22.6 | 1.6 | 21.5 | 2.9 | 0.28 | * 2.59 | <0.04 | 0.05 +0.03-0.01 | 0.4010 |
|
- | ||
| 142 PM3_5 | 36:35.60 | 14:24.4 | 0.5 | 2 | 0.3 | 1 | 0.5 | 0 | 23.9 | 1.2 | 23.5 | 4.5 | 0.28 | * 2.82 | - | 0.44 +0.04-0.08 | 2.0116 | - | 2 | ||
| 134 PM3_2 | 36:34.46 | 12:12.9 | 0.3 | 0 | 0.6 | 0 | 1.0 | 0 | 21.1 | 2.0 | 18.8 | 2.7 | 0.23 | <0.27 | <41.63 | - | 0.45 +0.07-0.06 | >1.56 | 0.4560 |
|
- |
| 176 PS2_3 | 36:48.05 | 13:09.1 | 0.3 | 0 | 0.9 | 1 | 0.9 | 2 | 22.5 | 2.5 | 20.4 | 3.2 | 0.18 | * 0.63 | 0.04 +0.06-0.03 | < 0.07 | <1.30 | 0.4752 |
|
- | |
| 172 PM3_21 | 36:46.41 | 15:29.2 | 0.2 | 0 | 0.6 | 2 | 0.7 | 0 | 24.6 | 3.1 | 23.2 | 4.2 | 0.14 | * 0.40 | - | 0.42 +0.09-0.09 | (0.6) | - | - | ||
| 160 PM3_12 | 36:41.80 | 11:32.0 | 1.5 | 2 | 1.4 | 1 | 2.7 | 5 | 20.6 | 0.9 | 19.4 | 1.7 | 0.13 | <0.26 | <39.78 | <0.07 | 0.24 +0.06-0.06 | >1.50 | 0.0891 |
|
- |
| 136 PM3_3 | 36:34.51 | 12:41.6 | 0.7 | 4 | 1.2 | 11 | 1.1 | 0 | 24.2 | 2.0 | 23.2 | 4.5 | 0.10 | <0.27 | <42.87 | - | 0.36 +0.08-0.04 | >1.53 | 1.2190 |
|
- |
| 161 PS3_6e | 36:42.11 | 13:31.6 | - | - | - | - | 1.3 | 6 | - | - | >26 | >4.6 | 0.10 | <0.21 | <44.66 | <0.07 | 0.02 +0.01-0.01 | >1.29 | 4.4244 |
|
1 |
| 188 PM3_28 | 36:51.11 | 10:30.7 | 0.3 | 0 | 0.4 | 0 | 0.5 | 0 | 21.9 | 2.0 | 20.2 | 3.6 | 0.10 | <0.26 | <41.42 | - | 0.34 +0.04-0.07 | >1.53 | 0.4101 |
|
- |
| 194 PM3_32 | 36:53.41 | 11:39.6 | 0.6 | 2 | 2.1 | 27 | 1.8 | 3 | 23.3 | 1.4 | 23.2 | 4.0 | 0.09 | <0.15 | <42.67 | - | 0.18 +0.06-0.04 | >1.52 | 1.2750 |
|
- |
| Var PM3_17 | 36:44.20 | 12:51.0 | 1.9 | 6 | 1.8 | 6 | 0.2 | 0 | 22.6 | 2.1 | 21.4 | 2.1 | 0.08 | <0.29 | <41.93 | <0.05 | 0.28 +0.06-0.06 | >1.50 | 0.5570 |
|
2 |
| 155 PM3_11 | 36:40.00 | 12:50.2 | 0.8 | 2 | 1.1 | 4 | 0.9 | 1 | 23.2 | 2.2 | 21.5 | 3.6 | 0.07 | 0.27 | <0.06 | 0.30 +0.07-0.06 | 0.8480 |
|
- | ||
| 175 PS3_14 | 36:47.95 | 10:19.9 | - | - | - | - | 2.3 | 8 | - | - | - | - | 0.07 | 0.89 | - | - | 0.10 +0.09-0.02 | 1.30 | - | - | - |
| 185 PM3_27 | 36:49.76 | 13:13.0 | 2.0 | 11 | 0.4 | 0 | 2.0 | 6 | 23.0 | 2.0 | 21.5 | 3.4 | 0.07 | <0.17 | <41.41 | 0.14 +0.07-0.06 | 0.16 +0.04-0.04 | >1.51 | 0.4751 |
|
- |
| 178 PM3_24 | 36:48.38 | 14:26.2 | 0.7 | 0 | 1.4 | 1 | 1.1 | 1 | 19.5 | 1.0 | 18.7 | 2.0 | 0.06 | <0.17 | <40.04 | 0.25 +0.07-0.07 | 0.31 +0.06-0.07 | >1.56 | 0.1390 |
|
- |
| 220 PM3_42 | 37:02.04 | 11:22.4 | 0.3 | 0 | 2.0 | 2 | 2.0 | 4 | 20.3 | 1.2 | 18.7 | 2.2 | 0.06 | <0.18 | <40.04 | - | 0.16 +0.08-0.05 | >1.50 | 0.1362 |
|
- |
| 183 PM2_3 | 36:49.45 | 13:47.2 | 0.6 | 0 | 0.8 | 0 | 1.0 | 3 | 19.2 | 1.5 | 18.0 | 2.4 | 0.05 | <0.18 | <39.62 | 0.04 +0.07-0.03 | < 0.05 | - | 0.0891 | - | - |
| 148 PM3_7 | 36:37.01 | 11:34.9 | 1.3 | 1 | 1.4 | 1 | 1.2 | 1 | 19.6 | 1.0 | 17.7 | 1.8 | 0.04 | <0.09 | <39.19 | <0.14 | 0.30 +0.06-0.07 | >1.62 | 0.0781 |
|
- |
| 229 PS3_37 | 37:04.66 | 14:29.0 | 0.2 | 0 | 1.4 | 3 | 1.5 | 5 | 22.7 | 2.3 | 21.0 | 3.2 | <0.05 | 0.29 | - | 0.07 +0.06-0.02 | 0.5611 |
|
- | ||
| 149 PS3_6b | 36:38.50 | 13:39.5 | 0.7 | 2 | 1.0 | 5 | 1.2 | 4 | 23.6 | 2.0 | 22.3 | 3.3 | <0.04 | 0.75 | - | 0.05 +0.03-0.01 | 0.3575 |
|
- | ||
In the case of the Lockman Hole observations, XMM sources have position
errors of 1-3'' (Hasinger et al. 2001), while 15 ![]() m and 6.75
m and 6.75 ![]() m ISOCAM sources have position errors of 2-4'' (depending on the
redundancy of mid-IR observation, see Fadda et al. 2002). In
practice, we match X-ray and mid-IR sources within a circle of 4''. In
total, we found 22 matches with 15
m ISOCAM sources have position errors of 2-4'' (depending on the
redundancy of mid-IR observation, see Fadda et al. 2002). In
practice, we match X-ray and mid-IR sources within a circle of 4''. In
total, we found 22 matches with 15 ![]() m sources detected at the
3
m sources detected at the
3![]() level and 7 with 6.75
level and 7 with 6.75 ![]() m sources at the 4
m sources at the 4![]() level. For the sake of completeness, we list also upper limits of the
LW2 and LW3 fluxes when a source is detected in only one of the two
ISOCAM filters.
level. For the sake of completeness, we list also upper limits of the
LW2 and LW3 fluxes when a source is detected in only one of the two
ISOCAM filters.
In the case of the Hubble Deep Field image, we have reprocessed the
ISOCAM data to recompute more accurate positions
of the LW3 sources. We
have used the I-band image of Barger et al. (1999) available on the
Web![]() to which
we added the astrometry according to the catalogue of Hogg et al. (2000). Position errors of the Chandra sources are estimated to be
less than 1'' (Brandt et al. 2001a), while ISOCAM sources thanks to the microscan technique of
observation have errors less than 2''. Therefore, we match X-ray and
mid-IR sources within a circle of 2''.
to which
we added the astrometry according to the catalogue of Hogg et al. (2000). Position errors of the Chandra sources are estimated to be
less than 1'' (Brandt et al. 2001a), while ISOCAM sources thanks to the microscan technique of
observation have errors less than 2''. Therefore, we match X-ray and
mid-IR sources within a circle of 2''.
For each source we have computed the probability of random association
of the X-ray source with its mid-IR and optical counterparts, and
of the mid-IR source with its optical counterpart. Assuming that the
counterpart belongs to a Poissonian distributed population of sources,
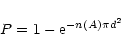 |
(1) |
Contours of the matched sources are also plotted on optical images in Figs. 2 and 3. In most of the cases there is a clear correspondence between X-ray and mid-IR sources. Only in a few cases (#149 in the Hubble Deep Field and #41, #79 in the Lockman Hole) optical counterparts are uncertain and the match relies only on the distance criterion. Three sources are optically faint (see Alexander et al. 2001a).
Results of these cross-correlations are reported in Tables 3 and 4 which contain positions of the X-ray sources, distances, and probability of random associations between sources and proposed counterparts, optical magnitudes in the V, I, R and K bands, X-ray and mid-IR fluxes, redshifts and AGN types when known, as well as other quantities described in the following.
For the sources without spectroscopic redshifts, we have estimated photometric redshifts using four optical magnitudes (V, I, R and K) under the assumption that the optical emission is dominated by the host galaxy. We used a library of synthetic SEDs generated with PEGASE2.0 (Fioc & Rocca-Volmerange 1997) to fit the distribution of optical magnitudes. The median error on photometric redshifts, derived from a study on the Hubble Deep Field South (Franceschini et al., in prep.), is 0.1.
Up to now, only two ISOCAM surveys have been studied in the X-ray
bands: the Elais-S1 field (Alexander et al. 2001) and the HDF-N
field (Hornschemeier et al. 2001). In this paper we extend the study
of mid-IR-X-ray cross-correlation in the HDF-N field
and flanking fields using the new observations of Brandt et al. (2001a)
and justifying the associations between X-ray and mid-IR sources.
Figure 4 compares the mid-IR and X-ray fluxes of the
sources detected in these surveys as well as the sensitivity limits of
the X-ray observations and the 80% completeness limits of the 15 ![]() m surveys. The survey in the Lockman Hole region is intermediate
between the Elais-S1 and HDF-N surveys. It covers an area of 218
square arcminutes that is
m surveys. The survey in the Lockman Hole region is intermediate
between the Elais-S1 and HDF-N surveys. It covers an area of 218
square arcminutes that is ![]() 30 times smaller than the Elais-S1
survey (
30 times smaller than the Elais-S1
survey (![]() 6000 square arcminutes) and
6000 square arcminutes) and ![]() 10 times larger than
the HDF-N survey (24 square arcminutes). In terms of sensitivity
it is approximately one order of magnitude shallower than the
HDF-N in the soft and hard X-ray bands, but it is two orders of
magnitudes deeper than the Beppo-SAX observations. Moreover, the
XMM-Newton data allow us to explore with a good sensitivity the
ultra-hard energy band (4.5-10 keV), which has been pioneered by
Beppo-SAX and is not well covered by Chandra. As we have already
seen, this band is very interesting because more than 60% of the
ultra-hard sources in the Lockman Hole have mid-IR counterparts.
10 times larger than
the HDF-N survey (24 square arcminutes). In terms of sensitivity
it is approximately one order of magnitude shallower than the
HDF-N in the soft and hard X-ray bands, but it is two orders of
magnitudes deeper than the Beppo-SAX observations. Moreover, the
XMM-Newton data allow us to explore with a good sensitivity the
ultra-hard energy band (4.5-10 keV), which has been pioneered by
Beppo-SAX and is not well covered by Chandra. As we have already
seen, this band is very interesting because more than 60% of the
ultra-hard sources in the Lockman Hole have mid-IR counterparts.
Taking into account the limits in sensitivity, the three surveys are
compatible in terms of source density. Within the sensitivity limits
of the Lockman Hole observations (
![]() mJy and
mJy and
![]() erg cm-2 s-1,
erg cm-2 s-1,
![]() erg cm-2 s-1) we find 13 and 11
sources in the soft and hard X-ray bands, respectively. Therefore, we
expect to detect in the HDF-N within the same flux limits
1.4
+0.5-0.4 and 1.2
+0.5-0.4 sources in the soft and
hard band, respectively, while we detect one and two sources.
Moreover, in the hard X-ray band within the sensitivity limits of
Elais-S1, we expect to detect
erg cm-2 s-1) we find 13 and 11
sources in the soft and hard X-ray bands, respectively. Therefore, we
expect to detect in the HDF-N within the same flux limits
1.4
+0.5-0.4 and 1.2
+0.5-0.4 sources in the soft and
hard band, respectively, while we detect one and two sources.
Moreover, in the hard X-ray band within the sensitivity limits of
Elais-S1, we expect to detect
![]() sources in the Lockman Hole
and
sources in the Lockman Hole
and
![]() sources in the HDF-N while no sources have been
detected in these two surveys.
sources in the HDF-N while no sources have been
detected in these two surveys.
In conclusion, the survey in the Lockman Hole is intermediate between the surveys in the Elais-S1 and HDF-N fields. Due to its large sky coverage, the Elais-S1 survey picks up very powerful and rare hard-X ray sources. On the other hand, the deep X-ray survey in the HDF-N allows the detection of very faint X-ray sources, and therefore also normal and starburst galaxies, in a small region of sky. So far, only the survey in the Lockman Hole region has sufficient depth and sky coverage to study a representative population of AGNs detected in the ISOCAM mid-IR surveys.
Copyright ESO 2002