Semi-analytic models of X-ray clusters and groups of galaxies, relying on the idea that there was a non-gravitational energy injection in these systems, are able to reproduce many observed correlations, in particular the
A&A 383, 450-471 (2002)
DOI: 10.1051/0004-6361:20011750
S. Dos Santos1 - O. Doré2
Department of Physics & Astronomy, University of Leicester, 1 University Road, Leicester LE1 7RH, UK
1 - Institut d'Astrophysique de Paris, 98bis boulevard Arago, 75014 Paris, France
Received 27 June 2001 / Accepted 6 December 2001
Abstract
Semi-analytic models of X-ray clusters and groups of galaxies,
relying on the idea that there was a non-gravitational energy injection in
these systems, are able to reproduce many observed correlations, in
particular the
![]() relation and the "central entropy floor'' in
groups. Limiting models exist which describe the behaviour of clusters and
groups separately, but no analytic modeling has yet been found to unify both
mass ranges. It is the aim of this paper to provide such an analytic
model. Our description relies on a now standard description of the shock
thought to occur in these systems near the virial radius (Cavaliere et al. 1998), the
isothermality and spherical symmetry of the intracluster medium, as well as
the reinterpretation of observed quantities (like the X-ray luminosity, the
gas mass
relation and the "central entropy floor'' in
groups. Limiting models exist which describe the behaviour of clusters and
groups separately, but no analytic modeling has yet been found to unify both
mass ranges. It is the aim of this paper to provide such an analytic
model. Our description relies on a now standard description of the shock
thought to occur in these systems near the virial radius (Cavaliere et al. 1998), the
isothermality and spherical symmetry of the intracluster medium, as well as
the reinterpretation of observed quantities (like the X-ray luminosity, the
gas mass
![]() and the central SZ effect y0) in terms of the specific
entropy. This allows the derivation of analytic expressions for several
observed correlations (
and the central SZ effect y0) in terms of the specific
entropy. This allows the derivation of analytic expressions for several
observed correlations (
![]() ,
,
![]() ,
y0-T,...) and their
normalisation encompassing both the group and the cluster regimes. The
analytic predictions compare very well with observations, as well as with
more elaborated semi-analytic schemes. This agreement allows a
reinterpretation of the
,
y0-T,...) and their
normalisation encompassing both the group and the cluster regimes. The
analytic predictions compare very well with observations, as well as with
more elaborated semi-analytic schemes. This agreement allows a
reinterpretation of the
![]() relation (via the quantity
relation (via the quantity
![]() )
and
the y0-T relation (via
y0/T5/2) as indirect measures of the
non-gravitational entropy content of groups and clusters of galaxies. We
emphasize the need for shock heating, even in the group mass range:
shocks can not be completely suppressed in groups (and thus groups can
not be entirely isentropic) unless an unacceptably high entropy floor is
needed in order to break the self-similarity in the
)
and
the y0-T relation (via
y0/T5/2) as indirect measures of the
non-gravitational entropy content of groups and clusters of galaxies. We
emphasize the need for shock heating, even in the group mass range:
shocks can not be completely suppressed in groups (and thus groups can
not be entirely isentropic) unless an unacceptably high entropy floor is
needed in order to break the self-similarity in the
![]() relation. Our
model shows that the normalisation of the entropy after the shock (which is
mass-dependent) is a key ingredient and that this quantity alone can
explain the shape of the observed correlations between integrated X-ray and
SZ quantities over and below 2 keV.
relation. Our
model shows that the normalisation of the entropy after the shock (which is
mass-dependent) is a key ingredient and that this quantity alone can
explain the shape of the observed correlations between integrated X-ray and
SZ quantities over and below 2 keV.
Key words: hydrodynamics - shock waves - galaxies: clusters: general - X-rays: galaxies: clusters - cosmology: large-scale structure of Universe
For ten years, it has been known that X-ray observations of clusters of
galaxies can not be reproduced in simple self-similar models, where the
central gas density is proportional to dark matter density. Kaiser (1991)
and Evrard & Henry (1991) advocated a preheating of the gas before it fell into the
cluster potential to recover the observed correlations. Later, X-ray
observations of groups of galaxies have strengthened the case for a
non-gravitational entropy injection in these systems, in particular by the
observation of the so-called "entropy floor'' (Ponman et al. 1999). These authors
showed that the central entropy level in groups (outside the cooling-flow
radius) is higher than the level the sole cosmological shocks can provide,
while being well in accord with adiabatic numerical simulations (e.g., including no dissipative physics) in clusters. This entropy
injection could be due to supernovae explosions (the so-called feedback from
star formation) or other sources as active galactic nuclei. Several
semi-analytic schemes that elaborate on this idea have been proposed to
reproduce the curvature of the
![]() relation in the groups' mass range
(where the effects of the preheating are thought to be the highest,
see Cavaliere et al. 1997; Bower 1997; Valageas & Silk 1999; Valageas & Schaeffer 2000; Wu et al. 2000; Bower et al. 2000). In particular,
Cavaliere et al. (1997, 1998, 1999, hereafter CMT) have introduced a simple model,
where the bending is provided by the differential strength of a shock
occurring at the virial radius in a preheated gas. Their description relies on
the physical modeling of the shock interface, using Hugoniot relations, and
reproduces naturally the central observed entropy floor. While this model
highlights the important role of shocks and entropy floor in the formation of
clusters and groups, no analytic description of the X-ray observed
relations has yet been found to encompass both groups and clusters.
The aim of this paper is to present such a model and compare it to
observations.
relation in the groups' mass range
(where the effects of the preheating are thought to be the highest,
see Cavaliere et al. 1997; Bower 1997; Valageas & Silk 1999; Valageas & Schaeffer 2000; Wu et al. 2000; Bower et al. 2000). In particular,
Cavaliere et al. (1997, 1998, 1999, hereafter CMT) have introduced a simple model,
where the bending is provided by the differential strength of a shock
occurring at the virial radius in a preheated gas. Their description relies on
the physical modeling of the shock interface, using Hugoniot relations, and
reproduces naturally the central observed entropy floor. While this model
highlights the important role of shocks and entropy floor in the formation of
clusters and groups, no analytic description of the X-ray observed
relations has yet been found to encompass both groups and clusters.
The aim of this paper is to present such a model and compare it to
observations.
However, despite the success of these semi-analytic schemes when confronted
with observations, difficult problems remain, as for example the fact that a
reheating by supernovae (hereafter SN) explosions requires an incredibly high
efficiency of the transfer of energy from SN remnants to the intergalactic
medium (Valageas & Silk 1999; Bower et al. 2000). In particular, the cooling of the SN remnants
will obviously decrease this transfer efficiency, and must be ignored in
these models. While a combination of SN and quasars (hereafter QSOs)
reheating is probable and would alleviate this problem, Bryan (2000) has
proposed that differential galaxy formation between groups and clusters
(which would lower the central entropy in groups and allow higher entropy gas
to flow into the center) can explain the curvature of the
![]() relation
and the entropy floor. However, it is well known that without preheating,
most of the available gas in the universe would have formed stars today,
which is not observed
(this the so-called "overcooling problem'', see Blanchard et al. 1992; Balogh et al. 2001). This much-needed feedback in galaxy formation would
certainly have an impact on the formation of clusters and
groups. Valageas & Silk (1999) have indeed shown that galaxy and cluster feedback
differing requirements are likely to provide a tight constraint on the amount
of preheating in the universe. But, even in the preheated scenarios, there is
actually no consensus on the entropy injection epoch. While most of the
studies have focussed on "external preheating'' models (where the entropy
injection occurs before the formation of groups and clusters e.g.,
before the gas is compressed by shocks) because low density gas requires much
less energy than high density one to be raised to a given entropy level (and
also because the star formation rate seems to peak rather early in the
universe evolution), Loewenstein (2000), from a series of approximate
static hot gas models and Brighenti & Mathews (2001), from 1D numerical simulation with
cooling, mass dropout and star formation feedback, have argued that most of
the heating occurred during or after the assembly of the group or cluster
gas. The efficiency problem of SN explosion is still present, but can be
alleviated by an initial mass function flatter than the Salpeter one
(Brighenti & Mathews 2001). These are the so-called "internal preheating'' models.
relation
and the entropy floor. However, it is well known that without preheating,
most of the available gas in the universe would have formed stars today,
which is not observed
(this the so-called "overcooling problem'', see Blanchard et al. 1992; Balogh et al. 2001). This much-needed feedback in galaxy formation would
certainly have an impact on the formation of clusters and
groups. Valageas & Silk (1999) have indeed shown that galaxy and cluster feedback
differing requirements are likely to provide a tight constraint on the amount
of preheating in the universe. But, even in the preheated scenarios, there is
actually no consensus on the entropy injection epoch. While most of the
studies have focussed on "external preheating'' models (where the entropy
injection occurs before the formation of groups and clusters e.g.,
before the gas is compressed by shocks) because low density gas requires much
less energy than high density one to be raised to a given entropy level (and
also because the star formation rate seems to peak rather early in the
universe evolution), Loewenstein (2000), from a series of approximate
static hot gas models and Brighenti & Mathews (2001), from 1D numerical simulation with
cooling, mass dropout and star formation feedback, have argued that most of
the heating occurred during or after the assembly of the group or cluster
gas. The efficiency problem of SN explosion is still present, but can be
alleviated by an initial mass function flatter than the Salpeter one
(Brighenti & Mathews 2001). These are the so-called "internal preheating'' models.
In this paper, we focus explicitly on an external preheating model. Internal
preheating models require spatially-dependent and time-dependent star
formation rates to provide the amount of injected entropy, while external
preheating models only require the level of entropy before the gas falls in a
cluster or a group. This simplification allows us to obtain a completely
analytic model that describes both groups and clusters.The physical approach
we follow consists of deriving scaling relations, e.g.
![]() ,
y-T,
,
y-T,
![]() by linking these observed quantities to the specific entropy profile in the
system. For this purpose we first derive an analytic expression for
the entropic profile normalisation at the virial radius of clusters and
groups by discussing shocks, as in CMT. Using this relation we then derive
analytically the relevant scaling relations and compare them to data.
Following Tozzi & Norman (2001), we highlight the key role of entropy and argue that
it indeed constitutes the best observable in clusters, allowing to derive
analytical expressions for standard X-ray and Sunyaev-Zeldovich (hereafter
SZ) correlations. This leads us to reinterpret these relations in terms of
global entropy content in a well physically motivated manner.
by linking these observed quantities to the specific entropy profile in the
system. For this purpose we first derive an analytic expression for
the entropic profile normalisation at the virial radius of clusters and
groups by discussing shocks, as in CMT. Using this relation we then derive
analytically the relevant scaling relations and compare them to data.
Following Tozzi & Norman (2001), we highlight the key role of entropy and argue that
it indeed constitutes the best observable in clusters, allowing to derive
analytical expressions for standard X-ray and Sunyaev-Zeldovich (hereafter
SZ) correlations. This leads us to reinterpret these relations in terms of
global entropy content in a well physically motivated manner.
The plan of the paper is as follows: in Sect. 2, we present
the shock model and derive an expression for the normalisation of the entropy
profile at the virial radius. This expression, containing a free
normalisation, is fitted to observations. In Sect. 3, we relate
the X-ray luminosity to the entropy profile and derive an analytic expression
for the shape of the
![]() relation, which is subsequently compared to
observations using only the fitted parameter of the last section.. The
same method is followed in Sects. 4-6 to obtain analytic expressions for the
relation, which is subsequently compared to
observations using only the fitted parameter of the last section.. The
same method is followed in Sects. 4-6 to obtain analytic expressions for the
![]() ,
,
![]() ,
y0-T and y0-Lx correlations (where
,
y0-T and y0-Lx correlations (where
![]() is the gas mass,
is the gas mass,
![]() is the gas fraction and y0 is the central
Compton parameter). In each of these parts, we provide a detailed comparison
with previous work. Section 7 discusses a reinterpretation
of these correlations in terms of the total entropy content in groups and
clusters, tests it using a semi-analytic model and discusses the main
hypotheses we make. Moreover, a comparison of our results for the entropy
floor with other theoretical models is made. Section 8
summarises the present work and concludes. We also compute the numerical
values of the normalisations of the correlations found and summarise all
these results in Appendix A, allowing them to be easily used in another
context. Appendix B computes the infalling velocity as a function
of the mean mass of the system and compares it to hydrodynamic
simulations. Finally, Appendix C, introducing a simple
model for the entropy profile of groups, computes the shape
factors appearing in the different normalisations.
is the gas fraction and y0 is the central
Compton parameter). In each of these parts, we provide a detailed comparison
with previous work. Section 7 discusses a reinterpretation
of these correlations in terms of the total entropy content in groups and
clusters, tests it using a semi-analytic model and discusses the main
hypotheses we make. Moreover, a comparison of our results for the entropy
floor with other theoretical models is made. Section 8
summarises the present work and concludes. We also compute the numerical
values of the normalisations of the correlations found and summarise all
these results in Appendix A, allowing them to be easily used in another
context. Appendix B computes the infalling velocity as a function
of the mean mass of the system and compares it to hydrodynamic
simulations. Finally, Appendix C, introducing a simple
model for the entropy profile of groups, computes the shape
factors appearing in the different normalisations.
Unless otherwise stated, we use
![]() with
h2/3 = 2/3, which gives approximately
with
h2/3 = 2/3, which gives approximately
![]() .
We rescale all the data used in this paper
to this value.
.
We rescale all the data used in this paper
to this value.
The study of the equilibrium state of X-ray clusters and groups of galaxies requires the physical description of the complex interplay between baryonic and non-baryonic dark matter. To tackle this problem analytically requires several simplifying hypotheses. The following assumptions are reasonable and will be thus assumed henceforth (see Sarazin 1988, for a review and a discussion of the main assumptions).
First, the hot and diluted plasma of ions and electrons constituting the intracluster medium (hereafter ICM) is treated as a single species perfect gas satisfying
To solve this set, boundary conditions are required. In the present paper, we
are interested in the variations of these boundary conditions with the total mass
of the system (or equivalently with its mean temperature). Indeed, the
previous equations will describe the equilibrium of baryonic gas in the
underlying potential, whatever the total mass of the system. We argue and
show in the following that changes in the boundary conditions, when explicitly
written as a function of the mean temperature, allow us to derive the change
in global correlations, such as the
![]() relation, on a scale going from
clusters to groups of galaxies. For this purpose, we use the fact that the
flow of gas on a cluster becomes supersonic in the vicinity of the virial
radius
relation, on a scale going from
clusters to groups of galaxies. For this purpose, we use the fact that the
flow of gas on a cluster becomes supersonic in the vicinity of the virial
radius ![]() (Teyssier et al. 1997). We will then show that a
standard modeling of the resulting shock (following CMT) leads to
the appropriate boundary conditions. We will consider hereafter that the
boundary conditions take place after the last major merger of the system, as
appropriate in a hierarchical picture of structure formation.
(Teyssier et al. 1997). We will then show that a
standard modeling of the resulting shock (following CMT) leads to
the appropriate boundary conditions. We will consider hereafter that the
boundary conditions take place after the last major merger of the system, as
appropriate in a hierarchical picture of structure formation.
The last hypothesis we will use is that within the virial radius, the ICM is isothermal. This hypothesis will not be used in the derivation of the boundary conditions (Sect. 2.1) but in the derivation of the global correlations in groups and clusters (Sects. 3 and 5). Both observations Markevitch et al. (1998) and simulations (Teyssier 2001) show that this approximation is good into a factor two and is thus sufficient for our purpose.
Finally, let us recall an hypothesis necessarily underlying every work published
using the entropy of the ICM, but rarely stated: the local
thermodynamic equilibrium hypothesis (hereafter LTE). By
definition, in a state of global thermodynamic equilibrium,
temperature and pressure (and thus density) are constant throughout
the system, and the state functions of the system (e.g. entropy) have a
determined dependency on the state variables chosen (and so a fixed
value). In the LTE however, temperature and pressure can vary from point to
point (as is obvious in clusters from X-ray observations for example) and,
locally only, the system is in thermodynamical equilibrium. Thus, the state
functions have the same dependency on state variables as in global
equilibrium, but vary now from point to point as do the latter. Note
that this hypothesis is likely to break down at smaller scales than the
ones of interest to us, due to turbulence or magnetic effects. This
hypothesis is crucial if we want to use
the usual analytic expression of the specific entropy of the ICM,
s, defined as
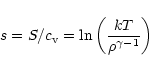 |
(4) |
We first aim at deriving adiabat boundary conditions based on the Rankine-Hugoniot relations, used in the same form as CMT.
Let the infalling gas velocity reach the sound speed at
![]() and
consider subsequently that a shock forms at this radius. Let the
temperature, the density and the velocity of the infalling gas before
the shock be respectively T1, n1 and v1, and the post-shock
temperature, density and velocity be T2, n2 and v2. If the
shock efficiency is very high, i.e. the post-shock velocity
v2 is null in the rest-frame of the cluster center of mass,
the Rankine-Hugoniot relations yield (see CMT):
and
consider subsequently that a shock forms at this radius. Let the
temperature, the density and the velocity of the infalling gas before
the shock be respectively T1, n1 and v1, and the post-shock
temperature, density and velocity be T2, n2 and v2. If the
shock efficiency is very high, i.e. the post-shock velocity
v2 is null in the rest-frame of the cluster center of mass,
the Rankine-Hugoniot relations yield (see CMT):
Using the formulas above, we will now derive a general expression for the adiabat jump at the shock, which will depend on the system mean temperature. This virial adiabat normalisation will provide us with the change in the boundary conditions necessary to describe groups and clusters in a unique analytic model.
To find a general expression for the post-shock adiabat, we
first express the ratio T1/T2 as a function of ![]() :
:
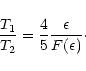 |
(10) |
| K2 | = | ||
| = | (12) |
Checking the validity of this expansion in the range
![]() we find an agreement better than
we find an agreement better than ![]() (Fig. 1) which is enough for our purpose (the error of the
approximation reaches a constant
(Fig. 1) which is enough for our purpose (the error of the
approximation reaches a constant ![]() level at large
level at large
![]() ). Thus we will neglect higher order corrections.
). Thus we will neglect higher order corrections.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{happrox.ps} \end{figure}](/articles/aa/full/2002/08/aah2972/Timg68.gif) |
Figure 1:
Top: plot of the function
|
| Open with DEXTER | |
As a consequence, for the all range from groups to rich clusters, one can write to a very
good approximation:
Since rich clusters of galaxies accrete mainly small clumps and diffuse gas,
the cold inflow or strong shock limit is
appropriate. Consequently it is usually argued that the entropy of
rich clusters is dominated by shock created entropy. Indeed,
for this approximation we have
![]() and
and
![]() ,
and so (from Eq. (15))
,
and so (from Eq. (15))
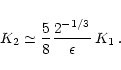 |
(16) |
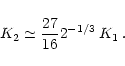 |
(17) |
The analytic expression in Eq. (15) thus provides a well physically motivated expression for the competition between shocks and entropy floor that rules the adiabat virial normalisation from groups to clusters.
We now want to make use of the previously derived expression (15) to predict a general relation for the K-Trelation for groups and clusters.
First, making use of Eqs. (8) and (15) we rewrite
 |
(18) |
This leads naturally to:
Deriving the value of K1 requires a whole semi-analytic scheme, which would require a model of the entropy evolution of the intergalactic medium (hereafter IGM) as the universe evolves (see e.g. Valageas & Silk 1999). This is clearly beyond the scope of the present paper, and we will thus constrain K1 by comparison with observations (which only means that the normalisation of our model is left free). However, K0 and T0 are not independent parameters and can be related by simple physical considerations as will be shown in the next section.
Once this is done, the scaling relation (21) is left with only one normalisation parameter K0.
First, to derive an explicit relation between K0 and T0, we need to
specify the value of both ![]() and T1 in
Eq. (23). Using the results of Miniati et al. (2000) for
the infall velocity in hydrodynamic simulations (see Eq. (B.15)
and Appendix for notations), a value for
and T1 in
Eq. (23). Using the results of Miniati et al. (2000) for
the infall velocity in hydrodynamic simulations (see Eq. (B.15)
and Appendix for notations), a value for ![]() can be derived by equating
Eq. (B.15) and Eq. (19):
can be derived by equating
Eq. (B.15) and Eq. (19):
The relation between K0 and T0 will appear when expliciting
T1. Indeed we can write it as a function of the pre-shock adiabat
K1:
By definition of the baryonic fraction ![]() and the overdensity
and the overdensity
![]() we can write:
we can write:
Consequently, to fix the numerical value of T0 we need to specify a
value of K1. We choose to assume the value of the
observed entropy floor visible in groups of galaxies. A value of
![]() is inferred from the
data (Lloyd-Davies et al. 2000, see the next section).
is inferred from the
data (Lloyd-Davies et al. 2000, see the next section).
Then we assume a flat
![]() universe with
universe with
![]() and the baryonic fraction as fixed by Big-Bang
Nucleosynthesis standard, i.e.
and the baryonic fraction as fixed by Big-Bang
Nucleosynthesis standard, i.e.
![]() (Olive et al. 2000).
For a spherical collapse model
(Olive et al. 2000).
For a spherical collapse model
![]() .
Note however that
in the widely used hierarchical structure formation paradigm, this monolithic
formation model is too
simplistic. Indeed, since the majority of the infall of group of
galaxies occurs through filaments, an overdensity of
.
Note however that
in the widely used hierarchical structure formation paradigm, this monolithic
formation model is too
simplistic. Indeed, since the majority of the infall of group of
galaxies occurs through filaments, an overdensity of
![]() should be more appropriate. Considering then the values of
should be more appropriate. Considering then the values of
![]() and
and ![]() specified in the Appendix, we find
that
specified in the Appendix, we find
that
![]() for
for
![]() and
and
![]() for
for
![]() .
This is quite
insensitive to the adopted cosmology, since for an
.
This is quite
insensitive to the adopted cosmology, since for an
![]() universe,
one finds
universe,
one finds
![]() and
and
![]() respectively. It
is thus obvious that we can take for T0 an intermediate value
between these two extremes.
respectively. It
is thus obvious that we can take for T0 an intermediate value
between these two extremes.
In the following, we will thus consider that T0 is fixed at 2 keV, and that the only free parameter of the model will be the normalisation factor K0. Moreover, choosing a value of T0 between 1.5 and 2.5 keV does not alter the quality of the fits we present in the next sections.
Looking at Eq. (21), T0 has a simple physical
interpretation: it is the system mean temperature where the effect of
an entropy floor begins to change the adiabat jump during the virial
shock. For systems with T < T0, the pre-shock entropy is high enough to
reduce the shock and a quasi-adiabatic inflow takes places (but the shocks are
not completely suppressed, see Sect. 7.4). For T>T0, the
shock adiabat jump brings the post-shock adiabat to values much higher that
the entropy floor, the latter having less and less incidence as T increases.
Thus we find that this transition occurs around
![]() .
.
X-ray observations of groups and clusters of galaxies have brought a great
amount of information on the gas equilibrium in these systems. Unfortunately,
due mostly to the high background of the instruments and the gas density
decline with radius, there are not yet entropy observations available up to
the virial radius, that would allow to test directly our model (and more
generally the scheme invented by CMT). The new
generation of satellites (Chandra and XMM-Newton) is expected to bring new
observations near the virial radius, allowing to test different formation
scenarios of clusters and groups (see e.g., Tozzi et al. 2000).
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{KTanalytic.ps} \end{figure}](/articles/aa/full/2002/08/aah2972/Timg118.gif) |
Figure 2:
Post-shock adiabat K2 as a function of the mean temperature of
the system. The solid line is obtained with Eq. (21),
with
|
| Open with DEXTER | |
Nevertheless, some data on the central adiabat value of the gas in groups and
clusters are available. Ponman et al. (1999) were the first to show that groups have
a central adiabat higher than the one they would have if it had been imposed
by shocks only. Recently, Lloyd-Davies et al. (2000) have refined these observations,
taking into account the temperature gradients, while increasing the
statistics. This is the so-called observed "entropy floor''. While cool
systems have a constant central adiabat, hotter clusters follow naturally the
results of numerical simulations without a preheating phase (which predict
that
![]() ). Note that our model predicts exactly
the same behaviour, exhibited in the post-shock adiabat analytic expression of
Eq. (21). However, we compute the adiabat near the virial radius,
while the data come from the central parts of the systems. Nevertheless,
observations and theory can be compared if we assume that the adiabat
difference between two different temperature systems is conserved when
going from the virial radius to the central part. This implies that the
physical mechanism responsible for the post-shock adiabat value (competition
between shocks and an entropy floor) is the same as the one responsible for
the central adiabat value. This is indeed a reasonable assumption, since 3D
hydrodynamical simulations of the formation of clusters show that, after the
last major merger, a quasi-spherical shock forms and expands, that leaves
behind an increasing adiabat profile (see e.g., Evrard 1990; Frenk et al. 1999). The same physics is thus at work in the center
and in the outer parts of clusters, allowing the physical description of the
two regions to coincide. Indeed, the only difference between these two
regions is that the universe will have evolved when the shock reaches
the present-day virial radius, as compared to the time when the central
entropy is set. We thus don't expect the observational value of K1 (found
by normalisation to the observations) to be
representative of the present adiabat of the universe, but it should instead be
representative of the IGM at the time when the smaller mass systems
formed. If virial radius observations of the adiabat were available for the
same systems, we expect then that the same analytic expression as in
Eq. (21) would be a good description of the data, with a
different value of K1, representative of the present-day adiabat of the IGM.
). Note that our model predicts exactly
the same behaviour, exhibited in the post-shock adiabat analytic expression of
Eq. (21). However, we compute the adiabat near the virial radius,
while the data come from the central parts of the systems. Nevertheless,
observations and theory can be compared if we assume that the adiabat
difference between two different temperature systems is conserved when
going from the virial radius to the central part. This implies that the
physical mechanism responsible for the post-shock adiabat value (competition
between shocks and an entropy floor) is the same as the one responsible for
the central adiabat value. This is indeed a reasonable assumption, since 3D
hydrodynamical simulations of the formation of clusters show that, after the
last major merger, a quasi-spherical shock forms and expands, that leaves
behind an increasing adiabat profile (see e.g., Evrard 1990; Frenk et al. 1999). The same physics is thus at work in the center
and in the outer parts of clusters, allowing the physical description of the
two regions to coincide. Indeed, the only difference between these two
regions is that the universe will have evolved when the shock reaches
the present-day virial radius, as compared to the time when the central
entropy is set. We thus don't expect the observational value of K1 (found
by normalisation to the observations) to be
representative of the present adiabat of the universe, but it should instead be
representative of the IGM at the time when the smaller mass systems
formed. If virial radius observations of the adiabat were available for the
same systems, we expect then that the same analytic expression as in
Eq. (21) would be a good description of the data, with a
different value of K1, representative of the present-day adiabat of the IGM.
Figure 2 shows the comparison of Eq. (21) with
data from Lloyd-Davies et al. (2000). Only the normalisation was fitted here, with a
value of
![]() (giving
(giving
![]() ), while we have taken
), while we have taken
![]() ,
derived with the same value
of K1 in the last section. Replacing Eq. (28) in
Eq. (21) instead, and fitting
for K1 gives an undistinguishible analytic curve. The dashed line is
the result of a
,
derived with the same value
of K1 in the last section. Replacing Eq. (28) in
Eq. (21) instead, and fitting
for K1 gives an undistinguishible analytic curve. The dashed line is
the result of a
![]() fit to the systems above
fit to the systems above
![]() found
by Helsdon & Ponman (2000). This temperature dependence of the adiabat is
taken from numerical simulations (see Ponman et al. 1999). The dot-dashed line is a
constant gas entropy fitted to the four lowest temperature systems by
Lloyd-Davies et al. (2000) and has a value of
found
by Helsdon & Ponman (2000). This temperature dependence of the adiabat is
taken from numerical simulations (see Ponman et al. 1999). The dot-dashed line is a
constant gas entropy fitted to the four lowest temperature systems by
Lloyd-Davies et al. (2000) and has a value of
![]() .
The agreement between
the analytic formula and the data is remarkable. Indeed, using the
fitted value of K1, the computed T0 value agrees very well with the
temperature of the intersection between these two limiting behaviours (see
last section). This shows that Eq. (21) is not a mere analytic
formula (which could have been inferred from the observations), but succeeds
in capturing both ingredients which fix the central
entropy value: the entropy floor (dot-dashed line in the groups mass range)
and the shocks (dashed line, in the cluster mass range).
.
The agreement between
the analytic formula and the data is remarkable. Indeed, using the
fitted value of K1, the computed T0 value agrees very well with the
temperature of the intersection between these two limiting behaviours (see
last section). This shows that Eq. (21) is not a mere analytic
formula (which could have been inferred from the observations), but succeeds
in capturing both ingredients which fix the central
entropy value: the entropy floor (dot-dashed line in the groups mass range)
and the shocks (dashed line, in the cluster mass range).
By adjusting the normalisation of our analytic model using the data we derive
a value for K1. Then making use of this relation we get directly for any
system at a given temperature T (either a group or a cluster) the
normalisation of the adiabat profile. It is now important to check whether we
are able to use this relation to derive realistic
![]() and y-T relations
for both groups and clusters.
and y-T relations
for both groups and clusters.
The total X-ray luminosity of a local cluster (group) of galaxies is expressed as:
We can now express Eq. (29) as a function of K and thus link
the X-ray luminosity with the temperature and the adiabat:
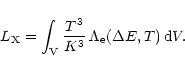 |
(30) |
Equation (31) gives us a direct link between ![]() ,
T and K. Were the expression of K as a function of T known, it would
enable us to predict the shape of the
,
T and K. Were the expression of K as a function of T known, it would
enable us to predict the shape of the
![]() relation. However,
the result of the previous section (21) gives us the change in the adiabat
normalisation as a function of temperature, but since the
integral in Eq. (31) is computed over all the system
volume, in principle we need the adiabat profile to compute it. However, if we
make the further assumption that the adiabat profiles are self-similar in
temperature, i.e. the temperature enters the analytic expression of
relation. However,
the result of the previous section (21) gives us the change in the adiabat
normalisation as a function of temperature, but since the
integral in Eq. (31) is computed over all the system
volume, in principle we need the adiabat profile to compute it. However, if we
make the further assumption that the adiabat profiles are self-similar in
temperature, i.e. the temperature enters the analytic expression of
![]() by its normalisation only, then we can derive an expected
by its normalisation only, then we can derive an expected
![]() relation. This assumption is justified by the fact that our
theoretical expression for the adiabat normalisation
(Eq. (21)), which is computed at the virial radius, provides
a very good fit to the central entropy data in groups and clusters. This
simple fact ensures that the difference in normalisation between two
clusters of different temperature (which is due to shocks and preheating) is
leaved approximately unchanged from the virial radius to the center. This
important side aspect of our work will be discussed in
Sect. 7. We thus write:
relation. This assumption is justified by the fact that our
theoretical expression for the adiabat normalisation
(Eq. (21)), which is computed at the virial radius, provides
a very good fit to the central entropy data in groups and clusters. This
simple fact ensures that the difference in normalisation between two
clusters of different temperature (which is due to shocks and preheating) is
leaved approximately unchanged from the virial radius to the center. This
important side aspect of our work will be discussed in
Sect. 7. We thus write:
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{lxtanalytic.ps} \end{figure}](/articles/aa/full/2002/08/aah2972/Timg136.gif) |
Figure 3:
|
| Open with DEXTER | |
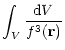 |
= | 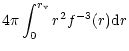 |
(34) |
| = | 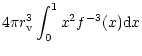 |
(35) | |
| (36) |
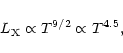 |
(39) |
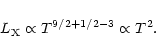 |
(40) |
The normalisation of the local
![]() relation (Eq. (38)) depends
on the value of the IGM adiabat K0 and the shape factor
relation (Eq. (38)) depends
on the value of the IGM adiabat K0 and the shape factor ![]() .
The former
has been obtained in Sect. 2.3.3 (
.
The former
has been obtained in Sect. 2.3.3 (
![]() )
by comparing our analytic formula for the adiabat jump to
observations. The latter is more difficult to obtain since it will depend on
the exact adiabat profile of clusters and groups. We show in
Appendix C that we can compute a value for
)
by comparing our analytic formula for the adiabat jump to
observations. The latter is more difficult to obtain since it will depend on
the exact adiabat profile of clusters and groups. We show in
Appendix C that we can compute a value for ![]() by considering a reasonable model for the adiabat profile, relying on
isothermality and a
by considering a reasonable model for the adiabat profile, relying on
isothermality and a ![]() -model for the gas density profile
(Cavaliere & Fusco-Femiano 1976). The computed value is
-model for the gas density profile
(Cavaliere & Fusco-Femiano 1976). The computed value is
![]() .
.
To validate this relation, we plot in Fig. 3 the
![]() relation of Eq. (37) together with data taken for
groups (from Helsdon & Ponman 2000) and clusters of galaxies
(Markevitch 1998; Arnaud & Evrard 1999). The quality of the fit is obviously
excellent. Note that we adopt for T0 the value computed in
Sect. 2.3.2 and used
relation of Eq. (37) together with data taken for
groups (from Helsdon & Ponman 2000) and clusters of galaxies
(Markevitch 1998; Arnaud & Evrard 1999). The quality of the fit is obviously
excellent. Note that we adopt for T0 the value computed in
Sect. 2.3.2 and used
![]() .
There is thus no free
parameter in the solid curve computation, since K0 has been already fixed.
.
There is thus no free
parameter in the solid curve computation, since K0 has been already fixed.
Note that the hotter groups seem to be overluminous when compared to the
cluster data as well as to the analytic relation. There are indeed several
uncertainties concerning these systems, both observational and
theoretical. Groups are much less luminous than clusters, which has some
important consequences: first, the radius of detection (in units of the
virial radius) is small and varies among groups: this effect is very hard to
correct since the value of the asymptotic slope of the surface brightness
(![]() in a
in a ![]() -model) is very uncertain. Second, it is very difficult
to separate the intra-group medium emission from the galactic emission, which
can lead to an important misestimation of the total flux
(see in particular the discussion on HCG 16 by Dos Santos & Mamon 1999). Third, the central
cooling-flows were cut (Markevitch 1998) or the sample was chosen
explicitly to contain only clusters with known weak cooling-flows
(Arnaud & Evrard 1999). On the contrary, the groups luminosity in Helsdon & Ponman (2000) are
not cooling-flow corrected, since it is very delicate to separate the
cooling-flow from the ICM emission with ROSAT's PSPC resolution. This could
also explain that the hotter groups (which are expected to have the greatest
fraction of their luminosity coming from their cooling-flow because of their
higher central density) show the greatest departure. Our model does not take
into account a possible cooling-flow component, which explains that it fits
very well the cluster data, while lying near the lower envelope of the hotter
groups. It fits nevertheless very well the lower temperature
groups
-model) is very uncertain. Second, it is very difficult
to separate the intra-group medium emission from the galactic emission, which
can lead to an important misestimation of the total flux
(see in particular the discussion on HCG 16 by Dos Santos & Mamon 1999). Third, the central
cooling-flows were cut (Markevitch 1998) or the sample was chosen
explicitly to contain only clusters with known weak cooling-flows
(Arnaud & Evrard 1999). On the contrary, the groups luminosity in Helsdon & Ponman (2000) are
not cooling-flow corrected, since it is very delicate to separate the
cooling-flow from the ICM emission with ROSAT's PSPC resolution. This could
also explain that the hotter groups (which are expected to have the greatest
fraction of their luminosity coming from their cooling-flow because of their
higher central density) show the greatest departure. Our model does not take
into account a possible cooling-flow component, which explains that it fits
very well the cluster data, while lying near the lower envelope of the hotter
groups. It fits nevertheless very well the lower temperature
groups![]() . As usually done, we thus assume that the discrepancies affecting
the high temperature groups is mainly due to observational uncertainties and
does not compromise our overall simplified picture.
. As usually done, we thus assume that the discrepancies affecting
the high temperature groups is mainly due to observational uncertainties and
does not compromise our overall simplified picture.
Both the cluster slope and the group steeper slope come out naturally of our relation. This agreement is remarkable and is the first to our knowledge based on an analytic discussion to encompass both groups and clusters.
This good agreements is a strong sign in favor of the consistency of our
approach. It is thus natural to try to apply
an analogous method to the correlation between the mass of gas and the mean
temperature, as well as to the SZ effect, and compare cluster observations with
our analytic predictions. Unfortunately, gas mass observations are sparse and
heterogeneous for groups, while no SZ effect in a group has yet been
observed. We can nevertheless make predictions for the
![]() and
y-T relation in this range, which could be validated by undoubtly
forthcoming SZ measurements.
and
y-T relation in this range, which could be validated by undoubtly
forthcoming SZ measurements.
Another tight correlation found in reducing ICM data of clusters is the link
between the ICM mass and the mean temperature. For a perfectly self-similar
model, one expects theoretically
![]() .
In fact, several
groups have reported recently a steepening of this relation, which could be
due to entropy injection. Vikhlinin et al. (1999) have studied the outer regions of a
ROSAT sample of clusters, and found that the above correlation could be
written
.
In fact, several
groups have reported recently a steepening of this relation, which could be
due to entropy injection. Vikhlinin et al. (1999) have studied the outer regions of a
ROSAT sample of clusters, and found that the above correlation could be
written
![]() ,
steeper but nevertheless close to the
self-similar value. On the other hand, Mohr et al. (1999) have fitted double
,
steeper but nevertheless close to the
self-similar value. On the other hand, Mohr et al. (1999) have fitted double
![]() -models to another large sample of clusters and found that
-models to another large sample of clusters and found that
![]() ,
much steeper than the self-similar model. It is not clear
if this discrepancy (at only
,
much steeper than the self-similar model. It is not clear
if this discrepancy (at only
![]() level) is real and if so, what are
the reasons behind it.
level) is real and if so, what are
the reasons behind it.
It is easy to compute this correlation in our framework and
worth comparing our predictions with observations. The ICM mass of gas
can be written (assuming spherical symmetry):
The slope of the correlation also steepens from very hot clusters (
![]() ,
analogous to the self-similar correlation) to groups (
,
analogous to the self-similar correlation) to groups (
![]() ). The temperature range probed by Mohr et al. (1999) is intermediate
between these two behaviours.
). The temperature range probed by Mohr et al. (1999) is intermediate
between these two behaviours.
Figure 4 shows the data from Mohr et al. (1999), as well
as their best-fit linear correlation
![]() (dashed
line). The solid line is our predicted relation using the computed value
(dashed
line). The solid line is our predicted relation using the computed value
![]() .
The predicted slope matches perfectly the data. The steepening of
the relation compared to the self-similar one is thus, in our particular
model, simply a consequence of the differential shock strength and the
entropy floor.
.
The predicted slope matches perfectly the data. The steepening of
the relation compared to the self-similar one is thus, in our particular
model, simply a consequence of the differential shock strength and the
entropy floor.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{mgas_t.ps}
\end{figure}](/articles/aa/full/2002/08/aah2972/Timg169.gif) |
Figure 4:
|
| Open with DEXTER | |
The gas fraction is very important in that it is supposed to give a direct lower limit on the universe baryon fraction, if clusters are a fair sample of the universe (White et al. 1993). Such measurements have proven to be tight constraints to the total mass density of the universe.
Using Eq. (42) and the observed M-T relation of
Eq. (B.11), i.e. the observed scaling between total mass and
temperature, it is straightforward to compute the gas fraction
variation with temperature:
Equation (45) is shown in Fig. 5,
together with observations. The data points are from
Mohr et al. (1999). These data were fitted by the authors with a power-law,
namely
![]() .
The shaded area, limited in abscissa by the minimum and
maximum temperature of the sample, represents the area covered by similar power-laws
increased and decreased by
.
The shaded area, limited in abscissa by the minimum and
maximum temperature of the sample, represents the area covered by similar power-laws
increased and decreased by
![]() (both in normalisation and in
slope). It is obvious that the data are dispersed, but the trend found by
Mohr et al. (1999) is very well recovered by Eq. (45), as well as
the normalisation.
(both in normalisation and in
slope). It is obvious that the data are dispersed, but the trend found by
Mohr et al. (1999) is very well recovered by Eq. (45), as well as
the normalisation.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{fgas_t.ps}
\end{figure}](/articles/aa/full/2002/08/aah2972/Timg174.gif) |
Figure 5:
|
| Open with DEXTER | |
Looking at Eq. (45), one sees that for ![]() ,
i.e.
for rich clusters, the gas fraction becomes independent of the
temperature. This regime is only reached asymptotically in the figure.
On the other end the slope steepens from clusters to groups, since we have:
,
i.e.
for rich clusters, the gas fraction becomes independent of the
temperature. This regime is only reached asymptotically in the figure.
On the other end the slope steepens from clusters to groups, since we have:
The observations against which our model was validated above were only in the X-ray wavelengths. We are now turning to the radio and sub-millimeter bandwidth, which also probes the hot gas in clusters (via the Sunyaev-Zeldovich effect) and offers independent observations, with different possible systematics and errors. This allows us to independently validate the model and make some predictions about the group behaviour in this band.
Inverse-Compton scattering of incoming CMB photons on ICM thermal
electrons cause a well observed change in the spectral dependence of the
CMB (Rephaeli 1995; Birkinshaw 1999). The amplitude of the CMB temperature brightness
variation can be written:
For current SZ experiments resolution (especially interferometric ones), the beam smearing is still a critical issue as long as we want to determine a central value. Most authors use X-ray determined temperature as well as the X-ray surface brightness to correct for the beam and to obtain the central value of the SZ effect y(0). This might be a source of uncertainty but we will nevertheless express this quantity in our physical framework, and compare it to observations.
The beam-corrected quantity can be obtained in the following way: going back
to Eq. (51) we write (assuming spherical symmetry)
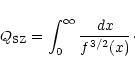 |
(56) |
Finally, let us make a comment about the shape of the y-Trelation. For ![]() ,
we get:
,
we get:
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{ytanalytic.ps}
\end{figure}](/articles/aa/full/2002/08/aah2972/Timg195.gif) |
Figure 6:
Central SZ decrement - X-ray temperature relation. The data
points are taken from Zhang & Wu (2000). The solid
line is the predicted y0 using
|
| Open with DEXTER | |
Taking observational data from Zhang & Wu (2000) (diamonds), we can compare our predicted relation of Eq. (54) to observed correlations.
In Fig. 6 we plot
data and their associated error bars, our prediction for
![]() (solid line, computed in Appendix C) and
the best fit of (Cooray 1999 dot-dashed line)
(solid line, computed in Appendix C) and
the best fit of (Cooray 1999 dot-dashed line)![]() . The fact that only rich cluster data
are yet available (which limits the leverage on the slope) and the large
dispersion on the observed y-T correlation translates into a large
uncertainty on the best-fit slope:
. The fact that only rich cluster data
are yet available (which limits the leverage on the slope) and the large
dispersion on the observed y-T correlation translates into a large
uncertainty on the best-fit slope:
![]() .
.
Our prediction for the beam-corrected value is steeper than the Cooray's
best-fit relation but still consistent with it at the 1![]() level. It seems to be in better agreement with Zhang's data set,
which extends to slightly higher and lower temperatures than
Cooray's. Note that we will further show that Eq. (54) is also
in very good agreement with semi-analytic models for both groups and
clusters.
level. It seems to be in better agreement with Zhang's data set,
which extends to slightly higher and lower temperatures than
Cooray's. Note that we will further show that Eq. (54) is also
in very good agreement with semi-analytic models for both groups and
clusters.
The overall agreement with both data sets is less impressive than for the
previously derived
![]() relation, but is still very reasonable, given the
observational dispersion.
relation, but is still very reasonable, given the
observational dispersion.
Since X-ray and SZ observations are completely independent, the agreement between our analytic model with the latter is another independent confirmation of its validity. A robust confirmation would come from SZ observations of groups of galaxies (unfortunately not yet feasible) and from the change in the correlation slopes. Nevertheless, we can compare our simple model to more elaborate semi-analytic models and their predictions.
Menci & Cavaliere (2001) have presented semi-analytic predictions for the
observed SZ effect in groups and clusters. Their semi-analytic model takes
into account the preheating due to star formation, in order to bend the
![]() relation in the groups mass range. Our predictions for the y(0)-Trelation (namely Eq. (57) for clusters and (58)
for groups) are in complete accord with their preheated models. They found a
self-similar relation for high mass systems (
relation in the groups mass range. Our predictions for the y(0)-Trelation (namely Eq. (57) for clusters and (58)
for groups) are in complete accord with their preheated models. They found a
self-similar relation for high mass systems (
![]() )
which is
exactly our prediction. The slope in the groups mass range depends on the
feedback model they chose, but our prediction (
)
which is
exactly our prediction. The slope in the groups mass range depends on the
feedback model they chose, but our prediction (
![]() )
is
also similar to their computed moderate feedback model (which looks to
be a better choice, since their strong feedback model is likely to give only an upper
limit on the feedback effect). We are thus able to reproduce their Figs. 3
and 4 with our simple analytic model. Even if this is not a confirmation of
the model (since we use an analytic version of their model of shocks and our
hypotheses on the preheating are very similar), we find it extremely
satisfying to reproduce analytically, and in a physically
straightforward and motivated way,
the results of a more complicated and non-analytic model. This gives us more
confidence in the fact, that we have captured in this simple physical scheme
the essential ingredients of the clusters and groups formation.
)
is
also similar to their computed moderate feedback model (which looks to
be a better choice, since their strong feedback model is likely to give only an upper
limit on the feedback effect). We are thus able to reproduce their Figs. 3
and 4 with our simple analytic model. Even if this is not a confirmation of
the model (since we use an analytic version of their model of shocks and our
hypotheses on the preheating are very similar), we find it extremely
satisfying to reproduce analytically, and in a physically
straightforward and motivated way,
the results of a more complicated and non-analytic model. This gives us more
confidence in the fact, that we have captured in this simple physical scheme
the essential ingredients of the clusters and groups formation.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{ylx.ps} \end{figure}](/articles/aa/full/2002/08/aah2972/Timg200.gif) |
Figure 7:
Central SZ decrement - X-ray luminosity relation. The solid line
represents the analytic predicted correlation, using the predicted values
of
|
| Open with DEXTER | |
To link SZ and X-ray measurements, it is natural to determine a
correlation between y and ![]() .
It is expected to be much tighter than the
.
It is expected to be much tighter than the ![]() relation (see Cooray 1999), but is more intricate to obtain
analytically. In this section, we will give two analytic expressions for
this correlation in the rich clusters's and in the groups' range mass respectively.
relation (see Cooray 1999), but is more intricate to obtain
analytically. In this section, we will give two analytic expressions for
this correlation in the rich clusters's and in the groups' range mass respectively.
Indeed using Eqs. (54) and (37), we can write:
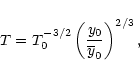 |
(60) |
Finally, one can compute this correlation in the groups mass range (![]() ), yielding a steeper correlation:
), yielding a steeper correlation:
We have shown that a simple modeling of the main process in charge of the
formation of clusters (namely the shocks which thermalise the gas inside the
virial radius) allows us to derive a general K-T relation that reproduces
very well the observed one. Moreover, we were able to deduce most of the
observed scaling laws with the adequate normalisation, encompassing both
groups and clusters. Thus, the physical meaning of e.g. the
![]() and y-T relations, and in particular of the break in their self-similarity when
going from clusters to groups (only evidenced in X-rays for the moment) can
be understood as a relic of the formation process of these systems: a
competition between an entropy floor prior to the shock and the shock
process itself. This suggests naturally that entropy constitutes the best
"observable'' in clusters, as already emphasized by the modified spherical
model of Tozzi & Norman (2001). What we add here is that we show that entropy (in
fact, the adiabat) is also suitable to seek analytic expressions for the
different correlations found observationally in groups and
clusters. Reversing this argument, these scaling laws
should be an appropriate probe of the entropy content of clusters.
and y-T relations, and in particular of the break in their self-similarity when
going from clusters to groups (only evidenced in X-rays for the moment) can
be understood as a relic of the formation process of these systems: a
competition between an entropy floor prior to the shock and the shock
process itself. This suggests naturally that entropy constitutes the best
"observable'' in clusters, as already emphasized by the modified spherical
model of Tozzi & Norman (2001). What we add here is that we show that entropy (in
fact, the adiabat) is also suitable to seek analytic expressions for the
different correlations found observationally in groups and
clusters. Reversing this argument, these scaling laws
should be an appropriate probe of the entropy content of clusters.
While the entropy spatial variations of the baryonic gas in clusters is a
valuable piece of information on their present thermodynamic state
(in particular for merging clusters, see e.g., Markevitch et al. 1999), the total
entropy content
![]() (hereafter TEC), defined as
(hereafter TEC), defined as
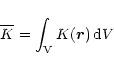 |
(64) |
The analytic model we have presented in the last sections allows us to shed
some light in the TEC and its link to the
![]() relation. On the one hand,
given our assumption of isothermality, Eq. (31) indicates that
relation. On the one hand,
given our assumption of isothermality, Eq. (31) indicates that
![]() is related to the TEC in a given system. On the other
hand, the self-similar models of cluster formation (Kaiser 1986) predict
that
is related to the TEC in a given system. On the other
hand, the self-similar models of cluster formation (Kaiser 1986) predict
that
![]() ,
which gives directly (using
,
which gives directly (using
![]() ):
):
To this purpose, we will use a semi-analytic model (hereafter SAM)
developed independently by one of us (Dos Santos 2001, in
preparation). This particular model uses the conduction-structured
temperature profile (which was shown by Dos Santos (2001) to describe very
well the temperature and surface brightness profile of clusters of
galaxies), together with an NFW profile for the dark matter density
profile. A shock model at the virial radius, together with entropic
constraints at the center allow to predict the temperature profile without
the hypothesis of isothermality or the unphysical polytropic link between
temperature and density. The evolution of the central entropy is governed by
the entropy evolution of the IGM in the universe obtained from the model of
Valageas & Silk (1999) in two different cases: in the first one, the reheating is
provided by SN explosions only, while in the second one, AGN and quasar
activity provide the entropy injection. Both cases were validated against a
number of observations, including the
![]() relation, the change in
surface brightness profiles from clusters to groups, the baryon fraction in
these systems and the entropy floor.
relation, the change in
surface brightness profiles from clusters to groups, the baryon fraction in
these systems and the entropy floor.
Figure 8 shows the comparison between observations and the
SAM. The solid (SN case) and dashed lines (QSO case) show the quantity
![]() computed directly using the model. Since
the specific entropy is known up to an additive constant, both lines were
normalised to match the high temperature clusters. The dot-dashed line shows the
self-similar prediction for
computed directly using the model. Since
the specific entropy is known up to an additive constant, both lines were
normalised to match the high temperature clusters. The dot-dashed line shows the
self-similar prediction for
![]() (Eq. (65)), also renormalised to match rich clusters. The
preheated models high temperature slopes match naturally the self-similar
prediction. They also match very well the cluster data and their trend in
temperature. It is in particular remarkable that the three clusters with the
smallest temperatures (
(Eq. (65)), also renormalised to match rich clusters. The
preheated models high temperature slopes match naturally the self-similar
prediction. They also match very well the cluster data and their trend in
temperature. It is in particular remarkable that the three clusters with the
smallest temperatures (
![]() )
depart notably from the
self-similar prediction, and lie exactly on top of the semi-analytic
prediction. The lower envelope of groups is well followed by the SAM, while
some points are over this prediction. We think that, as in
Sect. 3.2, this is due partly to the fact that the central
cooling regions of groups were not removed, unlike the clusters, and partly
to an intrinsic scatter.
)
depart notably from the
self-similar prediction, and lie exactly on top of the semi-analytic
prediction. The lower envelope of groups is well followed by the SAM, while
some points are over this prediction. We think that, as in
Sect. 3.2, this is due partly to the fact that the central
cooling regions of groups were not removed, unlike the clusters, and partly
to an intrinsic scatter.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{k3dv_Trelation_allmodels.ps}
\end{figure}](/articles/aa/full/2002/08/aah2972/Timg217.gif) |
Figure 8:
Lx/T7/2 (observational points) compared to the direct
computation of
|
| Open with DEXTER | |
The figure shows why our simple model works well in recovering slope and
normalisation of the
![]() relation (and of the other relations we
studied): the equality (31) is also verified in a more general
semi-analytic model where the adiabat profile is fully known and the ICM is
not isothermal. At a given temperature, the difference in location between
observations and the self-similar curve will give a measure of the
non-gravitational entropy injection in systems with this mean
temperature. This measure does not depend at all on hydrostatic
equilibrium or spherical symmetry. Nor does it require either that the
preheating was external. In fact, Eq. (33) is completely
independent of any modeling of the entropy injection. It only requires
isothermality and local thermodynamic equilibrium on the scales probed by
the observations. It thus can be used as a powerful, model-independent,
constraint on all the internal or external preheating models, as well as on
differential galaxy formation efficiency between groups and clusters
(Bryan 2000). Unfortunately, the TEC is not measured directly, but the
integral of the right-hand side of Eq. (31) will obviously
decrease as the entropy injection amount is increased. Thus, if the adiabat
profile is known in a given model, it will be easy to relate this integral
to the TEC, even if a certain amount of degeneracy will obviously be present
(this measure being integrated in space and time, different entropy
injection histories can lead to the same final amount of entropy at z=0).
relation (and of the other relations we
studied): the equality (31) is also verified in a more general
semi-analytic model where the adiabat profile is fully known and the ICM is
not isothermal. At a given temperature, the difference in location between
observations and the self-similar curve will give a measure of the
non-gravitational entropy injection in systems with this mean
temperature. This measure does not depend at all on hydrostatic
equilibrium or spherical symmetry. Nor does it require either that the
preheating was external. In fact, Eq. (33) is completely
independent of any modeling of the entropy injection. It only requires
isothermality and local thermodynamic equilibrium on the scales probed by
the observations. It thus can be used as a powerful, model-independent,
constraint on all the internal or external preheating models, as well as on
differential galaxy formation efficiency between groups and clusters
(Bryan 2000). Unfortunately, the TEC is not measured directly, but the
integral of the right-hand side of Eq. (31) will obviously
decrease as the entropy injection amount is increased. Thus, if the adiabat
profile is known in a given model, it will be easy to relate this integral
to the TEC, even if a certain amount of degeneracy will obviously be present
(this measure being integrated in space and time, different entropy
injection histories can lead to the same final amount of entropy at z=0).
In fact, this constraint will be more or less the same as the constraint
given by the
![]() relation (already used to constrain the models), even
if the interpretation in terms of entropy is physically more satisfying.
However, the same remarks can be made with the surface integrated SZ
decrement. Indeed, the SZ y-Compton parameter integrated over the whole
surface of a cluster can be written:
relation (already used to constrain the models), even
if the interpretation in terms of entropy is physically more satisfying.
However, the same remarks can be made with the surface integrated SZ
decrement. Indeed, the SZ y-Compton parameter integrated over the whole
surface of a cluster can be written:
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{scaledadiabatprof.ps}\vspace*{2mm}
\includegraphics[width=8.4cm,clip]{scaledadiabatcentre.ps}
\end{figure}](/articles/aa/full/2002/08/aah2972/Timg220.gif) |
Figure 9:
Upper panel: average scaled adiabat profiles for systems
grouped by mean temperature (solid: 6-14 keV; dashed: 3.7-6 keV;
dot-dashed: 1.3-3.7 keV; dotted: 0.5-1.3 keV). Each individual profile was
obtained from the best-fit gas and density profiles given by Lloyd-Davies et al. (2000)
and scaled by
|
| Open with DEXTER | |
To derive the analytic scaling relations presented in this paper, we have used a strong assumption: the self-similarity of rescaled adiabat profiles (see Eq.(32)) i.e., the fact that the temperature enters only the normalisation of the adiabat profile. The validity of this assumption is questionable, both on observational and theoretical grounds.
Ponman et al. (1999) show that density profiles are shallower in groups than in clusters (even if this result is still uncertain, see Roussel et al. 2000, for an alternative view), while preheating models predict naturally that entropy gradients in lower temperature systems are smaller than in clusters (due to adiabatic infall during their lifetime, see Balogh et al. 1999; Tozzi & Norman 2001). However, these models predict also large temperature gradients in groups which are not observed (Tozzi & Norman 2001). Moreover, using 1D hydrodynamic models with internal or external preheating, Brighenti & Mathews (2001) obtain linearly rising entropy profiles in groups (outside an isentropic core for external preheating models) as well as in clusters. They thus produce naturally self-similar adiabat profiles in groups and clusters. The reasons for such discrepancies are unclear, but are certainly linked with widely differing simulation methods. Note however that Knight & Ponman (1997), using similar 1D hydrodynamic simulations, have found shallower slopes in groups compared to clusters, without taking into account any preheating (whose effect is expected to widen the slope difference).
Spatially-resolved spectroscopic observations of groups and clusters provide
directly adiabat profiles in groups and clusters and can then help to settle
this debate. Unfortunately, the low surface-brightness of groups allows this
type of study only to small radii![]() . Indeed, Lloyd-Davies et al. (2000) obtained the adiabat profile for 12 systems with
. Indeed, Lloyd-Davies et al. (2000) obtained the adiabat profile for 12 systems with
![]() up to
up to
![]() .
Even if this
maximum extent radius is small, the study of the adiabat profiles behaviour
with temperature inside it is still worthwhile, since the X-ray luminosity comes
mainly from this central part of the cluster (due to the n2 scaling of
.
Even if this
maximum extent radius is small, the study of the adiabat profiles behaviour
with temperature inside it is still worthwhile, since the X-ray luminosity comes
mainly from this central part of the cluster (due to the n2 scaling of
![]() ). These authors have rescaled their observed entropy profiles by a
factor
T-1(1+z)2, removing the effect of system mass and of the
evolution of the mean density of the universe. They found that the scaled
adiabat profiles normalisations do not coincide, the less massive systems
having higher
scaled entropy profiles (see their Fig. 4), although the profiles
themselves are similar. However, this particular
scaling does not take into account the physical processes that change the
adiabat normalisation with mass. What we have shown in this paper is that
the adiabat profiles of groups and clusters should be rescaled (i.e., divided) by the quantity:
). These authors have rescaled their observed entropy profiles by a
factor
T-1(1+z)2, removing the effect of system mass and of the
evolution of the mean density of the universe. They found that the scaled
adiabat profiles normalisations do not coincide, the less massive systems
having higher
scaled entropy profiles (see their Fig. 4), although the profiles
themselves are similar. However, this particular
scaling does not take into account the physical processes that change the
adiabat normalisation with mass. What we have shown in this paper is that
the adiabat profiles of groups and clusters should be rescaled (i.e., divided) by the quantity:
Using the best-fit ![]() model for the gas density and the best-fit linear
ramp for the temperature profile, we reproduced their adiabat profiles, and
rescaled them individually by the quantity in
Eq. (67). Then we grouped the systems by temperature and
computed the mean scaled profile, as in Lloyd-Davies et al. (2000). The scaled profiles
are displayed in the upper panel of Fig. 7.3
(we used the same line styles as Lloyd-Davies et al. 2000). The profiles now lie on top
of each other, i.e., their normalisation does not depend on the
system temperature
(as opposed to the result of the scaling in Lloyd-Davies et al. 2000). To confirm this, one can do the same scaling with the central
adiabat values (at
model for the gas density and the best-fit linear
ramp for the temperature profile, we reproduced their adiabat profiles, and
rescaled them individually by the quantity in
Eq. (67). Then we grouped the systems by temperature and
computed the mean scaled profile, as in Lloyd-Davies et al. (2000). The scaled profiles
are displayed in the upper panel of Fig. 7.3
(we used the same line styles as Lloyd-Davies et al. 2000). The profiles now lie on top
of each other, i.e., their normalisation does not depend on the
system temperature
(as opposed to the result of the scaling in Lloyd-Davies et al. 2000). To confirm this, one can do the same scaling with the central
adiabat values (at
![]() ), which is shown in the bottom panel
of Fig. 7.3. Instead of finding an excess for
), which is shown in the bottom panel
of Fig. 7.3. Instead of finding an excess for
![]() as in the Fig. 5 of Lloyd-Davies et al. (2000), we find now that all the
systems lie on the same central adiabat symbolised by the dashed line and
giving directly the value of K0 in our model (i.e.,
as in the Fig. 5 of Lloyd-Davies et al. (2000), we find now that all the
systems lie on the same central adiabat symbolised by the dashed line and
giving directly the value of K0 in our model (i.e.,
![]() ). The slight dispersion can be attributed to the assumption
that the observation time equals the formation time of a system. This clearly
means that our whole approach of taking into account not only hydrodynamic
shocks but also an entropy floor established before them is valid and
describes appropriately the dynamics of formation of clusters and groups.
). The slight dispersion can be attributed to the assumption
that the observation time equals the formation time of a system. This clearly
means that our whole approach of taking into account not only hydrodynamic
shocks but also an entropy floor established before them is valid and
describes appropriately the dynamics of formation of clusters and groups.
But, the main point of this rescaling is that, without changing the adiabat
profiles shape, it allows us to compare them more directly. From the upper
panel of Fig. 7.3, it is obvious that the four profiles
are very similar between
![]() (the mean cooling-flow radius,
inside which entropy loss is achieved by cooling) and the outer radius. This
means that our assumption of scaled self-similar adiabat profiles is indeed
right, at least in the core of the systems. This explains why our slope and
normalisation work so well for the
(the mean cooling-flow radius,
inside which entropy loss is achieved by cooling) and the outer radius. This
means that our assumption of scaled self-similar adiabat profiles is indeed
right, at least in the core of the systems. This explains why our slope and
normalisation work so well for the
![]() and y0-T relations, which put
more weight on the core of the systems. It also enlights the fact that our
shape factor for the gas mass is less accurate, since most of the mass lies
at large radius where the self-similarity assumption breaks down (see
Appendix C).
and y0-T relations, which put
more weight on the core of the systems. It also enlights the fact that our
shape factor for the gas mass is less accurate, since most of the mass lies
at large radius where the self-similarity assumption breaks down (see
Appendix C).
First of all, let us remind the reader that, unlike most of the current
models of cluster and group equilibrium, we do not predict the density
and temperature profiles. Instead, we are interested in integrated
quantities as the luminosity. As such, our model has not the predictive power
of some others, but allows us to find analytic expressions for these
integrated quantities. In particular, since we assume isothermality and
self-similarity of the adiabat profiles, the density profiles do not change
with mean temperature (e.g., no evolution of ![]() with T), as
Ponman et al. (1999)'s analysis would suggest. The satisfying results we obtain show
first that the key point is the appropriate modeling of the competition
between shocks and an pre-existing entropy floor. Second, this means as well
that the prediction of integrated quantities is not very sensitive to the
precise knowledge of the profiles and/or that our assumptions are not far
from reality (it is known
with T), as
Ponman et al. (1999)'s analysis would suggest. The satisfying results we obtain show
first that the key point is the appropriate modeling of the competition
between shocks and an pre-existing entropy floor. Second, this means as well
that the prediction of integrated quantities is not very sensitive to the
precise knowledge of the profiles and/or that our assumptions are not far
from reality (it is known ![]() evolves very slightly with temperature).
evolves very slightly with temperature).
We have compared most of our analytic results with predictions from
semi-analytic models and found good agreement (in particular for the trends
of the gas fraction with total mass and the SZ effect with temperature in low
temperature systems). Let us now compare the value of the entropy floor we
need to reproduce the curvature of the
![]() relation with values assumed
in other theoretical models of energy injection. Balogh et al. (1999) assume a
constant entropy injection value of
relation with values assumed
in other theoretical models of energy injection. Balogh et al. (1999) assume a
constant entropy injection value of ![]()
![]() and
Tozzi & Norman (2001)'s model needs a value in the range
and
Tozzi & Norman (2001)'s model needs a value in the range
![]() in order to steepen
in order to steepen
![]() .
These values, as noted by Lloyd-Davies et al. (2000),
are higher than the observed value, which are likely to be upper limits. On
the other hand, our model needs a value of
.
These values, as noted by Lloyd-Davies et al. (2000),
are higher than the observed value, which are likely to be upper limits. On
the other hand, our model needs a value of
![]() ,
well within the observational range of
,
well within the observational range of
![]() .
.
As we have indeed fitted this value to the observations, it may be
asked if we do not force in fact this agreement. The answer is clearly no,
as, first, the agreement of the K-T relation with the observations does not
guarantee that the same value of K0 will provide the a good description of
the other relations (both their shape, via the temperature at which the
self-similarity is broken, T0, and their normalisation) which range
from radio to X-ray data. Second, the other models reproduce as well the
K-T relation, together with the
![]() one
(at least Tozzi & Norman 2001's model is compared to these observations)
with the same high
value of the entropy floor. A lower value compatible with observations would
not fit this relation.
one
(at least Tozzi & Norman 2001's model is compared to these observations)
with the same high
value of the entropy floor. A lower value compatible with observations would
not fit this relation.
The main difference between our present work and these models is the fact that their low temperature systems are entirely isentropic i.e., no shocks occur at all in groups. This is the claimed approximation made by Balogh et al. (1999), who want to investigate a limiting model (which naturally fails also in the clusters' mass range). However, Tozzi & Norman (2001) model shocks and adiabatic infall, and it is not clear why shocks do not raise the adiabat profiles of their groups.
This clearly shows that shocks can not be completely
suppressed in groups unless an unacceptably high entropy floor is needed in
order to break the self-similarity in the
![]() relation. Our model takes
shocks and the entropy floor into account by construction both in clusters
and groups and is thus able to reproduce nicely all the X-ray correlations
with the observed value of K0.
relation. Our model takes
shocks and the entropy floor into account by construction both in clusters
and groups and is thus able to reproduce nicely all the X-ray correlations
with the observed value of K0.
Throughout this paper, we have shown that the adiabat constituted a "key
observable'' in the ICM, not only because it is a record of the thermodynamic
past history of diffuse baryons in groups and clusters, but also because it
allowed us to derive for the first time unifying analytic expression
for the slope and normalisation of observed correlations of groups and
clusters in X-rays and SZ. We have thus derived analytic expressions and
their normalisation for the
![]() ,
,
![]() ,
,
![]() ,
y0-T and
,
y0-T and
![]() correlations (for the latter, two limiting expressions have been
provided in the case of groups and of clusters respectively). The
Appendix A summarises these correlations and gives the
corresponding numerical values of their normalisations. We will conclude by
discussing some applications of the model.
correlations (for the latter, two limiting expressions have been
provided in the case of groups and of clusters respectively). The
Appendix A summarises these correlations and gives the
corresponding numerical values of their normalisations. We will conclude by
discussing some applications of the model.
Clusters of galaxies, and in particular their baryonic content observed
through its X-ray emission, have often been used to provide cosmological
constraints (Perrenod 1980; Kaiser 1986, Oukbir et al. 1997; Blanchard et al. 2000, and references therein). These studies have shown that the
cluster population can provide tight constraints, but have also revealed two
problems (apart from purely statistical problems due to large error bars of
e.g., the temperature in high-redshift clusters): first, the
difficulty to model the luminosity in a cluster, mostly due to the fact that
it depends on the core properties, whose formation is still
uncertain. Second, the small available number of rich clusters, in particular
at high redshift, which precludes yet a reliable use of these
tests![]() .
.
We think that the present work, together with the new generation of X-ray
observatories, can alleviate both of these problems. First, our model
of the cluster luminosity does rely on the physical processes being at work
during the formation of a cluster, and not on an hypothetical density
profile. Therefore, the luminosity does not depend on an arbitrary core
radius and is thus more reliable than previous attempts
(in particular, we don't have to assume anything on the core radius evolution like
e.g., Romer et al. 2001). Second, we extend the analytic relations to the
groups mass scale, taking into account the competition between an external
entropy floor and hydrodynamic shocks (thus recovering the curvature of the
![]() relation) and make predictions for other properties of groups. This
is useful since the group population is thought (in a hierarchical structure
formation cosmology) to be much larger than rich clusters. However, its
redshift evolution has never been used to constrain cosmology, partly because
of the lack of reliable data and partly because no analytic model of the
groups baryonic properties was available (extrapolating the cluster baryonic
properties was obviously wrong, as the recent observations show). The first
problem will be solved, at least locally, by Chandra and especially
XMM-Newton. Our model provides an attempt to solve the second problem. Of
course, groups will certainly be much more dispersed than clusters (because
the entropy injection will have more effect on them, and any spatial
variation of this injection level will affect the properties of a given
group), but the number of groups detected will be large: Romer et al. (2001)
have estimated that more than 100 clusters with
relation) and make predictions for other properties of groups. This
is useful since the group population is thought (in a hierarchical structure
formation cosmology) to be much larger than rich clusters. However, its
redshift evolution has never been used to constrain cosmology, partly because
of the lack of reliable data and partly because no analytic model of the
groups baryonic properties was available (extrapolating the cluster baryonic
properties was obviously wrong, as the recent observations show). The first
problem will be solved, at least locally, by Chandra and especially
XMM-Newton. Our model provides an attempt to solve the second problem. Of
course, groups will certainly be much more dispersed than clusters (because
the entropy injection will have more effect on them, and any spatial
variation of this injection level will affect the properties of a given
group), but the number of groups detected will be large: Romer et al. (2001)
have estimated that more than 100 clusters with
![]() will be
detected in a serendipitous survey for z<0.2 (irrespective of the
cosmology), a number 10 times higher than for cluster with
will be
detected in a serendipitous survey for z<0.2 (irrespective of the
cosmology), a number 10 times higher than for cluster with
![]() and 50 times highers than for
and 50 times highers than for
![]() for a survey surface of
for a survey surface of
![]()
![]() .
The number of groups with
.
The number of groups with
![]() will
obviously be superior, certainly not by a factor 10 because of the reduced
size and steepening of the
will
obviously be superior, certainly not by a factor 10 because of the reduced
size and steepening of the
![]() relation, but at least by a factor of a
few. This number of well observed groups (together with pointed observations)
will allow an unprecedent local calibration of the group ensemble
properties. Using our model, it will be possible to use groups and clusters
to constrain cosmology and the cluster LF, TF and
relation, but at least by a factor of a
few. This number of well observed groups (together with pointed observations)
will allow an unprecedent local calibration of the group ensemble
properties. Using our model, it will be possible to use groups and clusters
to constrain cosmology and the cluster LF, TF and
![]() evolution to add
further constraints. Moreover, groups will provide useful constraints on the
total amount of reheating the present universe underwent and its redshift
evolution if high redshift groups are available (see Sect. 7).
evolution to add
further constraints. Moreover, groups will provide useful constraints on the
total amount of reheating the present universe underwent and its redshift
evolution if high redshift groups are available (see Sect. 7).
Acknowledgements
We are deeply grateful to Romain Teyssier whose critical reading improved significantly the quality of an earlier draft of this paper. S. Dos Santos aknowledges also very enlightening discussions with G. C. Stewart. The quality and clarity of this paper was also greatly enhanced thanks to the comments of A. Evrard, G. Mamon, T. Ponman and P. Tozzi. Useful comments from F. R. Bouchet and Y. Mellier are also gratefully aknowleged.
We first describe one relation (external to the model and independent from
it), the M-T relation, that we used to relate the virial radius to
the temperature. Then, we write the different
correlations presented in this work, namely
![]() ,
,
![]() ,
,
![]() ,
y0-T and
,
y0-T and
![]() .
.
This relation is crucial, in that it allows us to relate the virial radius
(where the shock is assumed to take place) with the temperature of the
system, via the definition of M in terms of ![]() .
The simulation results
of (Evrard et al. 1996) are frequently used for mass-temperature scaling, but they
seem to provide systematically a higher normalisation than the observed one,
whatever the method used to measure M
(Nevalainen et al. 2000 and references therein). We used the observational results of Nevalainen et al. (2000),
derived from observed density and temperature profile, because their sample,
although small, goes all the way from groups to clusters. These authors give
the M-T relation at different scaled radii, from r2000 to r500(where
.
The simulation results
of (Evrard et al. 1996) are frequently used for mass-temperature scaling, but they
seem to provide systematically a higher normalisation than the observed one,
whatever the method used to measure M
(Nevalainen et al. 2000 and references therein). We used the observational results of Nevalainen et al. (2000),
derived from observed density and temperature profile, because their sample,
although small, goes all the way from groups to clusters. These authors give
the M-T relation at different scaled radii, from r2000 to r500(where ![]() is the radius whose mean interior density is
is the radius whose mean interior density is ![]() times
the critical density). Since Evrard et al. (1996) have shown that, inside a radius
r500, the baryonic gas is in hydrostatic equilibrium to a very good
approximation and that hydrostatic masses measured within this radius should
be reliable, we choose this radius to normalise the M-T relation. Moreover,
while at smaller radius Nevalainen et al. (2000) find that the M-T relation is
significantly steeper (
times
the critical density). Since Evrard et al. (1996) have shown that, inside a radius
r500, the baryonic gas is in hydrostatic equilibrium to a very good
approximation and that hydrostatic masses measured within this radius should
be reliable, we choose this radius to normalise the M-T relation. Moreover,
while at smaller radius Nevalainen et al. (2000) find that the M-T relation is
significantly steeper (![]() confidence at r1000) than the
self-similar prediction (
confidence at r1000) than the
self-similar prediction (
![]() ), the slope they measure at
r500 is consistent with 3/2 (
), the slope they measure at
r500 is consistent with 3/2 (
![]() ,
but note that the best
fit has a slope of 1.84)
,
but note that the best
fit has a slope of 1.84)![]() . We thus used throughout the paper the
following relation:
. We thus used throughout the paper the
following relation:
Finally, let us state that introducing a steeper slope for the M-T relation is straightforward within the physical scheme we used in this work, but does not change much the predicted relations gathered in this appendix and their agreement with observations. Since we wanted to discuss the generic effect of shocks and preheating, the same effects which are thought to steepen the M-Trelation, we found natural to keep a self-similar scaling.
We now compute the different normalisations given in
Eqs. (38), (43), (46),
(55) and (62). For this purpose, we will use the values
of M*, T* and ![]() from the
last section. The critical density is defined as usual as:
from the
last section. The critical density is defined as usual as:
Finally, we take for T0 the value computed from K0 in the
Sect. 2.3.2 i.e.,
![]() and the values of
the shape factors
and the values of
the shape factors ![]() ,
,
![]() and
and ![]() computed in Appendix
C. Therefore, the only adjusted quantity used to produce
these relations is K0, which was fitted to the data of Helsdon & Ponman (2000) in
Sect. 2.3.3 to find
computed in Appendix
C. Therefore, the only adjusted quantity used to produce
these relations is K0, which was fitted to the data of Helsdon & Ponman (2000) in
Sect. 2.3.3 to find
![]() .
Once this
quantity was fixed by comparison with the central entropy observations,
no renormalisation of the following relations is allowed.
All the numbers are computed here at z=0, but it is easy, within a given
cosmology, to extend the formulae in the text to higher redshift (note that
the value of K0(z) must be assumed as well). The analytic correlations
found are then
.
Once this
quantity was fixed by comparison with the central entropy observations,
no renormalisation of the following relations is allowed.
All the numbers are computed here at z=0, but it is easy, within a given
cosmology, to extend the formulae in the text to higher redshift (note that
the value of K0(z) must be assumed as well). The analytic correlations
found are then
![\begin{displaymath}L_{\rm X} = 5.643 \times 10^{42} \, T^5 \left[ 1 + \frac{T}{T_0}
\right]^{-3} \, h^{-2}_{2/3} \, \, \rm erg \, \, s^{-1}
\end{displaymath}](/articles/aa/full/2002/08/aah2972/img252.gif) |
(A.4) |
![\begin{displaymath}M_{\rm ICM} = 2.405 \times 10^{12} \, T^3 \left[ 1 + \frac{T}{T_0} \right]^{-3/2} \,
h^{-2}_{2/3} \, \, M_\odot
\end{displaymath}](/articles/aa/full/2002/08/aah2972/img254.gif) |
(A.5) |
![\begin{displaymath}f_{\rm gas} = 0.0792 \, T^{3/2} \left[ 1 + \frac{T}{T_0} \right]^{-3/2} \,
h^{-1}_{2/3}
\end{displaymath}](/articles/aa/full/2002/08/aah2972/img256.gif) |
(A.6) |
![\begin{displaymath}y_0 = 3.506 \times 10^{-6} \, T^3 \left[ 1 + \frac{T}{T_0} \right]^{-3/2} \,
h^{-2/3}_{2/3} \:,
\end{displaymath}](/articles/aa/full/2002/08/aah2972/img257.gif) |
(A.7) |
![$\displaystyle \Delta T(0) = -1.914\times 10^{-2} \, T^3 \left[ 1 + \frac{T}{T_0} \right]^{-3/2}
h^{-2/3}_{2/3} \, \rm mK.$](/articles/aa/full/2002/08/aah2972/img259.gif) |
(A.8) |
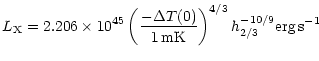 |
(A.9) |
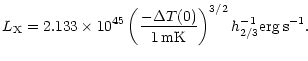 |
(A.10) |
We will then compare our result to hydrodynamic simulations, which will validate the use of the analytic expression found in the groups mass range.
Let's assume that the gas inflow is stationary. In a spherical collapse
model, the gas is assumed to be at rest at a radius
![]() (the so-called
"turn-around radius'') before falling into the cluster potential. Since the
gas will not be subjected to many processes changing its internal energy during
this inflow, we can assume that the flow is isentropic. Thus, applying
the Bernouilli equation between
(the so-called
"turn-around radius'') before falling into the cluster potential. Since the
gas will not be subjected to many processes changing its internal energy during
this inflow, we can assume that the flow is isentropic. Thus, applying
the Bernouilli equation between
![]() and
and ![]() (just before the
shock) we obtain (see e.g. Landau & Lifshitz 1959):
(just before the
shock) we obtain (see e.g. Landau & Lifshitz 1959):
![\begin{displaymath}v_1^2 = -2 \phi_{\rm v} \left[ 1 - \frac{\phi_{\rm ta}}{\phi_...
...left(\frac{\rho_{\rm ta}}{\rho_1}\right)^{2/3}\right)\right] .
\end{displaymath}](/articles/aa/full/2002/08/aah2972/img272.gif) |
(B.2) |
We can thus write:
![\begin{displaymath}v_1^2 = -2 \phi_{\rm v} \left[ 1 - \frac{\phi_{\rm ta}}{\phi_{\rm v}} + \frac{c_{\rm p}}{4}
\frac{T_1}{\phi_{\rm v}} \right] .
\end{displaymath}](/articles/aa/full/2002/08/aah2972/img273.gif) |
(B.3) |
We have thus:
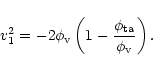 |
(B.4) |
Note that the established fact that the square of the infall velocity is
proportionnal to the
gravitational potential, both taken at the virial radius, is actually
not a surprise. Indeed, before the shock, the gas is thought to follow
the dark matter evolution, its velocity being equal to the dark matter
one up to the virial radius (see for example the Fig. 15 of Frenk et al. 1999). Since it has been shown that the dark matter infall velocity in a
spherical model scales as M1/3, while the mean potential
![]() scales as M2/3 (Ryu & Kang 1997, based on the work of
Bertschinger 1985), it is thus natural that
scales as M2/3 (Ryu & Kang 1997, based on the work of
Bertschinger 1985), it is thus natural that
![]() .
.
We now look for a useful expression for
![]() without assuming any
particular analytic expression for
without assuming any
particular analytic expression for
![]() .
First, since the
Poisson equation states:
.
First, since the
Poisson equation states:
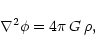 |
(B.6) |
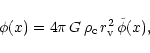 |
(B.7) |
An even more practical form for Eq. (B.8) does involve the
(supposed isothermal) ICM temperature T. It is achievable through the use
of the virial theorem. It indeed provides us with general relations between
![]() and M-T in the following form:
and M-T in the following form:
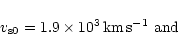
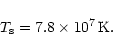
The normalisations of the three relations cited above are defined in
Eqs. (38), (42) and (54), where the
temperature is in keV. The temperature at which the normalisation must be
evaluated is obtained by equating the temperature shape function in each of
these relations to 1. This is illustrated in Fig. C.1, which
shows the following functions (the last two ones being the same):
![\begin{displaymath}L_{\rm X}(T) = \frac{T^5}{\left[ 1 + T/T_0\right]^3} \, \, \, {\rm (solid
\, \, line)}
\end{displaymath}](/articles/aa/full/2002/08/aah2972/img303.gif)
![\begin{displaymath}y(T) = \frac{T^3}{\left[ 1 + T/T_0\right]^{3/2}} \, \, \, {\rm (dashed
\, \, line)}
\end{displaymath}](/articles/aa/full/2002/08/aah2972/img304.gif)
![\begin{displaymath}M_{\rm ICM}(T) = \frac{T^{3}}{\left[ 1 + T/T_0\right]^{3/2}} \, \, \,
{\rm (dashed \, \, line),}
\end{displaymath}](/articles/aa/full/2002/08/aah2972/img305.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{norm.ps}
\end{figure}](/articles/aa/full/2002/08/aah2972/Timg307.gif) |
Figure C.1:
Normalisation temperature of the
|
Groups have a low surface brightness in X-rays and are thus difficult to
observe up to their virial radius. Obtaining a temperature profile at this
radius is obviously even more challenging. While the new generation of X-ray
satellites (Chandra and XMM-Newton in particular with its exceptional
sensitivity) is expected to produce constraints on low density regions,
ROSAT (whose energy band was perfectly adapted to the groups
observation) has provided data mostly on the inner parts of these systems
(see e.g., Helsdon & Ponman 2000). Nevertheless, David et al. (1996) have
published adiabat profiles for two cool clusters (
![]() )
nearly reaching the virial radius (as well as for even cooler groups, see
their Fig. 10), using a
)
nearly reaching the virial radius (as well as for even cooler groups, see
their Fig. 10), using a ![]() model for the density and the best-fit
power-law model for the temperature (despite large error bars). They found a
isentropic core, followed by a very modest increase compared to clusters
(where the virial value of the adiabat is at least 20 times higher than the
core value).
model for the density and the best-fit
power-law model for the temperature (despite large error bars). They found a
isentropic core, followed by a very modest increase compared to clusters
(where the virial value of the adiabat is at least 20 times higher than the
core value).
This can be easily understood, if one recalls that groups are thought to
accrete most of their gas adiabatically, and should thus have constant
adiabat profiles (Balogh et al. 1999; Tozzi & Norman 2001). However, this produces unacceptably
large temperature gradients in small groups and the quasi-absence of the
cooling-flow phenomenon, except in the largest clusters
(Tozzi & Norman 2001, see their Figs. 4c and 7b). It shows that somewhere between the center and
the virial radius, shocks must increase somewhat the adiabat, in order to
lower the temperature gradient, giving rise to an adiabatic inner core (much
larger than the core radius) followed by a modestly increasing adiabat
profile![]() .
.
One can seek an analytic expression for the adiabat profile by making use of
the isothermal ![]() model (Cavaliere & Fusco-Femiano 1976). Suppose that the gas density
profile is describe by this model i.e.,
model (Cavaliere & Fusco-Femiano 1976). Suppose that the gas density
profile is describe by this model i.e.,
![\begin{displaymath}n(x) = n_0 \left[1+\left(\frac{x}{x_0}\right)^2\right]^{-3\beta/2} \:,
\end{displaymath}](/articles/aa/full/2002/08/aah2972/img310.gif) |
(C.1) |
The shape factor for the y-T relation is given by:
The shape factor for the
![]() relation is given by:
relation is given by:
| |
= | ![$\displaystyle \int_0^{0.8} \left[1+\left(\frac{x}{0.7}\right)^2\right]^{-3/4}$](/articles/aa/full/2002/08/aah2972/img324.gif) |
|
| 0.1136, |
The luminosity of a cluster is dominated by the core gas (since it scales
as the square of the density) and the SZ effect computed here is a central
value (taking into account the beam smearing effect), while the gas mass
depends mainly on the outer parts of the profile, where ourassumption of
self-similarity of the scaled adiabat profiles is more likely to break down
(see Sect. 7.3). This explains naturally why
the predictions for ![]() and
and
![]() are much more accurate than for
are much more accurate than for
![]() .
Nevertheless, we consider the agreement between the theoretical
values and the observed normalisations very satisfying.
The fact that with the same model for the adiabat profile we can predict the
correct normalisations of the cluster correlations in two very different
wavebands is obviously a sign of coherence of the whole scheme. Since the
shape factors are predicted, the only parameter of the model is the
central entropy in groups K0, which was fit to the observations of
central adiabat value.
.
Nevertheless, we consider the agreement between the theoretical
values and the observed normalisations very satisfying.
The fact that with the same model for the adiabat profile we can predict the
correct normalisations of the cluster correlations in two very different
wavebands is obviously a sign of coherence of the whole scheme. Since the
shape factors are predicted, the only parameter of the model is the
central entropy in groups K0, which was fit to the observations of
central adiabat value.