A&A 383, 338-351 (2002)
DOI: 10.1051/0004-6361:20011713

Quasi-linear theory of the Jeans instability
in disk-shaped galaxies

E. Griv1 - M. Gedalin1 - C. Yuan2


1 - Department of Physics, Ben-Gurion University of the Negev, PO Box 653, Beer-Sheva 84105, Israel
2 - Academia Sinica Institute of Astronomy and Astrophysics (ASIAA), PO Box 23, Taipei 106, Taiwan

Received 4 September 2001 / Accepted 29 November 2001

Abstract
We analyse the reaction between almost aperiodically growing Jeans-unstable gravity perturbations and stars of a rotating and spatially inhomogeneous disk of flat galaxies. A mathematical formalism in the approximation of weak turbulence (a quasi-linearization of the Boltzmann collisionless kinetic equation) is developed. A diffusion equation in configuration space is derived which describes the change in the main body of equilibrium distribution of stars. The distortion in phase space resulting from such a wave-star interaction is studied. The theory, applied to the Solar neighborhood, accounts for the observed Schwarzschild shape of the velocity ellipsoid, the increase in the random stellar velocities with age, and the essential radial migration of the Sun from its birth-place in the inner part of the Galaxy outwards during its lifetime.

Key words: galaxies: kinematics and dynamics - galaxies: structure - waves - instabilities


1 Introduction

The theory of spiral structure of rotationally supported galaxies has a long history, but, as we emphasize below, is not yet complete. Even though no definitive answer can be given at the present time, the majority of experts in the field is yielded to opinion that the study of the stability of collective vibrations in disk galaxies of stars is the first step towards an understanding of the phenomenon. This is because the bulk of the total optical mass in the Milky Way and other flat galaxies is in stars. Recent measurements of the local dynamical density by Hipparcos rule out any disk-shaped dark matter (Crézé et al. 1998). Hipparcos data indicate a moderate contribution of unseen matter to the local potential (Haywood et al. 1997). In addition, spiral arms are smoother in images of galaxies in the near IR (Rix & Zaritsky 1995) indicating that the old disk stars participate in the pattern. Therefore, the spiral structures are intimately connected with the stellar constituent of a galaxy. We regard spiral structure in most flattened galaxies of stars as a wave pattern, which does not remain stationary in a frame of reference rotating around the center of the galaxy at a proper speed, excited as a result of the Jeans instability of gravity perturbations (those produced by a bar or oval structure in a galactic center, a spontaneous spiral perturbation, and/or a companion galaxy). It is our purpose to extend the investigation by studying the nonlinear effects. The problem is formulated in the same way as in plasma kinetic theory.

In the Solar neighborhood the random velocity distribution function of stars with an age $t \gtrsim 10^8$ yr is close to a Schwarzschild distribution - a set of Gaussian distributions along each coordinate in velocity space, i.e., close to equilibrium along each coordinate (Binney & Tremaine 1987; Gilmore et al. 1990). In addition, older stellar populations have a higher velocity dispersion than younger ones (Mayor 1974; Wielen 1977; Strömgren 1987; Meusinger et al. 1991; Fuchs et al. 1994; Dehnen & Binney 1999). High-quality Hipparcos data for a complete sample of nearly $12\,000$ main-sequence and subgiant stars show that the velocity dispersion of a coeval group is found to increase with time (Binney et al. 2000). The latter means that an unknown mechanism increases the velocity dispersion of stars in the Galaxy's disk after they are born. It is argued that the increase in velocity dispersion (and the diffusion of stellar orbits in coordinate space) with time is predominantly a gradual process. Grivnev & Fridman (1990) have shown, by using the observed stellar velocities, that the random velocity distribution of youngest stars is close to a $\delta$-like one. As the age of stars of spectral types B5-A9 increases from $t \approx 5 \times 10^7$ yr to $t \approx 5 \times 10^8$ yr, the distribution functions of the residual velocities of stars along each coordinate in the momentum space approach a normal distribution. On the other hand, a simple calculation of the relaxation time of the local disk of the Galaxy due to pairwise star-star encounters brings the value $\sim$1014 yr (Chandrasekhar 1960; Binney & Tremaine 1987, p. 187), which considerably exceeds the lifetime of the universe. Thus, observations indicate that the local disk is well relaxed, so some form of scattering process is going on most likely in the form of collisionless processes.

During the years several mechanisms have been proposed to explain the growth of the velocity dispersion: encounters of stars with massive gaseous clouds (Spitzer & Schwarzschild 1951, 1953), heating of the galactic disk by transient spiral waves (Barbanis & Woltjer 1967), a systematic increase in the velocity dispersion of protostellar gas clouds as the region of space increases (Larson 1979; Myers 1983), heating by proposed black holes in the Galactic dark halo (Lacey & Ostriker 1985) or by dwarf galaxies (Quinn & Goodman 1986). To date, a convincing mechanism to explain the observed amount of the disk heating has not been found. For instance, it is difficult to explain the observed relaxation by the usual binary encouters between stars and giant molecular clouds. This is because Binney & Lacey (1988) have shown that binary encounters with giant clouds of an interstellar medium result in a stellar velocity dispersion which will increase with age as t1/4, instead of the observed roughly $c_{\rm r} \propto t^{1/2}$ law (Wielen 1977). Also, if only giant molecular clouds are responsible for heating the ratio of the vertical-to-radial velocity dispersion $c_z/c_{\rm r}$will approach 0.75 and, if spiral structure also contributes to the disk heating the ratio will be lower. The most accurate measurements using the Hipparcos data indicate a ratio $c_z/c_{\rm r}$ of $0.53 \pm 0.07$ (Dehnen & Binney 1999). This behaviour is again consistent with the predictions of disk-heating by spiral structure. Scattering by giant molecular clouds plays only a modest role (Binney & Tremaine 1987, p. 470; Gilmore et al. 1990, p. 174; Binney 2001)[*].

In this paper a statistical mechanism of smoothing out stellar plane velocities, necessary to make them agree with a Schwarzschild distribution is suggested. This mechanism explains the observable increase in stellar velocity dispersion with age. In our approach, collisionless relaxation by virtue of interaction between Jeans-unstable density waves and stars does play a determining role in the evolution of stellar populations of the Galactic disk. In this regard, recent data from the Hipparcos satellite already made it clear that the Galaxy is by no means in a steady state (Dehnen & Binney 1999; Binney 2001). There are preliminary indications that we see in the local phase-space distribution the dynamical footprints of long-dissolved unstable waves.

The classical Jeans instability of gravity disturbances is one of the most frequent and most important instabilities in the stellar and in the planetary cosmogony, and galactic dynamics. The instability is driven by a strong interaction of the gravity fluctuations with the bulk of the particle population, and the dynamics of Jeans perturbations can be characterized as a fluidlike interaction. The gravitational Jeans-type instability does not depend on the behavior of the particle distribution function in the neighborhood of a particular speed, but the determining factors of the instability are macroscopic parameters like the random velocity spread, mean density, and angular velocity of regular rotation. The Jeans instability associated with departures of macroscopic quantities from the thermodynamic equilibrium is hydrodynamical in nature and has nothing to do with any explicit resonant effects; a relatively simple hydrodynamical model can be used to investigate the instability (Lovelace & Hohlfeld 1978; Lin & Lau 1979; Drury 1980).

The criterion for a rotationally flattened stellar disk to be Jeans-unstable to substructure formation by self-gravitation is that Toomre's (1964) stability parameter Q be less than $Q_{{\rm crit}} = 2$-2.5 (see Sect. 3.3 below). Here Toomre's Q-value, $Q = c_{\rm r}/ c_{{\rm T}}$, is a measure of the ratio of thermal and rotational stabilization to self-gravitation, $c_{\rm r}$ is the radial dispersion of residual (random) velocities of stars, $c_{{\rm T}} \approx 3.4 G \sigma_0 / \kappa$ is the Toomre (Toomre 1964; see also Safronov 1960) critical velocity dispersion, $\sigma_0$ is the local projected surface density of stars, and $\kappa$is the local epicyclic frequency. Combined with the Lin-Shu type dispersion relation for density waves, this is a venerable suggestion as to why disk galaxies almost always exhibit spiral structure.

The reaction of the distribution function of stars to the Jeans-unstable field fluctuations is such that the random velocity dispersion (or "temperature'') increases until the difference $Q - Q_{{\rm crit}} \rightarrow 0$, and the system tends toward marginal stability. Hence, in differentially rotating galaxies, once the entire disk has been heated to values $Q \approx Q_{{\rm crit}}$, no further spiral waves can be sustained by virtue of the Jeans instability - unless some "cooling'' mechanism is available leading to Toomre's Q-value, under approximately 2. By using N-body simulations, first Miller et al. (1970), Hohl (1971), and then Sellwood & Carlberg (1984), Tomley et al. (1991), and Griv & Chiueh (1998) have shown that the process of formation of fresh particles, which move on nearly circular orbits, plays a vital role in prolonging spiral activity in the plane of the disk by reducing the random velocity dispersion of the entire stellar component. Also, in good conformity with observations (van der Kruit & Freeman 1986; Bottema 1993) and the theory outlined above, both N-body simulations (Sellwood & Carlberg 1984; Tomley et al. 1991) and numerical solutions of the collisionless Boltzmann equation (Nishida et al. 1984) showed that the stability number Q of Toomre in relaxed equilibrium disks does not fall below a critical value, which lies about 2-2.5. Liverts et al. (2000) used computer simulations to test the validity of the modified stability criterion $Q_{{\rm crit}}$.

The investigations carried out in the linear approximation allow us to determine only the spectrum of the excited oscillations and their growth rates during the first stages of the excitation. Arbitrary perturbations can be expressed as a superposition of eigenmodes, with each eigenmode evolving independently. Other problems, which can be treated within the framework of nonlinear theory, are account of the reaction of the oscillations on the equilibrium parameters of the system and the determination of the amplitude of the oscillations that are produced. The quasi-linear approach to nonlinear plasma theory is usually referred to as the theory of weak turbulence, i.e., the case when the dynamics of the system can be described in the language of weakly interacting linear waves. That is, there are many random collective oscillations present in the system and it is permissible to treat the phases of these oscillations as being random in some sense. It can be justified if the energy in the excited spectrum is small compared with the total mechanical energy in particles but large compared to thermal noise. The theory of strong turbulence is still far from complete.

As applied to the fluidlike Jeans instabilities connected with a "thermodynamic nonuniformity'' of the stellar disk (the system is not sufficiently "hot'' in the equatorial plane), the nonlinear effects appear in the following fashion. The velocity dispersion of a young stellar population is small, and their space and velocity distribution are not completely relaxed. As the result of the reaction of the oscillations, the velocity dispersion of the main part of the distribution function of young stars would be expected to increase in the field of unstable waves with an amplitude increasing with time. Because the Jeans instability is characterized by the critical value of velocity dispersion $c_{{\rm crit}} = c_{{\rm T}} Q_{{\rm crit}}$, the rise in temperature in turn leads to a decrease in the growth rate of the wave amplitude. Eventually, as a result of such "heating'', the Jeans instability will be switched off and finally the spiral cannot be maintained (Binney & Tremaine 1987, p. 479). This process of the self-suppression of instability by the growing wave amplitude is reminiscent of the nonresonant relaxation in a plasma, which can effectively heat the medium even in the absence of collisions between particles (Alexandrov et al. 1984, p. 420; Krall & Trivelpiece 1986, p. 520). Apparently, Toomre (1964, p. 1237) first advanced the idea that the stars in the galactic disk would tend to develop random motion from the gravitational energy via this tendency toward gravitational instability. In addition, the nonlinear relaxation causes the diffusion of stars in coordinate space, that is, mass re-distribution. Romeo (1990) already discussed the role played by instabilities in the disk's secular evolution. The collective relaxation of stars may be done by their interaction with the gravitational field of unstable waves, solely. In interaction with standing waves, with the exception of spatially small resonant regions, there is no energy exchange in the wave-star system (Binney & Tremaine 1987, p. 482).

At the qualitative level, Goldreich & Lynden-Bell (1965) and Marochnik (1968) have suggested instabilities as a cause of enhanced relaxation in galaxies. Lynden-Bell (1967) and later Shu (1978) considered the problem of the collisionless relaxation in a vigorously nonstationary process of formation of the equilibrium state. A very nonequilibrium initially configuration was studied (the virial theorem is strongly violated). Kulsrud (1972) also discussed the inverse effects of different instabilities of gravity oscillations on the averaged velocity distribution function of stars by collective interaction. It was stated that, because of its long-range Newtonian forces, a self-gravitating medium (a stellar "gas'', say) would possess collective motions in which all the particles of the system participate. These properties would be manifested in the behavior of small gravity perturbations arising against the equilibrium background. Collective processes are completely analogous to two-body collisions, except that one particle collides not with another one but with many which are collected together by some coherent process such as a wave. The collective processes are random, and usually much stronger than the ordinary two-body collisions and leads to a random walk of the particles that takes the complete system toward thermal quasi-steady state. Thus, relaxation in stellar systems could occur without binary star-star enconters through the influence of collective motions of the stellar gas upon the particle distribution.

Barbanis & Woltjer (1967) studied almost circular orbits of stars of a rotating galaxy in the gravitational field of spiral arms on the basis of both epicyclic theory (see also Binney & Tremaine 1987, p. 478) and numerical integration of the equations of motion. Lynden-Bell & Kalnajs (1972) treated the resonant regions separately. Carlberg & Sellwood (1985) re-derived Dekker's (1975) basic equation governing the response of a rotating stellar disk to any transient-perturbing potential, and then calculated numerically the resonant response to a model slowly-varying wave in the vanishing growth rate limit. Binney & Lacey (1988), Jenkins & Binney (1990), and Jenkins (1992) developed a formalism to describe a heating of the local disk due to gravitational scattering by an imposed weak, time-varying perturbing potential. They showed that such a heating process could be described by a diffusion equation in action space and solved the diffusion equation by Monte Carlo simulation for cloud and spiral wave scatterers. Although all of these studies showed that the disk perturbations affect the dynamical evolution significantly, they focused mainly on a test particle responce to a given field of waves having adopted the model form for spiral perturbation and assumptions as to the typical wavelength, etc. of the spiral waves (Carlberg & Sellwood 1985, p. 81; Jenkins 1992, p. 623). The exact velocity dependence of the velocity diffusion tensor, and the resultant evolution in velocity space, were not completely pinned down.

We present a self-consistent quasi-linear theory of dynamical relaxation of two-dimensional self-gravitating, rotating stellar disks toward a thermal quasi-steady state via collective effects. In the process a star "collides'' with almost aperiodically growing inhomogeneities of a galactic gravitational field which result from the development of the fierce Jeans instability. The dominant interactions, which change the velocities and orbits of stars, are those with transient, rapidly-varying gravity perturbations. We find that the theory successfully accounts for several basic observations of the Galaxy, given that the growth rate of the perturbations is comparable to the epicyclic period of stars. In particular, we find that the off-resonant character of the interaction leads to a velocity diffusion tensor that is independent of velocity, and leads to an anisotropic Maxwellian distribution whose velocity dispersion grows with time. Nonlinear effects near resonances in a Jeans-stable system deserve separate research (e.g., Rauch & Tremaine 1996). To emphasize it again, unlike Carlberg & Sellwood (1985), Binney & Jenkins (1988), and Jenkins & Binney (1990) we solve a self-consistent Boltzmann-Poisson system of equations. The relaxation mechanism suggested in the present paper has an essential dependence on the equilibrium of the disk matter, and it has nothing to do with Lynden-Bell's violent relaxation. Brief first reports have been published by Griv et al. (1994) and Griv et al. (2001).

2 Basic equations

A thin rotating disk is taken as a model of the flat galaxy in many papers for analysis of the gravity perturbations. This is because stars of the nonrotating spherical-like subsystem, if it exists at all, which have large random velocities, will make a relatively small contribution to the wave field (Marochnik & Suchkov 1969)[*]. In the spirit of Griv & Peter (1996a), we solve the system of the collisionless Boltzmann equation and the Poisson equation describing the motion of a self-gravitating ensemble of stars in such a system within an accuracy of up two orders of magnitude with respect to small parameters $1/\vert k_{\rm r}\vert r$ and $c_{\rm r}/r\Omega$ for radial wavenumber $k_{\rm r}$, radius r, and angular velocity $\Omega$, looking for waves which propagate in a two-dimensional galactic disk. This approximation of an infinitesimally thin disk is a valid approximation if one considers perturbations with a radial wavelength $\lambda = 2\pi /k_{\rm r}$ that is greater h, the typical disk thickness. In actual spiral galaxies for a subsystem of young, low-dispersion stars, $h \approx 200$ pc. The dimensionless parameters $1/\vert k_{\rm r}\vert r$ and $c_{\rm r}/r\Omega$ are small, and in addition $1/\vert k_{\rm r}\vert r \sim c_{\rm r} /r\Omega$. The fact is took into account that because of the nature of the gravitational force, disks of spiral galaxies are always spatially inhomogeneous and are far from uniform rotation.

2.1 Boltzmann and Poisson equations

We assume that the stars move in the disk plane so that vz=0. This allows us to use the two-dimensional distribution function $f(r,\varphi,v_{\rm r},v_\varphi,t)$ such that $\tilde{f}=f \delta(z) \delta (v_z)$, $f=\int \tilde{f}{\rm d}z{\rm d}v_z$, and $\int f{\rm d}v_{\rm r}{\rm d}v_\varphi =\sigma$, where $\sigma (\vec{r},t)$ is the surface density. In the rotating frame of a disk galaxy, the local distribution function of stars $f (\vec{r},\vec{v},t)$ must satisfy the collisionless Boltzmann equation (Lin et al. 1969)

 
$\displaystyle \frac{\partial f}{\partial t} + v_{\rm r} \frac{\partial f}{\part... ...ial \Phi}{\partial \varphi} \right) \frac{\partial f}{\partial v_\varphi} = 0 ,$     (1)

where the total azimuthal velocity of the stars was represented as a sum of $v_\varphi$ and the basic circular velocity $r \Omega$. Here $v_{\rm r}$ and $v_\varphi$ are the residual velocities in the radial and azimuthal directions, and r and $\varphi$ are the galactocentric cylindrical coordinates. As a rule, in spiral galaxies  $\vert v_{\rm r}\vert$ and $\vert v_\varphi\vert \ll r \Omega$. In Eq. (1), $\Phi (\vec{r},t)$ is the total gravitational potential determined self-consistently from the Poisson equation $\Delta \Phi = 4 \pi G \sigma \delta (z)$.

As the equilibrium state an axisymmetric, weakly inhomogeneous in the radial direction stellar disk is adopted. The system in the equlibrium is described by the equation:

 \begin{displaymath}v_{\rm r} \frac{\partial f_{{\rm e}}}{\partial r} + \left( 2... ...right) \frac{\partial f_{{\rm e}}} {\partial v_\varphi} = 0\ \end{displaymath} (2)

or $\partial f_{{\rm e}}/\partial t=0$, and the angular velocity of rotation $\Omega (r)$ at a distance rfrom the center is such that the necessary centrifugal acceleration is exactly provided by the central gravitational force, $r\Omega^2 = \partial \Phi_{{\rm e}}/\partial r$. In these equations, $f_{{\rm e}} (r,\vec{v})$ and $\Phi_{{\rm e}} (r)$ are the equilibrium distribution function and the gravitational potential.

In the quasi-linear theory, one may follow the procedure of linearization by writing $f=f_0 (r,\vec{v},t) + f_1 (\vec{r},\vec{v},t)$ and $\Phi =\Phi_0(r,t)+\Phi_1(\vec{r},t)$ with $\vert f_1/f_0\vert \ll 1$ and $\vert\Phi_1 /\Phi_0\vert \ll 1$ for all $\vec{r}$ and t. The functions f1 and $\Phi_1$ are functions oscillating rapidly in space and time, while the functions f0 and $\Phi_0$ describe the slowly developing "background'' against which small perturbations develop; $f_0(t=0) \equiv f_{{\rm e}}$ and $\Phi_0(t=0) \equiv \Phi_{{\rm e}}$. Linearizing Eq. (1) and separating fast and slow varying variables one obtains the equation for the fast developing distribution function

 \begin{displaymath}\frac{{\rm d} f_1}{{\rm d}t} = \frac{\partial \Phi_1}{\partia... ...}{\partial \varphi} \frac{\partial f_0}{\partial v_\varphi} , \end{displaymath} (3)

where ${\rm d}/{\rm d}t$ means total derivative along the star orbit and f0 is a given equilibrium distribution function determined from Eq. (2). The equation for the slow part of the distribution function is

 \begin{displaymath}\frac{\partial f_0}{\partial t}={\Big\langle} \frac{\partial ... ...rphi} \frac{\partial f_1}{\partial v_\varphi} {\Big\rangle} , \end{displaymath} (4)

where $\langle \cdots \rangle$ denotes a time average.

2.2 Equilibrium distribution

Making use of expressions for the unperturbed epicyclic trajectories of stars in the equilibrium central field $\Phi_{{\rm e}}$,

 
r$\textstyle =r_0+\frac{v_\perp}{\kappa} \left[ \sin \phi_0 - \sin (\phi_0 - \kappa t) \right] , u_{\rm r} ={\rm d}r/{\rm d}t ,$    
$\displaystyle \varphi$$\textstyle = \Omega t + \frac{2\Omega}{\kappa} \frac{v_\perp}{r \kappa} \left[ ... ...kappa t) -\cos \phi_0 \right] , u_\varphi = r \frac{{\rm d}\varphi}{{\rm d}t} ,$   (5)

where $v_\perp$, $\phi_0$ are constants of integration, $v_\perp /\kappa r \approx \rho /r\ll~1$, and $\rho \sim v_\perp /\kappa$is the mean epicyclic radius, we can choose the Schwarzschild (the anisotropic Maxwellian) distribution function $f_0 (r,\vert\vec{v}\vert,t=0)$ satisfying the unperturbed part of the kinetic equation, that is, Eq. (2)[*]. In Eqs. (5), $u_{\rm r}$ and $u_\varphi$ are the components of the star's velocity relative to the disk center. To integrate Eq. (3) over t, we need to determine the components of the star's velocity at each point relative to the local standard of rest:
 
$\displaystyle v_{\rm r} = u_{\rm r} = v_\perp \cos (\phi_0 - \kappa t) ,$      
$\displaystyle v_\varphi = u_\varphi - r\Omega \approx (\kappa/2\Omega) v_\perp \sin (\phi_0 - \kappa t)$     (6)

(Spitzer & Schwarzschild 1953). As is seen, the motion of a star in the disk of a rotating galaxy is represented as in epicyclic motion along the small Hipparchus epicycle with a simultaneous circulation of the epicenter about the galactic center. The problem of epicyclic motion in its most general form is equivalent to the problem of the motion of a charged particle in a given electromagnetic field, in which the solution can be decomposed into the guiding center motion and the epicyclic motion. The epicycle radius is analogous to the gyroradius in a plasma (Marochnik 1966). The Schwarzschild distribution function, which is a function of the two epicyclic constants of motion $v_\perp^2 /2$ and $r_0^2 \Omega (r_0)$, has been given by Shu (1970):

 \begin{displaymath}f_0 = \frac{2\Omega (r_0)}{\kappa (r_0)} \frac{\sigma_0 (r_0)... ...p \left[ - \frac{v_\perp^2}{2c_{\rm r}^2 (r_0)} \right] \cdot \end{displaymath} (7)

In Eq. (7), r0 is the radius of the circular orbit, which is chosen so that the constant of areas for this circular orbit $r_0^2 \dot{\varphi}_0$ is equal to the angular momentum integral $r^2 \dot{\varphi}$, $v_\perp^2 = v_{\rm r}^2 +(2\Omega/\kappa)^2 v_\varphi^2$, $\dot{\varphi}_0^2 \equiv \Omega^2 (r_0)=(1/r_0)(\partial \Phi_0 /\partial r)_0$, and $\Omega$ as well as $\kappa$ and and $c_{\rm r}$ are evaluated at r0. In the equation above the fact is used that in a rotating reference frame the radial velocity dispersion $c_{\rm r}$ and the azimuthal velocity dispersion $c_\varphi$ are not independent but connected through (Eqs. (6)) $c_{\rm r} \approx (2\Omega / \kappa) c_\varphi$. In the Solar vicinity a velocity distribution of the early O and B stars with ages $t < (5-7) \times 10^7$ yr is almost the spherical Maxwellian distribution with the velocity dispersion near 8 kms-1 (Grivnev & Fridman 1990). Such a distribution function f0(t=0) for the unperturbed system is particularly important because it fits observations for all stars in the Galaxy (Shu 1970). It is this metaequilibrium that is examined for stability.

The partial derivatives in Eqs. (3) and (4) transform as follows (Shu 1970; Morozov 1980; Griv & Peter 1996a):

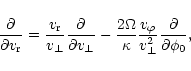\begin{displaymath}\frac{\partial}{\partial v_{\rm r}} = \frac{v_{\rm r}}{v_\per... ...ac{v_\varphi}{v_\perp^2} \frac{\partial}{\partial \phi_0} ,\\ \end{displaymath} (8)


 \begin{displaymath}\frac{\partial}{\partial v_\varphi} \approx \left( \frac{2\O... ...c{v_{\rm r}}{v_\perp^2} \frac{\partial}{\partial \phi_0}\cdot \end{displaymath} (9)

3 Linear theory

To determine oscillation spectra, let us consider the stability problem in the lowest (or local) WKB approximation; this is accurate for short wave perturbations only, but qualitatively correct even for perturbations with a longer wavelength, of the order of the disk radius R. In galaxies, $R \approx 15$ kpc. In the local WKB approximation in Eqs. (3) and (4), assuming the weakly inhomogeneous disk, the perturbation of equilibrium parameters is selected in the form of a plane wave (in the circular rotating frame) $\aleph_1 (\vec{r},t)=0.5\sum_{\vec{k}} \aleph_{\vec{k}} \left( {\rm e}^{ik_{\rm r} r +im\varphi -i\omega_* t} + {\rm c. \, c.} \right)$, where $\aleph_{\vec{k}}$ is an amplitude that is a constant in space and time, m is the nonnegative azimuthal mode number (= number of spiral arms), $\omega_* =\omega - m\Omega$ is the Doppler-shifted complex wavefrequency, $\omega_{*,\vec{k}} = \Re \omega_{*,\vec{k}} + i\Im \omega_{*,\vec{k}}$, $\vert k_{\rm r}\vert R \gg 1$, suffixes $\vec{k}$ denote the $\vec{k}$th Fourier component, and ${\rm c. \, c.}$ means the complex conjugate. In the local WKB approximation it is assumed that the wave vector and the wavefrequency vary continuously. By utilizing the more accurate nonlocal WKB approximation, it may be shown that in fact the characteristic oscillation frequencies of an inhomogeneous disk must be quantized, i.e., must pass through a discrete series of values. In galaxies, discrete spiral modes were already found in stellar population by Rix & Zaritsky (1995), Zaritsky & Rix (1997), Rudnick & Rix (1998), and Block & Puerari (1999). In the near-infrared, the morphology of older star-dominated disk indicates a simple classification scheme: the dominant Fourier m-mode. Fridman et al. (1998) and Burlak et al. (2000) detected m=1-9 spiral modes in relatively young stellar population of the nearly face-on galaxies from observations in the H$_\alpha$ line. A ubiquity of low-m (m=1-4) modes was confirmed. In the linear theory, one can select one of the Fourier harmonics: 0.5 [ $\aleph_{\vec{k}} \exp ( ik_{\rm r} r+im\varphi - i\omega t) + {\rm c.} \, {\rm c.}]$. The solution in such a form represents a spiral wave with m arms.

3.1 Perturbed distribution function

Using the transformation of the partial derivatives $\partial / \partial v_{\rm r}$ and $\partial / \partial v_\varphi$ given by Eqs. (9), the solution of the linearized kinetic Eq. (3) may be written immediately:

 \begin{displaymath}f_1 = \int_{-\infty}^t {\rm d} t^\prime \left( \frac{\vec{v}_... ...}{\partial \varphi} \frac{\partial f_0}{\partial r} \right) , \end{displaymath} (10)

where f0 is given by Eq. (7), and $f_1 (t \to -\infty) =0$, so by considering only growing perturbations we neglected the effects of the initial conditions. Paralleling the analysis leading to Eq. (13) of Griv & Peter (1996a), from Eq. (10) it is straightforward to show that
 
$\displaystyle f_1 = \Phi_1 \left[ \frac{\kappa}{v_\perp} \frac{\partial f_0}{\p... ... e}^{i(n-l)(\phi_0-\zeta)} J_l (\chi) J_n (\chi)}{\omega_* - l\kappa} \right] ,$     (11)

where $J_l (\chi)$ is the Bessel function of the first kind, $\chi = k_* v_\perp /\kappa$, $\tan \zeta = (2\Omega/\kappa) \tan \psi$, and $k_*=k\{ 1+[(2\Omega/\kappa )^2 - 1] \sin^2 \psi \}^{1/2}$ is the effective wavenumber. In Eq. (11) the denominators vanish when $\omega_* - l\kappa =0$. This occurs near corotation and other resonances. The Lindblad resonances occur at radii where the field $(\partial/ \partial \vec{r}) \Phi_1$ resonates approximately with the harmonics l=-1 (inner resonance) and l=1 (outer resonance) of the epicyclic (radial) frequency of equilibrium oscillations of stars $\kappa$. Clearly, the location of these resonances depends on the rotation curve and the spiral pattern speed $\Re \omega_* /m$; the higher the m value, the closer in radius the resonances are located (Lin et al. 1969). The corotation resonance occurs at a radius where l=0 in Eq. (11). Resonances are places where linearized equations describing the motion of particles do not apply. In the vicinity of the resonances it is necessary to use nonlinear equations, or to include terms of higher orders into the approximate form of the equations. The former approach was adopted by Contopoulos (1979) and the latter one was adopted by Griv et al. (2000a,b).

3.2 Generalized dispersion relation

Integrating Eq. (11) over velocity space and equating the result to the perturbed surface density given by the improved solution of the Poisson equation $\sigma_1 = - \vert k\vert \Phi_1 /2\pi G$ (Lin & Lau 1979; Griv & Peter 1996a), the generalized dispersion relation may easily be obtained

 \begin{displaymath}\frac{k^2c_{\rm r}^2}{2\pi G\sigma_0\vert k\vert}=\kappa \sum... ...\infty}^\infty \frac{{\rm e}^{-x}I_l(x)}{\omega_* -l\kappa} , \end{displaymath} (12)

where $\kappa \sim 2\Omega$, $\omega_* \ne l \kappa$, $x = k_*^2 c_{\rm r}^2/\kappa^2 \approx k_*^2 \rho^2$, $\rho = c_{\rm r} / \kappa$ is now the mean epicyclic radius, and Il (x) is the Bessel function of imaginary argument. In the second term on the right-hand side, $\vert L\vert \approx \left \vert\partial \ln (2\Omega \sigma_0 /\kappa c_{\rm r}^2) /\partial r \right\vert^{-1}$ is the radial scale of a spatial inhomogeneity, and in the local WKB approximation $\rho^2 / r\vert L\vert \ll 1$. The dispersion relation (12) connects the frequency of excited oscillations $\omega_*$ with the wavenumber $\vec{k}$ for every $\vec{r}$ and describes the ordered behavior of a medium near its equilibrium state.

The asymptotic expansion of the Bessel function Il (x) in the short-wavelength limit, $x \approx k_*^2 \rho^2 \gg 1$ (the case of epicyclic radius that is large compared with wavelength):

 \begin{displaymath}I_l (x) \simeq \frac{{\rm e}^x}{\sqrt{2 \pi x}} \left[ 1 + O \left( \frac{1}{x} \right) \right] . \end{displaymath} (13)

In the opposite long-wavelength limit, $x \approx k_*^2 \rho^2 \mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{... ...r{\offinterlineskip\halign{\hfil$\scriptscriptstyle ...:

 \begin{displaymath}I_l (x) = \sum_{n=0}^\infty \left( \frac{x}{2} \right)^{l+2n} \frac{1}{n \mbox{!} (n+l) \mbox{!} } \cdot \end{displaymath} (14)

In the later limit the epicyclic radius is small (or comparable to) compared with wavelength.

In Eq. (12), the functions $\Lambda_l (x) ={\rm e}^{-x} I_l (x)$ appear commonly in a theoretical treatment of Maxwellian plasmas in a magnetic field. It is instructive to note: (a) $0 \leq \Lambda_l (x) \leq 1$; (b) $\Lambda_0 (x)$ decreases monotonically from $\Lambda_0 (0)=1$; and (c) $\Lambda_l (x)$ for $l\ne 0$ start from $\Lambda_l (0)=0$, reach maxima, and then decrease.

Equation (12) replaces the standard Lin-Shu dispersion relation (Lin & Shu 1966; Lin et al. 1969; Shu 1970), to take into account all terms up to 2 orders in small parameters $\rho /r$ and $1/\vert k_{\rm r}\vert r$. Also, the terms $\propto L^{-1}$ were omitted in Toomre (1964), Lin & Shu (1966), Lin et al. (1969), Shu (1970), Mark (1977), Lynden-Bell & Kalnajs (1972) studies. The main difference from the original Lin-Shu dispersion relation is in the factor $\psi \ne 0$, which makes the generalized dispersion relation to be correct even in the regime of open perturbations (see Griv & Peter 1996a for a discussion). Actually, Lin & Shu (1966), Lin et al. (1969), Shu (1970), and Mark (1977) allowed for a departure from axial symmetry of the perturbations only partially by introducing a Doppler-shifted in a rotating reference frame wavefrequency $\omega_* =\omega - m\Omega$but omitting all other m and $\psi$-dependent terms in Eq. (12), on the grounds that they were interested in almost axisymmetric perturbations. Therefore, in fact these authors as well as Toomre (1964) obtained a criterion for an instability of axisymmetric perturbations of the Jeans kind only - the widely used Toomre critical radial velocity dispersion. It says nothing about the stability of Jeans modes which are not tightly wound, particularly the dominant open instabilities of the differentially rotating disks. The effects of the azimuthal forces have been analyzed by Lin & Lau (1979) by adopting the hydrodynamical model. Important conclusions were obtained about the enhanced amplification of nonaxisymmetric density waves in a differentially rotating system (Bertin & Mark 1978; Lin & Lau 1979; Bertin 1980). The free kinetic energy associated with the differential rotation of the system under study is one possible source for the growth of the energy of these spiral perturbations, and appears to be released when angular momentum is transferred outward.

In disk-shaped galaxies, $L \sim ({\rm d}\ln \sigma_0 /{\rm d}r)^{-1} < 0$. In the Solar vicinity of the Galaxy the value of the radial scale length |L| is about 3 kpc, which is a typical value for the radial scale length of the exponential component of the disk when compared with external galaxies of similar morphological types (Porcel et al. 1998).

The dispersion relation (12) is valid for relatively open spirals throughout a weakly inhomogeneous disk excluding resonance zones[*]. The existence of solutions of Eq. (12) $\omega_* = \omega_* (k_*)$ with $\Re \omega_* \ne 0$, $\vert\Im \omega_* / \Re \omega_*\vert \ll 1$, and $\Im \omega_* > 0$ implies oscillating instability, while the solutions with $\Re \omega_* \ne 0$ and $\Im \omega_* < 0$ describe the absorption of waves. The solutions with $\Im \omega_* = 0$ and $\Re \omega_* \ne 0$ describe the natural (harmonic) oscillations, and the solutions with $\Im \omega_* > 0$, $\vert\Im \omega_* / \Re \omega_*\vert \gg 1$describe the Jeans instability. The quantity $\Omega_{{\rm p}} = \Re \omega_* /m$characterizes the rate of rigid-body rotation of the wave pattern.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{figure-first.eps}\end{figure} Figure 1: The generalized Lin-Shu dispersion relation of a homogeneous ( $\vert L\vert \rightarrow \infty $) stellar disk in the case $2\Omega / \kappa = \sqrt {2}$ and $\vert\sin \psi\vert = 1$ for the different Toomre's Q-values: a) $Q=0.5 (2 \Omega / \kappa )$, b) $Q=0.8 (2 \Omega / \kappa )$, c) $Q=2 \Omega / \kappa $, and d) $Q=1.5 (2 \Omega / \kappa )$. The solid curves represent the real part of the dimensionless Doppler-shifted wavefrequency of low-frequency, $\vert\omega _*\vert < \kappa $, long-wavelength (1) and short-wavelength (2) Jeans oscillations we are interested in. The dashed curves represent the imaginary part of the dimensionless wavefrequency of low-frequency vibrations. The dot-dashed curves represent the wavefrequencies of additional high-frequency, $\vert\omega _*\vert > \kappa $, Jeans modes. Long-wavelength vibrations are the most unstable ones.
Open with DEXTER

(those with $k_*^2\rho^2 \protect\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hf... ...r{\offinterlineskip\halign{\hfil$\scriptscriptstyle ...)

A general impression of how the spectrum of nonaxisymmetric Jeans perturbations behaves in a homogeneous nonuniformly rotating disk can be gained from Fig. 1, which shows the dispersion curves in the cases of Jeans-unstable systems ((a) and (b)), a marginally Jeans-stable system (c), and a Jeans-stable one (d) for values of $l=0,\pm 1,\pm 2$, and $\pm 3$ (as determined on a computer from Eq. (12)). In this figure, the ordinate is the effective wavenumber k* measured in terms of the inverse epicyclic radius $\rho$and the abscissa is $\nu = \omega_*/\kappa$, i.e., the dimensionless angular frequency at which the stars meet with the pattern, measured in terms of the epicyclic frequency $\kappa$. In general, for fixed dimensionless wavefrequency $\omega_*/\kappa$there are two solutions in $k_* \rho$, comprising a long-wavelength wave, $k_* \rho \mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displa... ...r{\offinterlineskip\halign{\hfil$\scriptscriptstyle ..., and a short-wavelength wave, $k_*\rho > 1$. A property of the solution (12) is that in a homogeneous system the Jeans-stable modes those with $Q > 2 \Omega / \kappa$ are separated from each other by frequency intervals where there is no wave propagation: gaps occur between each harmonic (cf. the Bernstein modes in a magnetized plasma).

In summary, the generalized dispersion relation (12) can be explored to investigate detailed stability properties of an inhomogeneous stellar disk for the Schwarzschild distribution function $f_0 (r_0, v_\perp^2)$. In particular this relation can be applied to study the excitation of Jeans-unstable density waves. This problem has been studied by Morozov (1980, 1981a), Polyachenko (1989), Griv & Peter (1996a), Polyachenko & Polyachenko (1997), Griv et al. (1999). In Sect. 4 of the present paper, the problem is studied in the framework of the quasi-linear theory.

The generalized dispersion relation (12) is complicated: the basic dispersion relation above is highly nonlinear in the frequency $\omega_*$. Therefore, in order to deal with the most interesting oscillation types analytically, only various limiting cases of perturbations described by some simplified variations of dispersion relation may be considered.

3.3 Simplified dispersion relation

Let us first restrict ourselves to consideration of the principal part of a system between the inner and outer Lindblad resonances, $\vert l\vert\le 1$, by considering low-frequency perturbations with $\vert\omega_*\vert \mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfi... ...interlineskip\halign{\hfil$\scriptscriptstyle ... (which dispersion laws are given in Fig. 1 by curves 1 and 2). That is, $\vert\omega_*\vert$ less than the epicyclic frequency of any disk stars, and the consideration is limited to the transparency region between the turning points in a disk. In the opposite case of the high perturbation frequencies, $\vert\omega _*\vert > \kappa $, the effect of the disk rotation is negligible and therefore not relevant to us: in this "rotationless'' case the star motion is approximately rectilinear on the time and length scales of interest which are the wave growth/damping periods and wavelength (cf. Alexandrov et al. 1984, p. 110). Resonances of a higher order, $l=\pm 2, \pm 3, \dots$, are dynamically less important. Secondly, in Eq. (12) one can consider two asymptotic limits: the limit of long-wavelength perturbations, $x \mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle ..., and the opposite limit of short-wavelength perturbations, $x \gg 1$. Finally, we consider the weakly inhomogeneous system and the most important for the problem of spiral structure low-m perturbations: from now on in all equations $2 \Omega (m\rho^2 /rL) \ll 2 \Omega \sim \kappa$ and $m \sim 1$. Additionally, in the local version of the WKB method $\vert k_{\rm r}\vert^{-1} <\vert L\vert<r$. Therefore, in small terms proportional to L-1 we include only l=0 harmonics. As a result, from Eq. (12) the simplified dispersion relation reads

 \begin{displaymath}\omega_*^3 - \omega_* \omega_{{\rm J}}^2 + \Omega \kappa^2 \frac{m \rho^2}{rL} \frac{I_0 (x)}{I_1 (x)} = 0 , \end{displaymath} (15)

where the squared Jeans frequency is given by

 \begin{displaymath}\omega_{{\rm J}}^2 \approx \kappa^2 -2\pi G \sigma_0 \vert k\vert F(x) . \end{displaymath} (16)

In Eq. (16), $F \approx 2 \kappa^2 {\rm e}^{-x} I_1 (x)/k^2 c_{\rm r}^2$is the so-called reduction factor, which takes into account the fact that the wave field only weakly affects the stars with high peculiar velocities. Thus, Lin-Shu density waves or local gravity perturbations disturb essentially only the dynamically cold ( $c_{\rm r} < 20-25$ kms-1) stellar subpopulations. Making use of expansions (13) and (14), we can use the following asymptotic forms of the reduction factor. In the long-wavelength limit

\begin{displaymath}F (x) \approx (k_* / k)^2 [1-x+(3/4)x^2] \quad \mbox{and} \qu... ...halign{\hfil$\scriptscriptstyle ...

and in the opposite short-wavelength limit

\begin{displaymath}F (x) \approx (1 / k \rho)^2 [1 - (1/2\pi x)^{1/2}] \quad \mbox{and} \quad k \rho > 1 , \, x > 1 . \end{displaymath}

Analyzing the dispersion relation (15), it is useful to distinguish between the cases of axisymmetric (m=0) and nonaxisymmetric ($m \ne 0$) perturbations.

The resulting dispersion relation (15) is a third order equation with respect to $\omega_*$ with real coefficients, which describes three branches of oscillations: two Jeans branches (short-wavelength and long-wavelength ones) modified by the inhomogeneity, and an additional gradient branch. The frequency of the most important for the problem of disk's stability Jeans oscillations slightly modified by the inhomogeneity gradient in the frequency range

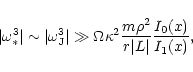
\begin{displaymath}\vert\omega_*^3\vert \sim \vert\omega_{{\rm J}}^3\vert \gg \O... ...a^2 \frac{m \rho^2}{r\vert L\vert} \frac{I_0 (x)}{I_1 (x)} , \end{displaymath}

is determined from Eq. (15):

 \begin{displaymath}\omega_{*1,2}\approx \pm p\vert\omega_{{\rm J}}\vert-\Omega \... ...{{\rm J}}^2} \frac{m \rho^2}{rL} \frac{I_0 (x)}{I_1 (x)}\cdot \end{displaymath} (17)

In Eq. (17), p=1 for Jeans-stable $(\omega_{{\rm J}}^2 > 0)$ perturbations and p=i for Jeans-unstable $(\omega_{{\rm J}}^2<0)$ perturbations, the term involving L-1 is the small correction, and in general $\vert\omega_{{\rm J}}\vert \sim \Omega$. This is qualitatively similar to the original dispersion relation of Lin & Shu (1966), Lin et al. (1969), and Shu (1970) in that $\omega_{*1,2}^2 \rightarrow \kappa^2$ in the high wavenumber limit as well as at zero wavenumber. Accordingly, a spatial inhomogeneity will not influence the stability condition of Jeans modes. In the gravitationally stable system ( $\omega_{{\rm J}}^2 > 0$) the Jeans oscillations are the natural ones ( $\Re \omega_{1,2} \ne 0$ and $\Im \omega_{*1,2} = 0$). In the gravitationally unstable disk ( $\omega_{{\rm J}}^2 < 0$) they grow almost aperiodically: in the unstable range $\Im \omega_{*1,2} > 0$, $\Re \omega_* \propto L^{-1}$, and $\vert\Im \omega_{*1,2} / \Re \omega_{*1,2}\vert \gg 1$. A very important feature of the instability under consideration is the fact that it is almost aperiodic (the real part of the wavefrequency almost vanishes in a rotating reference frame we are using).

The Jeans perturbations can be stabilized by the random velocity spread. Indeed, if one recalls that such unstable perturbations are possible only when $\omega_{* 1,2}^2 \approx \omega_{{\rm J}}^2 < 0$, then by using the condition $\omega_{{\rm J}}^2 \ge 0$ for all possible k, from Eq. (15) the stability criterion to suppress the instability of all Jeans perturbations can be obtained. At the limit of gravitational stability, the two conditions $\partial \omega_{{\rm J}}^2/\partial k=0$ and $\omega_{{\rm J}}^2 \ge 0$ are fulfilled. The first condition determines the most unstable Jeans wavelength $\lambda_{{\rm crit}} \approx (4\pi \Omega /\kappa)(c_{\rm r} /\kappa) = (4\pi \Omega /\kappa) \rho$, corresponding to the minimum on the dispersion curve $\omega_* = \omega_* (k_*)$. In the Solar vicinity for the subsystem of young, low-dispersion stars, $\lambda_{{\rm crit}} \approx 2$ kpc.[*] Interestingly, from observations in the Galaxy, the distance between spiral arms is also $\lambda \approx 2$ kpc. So, the radial scale of the perturbations is small, $\lambda_{{\rm crit}} \ll R$.

Use of the second condition determines the marginal radial velocity dispersion for the stability of arbitrary but not only axisymmetric perturbations:

 \begin{displaymath}c_{\rm r} \ge c_{{\rm crit}}\approx \frac{2\Omega}{\kappa}c_{... ... \Big\vert \frac{c_{\rm r}}{\kappa L} \Big\vert^{2/3} \right] \end{displaymath} (18)

or

\begin{displaymath}Q \ge Q_{{\rm crit}} = (2\Omega/\kappa)[1+(c_{\rm r}/\kappa \vert L\vert) ^{2/3}] , \end{displaymath}

respectively, where $c_{\rm r}/\kappa \vert L\vert\approx \rho/\vert L\vert < 1$. In galaxies, $Q_{{\rm crit}} = 2{-}2.5$. Equation (18) improves the Toomre stability criterion by including a destabilizing effect resulting from shear $\propto {\rm d}\Omega/{\rm d}r$, azimuthal forces $\propto m$, and spatial inhomogeneity $\propto L$. Morozov (1981b) took into account the additional weak stabilizing effect resulting from the small thickness of the disk. Bertin & Romeo (1988) estimated the destabilizing effect of a cold interstellar material. According to Polyachenko (1989) and Polyachenko & Polyachenko (1997) the marginal stability condition for Jeans perturbations of an arbitrary degree of axial asymmetry has been available since 1965 (Goldreich & Lynden-Bell 1965), though in a slightly masked form. In general, the growth rate of Jeans modes is large,

 \begin{displaymath}\Im \omega_{*1,2} \approx \Im \omega_{{\rm J}} \sim \sqrt{2\pi G \sigma_0 \vert k\vert F (x)} \sim \Omega , \end{displaymath} (19)

and depends on the azimuthal mode number. The instability develops on the dynamical time scale, $\sim$ $ \Omega^{-1}$. To repeat ourselves, N-body simulations have already indicated the same behavior of the numerical models: the azimuthal gravitational forces and the azimuthal dependence of the radial forces maintain the rapidly developing (on a time scale of single revolution) spiral density wave structure in a nonuniformly rotating disk, which was initially stable at each point only with respect to axisymmetric Jeans perturbations (Miller et al. 1970; Hohl 1971; Quirk 1972; Sellwood & Carlberg 1984; Griv et al. 1999).
  \begin{figure} \par\includegraphics[width=8.8cm,clip]{figure-second.eps}\end{figure} Figure 2: The growth rate of the Jeans instability of a homogeneous stellar disk (arbitrary units) in the case $2\Omega / \kappa = \sqrt {2}$, r0=8, $\vert k_{\rm r}\vert=1$, $\rho =1$, and $\vert\sin \psi\vert = 1$ for the different values of the azimuthal mode number m. The growth rates have maxima with respect to the critical mode number $m_{{\rm crit}} \sim 1$.
Open with DEXTER

The growth rate of the Jeans instability as determined on a computer from the expression $\sqrt{2\pi G\sigma_0 \vert k\vert F(x)}$ is shown in Fig. 2. As one can see visually in this figure, the growth rates have maxima with respect to $m_{{\rm crit}} \sim 1$. It means that of all harmonics of initial perturbation, one perturbation with the maximum of the growth rate $\sim \Omega$ and with $m=m_{{\rm crit}} \sim 1$ will be formed asymptotically in time. The low-m spiral modes (m < 10) are more unstable than the radial one (m=0) and the high-m ones ( $m \mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle ...). These low-m spiral modes are only important in the problem of galactic spiral structure because in contrast to the high-m modes, they do extend essentially over a large range of the galactic disk (Lin et al. 1969; Shu 1970). Interestingly, the study of the azimuthal structure of the stellar disk of 18 face-on spiral galaxies, using $K^\prime$-band photometry, shows that most of them exhibit lopsided (m=1) or two-armed structures (Rix & Zaritsky 1995). Fourier analysis of the spiral structure of the galaxy NGC 4254 already revealed the dominance of the m=1 component (Iye et al. 1982). It was stressed that theories of the origin of spiral structure of galaxies must explain the asymmetric structure of this galaxy without the help of spiral exciters such as tidal companions or a bar. About $20\%$ of all late-type spiral galaxies and 54 early-type disk galaxies have the strong m=1azimuthal component of the surface brightness in the near $\rm IR$-band and the R-band, confirming lopsidedness as a dynamical phenomenon (Zaritsky & Rix 1997; Rudnick & Rix 1998). A similar fraction of galaxies $\approx $ $30\%{-}50\%$ has lopsided H I distributions or kinematic asymmetries (Baldwin et al. 1980; Bosma 1981; Richter & Sancisi 1994; Swaters et al. 1999; Kornreich et al. 2000). In the single-arm galaxy NGC 4378 the spiral arm can be traced over most $1 \frac{1}{4}$ revolutions (Kormendy & Norman 1979). Disk ellipticity (m=2) may also be common (Andersen et al. 2001).

The shape and the number of spiral arms depend on the equilibrium parameters of a galaxy. For the Galaxy the most unstable pattern is that of 1-4 arms, the radial distance between the arms being about 2 kpc.

In the another frequency range, $\vert\omega_*\vert \ll \vert\omega_{{\rm J}}\vert$, Eq. (15) has another root, which describes the gradient, $L^{-1} \ne\,0$, branch of oscillations. The gradient perturbations are stable and are independent of the stability of Jeans modes (Griv & Peter 1996b). These low-frequency, $\vert\omega_{*3}\vert \ll \Omega$, oscillations are not important in dynamics of galaxies.

Although Eq. (15) can be analyzed directly and even solved analytically in the case $\vert l\vert\le 1$, graphical representation of the roots is much more convenient. A graphic method of solution of Eq. (15) is indicated in Fig. 3. It is seen in Fig. 3 how the usual Jeans oscillations with $\vert\omega_*\vert /\kappa \mathrel{\mathchoice {\vcenter{\offinterlineskip\hal... ...r{\offinterlineskip\halign{\hfil$\scriptscriptstyle ... as shown in Fig. 1 by curves 1 and 2 are deformed and the additional low-frequency $(\vert\Im \omega_{*3}\vert/\kappa \ll 1)$ gradient oscillations appear in an inhomogeneous disk.

  \begin{figure} \par\includegraphics[width=12cm,clip]{figure-third.eps}\end{figure} Figure 3: The behavior of the simplified dispersion relation of an inhomogeneous disk for reasonable galactic parameters L=-0.01, $2\Omega / \kappa = \sqrt {2}$, $\vert\sin \psi\vert = 1$ and for the different Toomre's Q-values (upper panels - $Q=0.5 (2 \Omega / \kappa )$ and lower panels - $Q=1.5 (2 \Omega / \kappa )$). Unlike in Fig. 1, only low-frequency modes are shown, |l| < 2 or $\vert\omega_* /\kappa\vert \protect\mathrel{\mathchoice {\vcenter{\offinterlin... ...r{\offinterlineskip\halign{\hfil$\scriptscriptstyle .... The solid curves represent the real part of the dimensionless Doppler-shifted Jeans wavefrequency (1 and 2) and the additional gradient frequency (3), and the dashed curves represent the imaginary part of the wavefrequency. A feature of this dispersion relation is the existence of the gradient branch of oscillations both in the case of the Jeans-unstable disk (panel c)) and in the case of the Jeans-stable one (panel f)). The gradient perturbations are stable, $\Im \omega_{*3} \protect\le 0$, and are low-frequency ones, $\vert\omega_{*3}\vert\protect\ll\Omega$.

4 Quasi-linear equations

We anticipate that the fluidlike Jeans-unstable oscillations must influence the distribution function of the main part of stars in such a way as to hinder the wave excitation, i.e., to increase the random velocity spread ultimately at the expense of circular motion or gravitational energy. This is because the Jeans instability, being essentially a gravitational one, tends to be stabilized by random motions of stars (Eqs. (16) and (17)). Therefore, along with the growth of the oscillation amplitude the velocity dispersion must increase, and finally in the disk there can be established a stationary distribution so that the Jeans-unstable perturbations are completely vanishing. Eventually the disk evolves toward a quasi-stationary, marginally Jeans-stable distribution. (In turn, the Jeans-stable perturbations are subject to a weak Landau-type oscillating instability; Griv et al. 2000a,b.)

Next, we substitute the solution (11) into Eq. (4) and average the latter over time. Taking into account that the terms $l \ne n$ vanish for axially symmetric functions f0, after averaging over $\phi_0$ we obtain the equation

 
$\displaystyle \frac{\partial f_0}{\partial t}$ = $\displaystyle i\frac{\pi}{2} \sum_{\vec{k}} \sum_{l=-\infty}^\infty {\cal{E}}_{... ...2(\chi)}{\omega_*-l\kappa} - \frac{l^2 J_l^2(\chi)}{\omega_*^*-l\kappa} \right]$  
  $\textstyle \;\times$ $\displaystyle \frac{\partial f_0}{\partial v_\perp} + i\frac{\pi}{2} \sum_{\bf ... ...}{\kappa^2} \frac{m}{r} \left[ \frac{J_l^2 (\chi)} {\omega_* - l\kappa} \right.$  
  $\textstyle \;-$ $\displaystyle \left. \frac{J_l^2 (\chi)} {\omega_*^* - l\kappa} \right] \frac{\partial f_0}{\partial r} ,$ (20)

where ${\cal{E}}_{\vec{k}}=\vert\Phi_{\vec{k}}\vert^2 \exp (2\Im \omega_* t)$and $\omega_*^*$ is the complex conjugate wavefrequency.

As usual in the quasi-linear theory, in order to close the system one must engage an equation for ${\cal{E}}_{\vec{k}}$. Averaging over the fast oscillations, we obtain

 \begin{displaymath}(\partial/\partial t) {\cal{E}}_{\vec{k}} =2\Im \omega_* {\cal{E}}_{\vec{k}} . \end{displaymath} (21)

Equations (20) and (21) form the closed system of quasi-linear equations for Jeans oscillations of the rotating inhomogeneous disk of stars, and describe a diffusion in velocity and coordinate space. The distortion of the wave packet due to the disk inhomogeneity is included through the second term on the right-hand side in Eq. (20). The spectrum of oscillations and their growth rate are given by Eqs. (12) and (19), respectively. In the Solar vicinity, $\Im \omega_{{\rm J}} \sim \Omega \approx 2 \times 10^{-8}$ yr-1. Equations (20) and (21) are clearly very approximate, since the local WKB, epicyclic, and weakly nonlinear approximations were used.

Two general physical conclusions can be deduced without solving Eq. (20). First, the initial distribution of stars will change upon time only under the action of growing perturbations ( $\Im \omega_* > 0$). Therefore, only transient, gravitationally unstable patterns heat the disk and cause star's guiding centers to diffuse radially[*]. Secondly, the distribution function of random velocities $\propto (\partial/\partial v_\perp)(\partial f_0 /\partial v_\perp)$ will change under the action of both the radial and the tangential forces (this is because in Eq. (20) $k_* \propto \sqrt{k_{\rm r}^2 + k_\varphi^2} \ne 0$). But the mean surface mass density (that is, star's guiding centers positions) $\propto (\partial / \partial r)(\partial f_0 / \partial r)$ will change under the action of only the azimuthal forces ($m \ne 0$): the requirement that $m \ne 0$ is required for shifts in guiding centers. Since the guiding center encodes angular momentum, this is merely a statement of angular-momentum conservation. As angular momentum is transferred outward, inner material falls to the center and outer material migrates outward (Lynden-Bell & Pringle 1974). Thus, the diffusion of star's guiding centers leads to the core-dominated mass density profile in rotating galaxies, together with the buildup of an extended outer envelope.

In the most important low-frequency limit, $\vert l\vert\le 1$, the function $\Lambda (x) = \exp (-x) I_1 (x)$ starts from $\Lambda (0)=0$, reaches a maximum $\Lambda_{{\rm max}}<1$at $x\approx 0.5$ (Figs. 1 and 3), and then decreases. Hence, the growth rate has a maximum at $x\approx 0.5<1$ (or $k_* = k_{{\rm crit}}\approx \kappa^2/4\pi \Omega c_{\rm r}$).

5 Astronomical implications

As an application of the quasi-linear theory we investigate the relaxation of low-frequency and Jeans-unstable ( $\vert\omega _*\vert < \kappa $ and $\omega_{{\rm J}}^2 < 0$, respectively) oscillations in the weakly inhomogeneous ( $\rho^2 / r\vert L\vert \ll 1$) disk of the Galaxy.

5.1 Dynamical evolution of the stellar disk

In the following, we restrict ourselves to the fastest growing long-wavelength, $\chi^2$ and $x^2 \ll 1$, and low-frequency, $\vert\omega_*\vert \mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfi... ...interlineskip\halign{\hfil$\scriptscriptstyle ... perturbations (see the explanation just at the end of Sect. 4 and Fig. 1). Then in Eqs. (12) and (20) one can use the expansions $J_0^2 (\chi) \approx 1$, $J_1^2 (\chi) = J_{-1}^2 (\chi) \approx \chi^2/4$ and e $^{-x} I_1 (x) \approx (1/2)x - (1/2)x^2 + (5/16)x^3$. Equation (20) takes the simple form

 \begin{displaymath}\frac{\partial f_0}{\partial t}-{\cal D}_{\rm v} \frac{\parti... ...2}-{\cal D}_{\rm r} \frac{\partial^2 f_0} {\partial r^2}=0 , \end{displaymath} (22)

where ${\cal D}_{\rm v} =(\pi/2\kappa^2) \sum_{\vec{k}}k_*^2 \Im \omega_* {\cal{E}}_{\vec{k}}$, ${\cal D}_{\rm r}=\pi \sum_{\vec{k}} m^2 {\cal{E}}_{\vec{k}}/\eta^2 \Im \omega_*$, both $\Im \omega_*$ and ${\cal{E}}_{\vec{k}}$ are functions of t, and we took into account the fact that in actual spiral galaxies with a flat rotation curve $2 \Omega /\kappa^2 \approx r/\eta$, where $\eta \sim \sqrt{(GM/r_0) \ln (r/r_0)}$ and M is a galaxy's mass. The term $\propto {\cal D}_{\rm r} (t)$ describes a diffusion of stellar guiding centers in coordinate space. As is seen, the velocity diffusion coefficient for stars ${\cal D}_{\rm v}(t)$ is independent of $\vec{v}_\perp$ (to lowest order). This is a qualitative result of the nonresonant character of the star's interaction with collective aggregates. Whereas Binney & Lacey (1988), Jenkins & Binney (1990), and Jenkins (1992) attributed the effect to some unspecified time behavior of the spiral density wave, we attribute the effect to the term resulting from wave growth of Jeans-unstable almost aperiodic perturbations. Hence we obtain a velocity diffusion coefficient that is independent of velocity $\vec{v}_\perp$, without any further assumptions. In addition, in actual spiral galaxies ${\cal D}_{\rm r}$ is independent of r. By contrast, Lynden-Bell & Kalnajs (1972) and Carlberg & Sellwood (1985) considered a model slowly-varying density wave in the vanishing growth rate limit, $\Im \omega_* \to 0$. Therefore, the density wave and the basic state stars could interact only at the limited radially wave-particle resonances.

An expression for f0 at $t \rightarrow \infty$ can be deduced from Eq. (22). We introduce the substitution ${\rm d}\tau / {\rm d}t = {\cal D}_{\rm v}(t)$, ${\rm d}/{\rm d}t=({\rm d}\tau/{\rm d}t) ({\rm d}/{\rm d}\tau)$. Then Eq. (22) can be re-written

 \begin{displaymath}\frac{\partial f_0}{\partial \tau} - \frac{\partial^2 f_0} {... ...rac{\partial {\cal D}_{\rm v}}{\partial \tau}=2\Im \omega_* . \end{displaymath} (23)

The particular solutions of the system (23) are

 \begin{displaymath}f_0(v_\perp,\tau)=\frac{{\rm const}}{\sqrt{\tau +c_{\rm r}^2/2}} \exp \left[ \frac{-v_\perp^2}{4(\tau +c_{\rm r}^2/2)}\right] \end{displaymath} (24)

and

 \begin{displaymath}f_0(r,\tau)\approx\frac{{\rm const}}{\sqrt{r_0^2+ ({\cal D}_{... ...\cal D}_{\rm r}/{\cal D}_{\rm v})\tau \right]} \right\} \cdot \end{displaymath} (25)

(The observations have taken into account that most spiral and S0 galaxies have an exponential disk with radial surface distribution of oldest stellar populations, $\sigma_0 \propto \exp [-(r/r_0)^2]$.) Accordingly, during the development of the Jeans instability, the Schwarzschild distribution of random velocities (i.e., Gaussian spread along $v_{\rm r}, v_\varphi$ coordinates in velocity space) is established. As the perturbation energy increases, the initial distribution spreads ( $f_0 (v_\perp^2)$ becomes less peaked), the effective temperature grows with time (i.e., Gaussian spread increases), and the effective velocity dispersion attains the value: $\langle v^2 \rangle =2\tau = 2\int {\cal D}_{\rm v}(t) {\rm d}t = (\pi /2\kappa^2) \sum_{\vec{k}} k_*^2 {\cal{E}}_{\vec{k}}$. The energy of the oscillation field $\sum_{\vec{k}} (k_*^2/\kappa^2) {\cal{E}}_{\vec{k}}$ thus plays the role of a "temperature'' T in the particle distribution. Subsequently, sufficient velocity dispersion prevents the Jeans instability from occuring. The diffusion in configuration space is due entirely to the growth of the Jeans-unstable modes in a self-gravitating collisionless system subject to a time-dependent potential.

This mechanism increases (a) the velocity dispersion of stars in the Galaxy's plane after they are born (Eq. (24)), and (b) the radial spread of the disk (Eq. (25)). The collisionless relaxation mimics thermal relaxation in a two-dimensional stellar disk, leading to Maxwell-Boltzmann type velocity distributions with an effective temperature that increases with time. To repeat ourselves, sufficient random velocity spread prevents the Jeans instability from occuring (Griv et al. 1994; Griv et al. 1999). The diffusion of the bulk of stars in configuration space takes place because they gain wave energy as the instability develops. The instability-induced diffusion, however, presumably tapers off as Jeans stability is approached: the radial velocity dispersion $c_{\rm r}$ becomes greater than the critical one $c_{{\rm crit}}$. Observations already convincingly indicated a secular dynamical evolution in spiral galaxies on the Hubble time scale or even smaller (Martinet 1995).

Thus, the true time scale for relaxation in the Galaxy may be much shorter than its standard value $\sim$1014 yr for the Chandrasekhar collisional relaxation; it may be of the order $(\Im \omega_{{\rm J}})^{-1} \mathrel{\mathchoice {\vcenter{\offinterlineskip\ha... ...ineskip\halign{\hfil$\scriptscriptstyle ... yr, i.e., comparable with 2-3 periods of the Galaxy rotation. This short relaxation time is in agreement with both observations (Binney & Tremaine 1987, p. 473; Grivnev & Fridman 1990) and N-body simulations (Hohl 1971; Morozov 1981a; Sellwood & Carlberg 1984; Tomley et al. 1991; Griv & Chiueh 1998).

5.2 Time evolution of the velocity dispersion

We have shown above that the squared plane velocity dispersion of stars increases with time t as

 \begin{displaymath}\langle v^2 \rangle \approx (\pi/2\kappa^2) k_*^2 {\cal{E}}_{\vec{k}} \propto \exp (\Im \omega_* t) , \end{displaymath} (26)

where k* and $\Im \omega_* \sim \Omega$ are the effective wavelength and the growth rate of the most unstable oscillations. For young stellar populations, say, with ages t < 109 yr, $\Im \omega_* t < 1$ and we see that heating by a Jeans-unstable density wave can produce the observed $\langle v^2 \rangle \propto t$ law for the age-velocity dispersion rate (Wielen 1977). However, over a long time span, the unstable mode itself would change its properties as the basic state evolves. That is, the wave-star interaction is a nonlinear process, which should take into account the fact that the wave field affects only weakly the stars with high peculiar velocities. Mathematically, this fact is expressed by the inverse dependence of the reduction factor F(x) in Eqs. (15) and (19) on the velocity dispersion: only the young stars, with their small velocity dispersion, are extremely sensitive to any gravity perturbation. Thus, we expect the decrease in the growth of unstable modes, and, consequently, the decrease in the growth of the velocity dispersion with age of stars, and the growth will not lead to $\langle v^2 \rangle > v^2_{{\rm obs}}$ in less than a Hubble time. Here $v_{{\rm obs}} \approx 40$km s-1 is the observed velocity dispersion of the oldest disk stars. The latter is consistent with the observed age-velocity correlation in the Galaxy which tapers off beyond a certain age $\sim$3 Gyr (Wielen 1977; Strömgren 1987; Haywood et al. 1997; Dehnen & Binney 1999; Binney 2001). This process of diffusion in phase-space, with the velocity distribution function scattering into a smoother and hotter distribution, lead naturally to definitions of young disk, of age less than about 1-2 Gyr, and old disk, of age older than about 3 Gyr.

One concludes that the proposed mechanism of wave-star interaction is able to account for both the shape of the velocity ellipsoid (the anisotropic Maxwellian, that is, Schwarzschild distribution) and the form of the age-velocity dispersion law in the plane of the Galaxy.

5.3 Velocity diffusion in the Solar vicinity

Transient spiral arms excite random motions parallel to the equatorial plane. According to Eq. (24), the heating efficiency of unstable density wave features depends on their spatial and temporal form. Let us evaluate the heating $\Delta v$ for a realistic model of the disk of the Galaxy in the Solar vicinity. In accordance with the theory as developed above, we consider the fastest growing mode with $k_* = k_{{\rm crit}} \approx \kappa^2/4\pi \Omega c_{\rm r} \approx \pi$ kpc-1 and $\Im \omega_* \approx \Omega$. According to observations, in the Solar vicinity ${\cal{E}}_{\vec{k}}/\Phi_0^2 \approx 10^{-3}$ (Lin et al. 1969; Yuan 1969), $\Phi_0 \approx 0.5 r_0^2 \Omega^2$, $r_0 \approx 8.5$ kpc, $c_{\rm r} (t=0) \approx 10$ kms-1, and $\kappa \approx 1.5 \Omega$. From Eq. (24), one obtains $\Delta v \approx \sqrt{{\cal D}_{\rm v} t} = 20{-}30$ kms-1, where t=109 yr. This value of $\Delta v$ is in agreement with both estimates based on the observed stellar velocities (Mayor 1974; Wielen 1977; Strömgren 1987; Meusinger et al. 1991; Grivnev & Fridman 1990; Dehnen & Binney 1999) and N-body simulations (Hohl 1971; Quirk 1972; Sellwood & Carlberg 1984; Tomley et al. 1991). Thus already in the first 4-5 galactic revolutions, in say about 109 yr, the stellar populations see their epicyclic energy vary by a factor of ten.

5.4 Migration of the Sun's guiding center

There is considerable scatter in the metallicities of stars that have a common guiding center and age. On the other hand, it is widely believed that all interstellar material at a given time and radius has a common metallicity. The paradox can be resolved if one assumes that these stars were born at different radii and then migrated to its present locations as a result of a series of uncorrelated scattering events (Wielen et al. 1996; Binney 2001).

The migration may be explained naturally by "collisions'' of stars with the Jeans-unstable density waves. Let us estimate the scale of radial migration $\Delta R_\odot$ of the Sun's guiding center. According to observations, we adopt the ratio ${\cal{E}}_{\vec{k}}/\Phi_0^2 \approx 10^{-3}$, $\eta^2\approx \Omega^2 r^2$, $m \approx 1$, $r_0 \approx 8.5$ kpc, and $\Im \omega_* \approx \Omega$, $k_* \approx k_{{\rm crit}}$. Then from Eq. (22) we obtain $\Delta R_\odot \approx \sqrt{{\cal D}_{\rm r} t} = 2{-}3$ kpc. This $\Delta R_\odot$ is in fair agreement with the estimate of Wielen et al. (1996) $\Delta R_\odot = 1.9$ kpc based on a radial galactic gradient in metallicity. We conclude that the Sun has migrated from its birth-place at r = 6-7 kpc in the inner part of the Galaxy outwards by 2-3 kpc during its lifetime of $t \approx 4.5 \times 10^9$ yr.

5.5 Problem of the spiral structure

Under the influence of Jeans-unstable perturbations, the random velocity dispersion of the main part of the stellar distribution function increases essentially on a dynamical time scale (on the time scale of only 2-3 galactic rotations). Because the Jeans instability is characterized by the critical value of velocity dispersion $c_{{\rm crit}}$, eventually as a result of such heating the gravitational instability will be switched off rapidly. Therefore, from the theoretical point of view, the Jeans-unstable density waves in a collisionless stellar disk have to be short-lived, and they should dissipate after a few rotations of the system.

N-body experiments have shown similar behavior for a hot system of stars repeatedly. A spiral structure usually develops in a numerical model during the first rotation of the system. These spirals are evidently Jeans-unstable density waves and not material arms, since test particles pass right through them (Miller et al. 1970; Quirk 1972). Sellwood & Carlberg (1984), Sellwood & Athanassoula (1986), and Griv et al. (1999) presented evidences that the spirals arise from collective processes. The growth of these perturbations then saturates due to the increasing velocity dispersion of the particles, and the Jeans-unstable modes decay during the next two to three rotations. The increase of velocity dispersion in those experiments cannot be explained by usual two-body encounters (Hohl 1973; Griv et al. 1999). It seems likely, the fast heating in the N-body models is due to collective effects discussed in the present paper, i.e., due to density fluctuations as a result of the Jeans instability. The violent Jeans instability occurs in numerical models because the Toomre stability criterion, satisfied for an initial computer model, is not applicable to nonaxisymmetric gravity perturbations in a differentially rotating, inhomogeneous disk. Density perturbations arising from the instabilities of the nonaxisymmetric perturbations grow into spiral structures. These density waves, which have growth rates comparable to the mean orbital frequency, dynamically heat the disk and exert torques which redistribute both mass and angular momentum. In a final, quasi-steady state after two to three rotations, the stars in acomputer model acquire large random velocities about 2 times more than Toomre's criterion predicts (Hohl 1971; Morozov 1981a; Sellwood & Carlberg 1984; Tomley et al. 1991; Griv et al. 1999). Thus, in the nonlinear regime, the stars (and indeed also the gas before their formation) can continue developing Jeans-unstable condensations only if some effective mechanism of cooling exists, leading to Toomre's Q-values smaller than 2-2.5.

Cooling of a numerical model through dissipation in the gas layer, accretion, and/or star formation (injection of new-born stars which are formed on almost purely circular orbits) has already been proposed as a mean to prolong collective instabilities in the plane of the stellar disk (Miller et al. 1970; Quirk 1972; Sellwood & Carlberg 1984; Tomley et al. 1991; Griv & Chiueh 1998). The cold interstellar medium may play a dominant role in determining the wave-like structure in galaxies with a high star formation rate because it is the site of the generation of dynamically cold objects. The star formation process fuels the Jeans instability, favoring the excitation of short-lived spiral modes exponentially growing through a recurrent instability cycle in the disk of newly formed stars. In this regard, no prominent spirals are seen in S0 galaxies that have little or no interstellar matter. Martinet (1995) already pointed out the connection between dynamical evolution and efficiency of star formation in galaxies of various morphological types. We expect that stellar disks of flat galaxies are rife with many transient, chaotic-looking Jeans-unstable wakes. Such short-lived spirals develop in young stellar population in rapid succession and possible interaction (cf. Sellwood & Carlberg 1984; Tomley et al. 1991). Summarizing, multiple armed spiral patterns in gas-rich galaxies may result from the simultaneous excitation and superposition of different Jeans-unstable modes. The coexistence of several spiral waves is possible. The low-m modes (m=1-4) are the dominant ones. Interestingly, many spiral structures in galaxies do not appear to be well-organized grand designs. Galaxies dominated by a single and symmetric pattern are exceedingly rare (Binney & Tremaine 1987, p. 391; Elmegreen & Elmegreen 1989).

6 Summary

The kinetic theory of the Jeans instability is extended by deriving a diffusion equation in configuration space for the main part of the distribution function of stars in the rotating disk of a flat galaxy. The analytical method of the quasi-linear kinetic theory is applied. It is shown that in the collisionless case diffusion leads to effective temperatures, i.e., to velocity dispersions relative to the bulk velocities of the galaxy stars, increasing in time in the field of the Jeans-unstable waves. Fluidlike stellar encounters with almost aperiodically growing Jeans-unstable gravity perturbations can explain the observed form of the age-velocity dispersion correlation, the observed amount heating of the local stellar disk in the plane of the Galaxy $\Delta v = 20-30$ kms-1 as well as the observed Schwarzschild shape of the stellar random velocity distribution. This result is in agreement with suggestions of previous work (Griv et al. 1994; Griv & Peter 1996a; Griv et al. 1999; Griv et al. 2000b). Sufficient velocity dispersion prevents the Jeans instability from occurring but cooling of a galaxy through dissipation in the gas layer, accretion, and/or star formation (injection of new-born dynamically cold stars) reduce the residual velocities of stars so that the Jeans instability may be an effective long-term generating mechanism for the spiral $\sim$2 kpc structure of a disk galaxy. We conclude that the spiral arms in gas-rich galaxies may be of transient nature in systems with gas cooling, accretion, and/or star formation. In such a way, we are able to reconcile the apparent conflict between the theory of the Jeans instability and the fact that spiral patterns in disk galaxies of stars must be long lived.

The diffusion of stellar orbits in coordinate space leads to the core-dominated mass density profile in disk galaxies. As a result of wave-star scattering, the Sun's guiding center diffused radially from its birth-place in the inner part of the Galaxy outwards; $\Delta R_\odot = 2{-}3$ kpc.

Acknowledgements
We have benefited from numerous discussions with Tzihong Chiueh, David Eichler, Alexei Fridman, Muzafar Maksumov, Frank Shu, Irina Shuster, and Jun-Hui Zhao. This work was supported in part by the Israel Science Foundation and the Israeli Ministry of Immigrant Absorption.

References

 
Copyright ESO 2002