| Phase | density (cm-3) | temperature (K) | volume filling factor ( |
| molecular cloud |
|
||
| cold neutral medium | 10-100 | ||
| HII envelopes | 5-10 | 8000 | |
| diffuse intercloud gas | 0.1-0.5 | 8000 | |
| coronal | 10-3 | 106 | 20-80 |
A&A 383, 319-325 (2002)
DOI: 10.1051/0004-6361:20011688
I. Lerche 1,2 - R. Schlickeiser 1
1 - Institut für Theoretische Physik, Lehrstuhl IV:
Weltraum- und Astrophysik, Ruhr-Universität Bochum,
44780 Bochum, Germany
2 -
Permanent address: Department of Geological Sciences, University of South
Carolina, Columbia, SC 29208, USA
Received 16 July 2001 / Accepted 27 November 2001
Abstract
In order to describe correctly the heating rate of the interstellar medium by
plasma wave energy losses, we investigate the influence of
non-linear amplitude effects on wave characteristics, using the
Rogister-Mjølhus-Wyller equation, which is the most complete
plasma kinetic description for nonlinear magnetohydrodynamic (MHD) waves
propagating parallel to an ambient magnetic field. It is demonstrated
(1) that any energy change arises only as a consequence of the nonlocal term in
this equation, and (2)
that the energy transfer rate can be evaluated in terms of quadratures
dependent on the initial and/or boundary conditions imposed on exact
solutions to the derivative non-linear Schrödinger equation.
Moreover, the Rogister-Mjølhus-Wyller equation
implies the presence of oscillatory solutions, independent of
the strength of the nonlocal term, indicating that
such waves play a role in the
long-term evolution of the interstellar medium. These waves propagate in
both positive and negative senses
(depending on their wavenumbers), suggesting a bifurcation of energy flux
directions at large and small spatial scales. Such a division is of significance
not only for the long term behavior of the interstellar medium, but also for
particle energization.
Key words: ISM: magnetic fields - plasmas - waves - turbulence - magnetohydrodynamics (MHD)
| Phase | density (cm-3) | temperature (K) | volume filling factor ( |
| molecular cloud |
|
||
| cold neutral medium | 10-100 | ||
| HII envelopes | 5-10 | 8000 | |
| diffuse intercloud gas | 0.1-0.5 | 8000 | |
| coronal | 10-3 | 106 | 20-80 |
The plasma wave models allow consideration
of the damping processes of the turbulence that is important for the
heating of the interstellar medium (Lerche & Schlickeiser 2001).
In this context, in order to
describe correctly wave energy loss in
the interstellar medium, it is necessary to investigate the influence of
non-linear amplitude effects on wave characteristics. Estimates of small
amplitude wave energy loss rates are
radically different in spatial and temporal behaviour from estimates pertaining
to large amplitude waves (Mjølhus & Wyller 1986,1988;
Spangler 1990,1991; Dawson & Fontan 1990; Flå et al. 1989). Here we investigate this problem on the basis of the
Rogister-Mjølhus-Wyller equation, which, to date, is the most complete
plasma kinetic description for nonlinear magnetohydrodynamic (MHD) waves
propagating parallel to an
ambient magnetic field (Rogister 1971;
Mjølhus & Wyller 1986,1988). With some minor modifications to
the notation presented in Spangler (1991), the wave evolution is described
through
From the requirement that ![]() be real for all
be real for all ![]() ,
it follows that
F0, c2, c1 and h02 all be real. Further c1 must be greater than
or equal to zero to avoid
,
it follows that
F0, c2, c1 and h02 all be real. Further c1 must be greater than
or equal to zero to avoid
![]() turning negative, which would
drive
turning negative, which would
drive ![]() complex, and thus violate the ansatz. From Eqs. (8)
and (11) it then follows that
complex, and thus violate the ansatz. From Eqs. (8)
and (11) it then follows that
With
![]() ,
,
![]() real, Eq. (3) can be written in
the general form
real, Eq. (3) can be written in
the general form
For c1=0, however, one has ![]() ,
,
![]() and then one is interested in
solutions to
and then one is interested in
solutions to
If N2 is small, then the global energy loss rate
![]() is
obtained by taking the solutions of Eq. (1) in the absence of
the term containing N2, i.e. solutions of the standard DNLS, and then using
them directly in the right hand side of Eq. (18). According to
property (16) only solutions with c1=0 are of interest
here. We denote solutions to Eq. (17) obtained with N2=0 by D(s).
Then with N2=0,
is
obtained by taking the solutions of Eq. (1) in the absence of
the term containing N2, i.e. solutions of the standard DNLS, and then using
them directly in the right hand side of Eq. (18). According to
property (16) only solutions with c1=0 are of interest
here. We denote solutions to Eq. (17) obtained with N2=0 by D(s).
Then with N2=0,
Using the solution (29) in Eq. (25) yields
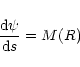 |
(38) |
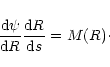 |
(39) |
To obtain wave solutions to Eq. (17) is relatively easy. Set
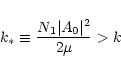 |
(44) |
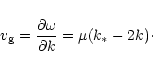 |
(46) |
This difference in propagation character at short and
long wavelengths, dependent
on the amplitude of the wave (through
![]() ), would
suggest that there should be at least one choice of k that could lead to
particle acceleration. This part of the problem is now considered.
), would
suggest that there should be at least one choice of k that could lead to
particle acceleration. This part of the problem is now considered.
The condition for acceleration
![]() can be written
with Eq. (45) as
can be written
with Eq. (45) as
(1) First, some of the basic properties of spatially bounded soliton-like solutions were provided indicating how such structures can develop.
(2) Second, particular structured forms, spatially bounded, were reduced to simple quadratures, thereby providing general analytic solutions in quadrature form. The patterns of behaviour for such soliton-like solutions were shown to be dependent on the initial and/or boundary conditions one chooses to impose, leading to a rich diversity of possible behaviors.
(3) Third, a class of wave-like solutions were derived that do not damp with time, independent of the value for the so-called "non-local" term in the equation that controls energy loss. These wave-like solutions were shown to be capable of accelerating charged particles. It may be that more general conditions for particle acceleration can be found than those developed here. However, the fact that some particles, at the least, can reach higher energies using the waves, suggests that a more general investigation of the spatially bounded soliton-like behaviours should also provide acceleration capabilities. The complexity and diversity of possible structural soliton patterns has so far precluded a detailed investigation of the particle acceleration capabilities of all classes of solutions to the non-linear Landau damping wave kinetic equation. But that one class of solutions does provide for such acceleration augers well for any further investigation involving more general classes of solutions.
The main point is that the influence of non-linear effects on wave
characteristics for energy gain and/or loss in the interstellar medium
is not to be lightly dismissed. In particular, for heating of the interstellar
medium, the investigation in Sect. 2.2 shows that the energy transfer rate (as
approximated by Eq. (21)) can be evaluated in terms of quadratures
dependent on the initial and/or boundary conditions imposed. This use of exact
solutions to the DNLS equation is a major improvement over the ad hoc
suggestions (Spangler 1991) for the structured solutions. The ad hoc
behaviors do not come even close to satisfying the basic equations under
consideration by direct insertion into the equations. For the classes of
solutions described by decaying soliton behaviors, the influence of such heating
(cooling) events can seriously affect the understanding of the balance of wave
heating and radiative cooling in the interstellar medium. The basic solutions
exhibited here would, seemingly, be a significant step forward in our long-term
attempts to understand this problem.
Equally, the presence of oscillatory solutions, independent of N2 for any and
all values of N2, would seem to indicate that such waves play a role in the
long-term evolution of the interstellar medium. If the soliton-like structures
decay (for ![]() )
then one is eventually left with a body of non-linear
oscillating waves. These waves propagate in both positive and negative senses
(depending on their wavenumbers), suggesting a bifurcation of energy flux
directions at large and small spatial scales. Such a division is of significance
not only for the long term behavior of the interstellar medium, but also for
particle energization.
This paper has shown how all of these problems can be addressed using the
one-dimensional non-local DNLS equation. It is clear that the richness of
patterns can only increase with multi-dimensional equations of similar sort.
)
then one is eventually left with a body of non-linear
oscillating waves. These waves propagate in both positive and negative senses
(depending on their wavenumbers), suggesting a bifurcation of energy flux
directions at large and small spatial scales. Such a division is of significance
not only for the long term behavior of the interstellar medium, but also for
particle energization.
This paper has shown how all of these problems can be addressed using the
one-dimensional non-local DNLS equation. It is clear that the richness of
patterns can only increase with multi-dimensional equations of similar sort.
The total effect of all such possibilities on the long term evolution of the interstellar medium is seen but murkily at present, but also represents an exciting challenge. The soliton behaviors, the forward and reverse propagating oscillatory waves, and the particle acceleration by the non-linear waves, all provide processes that are fundamentally beholden to the non-linear terms, without which all such effects would vanish. And these non-linear processes form the start of a significant combined integration of information in our attempts to understand the intertwined evolution of waves and charged particles in the interstellar medium.
Acknowledgements
We are grateful to Drs. M. Goossens and Y. Voitenko for pointing out to us the underlying assumptions in the derivation of the Rogister-Mjølhus-Wyller equation. We gratefully acknowledge support by the Deutsche Forschungsgemeinschaft through Sonderforschungsbereich 191.
The Rogister-Mjølhus-Wyller Eq. (1) is a "Kinetically Modified Derivative Nonlinear Schrödinger equation" (KMDNLS) where the modification arises from the nonlocal term scaling with N2. It reduces to the Derivative Nonlinear Schrödinger equation (DNLS) when N2=0.
The derivation of the DNLS equation has been reviewed by
Dawson & Fontan (1990) and Mjølhus & Wyller (1986).
It has been originally
obtained from the set of
nondissipative MHD equations, where all variables are supposed to depend only on
the z-coordinate (Sakai & Sonnerup 1983; Spangler & Sheerin
1982) by means of a reductive perturbation method (Taniui & Wei
1968). Due to this geometric restriction, the model obtained is
unidirectional and Bz=B0 always, so that longitudinal perturbations of
the magnetic field cannot be described.
The complex variable
![]() represents the real valued transverse field
components Bx,y according to
represents the real valued transverse field
components Bx,y according to
![\begin{displaymath}b=\epsilon ^{-1/2}[B_x+\imath B_y]
\end{displaymath}](/articles/aa/full/2002/07/aah3005/img141.gif) |
(66) |
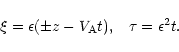 |
(67) |
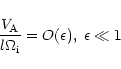 |
(68) |
Rogister (1971) was the first in deriving the DNLS from the full three
dimensional quasi-neutral Vlasov equations together with the pre-Maxwell's
equations (without the displacement current). A perturbation expansion
equivalent to the reductive perturbation method led to an equation containing
all the terms of the DNLS, but also with the additional non-local term
representing resonant particles. Mjølhus & Wyller (1988) started
from the guiding center plasma model to infer the KMDNLS Eq. (1). At least two assumptions are hidden in the
derivation of the KNDLS equation
that can make the applicability of the KNDLS equation to nonlinear MHD waves
in the interstellar medium less than optimal:
(1) The assumption that the velocity distribution of resonant particles
is constant in time leads to the dissipative coefficient N2 in Eq.
(1) being independent of time. If the velocity
distribution of the resonant particles, which causes the wave-particle
interaction, evolves much faster than the wave amplitudes then the
quasilinear diffusion smoothes out the velocity
distribution, thus quenching the Landau resonance and the coefficient N2.
Then one again would have the DNLS Eq. (1) with N2=0.
(2) The assumption of time reversibility of Landau damping, which
gives rise to the Hilbert transform operator in the nonlocal term of Eq.
(1), might be violated. Such an effect
can happen because of a change of the
dissipative term due to scattering of particles at small angles.
A non-local term would persist but would be more complexly described than by a
Hilbert transform.
Both assumptions become especially crucial for the asymptotic states of the turbulence at long times.
Unfortunately, compared to the interplanetary medium, where in-situ measurements
on spacecrafts of the turbulent properties of the interplanetary medium
are available, the observational data for interstellar medium turbulence is
scarce, and, as mentioned already, is mainly based on line-of-sight electron
density fluctuation measurements through a multi-phase interstellar medium
from scintillation, dispersion measure and Faraday rotation measure
observations. Therefore no direct
observational clue on the validity of the underlying assumptions (1) and (2)
in the interstellar medium can be provided. It is, however, important to keep
these hidden assumptions in mind when applying the solution properties of the
KNDLS equation presented in this work to the interstellar medium.
We finally mention that Dawson & Fontan (1990) have investigated the
soliton-behaviour of Eq. (1) with N2=0, whereas Flå et al. (1989) found numerically that with ![]() the soliton-like modes damp with time.
the soliton-like modes damp with time.