A&A 383, 14-29 (2002)
DOI: 10.1051/0004-6361:20011648

Oxygen and nitrogen abundances in Virgo and field spirals

L. S. Pilyugin 1 - M. Mollá 2 - F. Ferrini 3,4 - J. M. Vílchez 5


1 - Main Astronomical Observatory of National Academy of Sciences of Ukraine, 27 Zabolotnogo Str., 03680 Kiev, Ukraine
2 - Departamento de Física Teórica, Universidad Autónoma de Madrid, 28049 Cantoblanco, Spain
3 - Department of Physics, Section of Astronomy, University of Pisa, Piazza Torricelli 2, 56100 Pisa, Italy
4 - INTAS, 58 avenue des Arts, 1000 Bruxelles, Belgium
5 - Instituto de Astrofísica de Andalucía, Apdo. 3004, 18080 Granada, Spain

Received 20 September 2001 / Accepted 6 November 2001

Abstract
The oxygen and nitrogen abundances in the H II regions of the nine Virgo spirals of the sample from Skillman et al. (1996) and in nine field spiral galaxies are re-determined with the recently suggested P-method. We confirm that there is an abundance segregation in the sample of Virgo spirals in the sense that the H I deficient Virgo spirals near the core of the cluster have higher oxygen abundances in comparison to the spirals at the periphery of the Virgo cluster. At the same time both the Virgo periphery and core spirals have counterparts among field spirals. Some field spirals have H I to optical radius ratios, similar to that in H I deficient Virgo core spirals. We conclude that if there is a difference in the abundance properties of the Virgo and field spirals, this difference appears to be small and masked by the observational errors.

Key words: galaxies: abundances - galaxies: evolution - galaxies: ISM - galaxies: spiral


1 Introduction

There is evidence that the environment affects the properties of galaxies in clusters (see review of Balkowski 1992). The most obvious effect is probably that concerning the H I content of galaxies in clusters (Haynes & Giovanelli 1986; Huchtmeier & Richter 1989; Cayatte et al. 1994). It is well established that the spiral galaxies of the Virgo cluster have a tendency to be H I deficient in comparison with normal field spirals (Solanes et al. 1996, 2001) and this deficiency is correlated with distance to the cluster center, the proportion of gas-poor spirals increasing continuously towards the cluster center. Thus, a cluster galaxy (especially a galaxy near the center of the cluster) evolves in a different surrounding gaseous medium in comparison to a field galaxy.

The gas exchange between a galaxy and its ambient medium (loss of gas by the galaxy or gas infall onto the galaxy) changes the course of the chemical evolution of the galaxy. Then, it can be expected that the environment affects the chemical properties of galaxies in clusters. Oxygen plays a key role in understanding the (chemical) evolution of galaxies. The origin of oxygen seems to be reliably established in contrast to other elements like carbon or nitrogen. The oxygen abundance can be considered as a tool to investigate the evolution of galaxies. For example, the value of oxygen abundance in a galaxy combined with the value of the gas mass fraction can tell us about the efficiency of mass exchange between a galaxy and its environment (Pilyugin & Ferrini 1998, 2000).

A number of works have been devoted to searching for the possible effects of cluster environment on the chemical properties of spiral galaxies (Shields et al. 1991; Henry et al. 1992, 1994, 1996; Skillman et al. 1996). The conclusions of these works are: i) the spirals at the periphery of the cluster are indistinguishable from the field galaxies, ii) the H I deficient Virgo core galaxies have larger oxygen abundances at a predetermined galactocentric distance r = 0.4 R25 (where R25is the isophotal radius) than the field galaxies of comparable luminosity or Hubble type.

Accurate oxygen abundances can be derived from measurement of temperature-sensitive line ratios, such as [OIII]4959, 5007/[OIII]4363. This method will be referred to as the $T_{\rm e}$-method. Unfortunately, in oxygen-rich H II regions the temperature-sensitive lines such as [OIII]4363 are too weak to be detected. For such H II regions, empirical abundance indicators based on more readily observable lines were some years ago suggested (Pagel et al. 1979; Alloin et al. 1979). The empirical oxygen abundance indicator $R_{23} =\, $([OII]3727, 3729 + [OIII]4959, 5007)/H$_{\beta}$, suggested by Pagel et al. (1979), has found widespread acceptance and it has been used for the oxygen abundance determination in H II regions where the temperature-sensitive lines are undetectable. This method will be referred to as the R23-method. Using the R23-method, the characteristic oxygen abundances (the oxygen abundance at a predetermined galactocentric distance) and radial oxygen abundance gradients were obtained for a large sample of field spiral galaxies (Vila-Costas & Edmunds 1992; Zaritsky et al. 1994; van Zee et al. 1998, among others).

However, the basic problem whether R23 is an accurate abundance indicator is open to discussion (Zaritsky 1992; Kinkel & Rosa 1994, among others). It has been found (Pilyugin 2000) that the error in the oxygen abundance derived with the R23-method involves two parts: the first is a random error and the second is a systematic error depending on the excitation parameter. A new way of oxygen abundance determination in H II regions (P-method) has been recently suggested (Pilyugin 2000, 2001a). By comparing oxygen abundances derived through the $T_{\rm e}$-method in high-metallicity H II regions with those derived through the P-method, it has been found that the precision of oxygen abundance determination with the P-method is comparable to that of the $T_{\rm e}$-method (Pilyugin 2001a,b). It has been also shown that the R23-method provides more or less realistic oxygen abundances in high-excitation H II regions but it produces overestimated oxygen abundances in low-excitation H II regions. Taking into account this fact together with the fact known for a long time (Searle 1971; Smith 1975) that galaxies can show strong radial excitation gradients, in the sense that only the low-excitation H II regions populate the central parts of some galaxies, one can expect that the oxygen abundances of the inner H II regions and the gradient slopes based on the (O/H)R23 data can be appreciably overestimated. This speculation has been confirmed by comparison of the radial (O/H)R23 abundance distribution with the radial (O/H) $_{T_{\rm e}}$ abundance distribution within the disk of the well-observed spiral galaxy M 101 (Pilyugin 2001b).

The problem whether the cluster environment affects the chemical evolution of galaxies will be considered here based on the (O/H)$_{\rm P}$and (N/H)$_{\rm P}$ abundances obtained in Sect. 2. In Sect. 3 we analyze these data with the multiphase model applied to three Virgo galaxies, considered as typical examples. A dicussion is included in Sect. 4 and Conclusions are in Sect. 5.

2 Virgo and field spiral abundances

2.1 Oxygen


 

 
Table 1: The galaxy sample.
            P method   R23 method
Galaxy d ref log$L_{\rm B}$ R25 T type O/H0 gradient literature sources O/H0 gradient
  Mpc     (')     dex/R 25 for the spectra   dex/R 25
                     
                     
Virgo cluster galaxies
                     
NGC 4254 16.8 SKSZ 10.61 2.81 5 8.94 -0.65 HPC, MRS, SSK 9.44 -0.65
NGC 4303 16.8 SKSZ 10.62 3.23 4 8.84 -0.72 HPLC, SSK 9.43 -1.05
NGC 4321 16.8 SKSZ 10.66 3.79 4 8.86 -0.37 MRS, SSK 9.36 -0.38
NGC 4501 16.8 SKSZ 10.70 3.54 3 8.99 -0.52 SKSZ 9.48 -0.45
NGC 4571 16.8 SKSZ 9.94 1.86 6 8.90 -0.20 SKSZ, SSK 9.34 -0.10
NGC 4651 16.8 SKSZ 10.24 2.04 5 8.71 -0.64 SKSZ 9.25 -0.85
NGC 4654 16.8 SKSZ 10.34 2.45 6 8.84 -0.77 SKSZ 9.34 -0.84
NGC 4689 16.8 SKSZ 10.10 2.18 4 8.88 -0.41 SKSZ 9.40 -0.39
NGC 4713 16.8 SKSZ 9.88 1.35 7 8.71 -0.73 SKSZ 9.24 -1.02
                     
Field galaxies
                     
NGC 628 9.7 ZKH 10.25 5.36 5 8.71 -0.48 MRS, vZ, FGW 9.31 -0.77
NGC 1232 21.5 vZ 10.69 3.71 5 8.73 -0.58 vZ 9.36 -0.88
NGC 2903 8.9 DK 10.45 6.29 4 8.94 -0.73 MRS, ZKH, vZ 9.44 -0.76
NGC 3184 8.7 vZ 9.93 3.71 6 8.97 -0.63 MRS, ZKH, vZ 9.53 -0.80
NGC 3351 8.1 ZKH 9.90 3.79 3 8.94 -0.31 MRS, OK, FGW 9.43 -0.33
NGC 5194 7.7 ZKH 10.49 5.61 4 8.92 -0.40 MRS, D, BKG 9.43 -0.45
NGC 5236 4.5 S 10.31 6.59 5 8.75 -0.24 DTJS, WS 9.26 -0.27
NGC 5457 7.5 KG, vZ 10.67 14.42 6 8.76 -0.77 KG 9.37 -1.52
NGC 6946 5.9 KSH 10.60 8.30 6 8.73 -0.49 MRS, FGW 9.24 -0.62

List of references:

BKG - Bresolin et al. (1999); D - Díaz et al. (1991); DK - Drozdovsky & Karachentsev (2000); DTJS - Dufour et al. (1980); FGW - Fergurson et al. (1998); HPC - Henry et al. (1994); HPLC - Henry et al. (1992); KG - Kennicutt & Garnett (1996); KSH - Karachentsev et al. (2000); MRS - McCall et al. (1985); OK - Oey & Kennicutt (1993); S - Schmidt et al. (1994); SKSZ - Skillman et al. (1996); SSK - Shields et al. (1991); vZ - van Zee et al. (1998); WS - Webster & Smith (1983); ZKH - Zaritsky et al. (1994).


The (O/H)$_{\rm P}$ oxygen abundances in H II regions are determined with the expression suggested in (Pilyugin 2001a) 0pt

 
    $\displaystyle 12+\log({\rm O/H})_{\rm P} =$  
    $\displaystyle \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \frac{R_{23} + 54.2 + 59.45~ P + 7.31~ P^{2}} {6.07 + 6.71~ P + 0.37~ P^{2} + 0.243~ R_{23}} ,$ (1)

where R23 =R2 + R3, $R_{2} = I_{\rm [OII] \lambda 3727+ \lambda 3729} /I_{\rm H\beta }$, $R_{3} = I_{\rm [OIII] \lambda 4959+ \lambda 5007} /I_{\rm H\beta }$, and P = R3/R23.

For comparison, the (O/H)R23 oxygen abundances are also determined. Several workers have suggested calibrations of the R23 in terms of the oxygen abundance (Edmunds & Pagel 1984; McCall et al. 1985; Dopita & Evans 1986; Zaritsky et al. 1994, among others). Abundances for a large sample of spiral galaxies were derived by Zaritsky et al. (1994). The Zaritsky et al's calibration is an average of the three calibrations by Edmunds & Pagel (1984), McCall et al. (1985), and Dopita & Evans (1986). The oxygen abundances in Virgo spiral galaxies were determined by Skillman et al. (1996) using this same empirical R23-abundance calibration. Then this latter R23 calibration has been adopted here for the determination of the (O/H)R23 oxygen abundances.

The set of available spectra from the literature has been used for the determination of the (O/H)$_{\rm P}$ and (O/H)R23 oxygen abundances. There exist nine Virgo spirals with line intensity measurements for at least four H II regions (Skillman et al. 1996). We will compare the abundance properties of this Virgo sample to a sample of field spiral galaxies. This sample of field spiral galaxies also consists of nine galaxies, which were chosen in such way that 1) they lie in the same range of luminosity as the Virgo sample spirals, 2) they cover the same range of morphological type as the Virgo spirals, and 3) they have large enough number of H II regions with measurements of oxygen and nitrogen lines. The adopted and computed parameters of Virgo and field spiral galaxies are summarized in Table 1. The NGC number is listed in Col. 1. The adopted distance is reported in Col. 2 (source for the distance in Col. 3). The blue luminosity of the galaxy is reported in Col. 4. The isophotal radius R25 in arcmin and the numerical Hubble type of the galaxy (T type) taken from de Vaucouleurs et al. (1991) (RC3) are given in Cols. 5 and 6, correspondingly. The central (O/H)$_{\rm P}$ oxygen abundance and the gradient expressed in terms of dex/R25 are listed in Cols. 7 and 8. The source(s) for the line intensity measurements is reported in Col. 9. The central (O/H)R23 oxygen abundance and the gradient expressed in terms of dex/R25 are listed in Cols. 10 and 11, respectively.

  \begin{figure} \includegraphics[width=17.0cm,clip]{m1927f01.eps}\end{figure} Figure 1: Oxygen abundances and values of excitation parameter Pversus galactocentric distance for Virgo spiral galaxies. The oxygen abundances determined with the R23-method calibrated by Zaritsky et al. (1994) are shown by pluses, the best fits to these data are presented by dashed lines. The oxygen abundances determined with the P-method calibrated by Pilyugin (2001a) are shown by circles, the best fits to these data are presented by solid lines. The values of excitation parameter P are shown by triangles. The galactocentric distances are normalized to the isophotal radius.
Open with DEXTER

Figure 1 shows the derived (O/H)$_{\rm P}$ and (O/H)R23 oxygen abundances and excitation parameter P for H II regions in Virgo spirals as a function of galactocentric distance (normalized to the isophotal radius). The radial (O/H)R23 gradients in the Virgo spiral galaxies derived here are close to those determined by Skillman et al. (1996), with the exception of the galaxy NGC 4651. For this galaxy, those authors have found a value of the gradient of -0.42 (dex/R25), while a value -0.85 (dex/R25) is obtained here. The H II region +131, +021 with galactocentric distance 1.08 R25 is responsible for the small value of the gradient derived by those authors for that galaxy. Close examination of the radial distribution of (O/H)$_{\rm P}$ oxygen abundance within the disk of NGC 4651 (Fig. 1) shows that the oxygen abundance at galactocentric distances larger than $\sim$0.8 R25 is expected to be below 12+log(O/H)=8.2. Therefore it is unlikely that the H II regions within the disk of NGC 4651 at galactocentric distances larger than $\sim$0.8 R25 belong to the upper branch of the O/H-R23 diagram and, as consequence, the R23 calibrations of the upper branch of the O/H-R23 diagram should not be used for the oxygen abundance determination in the H II region +131, +021. Therefore this region has been excluded from consideration here, resulting in a larger value of the gradient as compared to the previous value of the gradient in Skillman et al. (1996).

As we can see in Fig. 1 most of the H II regions observed in the Virgo spiral galaxies are of low-excitation and they do not show (or show marginal) radial excitation gradients. Therefore the (O/H)$_{\rm P}$ gradients are close to the (O/H)R23 gradients, but the abundance (O/H)$_{\rm P}$ at any given galactocentric distance is significantly lower than the value estimated from the (O/H)R23 calibration. This reflects the fact that the R23-method may provide more or less realistic oxygen abundances for high-excitation H II regions but produce overestimated oxygen abundances in low-excitation H II regions. As an example, we see that a more or less distinct radial excitation gradient can be seen in the Virgo spiral NGC 4303. In consequence the (O/H)$_{\rm P}$ gradient in the NGC 4303 is shallower than the (O/H)R23 gradient, Fig. 1.


  \begin{figure} \includegraphics[width=17cm,clip]{m1927f02.eps}\end{figure} Figure 2: The same than Fig. 1 for the field spiral galaxies.
Open with DEXTER

Figure 2 shows the derived (O/H)$_{\rm P}$ and (O/H)R23 oxygen abundances and excitation parameter P for H II regions in field spiral galaxies. Some of them (NGC 628, NGC 1232, NGC 5457) show an appreciable radial excitation gradients and, as a consequence, the (O/H)$_{\rm P}$ gradients in these galaxies are shallower than the (O/H)R23 gradients, Fig. 2.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{m1927f03.eps}\end{figure} Figure 3: Oxygen abundance at r=0.4 R25 as a function of blue luminosity a) and as a function of T type b) for the Virgo and field spirals. The pluses correspond to the field galaxies (NGC 628, NGC 1232, NGC 2903, NGC 3184, NGC 3351, NGC 5194, NGC 5236, NGC 5457, NGC 6946), the squares represent the H I deficient (Virgo core) spirals (NGC 4501, NGC 4571, NGC 4689), the triangles represent the intermediate galaxies (NGC 4254, NGC 4321, NGC 4654), and the open circles represent the Virgo galaxies with normal H I disks (NGC 4303, NGC 4651, NGC 4713).
Open with DEXTER

Figure 3 shows oxygen abundances at r=0.4 R25 as a function of blue luminosity (a) and as a function of the morphological type T (b) for the Virgo and field spirals. The oxygen abundances at r=0.4 R25 have been used instead of the central oxygen abundances because the central oxygen abundances in these galaxies can be affected by large uncertainties: the number of H II regions in the Virgo core galaxies is low and they cover a small interval of galactocentric distances, see Fig. 1, implying that the extrapolation method used to estimate these central data is uncertain. Since the value of r=0.4 R25 is within the interval of galactocentric distances covered by the observed H II regions in each galaxy, we believe the oxygen abundance at r=0.4 R25 is more reliable than the central oxygen abundance.

Skillman et al. (1996) divided the nine Virgo spirals in their sample into three groups of three galaxies each: those with strong H I deficiencies (NGC 4501, NGC 4571, and NGC 4689), intermediate cases (NGC 4254, NGC 4321, and NGC 4654), and those with no H I deficiencies (NGC 4303, NGC 4651, and NGC 4713). The three subgroups into which the sample has been divided are coded with different symbols in Fig. 3. The pluses correspond to the field galaxies, the squares represent the H I deficient (Virgo core) spirals, the triangles correspond to the intermediate galaxies, and the open circles represent the Virgo galaxies with normal H I disks.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{m1927f04.eps}\end{figure} Figure 4: 12+logO/H at r=0.4 R25 versus $R_{\rm H}/R_{25}$ diagram for Virgo (circles) and field (pluses) spiral galaxies.
Open with DEXTER

The examination of Figs. 3a,b shows that there is an abundance segregation in the sample of Virgo spirals in the sense that the H I deficient Virgo core galaxies are all near the top of the abundance distributions of galaxies with similar properties, such as it was obtained by Skillman et al. (1996). At the same time, some field spiral galaxies have oxygen abundances similar to those ones from the most oxygen-rich (H I deficient) Virgo spirals.

Those authors also found that the characteristic oxygen abundance (oxygen abundance at r=0.4 R25) for the Virgo cluster galaxies correlates with the H I to optical radius ratio, $R_{\rm H}/R_{25}$, where $R_{\rm H}$ is the H I radius at the isophotal level of $1~M_{\odot}$pc-2 after Warmels (1988). Our O/H abundances at r=0.4 R25versus $R_{\rm H}/R_{25}$ for Virgo spiral galaxies are shown in Fig. 4 with circles. A trend of decreasing characteristic O/H value with increasing $R_{\rm H}/R_{25}$ is evident for these galaxies. We also derive the H I to optical radius ratio for the field spiral galaxies for which 21 cm observations are available. We find $R_{\rm H}/R_{25} = 1.91$ for NGC 628, 1.35 for NGC 1232, 1.14 for NGC 2903, 1.02 for NGC 5194, 3.76 for NGC 5236 , 1.75 for NGC 5457 and 1.49 for NGC 6946, with 21 cm data from Shostak & van der Kruit (1984), van Zee & Bryant (1999), Wevers et al. (1986), Shane (1975), Huchtmeier & Bohnenstengel (1981), Boulanger & Viallefond (1992). Our O/H abundances at r=0.4 R25 versus $R_{\rm H}/R_{25}$ for field spiral galaxies are shown in Fig. 4 with pluses. Figure 4 shows that some field spirals have a small H I to optical radius ratios, similar to that in H I deficient Virgo core spirals. The field galaxies from our limited sample, with the exception of NGC 5236, show a similar trend of decreasing characteristic O/H value with increasing $R_{\rm H}/R_{25}$ as the Virgo spiral galaxies.

Thus, the consideration of the O/H$_{\rm P}$ oxygen abundances in H II regions in the Virgo and field spiral galaxies suggests that in general the Virgo spirals are indistinguishable from the field spirals, both the Virgo periphery and core spirals have counterparts among field spirals. There are no H I deficient Virgo spirals with low oxygen abundances. This fact together with the larger number of H I deficient galaxies in the core of the cluster causes the apparent segregation of high abundances in the center galaxies.

2.2 Nitrogen

The N/O abundance ratio in H II regions have been determined using algorithms following below. It was adopted

 \begin{displaymath}\frac{\rm N}{\rm O} = \frac{\rm N^+}{\rm O^+}\cdot \end{displaymath} (2)

The $\frac{\rm N^+}{\rm O^+}$ value is derived from the expression (Pagel et al. 1992)
 
$\displaystyle \log ({\rm N^+/O^+}) = \log \frac{I_{\rm [NII] \lambda 6548 + \la... ... + \lambda 3729}} + 0.307 - \frac{0.726}{t_2} + 0.40 \log t_2 - \log (1+1.35 x)$     (3)

where

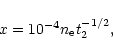\begin{displaymath}x= 10^{-4} n_{\rm e} t_2^{-1/2}, \end{displaymath} (4)

and $n_{\rm e}$ is the electron density in cm-3, t2 = $t_{\rm [NII]}$ is the electron temperature in units of 104 K. It was adopted $t_2 = t_{\rm [NII]} = t_{\rm [OII]}$. The t2 value can be determined from the following equations:
  
$\displaystyle 12+ \log ({\rm O}^{++}/{\rm H}^+) = \log \frac{I_{\rm [OIII] \lam... ...lambda 5007}} {I_{\rm H_{\beta}}} + 6.174 + \frac{1.251}{t_3} - 0.55 \log t_3 ,$     (5)
$\displaystyle 12+ \log ({\rm O}^{+}/{\rm H}^+) = \log \frac{I_{\rm [OII] \lambd... ...{\rm H_{\beta}}} + 5.890 + \frac{1.676}{t_2} - 0.40 \log t_2 + \log (1+1.35x) ,$     (6)


 \begin{displaymath}\frac{\rm O}{\rm H} = \frac{\rm O^+}{\rm H^+} + \frac{\rm O^{++}}{\rm H^+} , \end{displaymath} (7)


 \begin{displaymath}t_2 = 0.7 \, t_3 + 0.3 \end{displaymath} (8)

where t3 = $t_{\rm [OIII]}$ is in units of 104 K. Equations (5)-(7) were taken from Pagel et al. (1992), Eq. (8) was taken from Garnett (1992). Using the value of O/H derived from Eq. (1) and measured line intensities Eqs. (5)-(8) can be solved for $t_{\rm [OII]}$. The value of $n\rm _e$ was adopted to be equal to 100 cm-3 for every H II region.

The value of $t_{\rm [OII]}$ can be also found from the following expression for $t_{\rm P} = t_3$ (Pilyugin 2001a)

 \begin{displaymath}t_{\rm P} = \frac{R_{23} + 3.09 + 7.05 ~P + 2.87~ P^{2}} {9.90 + 11.86~ P + 7.05 ~P^{2} - 0.583~ R_{23}} \end{displaymath} (9)

and Eq. (8). The value of t2 determined from Eqs. (8), (9) coincides with the value of t2 derived from Eqs. (1), (5)-(8) for majority of H II regions considered. However, for H II regions, in which the bulk of oxygen is in the O+ stage, the two values of t2 are not in agreement. Equations (1), (5)-(8) give a more realistic values of t2 for these H II regions.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{m1927f05.eps}\end{figure} Figure 5: N/O versus O/H diagram for Virgo and field spiral galaxies. a) Virgo center galaxies: NGC 4501, NGC 4571, and NGC 4689 (squares) and field spiral galaxies: NGC 628, NGC 1232, NGC 2903, NGC 3184, NGC 3351, NGC 5194, NGC 5236, NGC 5457, and NGC 6946 (points). b) Virgo intermediate galaxies: NGC 4254, NGC 4321, and NGC 4654 (triangles) and field spiral galaxies (points). c) Virgo periphery galaxies: NGC 4303, NGC 4651, and NGC 4713 (circles) and field spiral galaxies (points).
Open with DEXTER

Using Eqs. (1), (5)-(8) the N/O abundance ratios were derived for all the H II regions in Virgo and field spiral galaxies for which the [NII] $\lambda \lambda 6548, 6584$ line measurements are available in the works cited in Table 1. If only the [NII] $\lambda 6584$ line measurement was available then the total [NII] $\lambda \lambda 6548, 6584$ line intensity was derived as $I_{\rm [NII]\lambda \lambda 6548, 6584} = 1.3\times I_{\rm [NII]\lambda 6584}$.

Figure 5 shows the N/O versus O/H diagram for Virgo and field spiral galaxies: Virgo core galaxies (NGC 4501, NGC 4571, and NGC 4689) are presented as squares, in panel a, the Virgo intermediate galaxies (NGC 4254, NGC 4321, and NGC 4654) are shown as triangles in panel b, and the Virgo periphery galaxies (NGC 4303, NGC 4651, and NGC 4713) are presented as circles in panel c. Points in all panels represent the field spiral galaxies (NGC 628, NGC 1232, NGC 2903, NGC 3184, NGC 3351, NGC 5194, NGC 5236, NGC 5457, and NGC 6946).

Panel a of Fig. 5 shows that the Virgo core spirals occupy the lower part of the band outlined by the field spirals in the N/O-O/H diagram. It looks as if the position of Virgo core spirals is slightly shifted (by around $0.05 \div 0.10$ dex) towards higher O/H values or towards lower N/O values relative to the overall position of field spirals. Is this small offset of Virgo core spirals in the N/O-O/H diagram real? Does it reflect a (marginal) difference between the evolution of the Virgo core and field spirals? It is more likely that this apparent small shift of positions of the Virgo core spirals in the N/O-O/H diagram is an artifact caused by error propagation in the abundance determination for H II regions in the core spirals, produced by the uncertainties in line measurements (only upper limit estimations of [OIII] $\lambda 5007$line intensities are available for those H II regions), or due to the uncertainty in the extrapolation of the P-method into an area of extreme values of the parameters P and R23 (the value of P is equal or close to zero, Fig. 1, for all the H II regions of the Virgo core spirals, and the R23 value is usually less than 1 while the calibration is based on the H II regions with R23 > 2). It should be particularly emphasized that we cannot discard the possibility that this apparent offset has an artificial origin, since it is small (around $0.05 \div 0.10$ dex), comparable to the expected errors in the oxygen and nitrogen abundances. Therefore error statistics prevent us from any possible data overinterpretation; though we stress that more and better data are needed to disentangle the actual nature of the offset revealed here.

Examination of Fig. 5 (panels b and c) shows that the Virgo periphery and intermediate spiral galaxies occupy the same band in the N/O-O/H diagram as do field spiral galaxies, i.e. they appear indistinguishable from field spirals in the N/O-O/H diagram.

Thus, the comparison of N/O abundance ratios in H II regions of the nine Virgo and nine field spiral galaxies confirms (or at least is not in conflict with) the above conclusion that Virgo spirals result indistinguishable from field spirals. If there is an actual difference between abundance properties of the Virgo and field spirals this difference should be small and appear entirely masked by the errors.

3 Virgo spirals and their multiphase chemical evolution models

Shields et al. (1991) and Skillman et al. (1996) argued that the high oxygen abundances in the HI deficient Virgo spirals can be explained by the fact that the infall of metal-poor gas onto the galaxy is inhibited in the cluster environment, and the Virgo core spirals may have evolved more nearly in the manner of the closed box "simple model" of chemical evolution. Field galaxies and galaxies on the periphery of the cluster would have their oxygen abundances depressed by infall of metal-poor gas. In the light of our results it can be concluded that some field spirals have also evolved in the same way as the Virgo core spirals do.

Another important result of the present study is the rather low values of the central oxygen abundances in spiral galaxies: the maximum central oxygen abundance is $\sim$12+log(O/H) = 9, about 0.3 dex higher than the solar value 12+log(O/H) $_{\odot} = 8.736$ (Holweger 2001) or 12+log(O/H)$_{\odot}$ = 8.69 (Prieto et al. 2001). The multiphase multizone models shown by Ferrini et al. (1992) predict a maximum value of oxygen abundance $12 + \log (\rm O/H) \sim 9.10$dex. This is indicative of that the oxygen production used in these models is closer to reality. Therefore, one can expect that these models can be used to test the influence of the environment, through the effect of the infall of gas on the disks of the Virgo galaxies and its dependence on distance to the center of the cluster.

 

 
Table 2: Galaxy characteristics.
Galaxy Type Arm $R_{\rm eff}$ Vel $_{\rm rot,max}$
Name   Class (arcsec) (kms-1)

NGC 4303		 4 9 62.6 150
NGC 4321 4 12 111.5 270
NGC 4501 3 9 77.1 300


3.1 Multiphase model description

The multiphase model used here was first applied to the Solar Neighborhood (Ferrini et al. 1992), and to the whole Galactic (MWG) disk (Ferrini et al. 1994 - hereafter FMPD) and bulge (Mollá & Ferrini 1995). The same model was then applied to disks (Mollá et al. 1996, 1999) and bulges (Mollá et al. 2000) of some spiral galaxies of different morphological types with reasonable success. We now present the application of this multiphase chemical evolution to three galaxies in Virgo, NGC 4501, close to the center, an intermediate galaxy as NGC 4321 and a HI normal galaxy NGC 4303, which is in the periphery of the cluster, as typical examples for these different zones.

The data used in our models for these three galaxies are presented in Table 2 where we display their morphological types (T) and Arm Class in Cols. (2) and (3) as derived by Tully (1988) and Biviano (1991), respectively. Effective radii from Tully (1988) are in Col. (4), with the exception of NGC 4303 for which the effective radii is from Henry et al. (1992). The adopted distance is 16.8 Mpc.

In the multiphase model a protogalaxy is assumed to be a spheroid composed of primordial gas with total mass M(R). For our galaxies the masses are calculated from the rotation curves (Table 2, Col. 5) obtained either via radio (Guhathakurta et al. 1988) or optical (Distefano et al. 1990) observations. Each galaxy is divided into concentric cylindrical regions 1 kpc wide. The model calculates the time evolution of the halo and disk components belonging to each cylindrical region. The halo gas falls into the galactic plane to form the disk, which is a secondary structure in the multiphase framework, formed by the gravitational accumulation of this gas at a rate which depends on the collapse time scale $\tau_{\rm coll}$.

In our framework an infall dependent on galactocentric distance and a two-steps star formation law, by forming molecular clouds and then stars, are assumed.

The infall rate f is inversely proportional to the collapse time scale $\tau_{\rm coll}$, which is assumed to depend on galactocentric radius, through an exponential function with a scale length l:

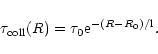\begin{displaymath}\tau_{\rm coll}(R)=\tau_{0}{\rm e}^{-(R-R_{0})/{\rm l}}. \end{displaymath} (10)

The characteristic time scale $\tau_{0}$ is defined for every galaxy as being appropriate to a region equivalent to the Solar Neighbourhood in MWG located at a radius R0 which is calculated from $R_{\rm eff}$. This characteristic time scale is calculated for every galaxy via the total mass of the galaxy. We compute, from the rotation curves, the total mass for each galaxy. This defines the collapse time scale for each one of them through the expression $\tau_{0} \propto M_{9}^{-1/2} T$ (Gallagher et al. 1984), where M9 is the total mass of the galaxy in 10 $^{9}~M_{\odot}$ and T is its age, assumed 13 Gyr. Thus, we obtain $\tau_{0}$ for each galaxy, through the proportion: $\tau_{0}=\tau_{\odot}(M_{9},{\rm gal}/M_{9,\rm MWG})^{-1/2}$, the value of $\tau_{\odot}=4 $ Gyr having been determined in Ferrini et al. (1992) for the Solar Region.


  \begin{figure} \par\includegraphics[width=16.8cm,clip]{m1927f06.eps}\end{figure} Figure 6: Predicted radial distributions at the present epoch for NGC 4303: a) oxygen abundance $12+\log (\rm O/H)$; b) star formation rate surface density normalized to the equivalent to solar region value $\Psi /\Psi _{0}$; c) diffuse or atomic gas H I and d) molecular gas H2 surface density. Model is represented by the lines while symbols are the observational data.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=16.8cm,clip]{m1927f07.eps}\end{figure} Figure 7: Predicted radial distributions at present time for NGC 4321 with the same panels and symbols than in Fig. 6.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=16.8cm,clip]{m1927f08.eps}\end{figure} Figure 8: Predicted radial distributions at present time for NGC 4501 with the same panels and symbols than in Fig. 6.
Open with DEXTER

Following the relation between collapse time scale and mass, it is evident that $\tau_{\rm coll}$ must be variable with the galactocentric radius. If the total mass surface density follows an exponential law, such as the surface brightness does for spiral disks, the resulting $\tau_{\rm coll}$ must increase along the radius with a scale length $ l \propto Re$ (where Re is the scale-length for the surface brightness radial distribution). We use l=4 kpc but we must take into account that Re usually decreases for later type galaxies and is larger for the earlier ones, and therefore the selection of this parameter have some uncertainties.

In the various regions of the galaxy we allow for different phases of matter aggregation: diffuse gas (g), clouds (c, only in the disk), low-mass ( $s_{1}, m < 4~ M_{\odot}$) and massive stars ( $s_{2}, m \ge 4~ M_{\odot}$), and remnants. The mass in the different phases changes through several conversion process:

1.
Star formation by the gas spontaneous fragmentation in the halo ( ${\propto} K g_{\rm H}^{1.5}$);
2.
Formation of the disk by the accumulation of diffuse gas from the halo ( ${\propto} f g_{\rm H}$);
3.
Cloud formation in the disk from diffuse gas ( ${\propto} \mu g^{1.5}$);
4.
Star formation from cloud-cloud collisions ( ${\propto} H c^{2}$);
5.
Induced star formation via massive star-cloud interactions ( ${\propto} a c S_{2}$);
6.
Diffuse gas restitution from these two star formation processes.
The rates for these processes are proportional to parameters $\mu $, H, a and K, which depend on galactocentric radius through the equations computed in FMPD. The proportionality factors of those equations are the corresponding efficiencies of processes, that is the probability of cloud formation, $\epsilon_{\mu}$, of cloud-cloud collision, $\epsilon_{\rm H}$, and of the interaction of massive stars with clouds, $\epsilon_{\rm a}$ in the disk, and the efficiency to form stars in the halo, $\epsilon_{\rm K}$. For each galaxy these characteristic efficiencies must be chosen, although the term of the induced star formation is associated to a local process and, as a result, its coefficient $\epsilon_{\rm a}$ is considered independent of both position and morphological type. The last term $\epsilon_{\rm K}$ is also assumed constant for all halos, thus being independent of morphological type. The other rates $\epsilon_{\mu}$ and $\epsilon_{\rm H}$, depend however on the Hubble type and/or the arm class, and their adopted variation range is determined following the arguments given by Ferrini & Galli (1988), as discussed in Mollá et al. (1996, 1999).


 

 
Table 3: Computed models.
Galaxy Model R0 $\tau_{0}$ $\epsilon_{\mu}$ $\epsilon_{\rm H}$
Name   (kpc) (Gyr)    

NGC 4303		 B 6 8 0.22 0.008
NGC 4303 M 6 16 0.20 0.005
NGC 4321 B 10 7.5 0.45 0.160
NGC 4321 M 10 15 0.45 0.320
NGC 4501 B 8 6.5 0.40 0.150


In order to reduce to a minimum the freedom degree due to the high number of parameters, the model has been applied following a precise strategy: first, it was used for the Solar Neighbourhood, followed by the MWG model, to determine the characteristic parameters of MWG. Then we afforded the final generalization for some other spiral galaxy, by assuming that the two efficiencies $\epsilon_{\rm a}$ and $\epsilon_{\rm K}$do not change from galaxy to galaxy. Therefore, we allow to change from galaxy to galaxy, only the characteristics collapse time scale, $\tau_{0}$, depending on the total mass and the two efficiencies, $\epsilon_{\mu}$ and $\epsilon_{\rm H}$, following the morphological type. The selection of each one of these input parameters in our models will be the matter of discussion in the following subsection.

The adopted initial mass function (IMF) is taken from Ferrini et al. (1990). The enriched material proceeds from the restitution from dying stars, considering their nucleosynthesis, their IMF (and the delayed restitution) and their final fate, via a quiet evolution, or types I or II supernova (SN) explosions. Nucleosynthesis yields are from Renzini & Voli (1981), and Woosley & Weaver (1995) for low-mass and intermediate, and massive stars, respectively. The type I supernova explosions release mostly iron following Nomoto et al. (1984) and Branch & Nomoto (1986) at a slower rate, by implying that the iron appear at least 1 Gyr later than the so-called $\alpha$-elements (oxygen, magnesium...) ejected by the massive stars.

3.2 Computed models

The collapse time scales have been chosen according to the above paragraph and their values are shown in Table 3. For the efficiencies, they usually turn out to be larger for earlier morphological types and lower for the later ones in MFD96, and this is useful for a first selection of the values for a given galaxy. The fine tuning is then performed, once the collapse time scale parameters $\tau_{0}$ and l chosen, when $\epsilon_{\mu}$ and $\epsilon_{\rm H}$ are constrained to reproduce the observational data. We use for this task the observed radial distributions for atomic gas H I (Warmels 1988; Cayatte et al. 1990), molecular gas H2, (Kenney & Young 1988; Kenney & Young 1989; Rownd & Young 1999), star formation rate surface densities, obtained from H$\alpha$ fluxes, from Kenney & Young (1989) and Rownd & Young (1999), and oxygen abundances of the gas phase $12+\log (\rm O/H)$ derived above. For NGC 4321 we also used the most recent data on H$\alpha$ fluxes and H I and H2 radial distributions from Knapen & Beckman (1996) and Knapen et al. (1996).

The set of models is shown in Table 3 where we give, for the region located at a distance R0, Col. (6), equivalent to the Solar Region, the corresponding values of the characteristic collapse time scale, Col. (7) and the two efficiencies $\epsilon_{\mu}$ and $\epsilon_{\rm H}$, Cols. (8) and (9).

3.3 The present-day radial distributions

In the following graphs we show the results derived from the chemical evolution models defined by the input data of Table 3, together with the corresponding observational data. Figures 6-8 show for each of the studied galaxies, the radial distribution of the oxygen abundance in panel (a); the star formation rate surface density normalized to its value for each equivalent solar region $\Psi_{0}$ in (b), the gas surface density of diffuse H I gas in (c), and the gas surface density of molecular gas H2 in (d).


  \begin{figure} \par\includegraphics[width=8.2cm,clip]{m1927f09.eps}\end{figure} Figure 9: Infall rate evolution for two regions in each galaxy, inner (4 kpc) - strong line - and outer (14 kpc) - slight line -.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.4cm,clip]{m1927f10.eps}\end{figure} Figure 10: Relation of oxygen abundances with the gas fraction $\mu $. The solid line represent the closed box model prediction, while points correspond to the radial distributions of oxygen abundances for the three galaxies at the present time as indicated in the figure.
Open with DEXTER

Abundances are really well reproduced for the three galaxies. By using the results derived in this work, the fit improves extraordinarily, in comparison with models from Mollá et al. (1999), where abundance estimates from the R23-method were used, thus supporting our new oxygen abundances.

Atomic gas radial distributions are quite well reproduced for all three galaxies, although they have a high gas surface density in the outer disks in comparison with the data. This difference between data and models does not appear in NGC 4303 models. For Model B of NGC 4321 it is ${\sim} 1{-}1.5~ M_{\odot}/\rm pc^{2}$ for $R > 10~\rm kpc$, while for Model M it does not exist. This implies that this last model is better able reproduce the outer disk, while the first one better fits the data in the inner regions. For the NGC 4501 model, the difference between data and models appears at $R> 8~\rm kpc$ and takes values comparable to the mean density in this outer disk. Summarizing, the discrepancy between models and data increases with decreasing distances to the center of the cluster, simulating perfectly the behavoir of the deficiency of the gas. This observed depletion of the diffuse gas from the outer regions of disks needs some mechanism producing this gas loss, which is not included in our models. Therefore we cannot reproduce this special feature of H I deficiency in the Virgo outer disks.

Molecular gas radial distributions differ slightly in the inner regions, but always close to the error bars. The uncertainties in the estimation of the molecular cloud masses, which are obtained from CO intensities through a calibration parameter $\chi$, are large because the dependence of $\chi$ on metallicity or galactocentric distance (Verter & Hodge 1995; Wilson 1995) in each galaxy is not completely well determinated.

These good results in the predicted gas radial distributions are, in fact, the consequence of searching models fitting these two distributions. Therefore the largest differences for a galaxy may only appear in the oxygen abundance and star formation rate radial distributions.

As we have already pointed out, abundances show a good behaviour, consistent with the data, while the shape of the star formation rate surface density radial distributions are well fit, showing exponential shapes, with the exception of Model B for NGC 4321 (panel d, Fig. 7). This model B predicts a star formation rate lower than the data in the inner regions. This also appears in Fig. 8 where a maximum rate is produced at 3-4 kpc and it implies that the model has a strong evolution, maybe more rapid than the actual evolution.

Thus, it seems that, following Figs. 6-8, our models reproduce the abundance data in Virgo galaxies well, and therefore we can use these models to explain the time evolution of Virgo galaxies. In order to see clearly the effects of the time evolution we show in Fig. 9 the infall rate for two regions, located at 4 and 14 kpc, and for model B of the three galaxies. We see that the infall rate is clearly higher in the inner region of NGC 4501 compared to the two other galaxies, NGC 4321 rests in middle of the two others, while NGC 4303 has a slow infall even in this central region. For the outer regions, the infall rate continues to be larger for NGC 4501, intermediate for NGC 4321 and low for NGC 4303, following the same trend as in the 4 kpc radial zone, but differences among galaxies are now smaller. All zones and galaxies show a similar and low infall rate at the present time. The most important difference resides in the fact that the infall rate had a very strong maximum during the first two Gyr for the inner diks in both NGC 4501 and NGC 4321, which finished at $\sim$5 Gyr, while NGC 4303 maintains a slow evolution, with an infall rate higher than that of the two others from 5 Gyr up to now.

These different infall rate histories have important effects on the oxygen abundances obtained along the galactic disk for these galaxies. We show in Fig. 10 the oxygen abundances, as 12 + log (O/H), for each radial region and galaxy vs. the gas fraction $\mu=M_{\rm gas}/M_{\rm disk}$. In this graph the solid line represents the closed box model prediction, while points correspond to the three disk radial distributions. The positions of NGC 4303 (circles), NGC 4321 (triangles), and NGC 4501 (squares) in the $\mu $-O/H diagram show that these galaxies evolve with some gas infall. We may see that the outer regions of NGC 4303 are close to the closed box model line, simulating a galaxy without mass exchange with the environment, while the inner regions have abundances smaller than the ones expected from their gas fraction according to the closed box model. NGC 4321 and NGC 4501 show a strong decrease in its abundances for their inner regions, and there is, even for the outer ones, some dilution effect. All these regions have very low gas fractions, which according to the closed box model should correspond to the highest abundances, 9.0-9.10; however this is not the case, and the abundances are lower than these values.

Thus, our models show that both H I normal and H I deficient galaxies have their oxygen abundances depressed by infall of metal-poor gas. Indded, the model for the NGC 4501 (a representative of the H I deficient Virgo core spirals) shows that the inner regions of NGC 4501 have very low gas fractions and therefore even a slow infall rate at the present epoch results in a dilution effect, and the evolution of Virgo core spirals are somehow similar to that of field spirals. Taking into account that our models reproduce the data well for the three galaxies, in particular the gas densities and abundances, this conclusion does not depend on the goodness of the hypotheses or theoretical assumptions.

4 Discussion

In order to make sure that our models are in agreement with the whole set of new results for the cluster galaxies and in particular for Virgo, we will summarize these observations. Solanes et al. (2001) have derived the atomic content for a total of 1900 galaxies in 18 nearby clusters, aiming to study possible connections between the gas deficiency and the characteristics of the galaxies or their environment. With these data it is well established that the proportion of gas-poor galaxies increases continuously toward the center of the cluster for a large number of them. Furthermore, there are clear indications that the removal of H I occurs mostly in the outer regions of disks, thus implying that the H I disk sizes are reduced (Warmels 1988; Cayatte et al. 1990; Cayatte et al. 1994), and that the degree of the H I depletion is related to the morphological type, early types and dwarfs being more easily emptied of gas than intermediate types.

On the other hand, the analysis of the spectroscopic catalog of distant clusters performed by Dressler et al. (1999) and Poggianti et al. (1999) show that the star formation rate has been quenched, rather than enhanced, in these galaxies. This conclusion has been also reached by Caldwell et al. (1999), who found that star formation takes place in the inner regions of these galaxies, but it is suppressed in the outer ones. Moreover the colors of these galaxies (Gavazzi et al. 1991; Gavazzi et al. 1998) do not differ significantly from those of field galaxies for the same morphological types, and the molecular gas content, usually more concentrated in the inner disks, show normal masses (Kenney & Young 1988, 1989).

Thus, the scenario necessary to reproduce all observations must be able to eliminate the gas of the outer regions, but not in the inner disk, and at the same time, it has to form stars at the early times of evolution, in order to obtain the red colors observed and the star formation rates estimated for the present time. The most extended idea is that the mechanism producing this removal of gas is the ram pressure stripping due to the orbit of each galaxy around the core of the cluster. Under this assumption the low density diffuse gas may be eliminated when the galaxy passes close to this core, while the higher density molecular clouds located in the inner disk should not be affected.

Recently, Vollmer et al. (2001) have performed some N-body simulations in order to study the effects of this mechanism on a galaxy suffering ram pressure stripping by its motion within the cluster. They find that the movement of the galaxy around the cluster center provokes an acceleration of the clouds located on the surface of the disk, which, in turn, produces a high surface density in the center of the galaxy. Thus, the star formation can suffer an enhancement in the inner disk. After this phase, the gas of the outer regions is removed and, without this fresh gas reservoir, the star formation decreases.

Within this scenario, the high density produced in the inner regions of the galaxy is the consequence of a strong infall rate on a short time scale. This is exactly what happens in the NGC 4501 model, where the inner disk suffers a large infall rate in a short time, by creating stars very rapidly. The consequence is the consumption of the gas, and therefore star formation stops. For a Virgo periphery galaxy, as NGC 4303, the infall is much slower, maintaining a more constant star formation rate along its evolution, similar to the typical one of a field galaxy. The model for NGC 4321 has a behavior intermediate between both of them. This explains why the star formation rate is, for the present time, higher for NGC 4303, which still has enough gas, while this rate has decreased for NGC 4321 from its maximum value, and it is very depressed for NGC 4501, which has almost no gas. These model predictions are supported by the observations from Koopmann & Kenney (1998) and Rownd & Young (1999) who find that the star formation efficiency decreases with increasing H I deficiency among the Virgo cluster galaxies. In fact the H$\alpha$ luminosities give values $\log L= 8.38$, 7.97 and 7.96 $L_{\odot}$ for NGC 4303, 4321 and 4501, respectively, following these latter authors.

We would like to add some other considerations about our models. Koopmann & Kenney (1998) found that the morphological classification for the Virgo cluster galaxies does not follow the same scheme as the one used for the field galaxies. In this last case the concentration index (measured as the bulge to disk luminosity ratio) is correlated with the star formation in the arms, while in the cluster galaxies it does not occur: due to the H I deficiency in the outer disk, the concentration index increases for a given H$\alpha$ flux, as a measure of the star formation rate. Thus if it corresponds to a Sc galaxy, the concentration index would define the galaxy as Sa. This fact implies that the Virgo galaxies would be classified as earlier types whereas their star formation rates would correspond to later types of galaxies. In this sense, it appears remarkable that our models reproduced the observed characteristics of the three selected galaxies with efficiency values lower than those typically used for their morphological types, and closer to the values corresponding to one unity later morphological types.

5 Conclusions

The oxygen and nitrogen abundances in H II regions in the nine Virgo spirals of the sample from Skillman et al. (1996) and in nine selected field spiral galaxies were re-determined with the recently suggested P-method.

It has been confirmed that there is an abundance segregation in the sample of Virgo spirals in the sense that the H I deficient Virgo spirals near the core of the cluster have higher oxygen abundances in comparison to the spirals at the periphery of the Virgo cluster. In general, both Virgo periphery and Virgo core spirals have counterparts among field spirals. Some field spirals have a small H I to optical radius ratios, similar to the one in H I deficient Virgo core spirals. It has been concluded that if there is an actual difference in abundance properties between the Virgo and field spirals this difference should be small or entirely masked by the errors.

These abundance results have been analyzed with the multiphase chemical evolution model, applied to three galaxies NGC 4501, 4321 and 4303, considered as typical examples of galaxies located at the center, at intermediate locations, and at the periphery of the cluster. These models are shown to be able to reproduce the observations of abundances, star formation rate and diffuse and molecular gas densities. Following these models the infall rate was strong at early times and it is very low now for the Virgo core galaxies, but with features continuously smoother for the periphery galaxies. The consequence of the infall of the gas is the dilution of the elements, and therefore lower abundances than those expected with the closed box model, for the gas fractions in the center galaxies, are predicted. Thus, the final abundances turn out to be similar to the ones present in field galaxies.

The scenario of the ram pressure stripping usually claimed to produce the observed characteristics in the cluster galaxies, such as a H I deficiency, which is larger for the galaxies closer to the cluster, was recently simulated with N-body models by Vollmer et al. (2001). Following this work, a large infall rate is produced in the inner regions of the disk of these galaxies, as a consequence of their movement towards the cluster core, with a posterior phase of quenching of the star formation; these results appear consistent with our conclusions.

Acknowledgements
We thank Prof. A. I. Díaz and Dr. M. Castellanos for useful discussions. L.S.P. is grateful to the staff of the Grupo de Astrofísica (Universidad Autónoma de Madrid) for hospitality during a visit when a part of this work was carried out. This study was partly supported by the NATO grant PST.CLG.976036 (L.S.P., M.M., and F.F.), the Joint Research Project between Eastern Europe and Switzerland (SCOPE) No. 7UKPJ62178 (L.S.P.), the grant No. 02.07/00132 of the Ukrainian fund for fundamental investigations (L.S.P.), and the Spanish Ministerio de Ciencia y Tecnologia project AYA-2000-093 (M.M.). We thank an anonymous referee for helpful comments.

References

 

Copyright ESO 2002