1 - Department of Computer Science, Jinan University, Guangzhou 510632, PR China and United Laboratory for Optical Astronomy, Chinese Academy of Sciences
2 - Institut de mécanique céleste et de calcul des éphémérides, Observatoire de Paris, UMR 8028 du CNRS and
Université de Lille, 59000 Lille, France
3 - Shanxi Astronomical Observatory, Chinese Academy of Sciences, Lintong, Shanxi 710600, PR China and Chinese National Astronomical Research Center

Abstract
A positional measuring procedure for the eight major satellites of Saturn (Mimas, Enceladus, Tethys, Dione, Rhea, Titan, Hyperion and Iapetus) is developed. Using this procedure, 199 frames of CCD images, obtained with the 1-meter telescope at the Yunnan Observatory from 1996-2000, are measured. These positions are compared to the ones computed with the Vienne & Duriez ephemerides (TASS1.7). The calibrated parameters of the CCD scale and orientation are determined by the comparison of their measurement coordinates with computed positions of four bright satellites: Tethys, Dione, Rhea and Titan. A catalog of 913 differential positions has been obtained. Analysis of the data as inter-satellite positions shows that these observations of the above-mentioned four satellites have root-mean-square residuals of 0.04 arcsec in the sense of (O-C) (Observed minus Computed). The positional measuring procedure is shown to be good enough to obtain a small dispersion in the observations for the major Saturnian satellites.

Key words: planets and satellites: individual: Saturn - techniques: image processing - astrometry

Astrometric observations of the eight major Saturnian satellites (S1-S8) have a long history of more than 100 years. Usually, traditional meridian observations, photographic observations, high precision mutual observations and CCD observations can be obtained. Nowadays, a CCD chip has been adopted as a regular receptor for many long-focus telescopes as a replacement for a photographic plate. Probably, CCD chips will be mainly used for a long time for the astrometry of the satellites. To refine their ephemerides to be compatible with the existing and planned spacecraft missions (CASSINI, for example), a large number of observations with high precision for the major saturnian satellites are continuously needed. Theoretical research on the Saturnian satellites has made a great progress. For instance, the theories of Taylor & Shen (1988), Dourneau (1993), Harper & Taylor (1993) and TASS 1.7 (Vienne & Duriez 1995; Duriez & Vienne 1997) have been developed in less than one decade. The internal precision for these theories are quite good. For example, TASS presents high precision of about ten kilometers (Vienne & Duriez 1995).

It is well known that, since the scattered light from Saturn and its rings can cause a strong gradient in the background level near its satellite, the center of its satellite is shifted towards the planet center. The shift is very significant and systematic in nature and needs to rectify to a flat background by subtracting the scattered light contributed by the planet and its rings.

Various techniques have been devised over the years for making this type of subtraction for other planets as well as Saturn. For example, an analytic subtraction of a planet and its scattered light was successfully adopted by Pascu et al. (1987) for Miranda. A similar method, which made a supposition of circular symmetry for the scattered light (see Eqs. (2) and (3) in Stone & Harris 2000), was developed for FASTT CCD observations at the USNO, Flagstaff. Another successful example was a planet-symmetry method devised by Veiga & Martins (1995) for Uranian satellites. Also, Colas & Arlot (1991) found the center of Phobos and Deimos from CCD observations, calculating the center of light after the subtraction of the background that is fitted by a polynomial surface. In addition, Beurle et al. (1993) calculated the center of each Saturnian satellite by using a centroid algorithm that chooses a small box in order to minimize the effects of gradients in the background close to the heavily over-exposed image of Saturn and its rings.

This paper presents an alternate positional measuring procedure, which is expected to remove the halo light of Saturn and its rings. Section 2 gives some specifications of the telescope and CCD chip for experimental observations. In Sect. 3, the procedure is described in detail. The following section includes the solution for calibration parameters for the CCD chip used. Section 4 deals with the calibrated positions. We present in Sect. 5 the comparison of the obtained positions with those deduced from the ephemerides. We also compare our results with some previous important ones and give a catalog of the corresponding astrometric data. Finally, concluding remarks are given in Sect. 6.

2 The instrumentation and observations

**Table 1:** Specifications of Yunnan Observatory 1-meter telescope and the attached CCD chip.
Focal length	1300 cm
F-Ratio	13
Diameter of Primary mirror	100 cm
CCD field of view	6 $.\mkern-4mu^\prime$ 4 $\times$ 6 $.\mkern-4mu^\prime$ 4
Size of pixel	24 $\mu$ $\times$ 24 $\mu$
Size of CCD array	1024 $\times$ 1024
Angular extent per pixel	0 $.\!\!^{\prime\prime}$ 37/pixel

During the years 1996-2000, 5 nights of observations with 199 frames of CCD images in total were obtained with the 1-meter telescope at the Yunnan observatory (Longitude E102 47 $.\mkern-4mu^\prime$ 3, Latitude N25 1 $.\mkern-4mu^\prime$ 5 and Height 2000 m above sea level). In Table 1, some specifications for the telescope and CCD chip are given.

**Table 2:** The number of pairs of pixel coordinates (x,y) of each satellite is given. The total is 1112 for all satellites. The first column denotes the data subset designation corresponding to observational dates (in Col. 2). The third column denotes the filter used, and the fourth column denotes the exposure time.
Subset	Date	Filter	Exp-time (s)	Mimas	Enceladus	Tethys	Dione	Rhea	Titan	Hyperion	Iapetus
1996	10/30	I	5-10	54	54	0	54	54	0	0	54
1997	10/10	I	1-5	0	24	24	24	24	24	0	0
1999	12/1 12/2	B	5-10	0	49	49	49	49	49	49	0
2000	11/17	I	5-8	0	34	72	34	72	72	72	72
total				54	161	145	161	199	145	121	126

For experimental observations, Johnson I-type and B-type filters were used. The use of the B-type filter was originally devised to decrease the brightness for both the primary planet and its satellites and to increase the exposure time so that the relative positions between satellites have quite good precision. We will see in Sect. 5.1 that the design is not profitable. Table 2 gives the raw measurement statistics for the number of pairs of pixel coordinates (x,y) of each satellite, observational dates, filter used and exposure time.

Unfortunately, Titan did not appeared in the CCD field of view for the data subset of 1996 due to the lack of experience.

3 Positional measuring procedure

In order to obtain raw pixel coordinates for some Saturnian satellites in the proximity of the planet and its rings (usually, Mimas, Enceladus, Tethys, Dione and Rhea), the following steps are adopted.

Step 1: by adjusting image brightness and contrast, we can see Saturn and its rings or parts of its rings (see Fig. 1). The pixel coordinates of two terminal points for the rings' maximum axis can be measured visually by a + type cursor. Therefore, the equations for the maximum axis and the minimum axis of the Saturnian ring image can be solved easily.

Step 2: suppose that the count distribution I(i,j) in the pixel coordinates (i,j) on an image is symmetric relative to the ring maximum axis or/and minimum axis. Then, the halo light in the area of a measured satellite is thought to be removed by a simple abstraction of its count distribution by its symmetric area (Fig. 2). The symmetric area may be chosen relative to the ring maximum or minimum axis, depending on which area is nearer to the measured satellite. The reason is that the above-mentioned supposition is thought to be satisfied better in this manner.

Step 3: determination of the satellite center. Theoretically, several centering algorithms for a star image can be used to determine the satellite center after the above two steps. However, a satellite, especially one close to Saturn and its rings is still located on an uneven background. Moreover, the planetary motion during the observation can elongate the satellites image. According to Stone (1989), a modified moment, method which suppressed the sky background through a process of image thresholding is a very good routine for dealing with high sky background levels. The method offers a significant gain in accuracy, particularly for weak images over the traditional treatment of the moment (Auer & van Altena 1978). Specifically, once the background level bis determined in the I(x,y) data array, each pixel in the array is thresholded according to the following precepts:

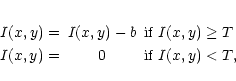
Now, a further modified version of the moment is developed in which Treplaces the b in the first precept. Experiment tests with actual observations (Ji & Wang 1996; Peng & Mao 1998) have shown that the new version of the moment method is even better, especially for weak stars or natural satellites. For Saturnian satellites, another slight modification is made to the threshold T. For Mimas, Enceladus and Hyperion, $T=b+2\sigma$ or even $T=b+\sigma$ is used depending on the signal-noise-ratio of the measured satellites. During our image processing, the moment method for a measured satellite center chooses a small rectangle, and the mean background band its rms (root-mean-square) error $\sigma$ are determined with another small rectangle near the satellite. The sizes of the two small rectangles can be conveniently adjusted. Usually, we keep them approximately equal (see Fig. 2). Last, for the satellites Titan, Hyperion and Iapetus, Step 1 and Step 2 are usually neglected.

4 Calibration

Most often, there is no good reference star on the frames which would allow us to do a complete astrometric reduction. So, we use an astrometric reduction for the case of inter-satellite measurements. The detailed description of this reduction can be seen in Vienne et al. (2001b). One can see also Vienne et al. (2001a) in which the reduction has been applied.

The frames registered and measured in pixels are comparable with ephemeris after taking into account some local effects: the atmospheric refraction, the stellar aberration, the central projection (projection of the celestial sphere on the tangential plane of the focal point), the light traveling time between the satellites and the diurnal parallax. These differential astrometric corrections done here were not automatically taken into account in previous works (see Vienne et al. 2001a).

We use TASS1.7 (Vienne & Duriez 1995; Duriez & Vienne 1997) for the saturnicentric positions of the satellites. According to Shen et al. (2001), TASS is now the best contemporary dynamical theory for Saturnian satellites and it is suggested to use TASS alone in the CCD reduction. We use the four satellites Tethys, Dione, Rhea and Titan to calibrate the scale and orientation of the CCD chip in each data subset. As we stated before, Titan was not observed in the 1996 data subset and only Dione and Rhea were used for the calibration. The positions of Saturn are given by the ephemerides SLP96 from the "Institut de mécanique céleste (IMCCE)'' (available at ftp://ftp.bdl.fr/pub/ephem/sun/slp96/) based on the VSOP87 planetary theory (Bretagnon & Francou 1988).

At a given date corrected for the light-travel time between the satellites, we compute the apparent coordinates, $X_{\rm c}$ and $Y_{\rm c}$ , of the satellites. We use the corresponding positions $(x_{\rm p},y_{\rm p})$ given in pixels from the observed frame. So, with the relation $\left( \begin{array}{rr}a & b\\ -b & a \end{array}\right) \left( \begin{arra... ...\right) -\left( \begin{array}{c} X_{\rm c}\\ Y_{\rm c} \end{array}\right) =0$ , we compute an estimation $\widetilde{a},\widetilde{b}$ of a and b by a least square procedure. We deduce the scale factor $\rho =\sqrt{\widetilde{a}^{2}+\widetilde{b}^{2}}$ and the orientation of the receptor (the angle from the $x_{\rm p}$ -axis of the camera to the true equator) $\varphi =\arctan (\widetilde{b},\widetilde{a})$ . This procedure is applied for a set of frames. A series of frames can cover several nights. So, we suppose that the receptor has been mounted in the same way for all frames of the series. Table 3 gives the solved scale and orientation for each data subset.

**Table 3:** The calibration parameters for the scale and orientation of CCD chip for each data subset. Note that $\Delta \rho \simeq \rho \Delta \varphi$ .
Subset	$\rho$ : Scale	$\varphi$ : Orientation
	(arcsec/pixel)	(radian)
1996	$0.3733478\pm .0000069$	-3.12607864
1997	$0.3737157\pm .0000173$	-3.10915524
1999	$0.3736810\pm .0000066$	+3.12735097
2000	$0.3737871\pm .0000045$	+3.10169865

The astrometric positions $(\Delta \alpha \cos \delta ,\Delta \delta )$ we have obtained are given in the J2000 system and all significant astrometric corrections have been done. But, for a given series, they are given apart from a scale factor and from a rotation. One can find in Vienne et al. (2001b) more details and a discussion of the method for the case of inter-satellites measurements. For example, as it is explained there, if we want to compute the astrometric coordinates in any other way (e.g.: with other ephemerides), we have only to touch up $\varphi$ and $\rho$ .

5 Results and comparisons

5.1 mean residuals (O-C) and comparisons

**Table 4:** Observed minus Computed (O-C in mas) of each satellite. Ngives the number of observations used. These residuals are relative to Titan (or Rhea for 1996 subset). The last lines give the global residuals of S3, S4, S5 and S6 (for which the positions have been used in the reduction).
1996		$\Delta \alpha \cos \delta$		$\Delta \delta$
satellites	N	means	rms	means	rms
S1-Mimas	54	-21	58	-16	47
S2-Enceladus	54	-6	24	-45	51
S4-Dione	54	+0	20	+0	17
S8-Iapetus	54	-150	150	-81	83
1997		$\Delta \alpha \cos \delta$		$\Delta \delta$
satellites	N	means	rms	means	rms
S2-Enceladus	24	+1	92	+20	90
S3-Tethys	24	+4	42	-2	42
S4-Dione	24	-10	65	-4	68
S5-Rhea	24	+8	86	+5	81
S3 S4 S5 S6	72	+1	67	+0	66
1999		$\Delta \alpha \cos \delta$		$\Delta \delta$
satellites	N	means	rms	means	rms
S2-Enceladus	49	+9	46	-11	49
S3-Tethys	49	+9	37	+0	53
S4-Dione	49	+6	34	-1	36
S5-Rhea	49	-19	38	-5	45
S7-Hyperion	49	-38	92	+104	138
S3 S4 S5 S6	147	-1	36	-2	45
2000		$\Delta \alpha \cos \delta$		$\Delta \delta$
satellites	N	means	rms	means	rms
S2-Enceladus	34	-57	62	+12	42
S3-Tethys	72	-5	23	-5	29
S4-Dione	34	-34	37	-5	25
S5-Rhea	72	+26	31	+1	20
S7-Hyperion	72	+2	22	-26	43
S8-Iapetus	72	-8	23	-20	39
S3 S4 S5 S6	178	+2	29	-3	25

Table 4 gives the mean residuals (O-C) (Observed minus Computed) and rms (root-mean-square) errors for each satellite with respect to Titan or Rhea (only for 1996 subset).

**Table 5:** Statistics in mas of all satellites and for the four satellites Tethys, Dione, Rhea relative to Titan (for 1996 data subset, all satellites are relative to Rhea).
	N	mean	rms	mean	rms
		$\Delta \alpha \cos \delta$	$\Delta \delta$
S1 to S8	913	$-14\pm 2$	58	$-7\pm 2$	56
S3 S4 S5 S6	451	$1\pm 2$	39	$-2\pm 2$	40

Table 5 gives the statistics of all eight satellites relative to Rhea or Titan and Table 6 gives the comparison of this work with some previous important photographic data or the latest CCD observations.

**Table 6:** Comparisons of our residuals with some important photographic or the latest CCD observations: AOC28 (Alden & O'Connel 1928), A29 (Alden 1929), VD92 (Veillet & Dourneau 1992), H+97 (Harper et al. 1997) and Q+99 (Qiao et al. 1999, in polar coordinates). Statistics are based upon residuals, in mas, of observations of Tethys, Dione, Rhea and Titan.
data set	$\Delta \alpha \cos \delta$			$\Delta \delta$
	N	mean	rms	N	mean	rms
AOC28	192	-40	90	192	+10	70
A29	108	-30	90	109	+0	60
VD92	434	-7	130	434	+12	100
H+97	891	-7	70	891	+1	90
Q+99,	381		80	381		90
this work	451	+1	40	451	-2	40

Tables 5 and 6 show that our residual dispersion between the inter- satellites of Tethys, Dione, Rhea and Titan is quite small in comparisons to the best photographic or the latest CCD observations. Poor tracking probably causes the slightly bigger rms error in the 1997 data subset (Table 4). Even so, no obvious systematic difference is found in the mean residuals. It shows that our positional measuring procedure would be good to deal with the situation. By comparing Table 2 with Table 4, when I-type and B-type filters are used, no obvious systematic difference is found, either.

5.2 Format of observations

Table 7: Extract of the catalog.
opp year m day (utc) tt-utc obs. ref. t obj. fl obs1 obs2 s f O-C1 O-C2 r - s xpix ypix

s arcsec (degree for C*) arcsec pixel

119 1996 10 30.5749132 62.184 286 302 1 15 11 -46.9204156 5.9172545 2 1 -0.118 0.049 5 0 1 125.874 -13.889

119 1996 10 30.5749132 62.184 286 302 1 25 11 -110.7493305 10.4010887 2 1 -0.009 -0.011 5 0 1 296.961 -23.235

119 1996 10 30.5749132 62.184 286 302 1 45 11 -132.9961025 12.0523440 2 1 -0.015 0.021 5 0 1 356.595 -26.729

119 1996 10 30.5749132 62.184 286 302 1 85 11 -45.2907571 -73.3128335 2 1 -0.178 -0.047 5 0 1 18.229 198.165

119 1996 10 30.5749132 62.184 286 302 1 C5 11 165.2981011 156.5448468 2 1 999.999 999.999 5 0 1 -436.203 -426.105

119 1996 10 30.5749132 62.184 286 302 0 C* 11 2.5913720 -1.6771020 2 1 999.999 999.999 5 0 1 99999.999 99999.999

119 1996 10 30.5791782 62.184 286 302 1 15 11 -46.6083017 5.8987671 2 1 0.065 0.005 5 0 1 125.038 -13.853

...

123 2000 11 17.7913715 64.184 286 302 0 C* 11 55.9767122 17.4245495 2 1 999.999 999.999 6 0 4 99999.999 99999.999

123 2000 11 17.7926910 64.184 286 302 1 86 11 -144.3442720 102.5517423 2 1 0.004 -0.038 6 0 4 374.639 -289.620

123 2000 11 17.7926910 64.184 286 302 1 76 11 26.3411600 -128.1610231 2 1 -0.011 -0.026 6 0 4 -56.637 345.324

123 2000 11 17.7926910 64.184 286 302 1 36 11 -184.5224289 -78.6382809 2 1 -0.001 -0.053 6 0 4 501.580 190.230

123 2000 11 17.7926910 64.184 286 302 1 56 11 -134.3295440 -26.6458330 2 1 0.048 -0.035 6 0 4 361.828 56.721

123 2000 11 17.7926910 64.184 286 302 1 26 11 -119.7285179 -69.6868116 2 1 -0.011 -0.026 6 0 4 327.454 173.319

123 2000 11 17.7926910 64.184 286 302 1 46 11 -125.4039624 -84.4916109 2 1 -0.023 -0.034 6 0 4 344.219 212.269

123 2000 11 17.7926910 64.184 286 302 1 C6 11 117.9793628 131.0317168 2 1 999.999 999.999 6 0 4 -329.373 -337.667

123 2000 11 17.7926910 64.184 286 302 0 C* 11 55.9763859 17.4246366 2 1 999.999 999.999 6 0 4 99999.999 99999.999

Using $\rho$ and $\varphi$ determined in Table 3, and applying once more, but inversely, the local deformations, we get the coordinates $(\alpha ,\delta )$ of each measured object. The coordinates $(\alpha ,\delta )$ are astrometric, but there is an absolute part $\alpha _{C}$ and $\delta _{C}$ which does not come from the observations. C is defined so the frame is the tangential plane of the celestial sphere at C. In order to not interpret the observations as absolute ones, we give them in inter-satellite form. That is $(\alpha _{\rm o}-\alpha _{\rm r})\cos \delta _{\rm r}$ and $\delta _{\rm o}-\delta _{\rm r}$ . The index $_{\rm o}$ is for the satellite object, and the index $_{\rm r}$ for the reference satellite. The catalog contains astrometric coordinates, in the J2000 system, of the observations. All raw pixel coordinates are also included in it. The dates correspond to the mid-time of the exposure. This date is not light-time corrected. Table 7 gives an extract from the first and last parts of the catalog of the 913 Saturnian satellites' differential positions for all observed satellites. The format of the catalog is the same as (Vienne et al. 2001a), and it is similar to that of Strugnell & Taylor (1990). The full catalog is available on request at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5). In FORTRAN code, one line is read with the format:

2(1x,f13.7),2i2,2(1x,f7.3),3i3,2f10.3).
Here is a rapid description of the content of each record:

6 Conclusion

A positional measuring procedure is developed with the main aim of removing the halo light effect from Saturn and its rings on the background of its near satellites. In the procedure, a modified moment method for centering algorithm for Saturnian satellites is used. When the procedure is applied to 199 frames of CCD observational images obtained with the 1-meter telescope at the Yunnan Observatory during the years 1996-2000, 913 pairs of inter-satellites observations were obtained. The root-mean-square residual for four satellites of Tethys, Dione, Rhea and Titan is 0.04 arcsec after analysis of the data. It is proved that the procedure is good enough to obtain high accuracy observations for Saturnian satellites. Besides, no obvious difference between the two residuals from the I type filter and the B-type filter is found. Even so, the use of B-type filter is not profitable. We will use a I-type filter in future observations.

Positional measuring procedure and CCD observations for Saturnian satellites

1 Introduction