A&A 383, 153-162 (2002)
DOI: 10.1051/0004-6361:20011719
A study of spatial structure of galactic open star clusters
Nilakshi 1 - R. Sagar1,2
- A. K. Pandey1
- V. Mohan1
1 - State Observatory, Manora Peak, Nainital 263 129, India
2 -
Indian Institute of Astrophysics, Bangalore 560 034, India
Received 14 May 2001 / Accepted 8 November 2001
Abstract
In order to study the relation between the core and corona in
galactic star clusters, the spatial structure of 38 rich open star clusters has
been studied using radial density profiles derived from the photometric data of
the Digital Sky Survey. The shape of the radial density profile indicates
that the corona, most probably, is the outer region around the cluster. It can
exist from the very beginning of the cluster formation and dynamical
evolution is not the reason for its occurrence. The study does not find any
relation between cluster size and age but indicates that the clusters with
galacto-centric distances >9.5 kpc have larger sizes. Further, we find that
the average value of the core radius is
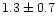 pc and that of annular width
of the corona is
pc and that of annular width
of the corona is
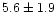 pc, while average values of densities of cluster
members in the core and corona are
pc, while average values of densities of cluster
members in the core and corona are
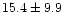 star/pc2 and
star/pc2 and
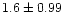 star/pc2 respectively. Average field star contaminations in the core and
corona are
star/pc2 respectively. Average field star contaminations in the core and
corona are 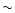 35% and 80% respectively. In spite of smaller densities
in the coronal region, it contains
35% and 80% respectively. In spite of smaller densities
in the coronal region, it contains 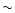 75% of the cluster members due to
its larger area in comparison to the core region. This clearly demonstrates
the importance of the coronal region in studies dealing with the entire stellar
contents of open star clusters as well as their dynamical evolution. In contrast
to the cluster cores, the structure of coronal regions differs significantly
from one cluster to other.
75% of the cluster members due to
its larger area in comparison to the core region. This clearly demonstrates
the importance of the coronal region in studies dealing with the entire stellar
contents of open star clusters as well as their dynamical evolution. In contrast
to the cluster cores, the structure of coronal regions differs significantly
from one cluster to other.
Key words: galaxy: open clusters and associations: general - stellar content
The stars of a stellar cluster are presumably the offspring of the same
interstellar dust and clouds that are born together. Hence, they are
dynamically associated and gravitationally bound and are located approximately
at the same distance. A spatial structure represents how sibling stars are
distributed within a family of stars (cluster) according to their
mass or brightness. The study of the spatial structure of a star cluster
therefore provides an opportunity to determine the mechanisms and conditions
of cluster formation at different stages of a galactic evolution. At the
beginning of the 20th century, Shapley (1916), pointed out that the dimensions
of star clusters considerably exceed the sizes that are obtained directly by
simple eye estimates. However, no detailed studies of outer regions of clusters
were carried out until the 1960s. Artyukhina & Kholopov (1959, 1963,
1966), Artyukhina (1966) and Kholopov (1969) suggested that all clusters, from
very sparse ones like Coma Bernices to the richest of all the Galactic globular
clusters have unity not only in origin and development (Elmegreen & Efremov
1997) but also show unity in the structure and have come to believe that these
extended regions represent very important structural properties of the star
clusters. Now, it is well established that every cluster consists of two main
regions: (i) nucleus (or core) which is the densest central part of the system,
the region that is perceived directly by the eye as a star cluster and (ii)
halo (or corona ) which is an outer and extended region with lower density
around a cluster, that contains a substantial number of cluster members.
Until recently most studies have been made of the nuclei which have been
taken to represent the clusters as a whole. Extensive studies of the coronal
regions have not been carried out mainly because of the non-availability of
photometry in a large field around the star clusters. The study of stars in the
coronal region is important for the following main reasons.
Wilner & Lada (1991) observed the presence of dip in luminosity function at
magnitudes
1.5 < Mv < 3.5 and they give two possible explanations for the
observed deficit of low luminosity stars in NGC 2362: (i) a significant
populations of low luminosity cluster stars are present in the outer part of the
cluster or (ii) the cluster IMF is different from Salpeter (1955) field star IMF
in the vicinity of Sun.
Until some years ago, unlike the coronal region of globular clusters, the
coronal regions of open clusters did not attract sufficient attention although
from a dynamical point of view they represent an exciting and challenging field
of study. On the observational side, the challenge is to isolate the
cluster members from the general field stars, as open star clusters (OCls) are
usually projected against rich stellar fields of the Galactic disk. On the theoretical side, open clusters are considered dynamically active systems.
Unlike globular clusters and galaxies, where two body relaxation
times are very much longer than the crossing times and the system can be
considered to be in quasi-static equilibrium, the crossing and relaxation times
of open clusters are more commensurate with each other. Thus the evolution of
clusters, velocity-distribution due to stellar encounters cannot be treated
independently of the orbital mixing of the distribution. It is thus essential
to study the dynamics of small number (N) stellar systems like the open clusters
as compared to large N systems because any differences in their velocity
distributions that occur due to the close stellar encounters with clouds in the
interstellar medium or passing molecular clouds or the effect of galactic tidal
field will appear primarily in the high energy tails of the distributions.
Turner (1982) recommend that it is necessary to fully delineate the boundaries
of the cluster nucleus and corona to strengthen the case for the cluster
membership of Cepheid variables e.g. of V Cent. in NGC 5662.
The above discussions clearly indicate that a systematic study of the spatial
stellar distribution in OCls would be desirable and the same has been presented
here. The criteria used to select the clusters for the present study are
described in the next section.
If existence of the corona observed in the open clusters is a reality then it is
important to know whether the corona is due to the dynamical evolution or is an
imprint of the star formation process itself. This question may be better
understood by studying and comparing the OCls of all ages, very young to
extremely old. Another significant aspect to be addressed is to determine if the
existence of a corona in an open cluster is position-dependent in the Galaxy. In
order to answer these questions, one would like to consider the OCls situated
not only in different locations of the Galaxy but also having a
statistically significant number of stars for the study of coronal regions.
We have therefore selected only rich clusters from the open clusters' catalogue
(Lyngå 1987) covering a range in age and galactic position, except
the binary and multiple clusters. We exclude them because their proximity
tends to influence each others dynamics which makes the determination of their
individual radial density profiles (RDPs) 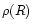 unreliable. If there is more
than one cluster in the
unreliable. If there is more
than one cluster in the
 area around the cluster in
consideration, they are treated as binary/multiple clusters and hence, not
considered for the study. Some of the clusters excluded in this way are indeed
found to be binary cluster e.g. NGC 869, NGC 884 and NGC 1912 (Subramaniam
et al. 1995). We have also excluded some clusters whose
area around the cluster in
consideration, they are treated as binary/multiple clusters and hence, not
considered for the study. Some of the clusters excluded in this way are indeed
found to be binary cluster e.g. NGC 869, NGC 884 and NGC 1912 (Subramaniam
et al. 1995). We have also excluded some clusters whose 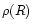 can not be
used in the present study due to the limitations discussed below.
can not be
used in the present study due to the limitations discussed below.
Table 1:
General information about the clusters under study with their
sequence and IAU names. Galactic longitude (l) and latitude (b) in degrees,
diameter (D) in arcmin and Trumpler concentration classification are taken form
Lyngå's (1987) catalogue while distance (d) in pc and log (t) where t is the
age in years are borrowed from Loktin et al. (1994) catalogue, if available.
Otherwise (asterisked clusters) they are taken from Lyngå's (1987) catalogue.
| Name |
IAU name |
l |
b |
Trumpler |
D |
d |
Log (t) |
| NGC 188 |
C0039+850 |
122.8 |
22.5 |
I2r |
13 |
1675 |
9.8 |
| NGC 654 |
C0140+616 |
129.1 |
-0.3 |
II2r |
5 |
2422 |
7.1 |
| NGC 663 |
C0142+610 |
129.5 |
-0.9 |
II3r |
16 |
2284 |
7.1 |
| NGC 1245 |
C0311+470 |
146.6 |
-8.9 |
II2r |
10 |
2608 |
9.2 |
| NGC 1817 |
C0509+166 |
186.1 |
-13.1 |
IV2r |
15 |
2132 |
8.9 |
| NGC 1960 |
C0532+341 |
174.5 |
1.0 |
I3r |
12 |
1285 |
7.5 |
| NGC 2099 |
C0549+325 |
177.6 |
3.1 |
I2r |
23 |
1356 |
8.5 |
| NGC 2244 |
C0629+049 |
206.4 |
-2.0 |
II3r |
23 |
1640 |
6.8 |
Trumpler 5 |
C0634+094 |
202.9 |
1.0 |
III1r |
7 |
977 |
9.9 |
| NGC 2301 |
C0649+005 |
212.6 |
0.3 |
I3r |
12 |
857 |
8.2 |
| NGC 2323 |
C0700-082 |
221.7 |
-1.2 |
II3r |
16 |
997 |
8.0 |
| NGC 2345 |
C0706-130 |
226.6 |
-2.3 |
II3r |
12 |
1947 |
7.6 |
| NGC 2354 |
C0712-256 |
238.4 |
-6.8 |
III2r |
20 |
2089 |
8.8 |
| NGC 2360 |
C0715-155 |
229.8 |
-1.4 |
I3r |
12 |
1459 |
9.0 |
| NGC 2420 |
C0735+216 |
198.1 |
19.6 |
I1r |
10 |
2464 |
9.3 |
| NGC 2421 |
C0734-205 |
236.2 |
0.1 |
I2r |
10 |
2001 |
7.2 |
| NGC 2437 |
C0739-147 |
231.9 |
4.1 |
II2r |
27 |
1491 |
8.4 |
| NGC 2447 |
C0742-237 |
240.1 |
0.2 |
I3r |
22 |
1014 |
8.7 |
| NGC 2477 |
C0750-384 |
253.6 |
-5.8 |
I2r |
27 |
1796 |
8.9 |
| NGC 2533 |
C0805-297 |
247.8 |
1.3 |
II2r |
3 |
1551 |
9.3 |
| NGC 3114 |
C1001-598 |
283.3 |
-3.8 |
II3r |
35 |
893 |
7.9 |
IC 2714 |
C1115-624 |
292.4 |
-1.8 |
II2r |
12 |
1138 |
8.3 |
| Mel 105 |
C1117-632 |
292.9 |
-2.5 |
I2r |
4 |
2035 |
8.3 |
| NGC 4755 |
C1250-600 |
303.2 |
2.5 |
I3r |
10 |
2105 |
7.3 |
| NGC 5617 |
C1426-605 |
314.7 |
-0.1 |
I3r |
10 |
1537 |
7.6 |
| NGC 6208 |
C1645-537 |
333.7 |
-5.8 |
III2r |
15 |
1248 |
9.3 |
| NGC 6250 |
C1654-457 |
340.8 |
-1.8 |
II3r |
7 |
942 |
7.3 |
| NGC 6451 |
C1747-302 |
359.5 |
-1.6 |
I2r |
7 |
1915 |
8.1 |
| NGC 6531 |
C1801-225 |
7.7 |
-0.4 |
I3r |
13 |
1285 |
7.0 |
| NGC 6546 |
C1804-233 |
7.3 |
-1.4 |
II1r |
13 |
927 |
7.9 |
| NGC 6705 |
C1848-063 |
27.3 |
-2.8 |
I2r |
13 |
1794 |
8.3 |
| NGC 6755 |
C1905+041 |
38.5 |
-1.7 |
II2r |
14 |
1563 |
7.8 |
| NGC 6811 |
C1936+464 |
79.4 |
11.9 |
III1r |
12 |
1292 |
8.8 |
| NGC 6819 |
C1939+400 |
74.0 |
8.5 |
I1r |
5 |
1689 |
9.4 |
| NGC 6866 |
C2002+438 |
79.5 |
6.9 |
II2r |
6 |
1490 |
8.8 |
NGC 6939 |
C2030+604 |
95.9 |
12.3 |
II1r |
7 |
1202 |
9.2 |
| NGC 6940 |
C2032+281 |
69.9 |
-7.2 |
III2r |
31 |
1042 |
8.9 |
| NGC 7654 |
C2322+613 |
112.8 |
0.5 |
II2r |
12 |
1490 |
7.7 |
To obtain the radius using RDPs is an arduous task. It has limitations such as:
- 1.
- dependency of
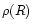 on the limiting magnitude of the members. The more
fainter stars considered, the larger the cluster radius, because such stars
occupy larger distances from the cluster center due to two body relaxation. We
have derived
on the limiting magnitude of the members. The more
fainter stars considered, the larger the cluster radius, because such stars
occupy larger distances from the cluster center due to two body relaxation. We
have derived 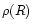 using the stars up to an absolute magnitude of MB =
+4;
using the stars up to an absolute magnitude of MB =
+4;
- 2.
- in some cases, the angular size is difficult to determine accurately due
to the weak contrast between cluster and field stars in the outer region;
- 3.
- sometimes the irregular shape of the cluster also makes it difficult
to accurately determine its boundaries;
- 4.
- the number of members diminishes with increasing distance from the
cluster center and it becomes difficult to detect them in the statistical
fluctuations of the field stars;
- 5.
- in the case of very sparse and poor clusters or in the clusters that
contain stars in clumps, it becomes difficult to locate the center.
Despite all these limitations, the method of RDP can still be used to study the
structure of rich galactic clusters.
On the basis of the above considerations, we found only 38 OCls in Lyngå's
(1987) catalogue as potential candidates for the present study and general
information about them is given in Table 1. The clusters are distributed in
the Galactic longitude along the Galactic plane representing different locations
in the Galaxy. They cover a range in ages from 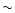 10 Myr to 8 Gyr; in visual
angular diameter from about 3' to 35' and in distance from 0.9 kpc
to 2.6 kpc. The method of RDP determination and its use to determine the core
and coronal regions, is described in the next section while the statistical
properties and other results are discussed in the remaining part of the paper.
10 Myr to 8 Gyr; in visual
angular diameter from about 3' to 35' and in distance from 0.9 kpc
to 2.6 kpc. The method of RDP determination and its use to determine the core
and coronal regions, is described in the next section while the statistical
properties and other results are discussed in the remaining part of the paper.
To cope with problems like interpreting the clusters' distinctive spatial
distribution, homogeneous data on the parameters of OCls are essential.
Accordingly, it is vital to adopt a definite instrumental system as well as a
common approach for studying the size and structure of all OCls. Our aim is
therefore also to include the outer region of the sample clusters. For this, the
photoelectric, photographic and most of the CCD photometric data published so
far are not sufficient as most of them are limited to the core regions only. We
therefore used the photometric results published in the U.S. Naval Observatory
(USNO)-A V2.0 catalogue (Monet et al. 1998). The data are derived from the
images which are Digitized Schmidt Survey (DSS) plates covering the entire sky.
Northern hemisphere images are constructed from Palomar Sky Survey while those
for Southern are from UK Science and Engineering Research Council sky survey.
Although the photometric quality of the USNO catalogue data is inferior (see
Appendix) to photoelectric and CCD, it is good enough to obtain cluster
structural parameters. The clusters showing indication of well defined corona
are planned for further extensive study using a large format CCD camera. In
fact, Pandey et al. (2001) and Nilakshi & Sagar (2002) have already carried out
such a study for our sample clusters NGC 7654 and NGC 2099 respectively.
In order to sketch the RDP well beyond the outer region of the sample clusters
whose angular diameter is less than
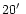 in Lyngå's (1987) catalogue, we
extract a circular area of
in Lyngå's (1987) catalogue, we
extract a circular area of 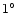 diameter centered on the cluster from the
USNO CDROMs. However, for the clusters having diameter >
diameter centered on the cluster from the
USNO CDROMs. However, for the clusters having diameter >
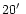 ,
the extracted area is of
,
the extracted area is of 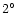 diameter. Thus, we determine the RDP far
beyond the cluster size and certainly include the field region.
To outline the RDPs, the first necessary step is to identify the cluster
center. We derive it (cf. Sagar & Griffiths 1998) iteratively by
calculating average X and Y position of stars within
diameter. Thus, we determine the RDP far
beyond the cluster size and certainly include the field region.
To outline the RDPs, the first necessary step is to identify the cluster
center. We derive it (cf. Sagar & Griffiths 1998) iteratively by
calculating average X and Y position of stars within
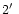 or
or
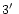 around
an eye-estimated center until it converged to a constant value. An error of
few tens of arcsec is expected in locating the cluster center.
around
an eye-estimated center until it converged to a constant value. An error of
few tens of arcsec is expected in locating the cluster center.
![\begin{figure}
\par\includegraphics[width=15.3cm,clip]{fig1.ps}
\end{figure}](/articles/aa/full/2002/07/aa1472/Timg37.gif) |
Figure 1:
The observed radial density profiles 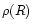 of the clusters under
study. Number of star per arcmin2 are plotted as filled circles against the
cluster radius in arcmin. The lengths of the bars represent errors due to
sampling statistics. The continuous curve is the fitted function
of the clusters under
study. Number of star per arcmin2 are plotted as filled circles against the
cluster radius in arcmin. The lengths of the bars represent errors due to
sampling statistics. The continuous curve is the fitted function
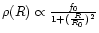 to the observed points using
to the observed points using 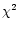 minimization technique.
minimization technique. |
| Open with DEXTER |
For determining the RDP of stars around a cluster region, the extracted area
has been divided into a number of concentric circles with respect to the above
estimated cluster-center in such a way that each zone contains a statistically
significant number of stars (generally more than 20). An annular width of
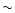
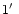 has been used for all the clusters under study. The stellar
surface density,
has been used for all the clusters under study. The stellar
surface density, 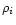 ,
in the ith zone is defined as:
,
in the ith zone is defined as:
where Ni is the number of stars up to absolute magnitude MB = +4 in the
the area Ai of the ith annulus whose outer and inner radii
are Ri and Ri-1 respectively. The RDPs derived in this way are shown in
Fig. 1 for all the clusters under study. The error bars are calculated
assuming that the number of stars in a zone is governed by Poisson statistics.
Following Kaluzny (1992), we describe the 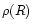 of an open star cluster as:
of an open star cluster as:
where the cluster core radius R0 is the radial distance at which the value of
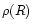 becomes half of the central density f0. We fit this function to the
observed data points of each cluster and use
becomes half of the central density f0. We fit this function to the
observed data points of each cluster and use 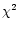 minimization technique to
determine R0 and other constants. As can be seen in Fig. 1, the fitting
of the function is satisfactory except for the clusters NGC 1817, NGC 6451 and
NGC 6940. The radial distance (
minimization technique to
determine R0 and other constants. As can be seen in Fig. 1, the fitting
of the function is satisfactory except for the clusters NGC 1817, NGC 6451 and
NGC 6940. The radial distance (
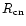 )
at which the
)
at which the 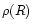 becomes constant
is defined as the extent of the cluster. These angular dimensions have been
converted to linear ones using values of the cluster distances given in Table 1.
The linear sizes derived in this way are listed in Table 2 along with
other parameters obtained from RDPs. The error in R0 is derived from the
becomes constant
is defined as the extent of the cluster. These angular dimensions have been
converted to linear ones using values of the cluster distances given in Table 1.
The linear sizes derived in this way are listed in Table 2 along with
other parameters obtained from RDPs. The error in R0 is derived from the
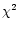 fitting. We expect
fitting. We expect 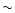
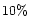 error in the estimation of
error in the estimation of
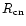 .
The mean stellar densities
.
The mean stellar densities
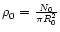 and
and
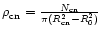 given in Table 2 are for the core and
coronal regions respectively where N0 and
given in Table 2 are for the core and
coronal regions respectively where N0 and
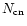 are the number of stars in
the corresponding regions. Assuming
are the number of stars in
the corresponding regions. Assuming
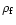 as the field star density, the
densities of cluster members in the core and coronal regions are
as the field star density, the
densities of cluster members in the core and coronal regions are
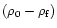 and
and
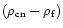 respectively. We estimate
respectively. We estimate
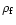 at the
cluster distance from its surrounding regions and use it to evaluate the field
star contaminations in the both core and coronal regions along with the fraction
of cluster members in the corona. The values thus derived are given in Table 2.
The field star density is minimum towards NGC 2420 with a value of 1.1 star/pc^
2 while maximum value of 26.1 star/pc2 is observed towards NGC 6451.
at the
cluster distance from its surrounding regions and use it to evaluate the field
star contaminations in the both core and coronal regions along with the fraction
of cluster members in the corona. The values thus derived are given in Table 2.
The field star density is minimum towards NGC 2420 with a value of 1.1 star/pc^
2 while maximum value of 26.1 star/pc2 is observed towards NGC 6451.
Table 3:
Exponential powers of the variation of stellar surface density
(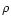 )
with radius (R) in relations
)
with radius (R) in relations
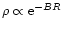 and
and
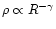 up to the core and cluster boundaries. c1 and c2
are correlation coefficients of least-square solutions of the linear relations
used to derive the values of B,
up to the core and cluster boundaries. c1 and c2
are correlation coefficients of least-square solutions of the linear relations
used to derive the values of B, 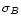 and
and 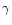 ,
,
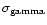 respectively.
respectively.
| |
Core region |
Core plus corona region |
| Name |
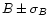 |
c1 |
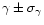 |
c2 |
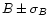 |
c1 |
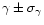 |
c2 |
| NGC 188 |
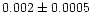 |
0.94 |
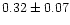 |
0.93 |
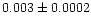 |
0.98 |
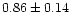 |
0.89 |
| NGC 654 |
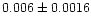 |
0.97 |
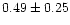 |
0.89 |
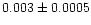 |
0.90 |
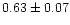 |
0.96 |
| NGC 663 |
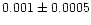 |
0.88 |
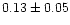 |
0.88 |
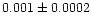 |
0.92 |
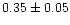 |
0.93 |
| NGC 1245 |
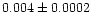 |
1.00 |
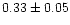 |
0.99 |
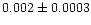 |
0.92 |
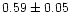 |
0.97 |
| NGC 1817 |
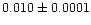 |
1.00 |
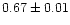 |
1.00 |
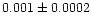 |
0.84 |
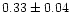 |
0.91 |
| NGC 1960 |
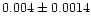 |
0.90 |
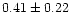 |
0.79 |
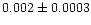 |
0.93 |
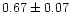 |
0.95 |
| NGC 2099 |
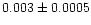 |
0.95 |
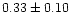 |
0.89 |
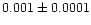 |
0.93 |
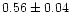 |
0.96 |
| NGC 2244 |
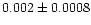 |
0.78 |
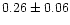 |
0.93 |
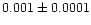 |
0.93 |
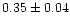 |
0.91 |
| Trumpler 5 |
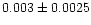 |
0.79 |
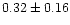 |
0.90 |
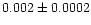 |
0.92 |
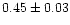 |
0.97 |
| NGC 2301 |
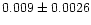 |
0.96 |
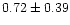 |
0.88 |
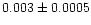 |
0.92 |
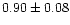 |
0.96 |
| NGC 2323 |
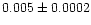 |
1.00 |
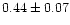 |
0.99 |
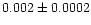 |
0.91 |
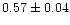 |
0.98 |
| NGC 2345 |
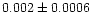 |
0.95 |
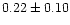 |
0.83 |
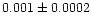 |
0.90 |
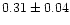 |
0.92 |
| NGC 2354 |
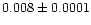 |
1.00 |
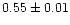 |
1.00 |
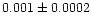 |
0.82 |
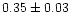 |
0.97 |
| NGC 2360 |
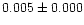 1 1 |
1.00 |
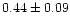 |
0.98 |
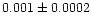 |
0.89 |
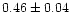 |
0.97 |
| NGC 2420 |
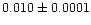 |
1.00 |
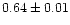 |
1.00 |
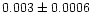 |
0.90 |
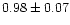 |
0.97 |
| NGC 2421 |
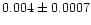 |
0.98 |
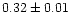 |
1.00 |
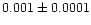 |
0.88 |
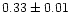 |
0.99 |
| NGC 2437 |
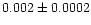 |
0.98 |
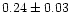 |
0.97 |
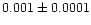 |
0.93 |
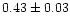 |
0.96 |
| NGC 2447 |
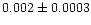 |
0.93 |
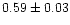 |
0.99 |
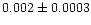 |
0.93 |
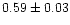 |
0.99 |
| NGC 2477 |
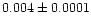 |
1.00 |
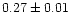 |
1.00 |
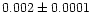 |
0.99 |
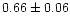 |
0.94 |
| NGC 2533 |
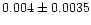 |
0.76 |
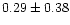 |
0.61 |
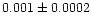 |
0.84 |
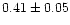 |
0.93 |
| NGC 3114 |
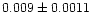 |
0.99 |
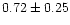 |
0.95 |
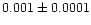 |
0.89 |
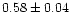 |
0.96 |
| IC 2714 |
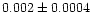 |
0.95 |
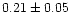 |
0.95 |
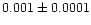 |
0.91 |
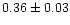 |
0.96 |
| Mel 105 |
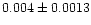 |
0.95 |
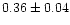 |
0.99 |
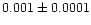 |
0.92 |
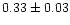 |
0.97 |
| NGC 4755 |
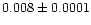 |
1.00 |
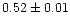 |
1.00 |
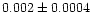 |
0.85 |
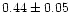 |
0.96 |
| NGC 5617 |
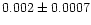 |
0.91 |
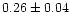 |
0.98 |
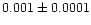 |
0.90 |
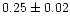 |
0.95 |
| NGC 6208 |
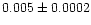 |
1.00 |
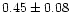 |
0.99 |
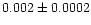 |
0.91 |
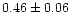 |
0.92 |
| NGC 6250 |
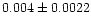 |
0.87 |
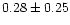 |
0.74 |
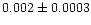 |
0.88 |
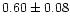 |
0.92 |
| NGC 6451 |
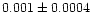 |
0.85 |
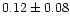 |
0.67 |
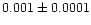 |
0.84 |
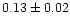 |
0.87 |
| NGC 6531 |
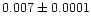 |
1.00 |
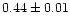 |
1.00 |
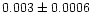 |
0.87 |
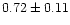 |
0.92 |
| NGC 6546 |
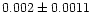 |
0.83 |
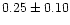 |
0.88 |
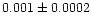 |
0.89 |
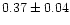 |
0.94 |
| NGC 6705 |
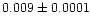 |
1.00 |
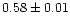 |
1.00 |
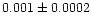 |
0.88 |
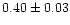 |
0.97 |
| NGC 6755 |
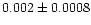 |
0.81 |
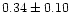 |
0.86 |
|
|
|
|
| NGC 6811 |
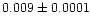 |
1.00 |
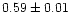 |
1.00 |
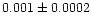 |
0.83 |
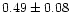 |
0.91 |
| NGC 6819 |
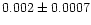 |
0.89 |
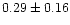 |
0.79 |
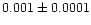 |
0.92 |
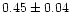 |
0.95 |
| NGC 6866 |
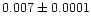 |
1.00 |
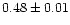 |
1.00 |
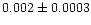 |
0.91 |
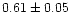 |
0.98 |
| NGC 6939 |
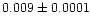 |
1.00 |
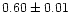 |
1.00 |
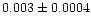 |
0.93 |
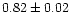 |
1.00 |
| NGC 6940 |
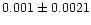 |
0.33 |
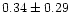 |
0.50 |
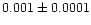 |
0.73 |
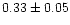 |
0.78 |
| NGC 7654 |
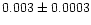 |
0.99 |
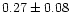 |
0.92 |
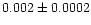 |
0.95 |
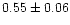 |
0.94 |
In order to see whether the 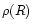 within a cluster radius follows
within a cluster radius follows
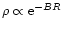 or
or
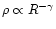 ,
we fit the linear relations
,
we fit the linear relations
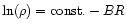 and
and
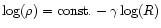 between
between 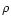 and R, up to both the core and cluster radii. The slopes B and
and R, up to both the core and cluster radii. The slopes B and 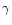 estimated using least-squares solution are listed in Table 3 along with their
standard deviations
estimated using least-squares solution are listed in Table 3 along with their
standard deviations
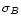 and
and
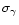 and correlation
coefficients c1 and c2 of the linear relations. As the values of c1 and
c2 are generally of the same order, the RDP within a cluster radius can be
represented by either
and correlation
coefficients c1 and c2 of the linear relations. As the values of c1 and
c2 are generally of the same order, the RDP within a cluster radius can be
represented by either
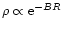 or
or
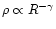 .
However, in some clusters one relation seems to fit data points better than
other one. The values of B and
.
However, in some clusters one relation seems to fit data points better than
other one. The values of B and 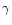 can be used to study differences
between the structure of the core and corona of the clusters under study. In the
core region, the values of B change from 0.001 to 0.01 with a median of
0.003. By including the coronal region, the value of B decreases, as expected
(see Fig. 1) by an average of 0.003. On the other hand, in the core the values
of
can be used to study differences
between the structure of the core and corona of the clusters under study. In the
core region, the values of B change from 0.001 to 0.01 with a median of
0.003. By including the coronal region, the value of B decreases, as expected
(see Fig. 1) by an average of 0.003. On the other hand, in the core the values
of 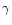 range from 0.12 to 0.72 with a median of 0.34. In contrast to B,
the value of
range from 0.12 to 0.72 with a median of 0.34. In contrast to B,
the value of 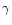 thus shows relatively larger variation and increases by
including the coronal region. This is due only to the role of the constants in
the relations under discussion. However, variation in both B and
thus shows relatively larger variation and increases by
including the coronal region. This is due only to the role of the constants in
the relations under discussion. However, variation in both B and 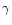 values by including the coronal region is not the same for all clusters,
indicating that the shape of the coronal regions is different for different
clusters, as can also be seen in Fig. 1. Differences in the structure of the
corona have also been observed by Durgapal & Pandey (2001) in a sample of 4
clusters. They may be due to various reasons e.g., (i) the dynamical relaxation
which causes mass segregation in the cluster (Nilakshi & Sagar 2002 and
references therein), (ii) the external environment, as we know that the corona
of the clusters are moulded by the Galactic tidal fields (Mathieu 1985).
values by including the coronal region is not the same for all clusters,
indicating that the shape of the coronal regions is different for different
clusters, as can also be seen in Fig. 1. Differences in the structure of the
corona have also been observed by Durgapal & Pandey (2001) in a sample of 4
clusters. They may be due to various reasons e.g., (i) the dynamical relaxation
which causes mass segregation in the cluster (Nilakshi & Sagar 2002 and
references therein), (ii) the external environment, as we know that the corona
of the clusters are moulded by the Galactic tidal fields (Mathieu 1985).
In order to obtain a general view of the real constitution of the galactic
clusters, the frequency distributions and the correlation between some of the
cluster parameters contained in Table 2 are studied in this section.
As the number of sample clusters is only 38, some of
the conclusions drawn below may not be definitive but indicative, which may be
worthwhile to study in detail when a larger sample becomes available.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig2.ps}
\end{figure}](/articles/aa/full/2002/07/aa1472/Timg275.gif) |
Figure 2:
Histograms of the core (R0) and corona (
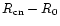 )
sizes;
their densities of cluster members and field star contamination along with
fraction of cluster members in corona of clusters under study are presented in
a-d) respectively. The solid and dashed lines in a-c) denote core and coronal regions respectively. )
sizes;
their densities of cluster members and field star contamination along with
fraction of cluster members in corona of clusters under study are presented in
a-d) respectively. The solid and dashed lines in a-c) denote core and coronal regions respectively. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig3.ps}
\end{figure}](/articles/aa/full/2002/07/aa1472/Timg276.gif) |
Figure 3:
The corona size (
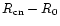 ), the cluster member density ( ), the cluster member density (
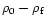 )
in the core and the percentage of field star contamination (F0) are
plotted as crosses against the core size in c), b) and a) respectively.
Binned data points along with their )
in the core and the percentage of field star contamination (F0) are
plotted as crosses against the core size in c), b) and a) respectively.
Binned data points along with their 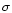 are shown by filled circles and
error bars respectively.
are shown by filled circles and
error bars respectively. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig4.ps}
\end{figure}](/articles/aa/full/2002/07/aa1472/Timg277.gif) |
Figure 4:
The cluster member density (
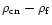 ), percentage of the
field stars ( ), percentage of the
field stars (
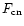 )
and the cluster members in coronal regions ( )
and the cluster members in coronal regions (
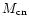 )
are plotted as crosses against the corona size ( )
are plotted as crosses against the corona size (
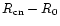 )
in c), b) and
a) respectively. Filled circles and error bars denote the same as in Fig. 3. )
in c), b) and
a) respectively. Filled circles and error bars denote the same as in Fig. 3. |
| Open with DEXTER |
Figure 2 illustrates the histograms of sizes, cluster member densities and field
star contamination in the core and coronal regions along with fraction of
cluster members in corona of clusters under study. The core size ranges from
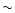 0.5 to 2.9 pc. Its histogram in Fig. 2a has a well defined peak
around 0.75 pc with an average of
0.5 to 2.9 pc. Its histogram in Fig. 2a has a well defined peak
around 0.75 pc with an average of
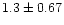 pc and a median of 1.2 pc. In
contrast, the histogram of width of the coronal region show a relatively flat
distribution with values ranging from 2.5 to 9.3 pc. Its mean and median
values are
pc and a median of 1.2 pc. In
contrast, the histogram of width of the coronal region show a relatively flat
distribution with values ranging from 2.5 to 9.3 pc. Its mean and median
values are
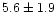 and 5.54 pc respectively. The coronal width is thus
more than 4 times the core size.
and 5.54 pc respectively. The coronal width is thus
more than 4 times the core size.
In Fig. 2b, histograms of the mean cluster member densities in the core
(
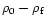 )
and corona (
)
and corona (
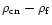 )
regions are displayed.
They have a mean and a median of
)
regions are displayed.
They have a mean and a median of
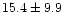 and 13.2 star/pc2 respectively
with large range from 0.6 to 53 star/pc2 in the core but relatively small
range from 0.3 to 4.5 star/pc2 with a mean and a median of
and 13.2 star/pc2 respectively
with large range from 0.6 to 53 star/pc2 in the core but relatively small
range from 0.3 to 4.5 star/pc2 with a mean and a median of
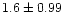 and
1.3 star/pc2 respectively in the corona. The density of cluster members in
the corona has a sharp peak around 1 star/pc2 while that in the core has
extended distribution which peaks around 11 star/pc2. All these indicate
that the density of cluster members in the core is about 10 times larger than
that of the corona.
Figure 2c shows the histograms of field star contamination in both the core and
coronal regions. The core region of NGC 1817 is least contaminated with a value
of 6% while that of NGC 5617 has the maximum contamination of 60%. The
histogram for the core region peaks around 25% with a median value of 28%.
As expected, the field star contamination in the corona is more in comparison
to the core. Its histogram has a peak around 80% with a median of 75%.
and
1.3 star/pc2 respectively in the corona. The density of cluster members in
the corona has a sharp peak around 1 star/pc2 while that in the core has
extended distribution which peaks around 11 star/pc2. All these indicate
that the density of cluster members in the core is about 10 times larger than
that of the corona.
Figure 2c shows the histograms of field star contamination in both the core and
coronal regions. The core region of NGC 1817 is least contaminated with a value
of 6% while that of NGC 5617 has the maximum contamination of 60%. The
histogram for the core region peaks around 25% with a median value of 28%.
As expected, the field star contamination in the corona is more in comparison
to the core. Its histogram has a peak around 80% with a median of 75%.
The histogram of cluster members population in corona is shown in Fig. 2d. It
peaks around 80%. This clearly indicates the importance of the corona in
studies dealing with entire stellar contents of the cluster e.g., study of
mass function. On the other hand, for the determination of cluster parameters
like distance and age, stars of the cluster core are best suited as they have
less field star contamination. The cluster sequences in photometric diagrams
can therefore be better identified in stars of the core region.
Figure 3 shows correlation of the core size with the corona size, the cluster
members density and the percentage of field star contamination (F0) in the
core. It indicates that both the corona size and F0 value generally increase
while the core density decreases with increasing size of the core. At a given
core size, the corona size varies by about 3 to 5 pc; the core density varies
from few to few tens of star/pc2 while the F0 value changes from few
tens to 50%. The scatter in Figs. 3a and c is almost independent of the
core size. However, the scatter in the density generally decreases as the core
size increases, being largest for a core size of around 0.6 pc. A larger sample
is needed to ascertain the behaviour.
In order to study correlation of the corona size (
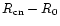 )
with its
cluster member density (
)
with its
cluster member density (
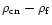 ), field star contamination
(
), field star contamination
(
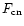 )
and fraction of cluster members (
)
and fraction of cluster members (
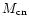 ), we plot them in Fig. 4.
The mean value of members' density in the coronal region is
), we plot them in Fig. 4.
The mean value of members' density in the coronal region is
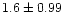 star/pc2. It slowly decreases with inceasing corona size and the value
becomes
star/pc2. It slowly decreases with inceasing corona size and the value
becomes 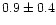 star/pc2 for a corona size larger than 8 pc (see Fig. 4c). Both the
star/pc2 for a corona size larger than 8 pc (see Fig. 4c). Both the
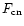 and
and
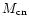 values are generally more than 60% with
no statistically significant dependence on the corona size (see Figs. 4a and b).
values are generally more than 60% with
no statistically significant dependence on the corona size (see Figs. 4a and b).
The open star clusters form from molecular clouds having mass in the range of
several thousands to hundreds of thousands of 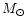 .
As the Galactic tidal
forces are different at different locations, it may be worthwhile to see how
they affect the sizes and member densities in open star clusters. For this, we
study the variation of cluster parameters with the Galacto-centric distance
(
.
As the Galactic tidal
forces are different at different locations, it may be worthwhile to see how
they affect the sizes and member densities in open star clusters. For this, we
study the variation of cluster parameters with the Galacto-centric distance
(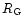 )
and height (z) above the Galactic plane in the following sub-sections.
)
and height (z) above the Galactic plane in the following sub-sections.
We plot the core and corona sizes, the central concentration and the member
densities ratio of the core to corona against the 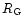 in Figs. 5a-d
respectively. Though the errors are large, it illustrates that the mean
core size is independent of
in Figs. 5a-d
respectively. Though the errors are large, it illustrates that the mean
core size is independent of 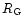 .
Similarly, both the ratio of corona to core
sizes and the (
.
Similarly, both the ratio of corona to core
sizes and the (
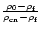 )
values seem to have
no statistically significant dependence on
)
values seem to have
no statistically significant dependence on 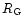 .
On the other hand, the mean
corona size of
.
On the other hand, the mean
corona size of 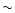 5 pc for
5 pc for
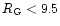 kpc increases systematically with
kpc increases systematically with
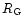 thereafter and becomes
thereafter and becomes 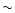 7.1 pc at
7.1 pc at
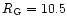 kpc. A careful inspection of the data reveals that the observed
correlations show no dependence on cluster ages.
kpc. A careful inspection of the data reveals that the observed
correlations show no dependence on cluster ages.
![\begin{figure}
\par\includegraphics[width=8.8cm]{fig5.ps}
\end{figure}](/articles/aa/full/2002/07/aa1472/Timg285.gif) |
Figure 5:
Plot of the core and coronal sizes; the central concentration defined
as ratio of the corona to core sizes and the members density ratios of core to
corona against 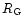 are shown in a-d) respectively. In order
to study the trend in variation, data points have been binned in
are shown in a-d) respectively. In order
to study the trend in variation, data points have been binned in 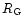 .
Error
bars are the .
Error
bars are the 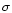 of data points in a bin. Crosses denote clusters younger
than 100 Myr while olders are shown by triangles.
of data points in a bin. Crosses denote clusters younger
than 100 Myr while olders are shown by triangles. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig6.ps}
\end{figure}](/articles/aa/full/2002/07/aa1472/Timg286.gif) |
Figure 6:
Plot of sizes and densities of both the core and coronal regions of the
cluster against z, its location above or below the Galactic plane. Crosses
denote clusters younger than 100 Myr while olders are shown by triangles. |
| Open with DEXTER |
Figure 6 outlines the plot of sizes and cluster member densities of both the core
and corona of the cluster against its height (z) above the Galactic plane.
None of the parameters seem to depend on the value of z. As expected, most of
the clusters with -200 pc < z < 200 pc are younger than 100 Myr while those
with z < -200 pc and z > 200 pc are older than that. We therefore conclude
that irrespective of the core and corona sizes, the clusters older than 100 Myr
are generally located away from while the younger ones are confined to the
Galactic plane.
Stellar encounters in a cluster can change the spatial position of members with
time due to equi-partition of energies amongst the cluster members. In order to
see its effect on parameters of open star clusters, we the plot core and corona
sizes, central concentration and density ratio of core to corona against
log (age) in Figs. 7a-d respectively. We observe no
statistically significant trend at all in the sizes of core and corona as well
as in the ratio of their cluster member densities with age. However, central
concentration appears to be somewhat smaller for clusters older than 1000 Myr.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig7.ps}
\end{figure}](/articles/aa/full/2002/07/aa1472/Timg287.gif) |
Figure 7:
The core and corona sizes; central concentration and density ratio of
core to corona are plotted against log of age in a-d)
respectively. Filled circles and error bars show the mean and 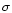 respectively of the data points binned in log (age).
respectively of the data points binned in log (age). |
| Open with DEXTER |
The present study of the spatial structures of 38 rich galactic open star
clusters leads to the following useful conclusions:
- 1.
- On average, annular size of the coronal region is about 5 times the
core radius. All the clusters including the very young ones have a corona.
Presence of a core and corona have also been detected in NGC 6611, an extremely
young (few Myr) star cluster by Belikov et al. (1999, 2000) using proper motion
data. As the RDP of the cluster (core plus corona) region can be fitted by a
function of
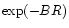 or
or
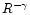 types, we consider the coronal region
as an integral outer part of a cluster existing from the time of its formation.
If the appearance of a corona is only due to the dynamical evolution in the
cluster, it should appear only for those clusters that are older than
types, we consider the coronal region
as an integral outer part of a cluster existing from the time of its formation.
If the appearance of a corona is only due to the dynamical evolution in the
cluster, it should appear only for those clusters that are older than 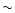 100 Myr.
100 Myr.
- 2.
- Field star contamination in the coronal region, on average, is 44%
greater to that of the core region. To determine the cluster
parameters from the observed colour-magnitude and colour-colour diagrams, stars
located in the core region should be considered. However, for the studies
dealing with the entire stellar content of the cluster, members present in the
coronal region must be included as they form a large fraction of cluster
members. This clearly demonstrates the importance of coronal regions in the
studies of IMF and dynamical evolution of the clusters.
- 3.
- In contrast to the coronal regions, the structure of the cluster cores
does not vary significantly from one cluster to other.
- 4.
- The mean radii of the core and cluster sizes are
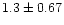 and
and
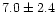 pc respectively while the corresponding median values are 1.2 and
6.8 pc respectively. The mean values
of cluster diameters determined by both Lyngå (1982) and Janes & Phelps
(1994) are
pc respectively while the corresponding median values are 1.2 and
6.8 pc respectively. The mean values
of cluster diameters determined by both Lyngå (1982) and Janes & Phelps
(1994) are 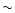 5.3 pc which lie between the values of core and cluster
diameter determined by us. Present values should be considered more reliable,
as they are derived from the RDP of an extended region around the cluster.
5.3 pc which lie between the values of core and cluster
diameter determined by us. Present values should be considered more reliable,
as they are derived from the RDP of an extended region around the cluster.
- 5.
- We find that the mean size of the clusters with
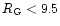 kpc is smaller
than that of those with
kpc is smaller
than that of those with
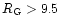 kpc. We thus confirm the earlier findings
of Burki & Maeder (1976), Lyngå (1982) and Janes et al. (1988).
kpc. We thus confirm the earlier findings
of Burki & Maeder (1976), Lyngå (1982) and Janes et al. (1988).
- 6.
- In agreement with Lyngå (1982) and Janes et al. (1988), we find that
sizes of the clusters are independent of age. Hence we believe that the cluster
size may depend on the properties of the parental molecular cloud rather than
the cluster age.
USNO-A V2.0: A catalogue of astrometric standards
USNO-A2.0 is a catalogue of 526280881 stars, and is based on a re-reduction
of the Precision Measuring Machine (PMM) scans for astrometric and photometric
data. These stars were detected by the PMM, built and operated by the U. S.
Naval Observatory, Flagstaff Station during the scanning and processing of the
Palomar Observatory Sky Survey I (POSS-I) O and E plates, the UK Science and
Research Council SRC-J survey plates, and the European Southern Observatory
ESO-R survey plates. For field centers with
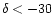 degrees, the data
come from POSS-I plates, while the data for the remaining part of the sky come
from SRC-J and ESO-R plates. The errors arising from the PMM are in the range
of 0.15 arcsec in astrometry and 0.15 mag in photometry. To avoid the necessity of
consulting many catalogues, objects brighter than 11th magnitude that appear in
the Guide Star Catalogue that were not detected by the PMM were inserted.
degrees, the data
come from POSS-I plates, while the data for the remaining part of the sky come
from SRC-J and ESO-R plates. The errors arising from the PMM are in the range
of 0.15 arcsec in astrometry and 0.15 mag in photometry. To avoid the necessity of
consulting many catalogues, objects brighter than 11th magnitude that appear in
the Guide Star Catalogue that were not detected by the PMM were inserted.
Acknowledgements
The valuable suggestions provided by the referee Dr. B. Chen improved the
scientific content of the paper.
We are thankful to Dr. A. E. Piskunov for useful discussions and to B. Kumar for
reading the manuscript critically. The present research has used the
USNO-A V2.0 catalogue and the WEBDA open cluster data base Web site at
http://obswww.unige.ch/webda/ maintained by Dr. J. C. Mermilliod.
- Artyukhina, N. M., & Kholopov, P. N. 1959, SvA-AJ, 3, 923
In the text
- Artyukhina, N. M., & Kholopov, P. N. 1963, SvA-AJ, 7, 840
In the text
- Artyukhina, N. M., & Kholopov, P. N. 1966, SvA-AJ, 10, 448
In the text
- Artyukhina, N. M. 1966, SvA-AJ, 10, 103
- Belikov, A. N., Kharchenko, N. V., Piskunov, A. E.,
& Schilbach, E. 1999, A&AS, 134, 525
In the text
NASA ADS
- Belikov, A. N., Kharchenko, N. V., Piskunov, A. E.,
& Schilbach, E. 2000, A&A, 358, 886
In the text
NASA ADS
- Burki, G., & Maeder, A. 1976, A&A, 51, 247
In the text
NASA ADS
- Durgapal, A. K., & Pandey, A. K. 2001, A&A, 375, 504
In the text
- Elmegreen, B. G., & Efremov, Yu. N. 1997, ApJ, 480, 235
In the text
NASA ADS
- Janes, K. A., Tilley, C., & Lyngå, G. 1988, AJ, 95, 771
In the text
NASA ADS
- Janes, K. A., & Phelps, R. L. 1994, AJ, 108, 1773
In the text
NASA ADS
- Kaluzny, J. 1992, Acta Astron., 42, 29
In the text
NASA ADS
- Kholopov, P. N. 1969, SvA-AJ, 12, 625
In the text
- Loktin, A. V., Matkin, N. V., & Gerasimenko, T. P. 1994, Astron. Astrophys. Trans., 4, 153
In the text
NASA ADS
- Lyngå, G. 1982, A&A, 109, 213
In the text
NASA ADS
- Lyngå, G. 1987, in Catalog of Open Cluster Data,
Computer Based Catalogue available through the CDS, Starsbourg, France and
through NASA Data Center, GreenBelt, MaryLand, USA, 5th edition, 4, 121
In the text
- Mathieu, R. D. 1985, IAU Symp., 113, 427
In the text
- Monet, D., Bird, A., Canzian, A., et al. 1998, USNO-A2.0,
(U.S. Naval Observatory, Washington DC)
In the text
- Nilakshi, & Sagar, R. 2002, A&A, 381, 65
In the text
NASA ADS
-
Pandey, A. K., Nilakshi, Ogura, K., Sagar, R., & Tarusawa, K. 2001, A&A, 374, 504
In the text
NASA ADS
- Sagar, R., & Griffiths, W. K. 1998, MNRAS, 299, 777
In the text
NASA ADS
- Salpeter, E. E. 1955, ApJ, 121, 161
In the text
NASA ADS
- Shapley, H. 1916, Contr. Mt. Wilson Obs., 117
In the text
- Subramaniam, A., Gorti, U., Sagar, R., & Bhatt, H. C. 1995, A&A, 302, 86
In the text
NASA ADS
- Turner, D. G. 1982, PASP, 94, 1003
In the text
NASA ADS
- Wilner, D. J., & Lada, C. J. 1991, AJ, 102, 1050
In the text
NASA ADS
Copyright ESO 2002
![\begin{figure}
\par\includegraphics[width=15.3cm,clip]{fig1.ps}
\end{figure}](/articles/aa/full/2002/07/aa1472/Timg37.gif)
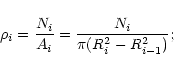
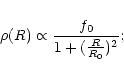
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig2.ps}
\end{figure}](/articles/aa/full/2002/07/aa1472/Timg275.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig3.ps}
\end{figure}](/articles/aa/full/2002/07/aa1472/Timg276.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig4.ps}
\end{figure}](/articles/aa/full/2002/07/aa1472/Timg277.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm]{fig5.ps}
\end{figure}](/articles/aa/full/2002/07/aa1472/Timg285.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig6.ps}
\end{figure}](/articles/aa/full/2002/07/aa1472/Timg286.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig7.ps}
\end{figure}](/articles/aa/full/2002/07/aa1472/Timg287.gif)