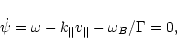 |
(1) |
A&A 382, 1061-1069 (2002)
DOI: 10.1051/0004-6361:20011601
V. G. Vlasov1 - A. A. Kuznetsov1 - A. T. Altyntsev2
1 - Irkutsk State Technical University,
Irkutsk, Russia
2 -
Institute of Solar-Terrestrial Physics, Irkutsk, Russia
Received 16 October 2001 / Accepted 5 November 2001
Abstract
The generation of solar millisecond spikes on the maser
cyclotron resonance is studied by taking into account the
large-scale monotonic magnetic field inhomogeneity and the
small-scale plasma inhomogeneity. It is shown that the presence of
these inhomogeneities can have a significant effect on the
generation of electromagnetic waves. In this case the structure
of the inhomogeneities determines the spectral and temporal
parameters of emission. A modeling of the spike dynamic
spectrum in the presence of a small-scale inhomogeneity of
coronal plasma is performed. It is shown that a simple
model of the plasma inhomogeneity (traveling density wave)
can account for many of the observed features of spikes.
Key words: Sun: flares - Sun: radio radiation - Sun: particle emission - masers
However, the spike generation mechanism remains unclear. Among the various coherent processes most often considered are the maser cyclotron resonance (Melrose & Dulk 1982) and different variants of the plasma mechanism when plasma waves are transformed into radio emission due to nonlinear processes (Zaitsev & Stepanov 1983; Willes & Robinson 1996). In this article we consider the maser mechanism of spike generation, namely the generation of the fundamental harmonic of the extraordinary wave (X1-mode). The emission frequency in this case virtually coincides with the electron cyclotron frequency in the source, which requires the presence of sufficiently strong magnetic fields in the solar corona (>100 G for the emission frequency >300 MHz). At the present time the existence of such magnetic fields is questionable; nevertheless, the electron cyclotron maser is still commonly considered to be the generation mechanism of solar radio emission (Fleishman & Melnikov 1998).
Most publications that have considered the maser mechanism of spike generation (Aschwanden 1990; Fleishman & Melnikov 1998; Fleishman & Arzner 2000; and other) are devoted mainly to the investigation of the mutual evolution of the electromagnetic wave and the unstable electron distribution. It is assumed that the main factor limiting the emission intensity is the quasilinear (or nonlinear) relaxation of this unstable distribution. Such a relaxation is very fast and therefore the generation of the emission takes place virtually in the area of formation of the unstable particle distribution. The influence of the inhomogeneities of the medium (magnetic field and plasma) is considered only when determining the spectral band of emission.
At the same time, as Le Quéau et al. (1985), Zarka et al. (1986), Vlasov (1991a, 1991b) have shown, inhomogeneities of the magnetic field and plasma essentially determine the characteristics of auroral kilometric radiation that is generated in the Earth's magnetosphere on the maser cyclotron resonance. The escape of the wave from resonance with the electron beam in the space of wave vectors proved to be the main factor limiting the emission intensity in this case. The combined influence of the large-scale monotonic magnetic field inhomogeneity and the small-scale plasma density inhomogeneity forms a complex dynamic spectrum of the auroral kilometric radiation.
In this paper the theory of the generation of radio emission on the maser cyclotron resonance that has been developed for the emission of the magnetospheres of the Earth and other planets (Vlasov 1991a, 1991b; Vlasov & Kuznetsov 1997), is used to interpret the solar millisecond spikes. In Sect. 2 of this article the basic equations of the process are given. In Sect. 3 it is shown that the unstable electron beams in the solar corona are stabilized by the large-scale longitudinal magnetic field inhomogeneity, the conditions allowing for the generation of the emission are determined, and the scenario for spike generation in an inhomogeneous medium is proposed. In Sect. 4 we introduce a simple model of a small-scale plasma inhomogeneity in the form of a traveling density wave, calculate the dynamic spectrum of the spike corresponding to this inhomogeneity and compare it with an experimental spike spectrum.
The equation of maser cyclotron resonance (MCR) of electrons and
electromagnetic waves at the fundamental harmonic has the form:
Within the semirelativistic approximation (![]() ), Eq. (1)
in the velocity space of electrons
), Eq. (1)
in the velocity space of electrons
![]() represents a
circle (or semicircle if we assume
represents a
circle (or semicircle if we assume
![]() )
with the center at
the point
)
with the center at
the point
![]() ,
,
![]() and the radius W (Melrose
& Dulk 1982)
and the radius W (Melrose
& Dulk 1982)
It was already noted (Melrose & Dulk 1982) that the growth
rate of the electromagnetic waves on MCR can be positive only when the
electron distribution function fb has an area with
a positive slope
![]() .
In this
paper the electron beam with the following distribution
function (Vlasov 1991a) is considered to be the emission source:
.
In this
paper the electron beam with the following distribution
function (Vlasov 1991a) is considered to be the emission source:
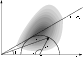 |
Figure 1: The model distribution function of the electron beam. |
| Open with DEXTER | |
The X1-mode dispersion equation near the cutoff point
(when
![]() ,
,
![]() )
has the form
)
has the form
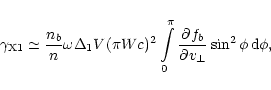 |
(6) |
For the model electron beam (3-4), the growth rate
is positive when
![]() ,
and the resonance semicircle
lies entirely in the area of the positive slope of the
distribution function, i.e.
,
and the resonance semicircle
lies entirely in the area of the positive slope of the
distribution function, i.e.
Figure 2 shows the regions of parameters, under which
electron beams with different energies can generate emission
with an arbitrary propagation direction. It is evident from
the figure that the interval of possible propagation angles is quite wide.
The angle that corresponds to a maximum growth rate varies
depending on particular generation conditions, but the
value of a maximum growth rate itself remains approximately
constant. The sole exception is the case of the wave propagation
at large angles to the magnetic field when their amplification
is less effective or impossible.
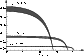 |
Figure 2:
The parameters, under which the hollow beam can
generate emission on MCR. The beam pitch-angle dispersion
|
| Open with DEXTER | |
Within the linear approximation the spectral density of electromagnetic
wave energy Wf increases exponentially with time, i.e.
![\begin{displaymath}%
W_{f}=W_{f0}\exp\left[
\left(2\gamma_{\rm X1}-\nu_{e}\right)
\Delta t\right],
\end{displaymath}](/articles/aa/full/2002/06/aah3228/img44.gif) |
(11) |
The spectral density of the emission intensity observed at the
Earth (neglecting the absorption during the propagation) can be
estimated as
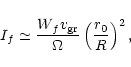 |
(12) |
The time of resonance ![]() is determined by the escape of the
wave from the generation region both in the ordinary space
and in the space of wave vectors, i.e. mainly by the
breakdown of the phase synchronism condition (1).
To determine this value
we expand the derivative of the relative phase of waves and
particles (1) in the vicinity of the point t=t0into a series at
is determined by the escape of the
wave from the generation region both in the ordinary space
and in the space of wave vectors, i.e. mainly by the
breakdown of the phase synchronism condition (1).
To determine this value
we expand the derivative of the relative phase of waves and
particles (1) in the vicinity of the point t=t0into a series at
![]() (Vlasov 1991a):
(Vlasov 1991a):
Instead of the exact solution of Eq. (13), it is
possible to use the approximate roots
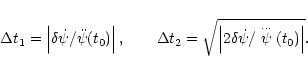 |
(15) |
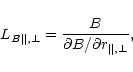 |
(16) |
The plasma density is characterized by the scales of
spatial inhomogeneity ![]() and
and ![]() ,
and by the time of
variation
,
and by the time of
variation ![]()
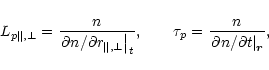 |
(17) |
Under these assumptions the second derivative of the relative
phase of waves and particles is
The derivatives
![]() and
and
![]() are
calculated using the Hamiltonian equations (see Vlasov 1991b)
and are
are
calculated using the Hamiltonian equations (see Vlasov 1991b)
and are
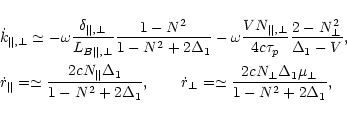 |
(19) |
The third derivative of the relative phase of waves and particles
has a more complicated expression. We give here its approximate
value for the wave with the propagation parallel to the magnetic field
(![]() ):
):
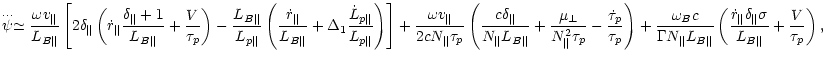 |
(20) |
The frequency range of the emission generated on MCR
![]() depends mainly on two factors. Firstly, it is the limited
spatial size of the generation region
depends mainly on two factors. Firstly, it is the limited
spatial size of the generation region
![]() .
The corresponding spectral bandwidth is
.
The corresponding spectral bandwidth is
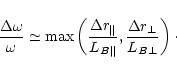 |
(22) |
 |
(23) |
The energy flux of the electron beam that is transferred through
a unit area per unit time is
| (25) |
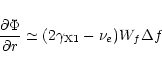 |
(26) |
As shown in the previous section, the duration of the resonance, and
hence the intensity of the radio emission generated on MCR
depend strongly on the scales and dynamics of magnetic field and
plasma inhomogeneities. First we consider the case where the plasma density
is time-independent and is characterized by constant scales of spatial
inhomogeneity ![]() and
and ![]() (i.e. it is assumed that
(i.e. it is assumed that
![]() ,
and
,
and
![]() ).
The main factors that influence the resonance time are
the scales of longitudinal inhomogeneity
).
The main factors that influence the resonance time are
the scales of longitudinal inhomogeneity ![]() and
and ![]() .
.
Tables 1-2 give an example of a calculation of the generation of radio emission on MCR. The electromagnetic wave propagation direction is parallel to the magnetic field. Table 1 presents the parameters that do not depend on the longitudinal inhomogeneity scale of plasma density. The chosen scales of magnetic field inhomogeneity are on the order of the coronal magnetic loop dimensions. The parameters of the electron beam distribution function are similar to electron beams observed in the Earth's magnetosphere.
If the scale of longitudinal inhomogeneity of plasma
density
![]() (or is comparable with the scale
of longitudinal inhomogeneity of the magnetic field, see
Table 2), then the resonance time is determined
by the time
(or is comparable with the scale
of longitudinal inhomogeneity of the magnetic field, see
Table 2), then the resonance time is determined
by the time
![]() ,
which, in turn, is proportional
to the scale of longitudinal inhomogeneity of the magnetic
field:
,
which, in turn, is proportional
to the scale of longitudinal inhomogeneity of the magnetic
field:
| Electron cyclotron frequency | fB, MHz | 350 |
| Magnetic field inhomogeneity scales | ||
| 5000 | ||
| Plasma density | n,
|
|
| Plasma frequency | fp, fB | 0.181 |
| Plasma temperature | T, K | 106 |
| Transverse scale of plasma density inhomogeneity | 5000 | |
| Thermal oscillation energy density at
|
Wf0,
|
|
| Energy of the electron beam | Eb, keV | 20 |
| Velocity of the electron beam | vb, c | 0.272 |
| Density of the electron beam | nb, n |
|
| Velocity dispersion of the electron beam |
|
1/3 |
| Pitch-angle dispersion of the electron beam |
|
1/3 |
| Growth rate of electromagnetic waves |
|
|
| Collision frequency | 3.90 | |
| Minimum spectral bandwidth of the emission | 2.97 | |
| Energy flux of the electron beam |
|
| Scale of longitudinal inhomogeneity of plasma density | 10000 | -356 | |
| Resonance times |
|
1.12 | |
|
|
9.09 | 8.26 | |
| Emission energy density | Wf,
|
|
|
| Emission intensity at the Earth* | If, sfu |
|
252 |
| Energy loss rate of the electron beam |
|
|
|
| Collective relaxation length of the electron beam | l, km |
|
52.8 |
We now consider the dependence of the resonance time on the scale
of longitudinal inhomogeneity of plasma. At the certain ratio of the
scales of longitudinal inhomogeneities of plasma and magnetic field,
namely at
Figure 3 shows the dependence of the resonance times
![]() and
and
![]() on the scale of
longitudinal inhomogeneity of plasma for different propagation
directions of the wave. The other parameters of the magnetic
field, plasma and electron beam are the same as in Table 1. An increase of the resonance time due to the
compensation of the longitudinal inhomogeneities occurs
at any angle between the wave propagation direction
and the magnetic field, but the exact condition of this
compensation can somewhat change. The resonance time
on the scale of
longitudinal inhomogeneity of plasma for different propagation
directions of the wave. The other parameters of the magnetic
field, plasma and electron beam are the same as in Table 1. An increase of the resonance time due to the
compensation of the longitudinal inhomogeneities occurs
at any angle between the wave propagation direction
and the magnetic field, but the exact condition of this
compensation can somewhat change. The resonance time
![]() decreases with an increase of the angle between the wave
propagation direction and the magnetic field, which makes the
quasilongitudinal propagation somewhat more favorable.
decreases with an increase of the angle between the wave
propagation direction and the magnetic field, which makes the
quasilongitudinal propagation somewhat more favorable.
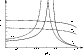 |
Figure 3:
The dependence of the resonance times on the scale
of longitudinal inhomogeneity of plasma density.
The solid and dashed lines correspond to the wave propagation
directions |
| Open with DEXTER | |
The resonance time
![]() (and therefore the conditions of
electron beam stabilization) does almost not depend
on the transverse inhomogeneities of the magnetic field
and plasma. However, as follows from the expression (29),
these inhomogeneities have a significant influence on the
resonance time
(and therefore the conditions of
electron beam stabilization) does almost not depend
on the transverse inhomogeneities of the magnetic field
and plasma. However, as follows from the expression (29),
these inhomogeneities have a significant influence on the
resonance time
![]() .
A detailed investigation of
the effects associated with the influence of the transverse
inhomogeneities of the magnetic field and plasma on the generation
of emission on MCR, is beyond the scope of this paper.
.
A detailed investigation of
the effects associated with the influence of the transverse
inhomogeneities of the magnetic field and plasma on the generation
of emission on MCR, is beyond the scope of this paper.
As the expression (28) suggests, for the breakdown of
the electron beam stabilization the required scale of the
longitudinal inhomogeneity of plasma density must be,
firstly, much smaller than the scale of longitudinal
inhomogeneity of the magnetic field and, secondly, the
longitudinal components of plasma and magnetic field gradients
must be oppositely directed. This is
possible only due to a small-scale plasma inhomogeneity
(turbulence). Accordingly, a breakdown of the stabilization
can take place only in relatively narrow height ranges,
which leads to a narrowband spectrum of the generated
emission. Note that if the spatial dimensions of the
generation region are determined only by the condition
of compensation of the inhomogeneities (28), then
the spatial escape of the electromagnetic waves from
the generation region is already taken into account
in the resonance time
![]() in view of the relations (21).
in view of the relations (21).
Thus we can propose the following scenario for generation of
the spikes on MCR in the inhomogeneous medium. The region
of formation of an unstable electron beam and the region
of generation of emission are spatially separated.
The large-scale longitudinal inhomogeneity of the magnetic
field stabilizes the beam both in the formation region and
during the propagation. The lifetime of the beam far exceeds the
duration of a single spike and corresponds to the duration of
a series of spikes. The generation of emission takes place
only in those local regions where the small-scale inhomogeneity
of plasma density slows down the escape of the electromagnetic
waves from resonance with the beam and thus breaks the stabilization.
The emission spectrum at any instant of time is the picture of
the structure of the plasma small-scale inhomogeneity. The
duration of a single spike is determined by the lifetime
of the corresponding inhomogeneity. The spatial movement of
the inhomogeneity results in a shift of the generation
region and in a frequency drift of the emission. The time variation
of the inhomogeneity forms the time profile of emission
intensity. The transverse size of the local generation region
is determined by the small-scale plasma inhomogeneity in
the same way as does the longitudinal size and is most likely to be much
smaller (
![]() is of the same order of magnitude as
is of the same order of magnitude as
![]() )
than the transverse size of the coronal magnetic
loop and the diameter of the electron beam.
)
than the transverse size of the coronal magnetic
loop and the diameter of the electron beam.
This scenario is supported by X-ray observations. As Güdel et al. (1991) pointed out, X-ray bursts correlate not with single spikes but with series of spikes, i.e. the duration of the X-ray burst is comparable with that of series of spikes and the spike occurrence rate in many cases is virtually proportional to the X-ray intensity. These features are easily explained if both the duration of the X-ray burst and the duration of series of spikes are determined by the lifetime of the electron beam. A change of the electron beam cross-section results in a proportional change of the X-ray intensity and, at the same time, in a proportional change of the number of local regions of generation of radio emission (if it is assumed that the plasma density inhomogeneities required for the generation of spikes arise with equal probability in different regions of the coronal magnetic loop).
Almost all spikes are accompanied by X-ray emission. At the same time, only about 2% of X-ray bursts are accompanied by spikes (Güdel et al. 1991). In the rest of cases either the electron beam distribution function is stable with respect to MCR or the nesessary (for the generation of radio emission) plasma inhomogeneity is missing.
Here we consider in more detail the generation of
radio emission on MCR in the presence of a small-scale
plasma inhomogeneity. Assume that the electromagnetic
wave propagation direction is parallel to the magnetic field.
The physical conditions in the generation region
depend only on the longitudinal coordinate (height)
![]() ,
which corresponds to a small transverse
size of the generation region (
,
which corresponds to a small transverse
size of the generation region (
![]() ).
The magnetic field decreases exponentially with height,
).
The magnetic field decreases exponentially with height,
![]() ,
and the electron beam density
is proportional to the magnetic field intensity as
particles move along the field lines.
,
and the electron beam density
is proportional to the magnetic field intensity as
particles move along the field lines.
The height dependence of the plasma density includes
large-scale and small-scale inhomogeneities. The large-scale
inhomogeneity is a global decrease in plasma density
with height with a typical scale Lp0. As has been noted
above, the breakdown of electron beam stabilization and
the generation of emission require the presence of a small-scale
plasma inhomogeneity with a sufficiently sharp gradient
that is directed oppositely to the magnetic field gradient.
Hence in some local region the plasma density must increase
with height. In addition, the interpretation of the emission
frequency drift requires the presence of a traveling inhomogeneity.
We use the following model dependence of the plasma density
on the height which satisfies the above mentioned requirements:
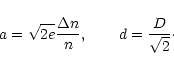 |
(31) |
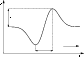 |
Figure 4: The profile of a model small-scale inhomogeneity of plasma density. |
| Open with DEXTER | |
The condition of compensation of the longitudinal inhomogeneities
of plasma and magnetic field (28) in a non-stationary
medium that is described by Eq. (30), somewhat changes
and takes the form:
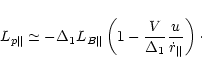 |
(32) |
As has been pointed out above, the lifetime of the electron beam
far exceeds the spike duration. Therefore when calculating
the emission parameters the beam can be considered
stationary. By varying the parameters of the electron beam (3-4) and the small-scale plasma inhomogeneity (30), we obtain different dynamic spectra of
radio emission, i.e. the dependence of the emission intensity
on the frequency and time. Figures 5-7 give
an example of such a dependence. The same parameters of the
magnetic field, plasma and electron beam as given in Table 1 were used, with the only difference that most of
them now depend on the coordinate ![]() ,
so instead of
"plasma density" there should be "plasma density at the point
where fB=350 MHz", etc. The scale of large-scale longitudinal
inhomogeneity of plasma density affects only slightly the
local process of generation of emission. It was taken to be
,
so instead of
"plasma density" there should be "plasma density at the point
where fB=350 MHz", etc. The scale of large-scale longitudinal
inhomogeneity of plasma density affects only slightly the
local process of generation of emission. It was taken to be
![]() km. The wave of the small-scale plasma
inhomogeneity had the following parameters: the amplitude
km. The wave of the small-scale plasma
inhomogeneity had the following parameters: the amplitude
![]() ,
the size D=150 km, and the velocity u=1000
,
the size D=150 km, and the velocity u=1000
![]() (the wave goes upwards). The beam energy losses due to emission are
small, so we can use a linear approximation.
(the wave goes upwards). The beam energy losses due to emission are
small, so we can use a linear approximation.
Figure 5 shows the calculated two-dimensional
dynamic spectrum of radio emission. The movement
of the inhomogeneity results in a frequency drift of
the emission with a rate of about 38
![]() .
The change of the emission intensity along the inhomogeneity wave trajectory
is caused by a change of the growth rate of the electromagnetic
waves. A total frequency range, over which the emission occurs, is
about 32 MHz, and is determined by the X1-mode generation
condition (9) and depends on the electron beam
parameters and the ratio of the large-scale longitudinal
inhomogeneities of plasma Lp0 and magnetic field
.
The change of the emission intensity along the inhomogeneity wave trajectory
is caused by a change of the growth rate of the electromagnetic
waves. A total frequency range, over which the emission occurs, is
about 32 MHz, and is determined by the X1-mode generation
condition (9) and depends on the electron beam
parameters and the ratio of the large-scale longitudinal
inhomogeneities of plasma Lp0 and magnetic field ![]() .
.
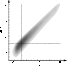 |
Figure 5: The calculated dynamic spectrum of radio emission. At the time t=0 s the small-scale plasma inhomogeneity wave is centered on the point where the electron cyclotron frequency fB=350 MHz. |
| Open with DEXTER | |
Figure 6 plots the emission
intensity versus frequency at a fixed time. The spectral
bandwidth at 1/e level is 6 MHz or 1.65% of the emission
frequency. The main factor that influence the bandwidth is the
shape of the electron beam distribution function, see the relation
(24). The observed relative bandwidth of spikes
(Csillaghy & Benz 1993; Messmer & Benz 2000)
varies from 4.1% to 0.17% (or smaller).
Emission with a relative spectral bandwidth of 0.17%
can be generated by a hollow beam with the pitch-angle dispersion
![]() and energy Eb=20 keV.
and energy Eb=20 keV.
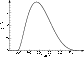 |
Figure 6: The calculated spectrum of radio emission (corresponds to the time t=-0.07 s in Fig. 5). |
| Open with DEXTER | |
Figure 7 plots the emission
intensity at the fixed frequency f=364 MHz versus time.
The burst duration at 1/e level is 154 ms. The
noticeable feature is the asymmetric shape of the time
profile - it consists of phases of fast rise and
nearly exponential decay. Spike observations with
high temporal resolution (Güdel & Benz 1990) show that such a
time profile is an essential characteristic of spikes
(for comparison, Fig. 8 shows an experimental
time profile). In earlier publications the temporal
dependence of the spike intensity was related to the
collisional damping (Güdel & Benz 1990) or the saturation of an
unstable electron distribution (Aschwanden 1990; Fleishman &
Arzner 2000). In the
case under investigation the time profile is determined by a complex
dependence of the resonance time and growth rate on the
varying conditions of generation of emission.
We are reminded that the time profile shown in Fig. 7
corresponds to the small-scale plasma inhomogeneity
wave with the size D=150 km moving upwards with
the velocity
![]() .
.
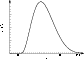 |
Figure 7: The calculated time profile of radio emission intensity (emission frequency f=364 MHz). |
| Open with DEXTER | |
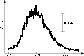 |
Figure 8: Experimental time profile of radio emission intensity at the frequency f=364 MHz. The figure is taken from (Güdel & Benz 1990). |
| Open with DEXTER | |
The theory of generation of radio emission on the maser cyclotron resonance in an inhomogeneous medium, developed earlier for radio emission of the planetary magnetospheres, has been used to interpret the solar millisecond spikes. A hollow electron beam was used as the emission source. It has been found that the main factor limiting the amplification of the electromagnetic waves is the escape of the waves from resonance with the beam in the space of wave vectors due to the influence of the inhomogeneities of the magnetic field and plasma density. The longitudinal inhomogeneity of magnetic field with a typical scale of about the the coronal magnetic loop size virtually stabilizes the unstable (with respect of MCR) electron beams and allows them to propagate to long distances. The generation of emission becomes possible only in some local regions where a small-scale inhomogeneity of plasma density compensates the longitudinal inhomogeneity of the magnetic field and slows down the wave escape from resonance. The dependence of the emission intensity on the frequency and time in this case is the reflection of the structure and dynamics of the plasma inhomogeneities. To investigate the dependence of emission parameters on the plasma small-scale inhomogeneity, an inhomogeneity model in the form of a traveling density wave has been introduced. The main criteria for choosing the inhomogeneity model were the agreement of the calculated emission parameters with observations, and a simplification of calculations. It has been shown that, despite its simplicity, this model can account for the observed features of spectra and time profiles of spikes. By varying the parameters of the electron beam, magnetic field and plasma and their inhomogeneities and comparing the calculated and observed parameters of radio emission, one can determine the physical parameters in the sources of solar spikes, and reconstruct the dynamics of plasma inhomogeneities in particular.
Acknowledgements
The authors would like to thank Dr. A. O. Benz and Dr. D. B. Melrose for helpful comments.This work was partially supported by the Competition Center for Fundamental Natural Sciences at St.-Petersburg University under grant No. E00-8.0-71 and by the Russian Foundation for Basic Research under grant No. 00-02-16819.