2 Method and results

Figure 1: The Dyer-Roeder angular-diameter distance in units of the Hubble-length for different values of the homogeneity-parameter $\alpha$ and $(\Omega _{\rm M} ,\Omega _\Lambda )=(0.3,0.7)$.

In Fig. 1, we have plotted the DR angular-diameter distance in units of the Hubble-length for different values of the homogeneity-parameter $\alpha$. The larger the value of $\alpha$, the larger the amount of focusing of the light-rays. Thus, the angular-diameter distance decreases monotonically with $\alpha$, i.e., it increases with the "inhomogeneity-parameter", $1-\alpha$. Note also that there is a simple relation between the luminosity distance, $d_{\rm L}$, and the angular-diameter distance $d_{\rm A}$,

$$d_{\rm L}=(1+z)^2\cdot d_{\rm A}.$$

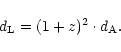
Using the simulation package SNOC (Bergström et al. 2000), we have used light-ray tracing to obtain angular-diameter distances with different inhomogeneity models and different values of the cosmological parameters. Gravitational lensing effects are calculated by integrating the geodesic deviation equation through a number of consecutive cells between the observer and the source. In each cell, we can specify the matter distribution governing the deviation. For more details of the method, see Holz & Wald (1998) and Bergström et al. (2000). In inhomogeneous models, there will not be a one-to-one correlation between the redshift and the distance since gravitational lensing will cause a dispersion in the Hubble diagram. Figure 2 shows one simulated data set of angular-diameter distances together with the DR angular-diameter distance for three different values of $\alpha$. Using $\chi^2$-tests, we determine the best-fit $\alpha$-value for each of our simulated data sets.

Figure 2: The dispersion in $d_{\rm A}$ for $(\Omega _{\rm M} ,\Omega _\Lambda )=(0.3,0.7)$ with a fraction 0.6 of the matter density in galactic dark matter halos and a fraction 0.4 in compact objects.

The case closest to the premises of the derivation of the DR distance-redshift relation is the case with one component of the matter density homogeneously distributed and another in very compact objects, e.g., point-masses.

A perhaps more realistic model of our Universe has one part of the total matter density in compact objects and another part in some smooth galaxy dark matter halo model, e.g., the Navarro-Frenk-White (NFW) density profile (Navarro et al. 1997). The compact component could, e.g., be dark matter in the form of massive compact halo objects (MACHOs) where the halo fraction deduced for the Milky Way from microlensing along the line of sight to the Large Magellanic Cloud, is of the order of 20% (Alcock et al. 2000). Note that the results are independent of the individual masses of the compact objects as well as their clustering properties on galaxy scales (Holz & Wald 1998; Bergström et al. 2000). Note also that the exact parametrization of the galaxy density profile does not significantly affect the results, see Bergström et al. (2000).

We have used three different sets of cosmological parameter values; one open with $(\Omega _{\rm M} ,\Omega _\Lambda )=(0.2,0)$ and two flat models with $(\Omega _{\rm M} ,\Omega _\Lambda )=(0.3,0.7)$ and $(\Omega _{\rm M} ,\Omega _\Lambda )=(1,0)$, respectively.

In Figs. 3 to 5 we present results for $(\Omega _{\rm M} ,\Omega _\Lambda )=(0.3,0.7)$ with one homogeneous component and one component in point-masses. Distances are calculated for z=1, z=2 and a distribution of redshifts, 0.1<z<3. For all models and redshifts, there is a linear relation between the fraction of the total matter density in point-masses, $f_{\rm p}$, and the inhomogeneity-parameter, $1-\alpha$. In the simulations using homogeneously distributed matter, we have added the condition that $1-\alpha =0$ for $f_{\rm p}=0$ when fitting the linear function.

Figure 3: Results for the homogeneity-parameter $\alpha$ for the case with one homogeneous component and one component in point-masses for z=1 and $(\Omega _{\rm M} ,\Omega _\Lambda )=(0.3,0.7)$.

Figure 4: Results for the homogeneity-parameter $\alpha$ for the case with one homogeneous component and one component in point-masses for z=2 and $(\Omega _{\rm M} ,\Omega _\Lambda )=(0.3,0.7)$.

Figure 5: Results for the homogeneity-parameter $\alpha$ for the case with one homogeneous component and one component in point-masses for 0.1<z<3 and $(\Omega _{\rm M} ,\Omega _\Lambda )=(0.3,0.7)$.

In Figs. 6 to 8, results for the more realistic case with one part of the total matter density in point-masses and another in dark matter halos parametrized by the NFW density profile are presented. Distances are calculated in a broad redshift interval 0.1<z<3.

Figure 6: Results for the homogeneity-parameter $\alpha$ for the case with one component with the NFW density profile and one in point-masses for 0.1<z<3 and $(\Omega _{\rm M} ,\Omega _\Lambda )=(0.3,0.7)$.

Figure 7: Results for the homogeneity-parameter $\alpha$ for the case with one component with the NFW density profile and one in point-masses for 0.1<z<3 and $(\Omega _{\rm M} ,\Omega _\Lambda )=(0.2,0)$.

Figure 8: Results for the homogeneity-parameter $\alpha$ for the case with one component with the NFW density profile and one in point-masses for 0.1<z<3 and $(\Omega _{\rm M} ,\Omega _\Lambda )=(1,0)$.