A&A 382, 1009-1015 (2002)
DOI: 10.1051/0004-6361:20011669

The influence of dynamic tides on the apsidal-motion rate
in close binaries with an evolved main-sequence star

B. Willems¹ - A. Claret²

1 - Department of Physics and Astronomy, The Open University, Walton Hall, Milton Keynes, MK7 6AA, UK
2 - Instituto de Astrofísica de Andalucía, CSIC, Apartado 3004, 18080 Granada, Spain

Received 18 May 2001 / Accepted 16 November 2001

Abstract
The validity of the classical formula for the rate of secular apsidal motion in close binaries is investigated for a sequence of models of a $5\, M_\odot$ star ranging from the last stages of the ${\rm C}^{12} \rightarrow {\rm N}^{14}$ reaction to the phase where hydrogen is exhausted in the core. For binaries with short orbital periods, the apsidal-motion rates predicted by the classical formula deviate from the rates determined within the framework of the theory of dynamic tides due to the effects of the compressibility of the stellar fluid and due to resonances of dynamic tides with free oscillation modes of the component stars (Smeyers & Willems 2001). As the star evolves on the main sequence, the deviations caused by the compressibility of the stellar fluid increase with increasing radius of the star. The additional deviations caused by the resonances are largest near the end of the core-hydrogen burning phase. Both of these deviations increase with increasing values of the orbital eccentricity.

Key words: binaries: close - stars: interiors - stars: evolution - stars: oscillations

1 Introduction

In close binary systems of stars, each star experiences the time-dependent tidal force exerted by its companion. The distortion caused by the tidal force leads to a perturbation of the external gravitational field, which in its turn causes secular variations of the position of the periastron in the relative orbit of the companion.

The most commonly used formula for the rate of secular apsidal motion due to the tidal deformation of the components of a close binary was derived by Cowling (1938) and subsequently by Sterne (1939) under the assumption that the orbital period is long in comparison with the free harmonic periods of the component stars. A generalisation of this classical formula taking into account the effects of an inclination of the equatorial planes of the stars with respect to the orbital plane of the binary was derived by Kopal (1959).

In a recent investigation, Smeyers & Willems (2001) (hereafter referred to as Paper I) reconsidered the derivation of the classical apsidal-motion formula in the light of the theory of dynamic tides. The authors concluded that, for sufficiently long orbital periods, the tide raised by the companion can be approximated at each instant by an appropriate linear combination of three static tides. For binaries with sufficiently long orbital periods, the classical formula then turns out to be valid up to high orbital eccentricities. When the orbital period is shorter, deviations arise due to the larger role of the stellar compressibility at higher forcing frequencies and due to the effects of resonances between dynamic tides and free oscillation modes. From the application of their results to $5\, M_\odot$, $10\,M_\odot$, and $20\,M_\odot$zero-age main sequence stars, Smeyers & Willems found the relative differences between the classical formula and the formula established within the framework of the theory of dynamic tides to be inversely proportional to the square of the orbital period. The relative differences also turned out to be larger for a model with a larger mass.

In this paper, we investigate the validity of the classical formula for the rate of secular apsidal motion in binaries with an evolved main-sequence star. Deviations between the classical formula and the formula established in the framework of the theory of dynamic tides may be expected to vary with the evolutionary stage of the star due to the changes in the central condensation and due to the growth of the stellar radius.

The plan of the paper is as follows. In Sects. 2 and 3, we present the basic assumptions and the ingredients necessary for the determination of the rate of secular apsidal motion in binaries with eccentric orbits. In Sect. 4, we briefly recall the classical formula for the rate of secular apsidal motion and the corresponding formula established within the framework of the theory of dynamic tides. In Sect. 5, we examine the influence of stellar evolution on the deviations between the apsidal-motion rates predicted by the classical formula and the rates given by the theory of dynamic tides for binaries with shorter orbital periods. Sect. 6 is devoted to concluding remarks.

2 Basic assumptions

Consider a close binary system of stars that are orbiting around each other in an unvarying Keplerian orbit with semi-major axis a and orbital eccentricity e. The first star, with mass M₁, is rotating uniformly around an axis perpendicular to the orbital plane with an angular velocity $\Omega$ which is assumed to be small in comparison to the inverse of the star's dynamical time scale:

$$\Omega \ll {1 \over \tau_{\rm dyn}} \equiv \left( {{G\, M_1} \over R_1^3} \right)^{1/2}.$$ (1)

Here G is the Newtonian constant of gravitation and R₁ the radius of the undistorted spherically symmetric equilibrium star. We treat the companion star, with mass M₂, as a point mass.

Let C₁xyz be an orthogonal right-handed frame of reference whose origin coincides with the mass centre C₁ of the tidally distorted star. The z-axis is normal to the orbital plane and is oriented in the sense of the binary's orbital angular momentum. The x- and y-axes are assumed to be corotating with the star. With respect to this frame of reference, we introduce a system of spherical coordinates $\vec{r} = (r,\theta,\phi)$ so that at each instant t the position of the companion is given by

$$r=u, \;\;\; \theta=\pi/2, \;\;\; \phi=v-\Omega\,t,$$ (2)

where u is the radial distance and v the true anomaly of the companion in its relative orbit.

The tidal force exerted by the companion is derived from the tide-generating potential $\varepsilon_{\rm T}\, W \left(r,t \right)$, where $\varepsilon_{\rm T}$ is a small dimensionless parameter defined as

$$\varepsilon_{\rm T} = \left( {R_1 \over a} \right)^3\, {M_2 \over M_1}\cdot$$ (3)

The parameter corresponds to the ratio of the tidal force to the gravity at the star's equator.

Following Polfliet & Smeyers (1990), we decompose the tide-generating potential in terms of unnormalised spherical harmonics $Y_\ell^m(\theta,\phi)$ and in Fourier series in terms of multiples of the companion's mean motion $n=2\pi/P_{\rm orb}$, where $P_{\rm orb}$is the orbital period. The decomposition takes the form

 

$$\varepsilon_{\rm T}\, W \left(r,t \right) = - \varepsilon_{\rm T}... ...\phi)\, \exp \left[ i \left( \sigma_{\rm T}\, t - k\, n\, \tau \right) \right],$$ (4)

where $\sigma_{\rm T} = k\, n + m\, \Omega$ is the forcing angular frequency with respect to the corotating frame of reference, $\tau$ is a time of periastron passage, and the $c_{\ell,m,k}$ are Fourier coefficients given by

 

$$c_{\ell,m,k} = \displaystyle {{(\ell-\vert m\vert)!} \over {(\ell... ... \pi} {\int_0^\pi (1 + e\, \cos v)^{\ell-1}\, \cos (k\, M + m\, v)\, {\rm d}v}.$$ (5)

In the latter expression, $P_\ell^{\vert m\vert}(x)$ is an associated Legendre polynomial of the first kind, and M is the mean anomaly of the companion.

The Fourier coefficients $c_{\ell,m,k}$ are equal to zero for odd values of $\ell+\vert m\vert$ and decrease with increasing values of the multiple k of the companion's mean motion. The decrease is slower for higher orbital eccentricities, so that the number of terms that has to be taken into account in the expansion of the tide-generating potential given by Eq. (4) increases with increasing values of the orbital eccentricity.

It follows that, for each degree $\ell$ of the spherical harmonics $Y_\ell^m(\theta,\phi)$, the tide-generating potential consists of a term giving rise to a static tide $(\sigma_{\rm T} = 0)$, and an infinite number of terms giving rise to partial dynamic tides $(\sigma_{\rm T} \ne 0)$. The static tides are not to be assimilated with equilibrium tides which occur when the orbit of the companion is circular and the rotation of the star is synchronised with the orbital motion of the companion.

3 The equations governing forced isentropic oscillations of a spherically symmetric star

When the effects of the Coriolis force and the centrifugal force are neglected, the uniformly rotating star can be considered to be spherically symmetric. In the isentropic approximation, a partial dynamic tide generated by a single term in the expansion of the tide-generating potential is then governed by the homogeneous fourth-order system of differential equations

   

$${{{\rm d} \left( r^2 \xi_{\rm T} \right)} \over {{\rm d}r}} = {g ... ... c^2}\, \sigma_{\rm T}^2 \right] \eta_{\rm T} + {r^2 \over c^2}\, \Psi_{\rm T},$$ (6)

$${{{\rm d} \eta_{\rm T}} \over {{\rm d}r}} = \left( 1 - {N^2 \over... ... g}\, \eta_{\rm T} - {1 \over \sigma_{\rm T}^2}\, {N^2 \over g}\, \Psi_{\rm T},$$ (7)

$${1 \over r^2}\, { {\rm d} \over {{\rm d}r}} \left( r^2 {{{\rm d}\... ...ver c^2} \left( \sigma_{\rm T}^2\, \eta_{\rm T} - \Psi_{\rm T} \right) \right].$$ (8)

In these equations, $\xi_{\rm T}(r)$ and $\eta_{\rm T}(r)$ are the radial parts of the radial and the transverse component of the tidal displacement with respect to the local coordinate basis $\partial/\partial r$, $\partial/\partial \theta$, $\partial/\partial \phi$, and $\Psi_{\rm T}(r)$is the sum of the radial parts of the tide-generating potential and the Eulerian perturbation of the star's gravitational potential. Furthermore, $\rho$ is the density, g the gravity, c²the square of the isentropic sound velocity, and N² the square of the Brunt-Väisälä frequency.

The solutions of the system of Eqs. (6)-(8) must satisfy boundary conditions at the star's centre and at the star's surface. At r=0, the radial component of the tidal displacement must remain finite. At r=R₁, the Lagrangian perturbation of the pressure must vanish, and the continuity of the gravitational potential and its gradient requires that

 

$$\left( {{{\rm d}\Psi_{\rm T}} \over {{\rm d}r}} \right)_{R_1} + {... ... = - \varepsilon_{\rm T} (2\, \ell + 1) {{G\, M_1} \over R_1^2}\, c_{\ell,m,k}.$$ (9)

Because of the non-homogeneous term in the right-hand member of this boundary condition, the solutions of the system of Eqs. (6)-(8) are proportional to the product $\varepsilon_{\rm T}\, c_{\ell,m,k}$.

In the case of static tides, the forcing angular frequency $\sigma_{\rm T}$is equal to zero and the radial component of the tidal displacement is determined by the homogeneous second-order differential equation

$${{{\rm d}^2 \xi_{{\rm T};0}} \over {{\rm d}r^2}}\! + 2\! \l... ...}r}} - {{\ell(\ell+1) - 2} \over r^2}\, \xi_{{\rm T};0} = 0.$$ (10)

This equation is equivalent to the equation of Clairaut which is usually derived within the framework of the theory of equilibrium tides in the limiting case of an infinite orbital period (Sterne 1939).

The solution of Eq. (10) must remain finite at r=0 and satisfy the boundary condition

$$\left( {{{\rm d} \xi_{{\rm T};0}} \over {{\rm d}r}} \right)_{... ..._{R_1} = \varepsilon_{\rm T}\, (2\, \ell + 1)\, c_{\ell,0,0}.$$ (11)

For the remainder of the paper, we restrict the expansion of the tide-generating potential given by Eq. (4) to the terms associated with $\ell=2$, which are dominant.

4 Apsidal motion due to the tidal deformation of a component of a close binary

The rate of secular apsidal motion due to the tidal distortion of the components of a close binary is usually determined by means of the classical formula established in the assumption that the orbital period is long in comparison to the periods of the free oscillation modes of the component stars (Cowling 1938; Sterne 1939). At each instant, the tide generated by the companion can then be approximated by a linear combination of three static tides (Paper I). The resulting formula takes the form

$$\left( {{{\rm d} \varpi} \over {{\rm d}t}} \right)_{\rm class... ...2\, \pi} \over P_{\rm orb}}\, k_2\, 15\, f\left({e^2}\right),$$ (12)

where $\varpi$ is the longitude of the periastron, and

$$f\left(e^2\right) = \left({1-e^2}\right)^{-5}\, \left({1 + {3\over 2}\, e^2 + {1\over 8}\, e^4 }\right).$$ (13)

The constant k₂ is known as the apsidal-motion constant and depends on the mass concentration of the tidally distorted star. The constant is determined as

$$k_2 = {{\displaystyle 3 - \left[ {{{\rm d}\, \ln (\xi_{{\rm... ..._{{\rm T};0}/r)} \over {{\rm d}\, \ln r}} \right]_{R_1}}}\cdot$$ (14)

Because of the logarithmic derivatives in the numerator and the denominator of this definition, the apsidal-motion constant is independent of the product $\varepsilon_{\rm T}\, c_{2,0,0}$ appearing in the boundary condition given by Eq. (11).

Within the framework of the theory of dynamic tides, the rate of secular apsidal motion is determined by adding the contributions to the apsidal motion stemming from the various partial static and dynamic tides which are generated by the individual terms in the expansion of the tide-generating potential given by Eq. (4). The resulting rate of secular change of the longitude of the periastron is given by

 

$$\left( {{{\rm d} \varpi} \over {{\rm d}t}} \right)_{\rm dyn} = \l... ...}\, G_{2,0,k} + F_{2,2,k}\, G_{2,2,k} + F_{2,-2,k}\, G_{2,-2,k} \right) \bigg],$$ (15)

where the G_2,m,k are functions of the orbital eccentricity defined as

 

$${ G_{2,m,k}(e) = {1 \over {e\, \left( 1 - e^2 \right)^2}}\, c_{2,... ...ggl[ 3 \int_0^\pi (1 + e\, \cos v)^2\, \cos (m\, v + k\, M)\, \cos v\, {\rm d}v$$

$$- m \int_0^\pi (1 + e \cos v)\, (2 + e \cos v) \sin (m\, v + k\, M)\, \sin v\, {\rm d}v \biggr]$$ (16)

(Smeyers et al. 1998).

The coefficients F_2,m,k render the star's responses to the various forcing angular frequencies $\sigma_{\rm T}$ and are related to the total perturbation of the gravitational potential at the star's surface as

$$2\, F_{2,m,k} = - \left[ {R_1\over {G\, M_1}} {{\Psi_{\rm T} ... ...right)} \over {\varepsilon_{\rm T}\, c_{2,m,k}}} + 1 \right].$$ (17)

In analogy with the apsidal-motion constant k₂, the coefficients F_2,m,k are independent of the product $\varepsilon_{\rm T}\, c_{2,m,k}$ which appears in the boundary condition given by Eq. (9).

In the limiting case of long orbital and rotational periods, the classical formula for the rate of secular apsidal motion agrees with the formula established within the framework of the theory of dynamic tides up to high orbital eccentricities (Smeyers et al. 1998). The agreement rests on the property that, in this limiting case, all forcing angular frequencies $\sigma_{\rm T}$ tend to zero, so that the coefficients F_2,m,k, with m=-2,0,2 and $k =1,2,3, \ldots$, tend to the apsidal-motion constant k₂.

For binaries with shorter orbital periods, deviations arise due to the increasing role of the stellar compressibility at higher forcing frequencies and due to resonances of dynamic tides with lower-order g⁺-modes of the component stars (Paper I). The extent of the deviations can be expected to depend on the evolutionary stage of the star due to the increase of the stellar radius and the redistribution of the mass as the star evolves on the main sequence.

5 Deviations of the classical apsidal-motion formula for binaries with an evolved main-sequence star

5.1 The models

 

We determined the deviations of the classical formula for the rate of secular apsidal motion in binaries with shorter orbital periods for a sequence of models of a $5\, M_\odot$ star with initial chemical composition X=0.70 and Z=0.02. The evolutionary track of the star in the Hertzsprung-Russell diagram is displayed in Fig. 1. The labels in the figure correspond to the numbers of the models considered in our investigation, which range from the last stages of the ${\rm C}^{12} \rightarrow {\rm N}^{14}$ reaction (model 20) to the phase where hydrogen is exhausted in the core (model 96).

	Figure 1: Evolutionary track of the $5\, M_\odot$ star with initial chemical composition X=0.70 and Z=0.02. The labels correspond to the numbers of the models considered in our investigation.
Open with DEXTER

The variation of the central hydrogen abundance $X_{\rm c}$, the apsidal-motion constant k₂, and the radius R₁ are displayed in Fig. 2 as a function of the age of the star. The central hydrogen abundance $X_{\rm c}$ decreases as the star evolves along the main sequence due to the conversion of hydrogen into helium via the CNO cycle. In addition, the conversion of hydrogen into helium increases the central condensation of the star, so that the value of the apsidal-motion constant k₂ decreases. At the end of the main sequence, when the star has reached an age of $8.4 \times 10^7$ years, the central hydrogen abundance has dropped to 0.001 and the apsidal-motion constant has decreased by a factor of two. The radius of the star expands during the major part of the evolution on the main sequence. It reaches a maximum value for model 72 and subsequently decreases again during the final stages of core-hydrogen burning. The ages, the radii, the central hydrogen abundances, and the apsidal-motion constants of the models used in our investigation are listed in Table 1.

	Figure 2: The variations of the central hydrogen abundance $X_{\rm c}$, the apsidal-motion constant k2, and the radius R1 as a function of the age of the $5\, M_\odot$ star.
Open with DEXTER

 

 

Table 1: Properties of the models of the $5\, M_\odot$ star considered in this investigation.

Model Nr.	age (yrs)	$R_1\, ({\rm km})$	$X_{\rm c}$	k2
20	$3.03 \times 10^5$	$1.93 \times 10^6$	0.699	0.00741
52	$5.65 \times 10^7$	$2.66 \times 10^6$	0.358	0.00505
72	$8.13 \times 10^7$	$3.63 \times 10^6$	0.060	0.00369
96	$8.44 \times 10^7$	$3.29 \times 10^6$	0.001	0.00348

Due to the growth of the radius with the age of the star, care needs to be taken that only orbital periods are considered for which the radius of the star remains smaller than the radius of its Roche lobe. For binaries with circular orbits, the star's Roche-lobe radius $R_{{\rm L},1}$ can be approximated by means of Eggleton's (1983) fitting formula

$${R_{{\rm L},1} \over a} = {{0.49\, q^{-2/3}} \over {0.6\, q^{-2/3} + \ln \left( 1 + q^{-1/3} \right)}},$$ (18)

where q = M₂/M₁. The relative error of the formula is smaller than 2% for all values of the mass ratio in the range of $0<q<\infty$.

The variation of the Roche-lobe radius of a $5\, M_\odot$ star, expressed in solar radii, is presented in Fig. 3 as a function of the orbital period for the mass ratios q=0.2, 0.5, 1.0. The solid lines in the figure correspond to the Roche-lobe radii for binaries with a circular orbit. The dotted horizontal lines represent the stellar radii at the evolutionary stages represented by the models 20, 52, 72, and 96.

	Figure 3: Variation of the Roche-lobe radius of a $5\, M_\odot$ star in the case of the orbital eccentricities e=0.0, 0.25, 0.5 and the mass ratios q=0.2, 0.5, 1.0. The dotted horizontal lines represent the radius of the star for models 20, 52, 72, and 96.
Open with DEXTER

In the case of a binary with an eccentric orbit, the Roche-lobe radius can be expected to be smallest when the companion is located in the periastron of its relative orbit. Therefore, we also determined the variations of the Roche-lobe radius for binaries with an eccentric orbit by substituting the periastron distance r_p=a(1-e) for the semi-major axis a in Eq. (18). The resulting Roche-lobe radii are represented by the long- and the short-dashed lines in Fig. 3 for the orbital eccentricities e=0.25 and e=0.5, respectively.

The Roche-lobe radii increase monotonically with increasing values of the orbital period and are larger for smaller values of the mass ratio. The restrictions on the orbital period imposed by the requirement that the star fit within its Roche-lobe are most stringent for higher orbital eccentricities. In the case of model 72, e.g., the orbital period must be larger than 3 days when the eccentricity takes the value e=0.25and larger than 5.5 days when the eccentricity takes the value e=0.5.

5.2 Deviations of the classical formula

An appropriate quantity to examine the deviations between the rate of secular apsidal motion given by the classical formula and the corresponding rate determined within the framework of the theory of dynamic tides is the relative difference

$$\Delta = {{\displaystyle \left( {{\rm d} \varpi/{\rm d}t} \ri... ...tyle \left( {{\rm d}\varpi/{\rm d}t} \right)_{\rm dyn}}}\cdot$$ (19)

This relative difference is independent of the product

$$\left(R_1/a\right)^5 \left(M_2/M_1\right) \left(2\, \pi/ P_{\rm orb}\right),$$

so that it depends on the orbital period only through the coefficients F_2,m,k.

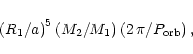
We determined the relative differences $\Delta$ as a function of the orbital period for the evolutionary models 20, 52, 72, and 96 of the $5\, M_\odot$ star, and the orbital eccentricities e=0.25 and e=0.5. The shortest orbital periods considered for each model are chosen such that the radius of the star is sufficiently small in comparison to the radius of its Roche lobe (Sect. 5.1). For the determination of the forcing angular frequencies $\sigma_{\rm T}$ with respect to the corotating frame of reference, we adopted the low angular velocity of rotation $\Omega=0.01\, n$, so that the companion's orbital period with respect to the corotating frame remains short. In the case of a resonance of a dynamic tide with a free oscillation mode, we limit the determination of $\Delta$to orbital periods for which the relative difference between the forcing angular frequency of the tide and the eigenfrequency of the oscillation mode is larger than $0.1\, \varepsilon_{\rm T}$(see Paper I). The resulting variations of the relative difference $\Delta$ are represented by the solid lines in the left- and right-hand panel of Fig. 4.

Figure 4: The relative differences $\Delta$ for models 20, 52, 72, and 96 of the $5\, M_\odot$ star in the case of the orbital eccentricities e=0.25 (left-hand panel) and e=0.5 (right-hand panel). The solid lines represent the relative differences in the presence of resonances of dynamic tides with free oscillation modes g+. The dashed lines correspond to the relative differences in the absence of resonances.

Open with DEXTER

The relative differences $\Delta$ are mostly negative so that for binaries with shorter orbital periods the classical formula yields somewhat too small values for the rate of secular apsidal motion, and thus somewhat too long apsidal-motion periods. The peaks observed at shorter orbital periods are caused by resonances of dynamic tides with free oscillation modes g⁺ of the tidally distorted star. These peaks are superposed on a basic curve which represents the systematic deviations caused by the increasing role of the stellar compressibility at shorter orbital periods.

The systematic relative differences $\Delta$ in the absence of resonances can be approximated by a formula of the form

$$\Delta_{\rm basic} = - \lambda\, T_{\rm orb}^{-2},$$ (20)

where $\lambda$ is a constant. For the determination of $\lambda$ we used a linear least-squares procedure described by Press et al. (1992) and fitted Eq. (20) to the relative differences $\Delta$displayed in Fig. 4. The resulting values of $\lambda$ are listed in Table 2 in the supposition that the orbital period is expressed in days. The associated basic curves determined by means of Eq. (20) are represented by the dashed lines in Fig. 4.

 

 

Table 2: The proportionality factor $\lambda$ for models 20, 52, 72, and 96 of the $5\, M_\odot$ star and the orbital eccentricities e=0.25 and e=0.5.

Model Nr.	$\lambda_{e=0.25}$	$\lambda_{e=0.5}$
20	0.13	0.52
52	0.27	1.1
72	0.88	3.2
96	0.68	2.3

The downwards slope of the basic curves is larger for a model representing a more evolved stage of the $5\, M_\odot$ star. The slope is largest for model 72, which is the model with the largest radius, and decreases again during the final stages of core-hydrogen burning. The underlying reason can be identified by expressing the forcing angular frequencies $\sigma_{\rm T}$ in units of the inverse of the star's dynamical time scale:

$$\sigma_{\rm T} = \left( {{G\, M_1} \over R_1^3} \right)^{1/2} \sigma_{\rm T}^\ast.$$ (21)

For a model with a constant mass, it then follows that the dimensionless forcing angular frequencies $\sigma_{\rm T}^\ast$ increase with increasing values of the stellar radius. The systematic deviations caused by the compressibility of the stellar fluid will therefore be larger for a model with a larger radius. In the case of the orbital eccentricity e=0.5 and the orbital period of 6 days, e.g., the relative differences $\Delta$ in the absence of resonances increase from 1.4% for model 20 to 8.9% for model 72.

In the case of a resonance of a dynamic tide with a free oscillation mode, the relative differences $\Delta$ may deviate substantially from the systematic trend represented by the basic curves. The largest deviations occur for resonances between the lower-order harmonics in the expansion of the tide-generating potential given by Eq. (4) and the lower-order g⁺-modes of the tidally distorted star. For these resonances the relative differences between the rates of secular apsidal motion predicted by the classical formula and the rates given by the theory of dynamic tides can amount to as much as a few tens of percents, especially for higher orbital eccentricities. This conclusion is in agreement with the conclusions reached by Papaloizou & Pringle (1980) and Quataert et al. (1996).

For a given range of orbital periods and a fixed orbital eccentricity, the deviations caused by the resonances increase as the star evolves on the main sequence. This behaviour is related to the growing radiative envelope which causes the eigenfrequencies of a more evolved stellar model to be smaller and closer to each other than those of a less evolved stellar model, so that resonances with lower-order g⁺-modes become increasingly important with increasing age of the star. A similar increase in the effectiveness of tidal forcing during the late stages of core hydrogen burning was found by Savonije & Papaloizou (1984) in an investigation on the spin-up of neutron stars and the circularization of orbits in massive X-ray binaries.

6 Concluding remarks

In this paper, we have examined the influence of stellar evolution on the deviations between the rates of secular apsidal motion predicted by the classical formula due to Cowling (1938) and Sterne (1939), and the rates of secular apsidal motion determined in the framework of the theory of dynamic tides. The deviations arise for binaries with shorter orbital periods due to the growing role of the stellar compressibility at higher forcing frequencies and due to resonances of dynamic tides with the free oscillation modes of the component stars (Smeyers & Willems 2001).

The extent of the deviations caused by the compressibility of the stellar fluid depends on the evolutionary stage of the star primarily through the evolution of the radius and the associated change of the star's dynamical time scale. As the star evolves on the main sequence, the radius and the dynamical time scale increase so that the orbital period effectively becomes shorter in comparison to the star's dynamical time scale. The deviations due to the compressibility of the stellar fluid are therefore larger for a model with a larger radius.

Besides varying the systematic deviations caused by the compressibility of the stellar fluid, the evolution of the star also affects the deviations caused by the resonances of dynamic tides with free oscillation modes of the component stars. The latter deviations are superposed upon the deviations caused by the stellar compressibility and can amount to as much as ten percent and more, especially for higher orbital eccentricities. In the case of the $5\, M_\odot$ star considered, the effects of the resonances are larger for a model near the end of core-hydrogen burning than for a model near the zero-age main sequence.

Acknowledgements

Bart Willems acknowledges the support of PPARC grant PPA/G/S/1999/00127.

References

 
• Cowling, T. G. 1938, MNRAS, 98, 734 In the text NASA ADS  
• Eggleton, P. P. 1983, ApJ, 268, 368 In the text NASA ADS  
• Kopal, Z. 1959, Close binary systems (Chapman & Hall, London) In the text  
• Papaloizou, J., & Pringle, J. E. 1980, MNRAS, 193, 603 In the text NASA ADS  
• Polfliet, R., & Smeyers, P. 1990, A&A, 237, 110 In the text NASA ADS  
• Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes, second edition (Cambridge, University Press) In the text  
• Quataert, E. J., Kumar, P., & Ao, C. O. 1996, ApJ, 463, 284 In the text NASA ADS  
• Savonije, G. J., & Papaloizou, J. C. B. 1984, MNRAS, 207, 685 In the text NASA ADS  
• Smeyers, P., & Willems, B. 2001, A&A, 373, 173 In the text NASA ADS  
• Smeyers, P., Willems, B., & Van Hoolst, T. 1998, A&A, 335, 622 In the text NASA ADS  
• Sterne, T. E. 1939, MNRAS, 99, 451 In the text NASA ADS