A&A 382, 974-983 (2002)
DOI: 10.1051/0004-6361:20011641

Time-resolved spectroscopy and photometry of the dwarf nova FS Aurigae in quiescence

V. V. Neustroev

Department of Astronomy and Mechanics, Udmurtia State University, Universitetskaia, 1, Izhevsk 426034, Russia

Received 2 September 1999 / Accepted 16 November 2001

Abstract
We present results of non-simultaneous time-resolved photometric and spectroscopic observations of the little-studied dwarf nova FS Aur in quiescence. The spectrum of FS Aur shows strong and broad emission lines of hydrogen and HeI, and of weaker HeII $\lambda4686$ and CIII/NIII blend, similar to other quiescent dwarf novae. All emission lines are single-peaked, however their form varies with orbital phase. Absorption lines from a late-type secondary are not detected. From the radial velocity measurements of the hydrogen lines H$\beta$ and H$\gamma$ we determined a most probable orbital period $P=0\hbox{$.\!\!^{\rm d}$ }059 \pm 0\hbox{$.\!\!^{\rm d}$ }002$. This period agrees well with the 0 $.\!\!^{\rm d}$0595 $\pm$ 0 $.\!\!^{\rm d}$0001 estimate by Thorstensen et al. (1996). On the other hand, the period of photometric modulations is longer than the spectroscopic period and can be estimated as 3 hours. Longer time coverage during a single night is needed to resolve this problem. Using the semi-amplitude of the radial velocities, obtained from measurements of hydrogen and helium lines, and some empirical and theoretical relations we limited the basic parameters of the system: a mass ratio $q \geq 0.22$, a primary mass $M_{1}=0.34{-}0.46~M_{\odot}$, a secondary mass $M_{2} \leq 0.1~M_{\odot}$, and an inclination angle $i=51^{\circ }{-}65^{\circ}$. Doppler tomography has shown at least two bright regions in the accretion disk of FS Aur. The first, brighter spot is located at phase about 0.6. The second spot is located opposite the first one and occupies an extensive area at phases about 0.85-1.15.

Key words: accretion, accretion disks - stars: binaries: spectroscopic - stars: cataclysmic variables - stars: individual: FS Aur

1 Introduction

FS Aur was discovered and first classified as a dwarf nova by Hoffmeister (1949). This little-studied system varies between aproximately $V=15\hbox{$.\!\!^{\rm m}$ }$4-16 $\hbox{$.\!\!^{\rm m}$ }$2 in quiescence and $V=14\hbox{$.\!\!^{\rm m}$ }4$ in outburst. Optical photometry during quiescence was reported by Howell & Szkody (1988) who found a modulation with period $P=97\pm10$ min, characteristic for SU Uma - type stars. The long term light curve was analysed by Andronov (1991). He found normal outbursts only with a probable interval between them of 12$^{\rm d}$ and no superoutburst. Therefore the SU Uma classification of this star is tentative.

Spectroscopic observations by Williams (1983) showed a typical dwarf nova spectrum with strong emission lines of hydrogen and HeI. H$\alpha$velocity variations with a period of $85.7\pm0.18$ min have been reported by Thorstensen et al. (1996; TPST hereafter). No other study of emission lines has been made for FS Aur. This motivated us to perform time-resolved spectroscopy and photometry of FS Aur in order to study its properties in more detail.

2 Observations and data reduction

2.1 Spectroscopy

The spectroscopic observations of FS Aur were obtained on January 18, 1996 with the 6 m telescope at the Special Astrophysical Observatory. The SP-124 spectrograph was used with a PHOTOMETRICS CCD, which has 1024$\times$1024 pixels. The seeing was around 2 arcsec and we selected a slit width of 1 $\hbox{$.\!\!^{\prime\prime}$ }$5. The spectra have a resolution of 2.6 Å, covering the range 4100-5000 Å. About 1.5 orbital cycles were covered with 29 spectra of 200 s long exposure (dead time between exposures was 30 s). He-Ne-Ar lamp exposures were taken typically every 30 min.

The spectra were reduced in the standard manner. All CCD frames were debiased, flat-fielded and wavelength calibrated using the MIDAS system. For the wavelength calibration of the spectra, interpolation was used between neighbouring arc spectra. The root mean square of the polynomial fits is $\sim$0.030 Å. One-dimensional spectra were extracted using the optimized algorithm proposed by Horne (1986). The resulting spectra were reduced to an absolute flux scale by calibration with standard star G191b2, which was observed in the same night. Note that substantial light losses at the slit edges occur. Therefore, our data cannot be used to obtain absolute fluxes though the obtained fluxes are good to approximately 10%. In view of this, from now on we shall use spectra normalized to the continuum.

2.2 Photometry

The photometric observations were obtained with the 1 m telescope at the Special Astrophysical Observatory (Nizhnij Arkhyz, Russia), using a 1024$\times$1024 CCD camera. 31 exposures in the V filter with 180 s integration time were obtained on February 12, 1997. The total observation time was more than 2 hours. Additional V-band CCD observations were carried out on October 11, 1997 during 4 hours using the same telescope with a 530$\times$580 CCD camera. A total of 34 frames were recorded with an integration time of 300 s.

All CCD images were debiased and flat-fielded using the MIDAS system. We calculated magnitudes of the source with respect to several "comparison'' stars within the field of view from Misselt (1996), using aperture photometry (we used standard stars C₁, C₃ and C₄). The differences between daily averages of the differential magnitudes (C₁-C₃, C₄-C₁, C₄-C₃) were within 0.01 mag during our observational runs.

	Figure 1: The single typical normalized spectrum (top panel) and the average spectrum (bottom panel) of FS Aur. The mean spectrum is an average of all spectra, corrected for wavelength shifts due to orbital motion.
Open with DEXTER

 

 

Table 1: Equivalent width (EW), Full Width at Half Maximum (FWHM), Full Width at Zero Intensity (FWZI) and Relative Intensity of the major emission lines.

Spectral line	EW	FWHM	FWZI	Relative
	(Å)	(km s-1)	(km s-1)	Intensity
H$\beta$	23.2	950	3900	2.16
H$\gamma$	21.7	1000	3500	2.03
H${\delta}$	14:	1000	3500:	1.81
HeI $\lambda4471$	6.7	1100	2700	1.36
HeI $\lambda4713$		1000		1.10
HeI $\lambda4921$	3.4	1050	2500	1.18
HeII $\lambda4686$	6.4	1300	3500:	1.29
CIII/NIII $\lambda4650$	1.9	1270:		1.10

3 Data analysis and results

3.1 The average spectrum

The single typical spectrum and the average spectrum of FS Aur are shown in Fig. 1. The mean spectrum is an average of all spectra, corrected for wavelength shifts due to orbital motion. The spectrum is typical for a dwarf nova. It is dominated by strong and broad emission lines of hydrogen and neutral helium. In addition to them HeII $\lambda4686$ and weak CIII/NIII blend are observed also. All emission lines are single-peaked. The Balmer decrement is flat, indicating that the emission is optically thick as is normal in dwarf novae. There is no evidence of a contribution from a late-type secondary star. The equivalent width, FWHM, FWZI, and Relative Intensity of the major emission lines are presented in Table 1.

	Figure 2: The variation of the H$\beta$ line profile around the orbit. The presence of a broad base component and a narrow line component is evident. There are orbital variations in the line profile. The narrow component remains practically symmetrical throughout an orbital cycle, but on the blue wing of the broad component at phases about 0.75-0.9 there appears a hump.
Open with DEXTER

3.2 Emission lines variations

In order to increase the signal to noise ratio of the spectra we have phased the individual spectra with the orbital period, derived in the next section, and then co-added the spectra into 15 separate phase bins. Figure 2 shows the H$\beta$ profiles from some of the obtained spectra. We note a broad base component and a narrower line component which is presented throughout the orbital cycle. There are orbital variations in the line profiles. But whereas the narrow component remains practically symmetric throughout the orbital cycle, on the blue wing of the broad component at phases about 0.75-0.9 a hump appears. A similar behavior is observed for all lines, but most notably for H$\beta$.

For a more accurate examination of the profiles for asymmetry we calculated the degree of asymmetry of all profiles as the ratio between the areas of the blue and the red parts of the emission line. This parameter is very similar to the V/R ratio for double-peaked emission lines. It strongly depends on the wavelength range of the line wings which was selected for calculation of the degree of asymmetry. Choosing a greater wavelength range, we can analyze the farther line wings.

We calculated the degree of asymmetry for two values of the wavelength range of the line wings, and plotted this parameter as a function of orbital phase (left-hand frame of Fig. 3, upper panel: for a wavelength range of 13 Å, and lower panel: for a wavelength range of 30 Å). In the right-hand frame of Fig. 3 are shown some profiles of the H$\beta$line in which the wavelength range used for the determination of the degree of asymmetry has been marked. One can see that the central narrow line component indeed remains practically symmetrical throughout the orbital period, showing only a slight skewness to the right from time to time (Fig. 3, top). At the same time the broad base component of the line shows strong variability, and it becomes most asymmetric at a phase of about 0.9 (Fig. 3, bottom). This variability seems to contain information on the structure of the accretion disk and give evidence for an unusually located emission region.

Figure 3: The degree of asymmetry of the emission line H$\beta$ folded on the adopted period of 0 $.\!\!^{\rm d}$0595. The degree of asymmetry is the ratio between the areas of blue and red parts of the emission line. This parameter is very similar to the V/R ratio for double-peaked emission lines. The degree of asymmetry was calculated for two values of the wavelength range of the line wings (left-hand frame, upper panel for a wavelength range of 13 Å, and lower panel for a wavelength range of 30 Å). In the right-hand frame are shown some profiles of the H$\beta$ line in which the wavelength range used for the determination of the degree of asymmetry has been marked. One can see that the central narrow line component remains practically symmetrical throughout an orbital period, showing only slight skewness to the right from time to time. The broad base component of the line shows strong variability, and it becomes quite asymmetric at a phase of about 0.9.

Open with DEXTER

3.3 Check of the period

Our photometric and spectral observations were carried out non-simultaneously and their short duration does not allow us to make any reliable period search. However as until now the orbital period of FS Aur was based only on spectra data (TPST), we have decided to check if our photometric data agree with spectral period.

Both our 2.1-hour and 4-hour light curves in the V-filter (Fig. 4) clearly show medium-amplitude (0 $.\!\!^{\rm m}$3) variations, although the flickering makes the light curves noisy. Although one can see a constant difference between two curves, their shape remains similar. However, no periodic modulations with spectroscopic period were detected, and thus the period of photometric modulations should be at least 3 hours.

As we detected a discrepancy between the photometric modulation period and the H$\alpha$ velocity variations period (from TPST), we decided also to check the spectral period using our spectral data. To verify the orbital period we measured the radial velocities in the H$\beta$ and H$\gamma$ emission lines using a Gaussian fit. To obtain an estimate of the period, a sine curve fit was made to the velocities, giving $P=0\hbox{$.\!\!^{\rm d}$ }059 \pm 0\hbox{$.\!\!^{\rm d}$ }002$ for H$\beta$ and H$\gamma$(Fig. 5). This period agrees well with the 0 $.\!\!^{\rm d}$0595 $\pm$ 0 $.\!\!^{\rm d}$0001 estimate by TPST. Additional evidence for this period, though less reliable, comes from the cyclic variations of the degree of asymmetry of the emission lines and their equivalent widths obtained from individual spectra, which oscillate with the same period.

Though we obtained different results based on photometric and spectral data, there are no reasons to doubt the reliability of the orbital (spectroscopic) period. Previous photometry of FS Aur over a 1.8-hour time span showed a 0 $.\!\!^{\rm m}$15 modulation in the B-filter with a period between 87-105 min (Howell & Szkody 1988) that is consistent with the spectroscopic period. Many CVs are known, for which the photometric behaviour varies for a short time. It is necessary to perform longer photometric observations of FS Aur during a single night to fully clarify this vagueness.

Note that henceforth we shall be using the period found by TPST because of its higher accuracy.

   
3.4 The radial velocity curve

In cataclysmic variables the most reliable parts of the emission line profile for deriving the radial velocity curve are the extreme wings. They are presumably formed in the inner parts of the accretion disk and therefore should represent the motion of the white dwarf with the highest reliability.

The velocities of the emission lines were measured using the double-Gaussian method described by Schneider & Young (1980) and later refined by Shafter (1983). This method consists of convolving each spectrum with a pair of Gaussians of width $\sigma$ whose centers have a separation of $\Delta$. The position at which the intensities through the two Gaussians become equal is a measure of the wavelength of the emission line. The measured velocities will depend on the choice of $\sigma$ and $\Delta$, and by varying $\Delta$ different parts of the lines can be sampled. The width of the Gaussians $\sigma$ is typically set by the resolution of the data.

	Figure 4: Light curves of FS Aur on February 12, 1997 (closed circles, bottom X axis) and October 11, 1997 (open circles, top X axis).
Open with DEXTER

	Figure 5: The radial velocity curve of the H$\beta$ and H$\gamma$ emission lines, derived from a single Gaussian fitting method. To obtain an estimate of the period, a sine curve fit was made to the velocities, giving $P=0\hbox{$.\!\!^{\rm d}$ }059 \pm 0\hbox{$.\!\!^{\rm d}$ }002$ for both H$\beta$ and H$\gamma$.
Open with DEXTER

	Figure 6: The diagnostic diagram for the H$\beta$ (left panel) and H$\gamma$(right panel) data, showing the response of the fitted orbital elements to the choice of the double-Gaussian separation. The best fit is reached with Gaussian separations of $\approx$1500 kms-1 for H$\beta$ and of $\approx$1300 kms-1 for H$\gamma$.
Open with DEXTER

We have measured the velocities in our binned spectra for the four emission lines (H$\beta ,$ H$\gamma$, HeI $\lambda$4471 and HeII $\lambda$4686) separately in order to test for consistency in the derived velocities. We measured the radial velocity using Gaussian separations ranging from 50 kms^-1 to 3200 kms^-1. All measurements were made using $\sigma =200$ kms^-1 and $\sigma =300$ kms^-1. For each value of $\Delta$ we made a non-linear least-squares fit of the derived velocities to sinusoids of the form

$$V(t,\Delta )=\gamma (\Delta )+K(\Delta )\sin \left[ 2\pi \left( T-T_0\left( \Delta \right) \right) /P+\pi\right]$$ (1)

where $\gamma$ is the systemic velocity, K is the semi-amplitude, T₀ is the time of inferior conjunction of the secondary star and P is the orbital period. The resulting "diagnostic diagram'' for H$\beta$ and H$\gamma$ with $\sigma =200$ kms^-1 is shown in Fig. 6. The diagram shows the variations of K, $\sigma(K)/K$ (the fractional error in K), $\gamma$ and T₀ with $\Delta$ (Shafter et al. 1986). The diagram for $\sigma =300$ kms^-1 looks the same.

To derive the orbital elements of the line wings we took the values that correspond to the largest separation just before $\sigma(K)/K$ shows a sharp increase (Shafter & Szkody 1984). Note that the dependence of parameter $\sigma(K)/K$ on Gaussian separation for both hydrogen lines is very similar (Fig. 6). For H$\beta$ it appears that $\Delta$ can be increased to $\sim$1500 kms^-1 before $\sigma(K)/K$ begins to increase. Similarly, the optimum value of $\Delta$ for H$\gamma$probably lies near 1300 kms^-1. Referring to the diagnostic diagram, the K values for H$\beta$, H$\gamma$, He I $\lambda$4471 and He II $\lambda$4686 are 73, 73, 81 and 69 kms^-1, respectively. The measured parameters of the best fitting radial velocity curves are summarized in Table 2. In Fig. 7 we show the radial velocity curves of H$\beta$ and H$\gamma$ emission lines.

 

 

Table 2: Elements of the radial velocity curves of FS Aur.

Emission	$\gamma$-velocity	K1	T0
line	(kms-1)	(kms-1)	(HJD)
H$\beta$	$46\pm 7$	$73\pm 10$	$2450101.264\pm0.001$
H$\gamma$	$68\pm 11$	$73\pm 15$	$2450101.265\pm 0.001$
HeI $\lambda$4471	$113\pm 10$	$81\pm 15$	$2450101.263\pm 0.002$
HeII $\lambda$4686	$50\pm 21$	$69\pm 29$	$2450101.265\pm 0.004$
Mean	$52\pm 7$	$73\pm8$	$2450101.264\pm0.001$

Basically, the radial velocity semi-amplitudes of the Balmer and Helium lines are consistent, while the $\gamma$-velocities are not. The reason for this is unknown. In the discussion to follow we will adopt a mean value of K and T₀ for these lines (using the $\sigma(K)$ and $\sigma(T_{0})$ as a weight factor): $K=73\pm8$ kms^-1 and $T_{0}({\rm HJD})=2450101.264\pm0.001$.

3.5 Equivalent width

We measured the equivalent widths of the H$\beta$ emission line in all individual spectra. They were investigated for a modulation with orbital period (Fig. 8). The errors have been obtained by calculating standard deviations from several independent measurements of the same lines.

Though the obtained equivalent widths exhibit rather significant dispersion, none the less one can see their modulation with orbital period. It is especially noticeable on the smoothed graph which was obtained by averaging adjacent data points (filled circles with dotted line in Fig. 8). We found that the EW is modulated with amplitudes not less than 25% of the mean value. We can confidently assert that there is a broad minimum in the EW around phase 0.1, and probably there is a secondary minimum near phase 0.6.

The observed minima could be due to an increase in the continuum luminosity when the enhanced emission region crosses the line-of-sight. If this is so then Fig. 8 testifies about complex and unusual accretion structure in FS Aur.

	Figure 7: The H$\beta$ (closed circles) and H$\gamma$ (open circles) radial velocities measured using the double-Gaussian method folded on the orbital period. All data are plotted twice for continuity. The K-velocity is $73\pm 10$ kms-1 and $73\pm 15$ kms-1 respectively.
Open with DEXTER

   
3.6 Possible system's parameters

It is impossible to measure the components' masses and the orbital inclination in a non-eclipsing, single-lined spectroscopic binary like FS Aur. However, we can determine preliminary values for the basic system's parameters, using the assumption that the secondary is a zero-age main-sequence (ZAMS) star (Patterson 1984) and that the secondary fills its Roche lobe. First of all, from our spectroscopic and photometric data we can limit the range of possible solutions.

Our observations reveal no evidence for eclipses, so we expected the inclination to be less than 65$^{\circ }$. Now, from the mass function for the system:

$$\frac{M_{2}\sin ^{3}i}{(1+q^{-1})^{2}}=\frac{PK^{3}}{2\pi G}$$ (2)

and any mass-period relations for the secondary stars we can obtain a lower limit to the mass ratio. Using any of the recently obtained empirical relations (see, for example, Caillault & Patterson 1990; Warner 1995; Smith & Dhillon 1998) we obtain a mass for the secondary less than $0.1~M_{\odot}$. Now, using Eq. (2) we find q>0.22 and, consequently, $M_{1}<0.46~M_{\odot}$.

	Figure 8: The variation of the H$\beta$ equivalent widths with orbital period. Open circles show individual values, filled circles with dotted line show data which were obtained by averaging adjacent data points. The data are plotted twice for continuity.
Open with DEXTER

Also we can place a stringent lower limit on M₁, assuming that the largest velocity in the emission line profile (FWZI/2) does not exceed the Keplerian velocity at the surface of the white dwarf:

$$\left( \frac{FWZI}{2\sin i}\right) ^{2}\frac{R_{1}}{G}<M_{1}$$ (3)

FWZI is not a well defined quantity because of the difficulty in establishing where the high velocity line wings end and the continuum begins. Besides, extensive wings due to Stark broadening can produce a spurious enhancement of emissivity at small radii. However, for the time being we assume that Stark broadening is not significant. The Balmer data show that the line wings extend to at least 1750 kms^-1from the line center. Using FWZI/2=1750 kms^-1, inclination angle $i<65^{\circ }$ and the mass-radius relation for white dwarfs (Hamada & Salpeter 1961),

$$\frac{{R_1 }}{{R_{\odot}}} = 0.0072\left( {\frac{{M_1 }}{{M_{\odot}}}} \right)^{ - 0.8},$$ (4)

we obtained $M_{1}>0.34~M_{\odot}$. And finally, using the last constraint on M₁ and Eq. (2), we can obtain a lower limit to the inclination: $i>51^{\circ }$. Table 3 summarizes all our calculated parameters.

 

 

Table 3: Adopted system's parameters for FS Aurigae.

Parameter	Value
T0 (Spectroscopic Phase 0.0)	$2450101.264\pm0.001$
Primary mass M1 ($M_{\odot}$)	0.34-0.46
Secondary mass M2 ($M_{\odot}$)	$\leq$0.1
Mass ratio q=M2/M1	$\geq$0.22
Inclination i	$51^{\circ}$- $65^{\circ}$

4 Doppler tomography

The orbital variation of the emission lines profiles detected by us indicates a non-uniform structure of the accretion disk. The distribution of the disk's emission can be explored by computing a Doppler map, using the method of Doppler tomography. Doppler tomography is an indirect imaging technique which can be used to determine the velocity-space distribution of the emission in close binary systems. A tomogram is constructed from the line profiles obtained at a variety of orbital phases. In other words, the Doppler map accumulates information about all profiles of the emission line in different phases of an orbital period. An accretion disk producing usually double-peaked emission lines should appear on the tomogram as a ring with an inner radius of $V_{\rm in} \sim 600{-}800$ kms^-1, plus additional emission that can be seen extending outward from the ring to a velocity of over $V_{\rm out} \sim 1200$ kms^-1 or more corresponding to the rest of the disk. This is because the outer edge of the disk becomes the inner edge in velocity coordinates, while the inner disk is represented by the outermost parts of the image. But we can also obtain single-peaked lines from the accretion disk. This can happen for many reasons, for example insufficient spectral resolution, a small inclination angle of the binary system, some line-broadening mechanisms. In this case the distribution of the emission on tomograms will not be ring-shaped but circular. Full technical details of the method are given by Marsh & Horne (1988) and Marsh (2001). Examples of the application of Doppler tomography to real data are given by Marsh (2001).

The Maximum Entropy Doppler maps of the H$\beta$, H$\gamma$, HeI $\lambda$4471 and HeII $\lambda$4686 emission were computed using the code developed by Spruit (1998). The resulting tomograms are displayed as a gray-scale image in Figs. 9 and 10. These figures also show trailed spectra in phase space and their corresponding reconstructed counterparts. A help in interpreting Doppler maps are additional inserted plots which mark the positions of the white dwarf, the center of mass of the binary and the Roche lobe of the secondary star. These markers are necessary to us only for facilitation of the interpretation of the tomograms, therefore the calculations of their positions can be done using our preliminary system parameters obtained in Sect. 3.6. Here we have used q=0.22, $M_{1}=0.46~M_{\odot}$ and $i=65^{\circ}$.

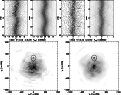Figure 9: Doppler tomograms for the H$\beta$ (left) and H$\gamma$(right) emission lines of FS Aur. These maps display a roughly symmetric and very nonuniform distribution of the emission centered near to the white dwarf. In addition to the symmetrically distributed emission, at least two additional emission sources can be seen. The first, brighter enhanced emission component is centered roughly on ( $V_x \approx -100$ kms-1, $V_y \approx -260$ kms-1) (the corresponding phase of the intersection of the line-of-sight with this bright region is about 0.6). The second source is located opposite the first one and occupies an extensive area at phases about 0.85-1.15. In addition, the tomogram of H$\gamma$ shows an emission ring with a radius of about 225 kms-1, which is centered on ( $V_x \approx 0$ kms-1, $V_y \approx -20$ kms-1). In the center of this ring there is a compact bright spot.

Open with DEXTER

The Balmer Doppler maps display a roughly symmetric and very nonuniform distribution of the emission centered near the white dwarf. So, on the H$\beta$ tomogram, in addition to the symmetrically distributed emission, at least two additional emission sources can be seen. The first, brighter enhanced emission component is centered roughly on ( $V_x \approx -100$ kms^-1, $V_y \approx -260$ kms^-1). The second occupies an area extending from azimuths about $300^{\circ}$ to $60^{\circ}$ (the corresponding phase of the intersection of the line-of-sight with this bright region is about 0.85-1.15). The first spot is well visible also on the Doppler maps of H$\gamma$ and HeI $\lambda$4471: in the case of HeI it is a primary radiating source. In addition, the tomograms of H$\gamma$ and HeII $\lambda$4686 show an emission ring with radius of about 225 kms^-1, which is centered on ( $V_x \approx 0$ kms^-1, $V_y \approx -20$ kms^-1). In the center of this ring there is a compact spot, which especially in HeII is a bright radiating source.

The interpretation of the spot structure detected in the accretion disk is ambiguous. Neither the first nor the second bright region can contribute to the emission from the bright spot on the outer edge of the accretion disk, as both areas of additional emission lie far from the region of interaction between the stream and the disk's particles. The brighter spot can be interpreted as due to an enhanced emission region located opposite to the bright spot expected by the standard model. Earlier Mennickent (1994) has shown that the bright spot region seems "to migrate" towards the back of the disk in systems with low mass ratios. This "reversed bright spot" phenomenon can be explained by a gas stream which passes above the disk and hits its back, or alternatively, by the disk thickening in resonating locations. We will analyze the nature of the detected structure of the accretion disk in the following section.

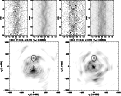Figure 10: Doppler tomograms for the HeI $\lambda$4471 (left) and HeII $\lambda$4686 (right) emission lines of FS Aur. The main emission source in HeI $\lambda$4471 is the first bright spot visible in H$\beta$(Fig. 9). The tomogram of HeII shows an emission ring with a radius of about 225 kms-1, which is centered at ( $V_x \approx 0$ kms-1, $V_y \approx -20$ kms-1). In the center of this ring there is a compact bright spot.

Open with DEXTER

5 Discussion

5.1 System's parameters

FS Aur is a non-eclipsing binary, so information on the system's parameters is difficult to obtain accurately. Usually for definition of the parameters of such systems some empirical formulae are used. However, it should be noted that these assessments are subject to unknown and potentially large errors and should be adopted with appropriate caution. In the present paper we have decided to restrict ourselves only to estimation of the parameters. To ensure some validation, we have used only stringent relations. Thus we believe that the restrictions on the basic system parameters for FS Aur obtained by us are correct, if the values of input data are correct too.

In this connection we pay attention to the obtained estimate of the mass of the white dwarf which is quite small. We have estimated the primary mass to be less (and possibly much less) than 0.46 $M_{\odot}$, which is near to the lower limit of the observed range for white dwarf masses in cataclysmic variables (Webbink 1990; Sion 1999). The estimate of M₁ depends strongly on the estimated K₁ value. Let us discuss possible errors in the definition of K₁.

The definition of the semi-amplitude of the radial velocities of the emission lines, really reflecting the orbital moving of a white dwarf, is a very complicated problem. The contribution to a broad emission line can be introduced by many emission areas of a binary system. For example, Balmer emission from the secondary star forms an additional component in an emission line moving with semi-amplitude K₁/q. This component upon condition of small q can deform the line wings. Any nonhomogeneity of the accretion disk can cause even greater distortion in the line profile.

In our case the contribution of the secondary to the Doppler maps is completely absent. At the same time, the Balmer and Helium emission is distributed very nonuniformly (Figs. 9 and 10). In general, this factor might affect the accuracy of the definition of K₁, but we hope that it has not occurred. Actually, though the areas of bright inhomogeneities can be detected rather clearly on the Balmer tomograms, nevertheless they reach distances of no more than about 500 kms^-1 from the center of the tomograms. We would like to recall, that we tested the line profiles at 650-750 km s^-1 from its center where inhomogeneities became less noticeable.

On the other hand it is necessary to note that TPST have found a somewhat smaller radial velocity semi-amplitude ( K₁ = 60 kms^-1). However they have noted that the main aim of their research was the definition of the orbital period, and their values of K₁ should not be used in dynamical solutions of the system. When we determined K₁ we adopted values of $\Delta$ much smaller than FWZI. The dependence of parameter $\sigma(K)/K$ on the Gaussian separation for H$\beta$and H$\gamma$ lines is very similar (Fig. 6). It can be seen that $\sigma(K)/K$ decreases monotonically with increasing $\Delta$. Having selected a greater value of $\Delta$ we can of course obtain a smaller value of K₁. However we cannot offer any convincing reasoning for increasing $\Delta$. It even seems undesirable to do so, as increasing $\Delta$ will lead us into the outer line wings, which are subject to contortion at some phases (Figs. 2 and 3).

Finally, it is necessary to pay attention to the emission ring, which is well noticeable on the H$\gamma$ and HeII tomograms. It is tempting to connect it with the accretion disk, and the bright spot in the ring center with the white dwarf. In this case it would become possible to independently determine K₁. Unfortunately, such a ring corresponds to a too large accretion disk, which cannot lie in the Roche lobe of the white dwarf.

Thus we believe and hope that the value of semi-amplitude of K₁(and system parameters) obtained by us is correct. Nevertheless we consider, that new, longer and better-quality observations are extremely necessary for a more precise definition of the system parameters of FS Aur.

5.2 The structure of the accretion disk

Another important result of this work is the spot structure detected in the accretion disk of FS Aur. Doppler tomography has shown at least two additional bright regions in this system. The first, brighter spot is located at phase about 0.6. The second spot is located opposite the first and occupies an extensive area at phases about 0.85-1.15. The detected spot structure of the accretion disk is confirmed by a dependence of equivalent widths on orbital phase (Fig. 8). The observed minima of EW can be due to an increase in the continuum luminosity when the enhanced emission region crosses the line-of-sight.

An enhancement of the emission coming from the back of the accretion disks of some cataclysmic variables was noted by many observers (see review by Livio 1993). Some theoretical and numerical studies indicate that high, free flowing gas could pass over the white dwarf and hit the back side of the disk (Lubow & Shu 1976; Lubow 1989; Kunze et al. 2001). In this case, the azimuth angle of the region of "secondary interaction" should be about $140^{\circ}$- $150^{\circ}$ for a wide range of the system's parameters, while the distance from the accreting component will change from 0.02 to 0.18 of the system's size, depending on the mass ratio (Lubow 1989). The phase where the line-of-sight crosses this bright spot must be about 0.6. This is where our observed bright spot is found!

In addition, recent numerical hydrodynamic calculations point to a possible difference in the thickness of the outer edge of the accretion disk in a close binary system. For example, Meglicki et al. (1993) identified three thicker regions of the disk at phases 0.2, 0.5, and 0.8. Armitage & Livio (1996) also pointed to a possible transfer of the stream matter above the plane of the accretion disk and an increase in the number of atoms along the line-of-sight relative to the average level at phases 0.1-0.2 and 0.7-1.0. Thus, the second bright region of FS Aur can be connected with one of the accretion disk's thickening regions found by Meglicki et al. (1993). The mechanism of the increase of its luminosity is not quite clear, but it is probably attributable to ionization by emission from the inner disk's region.

The nature of the ring-shaped structure visible on H$\gamma$ and HeII tomograms remains completely unintelligible. As was already noted above, this structure cannot be connected with the accretion disk, as its size should be so large, that it cannot lie in the Roche lobe of the white dwarf. Another possible site of origin is a nebula. However, the radial velocity of the nebula's center should coincide with the systemic velocity of the binary. In our case, though, the velocities are close, but still noticeably different. We again come to the conclusion, that new and better quality data are needed for the explanation of this puzzle.

6 Summary

In this paper we present the results of non-simultaneous time-resolved photometric and spectroscopic observations of the little-studied dwarf nova FS Aur in quiescence. We have obtained the following results:

$\bullet$

The spectrum of FS Aur shows strong and broad emission lines of hydrogen and HeI, and of weaker HeII $\lambda4686$ and CIII/NIII blend, similar to other quiescent dwarf novae.

$\bullet$

All emission lines in the spectrum of FS Aur are single-peaked, however their form varies with orbital phase.

$\bullet$

Absorption lines from a late-type secondary are not detected.

$\bullet$

From the radial velocity measurements of the hydrogen lines H$\beta$ and H$\gamma$ we have determined a most probable orbital period $P=0\hbox{$.\!\!^{\rm d}$ }059 \pm 0\hbox{$.\!\!^{\rm d}$ }002$. This period agrees well with the 0 $.\!\!^{\rm d}$0595 $\pm$ 0 $.\!\!^{\rm d}$0001 estimate by TPST. On the other hand, the period of photometric modulations is longer than the spectroscopic period and can be estimated as 3 hours. Longer time coverage during a single night is needed to resolve this problem.

$\bullet$

Using the semi-amplitude of the radial velocities, obtained from measurements of hydrogen and helium lines, and some empirical and theoretical relations we limited the basic parameters of the system: the mass ratio $q \geq 0.22$, the primary mass $M_{1}=0.34{-}0.46~M_{\odot}$, the secondary mass $M_{2} \leq 0.1~M_{\odot}$, and the inclination angle $i=51^{\circ }{-}65^{\circ}$.

$\bullet$

Doppler tomography has shown at least two bright regions in the accretion disk of FS Aur. The first, brighter spot is located at a phase of about 0.6. The second spot is located opposite the first one and occupies an extensive area at phases about 0.85-1.15.

Acknowledgements

I am grateful to Oksana van den Berg for contributing to a improved first version of this paper. I would like to thank the firm VEM (Izhevsk, Russia) and Konstantin Ishmuratov personally for the financial support rendered to me in the preparation of this paper. Thanks also to Alexander Khlebov for the computer and technical support. I acknowledge the referee Jet Katgert for detailed reading of the manuscript, improving the language of the manuscript, and useful suggestions concerning the final version.

References

 

• Andronov, I. I. 1991, IBVS, 3614 In the text  
• Armitage, P. J., & Livio, M. 1996, ApJ, 470, 1024 In the text NASA ADS  
• Caillault, J. P., & Patterson, J. 1990, AJ, 100, 825 In the text NASA ADS  
• Hamada, T., & Salpeter, E. E. 1961, ApJ, 134, 683 In the text NASA ADS  
• Hoffmeister, C. 1949, Veroff. Sternw. Sonneberg, 1, 3 In the text  
• Horne, K. 1986, PASP, 98, 609 In the text NASA ADS  
• Howell, S. B., & Szkody, P. 1988, PASP, 100, 224 In the text NASA ADS  
• Kunze, S., Speith, R., & Hessman, F. V. 2001, MNRAS, 322, 499 In the text NASA ADS  
• Livio, M. 1993, in Accretion Disks in Compact Stellar Systems, ed. J. C. Wheeler (Singapore: World Sci. Publ.), 243 In the text  
• Lubow, S. H. 1989, ApJ, 340, 1064 In the text NASA ADS  
• Lubow, S. H., & Shu, F. H. 1976, ApJ, 207, L53 In the text NASA ADS  
• Marsh, T. R., & Horne, K. 1988, MNRAS, 235, 269 In the text NASA ADS  
• Marsh, T. R. 2001, in Proceedings of the Astro-Tomography Workshop, ed. H. Boffin, & D. Steeghs, in press In the text  
• Meglicki, Z., Wickramasinghe, D., & Bicknell, G. V. 1993, MNRAS, 264, 691 In the text NASA ADS  
• Mennickent, R. E. 1994, A&A, 285, 979 In the text NASA ADS  
• Misselt, K. A. 1996, PASP, 108, 146 In the text NASA ADS  
• Patterson, J. 1984, ApJS, 54, 443 In the text NASA ADS  
• Schneider, D. P., & Young, P. 1980, ApJ, 238, 946 In the text NASA ADS  
• Shafter, A. W. 1983, ApJ, 267, 222 In the text NASA ADS  
• Shafter, A. W., & Szkody, P. 1984, ApJ, 276, 305 In the text NASA ADS  
• Shafter, A. W., Szkody, P., & Thorstensen, J. R. 1986, ApJ, 308, 765 In the text NASA ADS  
• Sion, E. M. 1999, PASP, 111, 532 In the text NASA ADS  
• Smith, D. A., & Dhillon, V. S. 1998, MNRAS, 301, 767 In the text NASA ADS  
• Spruit, H. C. 1998 [astro-ph/9806141] In the text  
• Thorstensen, J. R., Patterson, J. O., Shambrook, A., & Thomas, G. 1996, PASP, 108, 73 (TPST) In the text NASA ADS  
• Warner, B. 1995, Cataclysmic Variable Stars, Cambridge Astrophys. Ser., 28 (Cambridge: Cambridge Univ. Press) In the text  
• Webbink, R. F. 1990, in Accretion Powered Compact Binaries, ed. C. W. Mauche (Cambridge: Cambridge Univ. Press), 177 In the text  
• Williams, G. 1983, ApJS, 53, 523 In the text NASA ADS