A&A 382, 1070-1080 (2002)
DOI: 10.1051/0004-6361:20011694

Temporal aspects and frequency distributions of solar soft X-ray flares

A. Veronig¹ - M. Temmer¹ - A. Hanslmeier¹ - W. Otruba² - M. Messerotti³

1 - Institut für Geophysik, Astrophysik & Meteorologie, Universität Graz, Universitätsplatz 5, 8010 Graz, Austria
2 - Sonnenobservatorium Kanzelhöhe, 9521 Treffen, Austria
3 - Osservatorio Astronomico di Trieste, Via G. B. Tiepolo 11, 34131 Trieste, Italy

Received 13 September 2001 / Accepted 15 November 2001

Abstract
A statistical analysis of almost 50000 soft X-ray (SXR) flares observed by GOES during the period 1976-2000 is presented. On the basis of this extensive data set, statistics on temporal properties of soft X-ray flares, such as duration, rise and decay times with regard to the SXR flare classes is presented. Correlations among distinct flare parameters, i.e. SXR peak flux, fluence and characteristic times, and frequency distributions of flare occurrence as function of the peak flux, the fluence and the duration are derived. We discuss the results of the analysis with respect to statistical flare models, the idea of coronal heating by nanoflares, and elaborate on implications of the obtained results on the Neupert effect in solar flares.

Key words: methods: statistical - sun: flares - sun: X-rays

1 Introduction

With the availability of space-borne instrumentation, observations of solar flare phenomena in X-rays became possible in the 1960s. Disk-integrated soft X-ray emission measurements of the Sun have been collected more or less continuously since 1974 by the National Oceanic and Atmospheric Administration (NOAA), providing an almost unbroken record fully covering solar cycles 21 and 22 and the rising phase of cycle 23 (Garcia 2000).

Statistical investigations on temporal aspects of solar flares observed in various soft X-ray wavelengths have been carried out by Culhane & Phillips (1970), Drake (1971), Thomas & Teske (1971), Phillips (1972), Datlowe et al. (1974), and Pearce & Harrison (1988). In the meantime a wealth of data has accumulated, which makes worthwhile re-investigating the temporal characteristics of soft X-ray (SXR) flares on an extensive statistical basis. In the present analysis we make use of SXR flares observed by GOES during 1976-2000.

Moreover, on the basis of this comprehensive data set, we calculate frequency distributions of SXR flares as function of the peak flux, the fluence, i.e. the integrated flux from the start to the end of a flare, and the event duration. Frequency distributions of flare occurrence are related to the observational expectations from different flare models. Furthermore, they contain information about the possibility of coronal heating by nanoflares. Frequency distributions of solar flares from disk-integrated SXR measurements as function of the peak flux have been carried out by Drake (1971), Lee et al. (1995) and Feldman et al. (1997). However, only in the paper by Drake (1971) are frequency distributions of SXR fluence measurements also presented. Shimizu (1995) used spatially resolved observations from transient SXR brightenings and investigated frequency distributions as function of energy.

Soft X-ray measurements are an important counterpart to observations of flares in hard X-rays (HXR). From several observations it is reported that the SXR light curve has a similar shape as the time integral of the HXR curve. This led to the idea that there is a causal relationship between hard and soft X-ray emission of a flare, the so-called Neupert effect (Neupert 1968; Dennis & Zarro 1993). It supports a flare model, known as the thick-target model (Brown 1971), in which the HXR emission is electron-ion bremsstrahlung produced by energetic electrons as they reach the dense layers of the chromosphere. Only a small fraction of the electron beam energy is lost through radiation; most of the loss is due to Coulomb collisions, which serve to heat the ambient plasma. Due to the rapid deposition of energy by the particle beams, the energy cannot be radiated away at a sufficiently high rate and a strong pressure imbalance develops, causing the heated plasma to expand up into the corona ("chromospheric evaporation"), where this hot dense plasma gives rise to the enhanced SXR emission (e.g., Antonucci et al. 1984; Fisher et al. 1985; Antonucci et al. 1999, and references therein). In this paper we make use of the flare frequency distributions and the correlations among distinct flare parameters to infer information about the validity of the Neupert effect in solar flares by statistical means.

The paper is structured as follows. The data set is described in Sect. 2. In Sect. 3.1 a statistical investigation of temporal properties of SXR flares is presented. Correlations among various flare parameters, such as characteristic times, peak flux and fluence, are analyzed in Sect. 3.2. In Sect 3.3 frequency distributions as function of the peak flux, the fluence and the duration are derived. In Sect. 4 we give a summary and discussion of the main results. Finally, the conclusions are drawn in Sect. 5.

2 Data set

The present analysis is based on solar SXR flares observed by GOES in the 0.1-0.8 nm wavelength band during the period January 1976 to December 2000. We make use of the GOES flare listing in the Solar Geophysical Data (SGD), which contains almost 50000 single events for the time span considered.

2.1 GOES flare observations

Since 1974 broad-band soft X-ray emission of the Sun has been measured almost continuously by the meteorology satellites operated by NOAA: the Synchronous Meteorological Satellite (SMS) and the Geostationary Operational Environment Satellite (GOES). The first GOES was launched by NASA in 1975, and the GOES series extends to the currently operational GOES 8 and GOES 10. From 1974 to 1986 the soft X-ray records are obtained by at least one GOES-type satellite; starting with 1983, data from two co-operating GOES are generally available (Garcia 1994, 2000).

The X-ray sensor, part of the space environment monitor system aboard GOES, consists of two ion chamber detectors, which provide whole-sun X-ray fluxes in the 0.05-0.4 and 0.1-0.8 nm wavelength bands. The initial series of satellites maintained attitude control via spin-stabilization. GOES 8, launched in April 1994, and all subsequent GOES are three-axis stabilized, making it possible to observe the Sun uninterrupted by spacecraft rotations. This new operational mode facilitated an improved signal-to-background ratio and a higher time resolution, 0.5 s (prior to 1994, the time resolution was 3 seconds). Aside from the observing mode, the basic X-ray detector is unchanged with respect to the previous instrumentation (Garcia 2000). However, beginning with GOES 8, the dynamic range of the X-ray sensor was extended in order to permit the most energetic SXR events to be recorded.

Solar soft X-ray flares are classified according to their peak burst intensity measured in the 0.1-0.8 nm wavelength band by GOES. The letters (A, B, C, M, X) denote the order of magnitude of the peak flux on a logarithmic scale, and the number following the letter gives the multiplicative factor, i.e., ${\rm A}n = n \times 10^{-8}$, ${\rm B}n = n \times 10^{-7}$, ${\rm C}n = n \times 10^{-6}$, ${\rm M}n = n \times 10^{-5}$, and ${\rm X}n = n \times 10^{-4}$ W m^-2. In general, n is given as a float number with one decimal (prior to 1980, n is listed as an integer). No background subtraction is applied to the data.

In the present statistical analysis we utilize the 1-min average GOES data, as listed in the SGD. The definition of the start of a GOES X-ray event comprises the fulfillment of three conditions during four consecutive 1-min long intervals of observation: 1) all four values are above the B1 threshold; 2) all four values are strictly increasing; 3) the last value is greater than 1.4 times the value which occurred three minutes earlier. The maximum time is given by the 1-min averaged value of the SXR peak time. The end time is defined by the return of the flux to half the peak value above the pre-flare level. The temporal parameters calculated in the present analysis refer to these definitions of the start, end and maximum times of the SXR flares.

2.2 Data description and reduction

Table 1 lists the number of flares reported for the period January 1976 to December 2000, subdivided into the different SXR flare classes. No class A flares are listed, since the SGD cover only SXR events $\ge$B1 (see also the definition of flare onset in Sect. 2.1). As it can be seen from Table 1, the bulk of flares belongs to class C ($\approx$66%). Larger flares, i.e. M and X, are less frequent and occur primarily during times of maximum solar activity. Smaller flares, i.e. A and B, actually occur more frequently than C class flares. However, during periods of maximum activity the X-ray background is too high to detect A and B class flares from full-disk measurements (in extreme cases the X-ray background may even reach M-level). Thus, the distribution of detected flares among the SXR classes with the distinct maximum at class C results as an interaction of both these effects, i.e. the infrequent occurrence of large flares and the restriction of detecting small flares to periods of minimum solar activity. The increased X-ray background during maximum solar activity may be due to emission from many flare events as well as due to a steady coronal heating mechanism (e.g., Feldman et al. 1997).

 

 

Table 1: The number of flare events for the different SXR flare classes (B, C, M, X) and the corresponding percentage values are listed. T denotes the total number of flares occurring in the selected period (1976-2000).

Class	No. events	No. (%)
B	11558	23.4
C	32784	66.4
M	4708	9.5
X	359	0.7
T	49409	100.0

The present paper investigates temporal flare parameters as well as characteristics of the measured SXR flux. For the temporal analysis, the reported start, maximum and end times were checked. Moreover, due to the fact that prior to 1997 the reported SXR flare times were taken from the H$\alpha$ event, if there was a correlated one, also those flares were rejected from further analysis. Applying these selection criteria, for the temporal part of the analysis the data set was reduced to a number of 26745 events, covering 8844 B, 16507 C, 1331 M and 63 X class flares. Peak flux values are basically listed for each event and the respective analysis makes use of the overall data set as listed in Table 1. SXR fluence data, i.e. the integrated flux from the start to the end of an event, are available since January 1997, amounting to 8400 events.

3 Analysis and results

3.1 Statistics of temporal flare parameters

We statistically analyzed temporal aspects of SXR flares, i.e. the duration, rise and decay times. The temporal parameters have been derived only from those events, which fulfilled the selection criteria given in Sect. 2.2. Figure 1 shows the distributions of the duration, rise and decay times considering the total of events. Each histogram reveals a pronounced negative skewness.

	Figure 1: Histograms of duration, rise and decay times calculated from the total of flares passing the temporal selection criteria. The solid line indicates the median value of the distribution. The dotted line represents the 90th percentile, which indicates the abscissa range covering 90% of events.
Open with DEXTER

In Table 2 we list various statistical measures characterizing the distributions of the temporal parameters, the arithmetic mean, the median, the mode and the 90th percentile P₉₀. The obtained results for the mode of the duration, 7.0 min, is in agreement with previous studies, although different definitions of the start and end time of SXR events are used. Phillips (1972) and Pearce & Harrison (1988) report a mode in the range 5-10 min. Feldman et al. (1997) obtained SXR lifetime peaks in the range 6-8 min. Drake (1971) reports higher values, 16 min, considering only flares greater than about C2.

 

 

Table 2: Mean, median, mode and 90th percentile (P₉₀) values of the duration, rise and decay times of the total number of flares.

Stat. measure	Duration	Rise time	Decay time
	(min)	(min)	(min)
Mean	18.2	9.1	9.1
Median	12.0	5.0	6.0
Mode	7.0	4.0	3.0
P90	34.0	18.0	17.0

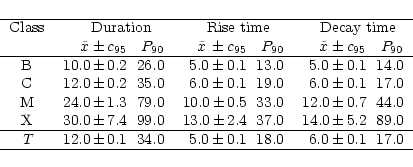
Figure 2 shows the distributions of the duration separately for the different classes of SXR flares. It can be seen that with increasing flare class the skewness of the distributions decreases and the center of the distribution moves to larger values. In Table 3 we list the median values (plus confidence intervals) and the 90th percentile values of the temporal parameters calculated for the different classes of SXR flares. Since the relevant distributions are significantly asymmetric (see Figs. 1 and 2), they are better represented by the median, $\tilde{x}$, than by the arithmetic mean. As a measure of statistical significance we make use of the 95% confidence interval, $\tilde{x} \pm c_{95}$, with

$$c_{95} = \frac{1.58~(Q_{3}-Q_{1})}{\sqrt{n}} \cdot$$ (1)

	Figure 2: Histograms of duration for the different SXR flare classes. The solid line indicates the median of the distribution, the dotted line the 90th percentile. The histograms of the B, C and M class flares are represented with a bin size of 2 min; for the X class flares it is 4 min to account for the poor statistics.
Open with DEXTER

Q₁ and Q₃ denote the first and the third quartile, respectively, n the total number of data values.

  

Table 3: Median values with 95% confidence interval, $~\tilde{x} \pm c_{95}$, and 90th percentiles, P₉₀, of the duration, rise and decay times for the different SXR classes (B, C, M, X) and the total number of flares ( T). All values are given in minutes.

$$\begin{tabular} {cc@{$\,\pm\,$}c@{~}rc@{$\,\pm\,$}c@{~}rc@{$\... ... & ~5.0 & 0.1 & 18.0 & ~6.0 & 0.1 & 17.0\\ \hline \end{tabular}$$

Table 3 reveals that on average the characteristic times increase with the flare class. The differences from one class to the other are larger than the 95% confidence limits, indicating the statistical significance of the effect. However, due to the rather poor statistics of X class flares, the respective 95% confidence limits are somewhat larger. From Tables 2 and 3 it follows that the median values of the rise and decay times are quite similar, for the overall number of flares as well as for the different flare classes. We want to stress that this fact is in particular related to the used definition of the end time of an event, i.e. the return of the flux to half the peak value above the background level at the time of the flare onset, which obviously underestimates the decay phase. However, the actual end of an X-ray event, i.e. the return of the coronal plasma to the state before the SXR flare, is difficult to determine, since the background level may change during the flare endurance and/or the decay phase may be overlaid by other events. Therefore, definitions of the characteristic times based on the peak flux are commonly used in statistical SXR flare studies (e.g., Culhane & Phillips 1970; Drake 1971; Pearce & Harrison 1988; Lee et al. 1995).

3.2 Correlations among flare parameters

	Figure 3: Scatter plots of the flare duration (top panel), rise time (middle panel) and decay time (bottom panel) as function of the peak flux. The solid line represents the linear regression fit to the data. For better illustration not the whole flare sample is plotted but a number of 1500 randomly chosen events from the period 1976-2000.
Open with DEXTER

Figure 3 shows the correlation scatter plots of the characteristic times, i.e. duration, rise and decay times, as function of the peak flux. The cross-correlation coefficients, calculated in log-log space, give similar values with $r \approx 0.25$, indicating a low correlation between the characteristic times and the peak flux.

	Figure 4: Scatter plots of the flare duration (top panel), rise time (middle panel) and decay time (bottom panel) as function of the fluence. The solid line represents the linear regression fit. 1500 randomly chosen events from the sample 1997-2000 are plotted.
Open with DEXTER

In Fig. 4 the scatter plots of the characteristic times as function of the fluence are shown. The cross-correlation coefficients give r=0.68 for the duration, r=0.64 for the rise times, and r=0.61 for the decay times. The outcome that the correlation between the fluence and the characteristic times is distinctly higher than those between the peak flux and the characteristic times is not unexpected, since the fluence intrinsically increases with the endurance of the event.

The top panel of Fig. 5 shows the scatter plot of the fluence versus the peak flux. The corresponding cross-correlation coefficient, r=0.88, is higher than that of the fluence and the duration, r=0.68. From the linear fit in log-log space we obtain the relation ${\cal F} \propto (F_{\rm P})^{1.10}$ with ${\cal F}$ denoting the fluence and $F_{\rm P}$ the peak flux. The bottom panel of Fig. 5 shows the scatter plot of the fluence versus the peak flux multiplied by the flare duration, yielding r=0.99. From this high cross-correlation coefficient it follows that the product of the peak flux and the duration, $F_{\rm P} \times t_{\rm dur}$, is a good estimate of the fluence, ${\cal F}$, without accounting for the actual time profile. From the regression analysis we obtain the relation: ${\cal F} \propto (F_{\rm P} \times t_{\rm dur})^{0.96}$.

	Figure 5: Scatter plots of the fluence as function of the peak flux (top panel) and as function of the peak flux times duration (bottom panel). The solid line represents the linear regression fit. 1500 randomly chosen events from the sample 1997-2000 are plotted.
Open with DEXTER

3.3 Frequency distributions

Frequency distributions have been calculated for various types of flare-associated activity, such as radio bursts, soft X-rays, hard X-rays, interplanetary type III bursts and interplanetary particle events (cf. Crosby et al. 1993; Aschwanden et al. 1998; and references therein). It has been shown that above a certain threshold (often attributed to the sensitivity of the observations) most of these frequency distributions can be represented by power-laws of the form

$${\rm d}N = A x^{-\alpha} {\rm d}x \; ,$$ (2)

where ${\rm d}N$ denotes the number of events recorded with the parameter x of interest in the interval $[x,x+{\rm d}x]$. A and $\alpha$ are constants, which can be determined from a fit to the data. For the distributions of different flare-related parameters, values in the range have been obtained (cf. Crosby et al. 1998). Theoretical considerations on various aspects concerning frequency distributions of flare-related phenomena, such as truncation effects, problems of the histogram method, time resolution of the observations, can be found, e.g., in Lee et al. (1993), Parnell & Jupp (2000) and Isliker & Benz (2001).

	Figure 6: Frequency distributions as function of the peak flux (top panel), fluence (middle panel) and duration (bottom panel). The dotted line indicates the least squares fit to the data.
Open with DEXTER

	Figure 7: Frequency distributions as function of the peak flux calculated separately for periods of minimum and maximum activity of solar cycle 22 (top panel) and solar cycle 23 (bottom panel). Frequency distributions for times of minimum activity are represented by full lines, for times of maximum activity by dashed-dotted lines.
Open with DEXTER

In Fig. 6 we show the frequency distributions for the peak flux, the fluence and the duration. The distributions of the peak flux and the fluence reveal power-laws over 2-3 decades. From the slopes of the distributions in log-log space we obtain $\alpha=2.11\pm0.13$ for the peak flux, and $\alpha=2.03\pm0.09$for the fluence. The frequency distribution of the event duration can also be well represented by a power-law, with $\alpha=2.93\pm0.12$.

Figure 7 illustrates the frequency distributions of the peak fluxes calculated separately for periods of minimum and maximum solar activity. The top panel shows the respective distributions of solar cycle 22 (calculated from the years 1986 and 1989), the bottom panel for the current cycle 23 (1996/2000). From the figure it can be clearly seen that during times of minimum activity the power-law behavior extends to smaller peak fluxes, since during these periods also less intense flares can be detected, evidence that the turn-over of the power-law distribution in fact is caused by the sensitivity of the observations, and the power-law is expected to extend to even smaller sizes. On the other hand, during times of maximum solar activity the power-law ranges to larger peak fluxes due to the enhanced occurrence of intense flares. However, as it can be inferred from Fig. 7, the slope of the distribution, i.e. the power-law index, does not reveal any remarkable change in the course of the solar cycle.

A few previous papers present frequency distributions as function of the SXR peak flux and fluence, respectively. Drake (1971) analyzed SXR flares measured in the 0.2-1.2 nm wavelength range from Explorer 33 and 35, finding $\alpha=1.75\pm 0.10$ for the peak flux distribution, and $\alpha=1.44\pm 0.01$ for the fluence distribution. Lee et al. (1995), investigating the peak fluxes of SXR flares with hard X-ray counterparts observed by GOES in the 0.1-0.8 nm band during 1981-1989, obtained $\alpha=1.86\pm 0.10$. Additionally, they investigated peak count rates for the Ca  XIX soft X-ray line emission measured by the BCS instrument aboard SMM, finding $\alpha=1.79\pm 0.01$. Feldman et al. (1997) investigated GOES peak fluxes observed in the 0.1-0.8 nm wavelength band during the period 1993-1995. By dividing the flares into domains according to the X-ray background level, they were able to extend the power-law relationship to A1 brightness level, obtaining an average value of $\alpha=1.88\pm0.21$ from a least squares fit and $\alpha=1.99$ from a non-parametric fit to the data.

It has to be noted that the value of $\alpha$ obtained in the present paper for the peak flux distribution is somewhat larger than those of the above cited papers. This difference might be caused by the fact that we did not apply a background subtraction, as some other authors did (e.g., Drake 1971; Feldman et al. 1997). Since the background subtraction is relatively stronger on smaller flares than large ones, it is expected to result in a slightly flattened frequency distribution. In the analysis of the peak flux distributions, Drake (1971) applied a correction in order to account for the effect that his data analysis method discriminates against small events on the basis of the actual background level. However, no such correction was applied in the analysis of the fluence distribution, which probably is the cause for the significantly smaller value of the power-law index of the fluence distribution he obtained.

4 Summary and discussion

4.1 Temporal flare characteristics

A loose correlation was found between the characteristic times and the flare peak fluxes, $r \approx 0.25$. This outcome is also reflected in the increasing values for the duration, rise and decay times with increasing flare class, as listed in Table 3. The average values of the duration (defined as the median of the distribution) give 10 min for B, 12 min for C, 24 min for M, and 30 min for X class flares. Thus, on average the duration increases from B to X class flares by a factor 3.

As it can be inferred from Table 3, this increase is caused in a similar manner by the rise as well as the decay times. This differs to what was found for H$\alpha$ flares (Temmer et al. 2001), revealing a distinctly more pronounced increase of the decay times than of the rise times with increasing flare importance, indicating that the cooling phase of the H$\alpha$ flare is more strongly affected by the event strength than the phase of heating-up the plasma at the flare site. However, we cannot exclude that a similar effect might exist in the case of the SXR flares, since the definition of the event end time by the return of the flux to half the peak value possibly causes a stronger underestimation of the actual decay time of intense events than weaker ones.

4.2 Statistical flare models

The distributions of the peak flux, the fluence and the duration revealed a power-law behavior over several decades, the determined power-law indices are $\alpha=2.11\pm0.13$, $\alpha=2.03\pm0.09$ and $\alpha=2.93\pm0.12$, respectively. The first attempt to explain the power-law distributions of flare-related phenomena was done by Rosner & Vaiana (1978), who developed a model based on a stochastic flaring probability and exponential energy build-up between successive events. However, the correlation between the strength of a flare and the elapsed time since the previous event, predicted by the model, is not supported by observations (Biesecker 1994; Crosby et al. 1998; Hudson et al. 1998; Wheatland 2000).

Lu & Hamilton (1991) were the first to propose an avalanche model of solar flares, relating the power-law distributions to the scale-invariant properties of a self-organized system in a critical state. Contrary to the energy storage model, no correlation between elapsed time and event size is expected from avalanche flare models. Moreover, since the avalanche size distribution is insensitive to much of the microphysics, from such a model it is also expected that the power-law distributions do not change over the solar cycle (see, e.g., Lu & Hamilton 1991; Lu et al. 1993). Crosby et al. (1993) and Lu et al. (1993) reported such invariance of $\alpha$in the course of the solar cycle for the occurrence of hard X-ray flares. In the present analysis we calculated peak flux distributions separately from periods of minimum and maximum solar activity (see Fig. 7), which confirms the invariance of $\alpha$ also for SXR flares. This outcome is similar to the finding of Feldman et al. (1997) that the power-law index of the peak flux distributions of SXR flares is insensitive to the actual SXR background level, which is closely related to the solar cycle (e.g., Wilson 1993).

4.3 Frequency distributions and correlations among flare parameters

Significant correlations among the characteristic times and the fluence, $r \approx 0.65$, were found. (Note that all cross-correlations were calculated in log-log space.) The correlation analysis of the fluence, ${\cal F}$, and the peak flux, $F_{\rm P}$, revealed a high cross-correlation coefficient, r = 0.88. From the regression analysis it follows ${\cal F} \propto (F_{\rm P})^{1.10}$. It is also shown that it is justified to estimate the fluence of an event by the product of the peak flux and the duration, since the respective cross-correlation coefficient amounts to r=0.99, whereas ${\cal F} \propto (F_{\rm P} \times t_{\rm dur})^{0.96}$.

The obtained power-law index of the peak flux distribution, $\alpha_{\rm P} = 2.11$, is similar to that of the fluence distribution, $\alpha_{\cal F} = 2.03$. Assuming that on average the fluence ${\cal F}$ of an event corresponds to its peak flux $F_{\rm P}$, which can be justified by the high correlation among these parameters, then $\frac{{\rm d}N({\cal F})}{{\rm d}{\cal F}} \, {\rm d}{\cal F} = \frac{{\rm d}N({F_{\rm P}})}{{\rm d}{F_{\rm P}}} \, {\rm d}{F_{\rm P}}$, where both quantities can be represented by power-law functions with power-law index  $\alpha_{\cal F}$ and $\alpha_{\rm P}$, respectively. On the other hand, from the scatter plot (Fig. 5, top panel) we find that ${\cal F}$ versus $F_{\rm P}$ is well fitted by the relation ${\cal F} \propto (F_{\rm P})^s$with s=1.10. Thus we obtain (cf. Lu et al. 1993):

$${\cal F} \propto F_{\rm P}^{(1-\alpha_{\rm P})/(1-\alpha_{\cal F})} = (F_{\rm P})^s \, .$$ (3)

With this relation, the power-law index of the fluence distribution, $\alpha_{\cal F}$, can be derived from the power-law index of the peak flux distribution, $\alpha_{\rm P}$, and the slope of the linear regression curve in log-log space, s, as:

$$\alpha_{\cal F} = 1 + \frac{(\alpha_{\rm P}-1)}{s} \cdot$$ (4)

With $\alpha_{\rm P} = 2.11$ and s=1.10 we obtain $\alpha_{\cal F}=2.01$, which is very close to the value determined from the fluence distribution, $\alpha_{\cal F} = 2.03$(cf. Fig. 6, middle panel). This means that the relation of the power-law indices for the distribution of the peak flux and the fluence can be interpreted in terms of the correlation between both quantities. Since s, the slope obtained from the regression analysis of the fluence versus the peak flux, is close to unity, the value of $\alpha_{\cal F}$ is close to $\alpha_{\rm P}$; if s is larger, then $\alpha_{\cal F}$ would decrease with respect to $\alpha_{\rm P}$.

4.4 The Neupert effect

Several observations revealed that the shape of the SXR light curve closely matches the time integral of the HXR emission. It has been argued that this observation is evidence for a causal relationship between the nonthermal hard X-ray emission and the thermal soft X-ray emission, the so-called Neupert effect (Neupert 1968; Dennis & Zarro 1993). The underlying idea is that the hard X-rays come from accelerated electrons impinging on coronal or chromospheric plasma, whereas the bulk of the energy deposited by the nonthermal electrons is converted into heating of the ambient thick-target plasma (Brown 1971). The soft X-ray emission is due to thermal bremsstrahlung from hot dense plasma that evaporated into the corona, as a consequence of the rapid energy deposition. In this case, the hard X-ray emission is proportional to the time profile of the accelerated electrons. The soft X-ray emission, which is emitted by the plasma heated by the same nonthermal electron population, is proportional to the accumulated energy deposited by the electrons up to a given time. Thus, it is expected to see the Neupert effect (see McTiernan et al. 1999).

The Neupert effect, as it is commonly stated in the literature, can be expressed as

$$F_{\rm P,SXR} = k \cdot {\cal F}_{\rm HXR} \, ,$$ (5)

where k is a proportionality factor that depends on several factors (e.g., the magnetic field geometry, the viewing angle, etc.), and therefore may vary from flare to flare. However, if k does not depend systematically on the flare size, then the HXR fluence and the SXR peak flux distributions should have the same shape. In particular, the respective power-law indices should be equal, i.e., $\alpha_{\rm P,SXR} = \alpha_{{\cal F}{\rm ,HXR}}$ (cf. Lee et al. 1993, 1995). However, the power-law index derived for the HXR fluence distribution, (cf. Lee et al. 1993, and references therein) is smaller than those of the SXR peak flux distribution, (Drake 1971; Lee et al. 1995; Feldman et al. 1997; this paper). It has already been pointed out by Lee et al. (1993, 1995) that such statistical considerations lead to a discrepancy with the Neupert effect in its simple form as stated in Eq. (5).

A possible explanation for this discrepancy might be that the HXR and SXR emissions are not necessarily indicative for the energies involved. As discussed in Lee et al. (1995), the Neupert effect should exist not necessarily between the X-ray emissions but between the energies. Namely the energy deposited by the nonthermal electrons, $\epsilon_{\rm e^-}$, should be equal to the maximum thermal energy contained in the plasma heated by the same electrons, $\epsilon_{\rm th,max}$, i.e.

$$\epsilon_{\rm e^-} = \epsilon_{\rm th,max} \, .$$ (6)

In this case, the proportionality factor k, which relates the X-ray emissions, may be a function of the flare size, still being compatible with the Neupert effect for the energies (Eq. (6)). One reason to expect that k indeed depends on the flare size is the finding of Feldman et al. (1996) that the observed SXR temperature tends to increase with flare size. Therefore, the amount of SXR emission per HXR electron may be different for large flares than for small ones (McTiernan 2001, private communication). Moreover, as shown by McTiernan et al. (1999), consistency of the observed HXR and SXR emission with the Neupert effect depends on the temperature response of the SXR detector used. It has been noted that the Neupert effect is more commonly associated with high than low temperature SXR emission.

Another possibility, of course, is that the Neupert effect is not working for the bulk of flares but just a subset of it. Most evidence for the Neupert effect indeed has been found for large and impulsive flares (e.g., Dennis & Zarro 1993; McTiernan 1999). Applying the same considerations as in Sect. 4.3, whereas

$${\cal F_{\rm HXR}} \propto (F_{\rm P, SXR})^s \, ,$$ (7)

we find

$$s = \frac{(\alpha_{{\rm P,SXR}} - 1)}{(\alpha_{{\cal F}{\rm ,HXR}} - 1)} \cdot$$ (8)

Since from observations it is known that $\alpha_{{\cal F}{\rm ,HXR}} < \alpha_{\rm P,SXR}$, it can be inferred from Eq. (8) that s is larger than 1. Under the assumption that the X-ray emissions are representative for the involved energies (i.e. the proportionality factor k does not depend systematically on the flare size), s is expected to be equal to 1 (cf. Eqs. (5) and (7)). In this case, the found difference of the power-law indices, $\alpha_{{\cal F}{\rm ,HXR}}$and $\alpha_{\rm P,SXR}$, indicate that the increase (decrease) of the SXR peak flux with increasing (decreasing) HXR fluence is smaller than it would be in the case of the Neupert effect. Any deviation from the Neupert effect basically means that the hot plasma giving rise to the SXR emission is not heated exclusively by the thermalization of the accelerated electrons responsible for the HXR emission (Dennis & Zarro 1993; Lee et al. 1993). Thus, the soft X-ray emission might be a better indicator of the total energy released in a flare than the HXR emission, and analogously the SXR flare frequency distributions might better reflect the total energy distribution of solar flares than the HXR frequency distributions (see also Lee et al. 1993; Feldman et al. 1997).

On the other hand, if we assume that the Neupert effect formulated for the energies (Eq. (6)) is valid for the bulk of flares, but the SXR and HXR emissions are not directly indicative for the nonthermal and thermal energies (i.e., k may depend systematically on the flare size), then the difference of the power-law indices of the HXR fluence and the SXR peak flux distributions can be considered to contain information on k as function of the flare size. Since s > 1, and comparing Eqs. (5) and (7), k is expected to decrease with increasing HXR fluence or increasing SXR peak flux, respectively. In that case, the functional dependency of k on the flare size gives an indication that the amount of SXR emission per HXR electron is smaller for large flares than for small ones. However, in the present study we cannot decide on these different possibilities.

4.5 Coronal heating by nanoflares

The actual value of the power-law index $\alpha$ determined from various flare-related phenomena is in particular of interest with respect to the idea of heating the corona by numerous small magnetic reconnection events extending below the observational limit, so-called nanoflares (Parker 1988). Hudson (1991) calculated that if the total power needed to heat the corona is generated by flare-like events of different sizes, then the total power is equal to the integral of event energies times their frequency of occurrence. Assuming that the frequency of events as function of the event energy follows a power-law of the form given in Eq. (2) and that the energies of the largest events are much larger than those of the smallest ones, Hudson (1991) has shown that if $\alpha < 2$, large events dominate the total power in the distribution and nanoflares cannot contribute much to it. Otherwise, if $\alpha \ge 2$, the more numerous small-scale events dominate and may provide a significant contribution to coronal heating.

However, the flare energy is not an observable quantity, and the investigations of flare frequency distributions most often rely on peak flux or peak count rate measurements. In a few papers though, the observed quantities have been transformed into flare energies, and frequency distributions as function of energy have been determined (see also Benz & Krucker 2001). Krucker & Benz (1998) and Parnell & Jupp (2000) analyzed energy distributions of events from quiet Sun regions, so-called network flares (Krucker et al. 1997), observed in Extreme Ultraviolet emission, finding $\alpha$ in the range 2.3-2.6 and 2.1-2.6, respectively. Such outcome suggests that the events at the low energy range dominate the total power in the distribution. However, using data from the Soft X-ray Telescope aboard Yohkoh, Shimizu (1995) studied transient brightenings discovered in solar active regions, obtaining frequency distributions as function of energy with $\alpha$ in the range 1.5-1.6. He estimated that the energy provided by small events is at most 20% of the total energy required to heat the active region corona. Crosby et al. (1993) analyzed frequency distributions of HXR flares. Assuming a thick-target model, they calculated the total energy in electrons and obtained from the distribution $\alpha \approx 1.5$.

In general, one has to be cautious in relating the frequency distributions of observed quantities to those of flare energies, as the energy available from flares in detail depends on their number, emission measure and temperature (e.g., Feldman et al. 1997). Hudson (1991) made use of empirical conversion formulae to obtain the frequency distributions of the total (radiated) flare energy from observed peak flux measurements in various wavelengths. The assumed proportionalities, which ensure a one-to-one correspondence of the respective power-law indices, are criticized, e.g., by Feldman et al. (1997). However, the fluence is a better representation of the total energy available in flares than peak flux measurements. Under the assumption that the fluence is proportional to the total radiated flare energy (e.g. Krucker & Benz 1998), the found power-law index of the fluence distribution, $\alpha_{\cal F}$, is also representative of the energy distribution.

Since the determined power-law index relevant to coronal heating, $\alpha_{\cal F} = 2.03 \pm 0.09$, is very close to the critical value of 2, we investigated the influence of the background subtraction on the fluence distribution, using the SXR flux just before the onset of the flare. For the analysis we integrated this background level over the event duration and subtracted it from the given fluence data for the subsample January 1997 - July 1999. As expected, from the distribution of the background subtracted fluence data we obtain a somewhat smaller power-law index, $\alpha_{\cal F} = 1.88 \pm 0.11$. However, within the given error limits this value is still rather close to 2. Moreover, it has to be noted that the derived power law index is still distinctly larger than those obtained by Drake (1971), with $\alpha_{\cal F} = 1.44 \pm 0.01$, which is the only other paper dealing with fluence distributions of SXR flares.

5 Conclusions

Frequency distributions of SXR flare occurrence as function of the peak flux, the fluence and the event duration have been calculated. All distributions can be described by power-law functions over several decades. The distributions, derived separately for the times of minimum and maximum solar activity do not reveal any remarkable change in the power-law index, consistent with the predictions of avalanche flare models (e.g., Lu & Hamilton 1991; Lu et al. 1993).

Relating the SXR fluence measurements to the total radiated flare energy, the determined power-law index $\alpha_{\cal F}$ is also representative of the flare energy distribution. The obtained values of $\alpha_{\cal F}$are 2.03 for the raw fluence data and 1.88 for the background subtracted fluence data. Both values are rather close to the critical value of 2, and no distinct conclusion can be drawn whether small-scale events provide a significant contribution to coronal heating or not. Moreover, deviations from the assumed proportionality between SXR fluence and flare energies would also cause deviations from the one-to-one correspondence of the respective power-law indices. If the slope of energy versus fluence in log-log space is less than one, then the power-law index of the energy distribution would be smaller than those of the fluence distribution, and vice versa.

The power-law index of SXR peak flux distributions (see Drake 1971; Lee et al. 1995; Feldman et al. 1997; this paper) is significantly larger than those reported for HXR fluence distributions (cf. Lee et al. 1993, and references therein), statistical evidence that the Neupert effect in its commonly stated form relating the X-ray emissions (Eq. (5)) is not valid for the bulk of flares. However, this outcome does not necessarily mean that the Neupert effect does not work for the more fundamental relationship between the energies (Eq. (6)). Depending on the validity of the Neupert effect for the bulk of solar flares, the differences in the power-law indices contain information upon additional energy sources for the SXR-emitting plasma, or upon the amount of SXR emission per HXR electron as a function of the flare size. From the present analysis, based only on SXR data, we cannot distinguish between these different possibilities. Moreover, a mixing of both cases might exist, making a distinction even more difficult. Therefore, a detailed statistical analysis of related SXR and HXR flares is in preparation in order to obtain deeper insight into the Neupert effect.

Acknowledgements

The authors are very grateful to Bojan Vrsnak for the careful reading of the manuscript and his helpful comments. A. V. thanks Hana Mészárosová for the provision of a cross-check on the flare frequency distributions. The authors also would like to thank James M. McTiernan for instructive comments on the Neupert effect. A. V., M. T. and A. H. acknowledge the Austrian Fonds zur Förderung der wissenschaftlichen Forschung (FWF grant P13655-PHY) for supporting this project. M. M. acknowledges the support of the Italian Space Agency (ASI) and the Ministry for University and Research (MURST).

References

 

• Antonucci, E., Gabriel, A. H., & Dennis, B. R. 1984, ApJ, 287, 917 In the text NASA ADS  
• Antonucci, E., Alexander, D., Culhane, J. L., et al. 1999, in The Many Faces of the Sun: A Summary of the Results from NASA's Solar Maximum Mission, ed. K. T. Strong, J. L. R. Saba, B. M. Haisch, & J. T. Schmelz (Springer), 331 In the text  
• Aschwanden, M. J., Dennis, B. R., & Benz, A. O. 1998, ApJ, 497, 972 In the text NASA ADS  
• Benz, A. O., & Krucker, S. 2001, in Recent Insights into the Physics of the Sun and Heliosphere: Highlights from SOHO and Other Space Missions, ed. P. Brekke, B. Fleck, & J. B. Gurman, IAU Symp., 203, 471 In the text  
• Biesecker, D. A. 1994, On the Occurrence of Solar Flares Observed with the Burst and Transient Source Experiment, Ph.D. Thesis, University of New Hampshire In the text  
• Brown, J. C. 1971, Solar Phys., 18, 489 In the text NASA ADS  
• Crosby, N. B., Aschwanden, M. J., & Dennis, B. R. 1993, Solar Phys., 143, 275 In the text NASA ADS  
• Crosby, N. B., Vilmer, N., Lund, N., & Sunyaev, R. 1998, A&A, 334, 299 In the text NASA ADS  
• Culhane, J. L., & Phillips, K. J. H. 1970, Solar Phys., 11, 117 In the text NASA ADS  
• Datlowe, D. W., Hudson, H. S., & Peterson, L. E. 1974, Solar Phys., 35, 193 In the text NASA ADS  
• Dennis, B. R., & Zarro, D. M. 1993, Solar Phys., 146, 177 In the text NASA ADS  
• Drake, J. F. 1971, Solar Phys., 16, 152 In the text NASA ADS  
• Feldman, U., Doschek, G. A., Behring, W. E., & Phillips, K. J. H. 1996, ApJ, 460, 1034 In the text NASA ADS  
• Feldman, U., Doschek, G. A., & Klimchuk, J. A. 1997, ApJ, 474, 511 In the text NASA ADS  
• Fisher, G. H., Canfield, R. C., & McClymont, A. N. 1985, ApJ, 289, 425 In the text NASA ADS  
• Garcia, H. A. 1994, Solar Phys., 154, 275 In the text NASA ADS  
• Garcia, H. A. 2000, ApJS, 127, 189 In the text NASA ADS  
• Hudson, H. S. 1991, Solar Phys., 133, 357 In the text NASA ADS  
• Hudson, H. S., Labonte, B. J., Sterling, A. C., Watanabe, T. 1998, in Observational Plasma Astrophysics: Five Years of Yohkoh and Beyond, ed. T. Watanabe, T. Kosugi, & A. C. Sterling (Kluwer Academic Publishers), 237 In the text  
• Isliker, H., & Benz, A. O. 2001, A&A, 275, 1040 In the text  
• Krucker, S., Benz, A. O., Acton, L. W., & Bastian, T. S. 1997, ApJ, 448, 499 In the text  
• Krucker, S., & Benz, A. O. 1998, ApJ, 501, L213 In the text NASA ADS  
• Lee, T. T., Petrosian, V., & McTiernan, J. M. 1993, ApJ, 412, 401 In the text NASA ADS  
• Lee, T. T., Petrosian, V., & McTiernan, J. M. 1995, ApJ, 448, 915 In the text NASA ADS  
• Lu, E. T., & Hamilton, R. J. 1991, ApJ, 380, L89 In the text NASA ADS  
• Lu, E. T., Hamilton, R. J., McTiernan, J. M., & Bromund, K. R. 1993, ApJ, 412, 841 In the text NASA ADS  
• McTiernan, J. M. 1999, AAS, 194.5402M In the text  
• McTiernan, J. M., Fisher, G. H., & Li, P. 1999, ApJ, 514, 472 In the text NASA ADS  
• Neupert, W. M. 1968, ApJ, 153, L59 In the text NASA ADS  
• Parker, E. N. 1988, ApJ, 330, 474 In the text NASA ADS  
• Parnell, C. E., & Jupp, P. E. 2000, ApJ, 529, 554 In the text NASA ADS  
• Pearce, G., & Harrison, R. A. 1988, A&A, 206, 121 In the text NASA ADS  
• Phillips, K. J. H. 1972, Ph.D. Thesis, University College London In the text  
• Rosner, R., & Vaiana, G. S. 1978, ApJ, 222, 1104 In the text NASA ADS  
• Shimizu, T. 1995, PASJ, 47, 251 In the text NASA ADS  
• Temmer, M., Veronig, A., Hanslmeier, A., Otruba, W., & Messerotti, M. 2001, A&A, 375, 1049 In the text NASA ADS  
• Thomas, R. J., & Teske, R. G. 1971, Solar Phys., 16, 431 In the text NASA ADS  
• Wheatland, M. S. 2000, Solar Phys., 191, 381 NASA ADS  
• Wilson, R. M. 1993, JGR, 98, 11477 In the text