A description of image motion characteristics is given for a general case of atmospheric turbulence. For this purpose the parameter p used in the expression
A&A 382, 1125-1137 (2002)
DOI: 10.1051/0004-6361:20011671
P. F. Lazorenko1
Main Astronomical Observatory, National Academy of Sciencies of the Ukraine, Golosiiv, 252680 Kyiv-127, Ukraine
Received 25 May 2001 / Accepted 4 October 2001
Abstract
A description of image motion characteristics is given for
a general case of atmospheric turbulence. For this purpose
the parameter p used in the expression
![]() for a
2-D power spectrum of a phase is considered as a variable term with a
typical 1/3-2/3 range of fluctuations. Dependence on p of the
variance
for a
2-D power spectrum of a phase is considered as a variable term with a
typical 1/3-2/3 range of fluctuations. Dependence on p of the
variance ![]() of differential image motion was studied
for stellar configurations with one, two, and a set of reference stars
located in a circular area, for a circular entrance pupil and
interferometers. It was shown that
for non-Kolmogorov turbulence,
of differential image motion was studied
for stellar configurations with one, two, and a set of reference stars
located in a circular area, for a circular entrance pupil and
interferometers. It was shown that
for non-Kolmogorov turbulence, ![]() is subject to
significant variations even when Fried's
parameter r0 and mean square absolute image motion are fixed.
The method allowing us to reduce atmospheric errors
by transition to 1-D
measurements of differential coordinates is considered.
Orientation of coordinate axes in this case depends on
the direction of wind and intensity of turbulence in atmospheric
layers. Atmospheric limitations of large ground-based telescopes
are discussed.
is subject to
significant variations even when Fried's
parameter r0 and mean square absolute image motion are fixed.
The method allowing us to reduce atmospheric errors
by transition to 1-D
measurements of differential coordinates is considered.
Orientation of coordinate axes in this case depends on
the direction of wind and intensity of turbulence in atmospheric
layers. Atmospheric limitations of large ground-based telescopes
are discussed.
Key words: atmospheric effects - instrumentation: interferometers - astrometry
The distorting influence of the Earth's atmosphere on light wave propagation essentially restricts opportunities for ground-based telescopes and considerably reduces their efficiency in comparison with telescopes working in Space. In differential astrometry atmospheric factors affect apparent relative positions of closely located stars so that they are subject to random displacements.
Theoretical deductions of atmospheric influence on the process of star image formation are usually based on some model of atmospheric turbulence. Most frequently, the Kolmogorov type of the turbulence is used. With this approximation basic relations for fluctuations of a phase and amplitude of the light wave propagating in a turbulent medium have been obtained, and a theoretical description of various atmospheric effects in optical astronomy is given (e.g. Tatarsky 1961; Fried 1965; Martin 1987; Sarazin & Roddier 1990). Lindegren (1980), in particular, has found dependence of the mean error of differential measurements on parameters of turbulent layers, angles between stars, and exposure. Temporal spectra and asymptotic power laws for a phase difference and differential angle of arrival were studied by Conan et al. (1995).
Meteorological data (e.g. Vinnichenko et al. 1976; Bull 1967) and theoretical studies (Weinstock 1980; Dalaudier & Sidi 1987), however, testify that the real atmosphere is not always in that physical state of fully developed 3-D turbulence which is described by the Kolmogorov theory. Strong evidence of deviations from the Kolmogorov model of turbulent spectrum have been frequently detected by astronomical observations, for example, with optical interferometers (Bester et al. 1992; Buscher et al. 1995).
In the present paper, we study differential image motion
suggesting a non-Kolmogorov type of the turbulence, and compare
results with those known for a classical case.
Description of differential
displacements of star images is based on the model of a
phase screen representing statistical properties of the
wavefront. Spatial power spectral
density of phase fluctuations is modeled by a power law
with a spectral slope which depends on the type of
turbulence in a layer.
Tentative limits of the spectral index variations are estimated.
A spectral approach to the problem allows one to take into
account various cases of
star relative positions and directions of image
centroid measurements by introducing or modifying some
necessary filters. Further, we derive expressions for the
variance ![]() of differential
image motion, either averaged, or non-averaged with respect to the model
spatial parameters, and discuss
the difference in performances of a filled single-aperture
telescope and interferometer in very narrow fields.
of differential
image motion, either averaged, or non-averaged with respect to the model
spatial parameters, and discuss
the difference in performances of a filled single-aperture
telescope and interferometer in very narrow fields.
Direct and remote sensing of an atmosphere shows that
intensive clear air turbulence exists only in a discrete set
of narrow turbulent layers isolated from each
other by laminar flows. A typical depth of turbulent
layer ![]() is much less than its height h above the surface,
and is in the limit of 10-100 m
(Barletti et al. 1977; Redfern 1991) to
100-800 m (Vinnichenko et al. 1976). According to Chunchuzov (1996),
existence of the layered structure of
turbulence is associated with features of a vertical
profile of the Brunt-Vaisala frequency N. He
also argues that near local maxima in the frequency
N, vertical profile gravitational internal waves can create
thin horizontal layers of a turbulence whose positions
are independent of the type of internal wave source.
is much less than its height h above the surface,
and is in the limit of 10-100 m
(Barletti et al. 1977; Redfern 1991) to
100-800 m (Vinnichenko et al. 1976). According to Chunchuzov (1996),
existence of the layered structure of
turbulence is associated with features of a vertical
profile of the Brunt-Vaisala frequency N. He
also argues that near local maxima in the frequency
N, vertical profile gravitational internal waves can create
thin horizontal layers of a turbulence whose positions
are independent of the type of internal wave source.
Small values of ![]() allow one to use the model of a thin phase
screen (Goodman 1985) for each turbulent layer. In the model,
a layer thickness and extinction of light transmitting through a layer
are neglected, only change of a phase is
considered. A plane wave entering the screen gains
some random phase
allow one to use the model of a thin phase
screen (Goodman 1985) for each turbulent layer. In the model,
a layer thickness and extinction of light transmitting through a layer
are neglected, only change of a phase is
considered. A plane wave entering the screen gains
some random phase
![]() on exit, where x, y are
rectangular coordinates of a point in the screen plane.
Though orientation of the coordinate frame x, y is arbitrary,
we assume for definiteness that its axes are parallel to
the axes of the equatorial coordinate system. By
statistical properties,
on exit, where x, y are
rectangular coordinates of a point in the screen plane.
Though orientation of the coordinate frame x, y is arbitrary,
we assume for definiteness that its axes are parallel to
the axes of the equatorial coordinate system. By
statistical properties,
![]() corresponds to a
homogeneous and isotropic random field, so 2-D
power spectral density
corresponds to a
homogeneous and isotropic random field, so 2-D
power spectral density
![]() of a phase has circular
symmetry:
of a phase has circular
symmetry:
![]() .
Here u, v are spatial frequencies corresponding
to x, y, and
.
Here u, v are spatial frequencies corresponding
to x, y, and
![]() is a circular frequency.
For the function
is a circular frequency.
For the function
![]() with a fairly complicated
dependence on q (Sect. 3) we use approximation by a simple function
with a fairly complicated
dependence on q (Sect. 3) we use approximation by a simple function
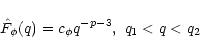 |
(1) |
The factor ![]() in (1) is determined by the intensity of turbulent
motions and is proportional to the coefficient C2n of the structure
function of refractive index n fluctations
in (1) is determined by the intensity of turbulent
motions and is proportional to the coefficient C2n of the structure
function of refractive index n fluctations
| Dn(r)=C2nrp , | (2) |
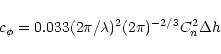 |
(3) |
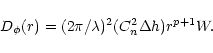 |
(4) |
![\begin{displaymath}D_{\phi} (r)=2\int _{0}^{\infty }\int _{0}^{2\pi}
[1-J_0 (2\pi qr)] \hat{F}_{\phi } (q)q\, {\rm d}q\, {\rm d}\varphi,
\end{displaymath}](/articles/aa/full/2002/06/aa1512/img44.gif) |
(5) |
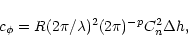 |
(6) |
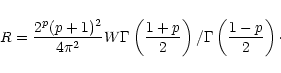 |
(7) |
Note that at greater scales isotropy is not maintained (Sect. 3) and Eqs. (4) and (6) are not valid.
In addition to the already introduced parameters, the model (1) is
supplemented with data on module V and
the angle
![]() that wind velocity
vector
that wind velocity
vector ![]() forms with the x-axis.
forms with the x-axis.
The spatial spectrum of phase fluctuations, besides being directly related to that of temperature t fluctuations in a turbulent layer, depends also on localization of a turbulence which can be either 3-D or 2-D, concentrated in a narrow horizontal quasi-2-D space.
To begin, let's refer to results of meteorological studies of a turbulent temperature spectrum under clear sky conditions on scales 1-105 m, of interest for this study.
By the data of airborne measurements in the troposphere and
lower stratosphere (Vinnichenko et al. 1976), a 1-D
temperature spectrum F't (q) in a low-frequency spectral
range usually follows a dependence
![]() which in
the higher frequency range is transformed to
which in
the higher frequency range is transformed to
![]() .
The position of the frequency qB separating these spectral
ranges is not permanent and depends on stratification. In
diagrams presented by Vinnichenko et al. (1976), qB corresponds to
scales of 200-1000 m. Spectral
slopes intermediate between -5/3 and -3 are also frequently found,
and sometimes spectra of
unregular shapes with local maxima and minima are detected.
.
The position of the frequency qB separating these spectral
ranges is not permanent and depends on stratification. In
diagrams presented by Vinnichenko et al. (1976), qB corresponds to
scales of 200-1000 m. Spectral
slopes intermediate between -5/3 and -3 are also frequently found,
and sometimes spectra of
unregular shapes with local maxima and minima are detected.
Observed features of the function F't (q) in general are
consistent with
modern theories of atmospheric turbulence. According to
Dalaudier & Sidi (1987), in low frequencies (buoyancy range)
temperature
fluctuations are caused by vertical displacements of
air particles in a stably stratified medium, some part
of kinetic energy is converted here to the potential form.
A spectral flux of potential energy (temperature) in the
buoyancy subrange is directed towards larger scales. In this
subrange both F't (q) and the kinetic energy spectrum
follow a dependency
![]() .
In higher frequencies (passive range
of temperature fluctuations corresponding to an inertial range
of kinetic energy)
temperature fluctuations are converted to heat in the usual way
described by the Kolmogorov theory. Here the spectral slope is
-5/3.
Dalaudier & Sidi (1987) theoretically
have substantiated a possibility of the so-called
"spectral gap" occurrence nearby qB, with an adjacent peak at
higher frequency. The slope of the spectral curve to the right of the
gap is much less than -5/3.
Weinstock (1980) suggested
some other mechanisms leading
to the formation of similar gaps in the kinetic energy spectrum
on scales of 30-1000 m.
.
In higher frequencies (passive range
of temperature fluctuations corresponding to an inertial range
of kinetic energy)
temperature fluctuations are converted to heat in the usual way
described by the Kolmogorov theory. Here the spectral slope is
-5/3.
Dalaudier & Sidi (1987) theoretically
have substantiated a possibility of the so-called
"spectral gap" occurrence nearby qB, with an adjacent peak at
higher frequency. The slope of the spectral curve to the right of the
gap is much less than -5/3.
Weinstock (1980) suggested
some other mechanisms leading
to the formation of similar gaps in the kinetic energy spectrum
on scales of 30-1000 m.
| spectral | spatial form of | structure | functions | power | spectrum | ||
| spatial scales | subrange | the turbulence | n and t | n and t | p | ||
| from 1 m to | |||||||
| 10-103 m | passive | 3-D | r2/3 | r5/3 | q-5/3 | q-11/3 | +2/3 |
| from 10-102 m | |||||||
| to 102-104 m | passive | 2-D | r2/3 | r2/3 | q-5/3 | q-8/3 | -1/3 |
| from 102-103 m | |||||||
| to 105 m and more | buoyancy | 2-D | r2 | r2 | q-3 | q-4 | +1 |
In Table 1, typical scales for buoyancy and passive subranges of turbulence, corresponding theoretical power laws for function F't (q) and structure functions of t and n quantities are given. It should be noted that "theoretical" power laws are deduced under the classical assumption of no additional sources and sinks of energy (wind shear, gravitational waves), and therefore are rather approximate.
The slopes of observed spectral functions F't (q) frequently and in a random way deviate from the "theoretical" ones. This was noticed, for example, by Bull (1967) who studied temporal spectra of n index measured with a microwave refractometer. While an average spectral slope was -1.68 at scales 2-100 m (temporal frequencies transformed into spatial scales with V=5 m/s), which is very close to the Kolmogorov's -5/3, sampled values of the spectral index varied from -1.2 to -2.5. Additional, modifying influences on the theoretically predicted temperature spectrum were affected by internal gravitational waves (Hogstrom et al. 1998).
The indicated details of the function F't (q) shape
directly affect the phase power spectral density
![]() .
Function
.
Function
![]() ,
besides, depends on the type of spatial
(2-D or 3-D) localization of the turbulent temperature field,
that is, on the dimensionality of space where the temperature
fluctuations can be considered as isotropic. On small
scales not exceeding the thickness of a turbulent layer
,
besides, depends on the type of spatial
(2-D or 3-D) localization of the turbulent temperature field,
that is, on the dimensionality of space where the temperature
fluctuations can be considered as isotropic. On small
scales not exceeding the thickness of a turbulent layer
![]() or
outer scale of turbulence L (these value estimates range
from 3-5 m (Coulman et al. 1988), to 30-100 m (Busher et al. 1995)
and to 100-1000 m (Vinnichenko et al. 1976),
fluctuations are 3-D and basic
functions of a phase are determined by expressions (1) and
(4). Therefore, with a "theoretical" spectrum
or
outer scale of turbulence L (these value estimates range
from 3-5 m (Coulman et al. 1988), to 30-100 m (Busher et al. 1995)
and to 100-1000 m (Vinnichenko et al. 1976),
fluctuations are 3-D and basic
functions of a phase are determined by expressions (1) and
(4). Therefore, with a "theoretical" spectrum
![]() we
have here (first line in Table 1)
we
have here (first line in Table 1)
![]() ,
,
![]() and p=2/3.
and p=2/3.
On scales
![]() and
and
![]() the turbulence is
essentially 2-D. The power spectral densities and
structure functions of n and t are described here (in a
horizontal plane) by the same power laws
as for 3-D turbulence. Corresponding
functions for a phase, however, are modified. Really, on
scales
the turbulence is
essentially 2-D. The power spectral densities and
structure functions of n and t are described here (in a
horizontal plane) by the same power laws
as for 3-D turbulence. Corresponding
functions for a phase, however, are modified. Really, on
scales
![]() one can
neglect changes of n and t across a
layer. Accordingly, a phase difference
one can
neglect changes of n and t across a
layer. Accordingly, a phase difference
![]() between two points of the screen
between two points of the screen
![]() and
and ![]() is proportional to the difference
is proportional to the difference
![]() ,
hence the phase structure function
,
hence the phase structure function
![]() is
proportional to the structure functions of n and t. So, in
a passive range
is
proportional to the structure functions of n and t. So, in
a passive range
![]() ,
while in
the buoyancy range
,
while in
the buoyancy range
![]() is expected
(Table 1). Now, using Eq. (5) it is easy to find spectral densities
of a phase
is expected
(Table 1). Now, using Eq. (5) it is easy to find spectral densities
of a phase
![]() (buoyancy range)
and
(buoyancy range)
and
![]() (passive range)
corresponding to these functions.
Two values of parameter p for 2-D turbulence are
therefore valid: p= + 1 at very large scales
q-1>qB-1,
and p=-1/3 for scales shorter than qB-1.
Thus, the function
(passive range)
corresponding to these functions.
Two values of parameter p for 2-D turbulence are
therefore valid: p= + 1 at very large scales
q-1>qB-1,
and p=-1/3 for scales shorter than qB-1.
Thus, the function
![]() relevant even to a very simplified
theoretical description of a turbulence, on scales 1-105 m
depends on frequency in a rather complicated way.
relevant even to a very simplified
theoretical description of a turbulence, on scales 1-105 m
depends on frequency in a rather complicated way.
Discussion of astronomical sources of data of the parameter p, in view of astronomical applicability of this analysis, is of a special value.
Diagrams of phase structure
functions, temporal spectra, and Allan functions are very typical for path
differences from a star to two telescopes of infrared
interferometer with baselines 4 and 13 m (Bester et al. 1992).
The peculiarity of these diagrams over spatial scales
![]() m (at wind velocity V=10 m/s corresponding to
temporal scales 2-1000 s and frequencies 10-0.5 Hz) is in a
strongly varying form of observed functions from sample to sample.
For scales indicated, the parameter p ranged from 0.2 to 1.0
with an average p=0.5.
m (at wind velocity V=10 m/s corresponding to
temporal scales 2-1000 s and frequencies 10-0.5 Hz) is in a
strongly varying form of observed functions from sample to sample.
For scales indicated, the parameter p ranged from 0.2 to 1.0
with an average p=0.5.
Similar results in the low-frequency spectral domain were obtained by Busher et al. (1995) with a MARK-III interferometer. Temporal spectra of phase differences at 0.001-0.1 Hz (scales 102-104 m at V=10 m/s) had distinct deviations from the Kolmogorov type of the spectrum, displayed mainly as the decrease of p. In 16% of cases the flat spectra relevant to p=0 were obtained. In the high-frequency 3-40 Hz region (scales 0.25-3 m) the dispersion of individual values of p was smaller, 90% of which did not exceed the limits 0.4-0.7. On average p=0.55.
Coulman & Vernin (1991) analysed observations of stars with NRAO's Very Large Array of radio telescopes (Armstrong & Sramek 1982) at baselines from 50 m up to 22 km.
At moderate baselines 100-1200 m they found that
![]() represents both autumn and
winter observations, and
represents both autumn and
winter observations, and
![]() does so for a spring and summer period. On scales considered,
the turbulence is intermediate between 2-D and 3-D,
thus logarithmic slopes of the phase structure functions in the 2/3-5/3
range are expected (Table 1). Observed
slopes, however, are consistent with the expected
range only for the spring to summer observations.
Corresponding mean values of p are -0.57 and +0.11
for the two periods.
does so for a spring and summer period. On scales considered,
the turbulence is intermediate between 2-D and 3-D,
thus logarithmic slopes of the phase structure functions in the 2/3-5/3
range are expected (Table 1). Observed
slopes, however, are consistent with the expected
range only for the spring to summer observations.
Corresponding mean values of p are -0.57 and +0.11
for the two periods.
It should be noted that the well-known Hog's (1968) model of the frequency spectra of absolute image motion based on observational data of various types has a parameter corresponding to p=0.5.
Lazorenko (1992), analyzing photographic and visual data on star image tracks obtained for site testing programmes, has shown that the shape of autocorrelation functions and power spectra of image motion is usually highly biased in consequence of a limited duration of observational series. The absolute image motion spectrum corrected for this effect should have a maximum at 0.01-0.015 Hz (scales 600-1000 m at V=10 m/s). It was found that p=0.97 at higher frequencies, and at lower frequencies p< 0, which agrees well with the data in Table 1.
This short review of meteorological, astronomical, and theoretical data allows us to make following conclusions:
1) the samplings of p have an intrinsic scatter caused by changes of physical conditions in the atmosphere,
2) on scales 1-300 m giving a main contribution to the variance of differential image motion, p varies at least from 1/3 up to 2/3, with a mean value of about 0.5,
3) on scales 200-1000 m the function
![]() has
a smaller slope, with p decreasing sometimes
to negative magnitudes.
has
a smaller slope, with p decreasing sometimes
to negative magnitudes.
The magnitude of differential displacement is a
function of the phase screen parameters ![]() ,
p, h, Vand
,
p, h, Vand
![]() ,
and depends on location of the program
object with respect to a reference frame.
The direction along which the differences
of coordinates of star image centroids are measured
is also of importance.
Taking into consideration a vast variety of possible
configurations of reference stars, we shall examine only
those which are most typical.
,
and depends on location of the program
object with respect to a reference frame.
The direction along which the differences
of coordinates of star image centroids are measured
is also of importance.
Taking into consideration a vast variety of possible
configurations of reference stars, we shall examine only
those which are most typical.
a) Two stars, located in the sky at angular distance ![]() .
At some points A and B a phase screen is crossed by light
beams passing from these stars to the centre of
the telescope pupil. Here and further, point A refers to
the target star while point B refers to the geometrical centre
of the reference frame (in this instance, to star B). The
line AB is the baseline of configuration.
.
At some points A and B a phase screen is crossed by light
beams passing from these stars to the centre of
the telescope pupil. Here and further, point A refers to
the target star while point B refers to the geometrical centre
of the reference frame (in this instance, to star B). The
line AB is the baseline of configuration.
b) Two reference stars B1 and B2, seen at an
angle ![]() .
The program star A is on a common arc with reference
stars shifted some angle
.
The program star A is on a common arc with reference
stars shifted some angle ![]() off their middle point B.
B1B2 is the baseline of configuration.
off their middle point B.
B1B2 is the baseline of configuration.
c) A set of some reference stars, located uniformly in a circular
area. In the limit stars completely fill in the area
forming a circle of angular diameter ![]() with the target
star A displaced some angle
with the target
star A displaced some angle ![]() off the circle centre B.
off the circle centre B.
Each configuration projected to the phase screen
is characterized by its linear size ![]() ,
the distance
between the geometrical centres of star systems
,
the distance
between the geometrical centres of star systems
![]() (for the elementary configuration "a" S=S' and
(for the elementary configuration "a" S=S' and
![]() is assumed), and angle
is assumed), and angle ![]() the baseline formed
with the x-axis.
the baseline formed
with the x-axis.
With light rays propagating perpendicularly to a wavefront,
the star image displacements
in the focal plane are proportional to the mean gradient of the
phase taken over the screen section involved
in image formation at exposure T. It should be noted that
axes of the coordinate
system ![]() ,
in reference to which positions and
displacements of stars are
measured, may not necessarily be parallel to the x,y axes fixed by
the celestial frame. The angle between the axes of these
coordinate frames is here denoted
,
in reference to which positions and
displacements of stars are
measured, may not necessarily be parallel to the x,y axes fixed by
the celestial frame. The angle between the axes of these
coordinate frames is here denoted ![]() .
Differential displacement
.
Differential displacement
![]() in the direction of the
in the direction of the
![]() -axis
is equal to the difference of displacements of the
target star and a system of reference stars. An
efficient approach for studying statistical
properties of various parameters relevant to the turbulent
wave-front phase, and based on the use of
convolution operators, was described by Conan et al. (1995).
Using his formalism, it is easy to derive the following
expression which we give in polar coordinates
-axis
is equal to the difference of displacements of the
target star and a system of reference stars. An
efficient approach for studying statistical
properties of various parameters relevant to the turbulent
wave-front phase, and based on the use of
convolution operators, was described by Conan et al. (1995).
Using his formalism, it is easy to derive the following
expression which we give in polar coordinates
![]() :
:
![\begin{displaymath}\Delta \xi ({\vec r})=\frac{\lambda }{2\pi }
\frac{\partial \...
...{VT} \right ]
\ast P({\vec r}/D) \ast \tilde{Q}({\vec r})\cdot
\end{displaymath}](/articles/aa/full/2002/06/aa1512/img78.gif) |
(8) |
- calculation of the phase gradient
![]() in the direction
of the
in the direction
of the ![]() -axis rotated by
-axis rotated by ![]() from the x-axis;
from the x-axis;
- calculation of the running average over a straight 1-D
line VT oriented along the wind
![\begin{displaymath}\mbox{rect}[z/(VT)]=\left \{ \begin{array}{ll}
(VT)^{-1}, & \...
...rt \leq VT/2\\
0, & \vert z \vert > VT/2;
\end{array} \right.
\end{displaymath}](/articles/aa/full/2002/06/aa1512/img82.gif) |
(9) |
- averaging over the telescope aperture D
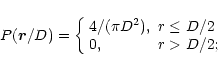 |
(10) |
- evaluation of a difference between two values of a function
in points A and B, which for configurations "a", "b",
and "c" is correspondingly:
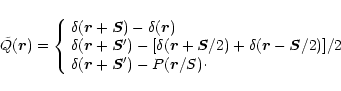 |
(11) |
Expressions of the type (11) may be easily modified for other stellar configurations. Note that Eq. (11) for configuration "b" is valid even if the star A is not in line with reference stars.
The use of convolution operators in Eq. (8) allows direct
proceeding to the analysis in
the spectral domain. In this case the spatial power
spectral density
of
![]() in polar coordinates
in polar coordinates
![]() is expressed as a sequential
product of
is expressed as a sequential
product of
![]() and four filters
originating from the corresponding functions in Eq. (8)
and their Fourier transforms:
and four filters
originating from the corresponding functions in Eq. (8)
and their Fourier transforms:
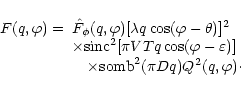 |
(12) |
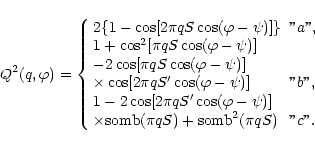 |
(13) |
![\begin{displaymath}\begin{array}{ll}
Q^2(q,\varphi )=&
1+\cos ^2[\pi qS\cos (\va...
...i - \psi )]
\cos (2\pi {\vec q}{\vec S'})\cdot \\
\end{array}\end{displaymath}](/articles/aa/full/2002/06/aa1512/img94.gif) |
(14) |
The effect of averaging over
![]() is created in a natural way
by fluctuations and changes with height
of the wind direction.
Though there are a few possible ways and sources of performing
averaging of the variance (16) over
angular parameters, further consideration shows that
in some instances the resulting quantities follow
a similar dependency
on T and angular size
is created in a natural way
by fluctuations and changes with height
of the wind direction.
Though there are a few possible ways and sources of performing
averaging of the variance (16) over
angular parameters, further consideration shows that
in some instances the resulting quantities follow
a similar dependency
on T and angular size ![]() ,
the details of reference
star distribution in the field being of less importance.
This Section deals with the variance
,
the details of reference
star distribution in the field being of less importance.
This Section deals with the variance ![]() which, owing to
averaging, does not depend on angular parameters.
which, owing to
averaging, does not depend on angular parameters.
Let's consider a case of some randomly distributed pairs of stars
(configuration "a") with equal
baseline length ![]() .
The
direction along which the angular distance between stars of the pair is
measured usually either coincides with the direction of the baseline
(
.
The
direction along which the angular distance between stars of the pair is
measured usually either coincides with the direction of the baseline
(
![]() ),
is perpendicular to that of (
),
is perpendicular to that of (
![]() ), or directed along
the x-axis (
), or directed along
the x-axis (![]() )
or y-axis (
)
or y-axis (
![]() ).
We shall denote the relevant quantities of
).
We shall denote the relevant quantities of ![]() as
as ![]() ,
,
![]() ,
,
![]() ,
and
,
and ![]() ,
and introduce their average
,
and introduce their average
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{1512f1.ps}\end{figure}](/articles/aa/full/2002/06/aa1512/Timg129.gif) |
Figure 1:
The function I(z) (solid), its
approximation by Eq. (21) (long dashed), and
the function
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1512f2.ps}\end{figure}](/articles/aa/full/2002/06/aa1512/Timg130.gif) |
Figure 2:
Dependence of the variance
|
| Open with DEXTER | |
The values of h/V and V in (22) are
approximately equal to the
weight-average parameters used by Lindegren (1980) for differential effect
evaluation at normal conditions of multi-layered atmosphere.
In this sense parameters (22) represent "typical" atmospheric
conditions, though they are used in this paper exceptionally
for the purpose of qualitative interpretation of
the expressions obtained. A normalizing coefficient ![]() is introduced in (22) implicitly, through
is introduced in (22) implicitly, through
![]() .
Such an approach to the
calibration of
.
Such an approach to the
calibration of ![]() in our opinion has some advantages. So, the
quantity
in our opinion has some advantages. So, the
quantity
![]() unlike
unlike ![]() has a clear astronomical sense
and a rich history of determinations. Besides,
has a clear astronomical sense
and a rich history of determinations. Besides,
![]() is equal to
the accuracy of meridian observations at
T30 =30 s, and is known
to be in the limits
0.12-0.14'', which follows also from the model of absolute motion
power spectrum derived by Hog (1968). The use of
is equal to
the accuracy of meridian observations at
T30 =30 s, and is known
to be in the limits
0.12-0.14'', which follows also from the model of absolute motion
power spectrum derived by Hog (1968). The use of
![]() instead of
instead of ![]() for calibration of the expression (19) is also more convenient,
as in some cases it reduces the number of
model parameters. For example, while two
parameters h and V are used in
Eq. (24), (25)
contains
only their ratio h/V which can be considered as a single
parameter.
for calibration of the expression (19) is also more convenient,
as in some cases it reduces the number of
model parameters. For example, while two
parameters h and V are used in
Eq. (24), (25)
contains
only their ratio h/V which can be considered as a single
parameter.
The expression relating
![]() and
and ![]() is found from (19) in the limit
is found from (19) in the limit
![]() ,
,
![]() :
:
For a single-layer model of an atmosphere with parameters (22),
p=2/3, and ![]() ,
the use
of Eqs. (25) and (26)
allows one to find
,
the use
of Eqs. (25) and (26)
allows one to find
![]() ,
where Tis expressed in seconds. At
arbitrary atmospheric parameters and
,
where Tis expressed in seconds. At
arbitrary atmospheric parameters and
![]()
A similar power law of ![]() dependence on geometric
size
dependence on geometric
size ![]() of a stellar group is seen for configurations
"b" and "c" (Fig. 2). Calculations were
carried out using Eqs. (12) and (16)
with the same parameters at which the curve "a" was plotted,
with a central
position of the target star (
of a stellar group is seen for configurations
"b" and "c" (Fig. 2). Calculations were
carried out using Eqs. (12) and (16)
with the same parameters at which the curve "a" was plotted,
with a central
position of the target star (![]() ), and with
averaging over two (one in the case "c") angles,
the function Q2(q) taken from (15).
Both curves at wide
), and with
averaging over two (one in the case "c") angles,
the function Q2(q) taken from (15).
Both curves at wide ![]() follow a power law
follow a power law
![]() ,
are parallel to, and below the curve "a". The most efficient,
of course, is filtration of phase distortions for configuration "c".
Equation (16) under the condition
,
are parallel to, and below the curve "a". The most efficient,
of course, is filtration of phase distortions for configuration "c".
Equation (16) under the condition
![]() in this case transformes to
in this case transformes to
Thus, a symmetric circular distribution of reference
stars, in comparison to one reference star,
ensures a decrease in the variance equivalent to a 5-9 times longer
exposure. If p=2/3, then
E(2/3)=0.8458, and
The use of configuration "b" with two reference stars
is also efficient. To find the relevant variance,
it is useful to take advantage of the similarity of the function Q2(q)for configurations "a" and "b".
The comparison of relevant expressions in Eq. (15) allows us to write
The value of ![]() is larger when the position of
a target star is displaced off the geometrical centre B of
reference frame. Estimation of this effect requires a term
with non-zero S' of Q2(q) function (13) to be included into
expression (29). The expression obtained for S'<Sand
is larger when the position of
a target star is displaced off the geometrical centre B of
reference frame. Estimation of this effect requires a term
with non-zero S' of Q2(q) function (13) to be included into
expression (29). The expression obtained for S'<Sand
![]() is easily transformed to
is easily transformed to
Differential motion for small ![]() has already been studied by Lindegren (1980) who found
has already been studied by Lindegren (1980) who found
We now derive analytical expressions for the filled aperture.
An approximate expression for
![]() (configuration "a")
in small
(configuration "a")
in small ![]() domain is found
from Eq. (19). Assuming
domain is found
from Eq. (19). Assuming
![]() for
for
![]() ,
and
,
and
![]() for
for
![]() ,
we find an expression of the type (35)
,
we find an expression of the type (35)
Concerning configurations "b" and "c", the use of
Eq. (29) with approximation
![]() at z>1,
or
at z>1,
or
![]() results in
results in
The power law in Eqs. (38)-(41) differs
from that in expression
(36) again by a factor S/D. Such a difference
is consistent with that in the second term of Eqs. (35)
and (37).
This may be explained using Lindegren's (1980) results.
Considering an arbitrary distribution of n stars, he derived
Using Eq. (44), and a filter (9) describing wind
(time) averaging, a power spectral density of image motion
is found
Evaluation of Eq. (46) for large separations S with
an accuracy to the leading term gives an
expression that exactly coincides with Eq. (24).
For very narrow angles ![]() an expression obtained
an expression obtained
Similarly, replacing a term
![]() in Eq. (46)
by a proper function Q2(q) allows us to obtain expressions
for other stellar configurations at small
in Eq. (46)
by a proper function Q2(q) allows us to obtain expressions
for other stellar configurations at small ![]() :
:
| conf.-n | offset | interferometer, d | filled pupil, D | ||
| type | 10 m | 100 m | 10 m | 100 m | |
| "a" | - | 1820 | 390 | 1530 | 330 |
| "b" | 0 | 180 | 18 | 70 | 2.3 |
| "c" | 0 | 150 | 15 | 30 | 1.0 |
| "b" | 15'' | 490 | 100 | 380 | 83 |
Table 2 shows the relative performance of an interferometer and
filled aperture of large d=D=10 m and very large d=D=100 m
size, ![]() ,
moderate T=100 s, Kolmogorov turbulence,
and atmospheric layer (22). Due to a strong dependence
of
,
moderate T=100 s, Kolmogorov turbulence,
and atmospheric layer (22). Due to a strong dependence
of ![]() on h, the data given are only illustrative.
Anyhow it clearly shows the great advantage of symmetric frames like
"b" and "c". To achieve
on h, the data given are only illustrative.
Anyhow it clearly shows the great advantage of symmetric frames like
"b" and "c". To achieve
![]() as level
with a D=100 m telescope, a target star, however, should be exactly at the
center of the reference frame. Analysis of Eq. (13) for a slightly non-central
position of the target star (0<S'<S) allows us to find approximation
as level
with a D=100 m telescope, a target star, however, should be exactly at the
center of the reference frame. Analysis of Eq. (13) for a slightly non-central
position of the target star (0<S'<S) allows us to find approximation
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1512f3.ps}\end{figure}](/articles/aa/full/2002/06/aa1512/Timg234.gif) |
Figure 3:
Differential image motion |
| Open with DEXTER | |
Let's consider measurements of
coordinate differences for a pair of stars at fixed spatial angles,
assuming a single-layer model of an atmosphere.
Taking into account that
integral (17) is a function of
![]() and
and
![]() differences,
the dependence of
differences,
the dependence of ![]() on
on
![]() at fixed
at fixed
![]() ,
15, 45, and 900 can be calculated.
Figure 3 shows the functions calculated with
,
15, 45, and 900 can be calculated.
Figure 3 shows the functions calculated with ![]() ,
T=100 s, and
parameters (22). Graphical data
in the region
,
T=100 s, and
parameters (22). Graphical data
in the region
![]() are well fitted by
a function
are well fitted by
a function
![]() ,
where
,
where
![]() is the variance at
is the variance at
![]() and some fixed
and some fixed ![]() .
The horizontal dashed line
marks a level of the mean variance
.
The horizontal dashed line
marks a level of the mean variance ![]() in the sense of
Eq. (19), with averaging over
in the sense of
Eq. (19), with averaging over ![]() and
and ![]() .
Figure 3 shows
that at some particular orientations
of a baseline (
.
Figure 3 shows
that at some particular orientations
of a baseline (![]() parameter) and
parameter) and ![]() -axis (
-axis (![]() angle)
the level of
angle)
the level of ![]() can be much lower than
can be much lower than ![]() .
There are two cases of interest to be discussed:
.
There are two cases of interest to be discussed:
1) The baseline AB connecting two stars formes a small angle
![]() with the wind direction, with
with the wind direction, with
![]() arbitrary;
arbitrary;
2) The ![]() -axis along which
positions are measured is oriented approximately
along the wind:
-axis along which
positions are measured is oriented approximately
along the wind:
![]() ,
with arbitrary
,
with arbitrary ![]() .
.
Condition (1) essentially limits the number of star
pairs which can be measured in the field. For that reason
the opportunity (2) that places no limitations on the orientation
of baselines is of greater practical value.
In the important case of
configuration "c", with a central position of a target star,
and ![]() angle varying over a set of reference stars,
this opportunity is unique. Note that improvement in precision
expected for
angle varying over a set of reference stars,
this opportunity is unique. Note that improvement in precision
expected for ![]() -coordinates is achieved at the expense of
an equivalent loss in the accuracy of
-coordinates is achieved at the expense of
an equivalent loss in the accuracy of ![]() -coordinates in
the perpendicular direction.
Such a feature actually causes transition to 1-D
mode of measurements. However, it is not necessarily a
shortcoming, as for example in parallax programs
where only 1-D, high precision differential
coordinates are practically of use.
-coordinates in
the perpendicular direction.
Such a feature actually causes transition to 1-D
mode of measurements. However, it is not necessarily a
shortcoming, as for example in parallax programs
where only 1-D, high precision differential
coordinates are practically of use.
The highest gain in precision for a single-layer
atmosphere is expected at
![]() .
In this case evaluation of
the integral (17) averaged over
.
In this case evaluation of
the integral (17) averaged over ![]() in the limits
in the limits ![]() for a small aperture
for a small aperture
![]() yields
yields
For a real multi-layered atmosphere,
the transition to measurements in
a selected direction is rarely justified, and only under
conditions of approximately parallel
orientation of wind velocity vectors
![]() of all
of all
![]() turbulent layers. In this case, to ensure
best filtering of a dominant layer i=1 with
the greatest index C2n, the
turbulent layers. In this case, to ensure
best filtering of a dominant layer i=1 with
the greatest index C2n, the ![]() -axis is positioned
parallel to the vector
-axis is positioned
parallel to the vector
![]() thus ensuring
thus ensuring
![]() .
It does not however garantee the decrease
of the total variance, which is achieved unconditionally
only when
.
It does not however garantee the decrease
of the total variance, which is achieved unconditionally
only when
![]() for each layer i.
for each layer i.
An important feature of atmospheric layer distribution in C2n is that at each moment of observations there are only a few layers which greatly dominate over others in the intensity of turbulence (Gendron & Lena 1996; Redfern 1991; Benkhaldoun et al. 1996). This circumstance brings up quasi-single-layer features to the atmospheric behaviour, and is favorable for 1-D techniques of measurements.
| layer | h, | V, |
|
|
||
| No. i | km | m/s | degr. |
|
mas | mas |
| 1 | 4 | 14 | 0 | 25.8 | 11.7 | 1.31 |
| 2 | 10 | 59 | -8 | 2.1 | 2.3 | 0.47 |
| 3 | 12 | 51 | -9 | 3.4 | 3.3 | 0.78 |
| 4 | 12 | 44 | -13 | 2.1 | 2.8 | 0.91 |
| 5 | 14 | 33 | -4 | 2.7 | 3.8 | 0.62 |
| 6 | 16 | 36 | 1 | 1.9 | 3.2 | 0.44 |
| 7 | 17 | 10 | 16 | 1.8 | 6.1 | 2.70 |
| 8 | 18 | 17 | 37 | 1.4 | 4.2 | 3.51 |
| Caccia et al. (1987) | total: | 41 | 15.5 | 4.8 | ||
| 1 | 3 | 9 | -45 | 15 | 10.0 | 10.0 |
| 2 | 6 | 6 | 0 | 28 | 21.5 | 4.3 |
| 3 | 10 | 4 | 63 | 9 | 17.9 | 21.7 |
| Rocca et al. (1974) | total: | 52 | 29.7 | 24.3 | ||
For discussion we shall consider some observational data.
In the upper part of Table 3, Cols. 2-5, are the parameters of
atmospheric layers h, V,
![]() ,
and
,
and
![]() found by Caccia et al. (1987) from
spatiotemporal correlation analysis of
single-star scintillations. Observations were obtained with the 1.93 m
telescope of the Haute-Provence observatory. In the second part of
Table 3, the data found by Rocca et al. (1974) from the
analysis of star scintillations on a 10 cm telescope
are presented. In Col. 6,
found by Caccia et al. (1987) from
spatiotemporal correlation analysis of
single-star scintillations. Observations were obtained with the 1.93 m
telescope of the Haute-Provence observatory. In the second part of
Table 3, the data found by Rocca et al. (1974) from the
analysis of star scintillations on a 10 cm telescope
are presented. In Col. 6,
![]() values for each layer calculated with Eq. (24)
at T=100 s, p=2/3,
values for each layer calculated with Eq. (24)
at T=100 s, p=2/3, ![]() and
averaged with respect to
and
averaged with respect to ![]() and
and ![]() ,
are given. Column 7 contains
image motion
,
are given. Column 7 contains
image motion ![]() measured in the
direction of the vector
measured in the
direction of the vector
![]() (that is
(that is
![]() ), and also with averaging over
), and also with averaging over
![]() .
Total values of
.
Total values of ![]() and
and ![]() integrated over the
depth of an atmosphere are also given. The transformation of
integrated over the
depth of an atmosphere are also given. The transformation of
![]() into
into ![]() was carried out using Eq. (3)
which is valid for 3-D isotropic turbulence.
was carried out using Eq. (3)
which is valid for 3-D isotropic turbulence.
The vertical structure of an atmosphere which is shown in the first
part of the table, at the optimal position of
the ![]() -axis allows us to reduce the variance of image motion
by a factor of 10. In this particular case
-axis allows us to reduce the variance of image motion
by a factor of 10. In this particular case
![]() for each layer.
The wind situation
described in the second part of Table 3 is much worse
and is characterized by a strong change of the wind orientation with
a height. As a result, the contribution of a layer i=3even encreases, and the total effect
for each layer.
The wind situation
described in the second part of Table 3 is much worse
and is characterized by a strong change of the wind orientation with
a height. As a result, the contribution of a layer i=3even encreases, and the total effect
![]() for
the whole atmosphere becomes negligable.
for
the whole atmosphere becomes negligable.
Barletti gives an even more unfavorable example of the
wind shifting 2500 at heights 13-17 km, where most layers of
intense turbulence were concentrated. The vertical profile
of the wind velocity given by Hogstrom et al. (1998) for heights
500 m-3 km, on the contrary, has very weak
variations of the
![]() angle, being in the limits
angle, being in the limits ![]() .
.
The above examples show that there is a certain possibility to come across a lucky meteorological situation allowing us to take advantage of anisotropic properties of differential image motion. Detection of atmospheric conditions favourable for a 1-D strategy of observations, however, implies a permanent control of atmospheric parameters using some remote methods of sensing with satisfactory precision of the vertical wind profile determination (Caccia et al. 1987; Rocca et al. 1974).
When the variance of differential image motion ![]() is calculated,
calibration is performed with some measured
quantity that characterizes the intensity of turbulence.
This procedure is however biased because there are usually no
reliable data on the p quantity available, so
p=2/3 is set tentatively. Besides,
we note that there are some quantities that specify
the turbulence in a different way, by refering to either one-point
or integral estimates of one of the phase-related functions
is calculated,
calibration is performed with some measured
quantity that characterizes the intensity of turbulence.
This procedure is however biased because there are usually no
reliable data on the p quantity available, so
p=2/3 is set tentatively. Besides,
we note that there are some quantities that specify
the turbulence in a different way, by refering to either one-point
or integral estimates of one of the phase-related functions
![]() ,
,
![]() or
Dn(r). Thus,
or
Dn(r). Thus, ![]() (measured in units
of m-p-1) is numerically equal to
the function
(measured in units
of m-p-1) is numerically equal to
the function
![]() at some
unit frequency (here 1 m-1) that
depends on the adopted system of units; a similar remark concerns
C2n. More frequently in use are integral estimates
such as FWHM, Fried's parameter r0, and rarely,
at some
unit frequency (here 1 m-1) that
depends on the adopted system of units; a similar remark concerns
C2n. More frequently in use are integral estimates
such as FWHM, Fried's parameter r0, and rarely,
![]() .
.
| Parameter |
| ||
|
|
|
- | |
|
|
|
|
- |
|
|
|
|
<0 |
| r0 |
|
|
>0 |
Let us estimate the bias in ![]() caused by assuming p=2/3when r0 and
caused by assuming p=2/3when r0 and
![]() are used as normalizing factors.
To express r0 via
are used as normalizing factors.
To express r0 via ![]() one may compare the expression for a
phase structure function
one may compare the expression for a
phase structure function
![]() where
where
![]() (Fried 1965)
with representation (5). Assuming that the turbulence is
completely developed, the use of Eqs. (4-7) yields
(Fried 1965)
with representation (5). Assuming that the turbulence is
completely developed, the use of Eqs. (4-7) yields
With typical
![]() ,
h=2-15 km, V=5-30 m/s,
,
h=2-15 km, V=5-30 m/s,
![]() m, and long T we find that
[S/(VT30)]<1 and
[D/(VT30)]<1, therefore the derivative
m, and long T we find that
[S/(VT30)]<1 and
[D/(VT30)]<1, therefore the derivative
![]() is always negative at any given
is always negative at any given
![]() .
On the contrary, when
using r0, expressions for
.
On the contrary, when
using r0, expressions for ![]() contain ratios S/r0>1and D/r0>1, so in this case
contain ratios S/r0>1and D/r0>1, so in this case
![]() .
Considering that usually 1/3<p<2/3 (Sect. 3), we find
.
Considering that usually 1/3<p<2/3 (Sect. 3), we find
![]() ,
where
,
where ![]() is the actual value
of
is the actual value
of ![]() ,
and
,
and
![]() is that calculated with p=2/3and measured
is that calculated with p=2/3and measured
![]() .
Using r0 results in inverse inequality
.
Using r0 results in inverse inequality
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1512f4.ps}\end{figure}](/articles/aa/full/2002/06/aa1512/Timg285.gif) |
Figure 4:
The variance |
| Open with DEXTER | |
In Table 5 we reproduce data of Table 2 for the non-Kolmogorov spectral
index p=1/3 and the former value of r0=83 mm. Comparison of Tables 2
and 5 shows that the largest change of image motion magnitude occures
when double-star separations are measured. Owing to the dependence
![]() ,
the effect is stronger for large
,
the effect is stronger for large
![]() telescopes. Concerning symmetric stellar groups,
one may note comparatively stable estimates of
telescopes. Concerning symmetric stellar groups,
one may note comparatively stable estimates of ![]() ,
especially
for interferometers.
,
especially
for interferometers.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1512f5.ps}\end{figure}](/articles/aa/full/2002/06/aa1512/Timg289.gif) |
Figure 5:
The same as in Fig. 4, for interferometer with a baseline
d=10 m (dashed) and filled aperture D=10 m (solid),
for triple star "b", |
| Open with DEXTER | |
In this Paper we derive necessary formulations and analyze
some effects which may be useful for
understanding the properties of differential image motion under
non-Kolmogorov distortions of the wave-front.
Non-classic statistics of the turbulent phase are due to three
effects:
non-Kolmogorov type of refractive index n fluctuations in
3-D space, 2-D spatial location of a turbulence, and
wind-dependent anisotropy of the phase. The two first sources
result in the decrease of p; the effect becomes stronger
at large scales. According to observational data, on scales
1-300 m which are effective for differential image motion, p is
typically in the range 1/3-2/3. Deviation of p from its
Kolmogorov value 2/3 affects all phase-related quantities,
in particular, causes divergence of the observed ![]() value
from that calculated at p=2/3. The bias may exceed 50% or more,
depending on which quantity, r0 or
value
from that calculated at p=2/3. The bias may exceed 50% or more,
depending on which quantity, r0 or
![]() ,
is taken
as a measure of the intensity of turbulence (Figs. 4 and 5), and which
stellar configuration is observed. Thus, when measuring double-star
separations,
,
is taken
as a measure of the intensity of turbulence (Figs. 4 and 5), and which
stellar configuration is observed. Thus, when measuring double-star
separations, ![]() is proportional to the factors
(D/r0)p and
(d/r0)p which practically do not depend on
p for small instruments. The situation
is quite different for the Keck 10 m telescope and some operating
interferometers with
is proportional to the factors
(D/r0)p and
(d/r0)p which practically do not depend on
p for small instruments. The situation
is quite different for the Keck 10 m telescope and some operating
interferometers with
![]() m, when small 1/3 to 2/3 variations
of p evoke a change of 5-10 in
m, when small 1/3 to 2/3 variations
of p evoke a change of 5-10 in ![]() ,
better accuracies
corresponding to small p.
,
better accuracies
corresponding to small p.
| conf.-n | offset | interferometer, d | filled pupil, D | ||
| type | 10 m | 100 m | 10 m | 100 m | |
| "a" | - | 1230 | 180 | 850 | 120 |
| "b" | 0 | 160 | 16 | 48 | 1.5 |
| "c" | 0 | 150 | 15 | 25 | 0.8 |
| "b" | 15'' | 350 | 48 | 220 | 30 |
In brief, we analyzed a third factor of non-Kolmogorov
distortions of the wave-front, a spatial anisotropy of the
phase brought in by the wind. We concluded that at certain
conditions it may be useful
for improving the accuracy of ground-based observations.
Examples given in the upper part of Table 3 show
that the use of a special
1-D strategy of measurements which takes advantage of
anisotropic properties of the turbulent phase may result in
a perceptible reduction of ![]() .
.
Rather unexpected results have been obtained when studying
the peformance of a classic circular pupil.
Expressions derived for ![]() do not follow power laws
predicted by Lindegren (1980) as his analysis is directly
valid for interferometers. For
symmetric stellar groups ("b" or "c") measured
in very narrow fields,
a new power law derived
do not follow power laws
predicted by Lindegren (1980) as his analysis is directly
valid for interferometers. For
symmetric stellar groups ("b" or "c") measured
in very narrow fields,
a new power law derived
![]() differs
by a factor of S/D from Lindegren's dependence
differs
by a factor of S/D from Lindegren's dependence
![]() .
This circumstance
results in an order smaller, as compared to current,
estimates of
.
This circumstance
results in an order smaller, as compared to current,
estimates of ![]() for observations with very large
for observations with very large
![]() m
apertures and small
m
apertures and small ![]() angles (Tables 2 and 5).
angles (Tables 2 and 5).
High-accuracy differential astrometry is required primarily
to study double-stars, determination of parallaxes,
and in searching for extrasolar planets.
These problems can be solved very effectively with
future astrometric satellites that will have an
expected accuracy of about 1-10 ![]() as.
The potential of ground-based
astronomy also looks rather promising,
considering projects of large-scale facilities.
The analysis of atmospheric effects made in this Paper allows us
to conclude that this source of errors can be reduced approximately
to the level expected for space missions, or 1
as.
The potential of ground-based
astronomy also looks rather promising,
considering projects of large-scale facilities.
The analysis of atmospheric effects made in this Paper allows us
to conclude that this source of errors can be reduced approximately
to the level expected for space missions, or 1 ![]() as per
100 s exposure.
as per
100 s exposure.
The largest operating 10 m Keck telescope has a potential
narrow-field accuracy of 30-70 ![]() as per 100 s exposure
at the Kolmogorov parameter p (Table 2), and 20-50
as per 100 s exposure
at the Kolmogorov parameter p (Table 2), and 20-50 ![]() as
at p=1/3 (Table 5). Due to a strong
as
at p=1/3 (Table 5). Due to a strong
![]() improvemnt with D, the 1
improvemnt with D, the 1 ![]() as per 100 s time level is already expected
at D=100 m. For interferometers, baselines of about 1000 m
are required because of the slower improvement of
as per 100 s time level is already expected
at D=100 m. For interferometers, baselines of about 1000 m
are required because of the slower improvement of
![]() .
Interferometers of this class should be able to measure
simultaneously at least three objects so as to detect
a minimal symmetric configuration of stars. Interferometers
of the Mark III type with two separate beam channels are
restricted to observations of asymmetric double-star systems,
and even at d=1000 m baselines will be limited by
.
Interferometers of this class should be able to measure
simultaneously at least three objects so as to detect
a minimal symmetric configuration of stars. Interferometers
of the Mark III type with two separate beam channels are
restricted to observations of asymmetric double-star systems,
and even at d=1000 m baselines will be limited by
![]() as (Sect. 5.3).
as (Sect. 5.3).
The above estimates relate to the dimeter ![]() of the reference
group; in other cases correction allowing for dependences
of the reference
group; in other cases correction allowing for dependences
![]() (filled apertures) and
(filled apertures) and
![]() (interferometers) should be applied.
Very high accuracies, however, require perfect centering of
the reference frame on the target object. Even very small
(interferometers) should be applied.
Very high accuracies, however, require perfect centering of
the reference frame on the target object. Even very small ![]() offsets will generate, depending on p, errors of 2-5
offsets will generate, depending on p, errors of 2-5 ![]() as
for a D=10 m telescope (Sect. 5.3), and about 0.5-1
as
for a D=10 m telescope (Sect. 5.3), and about 0.5-1 ![]() as with
D=100 m. Errors of this type are completely eliminated
with the symmetrizing procedure (Sect. 5.4).
An extra 1.5-2 fold improvement is expected at astronomical
sites with average
as with
D=100 m. Errors of this type are completely eliminated
with the symmetrizing procedure (Sect. 5.4).
An extra 1.5-2 fold improvement is expected at astronomical
sites with average
![]() on spatial scales 1-300 m.
on spatial scales 1-300 m.