A&A 382, 688-698 (2002)
DOI: 10.1051/0004-6361:20011599
Astronomical Institute, Academy of Sciences of the Czech Republic, Fricova 298, Ondrejov, 25165, The Czech Republic
Received 23 July 2001 / Accepted 8 November 2001
Abstract
Influence of non-thermal collisional rates, related to an electron
beam, on hydrogen Balmer line profiles is investigated. Semi-empirical
temperature structure of the flare model F1 has been used for computing non-LTE
profiles of H![]() ,
H
,
H![]() ,
and H
,
and H![]() .
Contribution functions and
their change due to different values of beam parameters are shown. Unlike the
line core intensity, the intensity of line wings considerably depends on beam
parameters and it is significantly enhanced for typical values of the beam
energy flux. The ratio of line intensities at a selected wavelength is proposed
to be used for diagnostics of electron beams during solar flares, particularly at
impulsive phases. Obtained H
.
Contribution functions and
their change due to different values of beam parameters are shown. Unlike the
line core intensity, the intensity of line wings considerably depends on beam
parameters and it is significantly enhanced for typical values of the beam
energy flux. The ratio of line intensities at a selected wavelength is proposed
to be used for diagnostics of electron beams during solar flares, particularly at
impulsive phases. Obtained H![]() line profiles are compared to those of
Fang et al. (1993).
line profiles are compared to those of
Fang et al. (1993).
Key words: Sun: flares - line: profiles - methods: numerical
Most of computations of spectral line profiles have been done for
static flare models.
One approach in theoretical static flare modelling is to specify mechanisms of
a flare heating. In such models the energy equation is solved
simultaneously with the equations describing the pressure balance, the
radiative transfer, and the statistical equilibrium.
Study of the effects of various heating mechanisms on H![]() line profiles
was done by Canfield et al. (1984) and Hawley & Fisher (1994).
Non-thermal electron collisional rates and heating by non-thermal
electrons were treated in Canfield et al. (1984), which is based on energy-balance
models
of Ricchiazzi & Canfield (1983). A set of one dimensional,
static models of flare atmospheres was developed, each
model was determined by four independent parameters describing the flare
corona: P0 (the coronal pressure), F5 (conductive flux at
line profiles
was done by Canfield et al. (1984) and Hawley & Fisher (1994).
Non-thermal electron collisional rates and heating by non-thermal
electrons were treated in Canfield et al. (1984), which is based on energy-balance
models
of Ricchiazzi & Canfield (1983). A set of one dimensional,
static models of flare atmospheres was developed, each
model was determined by four independent parameters describing the flare
corona: P0 (the coronal pressure), F5 (conductive flux at
![]() )
and the non-thermal electron flux above 20 keV
F20. H
)
and the non-thermal electron flux above 20 keV
F20. H![]() line profiles were calculated by solving
the probabilistic radiative transfer equation for a four-level plus
continuum hydrogen atomic model.
line profiles were calculated by solving
the probabilistic radiative transfer equation for a four-level plus
continuum hydrogen atomic model.
In their 1D static models, Hawley & Fisher (1994) assumed
an X-ray heating of the chromosphere and heating by non-thermal electrons.
The non-thermal collisional ionisation rates were also included into the
statistical equilibrium equations; the radiation transport equations were used
for obtaining H![]() line profiles.
The models were
divided into three types: impulsive (density distribution frozen in the
pre-flare state), evolving (hydrostatic equilibrium holds but energetic
equilibrium has not been established in the corona), and equilibrium (the whole
atmosphere in hydrostatic and energetic equilibrium). It was concluded that
observed H
line profiles.
The models were
divided into three types: impulsive (density distribution frozen in the
pre-flare state), evolving (hydrostatic equilibrium holds but energetic
equilibrium has not been established in the corona), and equilibrium (the whole
atmosphere in hydrostatic and energetic equilibrium). It was concluded that
observed H![]() profiles could be reproduced by the impulsive models of low
coronal pressure with strong non-thermal heating.
profiles could be reproduced by the impulsive models of low
coronal pressure with strong non-thermal heating.
Finally, Fang et al. (1993) included the non-thermal
collisional excitation and ionisation rates due to electron beams
into semi-empirical models.
Their computations are based on
the temperature distributions given by flare models F1 and F2 of
Machado et al. (1980).
These well-known semi-empirical models are based on spectral
observations of several flares obtained during various phases of their
evolution (note that some of these flares were observed after their maximum
and thus F1 or even F2 can be used as well for the gradual phase). The
presence of beams during the impulsive phase has two effects: (i) heating
due to energy dissipation and (ii) non-thermal excitation and ionisation
of various species.
The heating is implicitly included into the
semi-empirical temperature structure which Fang et al. (1993) assumed to be fixed.
Then they studied so called differential effect of non-thermal
collisional rates on spectral line intensities, i.e. they compared the
line profiles in presence and without presence of beams for the same
atmospheric model.
In their models the statistical equilibrium equations and the
radiative transfer equations, together with the equation of hydrostatic
equilibrium, were solved iteratively. H![]() and CaII line
profiles were calculated by using a four-level plus continuum
atomic model of hydrogen and a five-level plus continuum atomic model
of ionised calcium, respectively. H
and CaII line
profiles were calculated by using a four-level plus continuum
atomic model of hydrogen and a five-level plus continuum atomic model
of ionised calcium, respectively. H![]() line profiles obtained for chosen
beam parameters
show a substantial increase in line intensities by a factor up to 5.
Namely the line core intensities vary significantly with beam parameters.
Recently, the optical effects of the non-thermal particle bombardment of the
solar atmosphere have been reviewed by Fang et al. (2000), Hénoux (2000).
line profiles obtained for chosen
beam parameters
show a substantial increase in line intensities by a factor up to 5.
Namely the line core intensities vary significantly with beam parameters.
Recently, the optical effects of the non-thermal particle bombardment of the
solar atmosphere have been reviewed by Fang et al. (2000), Hénoux (2000).
In the present paper we follow the approach of Fang et al. (1993) in order to
demonstrate the differential effects of the non-thermal collisional rates
on other Balmer lines (H![]() ,
H
,
H![]() ). We analyse the contribution
functions of Balmer lines and study their depth variations due to beam energy
deposit on hydrogen for different parameters of the electron beam.
). We analyse the contribution
functions of Balmer lines and study their depth variations due to beam energy
deposit on hydrogen for different parameters of the electron beam.
The paper has been organised in the following manner:
Sect. 2 presents relations between the non-thermal collisional rates
and characteristics of the electron beam; values of beam parameters are set
there. Brief description of numerical models is given in Sect. 3. Effects of
the non-thermal collisional rates are
discussed in Sect. 4 by showing computed line profiles and contribution
functions
of H![]() ,
H
,
H![]() ,
and H
,
and H![]() .
Intensity ratio method as a possible
diagnostic tool is proposed there.
In Sect. 5 we compare our results for H
.
Intensity ratio method as a possible
diagnostic tool is proposed there.
In Sect. 5 we compare our results for H![]() with
the work of Fang et al. (1993). Section 6 summarises our results.
with
the work of Fang et al. (1993). Section 6 summarises our results.
The collisional logarithms ![]() ,
,
![]() ,
and
,
and
![]() are depth
dependent and can be expressed as functions of n and
the beam electron energy
are depth
dependent and can be expressed as functions of n and
the beam electron energy
![]() (Ricchiazzi 1982):
(Ricchiazzi 1982):
![]() ,
,
![]() ,
and
,
and
![]() .
We follow the approach of Hawley & Fisher (1994) and treat their values as
constants for the whole atmosphere. Assuming
.
We follow the approach of Hawley & Fisher (1994) and treat their values as
constants for the whole atmosphere. Assuming
![]() and
and ![]() ,
mean values of the collisional logarithms have been computed
by using average injected beam electron energies
(
,
mean values of the collisional logarithms have been computed
by using average injected beam electron energies
(
![]() ,
4, and 5).
,
4, and 5).
![]() ,
,
![]() ,
and
,
and
![]() .
.
The expression for the rate of the energy deposit (1) was derived
by keeping the parameter ![]() (Eq. (3))
constant along the path of a beam electron. However, Eq. (1)
varies only slightly with
(Eq. (3))
constant along the path of a beam electron. However, Eq. (1)
varies only slightly with ![]() .
Assuming a value of the mean ionised
fraction of hydrogen
.
Assuming a value of the mean ionised
fraction of hydrogen
![]() (middle chromosphere), we have set
(middle chromosphere), we have set
![]() and similarly
and similarly
![]() .
.
There is a direct connection between the rate of energy deposit on hydrogen
![]() and the
non-thermal collisional excitation
and the
non-thermal collisional excitation
![]() and ionisation
and ionisation
![]() rates of hydrogen.
We have adopted the same approach as Fang et al. (1993):
rates of hydrogen.
We have adopted the same approach as Fang et al. (1993):
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3033f1.eps}\vspace*{2mm}
...
...f2.eps}\vspace*{2mm}
\includegraphics[width=8.8cm,clip]{h3033f3.eps}\end{figure}](/articles/aa/full/2002/05/aah3033/Timg57.gif) |
Figure 1:
H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{h3033f4.eps}\vspace*{2mm}
...
...f5.eps}\vspace*{2mm}
\includegraphics[width=8.6cm,clip]{h3033f6.eps}\end{figure}](/articles/aa/full/2002/05/aah3033/Timg58.gif) |
Figure 2:
H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{h3033f7.eps}\vspace*{2mm}
...
...f8.eps}\vspace*{2mm}
\includegraphics[width=8.6cm,clip]{h3033f9.eps}\end{figure}](/articles/aa/full/2002/05/aah3033/Timg59.gif) |
Figure 3:
H |
| Open with DEXTER | |
Profiles of three Balmer lines H![]() ,
H
,
H![]() ,
and H
,
and H![]() computed
for different values of
computed
for different values of ![]() and
and
![]() by using the model F1
are plotted in
Figs. 1-3. Corresponding line profiles
without including the non-thermal collisional rates (dotted line) are also
displayed in
each figure. All figures show that the line-wing intensities significantly rise
with increasing
the total electron energy flux
by using the model F1
are plotted in
Figs. 1-3. Corresponding line profiles
without including the non-thermal collisional rates (dotted line) are also
displayed in
each figure. All figures show that the line-wing intensities significantly rise
with increasing
the total electron energy flux
![]() ,
while the effects in line
cores are only marginal.
In contrast, the line intensities are much less sensitive to different
values of the parameter
,
while the effects in line
cores are only marginal.
In contrast, the line intensities are much less sensitive to different
values of the parameter ![]() .
The line core intensity is increased in comparison with the line intensity of
profile without
including non-thermal collisional rates. However, there is only weak
dependence of the
line core intensity on values of
.
The line core intensity is increased in comparison with the line intensity of
profile without
including non-thermal collisional rates. However, there is only weak
dependence of the
line core intensity on values of ![]() or
or
![]() .
This latter
result contrasts with that of Fang et al. (1993) (see discussion below).
.
This latter
result contrasts with that of Fang et al. (1993) (see discussion below).
The effect of different
values of
![]() is considerably pronounced in the line wings. This
behaviour is closely associated with a formation depth of the line intensity in
specific wavelengths.
Figures 9-11 display the contribution functions
is considerably pronounced in the line wings. This
behaviour is closely associated with a formation depth of the line intensity in
specific wavelengths.
Figures 9-11 display the contribution functions ![]() as a 2D function of the line centre wavelength and the depth h. By definition
as a 2D function of the line centre wavelength and the depth h. By definition
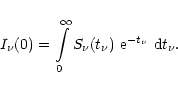 |
(6) |
On each of Figs. 9-11 the first image
refers to the contribution function of H![]() ,
H
,
H![]() ,
or H
,
or H![]() without including the non-thermal collisional rates. The
corresponding rate of the energy deposit on hydrogen is over-plotted
on subsequent four images. These figures clearly show that formation of the
line wing intensities moves to higher parts of the atmosphere as the
value of
without including the non-thermal collisional rates. The
corresponding rate of the energy deposit on hydrogen is over-plotted
on subsequent four images. These figures clearly show that formation of the
line wing intensities moves to higher parts of the atmosphere as the
value of
![]() rises, whereas the location of formation region of the
line core intensities remains approximately the same.
rises, whereas the location of formation region of the
line core intensities remains approximately the same.
Most of the contribution functions exhibit a gap of low values which
separates the regions where significant portions of the line intensity are
formed. The gap is caused by
a drop of the second level and high-level populations of hydrogen near
the temperature
minimum. The drop in the second level population results in more transparent
medium in the region of the gap and thus we see contributions from the
photospheric layers. Values of
![]() in the temperature minimum are also
lower because of the drop of high-level populations. Combination of these
effects leads to a decrease in the contribution functions.
in the temperature minimum are also
lower because of the drop of high-level populations. Combination of these
effects leads to a decrease in the contribution functions.
Keeping
![]() constant,
maximum of the rate of energy deposit on hydrogen
reaches deeper layers of atmosphere for
constant,
maximum of the rate of energy deposit on hydrogen
reaches deeper layers of atmosphere for ![]() than for the case of
than for the case of
![]() .
This behaviour is mainly a result of the form of Eq. (2) and the
condition for the maximum of
.
This behaviour is mainly a result of the form of Eq. (2) and the
condition for the maximum of
![]() :
:
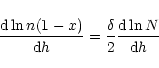 |
(8) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3033f10.eps}\vspace*{2mm}
\includegraphics[width=8.8cm,clip]{h3033f11.eps}\end{figure}](/articles/aa/full/2002/05/aah3033/Timg74.gif) |
Figure 4:
Intensity ratio of H
|
| Open with DEXTER | |
Concerning diagnostic tools suitable
for comparison of our theoretical line profiles with the observed ones,
we suggest to use the intensity ratios. Figure 4 shows the ratio of
H
![]() ,
resp. H
,
resp. H
![]() intensities
as a
function of the total energy flux
intensities
as a
function of the total energy flux
![]() at a selected wavelength.
In order to get a unique solution for
at a selected wavelength.
In order to get a unique solution for
![]() using the
intensity ratios, we require a monotonic dependence of the ratios on
using the
intensity ratios, we require a monotonic dependence of the ratios on
![]() .
However, the monotonic dependence seems to be a rather strong condition
since only few combinations of
.
However, the monotonic dependence seems to be a rather strong condition
since only few combinations of
![]() satisfy it. We have selected
satisfy it. We have selected
![]() for all considered lines which reveals
the most pronounced change of the intensity ratios over
for all considered lines which reveals
the most pronounced change of the intensity ratios over
![]() values.
The intensity ratios without including the non-thermal
collisional
rates are indicated by full line. The ratio of H
values.
The intensity ratios without including the non-thermal
collisional
rates are indicated by full line. The ratio of H
![]() for
for
![]() decreases
nearly by 50% compared with the case without including the non-thermal
collisional rates.
Ratio H
decreases
nearly by 50% compared with the case without including the non-thermal
collisional rates.
Ratio H
![]() is lowered by 40%. The intensity ratios
are little sensitive to different values of the power index
is lowered by 40%. The intensity ratios
are little sensitive to different values of the power index ![]() .
.
The contribution functions at
![]() together with the
rate of energy deposit are plotted in Fig. 5. These graphs show that
the place from which the intensity
together with the
rate of energy deposit are plotted in Fig. 5. These graphs show that
the place from which the intensity
![]() originates varies only slightly with
originates varies only slightly with
![]() in contrast with
in contrast with
![]() or
or
![]() .
Although the contribution
functions of
H
.
Although the contribution
functions of
H![]() ,
resp. H
,
resp. H![]() ,
at
,
at
![]() are almost by a order of
magnitude lower than for H
are almost by a order of
magnitude lower than for H![]() ,
the resultant line intensities are
comparable. This is caused by a different width of the region which
significantly contributes to the line intensity (see Eq. (5)).
,
the resultant line intensities are
comparable. This is caused by a different width of the region which
significantly contributes to the line intensity (see Eq. (5)).
The intensity ratios start to saturate for
![]() .
We have found out that in region where hydrogen ionisation degree
.
We have found out that in region where hydrogen ionisation degree ![]() populations of high levels
are only slightly sensitive to the values of
populations of high levels
are only slightly sensitive to the values of
![]() .
.
![]() comes from such part of atmosphere.
Hence,
comes from such part of atmosphere.
Hence,
![]() ,
,
![]() ,
and
,
and
![]() do not considerably vary with
do not considerably vary with
![]() (see Fig. 1). However,
(see Fig. 1). However,
![]() and
and
![]() contain contributions from deeper atmospheric layers in the case of
contain contributions from deeper atmospheric layers in the case of
![]() .
As value of
.
As value of
![]() is increased, second level
population
and thus
is increased, second level
population
and thus
![]() grow in these deeper layers due to higher values of
non-thermal collisional rates. Consequently, contribution
functions of H
grow in these deeper layers due to higher values of
non-thermal collisional rates. Consequently, contribution
functions of H![]() and H
and H![]() at
at
![]() show significant
values only at the higher atmospheric layers (see Fig. 5), which
are almost fully ionised. Therefore, resultant line intensities at
show significant
values only at the higher atmospheric layers (see Fig. 5), which
are almost fully ionised. Therefore, resultant line intensities at
![]() are
not sensitive to further increase of
are
not sensitive to further increase of
![]() .
This saturation effect is not a general behaviour but strongly
depends on selected
.
This saturation effect is not a general behaviour but strongly
depends on selected
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3033f12.eps}\vspace*{2mm}...
...3.eps}\vspace*{2mm}
\includegraphics[width=8.8cm,clip]{h3033f14.eps}\end{figure}](/articles/aa/full/2002/05/aah3033/Timg87.gif) |
Figure 5:
Dependence of the contribution function |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3033f15.eps}\end{figure}](/articles/aa/full/2002/05/aah3033/Timg89.gif) |
Figure 6:
H |
| Open with DEXTER | |
It must be pointed out that presented dependences of the intensity ratios
on
![]() reveal the effects of the non-thermal collisional rates
for the case of the fixed temperature structure of the model F1. However,
distinct temperature distribution may considerably influence the line
intensities. Therefore, the intensity ratios will be model dependent.
reveal the effects of the non-thermal collisional rates
for the case of the fixed temperature structure of the model F1. However,
distinct temperature distribution may considerably influence the line
intensities. Therefore, the intensity ratios will be model dependent.
![\begin{figure}
\includegraphics[width=8.8cm,clip]{h3033f16.eps}\end{figure}](/articles/aa/full/2002/05/aah3033/Timg90.gif) |
Figure 7:
Ratio of H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3033f17.eps}\vspace*{2mm}
\includegraphics[width=8.8cm,clip]{h3033f18.eps}\end{figure}](/articles/aa/full/2002/05/aah3033/Timg91.gif) |
Figure 8:
H |
| Open with DEXTER | |
At the beginning of our work we adopted the same approach as Fang et al. (1993) and
expected to obtain very similar H![]() line profiles. However, even though
our column mass dependence of the collisional ionisation rates
and electron density give almost the same
results as those presented in Hénoux et al. (1993, Fig. 5), or
Fang et al. (1993, Fig. 4), our H
line profiles. However, even though
our column mass dependence of the collisional ionisation rates
and electron density give almost the same
results as those presented in Hénoux et al. (1993, Fig. 5), or
Fang et al. (1993, Fig. 4), our H![]() line profiles do not show as strong intensity enhancements in the line
cores as those in the articles mentioned above.
line profiles do not show as strong intensity enhancements in the line
cores as those in the articles mentioned above.
In Fang et al. (2000) there were presented recalculated H![]() line profiles,
using higher relative precision, which exhibited lower intensity enhancements
compared to those in Fang et al. (1993).
Furthermore, according to Fang (private communication), a standard
Lambda-iteration scheme
was used as a method for solving the equation of radiative transfer in their
papers (Fang et al. 1993; Hénoux et al. 1993). Due to these facts, we have also performed
calculations by using the Lambda iterations. We have adopted the
same values of parameters
line profiles,
using higher relative precision, which exhibited lower intensity enhancements
compared to those in Fang et al. (1993).
Furthermore, according to Fang (private communication), a standard
Lambda-iteration scheme
was used as a method for solving the equation of radiative transfer in their
papers (Fang et al. 1993; Hénoux et al. 1993). Due to these facts, we have also performed
calculations by using the Lambda iterations. We have adopted the
same values of parameters ![]() and
and
![]() as in Fang's paper (
as in Fang's paper (
![]() ,
,
![]() ). All line
profiles presented in this section were convolved with a Gaussian
macroturbulence velocity of
). All line
profiles presented in this section were convolved with a Gaussian
macroturbulence velocity of
![]() in order to make
a comparison with Fang's line profiles possible.
Figure 6 shows H
in order to make
a comparison with Fang's line profiles possible.
Figure 6 shows H![]() line profiles after 600 Lambda
iterations for
line profiles after 600 Lambda
iterations for
![]() and various values of
and various values of
![]() .
These line profiles are quite comparable to those in Fang et al. (1993, Fig. 1).
.
These line profiles are quite comparable to those in Fang et al. (1993, Fig. 1).
Moreover, H![]() line source function after
600 Lambda iterations is also consistent with
the one obtained in Hénoux et al. (1993, Fig. 4). On the basis of these facts
we can speculate
that the slight difference between Fang's and our column mass dependence of
the electron density for the
model without including the non-thermal collisional rates is mainly due to the
chosen numerical
method. The electron density for the models with included non-thermal
collisional rates is significantly affected by the non-thermal ionisation,
which is the same in both Fang's and our calculations. Therefore, the
influence of the chosen numerical method of the radiative transfer is
suppressed and for the models with included non-thermal
collisional rates our and Fang's electron densities are almost identical.
line source function after
600 Lambda iterations is also consistent with
the one obtained in Hénoux et al. (1993, Fig. 4). On the basis of these facts
we can speculate
that the slight difference between Fang's and our column mass dependence of
the electron density for the
model without including the non-thermal collisional rates is mainly due to the
chosen numerical
method. The electron density for the models with included non-thermal
collisional rates is significantly affected by the non-thermal ionisation,
which is the same in both Fang's and our calculations. Therefore, the
influence of the chosen numerical method of the radiative transfer is
suppressed and for the models with included non-thermal
collisional rates our and Fang's electron densities are almost identical.
![\begin{figure}
\par\hspace*{4.5cm}\mbox{\includegraphics[width=7.5cm,clip]{h3033...
...}\hspace*{0.7cm}
\includegraphics[width=7.5cm,clip]{h3033f23.eps} }
\end{figure}](/articles/aa/full/2002/05/aah3033/Timg95.gif) |
Figure 9:
H |
| Open with DEXTER | |
![\begin{figure}
\par\hspace*{4.5cm}\mbox{\includegraphics[width=7.5cm,clip]{h3033...
...}\hspace*{0.7cm}
\includegraphics[width=7.5cm,clip]{h3033f28.eps} }
\end{figure}](/articles/aa/full/2002/05/aah3033/Timg96.gif) |
Figure 10:
H |
| Open with DEXTER | |
![\begin{figure}
\par\hspace*{4.5cm}\mbox{\includegraphics[width=7.5cm,clip]{h3033...
...}\hspace*{0.7cm}
\includegraphics[width=7.5cm,clip]{h3033f33.eps} }
\end{figure}](/articles/aa/full/2002/05/aah3033/Timg97.gif) |
Figure 11:
H |
| Open with DEXTER | |
Figures 7 and 8 demonstrate behaviour of convergence of
the standard Lambda-iteration method in the case of the flare atmosphere F1.
Figure 8 shows that more than 12 000 standard
Lambda iterations must be performed in order to obtain the H![]() line
profile comparable to that obtained by MALI method. Convergence of
H
line
profile comparable to that obtained by MALI method. Convergence of
H![]() source function for Lambda iterations and MALI iterations is
displayed in
Fig. 7. It is generally known that standard Lambda iterations
converge very slowly at large optical depths (Mihalas 1978). The solution usually
stabilises far from the true one after several tens or hundreds of iterations
(Auer 1991; Heinzel 1995).
source function for Lambda iterations and MALI iterations is
displayed in
Fig. 7. It is generally known that standard Lambda iterations
converge very slowly at large optical depths (Mihalas 1978). The solution usually
stabilises far from the true one after several tens or hundreds of iterations
(Auer 1991; Heinzel 1995).
Moreover, the intensity ratios of Balmer lines appear to be considerably
dependent on the
total energy flux
![]() .
We thus propose to use this effect as
a diagnostic tool for revealing the presence of electron beams during impulsive phases
of solar flares. However, one must bear in mind that the relations presented here
do not include possible changes of the temperature structure during the
flare evolution.
.
We thus propose to use this effect as
a diagnostic tool for revealing the presence of electron beams during impulsive phases
of solar flares. However, one must bear in mind that the relations presented here
do not include possible changes of the temperature structure during the
flare evolution.
In our case we have treated the atmosphere in a semi-empirical manner keeping same temperature distribution of model F1 for all our models. The model F1 was derived on base of flare spectra (mainly the UV continua) and does not include the non-thermal collisional rates. Therefore, in the presence of the beam, the F1 temperatures, which we use, are actually overestimated (the non-thermal excitations produce a part of the line and continuum emission). In this sense, our present simulations are only aimed at analysing the differential effects as discussed above.
Furthermore, we have assumed that beam of electrons penetrates through the atmosphere which is in hydrostatic equilibrium (model F1). This simplification is valid only when motions are negligible in the flare atmosphere. However, the equilibrium solution with the non-thermal collisional rates results in a change of electron density that modifies number density of hydrogen which subsequently changes the geometric depth scale. This leads to a new density distibution on h compared to the model F1. In reality, the presence of the beam will cause a dynamical evolution of an atmosphere.
Finally, using a five-level plus continuum model of hydrogen atom may not be
sufficient in the case of H![]() line. An atomic model with more levels
included should be considered to obtain quantitatively more accurate results
which could be compared with the observations.
line. An atomic model with more levels
included should be considered to obtain quantitatively more accurate results
which could be compared with the observations.
This analysis gives us an insight into the non-thermal effects introduced by electron beams which will be used in our future work. We plan to develop time-dependent models of the beam heating by a series of short duration pulses of accelerated beams of electrons and/or protons.
Acknowledgements
This work was partially supported by the grant A3003902 of the Academy of Sciences of the Czech Republic. The authors are indebted to J.-C. Hénoux for useful discussions and comments.