A&A 382, 600-609 (2002)
DOI: 10.1051/0004-6361:20011626

Diffuse far-infrared [C II] line emission from high Galactic latitude

S. Makiuti1 - H. Shibai2 - T. Nakagawa1 - H. Okuda3 - K. Okumura4 - H. Matsuhara1 - N. Hiromoto5 - Y. Doi6


1 - The Institute of Space and Astronautical Science (ISAS), 3-1-1 Yoshinodai, Sagamihara, Kanagawa 229-8510, Japan
2 - Graduate School of Science, Nagoya University, Furo-cho, Chikusa-ku, Nagoya 464-8602, Japan
3 - Gunma Astronomical Observatory, 6860-86 Nakayama, Takayama, Agatsuma Gunma, 377-0702, Japan
4 - Communications Reserch Laboratory, 4-2-1 Nukui-kitamachi, Koganei, Tokyo 184-8795, Japan
5 - Kansai Advanced Research Center, Communications Research Laboratory, 588-2 Iwaoka, Nishi-ku, Kobe 651-2492, Japan
6 - College of Arts and Sciences, University of Tokyo, Komaba 3-8-1, Meguro, Tokyo 153-8902, Japan

Received 23 July 2001 / Accepted 30 October 2001

Abstract
The Far-Infrared Line Mapper (FILM) onboard the Infrared Telescope in Space (IRTS) made a survey for the far-infrared [C II] 158 $\mu $m line emission with high sensitivity and moderate spatial resolution. We have found that diffuse [C II] line emission extends to high Galactic latitude regions. The [C II] line intensity at $\vert b\vert \sim 60^{\circ}$ ranges from $2\times10^{-7}$ to $1.5\times10^{-6}$  $\mbox{erg cm}^{-2}~\mbox{ s}^{-1}~\mbox{sr}^{-1}$. Comparisons of the distribution of the [C II] line emission with those of the H I column density and far-infrared radiation show some correlations, but the [C II] line emission differs from the far-IR and HI emission at high Galactic latitudes. These differences suggest that the [C II] line primarily comes from ionized gas in the high-latitude regions. The intensities of the [C II] line emission on the southern side ( $b< 0^{\circ }$) of the Galactic plane are systematically larger than those on the northern side ( $b> 0^{\circ }$). We infer from this difference that there is a displacement of the Sun with respect to the center of interstellar medium from which the [C II] line comes. When an exponential distribution is assumed for the [C II] emitting gas, it is expected that the Sun is located at the distance of about 17% of the scale height above the center of the gas. This is consistent with the previously reported displacement of the Sun from the Galactic plane.

Key words: lnfrared: ISM - ISM: lines and bands - ISM: structure - Galaxy: general


1 Introduction

The interstellar matter can be classified into several states of particular temperature and density depending on balances of energy (heating and cooling) and mass (evaporation and condensation of clouds) (Field et al. 1969; McKee & Ostriker 1977; Draine 1978; Shull 1987). The major components of the interstellar gases in high Galactic latitude regions can be classified into three phases (three-phase model): cold ($T \sim 50$ K) diffuse H I clouds (or cold neutral medium; CNM), warm ( $T \sim 8000$ K) medium, and hot ( $T \sim 10^{{\rm 6}}$ K) ionized medium (HIM or hot plasma). In addition, the warm medium can be distinguished into two phases according to the ionization degree; warm neutral medium (WNM; $n_{{\rm e}}/n \sim$ 10 $^{{\rm -1}})$ and warm ionized medium (WIM; $n_{{\rm e}}/n \sim$ 1). The WIM has been observed extensively with the optical recombination line H$\alpha $ and forbidden lines such as [S II] and [N II] (cf. Reynolds 1990). It is believed to be one of the major components in the interstellar gas (Reynolds 1991), but the details such as the fraction in the interstellar space and the relation to other phases have not been well known.

The far-infrared [C II] line ( 2P3/2- 2P1/2; 157.7 $\mu $m) is emitted from gases in a wide range of physical conditions from neutral to ionized hydrogen regions in the interstellar space. The emitting level lies only $\Delta E/k$ = 91 K above ground, which is relatively low. Therefore the [C II] line is one of the strongest line emissions from the interstellar gases and it is presumed that the [C II] line emission is a dominant coolant in the warm ionized medium in particular.

Past observations with balloons and airplane-borne telescopes revealed that the [C II] line emission in the Galactic plane comes not only from compact areas associated with high-temperature stars but also from extensive regions (Stacey et al. 1985; Shibai et al. 1991). Later observations by balloons surveyed the Galactic plane in detail and have shown that the [C II] line becomes more important in diffuse components rather than in compact sources (Nakagawa et al. 1998).

In high Galactic latitude regions, the [C II] line emission in limited regions was observed with a rocket-borne telescope (Bock et al. 1993; Matsuhara et al. 1997), and an all-sky survey was made by FIRAS onboard the COBE satellite (Bennett et al. 1994; Fixsen et al. 1999). The COBE/FIRAS revealed that the [C II] line emission spreads extensively to high-latitude regions, but the 7 degrees beam size of FIRAS was too large to resolve discrete sources. The IRTS/FILM has succeeded in observations of the high-latitude [C II] line emission with a moderate angular resolution and a high sensitivity although the observed region was limited owing to the short observation period. We present an analysis of the IRTS/FILM high-latitude [C II] observations here.

The WNM and Hot Plasma cannot emit the [C II] line efficiently since the densities inside those components are too small (Bakes & Tielens 1994; Wolfire et al. 1995). It seems that there are few photodissociation regions (PDRs) that are formed on molecular cloud surfaces in high Galactic latitude regions, because there are few molecular clouds (Magnani et al. 1996). Consequently the most important candidates for the source of the [C II] line emission are the WIM and the cold H I clouds.

Bennett et al. (1994) found that the [C II] line intensity observed by COBE/FIRAS is consistent with the predicted values from the neutral gas, when they assumed a column density of the H I gas averaged in the whole sky to be $N{\rm (H {\sc i})}/\csc\vert b\vert = 3.3 \times 10^{{\rm 20}}~ {\rm cm}^{{\rm -2}}$ (Lockman et al. 1986) and the neutral gas to be cold H I clouds that have typical temperatures of 80$\sim $100 K and densities of 10$\sim $30 cm $^{{\rm -3}}$. They concluded that cold H I clouds dominate the high Galactic latitude [C II] line emission. However, the percentage of the H I gas in cold clouds as well as most of the physical conditions of the interstellar medium in high Galactic latitude regions are not well known. The ionized gas is also believed to be a major component in high-latitude regions, so it can contribute largely to the [C II] line emission. In Sects. 4.1 and 4.2, we discuss the contribution of the WIM to the [C II] line emission in high-latitudes.

Systematic differences between at the northern and the southern side of the Galactic plane are seen in the [C II] line intensity observed by the IRTS/FILM. The Galaxy consists of various forms of matter such as stars, interstellar dust and gas. However, the structure of our Galaxy and the position of the Sun have not been elucidated in detail since we cannot get sufficiently unobstructed views at most wavelengths owing to the extinctions by interstellar matter. We have now a new data set to probe this. In Sect. 4.3, we will discuss the position of the Sun relative to the [C II] line emitting gas distributed around our solar system, founded on the distribution data of the [C II] line emission at high Galactic latitude.

2 Observations and data reduction

The Infrared Telescope in Space (IRTS) onboard the Space Flyer Unit (SFU) satellite was launched with an HII rocket in March 1995. The IRTS has a primary mirror 15 cm in diameter, cooled with liquid helium, and succeeded in the survey observation for about one month until all the helium was consumed (Murakami et al. 1996). The Far-Infrared Line Mapper (FILM) is one of the focal plane instruments of the IRTS (Shibai et al. 1994). It is a grating spectrometer dedicated to observations of the far-infrared [C II] 158 $\mu $m line emission and uses stressed Ge:Ga photoconductors as the detector (Hiromoto et al. 1992). It has a spectral scanner and the line intensity components were extracted as modulated signals (Shibai et al. 1996a). The IRTS/FILM surveyed the [C II] line emission in high Galactic latitude regions up to about $\vert b\vert \sim 60^{\circ}$ under the low background conditions of space. The beam size of the instrument was 8 $' \times 13'$ (FWHM).

The detector noise levels were stable during the observations. However the responsivity of the stressed Ge:Ga detector continually changed mainly due to cosmic ray impacts. The FILM has internal calibration lamps in order to correct the changes in the detector responsivities. Signals for the calibration lamps were acquired at 1024 s intervals during the observations and the slow components of responsivity changes have been corrected by the post-flight analysis with those data. Most of the fast components by cosmic rays have been removed.

The absolute calibration has been made independently from the preflight experiments (Shibai et al. 1994). However, the calibrated [C II] line intensity of the IRTS/FILM is different from the results of other observations at present. We compared the independent observations of the IRTS/FILM and the balloon-borne telescope BICE (Nakagawa et al. 1998) for objects near the Galactic plane. The [C II] line intensity from the IRTS/FILM is $\sim $65% for $I_{{\rm [C {\sc ii}]}}$(BICE) > 1 $\times$ 10 $^{{\rm -4}}$ erg cm $^{{\rm -2}}$ s $^{{\rm -1}}$ sr $^{{\rm -1}}$ and $\sim $85% for $I_{{\rm [C {\sc ii}]}}$(BICE) < 1 $\times$ 10 $^{{\rm -4}}$ erg cm $^{{\rm -2}}$ s $^{{\rm -1}}$ sr $^{{\rm -1}}$. It is also reported that the observation from the BICE is about 65% compared to the COBE/FIRAS (Nakagawa et al. 1998; Bennett et al. 1994). Therefore the [C II] line intensity of the FILM is (42-55)% of COBE/FIRAS. Recently the ISO satellite (Kessler et al. 1996) has also observed the [C II] line emission, but it is difficult to compare the ISO with the IRTS/FILM since the beam sizes are significantly different. The uncertainty of the absolute line intensity does not affect the discussions in this paper.

The IRTS/FILM has a cold shutter at an entrance aperture, and it was closed at 1024 seconds intervals. The zero flux level for the [C II] line intensity was determined by those data. The zero flux level is the dominant uncertainty for the estimation of high-latitude [C II] line emission that is very weak. The zero flux level was stable on the whole. The uncertainty in the determination of the zero level is estimated to be less than $3 \times 10^{{\rm -7}}$ erg cm $^{{\rm -2}}$ s $^{{\rm -1}}$ sr $^{{\rm -1}}$.

  
Table 1: Observed regions (definition $^{{\rm *}}$).

\begin{displaymath}{\begin{tabular}{c r @{ $l$ } l c} \hline {\bf Region name}... ...$^{\circ}$ & $b$ $<$ 0$^{\circ}$ \\ \hline \end{tabular}} \end{displaymath}
$^{{\rm *}}$ See also Fig. 1.


3 Results

  
3.1 Intensity distribution of the [C II] line emission


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms1722f1r.eps} % \end{figure} Figure 1: The region observed by the IRTS/FILM. It is along a great circle on the sky, which cut across the Galactic plane around l $\sim $ 50$^{\circ }$ and l $\sim $ 230$^{\circ }$ and reaches approximately up to $\vert b\vert \sim$ 60$^{\circ }$. There are two different data sets at each latitude. They are defined as data at inner and outer regions respectively in this analysis (see Table 1). Note that the two regions are not symmetric with respect to the Galactic center.
Open with DEXTER

The IRTS/FILM has succeeded in the detection of the [C II] 158 $\mu $m line emission from high-latitude regions of the Galaxy. The surveyed area consists of two bands along great circles about five degrees in width. In this paper, we use only the data from one of them, which includes high Galactic latitude regions up to $\vert b\vert \sim 60^{\circ}$ as shown in Fig. 1.

The observed data were averaged into one-degree bins in the Galactic latitude in order to obtain higher S/N ratios in high-latitude regions, although the instrumental beam size of the IRTS/FILM was 8 $' \times 13'$ (FWHM). The resultant integration time is nominally 1500 s and at least 500 s for every one-degree bin. The statistical error is $7 \times 10^{{\rm -8}}$ erg cm $^{{\rm -2}}$ s $^{{\rm -1}}$ sr $^{{\rm -1}}$ (1$\sigma)$ for bins having the nominal integration time. This statistical error in the diffuse [C II] line emission is about 30 times smaller than that of COBE/FIRAS with its beam size of 7 degrees (Bennett et al. 1994).

  \begin{figure} \includegraphics[width=8.8cm,clip]{ms1722f2r.eps} % \end{figure} Figure 2: Galactic latitudinal distribution of the far-infrared [C II] 158 $\mu $m line emission obtained by the IRTS/FILM. Each data point is calculated by averaging all data at intervals of one-degree in Galactic latitude. Error bars are $\pm 1\sigma $ values. It appears to have a discontinuity at $\vert b\vert = 0^{\circ}$ in outer regions owing to the shift of peak position to the south (see text).
Open with DEXTER

The obtained latitudinal profiles are shown in Fig. 2 for individual quadrants (defined in Fig. 1 and Table 1). The [C II] line emission was clearly detected at the high Galactic latitude regions, even at the region of $\vert b\vert \sim 60^{\circ}$. The errors indicated in Fig. 2 do not include the systematic error due to uncertainty of the estimation of the zero flux level. This systematic error is less than $3 \times 10^{{\rm -7}}$ erg cm $^{{\rm -2}}$ s $^{{\rm -1}}$ sr $^{{\rm -1}}$ as described in the previous section. Even if this systematic error is included, it can be concluded that the [C II] line emission was detected positively in high-latitude regions except for the inner north region.

However, the line intensity of the [C II] emission varies among the four regions at high latitudes. The outer south region has the largest intensity of ${\sim}1.5 \times 10^{-6}$ erg cm $^{{\rm -2}}$ s $^{{\rm -1}}$ sr $^{{\rm -1}}$, whereas the inner north region has the smallest, ${\sim}2 \times 10^{{\rm -7}}$ erg cm $^{{\rm -2}}$ s $^{{\rm -1}}$ sr $^{{\rm -1}}$. They show a tendency that the intensities on the southern side ( $b< 0^{\circ }$) are larger than those on the northern side ( $b> 0^{\circ }$), both in the inner regions and in the outer regions.

In regions near the Galactic plane, $\vert b\vert \le 10^{\circ}$, the [C II] line intensity rapidly increases as the Galactic latitude decreases. The present result is consistent with those of Shibai et al. (1996b) and Makiuti et al. (1996), who have also analyzed the data set obtained by the IRTS/FILM. According to their interpretation, the [C II] emission component from the inner low-latitude regions can predominantly be attributed to the emission from photodissociation regions (PDRs) that are consistent with the detailed model calculated by Mochizuki & Nakagawa (2000), whereas the emission from the outer low-latitude regions can be attributed to H I atomic gas clouds.

In the outer regions, the peak of the [C II] line emission is not on the Galactic plane but is shifted to the southern side from the plane (Fig. 2). This displacement of the peak is consistent with distributions of FIR radiation, H I emission and stars (Djorgovski & Sosin 1989; Freudenreich et al. 1994).

  
3.2 Comparisons of the [C II] distribution with the HI and FIR distributions


  \begin{figure} \par\includegraphics[width=17cm,clip]{ms1722f3r.eps} % \end{figure} Figure 3: Galactic latitudinal distribution of the [C II], H I (Dickey & Lockman 1990), and FIR (COBE/DIRBE 140 $\mu $m). The horizontal axis in sin $\vert b\vert$ (sin $\vert b\vert$ = 0.1 corresponds to $\vert b\vert$ = 5.7$^{\circ }$). When each interstellar matter component has a plane-parallel density distribution and follows the cosecant-law, the intensity profile is expected to be along the downward line shown in each panel. An intercept of the line at sin $\vert b\vert$ = 1 is proportional to the thickness of interstellar matter, or line intensity perpendicular to the Galactic plane. The left column shows the distributions in the inner regions. The right column shows those in the outer regions. a-b) The [C II] 158 $\mu $m line emission obtained by the IRTS/FILM. The intercepts of the lines at $\sin\vert b\vert = 1$ are $2 \times 10^{{\rm -7}}$ erg cm $^{{\rm -2}}$ s $^{{\rm -1}}$ sr $^{{\rm -1}}$. Error bars are $\pm 1\sigma $ values. c-d) H I column density calculated in the same regions observed by the IRTS/FILM. The intercepts at $\sin\vert b\vert = 1$ are $2 \times 10^{{\rm 20}}$ cm $^{{\rm -2}}$. e-f) FIR radiation (COBE/DIRBE 140 $\mu $m band) calculated in the same region observed by the IRTS/FILM. They are proportional to the total FIR luminosity since there are no large variations in dust temperature. The intercepts at $\sin\vert b\vert = 1$ are 3 MJy sr $^{{\rm -1}}$.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=12cm,clip]{ms1722f4r.eps} \end{figure} Figure 4:  Ratio of FIR radiation to H I column density vs. Galactic latitude (sin $\vert b\vert$) in the inner regions a) and the outer regions  b). The FIR radiation is 140 $\mu $m band data from COBE/DIRBE. In each panel, diamonds ( $\diamondsuit )$ show data on the northern side ( $b> 0^{\circ }$) and crosses ($\times )$ show the southern side ( $b< 0^{\circ }$) of the Galactic plane. The ratio increases with sin $\vert b\vert$ in the outer regions (see text).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=12cm,clip]{ms1722f5r.eps} % \end{figure} Figure 5:  Ratio of the [C II] 158 $\mu $m line emission obtained by the IRTS/FILM to FIR radiation (COBE/DIRBE 140 $\mu $m) vs. Galactic latitude (sin $\vert b\vert)$ in the inner regions a) and the outer regions  b). In each panel, diamonds ( $\diamondsuit )$ show data on the northern side (b $> 0^{\circ }$) and crosses ($\times )$ show the southern side ( $b< 0^{\circ }$) of the Galactic plane. The ratio at high-latitudes is larger than at low-latitudes (see text).
Open with DEXTER

Figure 3 shows the distributions of the [C II] 158 $\mu $m line intensity (present work), the H I column density (Dickey & Lockman 1990), and the far-infrared continuum intensity at 140 $\mu $m observed by COBE/DIRBE along the same area. If the interstellar matter has a plane-parallel distribution along the Galactic plane, the intensity profiles tracing each component would be proportional to $\csc \vert b\vert$ (the cosecant-law), or straight lines with the slope of -1 in Fig. 3.

As seen in Fig. 3, all distribution profiles decrease with $\sin \vert b\vert$ in an overall scale, but there is a wide variety in their profiles, as follows. Firstly, most parts of the Galactic latitudinal profiles are nearly proportional to $\csc \vert b\vert$ in the inner regions, which means that the interstellar matter has distributions similar to plane-parallel disks. However, the [C II] line profile has a remarkable excess emission component at $b < -35^{\circ}$, and the H I and FIR profiles have a peak at $b \sim -40^{\circ}$.

The [C II] and H I profiles in the outer regions do not show the same $\sin \vert b\vert$ dependence as that in the inner regions; the [C II] emission has gentler dependence, whereas the H I has steeper dependence. Only the FIR has dependence similar to that expected for the plane-parallel distribution.

In addition, there are some local features with scales of several degrees to some dozens of degrees on each latitudinal distribution of the [C II], H I, and FIR; for example, at $b = -15^{\circ}$ and $-40^{\circ}$ on the inner side and at $b = 30^{\circ}$ on the outer side. They correspond to high-latitude cirrus components (Low et al. 1984).

  
3.3 Ratios among the [C II] line, far-infrared radiation, and the H I gas

Although the FIR continuum and the H I gas locally have a good correlation with each other, there is some variation in FIR to H I ratios vs. Galactic latitude as is shown in Fig. 4. In the inner regions, the FIR/H I ratio is almost constant except for the region near the Galactic plane ( $\vert b\vert < 5^{\circ}$ or $\sin\vert b\vert < 0.1$). In the outer regions, the FIR/H I ratio is significantly smaller than that of the inner regions at low-latitudes and it increases rapidly as Galactic latitude increases.

We show the Galactic latitudinal profiles of the [C II] line to FIR continuum flux ratio in Fig. 5. In the outer regions, the [C II]/FIR ratio evidently increases with the Galactic latitude. In the inner regions, it is not conspicuous compared to that of the outer regions, but the ratios at $\vert b\vert > 10^{\circ}$ are 10 to 30% larger than those at $\vert b\vert < 10^{\circ}$. These ratios are liable to be affected by the uncertainty of zero flux level since the observed intensity at high-latitude is generally very weak. However, the tendency for the ratio to increase does not change within the range of uncertainty estimated for the zero level in the [C II] line intensity (see Sect. 2). This result is different to that reported by Bennett et al. (1994) with the COBE/FIRAS data (see Fig. 7 in their paper), in which the [C II]/FIR ratio decreases with latitude.

  
3.4 North-south difference of the [C II] line intensity profile

We have obtained four Galactic latitudinal distributions of the [C II] line emission in the range of 0$^{\circ }$ to about 60$^{\circ }$. There are evident differences in the average levels of the [C II] line intensity at high Galactic latitude between the four regions as shown in Fig. 2. The average [C II] line intensity on the southern side is larger than that on the northern side both in the inner regions and in the outer regions. We show the Galactic latitudinal profiles of the intensity ratio of the [C II] line emission between the northern side and the southern side in Fig. 6. The south-to-north intensity ratio of the [C II] line emission $I_{ {\rm (} b < 0^{\circ } {\rm )} } /I_{ {\rm (} b > 0^{\circ } {\rm )} }$ in the outer regions varies from 1 to 3 in $\vert b\vert < 50^{\circ}$, with an average value of 1.8.

In the inner regions, the averaged intensity of the [C II] line emission on the southern side is larger than that on the northern side as well as in the outer regions. However, the values of the south-to-north ratio are around the unity in low-latitude regions ( $\vert b\vert < 15^{\circ}$) and increase with the Galactic latitude, unlike in the outer regions.

4 Discussion

  
4.1 Origin of the [C II] line emission at high-latitudes

We have successfully detected diffuse [C II] line emission at high-latitudes. The COBE/FIRAS made an all-sky [C II] map, but with a coarse resolution of 7 degrees. The present results have a better resolution, of one-degree in latitude, and have better sensitivities, as described in Sect. 3.1. Therefore, a much more precise analysis could be made by the present result.

In lower latitudes ( $\vert b\vert < 30^{\circ}$) of the inner regions, the [C II], 21 cm, and 140 $\mu $m profiles follow those expected for a plane-parallel distribution. This fact suggests that the [C II] line emitting gas, the H I gas and the dust radiating far-infrared continuum, have mostly plane-parallel distributions in the Galactic disk.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms1722f6r.eps} \end{figure} Figure 6: Latitudinal profile of the [C II] 158 $\mu $m line intensity ratio between the southern side ( $b< 0^{\circ }$) and the northern side ( $b> 0^{\circ }$) of the Galactic plane; $I_{ {\rm (} b < 0^{\circ } {\rm )} } /I_{ {\rm (} b > 0^{\circ } {\rm )} }$. The inner region is represented with diamonds ( $\diamondsuit )$ and outer region with crosses ($\times )$. The values of ratio are generally more than the unity. The average value in the outer regions is about 1.8 (shown by the horizontal line), which has no systematic dependency on latitude. In the outer regions, the ratio increases with latitude (see text).
Open with DEXTER


  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{ms1722f7r.eps}} % \end{figure} Figure 7: Expected intensity of the [C II] 158 $\mu $m line emission from the warm ionized medium (WIM). The horizontal axis is effective thickness of the WIM. Solid lines represent the estimated intensities of the [C II] line emission that are calculated for the WIM with various peak densities when those distributions are assumed to be exponential. Two horizontal dashed lines show a range (maximum and minimum) of the [C II] line intensities in the direction of the Galactic pole estimated from the observational results of the IRTS/FILM.
Open with DEXTER

As shown in Fig. 3, the [C II] profiles in the inner regions have a remarkable excess emission over a cosecant-law component in southern high-latitudes, whereas the H I and FIR profiles have smaller excess emission component in the same region of the sky. In the outer regions, the [C II] profiles are obviously different from others. Furthermore, the H I and the FIR profiles have different distributions as described in Sect. 3.2.

Changes in the ratios among the [C II] line intensity, the H I gas column density and the FIR radiation can be caused by changes of gas-to-dust ratios, abundances of the elements, gas density, far-UV field strength, and temperature of gas and dust. However, it is hard to explain our results by changes in those physical parameters. Those changes are insufficient quantitatively or require unrealistic assumptions in order to fit the observational results.

The global difference of dependencies on Galactic latitude between the [C II] line emission and the H I gas indicates that the [C II] line does not solely arise from the atomic interstellar medium. If the density of gas increases with latitude, the [C II] line intensity exceeds the H I gas component at high-latitude because the [C II] line intensity must be proportional to an emission measure but the H I profile in Fig. 3 is a column density. However this is hard to believe. It is probable that the majority of the [C II] line radiation from the high-latitude regions does not arise from the atomic interstellar medium, but rather from the warm ionized medium (WIM). It seems to be general throughout the Galaxy although the observed high-latitude [C II] line might be coming from local ionized bubble.

Bennett et al. (1994) conclude from the observed decrease in [C II] to FIR with latitude in the COBE/FIRAS data that the fraction of H I in the (poorly [C II] emitting) WNM must be increasing in compensation for H I in the (efficiently [C II] emitting) cold clouds as a function of latitude. However, we observed an increase in the [C II] to FIR ratio with latitude (Fig. 5), suggesting instead, that there is no increase in the WNM fraction at high-latitude. One possible reason for the discrepancy in the results is that the region observed by the IRTS/FILM is a small part of the sky, but the COBE result, the Galactic latitudinal profile of the [C II]/FIR ratio, were obtained from the average of nearly all-sky data. However, we believe the FILM's data are more reliable at high-latitude because the source-to-noise ratio is much better than that of the COBE. From our observational results, increase in [C II] to FIR and H I with latitude, it seems that the contribution from ionized gas (WIM) is increasing at high Galactic latitude.

Another observational fact suggesting the presence of the WIM in high latitudes is a factor of two increment of the FIR/H I ratio compared to that in lower latitudes, as shown in Fig. 4. In low-latitudes of the outer regions, most of the interstellar dust radiating the FIR continuum is thought to be mixed in the H I gas (cf. Boulanger & Perault 1988), and then, the FIR/H I ratio must be the smallest value for a constant gas-to-dust ratio. On the other hand, the ratio in high-latitude regions may increase due to the presence of the ionized gas (WIM). A factor of two increment in the FIR/H I ratio can be explained with the same amount of the WIM as that of neutral medium in high-latitudes, which is consistent with the result of Reynolds (1991). In the low-latitudes ( $\vert b\vert < 10^{\circ}$) of the inner regions, molecular clouds as well as H II regions must contribute to larger values of the FIR/H I ratio.

  
4.2 Expected intensity of the [C II] line emission from WIM

Next, we make a quantitative discussion. It is expected from the transitions in the FIR/H I ratio from low- to high-latitude regions that roughly half of the interstellar gas is neutral and the other half is ionized in the high-latitude regions. The respective percentages of neutral gases that form the cold H I clouds and the WNM are not clear. On the other hand, ionized gas must nearly entirely be in the WIM phase. So we estimate the intensity of the [C II] line from the WIM, when it has roughly the same column density as neutral gas at high Galactic latitude.

If an electron density $n_{{\rm e}}$ in the WIM is expressed as a function of a vertical distance Z from the Galactic plane, we can assume the typical column density at high-latitude from the observed value as

          $\displaystyle % \left\langle N_{{\rm H^{+}}}\right\rangle$ = $\displaystyle \int n_{{\rm e}} (Z) {\rm d}Z \cdot \csc \vert b\vert$  
  = $\displaystyle 2.5\times 10^{20} \csc \vert b\vert~{\rm cm^{ - 2}}~\left( \approx \langle N_{{\rm H^{0}}}\rangle \right) ,$ (1)

which is consistent with whole sky average column density of H I gas (Lockman et al. 1986). When we assume that the density distribution of the WIM is exponential, $n_{{\rm e}}$(Z) is

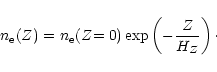\begin{displaymath}% n_{{\rm e}} (Z) = n_{{\rm e}} (Z{\rm =0}) \exp \left( - \frac{Z}{H_{Z}} \right)\cdot \end{displaymath} (2)

The intensity of the [C II] line depends on the local number density of the gas and significantly varies according to the degree of clumpiness. For example, we now assume the exponential distribution in which the density of the WIM on the Galactic plane is $n_{{\rm e}}$( Z=0) = 0.3 cm $^{{\rm -3}}$, which is typical for the WIM (Tielens 1995), and the scale height is HZ = 270 pc. The intensity of the [C II] line coming from the WIM in the direction of the Galactic pole can be estimated by equation:

\begin{displaymath}% I_{[C {\sc ii}]} = {\frac{1}{4\pi}} L(T_{{\rm e}} ) \int{ n... ...Z){\rm d}Z {\rm {\frac{[C]}{[H]}} {\frac{[C^{+}]}{[C]}} } }, \end{displaymath} (3)

when $L(T_{{\rm e}})$ is the cooling function in the case that the C $^{{\rm +}}$ ions are excited by collision with electrons (Hayes & Nussbaumer 1994). Assuming $T_{{\rm e}} = 8000$ K, [C]/ $\rm [H] = 3.6 \times 10^{-4}$ (Anders & Grevesse 1989) and [ $\rm C^{+}]/[C] = 0.5$, the [C II] line intensity is estimated as $I_{{\rm [C {\sc ii}]}} = 0.9 \times 10^{-6} \csc \vert b\vert$ erg cm-2 s-1 sr-1. If the scale height of the gas distribution is half of the above and the density in the Galactic plane is $n_{{\rm e}}(Z=0) = 0.6$ cm-3, the intensity of the [C II] line increases and is estimated to be $1.8 \times 10^{-6}$ csc $\vert b\vert$ erg cm-2 s-1 sr-1. The [C II] line intensities observed at the highest Galactic latitudes ( $\vert b\vert \sim 60^{\circ}$) by the IRTS/FILM is in the range of $2\times10^{-7}$ to $1.5 \times 10^{{\rm -6}}$ erg cm $^{{\rm -2}}$ s $^{{\rm -1}}$ sr-1. Consequently, the observational results by the IRTS/FILM can be explained by the emission from the WIM that has plausible parameters.

We represent the expected [C II] line intensity depending on the peak densities and effective thickness of the WIM in Fig. 7. The distribution function for the WIM is assumed to be exponential. Two horizontal lines in the figure express a range of the [C II] line intensities toward the Galactic pole expected by the results of the IRTS/FILM. In order to explain our observational results, we need to suppose that there is an ionized gas with peak density of $n_{{\rm e}} = 0.2$$\sim $0.7 cm $^{{\rm -3}}$ and scale height of a few tens to a few hundred parsecs. The range of values would be wider considering the uncertainty of an ionization degree and a volume-filling fraction of the WIM in the interstellar space.

Considering the circumstances mentioned above, the warm ionized medium (WIM), with typical densities and temperatures (cf. Minter et al. 2000) therefore appears to be a major source of the [C II] emission observed by the IRTS/FILM at high latitudes, and a major gas reservoir in high Galactic latitude regions.

  
4.3 The [C II] line emitting gas in the solar neighborhood and the position of the Sun

The north-south asymmetry in the [C II] intensity distribution in the outer regions shown in Fig. 6 suggests that the [C II] line emitting gas is abundant toward the southern side of the Galaxy compared with the northern side. This may be caused by the displacement of the Sun from the mid-plane of the distribution of the [C II] emitting gas in the local Galactic disk, or it may just be a local structure around the solar system.

  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{ms1722f8r.eps}} % \end{figure} Figure 8: Simple model of the displacement of the Sun and a systematically difference between $b> 0^{\circ }$ and $b< 0^{\circ }$.
Open with DEXTER

We derive the displacement in the position of the Sun from the [C II] asymmetry observed here; the average ratio $I_{ {\rm (} b < 0^{\circ } {\rm )} } /I_{ {\rm (} b > 0^{\circ } {\rm )} }$ is 1.8. If the distribution of the interstellar matter has a symmetric structure and the Sun is located away from the center of it, a systematic difference in observed intensity will occur (see Fig. 8). When there is a perpendicular displacement from the Galactic plane, the south-to-north intensity ratio $I_{ {\rm (} b < 0^{\circ } {\rm )} } /I_{ {\rm (} b > 0^{\circ } {\rm )} }$ should be independent of Galactic latitude, depending only on the solar position from the Galactic plane ( $Z_{{\rm Sun}}$).

The value of the ratio must be different between the FIR continuum radiation and the [C II] line emission (Fig. 9). The former is proportional to a column density of interstellar dust when it is optically thin. On the other hand, the high-latitude [C II] line intensity is in proportion to an emission measure because it comes from gases with density sufficiently lower than the critical density. The actual distribution of source matter emitting the [C II] line is not evident. However, an assumption that a density distribution is generally expressed as symmetric exponential function with respect to the Galactic plane seems to be practical (cf. Pritchet 1983; Kent et al. 1991).

Assuming that the [C II] emitting gas has an exponential density distribution in the Z-direction and that the [C II] emissivity is proportional to the emission measure as expected for WIM, we obtain about 17% of the scale height for the displacement of the Sun according to Fig. 9. Thus we can expect, for example, that for a scale height of 100 pc, the displacement of the Sun from the Galactic plane $Z_{{\rm Sun}}$ is about +20 pc.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms1722f9r.eps} % \end{figure} Figure 9: Relation between the south-to-north intensity ratio $I_{ {\rm (} b < 0^{\circ } {\rm )} } /I_{ {\rm (} b > 0^{\circ } {\rm )} }$ and the distance of the Sun $Z_{{\rm Sun}}$ from the center of interstellar matter distribution. A density distribution of the interstellar matter is assumed to be exponential function of Z. The south-to-north ratio increases with $Z_{{\rm Sun}}$. It is different by the case where observed intensity is proportional to a column density (ex. far-infrared radiation; dashed line), and the case where it is proportional to emission measure (ex. [C II] line from the WIM; solid line).
Open with DEXTER

The scale height of 100 pc is somewhat smaller than that often considered; from a few hundreds to a few thousands parsec (cf. Reynolds 1991), but it is not a significant difference. If the actual distribution of the gas differs from the simple exponential distribution assumed above, the estimated displacement of the Sun, $Z_{{\rm Sun}}$, will vary. For example, if the distribution is more strongly concentrated towards the Galactic plane, then a smaller value of $Z_{{\rm Sun}}$ will be estimated than above. On the contrary, if the density distribution is more distributed, and close to uniform, a larger value of $Z_{{\rm Sun}}$ is required.

Next, we compare this value with other results. Bahcall & Bahcall (1985) calculated the periodical oscillation of the Sun in the perpendicular direction to the Galactic plane. They demonstrated that half-periods in the perpendicular motion of the Sun should be 26-37 Myr and maximum distance from the Galactic plane $Z_{{\rm max}}$ should be 49-93 pc. Many attempts to find the distance of the Sun from the Galactic plane $Z_{{\rm Sun}}$ based on the asymmetry and so on have been made for various objects and wavelengths. The values of $Z_{{\rm Sun}}$ range from 0 to 40 pc at the present time (see Table 2). Our conclusion that the Sun is located above the center of the interstellar medium, which is emitting the [C II] line, is consistent with previous work.

In the inner regions, there are different features in the south-to-north ratio from the outer regions as described in Sect. 3.4. There is a dominant component that is highly concentrated upon the Galactic plane (Shibai et al. 1996b). It has an approximately symmetrical distribution with respect to the Galactic plane, so that the ratio is unity. The reason for the ratio increasing toward high-latitude regions could be because the inner region defined by us is shifted by +45$^{\circ }$ relative to the Galactic center, and the southern data is closer to the Galactic center than the northern data. It is expected that the actual distribution of interstellar matter is a function of distance from the Galactic center approximately (Unavane et al. 1998; Mandez & Altena 1998; Chen et al. 1999). When the interstellar medium emitting the [C II] line becomes denser or has a larger scale height as it is closer to the Galactic center, the south-to-north intensity ratio should vary according to the Galactic latitude as actually observed. The same effects might appear in the outer regions, but the dependency on the Galactic longitude is expected to be small in the outer regions, and it seems that little effect appears actually.

 

 
Table 2: Previous estimates of $Z_{{\rm Sun}}$.
Author Probe $Z_{{\rm Sun}}$
Gum et al. (1960) H I gas $+4\pm 12$ pc

Blaauw et al. (1960)

 Pop. I star count $+22\pm 2$ pc

Stenholm (1975)

 Wolf-Rayet stars $+26\pm 20$ pc

Lynga (1982)

 Open clusters +20 pc

Pandey & Mahra (1987)

 Interstellar dust distribution $+10\pm 4$ pc

Caldwell & Coulson (1987)

 Cepheids $+36\pm 6$ pc

Ratnatunga et al. (1989)

 Yale BSC sample and model +7 pc

Yamagata & Yoshii (1992)

 Faint red stars of the halo $+40\pm 3$ pc

Hammersley et al. (1995)

 COBE, IRAS, TMGS $+15.5\pm 3$ pc

Cohen (1995)

 PSC of IRAS12 & 25 $\mu $m, FUV counts $+15.0\pm 0.5$ pc

Freudenreich (1998)

 COBE/DIRBE $1.25-4.9~\mu$m +16.5 pc

Mandez & Altena (1998)

 Star counts from GSC and model $+27\pm 3$(3$\sigma)$ pc

Chen et al. (1999)

 Star counts and extinction model $+27.5\pm 6.0$ pc


5 Summary

We have obtained the Galactic latitudinal distributions of the [C II] 158 $\mu $m line emission up to high Galactic latitudes of approximately $\vert b\vert \sim 60^{\circ}$ using the IRTS/FILM. The observed region is along a great circle across $l \sim$ 50$^{\circ }$ and $l \sim 230^{\circ}$ of about 5$^{\circ }$ in width. We find that:

1.
We have detected the [C II] line emission in the range of $2 \times 10^{{\rm - }{\rm 7}}$ to $1.5 \times 10^{{\rm -6}}$ erg cm $^{{\rm -2}}$ s $^{{\rm -1}}$ sr $^{{\rm -1}}$ in high-latitude regions of $\vert b\vert \sim 60^{\circ}$.

2.
The distribution of the [C II] line emission does not agree with those of the H I column density and the FIR continuum on the large scale. The differences are conspicuous in the Galactic outer regions in particular.

3.
The [C II] line component that has globally different distribution to the H I column density is expected to come from the warm ionized medium (WIM). The WIM is believed to be the major component in the high-latitude regions. We conclude that the major source of the [C II] line emission observed by the IRTS/FILM is the WIM at high Galactic latitudes.

4.
The [C II] line intensities on the southern side ( $b< 0^{\circ }$) are systematically larger than those on the northern side ( $b> 0^{\circ }$) in both of the Galactic inner and outer regions respectively.

5.
This systematic difference seems to be due to the displacement of the Sun. The Sun is located above the center of the [C II] line emitting gas. A distance of the displacement is estimated to be about 17% of the scale height of the gas distribution, assuming an exponential distribution. This displacement above the plane is consistent with previous works based on star counts and various interstellar matters.

Acknowledgements
We are grateful to the IRTS and SFU development and operation teams. In particular, we thank T. Matsumoto and H. Murakami for their efforts in ensuring the success of the IRTS project. We acknowledge the people who contributed to the IRTS/FILM, particularly M. Yui, Y. Y. Yui, T. Toya. Finally, we thank M. Narita at ISAS for his kind support.

References

 
Copyright ESO 2002