A&A 382, 431-449 (2002)
DOI: 10.1051/0004-6361:20011675
Dynamics of gravitational clustering
III. The quasi-linear regime for some non-Gaussian initial conditions
P. Valageas
Service de Physique Théorique, CEN Saclay, 91191 Gif-sur-Yvette, France
Received 11 July 2001 / Accepted 23 November 2001
Abstract
Using a non-perturbative method developed in a previous work (Paper II), we derive the probability distribution
 of the density contrast within spherical cells in the quasi-linear regime for some non-Gaussian initial conditions. We describe three such models. The first one is a straightforward generalization of the Gaussian scenario. It can be seen as a phenomenological description of a density field where the tails of the linear density contrast distribution would be of the form
of the density contrast within spherical cells in the quasi-linear regime for some non-Gaussian initial conditions. We describe three such models. The first one is a straightforward generalization of the Gaussian scenario. It can be seen as a phenomenological description of a density field where the tails of the linear density contrast distribution would be of the form
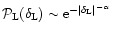 ,
where
,
where 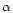 is no longer restricted to 2 (as in the Gaussian case). We derive exact results for
is no longer restricted to 2 (as in the Gaussian case). We derive exact results for
 in the quasi-linear limit. The second model is a physically motivated isocurvature CDM scenario. Our approach needs to be adapted to this specific case and in order to get convenient analytical results we introduce a simple approximation (which is not related to the gravitational dynamics but to the initial conditions). Then, we find a good agreement with the available results from numerical simulations for the pdf of the linear density contrast for
in the quasi-linear limit. The second model is a physically motivated isocurvature CDM scenario. Our approach needs to be adapted to this specific case and in order to get convenient analytical results we introduce a simple approximation (which is not related to the gravitational dynamics but to the initial conditions). Then, we find a good agreement with the available results from numerical simulations for the pdf of the linear density contrast for
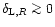 .
We can expect a similar accuracy for the non-linear pdf
.
We can expect a similar accuracy for the non-linear pdf
 .
Finally, the third model corresponds to the small deviations from Gaussianity which arise in standard slow-roll inflation. We obtain exact results for the pdf of the density field in the quasi-linear limit, to first-order over the primordial deviations from Gaussianity.
.
Finally, the third model corresponds to the small deviations from Gaussianity which arise in standard slow-roll inflation. We obtain exact results for the pdf of the density field in the quasi-linear limit, to first-order over the primordial deviations from Gaussianity.
Key words: cosmology: theory - large-scale structure of Universe
In usual cosmological scenarios, large-scale structures in the universe are generated by the growth of small primordial density perturbations, through gravitational instability. At large scales or at early times one can use a perturbative approach to obtain the first few moments of the evolved density field. Moreover, as described in Bernardeau (1992) and Bernardeau (1994a) one can actually sum up the perturbative series at leading order in the limit
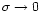 (where
(where 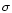 is the rms density fluctuation) to obtain all order cumulants. This yields the probability distribution function (pdf)
is the rms density fluctuation) to obtain all order cumulants. This yields the probability distribution function (pdf)
 of the density contrast within spherical cells. However, this method only applies to Gaussian initial conditions. Moreover, it may miss some non-perturbative effects.
of the density contrast within spherical cells. However, this method only applies to Gaussian initial conditions. Moreover, it may miss some non-perturbative effects.
In a previous paper (Paper II) we developed a non-perturbative method to derive the pdf
 in this quasi-linear regime. It is based on a steepest-descent approximation which yields asymptotically exact results in this limit. This allowed us to justify the results obtained by perturbative means and to correct some misconceptions related to non-perturbative effects. Another advantage of our approach is that in principle it can also be applied to non-Gaussian primordial density fluctuations. However, the determination of the relevant saddle-points needed in order to get simple analytic results may then be more difficult. In particular, the method may need to be adapted to specific cases.
in this quasi-linear regime. It is based on a steepest-descent approximation which yields asymptotically exact results in this limit. This allowed us to justify the results obtained by perturbative means and to correct some misconceptions related to non-perturbative effects. Another advantage of our approach is that in principle it can also be applied to non-Gaussian primordial density fluctuations. However, the determination of the relevant saddle-points needed in order to get simple analytic results may then be more difficult. In particular, the method may need to be adapted to specific cases.
Thus, in this article we show in details how to obtain the pdf
 for three specific non-Gaussian models, in the quasi-linear regime. Indeed, although observations are consistent with Gaussian initial conditions so far, it is of interest to investigate a broader class of models until any non-Gaussianity is definitely ruled out. Moreover, there exist some reasonable physical scenarios (though somewhat more contrived than the standard CDM model) which give rise to non-Gaussian primordial fluctuations. Finally, even standard inflationary scenarios lead to small deviations from Gaussianity for the primordial density fluctuations.
for three specific non-Gaussian models, in the quasi-linear regime. Indeed, although observations are consistent with Gaussian initial conditions so far, it is of interest to investigate a broader class of models until any non-Gaussianity is definitely ruled out. Moreover, there exist some reasonable physical scenarios (though somewhat more contrived than the standard CDM model) which give rise to non-Gaussian primordial fluctuations. Finally, even standard inflationary scenarios lead to small deviations from Gaussianity for the primordial density fluctuations.
This article is organized as follows. First, in Sect. 2 we recall the path-integral formulation which allows one to write an explicit expression for the pdf
 in terms of initial conditions. Then, in Sect. 3 we apply our method to a non-Gaussian model which is a straightforward generalization of the Gaussian case and could be used as a phenomenological tool to reproduce observations in case some departure from Gaussianity would be measured (e.g., in the CMB data). Then, in Sect. 4 we investigate a physically motivated model which describes an isocurvature cold dark matter scenario (Peebles 1999a). In particular, we obtain a good agreement with the available results from numerical simulations for the pdf of the linearly evolved density field. Finally, in Sect. 5 we consider the small primordial deviations from Gaussianity which arise in standard slow-roll inflation.
in terms of initial conditions. Then, in Sect. 3 we apply our method to a non-Gaussian model which is a straightforward generalization of the Gaussian case and could be used as a phenomenological tool to reproduce observations in case some departure from Gaussianity would be measured (e.g., in the CMB data). Then, in Sect. 4 we investigate a physically motivated model which describes an isocurvature cold dark matter scenario (Peebles 1999a). In particular, we obtain a good agreement with the available results from numerical simulations for the pdf of the linearly evolved density field. Finally, in Sect. 5 we consider the small primordial deviations from Gaussianity which arise in standard slow-roll inflation.
2 Generating functions. Gaussian initial conditions
In this article, we investigate the probability distribution function (pdf)
 of the density contrast
of the density contrast
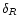 within a spherical cell of comoving radius R, volume V:
within a spherical cell of comoving radius R, volume V:
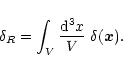 |
(1) |
Here
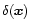 is the non-linear density contrast at the comoving coordinate
is the non-linear density contrast at the comoving coordinate 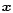 ,
at the time of interest. In this section, following the method developed in Paper II, we recall how one can express the pdf
,
at the time of interest. In this section, following the method developed in Paper II, we recall how one can express the pdf
 as a function of the initial conditions through a path-integral formalism. In order to introduce our approach we first briefly consider the case of Gaussian initial conditions which is most familiar. In the next section, we extend our formalism to a non-Gaussian model which can be seen as the simplest generalization of the usual Gaussian case.
as a function of the initial conditions through a path-integral formalism. In order to introduce our approach we first briefly consider the case of Gaussian initial conditions which is most familiar. In the next section, we extend our formalism to a non-Gaussian model which can be seen as the simplest generalization of the usual Gaussian case.
Rather than trying to directly evaluate the pdf itself, it is actually more convenient to study its Laplace transform  given by:
given by:
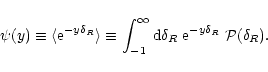 |
(2) |
Here, the symbol
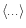 expresses the average over the initial conditions. Then, the last term in Eq. (2) can also be seen as the definition of the pdf
expresses the average over the initial conditions. Then, the last term in Eq. (2) can also be seen as the definition of the pdf
 .
Indeed, the pdf can be recovered from
.
Indeed, the pdf can be recovered from  through the standard inverse Laplace transform:
through the standard inverse Laplace transform:
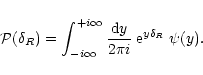 |
(3) |
Moreover, the generating function  also yields the moments
also yields the moments
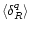 through:
through:
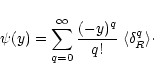 |
(4) |
Then, we need to compute  as an average over the initial conditions, using the first equality in Eq. (2). To do so, one simply needs two pieces of information. First, we must know the functional
as an average over the initial conditions, using the first equality in Eq. (2). To do so, one simply needs two pieces of information. First, we must know the functional
![$\delta_{R}[\delta_{\rm L}({\vec x})]$](/articles/aa/full/2002/05/aa1670/img30.gif) which yields the exact non-linear density contrast
which yields the exact non-linear density contrast
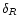 over the cell V which arises from the gravitational dynamics of the linear density field
over the cell V which arises from the gravitational dynamics of the linear density field
 .
Indeed, as shown for instance in Paper I the initial conditions can be defined by the linear density contrast
.
Indeed, as shown for instance in Paper I the initial conditions can be defined by the linear density contrast
 where we only keep the linear growing mode. This does not assume that the exact non-linear density field
where we only keep the linear growing mode. This does not assume that the exact non-linear density field
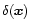 can be written as a series expansion over powers of the linear field
can be written as a series expansion over powers of the linear field
 .
In fact, such a series is only asymptotic (e.g., Papers I, V). Hereafter, we note
.
In fact, such a series is only asymptotic (e.g., Papers I, V). Hereafter, we note
 the growing mode of the linear density contrast at the time of interest, where we compute
the growing mode of the linear density contrast at the time of interest, where we compute
 (i.e., to simplify notations we do not write explicitly the time dependence). Second, in order to perform the average in Eq. (2) we need the weight which is associated with all possible fields
(i.e., to simplify notations we do not write explicitly the time dependence). Second, in order to perform the average in Eq. (2) we need the weight which is associated with all possible fields
 .
In other words, we must specify the probability distribution of the random field
.
In other words, we must specify the probability distribution of the random field
 .
Thus, the first point expresses the physics of gravitational interactions while the second point describes the initial conditions of the system.
.
Thus, the first point expresses the physics of gravitational interactions while the second point describes the initial conditions of the system.
In the case of Gaussian initial conditions, the statistics of the random field
 are fully defined by the two-point correlation:
are fully defined by the two-point correlation:
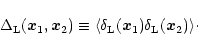 |
(5) |
The kernel
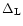 is symmetric, homogeneous and isotropic:
is symmetric, homogeneous and isotropic:
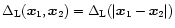 .
It is convenient to express
.
It is convenient to express
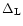 in terms of the power-spectrum P(k) of the linear density fluctuations. To do so, we define the Fourier transform of the density field as:
in terms of the power-spectrum P(k) of the linear density fluctuations. To do so, we define the Fourier transform of the density field as:
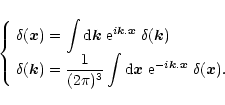 |
(6) |
Next, we define the Fourier transform of the kernel
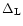 by the property:
by the property:
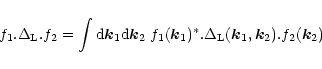 |
(7) |
for any real fields f1 and f2, where we introduced the short-hand notation:
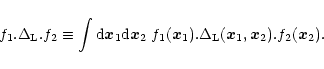 |
(8) |
Using Eq. (6) this implies:
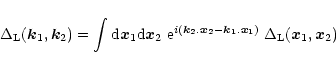 |
(9) |
which gives:
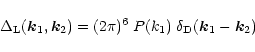 |
(10) |
where we defined the power-spectrum P(k) of the linear density contrast by:
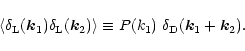 |
(11) |
Finally, the inverse
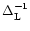 of the kernel
of the kernel
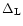 is (see Paper II):
is (see Paper II):
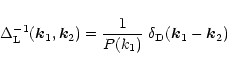 |
(12) |
which implies that
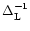 is positive definite since we have:
is positive definite since we have:
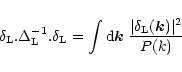 |
(13) |
where we used
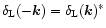 for real fields
for real fields
 ,
see Eq. (6).
,
see Eq. (6).
Thus, for Gaussian initial conditions the statistical properties of the random field
 are determined by the kernel
are determined by the kernel
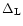 given in Eq. (10) (or equivalently by
given in Eq. (10) (or equivalently by
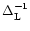 given in Eq. (12)). In particular, the average over the initial conditions in Eq. (2) can be written as the path-integral:
given in Eq. (12)). In particular, the average over the initial conditions in Eq. (2) can be written as the path-integral:
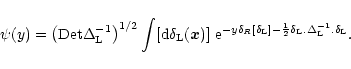 |
(14) |
This expression merely means that in order to compute the average
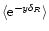 we simply need to sum up the contributions of all possible linear density fields
we simply need to sum up the contributions of all possible linear density fields
 to which we associate a Gaussian weight which is proportional to
to which we associate a Gaussian weight which is proportional to
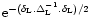 .
The normalization factor
.
The normalization factor
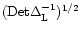 ensures that
ensures that 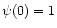 ,
as implied by the definition (2). Here
,
as implied by the definition (2). Here
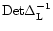 is the determinant of the kernel
is the determinant of the kernel
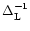 .
Thus, Eq. (14) yields an explicit expression for the Laplace transform
.
Thus, Eq. (14) yields an explicit expression for the Laplace transform  (though it may be difficult to obtain numerical results from such a path-integral). This provides in turn the pdf
(though it may be difficult to obtain numerical results from such a path-integral). This provides in turn the pdf
 through the inverse transform (3). In Paper II we showed how to get the generating function
through the inverse transform (3). In Paper II we showed how to get the generating function  from Eq. (14) in the limit
from Eq. (14) in the limit
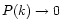 (i.e. for small rms density fluctuations) using a steepest-descent method. In the next section, we apply this method to a closely related non-Gaussian model.
(i.e. for small rms density fluctuations) using a steepest-descent method. In the next section, we apply this method to a closely related non-Gaussian model.
3 Generalization of the Gaussian weight
In this section, we describe a non-Gaussian model which can be seen as the simplest generalization of the Gaussian scenario. This model is not derived from physical principles. It simply provides a phenomenological tool which can describe initial conditions such that the tails of the linear pdf
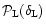 of the density field are of the form
of the density field are of the form
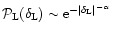 ,
where
,
where 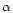 is no longer restricted to 2 (as in the Gaussian case). In addition, it allows us to show on a simple example the power of the method we developed in Paper II and how it can be applied to non-Gaussian initial conditions.
is no longer restricted to 2 (as in the Gaussian case). In addition, it allows us to show on a simple example the power of the method we developed in Paper II and how it can be applied to non-Gaussian initial conditions.
3.1 A non-Gaussian model
In the case of Gaussian primordial density fluctuations, the average involved in the definition (2) of the generating function  (i.e. the Laplace transform of the pdf
(i.e. the Laplace transform of the pdf
 )
is simply given by the Gaussian weight
)
is simply given by the Gaussian weight
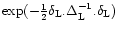 in the path-integral (14) which takes the average of
in the path-integral (14) which takes the average of
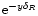 over all possible initial states, as we recalled in the previous section. A straightforward generalization of the Gaussian case (14) is to modify this weight. Thus, one can consider the case where the average over the field
over all possible initial states, as we recalled in the previous section. A straightforward generalization of the Gaussian case (14) is to modify this weight. Thus, one can consider the case where the average over the field
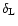 is given by:
is given by:
![\begin{displaymath}%
\psi(y) = {\cal N}\int [{\rm d}\delta_{\rm L}({\vec x})] \; {\rm e}^{-y \delta_{R}- W[\delta_{\rm L}]}
\end{displaymath}](/articles/aa/full/2002/05/aa1670/img56.gif) |
(15) |
with:
![\begin{displaymath}%
W[\delta_{\rm L}] = \sum_{i=1}^{N} \lambda_i \; (\delta_{\rm L}. \Delta_{\rm W}^{-1} . \delta_{\rm L})^{\alpha_i/2}
\end{displaymath}](/articles/aa/full/2002/05/aa1670/img57.gif) |
(16) |
where
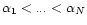 and
and
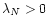 .
Here
.
Here 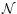 is a normalization constant, so that
is a normalization constant, so that 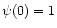 ,
and we still take the kernel
,
and we still take the kernel
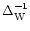 to be of the form (12) hence
to be of the form (12) hence
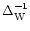 is positive definite. We also define a quantity
is positive definite. We also define a quantity
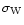 in terms of
in terms of
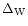 by:
by:
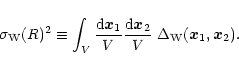 |
(17) |
However, contrary to the Gaussian case we now have:
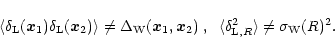 |
(18) |
The form (15) corresponds to a large density contrast tail of the form
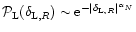 for the linear density field.
for the linear density field.
In order to compute the Laplace transform  we simply follow the steps of the calculation developed in Paper II. Thus, we first define a new generating function
we simply follow the steps of the calculation developed in Paper II. Thus, we first define a new generating function
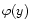 through:
through:
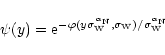 |
(19) |
in order to factorize the amplitude of the kernel
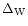 .
This yields from Eq. (15):
.
This yields from Eq. (15):
![\begin{displaymath}%
{\rm e}^{-\varphi(y,\sigma_{\rm W})/\sigma_{\rm W}^{\alpha_...
...x})] \; {\rm e}^{- S_{\rm W} /\sigma_{\rm W}^{\alpha_{\rm N}}}
\end{displaymath}](/articles/aa/full/2002/05/aa1670/img69.gif) |
(20) |
where the "action''
![$S_{\rm W}[\delta_{\rm L}]$](/articles/aa/full/2002/05/aa1670/img70.gif) is given by:
is given by:
![\begin{displaymath}%
S_{\rm W}[\delta_{\rm L}] = y \; \delta_{R}[\delta_{\rm L}]...
..._{\rm L}. \Delta_{\rm W}^{-1} . \delta_{\rm L})^{\alpha_i/2} .
\end{displaymath}](/articles/aa/full/2002/05/aa1670/img71.gif) |
(21) |
The quasi-linear regime corresponds to the limit
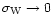 at fixed y. Then, we see that all terms with
at fixed y. Then, we see that all terms with
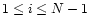 in the action
in the action 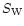 in Eq. (21) vanish as
in Eq. (21) vanish as
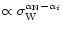 since
since
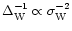 ,
see Eq. (17). Therefore, in the limit
,
see Eq. (17). Therefore, in the limit
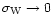 we are left with the action
we are left with the action
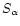 :
:
![\begin{displaymath}%
S_{\alpha}[\delta_{\rm L}] = y \; \delta_{R}[\delta_{\rm L}...
...elta_{\rm L}. \Delta_{\rm W}^{-1} . \delta_{\rm L})^{\alpha/2}
\end{displaymath}](/articles/aa/full/2002/05/aa1670/img78.gif) |
(22) |
with
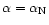 and we normalized
and we normalized
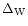 such that
such that
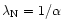 .
The fact that the terms with
.
The fact that the terms with
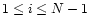 disappear in the quasi-linear limit expresses the fact that this limit is actually a "rare-event limit''. Indeed, as seen in Paper II for the Gaussian case (and this remains valid here) a finite y corresponds to a finite density contrast. Then, in the limit
disappear in the quasi-linear limit expresses the fact that this limit is actually a "rare-event limit''. Indeed, as seen in Paper II for the Gaussian case (and this remains valid here) a finite y corresponds to a finite density contrast. Then, in the limit
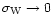 these finite density contrasts (even though small) become very rare events. On the other hand, the tails of the functional distribution
these finite density contrasts (even though small) become very rare events. On the other hand, the tails of the functional distribution
![${\cal P}[\delta_{\rm L}]$](/articles/aa/full/2002/05/aa1670/img81.gif) defined by the weight
defined by the weight
![$W[\delta_{\rm L}]$](/articles/aa/full/2002/05/aa1670/img82.gif) are governed by the highest power in Eq. (16). This implies that in the quasi-linear limit the only relevant term is the highest power
are governed by the highest power in Eq. (16). This implies that in the quasi-linear limit the only relevant term is the highest power
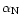 .
Note that we can expect the validity of the quasi-linear limit to extend to larger values of
.
Note that we can expect the validity of the quasi-linear limit to extend to larger values of
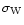 in the case N=1 than for N>1. Indeed, in this latter case we can expect the terms
in the case N=1 than for N>1. Indeed, in this latter case we can expect the terms
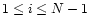 to make a significant contribution for
to make a significant contribution for
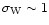 which is not taken into account at all by the quasi-linear limit.
which is not taken into account at all by the quasi-linear limit.
3.2 Steepest-descent method
The action
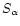 is independent of the normalization of the kernel
is independent of the normalization of the kernel
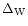 .
Thus, as in Paper II we can apply the steepest-descent method in the limit
.
Thus, as in Paper II we can apply the steepest-descent method in the limit
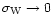 .
Indeed, it is clear than in this limit the path-integral (20) is dominated by the global minimum of the action
.
Indeed, it is clear than in this limit the path-integral (20) is dominated by the global minimum of the action
![$S_{\alpha}[\delta_{\rm L}]$](/articles/aa/full/2002/05/aa1670/img85.gif) while the contributions from other points
while the contributions from other points
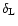 are exponentially damped. Then, the steepest-descent method yields asymptotically exact results in this limit. We briefly describe below the main steps of this steepest-descent method. Since the derivation is very close to the one performed in Paper II for the Gaussian case we refer the reader to that paper for the details of the calculation. Note that the Gaussian case actually corresponds to
are exponentially damped. Then, the steepest-descent method yields asymptotically exact results in this limit. We briefly describe below the main steps of this steepest-descent method. Since the derivation is very close to the one performed in Paper II for the Gaussian case we refer the reader to that paper for the details of the calculation. Note that the Gaussian case actually corresponds to 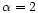 .
.
In order to apply the steepest-descent approximation we first need to find the global minimum of the action
![$S_{\alpha}[\delta_{\rm L}]$](/articles/aa/full/2002/05/aa1670/img85.gif) .
The condition which expresses that the point
.
The condition which expresses that the point
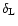 is an extremum (or a saddle-point) is:
is an extremum (or a saddle-point) is:
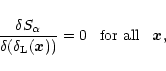 |
(23) |
where
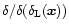 is the functional derivative with respect to
is the functional derivative with respect to
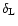 at the point
at the point 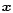 .
This constraint also writes:
.
This constraint also writes:
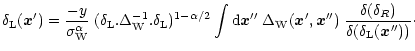 |
|
|
(24) |
Thus, we obtain exactly the same profile for the saddle-point as in the Gaussian case. Indeed, we can see that
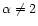 only modifies a numerical multiplicative factor in the r.h.s. of Eq. (24) (i.e. independent of
only modifies a numerical multiplicative factor in the r.h.s. of Eq. (24) (i.e. independent of 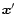 and
and
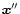 )
which could formally be absorbed into y through
)
which could formally be absorbed into y through
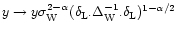 .
Then, as in Paper II we obtain a spherically symmetric saddle-point. Note that the existence of a spherical saddle-point could be expected a priori, since the initial conditions are homogeneous and isotropic and we study the density contrast within spherical cells. Therefore, the very problem we investigate is spherically symmetric. However, a priori this spherical saddle-point is not necessarily the global minimum of the action (in full generality it might as well be a maximum). This will need to be checked a posteriori.
.
Then, as in Paper II we obtain a spherically symmetric saddle-point. Note that the existence of a spherical saddle-point could be expected a priori, since the initial conditions are homogeneous and isotropic and we study the density contrast within spherical cells. Therefore, the very problem we investigate is spherically symmetric. However, a priori this spherical saddle-point is not necessarily the global minimum of the action (in full generality it might as well be a maximum). This will need to be checked a posteriori.
The fact that we obtain a spherical saddle-point greatly simplifies the problem since it means that this point
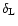 is described by the well-known spherical collapse solution of the gravitational dynamics. This reads:
is described by the well-known spherical collapse solution of the gravitational dynamics. This reads:
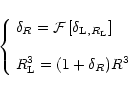 |
(25) |
where the function
![${\cal F}[\delta_{{\rm L},R_{\rm L}}]$](/articles/aa/full/2002/05/aa1670/img95.gif) is given by the usual spherical collapse solution of the equations of motion (e.g., Peebles 1980; Paper II). The second equation in (25) merely expresses the conservation of mass and the fact that the matter enclosed within the radius R in the actual non-linear density field actually comes from a Lagrangian comoving radius
is given by the usual spherical collapse solution of the equations of motion (e.g., Peebles 1980; Paper II). The second equation in (25) merely expresses the conservation of mass and the fact that the matter enclosed within the radius R in the actual non-linear density field actually comes from a Lagrangian comoving radius 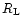 ,
for a spherical initial condition. The Eq. (25) provides the functional
,
for a spherical initial condition. The Eq. (25) provides the functional
![$\delta_{R}[\delta_{\rm L}({\vec x})]$](/articles/aa/full/2002/05/aa1670/img30.gif) for spherical states
for spherical states
 .
As shown in Paper II this is sufficient to derive the spherical saddle-point which obeys the condition (24). Using the results of Paper II with the substitution
.
As shown in Paper II this is sufficient to derive the spherical saddle-point which obeys the condition (24). Using the results of Paper II with the substitution
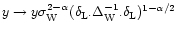 we eventually obtain:
we eventually obtain:
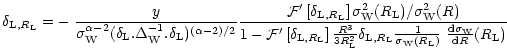 |
|
|
(26) |
together with:
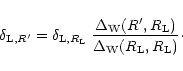 |
(27) |
These two equations fully define the spherically symmetric saddle-point
 .
The implicit Eq. (26) determines
.
The implicit Eq. (26) determines
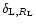 while the radial profile of this initial state is given by Eq. (27). In Eq. (27) we introduced the spherically averaged kernel
while the radial profile of this initial state is given by Eq. (27). In Eq. (27) we introduced the spherically averaged kernel
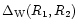 defined by:
defined by:
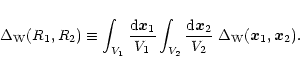 |
(28) |
As in Paper II these equations can be simplified by introducing the functions
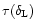 and
and
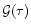 defined by:
defined by:
![\begin{displaymath}%
\tau(\delta_{\rm L}) \equiv \frac{- \; \delta_{\rm L}\; \si...
..._{\rm W} \left[ (1+{\cal F}[\delta_{\rm L}])^{1/3} R \right] }
\end{displaymath}](/articles/aa/full/2002/05/aa1670/img104.gif) |
(29) |
and:
![\begin{displaymath}%
{\cal G}(\tau) \equiv {\cal F}\left[\delta_{\rm L}(\tau)\right] = \delta_{R}
\end{displaymath}](/articles/aa/full/2002/05/aa1670/img105.gif) |
(30) |
where
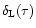 is defined by Eq. (29). Using Eq. (29), we note that for a power-law "power-spectrum''
is defined by Eq. (29). Using Eq. (29), we note that for a power-law "power-spectrum''
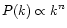 we have
we have
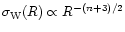 so that Eq. (30) simplifies to:
so that Eq. (30) simplifies to:
![\begin{displaymath}%
{\cal G}(\tau) = {\cal F}\left[ - \tau \; (1+{\cal G}[\tau])^{-(n+3)/6} \right].
\end{displaymath}](/articles/aa/full/2002/05/aa1670/img109.gif) |
(31) |
Note however that in this non-Gaussian case the "power-spectrum'' P(k) does not obey Eq. (11). Nevertheless, it still provides a measure of the power associated with the wavenumber k.
Finally, the limiting generating function
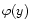 defined by
defined by
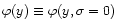 is given by the value of the action
is given by the value of the action
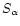 at this minimum which yields the implicit system:
at this minimum which yields the implicit system:
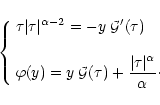 |
(32) |
Of course, this result is similar to the Gaussian case which can be recovered by taking 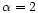 .
Note that Eq. (32) has only been derived for real y (hence
.
Note that Eq. (32) has only been derived for real y (hence 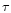 is real), so that
is real), so that 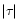 is the absolute value of
is the absolute value of 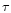 .
.
Thus, the steepest-descent method allows us to compute the Laplace transform  in the quasi-linear regime through Eq. (32) which yields
in the quasi-linear regime through Eq. (32) which yields  as in Eq. (19). This will give the pdf
as in Eq. (19). This will give the pdf
 through Eq. (3). However, we first need to check that the spherical saddle-point defined by Eq. (26) and Eq. (27) is the global minimum of the action
through Eq. (3). However, we first need to check that the spherical saddle-point defined by Eq. (26) and Eq. (27) is the global minimum of the action
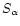 .
For small positive y this can be rigorously proved as for the Gaussian case, using the fact that the kernel
.
For small positive y this can be rigorously proved as for the Gaussian case, using the fact that the kernel
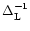 is positive definite. We shall not repeat this discussion here (see Sect. 3.4 in Paper II). For negative y this cannot be proved as it may actually happen that the spherical saddle-point is only a local minimum. This also occurs in the Gaussian case for a power-spectrum with n<0. This case is discussed in great details in Paper II where we show that the steepest-descent method remains useful but requires a careful justification. Since the same discussion can be applied to the non-Gaussian model we investigate here we refer the reader to Paper II for a description of such cases and we shall only give a brief comment on this point in the next section.
is positive definite. We shall not repeat this discussion here (see Sect. 3.4 in Paper II). For negative y this cannot be proved as it may actually happen that the spherical saddle-point is only a local minimum. This also occurs in the Gaussian case for a power-spectrum with n<0. This case is discussed in great details in Paper II where we show that the steepest-descent method remains useful but requires a careful justification. Since the same discussion can be applied to the non-Gaussian model we investigate here we refer the reader to Paper II for a description of such cases and we shall only give a brief comment on this point in the next section.
3.3 Geometrical construction
As for the Gaussian case studied in Paper II we can give a geometrical construction of the generating function
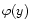 defined by Eq. (32). Indeed, this latter expression can also be written:
defined by Eq. (32). Indeed, this latter expression can also be written:
![\begin{displaymath}%
\varphi(y) = \min_{\tau} \left[ y \; {\cal G}(\tau) + \frac{\vert\tau\vert^{\alpha}}{\alpha} \right]\cdot
\end{displaymath}](/articles/aa/full/2002/05/aa1670/img114.gif) |
(33) |
The minimum which appears in this expression merely expresses the fact that by sheer definition of the steepest-descent method the generating function
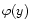 is governed by the global minimum of the action
is governed by the global minimum of the action
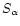 .
.
Then, we see that the geometrical construction displayed in Fig. 4 in Paper II still applies to this non-Gaussian case, with the modification that the parabola
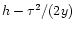 are replaced by the curves
are replaced by the curves
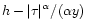 .
That is, the minimum point
.
That is, the minimum point 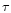 which yields
which yields
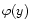 in Eq. (33) is given by the first contact of the curve
in Eq. (33) is given by the first contact of the curve
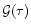 with the curves
with the curves
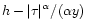 of varying height h. For y>0 we start from below at
of varying height h. For y>0 we start from below at 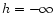 while for y<0 we start from above at
while for y<0 we start from above at  .
.
As in the Gaussian case, we find that for some values of n the action
 has no global minimum. This can be seen from the geometrical construction shown in Fig. 4 or simply from Eq. (33). Indeed, as noticed in Paper II from Eq. (31) we have the following asymptotic behaviour for
has no global minimum. This can be seen from the geometrical construction shown in Fig. 4 or simply from Eq. (33). Indeed, as noticed in Paper II from Eq. (31) we have the following asymptotic behaviour for
 :
:
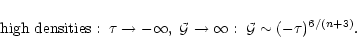 |
(34) |
Using this expression we see that for y<0 the term in the brackets in the r.h.s. of Eq. (33) is not bounded from below if
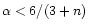 ,
since in this case it goes to
,
since in this case it goes to 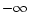 for
for
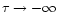 .
For the Gaussian case this occurs for n<0. However, as explained in Paper II the steepest-descent method developed in Sect. 3.2 remains useful and the pdf
.
For the Gaussian case this occurs for n<0. However, as explained in Paper II the steepest-descent method developed in Sect. 3.2 remains useful and the pdf
 is still governed by the spherical saddle-point defined by Eqs. (26) and (27). This can be seen by the following remark. If we consider the quantity
is still governed by the spherical saddle-point defined by Eqs. (26) and (27). This can be seen by the following remark. If we consider the quantity
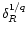 rather than
rather than
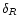 ,
where q is an odd integer, we can again apply the steepest-descent method which yields the associated generating function
,
where q is an odd integer, we can again apply the steepest-descent method which yields the associated generating function
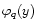 as in Eq. (33). However, the function
as in Eq. (33). However, the function
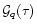 is now given by
is now given by
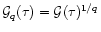 .
Then, if we choose a sufficiently large value for q the behaviour of the r.h.s. bracket in Eq. (33) is dominated by the term
.
Then, if we choose a sufficiently large value for q the behaviour of the r.h.s. bracket in Eq. (33) is dominated by the term
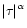 at large
at large 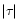 so that the action now exhibits a global minimum. Of course, this point is still the spherical saddle-point we obtained in Sect. 3.2 (since the initial conditions
so that the action now exhibits a global minimum. Of course, this point is still the spherical saddle-point we obtained in Sect. 3.2 (since the initial conditions
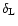 which give rise to a fixed value of
which give rise to a fixed value of
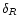 do not depend on whether we study
do not depend on whether we study
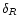 itself or
itself or
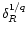 !). Then the pdf
!). Then the pdf
 could be recovered from
could be recovered from
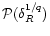 through a mere change of variable. This implies in turn that the pdf
through a mere change of variable. This implies in turn that the pdf
 is still governed by the standard spherical saddle-point, even though the latter is no longer the global minimum of the action. However, as described in Paper II the treatment of this case requires some additional care and it is actually associated with a break-up of perturbative theory.
is still governed by the standard spherical saddle-point, even though the latter is no longer the global minimum of the action. However, as described in Paper II the treatment of this case requires some additional care and it is actually associated with a break-up of perturbative theory.
3.4 Calculation of the pdf
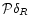
Finally, we describe how to compute the pdf
 itself from the results obtained in Sect. 3.2. We consider the case n=-1 and
itself from the results obtained in Sect. 3.2. We consider the case n=-1 and 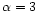 where the action
where the action
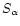 always shows a global minimum. Then, the Laplace transform
always shows a global minimum. Then, the Laplace transform  is fully defined by the generating function
is fully defined by the generating function
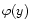 given by Eq. (32).
given by Eq. (32).
In order to compute the pdf from Eq. (32) we simply use the inverse relation (3) which yields:
![\begin{displaymath}%
{\cal P}(\delta_{R}) = \int_{-i\infty}^{+i\infty}\frac{{\rm...
... {\rm e}^{[y \delta_{R}- \varphi(y)]/\sigma_{\rm W}^{\alpha}}.
\end{displaymath}](/articles/aa/full/2002/05/aa1670/img129.gif) |
(35) |
Then, to perform the integration over y we need the analytic continuation of
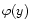 over the complex plane. Indeed, note that Eqs. (32) and (33) were actually derived for real y (hence
over the complex plane. Indeed, note that Eqs. (32) and (33) were actually derived for real y (hence 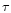 was real). In particular, we must continue the absolute value
was real). In particular, we must continue the absolute value 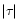 over the complex plane. Moreover, we need to specify the integration path over y (since
over the complex plane. Moreover, we need to specify the integration path over y (since
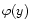 will usually be singular at the origin). First, the integration path starts from the real axis at the saddle-point
will usually be singular at the origin). First, the integration path starts from the real axis at the saddle-point
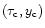 given by:
given by:
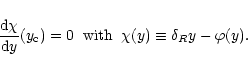 |
(36) |
From Eq. (32) we have:
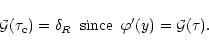 |
(37) |
Thus, as for the Gaussian case, we see from Eq. (30) that the triplet
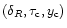 is also the triplet
is also the triplet
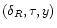 we obtained in Sect. 3.2 to get
we obtained in Sect. 3.2 to get
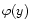 .
This simply means that
.
This simply means that
 at the point
at the point
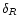 is governed by the neighbourhood of the saddle-point
is governed by the neighbourhood of the saddle-point
 obtained in Sect. 3.2, which obeys
obtained in Sect. 3.2, which obeys
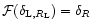 .
This is actually quite natural. Then, we need to continue the function
.
This is actually quite natural. Then, we need to continue the function
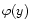 over the complex plane from the neighbourhood of the point
over the complex plane from the neighbourhood of the point 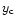 on the real axis. Thus, if
on the real axis. Thus, if
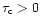 (i.e.
(i.e.
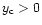 )
we replace
)
we replace 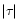 in Eq. (32) by
in Eq. (32) by 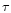 ,
while if
,
while if
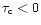 (i.e.
(i.e.
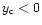 )
we replace
)
we replace 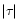 by
by 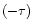 .
Then, we have the usual analytic continuation of the power-laws
.
Then, we have the usual analytic continuation of the power-laws
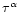 or
or
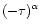 .
The argument of these power-laws is real positive at the starting point
.
The argument of these power-laws is real positive at the starting point
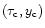 .
This provides the analytic continuation of the generating function
.
This provides the analytic continuation of the generating function
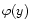 .
The function
.
The function
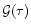 is also analytic around the real axis because the spherical collapse solution
is also analytic around the real axis because the spherical collapse solution
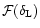 can be expressed in terms of analytic functions (e.g., trigonometric or hyperbolic functions for a critical density universe).
can be expressed in terms of analytic functions (e.g., trigonometric or hyperbolic functions for a critical density universe).
Next, the integration path in the complex plane follows the steepest-descent contour which runs through the saddle-point 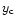 .
It is given by the constraint
.
It is given by the constraint
 and it is orthogonal to the real axis at the point
and it is orthogonal to the real axis at the point 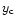 .
This path is also symmetric about the real axis which implies that the result for
.
This path is also symmetric about the real axis which implies that the result for
 is real. Note that in the quasi-linear limit
is real. Note that in the quasi-linear limit
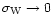 the contributions to the integral (35) only come from an infinitesimal neighbourhood of the saddle-point
the contributions to the integral (35) only come from an infinitesimal neighbourhood of the saddle-point
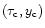 around the real axis.
around the real axis.
Usually the function
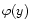 is not regular at the origin since we have
is not regular at the origin since we have
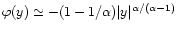 for small real y. Then, the pdf
for small real y. Then, the pdf
 is not analytic at
is not analytic at
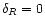 and the moments of the pdf cannot be recovered from the expansion (4). This is not the case for Gaussian initial conditions where both
and the moments of the pdf cannot be recovered from the expansion (4). This is not the case for Gaussian initial conditions where both
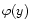 and
and
 are regular at the origin.
are regular at the origin.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{MS1670f1.eps}\end{figure}](/articles/aa/full/2002/05/aa1670/Timg148.gif) |
Figure 1:
The pdf
 for n=-1,
for n=-1,
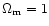 , ,
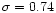 and
and 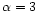 .
This corresponds to .
This corresponds to
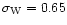 .
The solid line shows the theoretical prediction from (32). The dashed-line displays the linear pdf .
The solid line shows the theoretical prediction from (32). The dashed-line displays the linear pdf
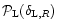 of the linearly evolved density field. The dotted-lines show the linear and non-linear pdfs obtained for Gaussian initial conditions with the same linear rms density fluctuation
of the linearly evolved density field. The dotted-lines show the linear and non-linear pdfs obtained for Gaussian initial conditions with the same linear rms density fluctuation 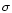 (the non-linear pdf is the asymmetric curve with the extended high-density tail).
(the non-linear pdf is the asymmetric curve with the extended high-density tail). |
| Open with DEXTER |
As an example, we show in Fig. 1 the pdf
 for the case
for the case 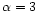 and n=-1 (solid line). We also have
and n=-1 (solid line). We also have
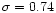 where
where
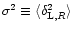 is the rms density fluctuation. Since
is the rms density fluctuation. Since
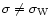 we numerically compute
we numerically compute 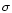 from the second moment of the linear pdf
from the second moment of the linear pdf
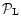 .
Indeed, the steepest-descent method developed in Sect. 3.2 also yields the linear pdf
.
Indeed, the steepest-descent method developed in Sect. 3.2 also yields the linear pdf
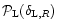 of the linearly-evolved density field. In this case we have
of the linearly-evolved density field. In this case we have
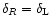 and
and
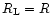 ,
hence we simply need to take
,
hence we simply need to take
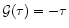 in Eq. (32) (of course, for
in Eq. (32) (of course, for 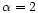 this gives back the Gaussian). The non-linear evolution of the density field increases the value of
this gives back the Gaussian). The non-linear evolution of the density field increases the value of
 at large positive
at large positive
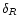 (it actually spreads the linear pdf towards larger value of the density) as in the Gaussian case but the cutoff remains much sharper. It also induces a cutoff at low densities
(it actually spreads the linear pdf towards larger value of the density) as in the Gaussian case but the cutoff remains much sharper. It also induces a cutoff at low densities
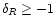 which expresses the fact that the actual density
which expresses the fact that the actual density 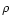 is positive.
is positive.
For comparison, we also display in Fig. 1 the results we obtain for Gaussian initial conditions with the same linear variance 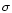 (dotted lines). These curves were derived in Paper II. As could be anticipated from Eq. (15) the large density contrast cutoff of the linear pdf is much sharper than for the Gaussian case: it goes as
(dotted lines). These curves were derived in Paper II. As could be anticipated from Eq. (15) the large density contrast cutoff of the linear pdf is much sharper than for the Gaussian case: it goes as
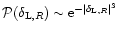 since here we take
since here we take 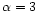 .
Moreover, we can check that for the actual non-linear pdfs this trend remains valid. More precisely, as shown in Paper II the high-density tail of the non-linear pdf for Gaussian initial conditions is of the form:
.
Moreover, we can check that for the actual non-linear pdfs this trend remains valid. More precisely, as shown in Paper II the high-density tail of the non-linear pdf for Gaussian initial conditions is of the form:
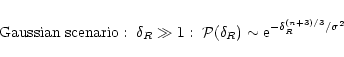 |
(38) |
while for non-Gaussian initial conditions we obtain:
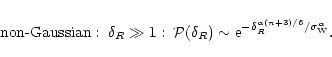 |
(39) |
These behaviours are obtained from Eqs. (32), (35) and (37) which yield:
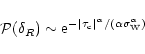 |
(40) |
while the asymptotic behaviour of
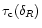 for large
for large
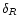 is given by Eqs. (34) and (37).
is given by Eqs. (34) and (37).
As noticed above, the non-Gaussian model (16) is not derived from a physical scenario of the primordial universe. It should be viewed as a simple model to describe initial density fluctuations which exhibit a non-Gaussian tail. Then, the analysis performed in the previous sections shows how one may derive in a rigorous manner the gravitational dynamics of density fluctuations in the quasi-linear regime. Moreover, we can expect the form (39) of the high-density tail to apply to any model which obeys
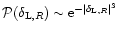 at large densities, whatever the details of the model. In fact, we have shown that in the quasi-linear regime the tail (39) (actually the generating function
at large densities, whatever the details of the model. In fact, we have shown that in the quasi-linear regime the tail (39) (actually the generating function
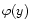 itself !) is common to all models of the class described by Eq. (16) with
itself !) is common to all models of the class described by Eq. (16) with
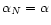 .
.
In practice, since observations have not shown any deviations from Gaussianity so far, the parameter 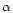 is constrained to be close to 2 (the Gaussian value). Note that this family of models presents the advantage of containing the usual Gaussian scenario as a particular case.
is constrained to be close to 2 (the Gaussian value). Note that this family of models presents the advantage of containing the usual Gaussian scenario as a particular case.
4 An isocurvature CDM model
In addition to generalized non-Gaussian models as the one studied in Sect. 3 which are rather ad-hoc tools, there exist some specific non-Gaussian models which arise from a physically motivated description of the primordial universe. These scenarios are of great interest as they could provide a reasonable alternative to the standard simple inflationary model. Moreover, it is prudent not to disregard a priori sensible models of structure formation in view of the rather indirect character of the probes of the early universe which are available to us.
4.1 Initial conditions
Thus, in this section we consider a specific isocurvature cold dark matter model which was presented in Peebles (1999a). This is an inflationary scenario which involves three scalar fields and it gives birth to non-Gaussian isocurvature CDM fluctuations. We refer the reader to Peebles (1999a) for a description of the physical processes which give rise to this scenario. Then, at the end of inflation (at time 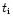 )
the CDM mass distribution is (Peebles 1999a):
)
the CDM mass distribution is (Peebles 1999a):
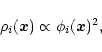 |
(41) |
where
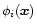 is a Gaussian random field with zero mean and power-spectrum
is a Gaussian random field with zero mean and power-spectrum
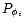 :
:
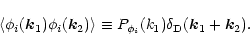 |
(42) |
On the scales of interest for structure formation we have:
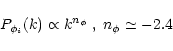 |
(43) |
while below the coherence length 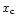 (i.e. for
(i.e. for
 )
the power-spectrum decreases as
)
the power-spectrum decreases as
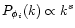 with s<-3. This coherence length ensures that
with s<-3. This coherence length ensures that
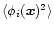 is finite, as required by Eq. (41). In the case of the model described in Peebles (1999a) we have
is finite, as required by Eq. (41). In the case of the model described in Peebles (1999a) we have
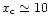 pc. In the linear regime below the horizon the CDM density perturbations grow as
pc. In the linear regime below the horizon the CDM density perturbations grow as
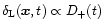 (we only keep the growing mode) hence we write:
(we only keep the growing mode) hence we write:
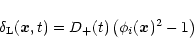 |
(44) |
where we normalized
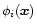 by
by
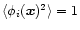 and the growing mode by
D+(ti)=1. Note that in Eq. (44) and in the following we only consider "small'' comoving scales
and the growing mode by
D+(ti)=1. Note that in Eq. (44) and in the following we only consider "small'' comoving scales
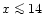 Mpc, where the isocurvature CDM transfer function is close to unity (Peebles 1999b). On larger scales the density fluctuations are damped with respect to Eq. (44) and we should take into account the decrease of the transfer function. Since we are interested in the statistics of the density field at an arbitrary time t it is convenient to rescale the Gaussian field
Mpc, where the isocurvature CDM transfer function is close to unity (Peebles 1999b). On larger scales the density fluctuations are damped with respect to Eq. (44) and we should take into account the decrease of the transfer function. Since we are interested in the statistics of the density field at an arbitrary time t it is convenient to rescale the Gaussian field 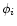 .
Thus, we define
.
Thus, we define
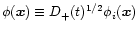 so that Eq. (44) now reads:
so that Eq. (44) now reads:
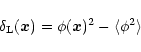 |
(45) |
at the redshift of interest. The power-spectrum
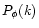 is still of the form (43). Note that the relation between the fields
is still of the form (43). Note that the relation between the fields
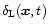 and
and
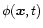 depends explicitly on time through the last term in Eq. (45) (to simplify notations we usually do not write explicitly the time dependence of the various random fields). Indeed, we must recall here that
depends explicitly on time through the last term in Eq. (45) (to simplify notations we usually do not write explicitly the time dependence of the various random fields). Indeed, we must recall here that
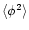 is not the spatial average of
is not the spatial average of
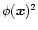 but the mean over all realizations of the Gaussian random field
but the mean over all realizations of the Gaussian random field 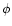 .
Therefore, it is independent of the peculiar realization
.
Therefore, it is independent of the peculiar realization 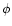 which gives rise to a given linear density field through Eq. (45) (even though by ergodicity both averages happen to be equal). We define the two-point correlation of the field
which gives rise to a given linear density field through Eq. (45) (even though by ergodicity both averages happen to be equal). We define the two-point correlation of the field
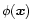 by:
by:
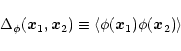 |
(46) |
and the linear variance over the scale R by:
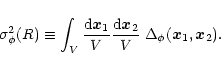 |
(47) |
Note that Eq. (46) also implies that we can define the average
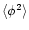 by:
by:
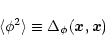 |
(48) |
which does not depend on 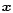 since the initial conditions are invariant through translations. From Eq. (45) and the fact that
since the initial conditions are invariant through translations. From Eq. (45) and the fact that
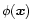 is Gaussian one obtains the variance
is Gaussian one obtains the variance 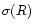 of the linearly-evolved density contrast as:
of the linearly-evolved density contrast as:
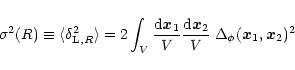 |
(49) |
since the two-point correlation
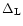 of the linear density field is given by:
of the linear density field is given by:
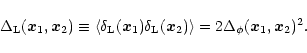 |
(50) |
From Eqs. (47) and (49) we see that for
 we get
we get
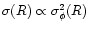 and the slope n of the linear power-spectrum P(k) of the density fluctuations is related to
and the slope n of the linear power-spectrum P(k) of the density fluctuations is related to 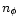 by:
by:
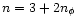 .
This implies
.
This implies
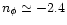 as in Eq. (43) in order to match observational constraints (Peebles 1999b). For numerical calculations we shall use:
as in Eq. (43) in order to match observational constraints (Peebles 1999b). For numerical calculations we shall use:
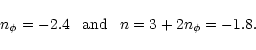 |
(51) |
4.2 Laplace transform
We again define the generating function  as in Eq. (2) but the Gaussian average over
as in Eq. (2) but the Gaussian average over
 which appeared in Eq. (14) must now be replaced by a Gaussian average over
which appeared in Eq. (14) must now be replaced by a Gaussian average over
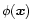 :
:
![\begin{displaymath}%
\psi(y) = {\cal N}\int [{\rm d}\phi({\vec x})] \; {\rm e}^{...
...elta_{R}[\phi] -\frac{1}{2} \phi . \Delta_{\phi}^{-1} . \phi}.
\end{displaymath}](/articles/aa/full/2002/05/aa1670/img200.gif) |
(52) |
Thus, our goal is now to estimate the Laplace transform  .
To do so, we shall not introduce a rescaled generating function
.
To do so, we shall not introduce a rescaled generating function
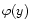 as in Eq. (19) and we work directly with
as in Eq. (19) and we work directly with  .
First, using Eq. (45) it is convenient to introduce the linear density field
.
First, using Eq. (45) it is convenient to introduce the linear density field
 into the expression (52) through the Dirac functional
into the expression (52) through the Dirac functional
![$\delta_{\rm D}[\langle\phi^2 \rangle+\delta_{\rm L}({\vec x}) - \phi({\vec x})^2]$](/articles/aa/full/2002/05/aa1670/img201.gif) :
:
![$\displaystyle %
\psi(y) = \int [{\rm d}\phi({\vec x})] [{\rm d}\delta_{\rm L}({...
...^{-y \delta_{R}[\delta_{\rm L}] -\frac{1}{2} \phi . \Delta_{\phi}^{-1} . \phi}.$](/articles/aa/full/2002/05/aa1670/img202.gif) |
|
|
(53) |
Here and in the following we do not write the normalization constant of the path-integral (it will be recovered in the final expressions). Then, using the integral representation of the Dirac functional we obtain:
![$\displaystyle %
\psi(y) = \int [{\rm d}\phi({\vec x})] [{\rm d}\delta_{\rm L}({...
... \rangle+\delta_{\rm L}- \phi^2) -\frac{1}{2} \phi . \Delta_{\phi}^{-1} . \phi}$](/articles/aa/full/2002/05/aa1670/img203.gif) |
|
|
(54) |
where
 is an auxiliary real field. Note that the exponent is actually quadratic over
is an auxiliary real field. Note that the exponent is actually quadratic over  and we can write Eq. (54) as:
and we can write Eq. (54) as:
![$\displaystyle %
\psi(y) = \int [{\rm d}\phi({\vec x})] [{\rm d}\delta_{\rm L}({...
...le+\delta_{\rm L}) -\frac{1}{2} \phi . (\Delta_{\phi}^{-1}+2 i \Lambda) . \phi}$](/articles/aa/full/2002/05/aa1670/img205.gif) |
|
|
(55) |
where we introduced the kernel:
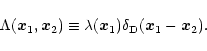 |
(56) |
Then, the Gaussian integration over
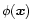 is straightforward and it yields:
is straightforward and it yields:
![$\displaystyle %
\psi(y) = \int [{\rm d}\delta_{\rm L}({\vec x})] [{\rm d}\lambd...
...\; {\rm e}^{-y \delta_{R}+ i \lambda . (\langle\phi^2 \rangle+\delta_{\rm L})}.$](/articles/aa/full/2002/05/aa1670/img207.gif) |
|
|
(57) |
Note indeed that the factor
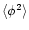 in Eq. (55) does not depend on the random field
in Eq. (55) does not depend on the random field
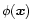 over which we integrate, as shown by Eq. (48). Next, multiplying the r.h.s. of Eq. (57) by
over which we integrate, as shown by Eq. (48). Next, multiplying the r.h.s. of Eq. (57) by
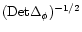 (i.e. we change the implicit normalization constant of the path-integral) and using the relation
(i.e. we change the implicit normalization constant of the path-integral) and using the relation
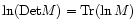 we get:
we get:
![$\displaystyle %
\psi(y) = \int [{\rm d}\delta_{\rm L}({\vec x})] [{\rm d}\lambd...
...\; {\rm e}^{-y \delta_{R}+ i \lambda . (\langle\phi^2 \rangle+\delta_{\rm L})}.$](/articles/aa/full/2002/05/aa1670/img207.gif) |
|
|
(58) |
At this point, it is instructive to consider the linear regime when the density field is linearly evolved:
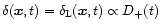 .
In this case, we have:
.
In this case, we have:
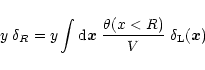 |
(59) |
where
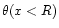 is a top-hat with obvious notations. Then, the integration over
is a top-hat with obvious notations. Then, the integration over
 is straightforward and it yields the Dirac functional
is straightforward and it yields the Dirac functional
![$\delta_{\rm D}[ \lambda({\vec x}) + i y \theta(x<R)/V ]$](/articles/aa/full/2002/05/aa1670/img213.gif) .
The integration over
.
The integration over
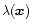 is now obvious and we obtain for the generating function
is now obvious and we obtain for the generating function
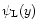 which describes the linear density field (again, the subscript "L'' refers to "linear''):
which describes the linear density field (again, the subscript "L'' refers to "linear''):
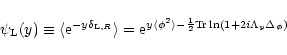 |
(60) |
where the matrix 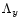 is given by:
is given by:
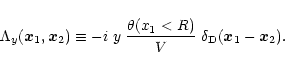 |
(61) |
The normalization of the result derived from the path-integral in Eq. (60) is obtained from the condition
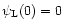 ,
as implied by the definition of
,
as implied by the definition of
 (since
(since
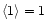 ). As shown in Eq. (4) the generating function
). As shown in Eq. (4) the generating function
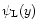 gives the moments
gives the moments
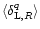 of the pdf
of the pdf
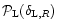 of the linear density contrast. However, it is usually convenient to introduce the generating function
of the linear density contrast. However, it is usually convenient to introduce the generating function
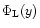 of the cumulants
of the cumulants
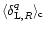 which is given by (see any textbook on statistical theory):
which is given by (see any textbook on statistical theory):
![\begin{displaymath}%
\Phi_{\rm L}(y) \equiv \ln \left[ \psi_{\rm L}(y) \right] =...
...{(-y)^{q}}{q!} \; \langle\delta_{{\rm L},R}^q \rangle_{\rm c}.
\end{displaymath}](/articles/aa/full/2002/05/aa1670/img223.gif) |
(62) |
Thus, from Eq. (60) we obtain the exact expression:
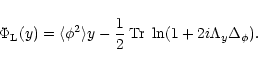 |
(63) |
One can easily check by expanding the logarithm over y that
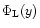 is actually quadratic over y (see also Eq. (75) below). Hence
is actually quadratic over y (see also Eq. (75) below). Hence
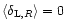 as it should. Moreover, we can check that we recover Eq. (49) for the variance of the linear density contrast.
as it should. Moreover, we can check that we recover Eq. (49) for the variance of the linear density contrast.
4.3 Saddle-point contributions
In the non-linear case it is not so easy to compute the expression (58) since the integration over
 no longer yields a Dirac functional. Besides, even for the linear density field the expression (63) is not very convenient since it is not obvious to compute the logarithm. Thus, for practical purposes it only provides the first few cumulants of
no longer yields a Dirac functional. Besides, even for the linear density field the expression (63) is not very convenient since it is not obvious to compute the logarithm. Thus, for practical purposes it only provides the first few cumulants of
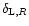 ,
which can be obtained by expanding the logarithm as a series over y and computing the trace of each power of
,
which can be obtained by expanding the logarithm as a series over y and computing the trace of each power of
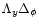 .
Hence we can try a steepest-descent approximation to the path-integral (58), in the spirit of the calculations presented in Paper II for the Gaussian case or in Sect. 3 for a simple non-Gaussian model. More precisely, we may try to evaluate the contributions of all possible saddle-points to the path-integral (58).
.
Hence we can try a steepest-descent approximation to the path-integral (58), in the spirit of the calculations presented in Paper II for the Gaussian case or in Sect. 3 for a simple non-Gaussian model. More precisely, we may try to evaluate the contributions of all possible saddle-points to the path-integral (58).
First, we can look for the saddle-points of the exponent with respect to
 .
This yields:
.
This yields:
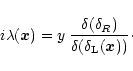 |
(64) |
Since the Gaussian random field
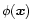 is homogeneous and isotropic we still have a spherical symmetry and we can again look for a spherical saddle-point. Then, taking the mean of Eq. (64) over a spherical cell V' we get:
is homogeneous and isotropic we still have a spherical symmetry and we can again look for a spherical saddle-point. Then, taking the mean of Eq. (64) over a spherical cell V' we get:
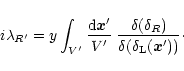 |
(65) |
From the very definition of derivatives we can also write Eq. (65) as:
![$\displaystyle %
i \lambda_{R'} = \lim_{\epsilon \rightarrow 0} \frac{y}{\epsilo...
...ambda}(R',R'') \right] - \delta_{R}\left[ \delta_{{\rm L},R''} \right] \right\}$](/articles/aa/full/2002/05/aa1670/img230.gif) |
|
|
(66) |
where R'' is a dummy variable and we introduced the kernel:
We again define the linear density contrast
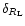 and the Lagrangian mass scale
and the Lagrangian mass scale 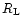 as in Eq. (25) and we obtain:
as in Eq. (25) and we obtain:
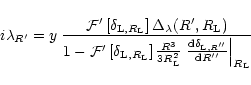 |
(68) |
in a fashion similar to the calculation presented in Paper II for the Gaussian case. The only term in the r.h.s. of Eq. (68) which depends on R' is the factor
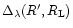 hence we have:
hence we have:
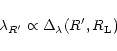 |
(69) |
which yields the profile:
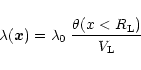 |
(70) |
which also defines the normalization 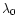 .
Note that this profile for the field
.
Note that this profile for the field
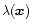 is of the same form as the one obtained for the linear regime which involved the Dirac functional
is of the same form as the one obtained for the linear regime which involved the Dirac functional
![$\delta_{\rm D}[ \lambda({\vec x}) + i y \theta(x<R)/V ]$](/articles/aa/full/2002/05/aa1670/img213.gif) ,
see the derivation of Eq. (60).
,
see the derivation of Eq. (60).
Then, for such a state
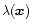 we can estimate the trace which appeared in Eq. (58) as follows. Let us note this trace as
we can estimate the trace which appeared in Eq. (58) as follows. Let us note this trace as
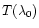 .
Then, we have:
.
Then, we have:
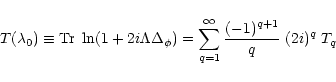 |
(71) |
with:
using the definition of the trace:
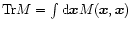 .
Next, from Eq. (56) we see that for the spherical state (70) the matrix
.
Next, from Eq. (56) we see that for the spherical state (70) the matrix
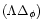 is given by:
is given by:
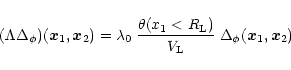 |
(73) |
which yields:
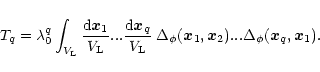 |
(74) |
The first term T1 (i.e. q=1) is simply:
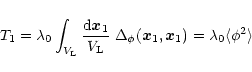 |
(75) |
where we used Eq. (46). Note that it is set by the short-distance behaviour (
 )
of the two-point correlation
)
of the two-point correlation
 ,
since we actually have x=0. On the other hand, for
,
since we actually have x=0. On the other hand, for
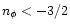 the other terms Tq with
the other terms Tq with 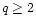 are set by the long-distance behaviour of the correlation
are set by the long-distance behaviour of the correlation
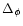 ,
i.e. by the scale R one is looking at by studying
,
i.e. by the scale R one is looking at by studying
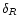 .
This is the case for the power-spectra
.
This is the case for the power-spectra 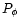 of cosmological interest, see Eq. (43). Moreover, for large q the different factors
of cosmological interest, see Eq. (43). Moreover, for large q the different factors
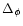 in Eq. (74) are almost uncorrelated and it makes sense to use the approximation:
in Eq. (74) are almost uncorrelated and it makes sense to use the approximation:
![\begin{displaymath}%
q \geq 2: \; T_q \simeq \lambda_0^q \; \left[ \sigma_{\phi}^2(R_{\rm L}) \right]^q.
\end{displaymath}](/articles/aa/full/2002/05/aa1670/img255.gif) |
(76) |
Besides, for a power-law power-spectrum
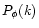 as in Eq. (43) we have (at scales larger than the coherence length
as in Eq. (43) we have (at scales larger than the coherence length 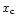 ):
):
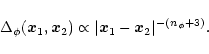 |
(77) |
Then, since
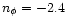 is close to -3 the correlation
is close to -3 the correlation
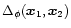 is almost constant over most of the integration volume so that the approximation (76) should be quite reasonable. This yields for the trace
is almost constant over most of the integration volume so that the approximation (76) should be quite reasonable. This yields for the trace
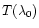 defined in Eq. (71):
defined in Eq. (71):
![\begin{displaymath}%
T(\lambda_0) \simeq 2 i \lambda_0 \langle\phi^2 \rangle- 2 ...
...n \left[ 1 + 2 i \lambda_0 \sigma_{\phi}^2(R_{\rm L}) \right].
\end{displaymath}](/articles/aa/full/2002/05/aa1670/img258.gif) |
(78) |
Next, we could try to consider a saddle-point with respect to both
 and
and
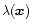 .
However, one can check that this procedure does not give meaningful results. In fact, as described above in the derivation of the exact Eq. (60) the generating function
.
However, one can check that this procedure does not give meaningful results. In fact, as described above in the derivation of the exact Eq. (60) the generating function
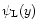 of the linear density field itself is not governed by a unique saddle-point. Indeed, we had to take into account the contributions from all real fields
of the linear density field itself is not governed by a unique saddle-point. Indeed, we had to take into account the contributions from all real fields
 in the path-integral to get the Dirac functional which eventually provides the correct result. Then, in order to keep this structure while using the spherical saddle-points (70) it is natural to try to approximate the path-integral (58) by:
in the path-integral to get the Dirac functional which eventually provides the correct result. Then, in order to keep this structure while using the spherical saddle-points (70) it is natural to try to approximate the path-integral (58) by:
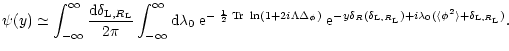 |
|
|
(79) |
Here
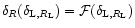 is given by the spherical collapse solution of the equation of motions, while the matrix
is given by the spherical collapse solution of the equation of motions, while the matrix
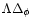 is given by Eq. (73). Thus, we have replaced the integration over the real fields
is given by Eq. (73). Thus, we have replaced the integration over the real fields
 and
and
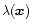 in Eq. (58) by an integration over the real numbers
in Eq. (58) by an integration over the real numbers
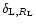 and
and 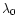 .
In other words, we have replaced the average over
.
In other words, we have replaced the average over
 and
and
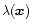 by an average over spherical saddle-points of the form (70). In the case of the linear regime when
by an average over spherical saddle-points of the form (70). In the case of the linear regime when
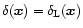 we simply have
we simply have
 and
and
 .
Then we can perform the integration over
.
Then we can perform the integration over
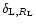 which yields the Dirac function
which yields the Dirac function
![$\delta_{\rm D}[\lambda_0+iy]$](/articles/aa/full/2002/05/aa1670/img264.gif) .
The integration over
.
The integration over 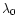 is now straightforward and we recover exactly the rigorous result (60) (this also justifies the normalization factor
is now straightforward and we recover exactly the rigorous result (60) (this also justifies the normalization factor  we introduced in Eq. (79)). Note in addition that the structure of the calculation is also the same (the Dirac functional is simply replaced by a Dirac function). Thus, the expression (79) is actually exact in the linear regime. We show in Appendix A how to rigorously derive the expression (79) from Eq. (58) in the linear regime. We also explain how it can be derived for the fully non-linear density field in the quasi-linear limit. Thus, Eq. (79) is actually exact to leading order in the limit
we introduced in Eq. (79)). Note in addition that the structure of the calculation is also the same (the Dirac functional is simply replaced by a Dirac function). Thus, the expression (79) is actually exact in the linear regime. We show in Appendix A how to rigorously derive the expression (79) from Eq. (58) in the linear regime. We also explain how it can be derived for the fully non-linear density field in the quasi-linear limit. Thus, Eq. (79) is actually exact to leading order in the limit
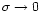 .
More precisely, for the non-linear density field it yields the exact exponential cutoff of the pdf
.
More precisely, for the non-linear density field it yields the exact exponential cutoff of the pdf
 which dominates the dependence on
which dominates the dependence on 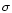 but the normalization is only correct up to a multiplicative factor of order unity which may depend on
but the normalization is only correct up to a multiplicative factor of order unity which may depend on
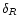 but not on
but not on 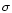 .
This factor arises from the Jacobians Ja and Jb in Eq. (A.15). We shall come back to this point below in Eq. (92).
.
This factor arises from the Jacobians Ja and Jb in Eq. (A.15). We shall come back to this point below in Eq. (92).
As explained above, the factor
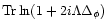 is not very convenient for practical calculations hence it is natural to use the approximation (78) which was derived for such spherical fields
is not very convenient for practical calculations hence it is natural to use the approximation (78) which was derived for such spherical fields
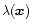 .
This yields:
.
This yields:
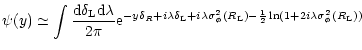 |
|
|
(80) |
where we removed the subscripts of the integration variables
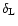 and
and 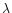 .
Note that in this approximation the term
.
Note that in this approximation the term
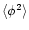 has disappeared. In the linear regime, where
has disappeared. In the linear regime, where
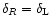 and
and
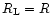 ,
we can again perform the integrations over
,
we can again perform the integrations over
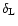 and
and 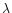 which yields:
which yields:
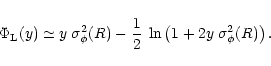 |
(81) |
Then, expanding the logarithm around y=0 we obtain the cumulants
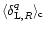 from Eq. (62). This leads to
from Eq. (62). This leads to
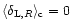 and:
and:
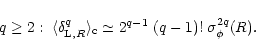 |
(82) |
In particular, we obtain for the variance:
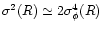 ,
which must be compared with Eqs. (47) and (49). Of course, the deviation from the exact result (49) is entirely due to the approximation (76). For a power-law power-spectrum
,
which must be compared with Eqs. (47) and (49). Of course, the deviation from the exact result (49) is entirely due to the approximation (76). For a power-law power-spectrum 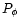 as in Eq. (43) with
as in Eq. (43) with
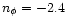 we obtain for this deviation
we obtain for this deviation 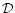 :
:
![\begin{displaymath}%
{\cal D}\equiv \frac{\sigma^2}{2 \sigma_{\phi}^4} = \frac{ ...
...; \Delta_{\phi}({\vec x}_1,{\vec x}_2) \right]^2 } \simeq 1.11
\end{displaymath}](/articles/aa/full/2002/05/aa1670/img274.gif) |
(83) |
where we used Eq. (77) and the result (see Peebles & Groth 1976):
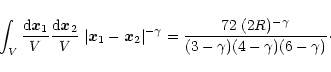 |
(84) |
Thus, we see that the approximation (76) is quite reasonable. Note that it becomes exact in the limit
 .
Then, from Eq. (82) we get for the skewness and the kurtosis:
.
Then, from Eq. (82) we get for the skewness and the kurtosis:
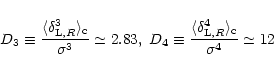 |
(85) |
since we have:
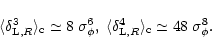 |
(86) |
On the other hand, for the same power-spectrum (
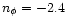 )
Peebles (1999b) obtains by a direct numerical calculation (i.e. without the approximation (76)):
)
Peebles (1999b) obtains by a direct numerical calculation (i.e. without the approximation (76)):
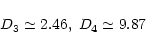 |
(87) |
and:
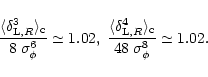 |
(88) |
Thus, we see that the approximation (76) is quite satisfactory. In particular, the behaviour of the high-order cumulants
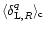 is very well reproduced as soon as
is very well reproduced as soon as
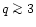 .
Then, we can expect the expression (80) to provide a good approximation to
.
Then, we can expect the expression (80) to provide a good approximation to  ,
both for the linear and the quasi-linear regimes, since we do not add any approximation in order to describe the non-linear effects encoded in the relations
,
both for the linear and the quasi-linear regimes, since we do not add any approximation in order to describe the non-linear effects encoded in the relations
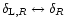 and
and
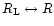 .
.
Going back to Eq. (80), we can make the change of variable
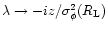 which yields:
which yields:
![$\displaystyle %
\psi(y) \simeq \int_{-\infty}^{\infty} \frac{{\rm d}\delta_{\rm...
...ta_{R}+ z [1+ \delta_{\rm L}/ \sigma_{\phi}^2(R_{\rm L})]} }{\sqrt{1+2 z}}\cdot$](/articles/aa/full/2002/05/aa1670/img285.gif) |
|
|
(89) |
Then, after a change of variable and using the integral representation of the Euler Gamma function:
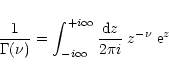 |
(90) |
we obtain:
![$\displaystyle %
\psi(y) \simeq \int_{-\infty}^{\infty} \frac{{\rm d}\delta_{\rm...
... \; \left[ 1 + \frac{\delta_{\rm L}}{\sigma_{\phi}^2(R_{\rm L})} \right]^{-1/2}$](/articles/aa/full/2002/05/aa1670/img287.gif) |
|
|
(91) |
where the factor  is the Heaviside function with obvious notations. Let us recall that in Eq. (91) we have:
is the Heaviside function with obvious notations. Let us recall that in Eq. (91) we have:
 and
and
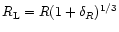 .
.
4.4 The pdf
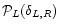 and
and
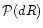
In fact, since the generating function is written in an integral form we can directly derive the pdf
 using the inverse Laplace transform (3). Indeed, the integration over y simply gives the Dirac function
using the inverse Laplace transform (3). Indeed, the integration over y simply gives the Dirac function
![$\delta_{\rm D}[\delta_{R}-{\cal F}(\delta_{\rm L})]$](/articles/aa/full/2002/05/aa1670/img291.gif) .
After a trivial integration over
.
After a trivial integration over 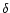 we obtain:
we obtain:
![$\displaystyle %
{\cal P}(\delta_{R}) \simeq \theta \left( 1 + \frac{\delta_{\rm...
...1/2} \; {\rm e}^{- \frac{1}{2} [1+ \delta_{\rm L}/ \sigma_{\phi}^2(R_{\rm L})]}$](/articles/aa/full/2002/05/aa1670/img293.gif) |
|
|
(92) |
where the quantity
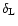 is given by the condition:
is given by the condition:
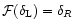 and
and
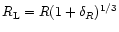 .
In particular, the pdf
.
In particular, the pdf
 of the linearly evolved density field is given by:
of the linearly evolved density field is given by:
![$\displaystyle %
{\cal P}_{\rm L}(\delta_{{\rm L},R}) \simeq \theta \left( 1 + \...
...^{-1/2} \; {\rm e}^{- \frac{1}{2} [1+ \delta_{{\rm L},R}/ \sigma_{\phi}^2(R)]}.$](/articles/aa/full/2002/05/aa1670/img295.gif) |
|
|
(93) |
It is obtained from Eq. (92) by setting
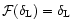 and
and
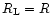 .
For Gaussian initial conditions the pdf
.
For Gaussian initial conditions the pdf
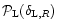 exhibits a specific scaling over the variable
exhibits a specific scaling over the variable
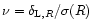 ,
which contains all the time and scale dependence of the pdf. As described above, within the approximation (76) we have
,
which contains all the time and scale dependence of the pdf. As described above, within the approximation (76) we have
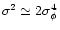 hence we get:
hence we get:
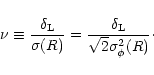 |
(94) |
Then, we see that the linear pdf (93) shows a scaling over  as in the Gaussian case:
as in the Gaussian case:
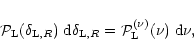 |
(95) |
but the pdf
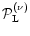 is now given by:
is now given by:
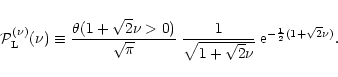 |
(96) |
As noticed in Paper II, in the Gaussian case the non-linear high-density tail is well described by a simple spherical model. In fact, this model gives the exact exponential dependence of the pdf on the variance  ,
at leading order in the limit
,
at leading order in the limit
 ,
as was also shown in Valageas (1998). Let us recall here how to build this simple model. It is based on the approximation:
,
as was also shown in Valageas (1998). Let us recall here how to build this simple model. It is based on the approximation:
 |
(97) |
which merely states that the fraction of matter within spherical cells of radius R with a non-linear density contrast larger than
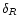 is approximately equal to the fraction of matter which was originally enclosed within spherical cells of radius
is approximately equal to the fraction of matter which was originally enclosed within spherical cells of radius  with a linear density contrast larger than
with a linear density contrast larger than
 .
Here
.
Here  and
and
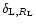 are related to the non-linear variables R and
are related to the non-linear variables R and
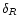 by the usual relation (25), as in Eq. (92). Note that this is similar to the usual Press-Schechter prescription (Press & Schechter 1974), without the factor 2. Then, substituting the scaling (95) into Eq. (97) and differentiating with respect to
by the usual relation (25), as in Eq. (92). Note that this is similar to the usual Press-Schechter prescription (Press & Schechter 1974), without the factor 2. Then, substituting the scaling (95) into Eq. (97) and differentiating with respect to
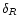 we obtain:
we obtain:
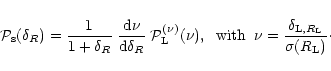 |
(98) |
Here the subscript "s'' refers to the "spherical'' model. In order to recover the variables used in the Gaussian case (Paper II) it is convenient to introduce the variable 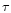 given by:
given by:
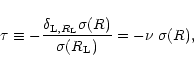 |
(99) |
which removes the dependence on the amplitude of the rms linear density fluctuation, and to define the function
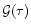 by:
by:
![\begin{displaymath}%
{\cal G}(\tau) \equiv {\cal F}[\delta_{{\rm L},R_{\rm L}}] = \delta_{R}
\end{displaymath}](/articles/aa/full/2002/05/aa1670/img307.gif) |
(100) |
which obeys again Eq. (31). Then, the relation (98) writes:
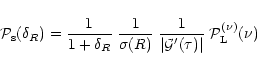 |
(101) |
which yields:
![$\displaystyle %
{\cal P}_{\rm s}(\delta_{R}) = \theta \left( 1 + \frac{\delta_{...
.../2} \; {\rm e}^{- \frac{1}{2} [1+ \delta_{\rm L}/ \sigma_{\phi}^2(R_{\rm L})]}.$](/articles/aa/full/2002/05/aa1670/img309.gif) |
|
|
(102) |
We can see that we recover the expression (92), except for the multiplicative factor where
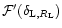 has been replaced by
has been replaced by
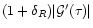 .
Thus, as in the Gaussian case, we find that the simple spherical model (97) yields the exact exponential
.
Thus, as in the Gaussian case, we find that the simple spherical model (97) yields the exact exponential  -dependent term of the pdf. However, the multiplicative factor may not be exact. Here, we note that the multiplicative factor which appears in Eq. (92) is not exact either, as stated above, below Eq. (79), see also Appendix A. In the Gaussian case, we checked by a comparison with numerical simulations (e.g., Valageas 1998; Paper II) that the spherical model (97) provides good results up to
-dependent term of the pdf. However, the multiplicative factor may not be exact. Here, we note that the multiplicative factor which appears in Eq. (92) is not exact either, as stated above, below Eq. (79), see also Appendix A. In the Gaussian case, we checked by a comparison with numerical simulations (e.g., Valageas 1998; Paper II) that the spherical model (97) provides good results up to
 .
We can expect a similar accuracy in the non-Gaussian case studied here. Therefore, the expression (102) should give a good description of the non-linear pdf. This means that the multiplicative factor which appears in Eq. (102) gives a reasonable approximation of the term induced by the Jacobians which arise in the non-linear case, see Eq. (A.15).
.
We can expect a similar accuracy in the non-Gaussian case studied here. Therefore, the expression (102) should give a good description of the non-linear pdf. This means that the multiplicative factor which appears in Eq. (102) gives a reasonable approximation of the term induced by the Jacobians which arise in the non-linear case, see Eq. (A.15).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS1670f2.eps}\end{figure}](/articles/aa/full/2002/05/aa1670/Timg313.gif) |
Figure 2:
The pdf
 for the isocurvature CDM scenario, with
for the isocurvature CDM scenario, with
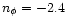 and
and
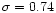 .
This corresponds to .
This corresponds to
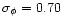 .
The solid line shows the theoretical prediction from (102) for .
The solid line shows the theoretical prediction from (102) for
 .
This corresponds to the "spherical'' model. The dotted line is given by Eq. (102) where no attempt is made to take into account the Jacobians which arise in the non-linear case. The solid line (spherical model) should give better results. The dashed-line displays the pdf .
This corresponds to the "spherical'' model. The dotted line is given by Eq. (102) where no attempt is made to take into account the Jacobians which arise in the non-linear case. The solid line (spherical model) should give better results. The dashed-line displays the pdf
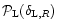 of the linearly evolved density field, from Eq. (93). The histogram shows the results of numerical simulations by Robinson & Baker (2000) for the linear pdf
of the linearly evolved density field, from Eq. (93). The histogram shows the results of numerical simulations by Robinson & Baker (2000) for the linear pdf
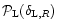 . . |
| Open with DEXTER |
We show in Fig. 2 our results for
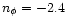 and
and
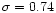 .
The dashed-line shows the pdf
.
The dashed-line shows the pdf
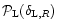 of the linearly evolved density field, from Eq. (93). As could be seen from Eq. (93) it is strongly non-Gaussian, whatever the value of
of the linearly evolved density field, from Eq. (93). As could be seen from Eq. (93) it is strongly non-Gaussian, whatever the value of
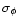 .
In particular, for large overdensities
.
In particular, for large overdensities
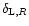 the pdf exhibits a simple exponential cutoff (multiplied by a power
the pdf exhibits a simple exponential cutoff (multiplied by a power
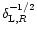 )
which is much smoother than a Gaussian cutoff. Hence the number of extreme events (i.e.
)
which is much smoother than a Gaussian cutoff. Hence the number of extreme events (i.e.
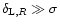 )
is much larger than for the Gaussian case, as can be checked by comparison with the lower dotted curve in Fig. 1. We can see that for
)
is much larger than for the Gaussian case, as can be checked by comparison with the lower dotted curve in Fig. 1. We can see that for
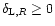 our predictions agree very well with the results of numerical simulations from Robinson & Baker (2000) for the linear density field (shown by the histogram). Note that for the theoretical curve we used the exact value of
our predictions agree very well with the results of numerical simulations from Robinson & Baker (2000) for the linear density field (shown by the histogram). Note that for the theoretical curve we used the exact value of
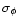 obtained from Eq. (83) in order to get a meaningful comparison. Hence the variance of the approximate pdf (93) underestimates the exact result by a factor
obtained from Eq. (83) in order to get a meaningful comparison. Hence the variance of the approximate pdf (93) underestimates the exact result by a factor
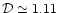 .
However, we can check that the agreement is quite good for
.
However, we can check that the agreement is quite good for
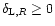 so that for practical purposes one can directly use Eq. (93). For instance, Robinson & Baker (2000) actually use the linear pdf to apply the usual Press-Schechter recipe (Press & Schechter 1974) in order to estimate the mass function of just-collapsed objects.
so that for practical purposes one can directly use Eq. (93). For instance, Robinson & Baker (2000) actually use the linear pdf to apply the usual Press-Schechter recipe (Press & Schechter 1974) in order to estimate the mass function of just-collapsed objects.
On the other hand, we note that our estimate (93) fails for
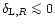 .
In particular, we see that the pdf vanishes for
.
In particular, we see that the pdf vanishes for
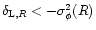 ,
that is the exact lower bound
,
that is the exact lower bound
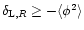 has been replaced by
has been replaced by
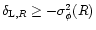 .
This is due to the approximation (76). Indeed, the exact linear pdf obtained from Eqs. (3) and (60) is:
.
This is due to the approximation (76). Indeed, the exact linear pdf obtained from Eqs. (3) and (60) is:
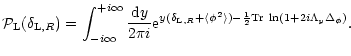 |
|
|
(103) |
This expression clearly shows that the linear density contrast obeys the lower bound
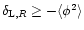 .
Indeed, for
.
Indeed, for
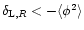 we can push the integration path over y to the right (i.e. Re
we can push the integration path over y to the right (i.e. Re
 )
so that the integral vanishes (we have
)
so that the integral vanishes (we have
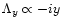 ). Note that this behaviour is rather different from the Gaussian case where the linear density contrast can take negative values of arbitrarily large amplitude. In fact, the lower bound for
). Note that this behaviour is rather different from the Gaussian case where the linear density contrast can take negative values of arbitrarily large amplitude. In fact, the lower bound for
 can be directly seen from Eq. (45). Note that this bound is directly related to the time ti at the end of inflation where Eq. (41) holds. Indeed, from Eq. (44) we see that
can be directly seen from Eq. (45). Note that this bound is directly related to the time ti at the end of inflation where Eq. (41) holds. Indeed, from Eq. (44) we see that
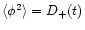 where the growing mode has been normalized by
D+(ti)=1. This minimum value of
where the growing mode has been normalized by
D+(ti)=1. This minimum value of
 is also overestimated by the numerical simulations which only start at a redshift
is also overestimated by the numerical simulations which only start at a redshift
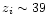 .
Nevertheless, it is clear that the approximate bound
.
Nevertheless, it is clear that the approximate bound
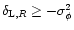 gives the value below which underdensities become very rare (i.e. the pdf should decline for
gives the value below which underdensities become very rare (i.e. the pdf should decline for
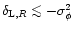 ). Besides, for practical purposes one is often mainly interested in the behaviour of overdensities
). Besides, for practical purposes one is often mainly interested in the behaviour of overdensities
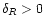 so that the expressions (92) and (93) should remain useful.
so that the expressions (92) and (93) should remain useful.
As noticed in Eq. (95), the linear pdf given by Eq. (93) exhibits a scaling over the one variable 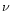 defined in Eq. (94), as in the usual Gaussian case. This scaling property was actually used in order to obtain
defined in Eq. (94), as in the usual Gaussian case. This scaling property was actually used in order to obtain
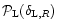 from the numerical simulations. However, this property is not exact and it fails for underdensities since as noticed above the linear density contrast also satisfies the lower bound
from the numerical simulations. However, this property is not exact and it fails for underdensities since as noticed above the linear density contrast also satisfies the lower bound
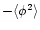 which does not scale as
which does not scale as 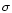 (e.g., contrary to
(e.g., contrary to 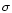 it is independent of scale).
it is independent of scale).
Next, we show the theoretical prediction
 from Eq. (92) (dotted line) and from Eq. (102) (solid line) from the spherical model (97) for the actual non-linear density field. In Fig. 2 we used the approximation:
from Eq. (92) (dotted line) and from Eq. (102) (solid line) from the spherical model (97) for the actual non-linear density field. In Fig. 2 we used the approximation:
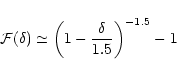 |
(104) |
which has been shown to provide a very good fit to the exact spherical collapse solution for all values of
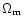 and
and
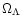 ,
see Fig. 2 in Bernardeau (1994b). This means that the dependence on
,
see Fig. 2 in Bernardeau (1994b). This means that the dependence on
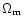 and
and
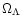 is negligible (in the quasi-linear regime where we do not consider virialized objects) and the pdf only depends on the rms fluctuation
is negligible (in the quasi-linear regime where we do not consider virialized objects) and the pdf only depends on the rms fluctuation 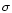 (and the slope
(and the slope 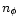 of the power-spectrum). Unfortunately, there are no available results from numerical simulations to compare with our prediction. However, in view of the reasonable accuracy of our prediction for the linear pdf
of the power-spectrum). Unfortunately, there are no available results from numerical simulations to compare with our prediction. However, in view of the reasonable accuracy of our prediction for the linear pdf
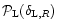 and the good results obtained for the Gaussian case (see Paper II) we can expect the expression (102) to provide a good estimate of the exact pdf
and the good results obtained for the Gaussian case (see Paper II) we can expect the expression (102) to provide a good estimate of the exact pdf
 .
It should perform better than Eq. (92) where no attempt was made to take into account the Jacobians which arise in the non-linear case, see Appendix A. Of course, we recover the usual features of the non-linear evolution which increases the high-density tail of the pdf. Note again the much larger number of high density events with respect to the Gaussian case with the same variance (see Fig. 1).
.
It should perform better than Eq. (92) where no attempt was made to take into account the Jacobians which arise in the non-linear case, see Appendix A. Of course, we recover the usual features of the non-linear evolution which increases the high-density tail of the pdf. Note again the much larger number of high density events with respect to the Gaussian case with the same variance (see Fig. 1).
5 Standard slow-roll inflation
5.1 Initial conditions
The two classes of models we investigated in Sects. 3 and 4 are strongly non-Gaussian (except for
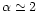 in the first case) and they apply to "non-standard'' scenarios for the generation of primordial density fluctuations. For instance, the second model is based on a multifield inflationary scenario. By contrast, in standard slow-roll inflation the primordial density perturbations should be very close to Gaussian. Nevertheless, they may still show some small deviations from Gaussianity. In particular, one is led to consider models where the perturbed primordial gravitational potential
in the first case) and they apply to "non-standard'' scenarios for the generation of primordial density fluctuations. For instance, the second model is based on a multifield inflationary scenario. By contrast, in standard slow-roll inflation the primordial density perturbations should be very close to Gaussian. Nevertheless, they may still show some small deviations from Gaussianity. In particular, one is led to consider models where the perturbed primordial gravitational potential
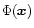 is given by:
is given by:
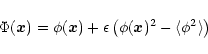 |
(105) |
where
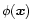 is a Gaussian random field with zero mean and power-spectrum
is a Gaussian random field with zero mean and power-spectrum
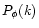 ,
as in Eq. (42). Such models arise in standard slow-roll inflation if we keep track of the perturbations of the inflaton up to the second-order (e.g., Gangui et al. 1994; Falk et al. 1993). In fact, Eq. (105) can be seen as the first two terms of a Taylor expansion so that it applies to a large class of slightly non-Gaussian models. Thus, the parameter
,
as in Eq. (42). Such models arise in standard slow-roll inflation if we keep track of the perturbations of the inflaton up to the second-order (e.g., Gangui et al. 1994; Falk et al. 1993). In fact, Eq. (105) can be seen as the first two terms of a Taylor expansion so that it applies to a large class of slightly non-Gaussian models. Thus, the parameter 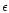 is taken to be small so that the primordial density fluctuations are close to Gaussian. Note that
is taken to be small so that the primordial density fluctuations are close to Gaussian. Note that 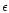 has the dimensions of
has the dimensions of 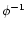 .
We shall define below what we mean by "
.
We shall define below what we mean by "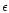 being small'' (see Eq. (138)). Then, our goal here is to obtain the pdf
being small'' (see Eq. (138)). Then, our goal here is to obtain the pdf
 of the density fluctuations in the quasi-linear regime up to first order in
of the density fluctuations in the quasi-linear regime up to first order in 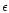 (to go beyond this order we should first take into account the possible higher-order terms in Eq. (105)). Note that for
(to go beyond this order we should first take into account the possible higher-order terms in Eq. (105)). Note that for
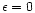 we must recover the case of Gaussian primordial density fluctuations studied in Paper II. The gravitational potential
we must recover the case of Gaussian primordial density fluctuations studied in Paper II. The gravitational potential
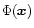 is related to the primordial linear density fluctuations
is related to the primordial linear density fluctuations
 by the Poisson equation (in comoving coordinates):
by the Poisson equation (in comoving coordinates):
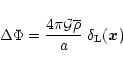 |
(106) |
where a(t) is the scale-factor and
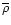 the mean comoving density. Taking the Fourier transform of Eq. (106) one can eventually write the linear density field
the mean comoving density. Taking the Fourier transform of Eq. (106) one can eventually write the linear density field
 at the time of interest as:
at the time of interest as:
![\begin{displaymath}%
\delta_{\rm L}({\vec x}) = \int {\rm d}{\vec x'} \; W({\vec...
...left( \phi({\vec x'})^2 - \langle\phi^2 \rangle\right) \right]
\end{displaymath}](/articles/aa/full/2002/05/aa1670/img344.gif) |
(107) |
where the kernel
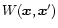 is given by:
is given by:
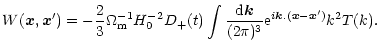 |
|
|
(108) |
Here we introduced the Hubble constant H0 and the density parameter
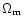 today, while D+(t) is the usual linear growing mode at the time of interest, normalized by
D+(t0)=1 today. The function T(k) is simply the adiabatic CDM transfer function (normalized to unity for
today, while D+(t) is the usual linear growing mode at the time of interest, normalized by
D+(t0)=1 today. The function T(k) is simply the adiabatic CDM transfer function (normalized to unity for
 ). Indeed, contrary to the isocurvature model described in Sect. 4 we need to take into account the deviations of T(k) from unity on the scales of interest for large-scale structure formation. The factor k2 arises from the Laplacian in the l.h.s. in Eq. (106). Note that the kernel
). Indeed, contrary to the isocurvature model described in Sect. 4 we need to take into account the deviations of T(k) from unity on the scales of interest for large-scale structure formation. The factor k2 arises from the Laplacian in the l.h.s. in Eq. (106). Note that the kernel
 is homogeneous, isotropic and symmetric since it only depends on
is homogeneous, isotropic and symmetric since it only depends on
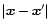 .
Hence for any real fields f1 and f2 we have:
.
Hence for any real fields f1 and f2 we have:
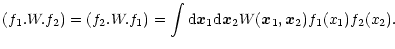 |
|
|
(109) |
Thus, Eq. (107) defines the initial conditions of our system.
We can note that the pdf
 of the linearly evolved density field was already studied in Matarrese et al. (2000) using path-integral methods like those described in Sect. 5.2 below. However, they did not investigate the effects of the non-linear dynamics. On the other hand, Verde et al. (2000) studied the observational tests which may constrain such deviations from Gaussian initial conditions.
of the linearly evolved density field was already studied in Matarrese et al. (2000) using path-integral methods like those described in Sect. 5.2 below. However, they did not investigate the effects of the non-linear dynamics. On the other hand, Verde et al. (2000) studied the observational tests which may constrain such deviations from Gaussian initial conditions.
5.2 Generating function
In order to derive the pdf
 we again introduce the Laplace transform
we again introduce the Laplace transform  as in Eq. (2), which yields again Eq. (52). Next, we introduce the linear density field through the Dirac functional
as in Eq. (2), which yields again Eq. (52). Next, we introduce the linear density field through the Dirac functional
![$\delta_{\rm D}[\delta_{\rm L}({\vec x}) - \int {\rm d}{\vec x'} W({\vec x},{\ve...
...\{ \phi({\vec x'}) + \epsilon ( \phi({\vec x'})^2 - \langle\phi^2 \rangle) \} ]$](/articles/aa/full/2002/05/aa1670/img350.gif) .
This Dirac functional can again be expressed through an auxiliary real field
.
This Dirac functional can again be expressed through an auxiliary real field
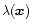 so that the analog of Eq. (54) now reads:
so that the analog of Eq. (54) now reads:
![$\displaystyle %
\psi(y) = \int [{\rm d}\phi({\vec x})] [{\rm d}\delta_{\rm L}({...
... (\delta_{\rm L}- W . [ \phi + \epsilon ( \phi^2 - \langle\phi^2 \rangle) ] ) }$](/articles/aa/full/2002/05/aa1670/img351.gif) |
|
|
(110) |
where we defined the inverse
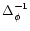 of the two-point correlation
of the two-point correlation
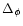 of the Gaussian random field
of the Gaussian random field 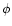 ,
which is again given by Eq. (46). The mean
,
which is again given by Eq. (46). The mean
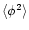 is again given by Eq. (48) and it does not depend on the field
is again given by Eq. (48) and it does not depend on the field
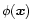 over which we integrate. As in Sect. 4 we do not write explicitly the normalization factor of the path-integrals. Next, we introduce the kernel
over which we integrate. As in Sect. 4 we do not write explicitly the normalization factor of the path-integrals. Next, we introduce the kernel
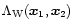 defined by:
defined by:
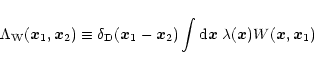 |
(111) |
so that Eq. (110) reads:
![$\displaystyle %
\psi(y) = \int [{\rm d}\phi({\vec x})] [{\rm d}\delta_{\rm L}({...
... . \Lambda_{\rm W} . \phi + i \epsilon \langle\phi^2 \rangle(\lambda . W . 1)}.$](/articles/aa/full/2002/05/aa1670/img355.gif) |
|
|
(112) |
As explained in Sect. 5.1 we only consider the first-order term in 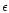 .
Therefore, we expand the exponential in Eq. (112) up to first-order in
.
Therefore, we expand the exponential in Eq. (112) up to first-order in 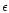 .
This yields:
.
This yields:
![$\displaystyle %
\psi(y) = \int [{\rm d}\phi({\vec x})] [{\rm d}\delta_{\rm L}({...
...\rangle(\lambda . W . 1) - i \epsilon (\phi . \Lambda_{\rm W} . \phi) \right] .$](/articles/aa/full/2002/05/aa1670/img356.gif) |
|
|
(113) |
This path-integral is Gaussian over the random field 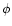 .
Thus, we first make the change of variable
.
Thus, we first make the change of variable
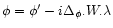 so that Eq. (113) writes:
so that Eq. (113) writes:
Here we used the fact that all kernels W,
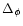 and
and
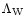 are symmetric. Then, using Wick's theorem we can perform the Gaussian integration over
are symmetric. Then, using Wick's theorem we can perform the Gaussian integration over
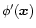 which yields:
which yields:
![$\displaystyle %
\psi(y) = \int [{\rm d}\delta_{\rm L}({\vec x})] [{\rm d}\lambd...
...bda . W . \Delta_{\phi}. \Lambda_{\rm W} . \Delta_{\phi}. W . \lambda) \biggl ]$](/articles/aa/full/2002/05/aa1670/img363.gif) |
|
|
(115) |
where we used
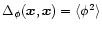 .
Next, we define the two-point correlation
.
Next, we define the two-point correlation
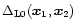 of the linear density field in the case
of the linear density field in the case
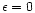 by:
by:
where we used Eq. (107). Here the subscript "0'' refers to "
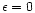 ''. The relation (116) also writes:
''. The relation (116) also writes:
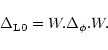 |
(117) |
The path-integral (115) is Gaussian over the field
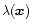 .
Thus, making the change of variable
.
Thus, making the change of variable
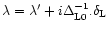 and integrating over
and integrating over
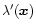 using Wick's theorem we finally get:
using Wick's theorem we finally get:
![$\displaystyle %
\psi(y) = \int [{\rm d}\delta_{\rm L}({\vec x})] \; {\rm e}^{-y...
...\; (\Delta_{\phi}^{-1}.W^{-1}.\delta_{\rm L}).(W^{-1}.\delta_{\rm L})^2 \right]$](/articles/aa/full/2002/05/aa1670/img372.gif) |
|
|
(118) |
where we used
 .
Here we introduced the short-hand notation
.
Here we introduced the short-hand notation
 for the vector:
for the vector:
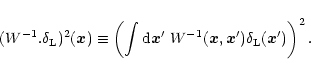 |
(119) |
Note that for
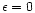 we recover the expression (14) derived for Gaussian initial conditions. This was to be expected since for
we recover the expression (14) derived for Gaussian initial conditions. This was to be expected since for
 the linear density field is actually Gaussian. Indeed, in this case we have
the linear density field is actually Gaussian. Indeed, in this case we have
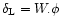 and
and 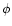 is a Gaussian random field. Of course, the procedure we described above can be extended up to any order in
is a Gaussian random field. Of course, the procedure we described above can be extended up to any order in 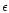 (provided we know the initial conditions up to the required order). Indeed, by expanding the exponential which appears in Eq. (110) up to the needed order in
(provided we know the initial conditions up to the required order). Indeed, by expanding the exponential which appears in Eq. (110) up to the needed order in 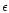 the integrations over the fields
the integrations over the fields
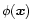 and
and
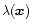 are Gaussian and can be easily performed using Wick's theorem. Then, one eventually obtains an expression of the form (118), where the term in brackets is an expansion over
are Gaussian and can be easily performed using Wick's theorem. Then, one eventually obtains an expression of the form (118), where the term in brackets is an expansion over 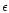 up to the required order. Note that this is similar to the standard Edgeworth expansion where one directly expands the Laplace transform
up to the required order. Note that this is similar to the standard Edgeworth expansion where one directly expands the Laplace transform  around the Gaussian value
around the Gaussian value
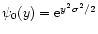 (see any textbook on probability theory). Therefore, the expansion over
(see any textbook on probability theory). Therefore, the expansion over  does not necessarily converge: it may only provide an asymptotic series (e.g., Cramer 1946).
does not necessarily converge: it may only provide an asymptotic series (e.g., Cramer 1946).
5.3 Steepest-descent method
We now need to evaluate the path-integral (118). As for the Gaussian case studied in Paper II or the non-Gaussian generalization described in Sect. 3 we can use a steepest-descent method for the quasi-linear regime. We refer the reader to Paper II for a detailed presentation of this method. First, we define the rescaled generating function
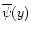 by:
by:
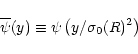 |
(120) |
where
 is the variance of the linear density field for
is the variance of the linear density field for
 :
:
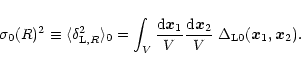 |
(121) |
Using Eq. (118) we get:
![$\displaystyle %
\overline{\psi}(y) = \int [{\rm d}\delta_{\rm L}({\vec x})] \; ...
...\; (\Delta_{\phi}^{-1}.W^{-1}.\delta_{\rm L}).(W^{-1}.\delta_{\rm L})^2 \right]$](/articles/aa/full/2002/05/aa1670/img382.gif) |
|
|
(122) |
where we introduced the "action''
![$S[\delta_{\rm L}]$](/articles/aa/full/2002/05/aa1670/img383.gif) given by:
given by:
![\begin{displaymath}%
S[\delta_{\rm L}] \equiv y \; \delta_{R}[\delta_{\rm L}] + ...
...2}{2} \; \delta_{\rm L}.\Delta_{{\rm L}0}^{-1}.\delta_{\rm L}.
\end{displaymath}](/articles/aa/full/2002/05/aa1670/img384.gif) |
(123) |
In the quasi-linear limit
 the path-integral (122) is governed by the minimum of the action S. As shown in Paper II this spherically symmetric saddle-point is given by:
the path-integral (122) is governed by the minimum of the action S. As shown in Paper II this spherically symmetric saddle-point is given by:
where  is a dummy variable. The variable
is a dummy variable. The variable
 is given by the implicit equation:
is given by the implicit equation:
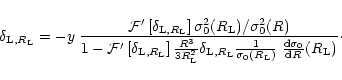 |
(125) |
Here the function
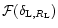 is the usual spherical collapse solution while
is the usual spherical collapse solution while 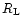 is the Lagrangian mass scale, see Eq. (25). These results were also used in Sect. 3.2 where we investigated a simple generalization of the Gaussian weight. Next, we introduce the functions
is the Lagrangian mass scale, see Eq. (25). These results were also used in Sect. 3.2 where we investigated a simple generalization of the Gaussian weight. Next, we introduce the functions
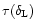 and
and
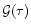 by:
by:
![\begin{displaymath}%
\tau(\delta_{\rm L}) \equiv \frac{- \; \delta_{\rm L}\; \si...
...\sigma_0 \left[ (1+{\cal F}[\delta_{\rm L}])^{1/3} R \right] }
\end{displaymath}](/articles/aa/full/2002/05/aa1670/img391.gif) |
(126) |
and:
![\begin{displaymath}%
{\cal G}(\tau) \equiv {\cal F}\left[\delta_{\rm L}(\tau)\right] = \delta_{R}
\end{displaymath}](/articles/aa/full/2002/05/aa1670/img105.gif) |
(127) |
as in Eqs. (29) and (30). Then, we define the function
![$\varphi_0(y) \equiv \min S[\delta_{\rm L}]$](/articles/aa/full/2002/05/aa1670/img392.gif) as the value of the action S at this spherically symmetric saddle-point (i.e. the minimum of the action). As shown in Paper II it is given by the implicit system:
as the value of the action S at this spherically symmetric saddle-point (i.e. the minimum of the action). As shown in Paper II it is given by the implicit system:
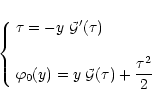 |
(128) |
in a fashion similar to Eq. (32). Then, at leading order in  we can write the path-integral (122) in the quasi-linear limit as:
we can write the path-integral (122) in the quasi-linear limit as:
![\begin{displaymath}%
\overline{\psi}(y) = {\rm e}^{-\varphi_0(y)/\sigma_0(R)^2} ...
...(R)^3} \; \frac{J_3(R_{\rm L})}{\sigma_0(R_{\rm L})^3} \right]
\end{displaymath}](/articles/aa/full/2002/05/aa1670/img395.gif) |
(129) |
where we defined:
 |
(130) |
Here
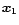 and
and
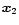 are dummy variables. The normalization of
are dummy variables. The normalization of
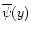 in Eq. (129) is set by the constraint
in Eq. (129) is set by the constraint
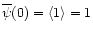 .
Next, we define the dimensionless quantity
.
Next, we define the dimensionless quantity
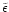 by:
by:
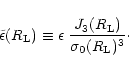 |
(131) |
It is convenient to express the quantities  and J3 in terms of the power-spectrum
and J3 in terms of the power-spectrum
 of the Gaussian random field
of the Gaussian random field
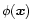 .
This yields:
.
This yields:
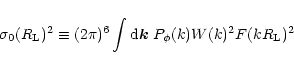 |
(132) |
and:
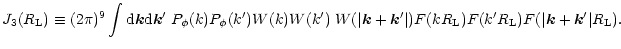 |
|
|
(133) |
Here
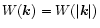 is the Fourier transform of the window function
is the Fourier transform of the window function
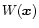 defined in Eq. (108) (i.e. it is related to the kernel W by
defined in Eq. (108) (i.e. it is related to the kernel W by
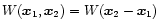 )
while F(kR) is the Fourier transform of the top-hat of radius R:
)
while F(kR) is the Fourier transform of the top-hat of radius R:
 |
(134) |
Note that in Eq. (134) we did not introduce the factor
 used in the definition (6) of the Fourier transform, in order to obtain the usual top-hat window F(kR). As in the previous sections we approximate the power-spectrum P0(k) of the linear density fluctuations (when
used in the definition (6) of the Fourier transform, in order to obtain the usual top-hat window F(kR). As in the previous sections we approximate the power-spectrum P0(k) of the linear density fluctuations (when
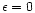 )
by a power-law. Since we have
)
by a power-law. Since we have
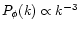 (i.e. a scale-invariant primordial power-spectrum, with small and large scale cutoffs) for the standard inflationary scenarios we investigate here this means that
(i.e. a scale-invariant primordial power-spectrum, with small and large scale cutoffs) for the standard inflationary scenarios we investigate here this means that
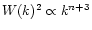 on the scales of interest. Indeed, the power-spectrum P0(k) is related to
on the scales of interest. Indeed, the power-spectrum P0(k) is related to
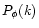 by:
by:
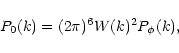 |
(135) |
as can be seen for instance from Eq. (132). Then, from Eqs. (132) and (133) we get:
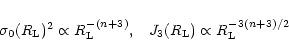 |
(136) |
which implies that the quantity
 defined in Eq. (131) does not depend on
defined in Eq. (131) does not depend on  ,
within this approximation. Moreover, from Eqs. (132) and (133) we see that we have the order of magnitude estimate:
,
within this approximation. Moreover, from Eqs. (132) and (133) we see that we have the order of magnitude estimate:
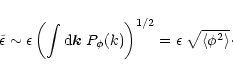 |
(137) |
Going back to the definition (105) of the initial conditions we see that we can write the primordial perturbations of the gravitational potential as:
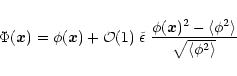 |
(138) |
where
 stands for a numerical factor of order unity. It is clear from this expression that for a scale-invariant primordial power-spectrum the initial conditions are close to Gaussian if
stands for a numerical factor of order unity. It is clear from this expression that for a scale-invariant primordial power-spectrum the initial conditions are close to Gaussian if
 .
Hence
.
Hence
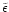 is the relevant dimensionless parameter which describes the amplitude of the deviations from Gaussianity and the usual inflationary scenarios lead to
is the relevant dimensionless parameter which describes the amplitude of the deviations from Gaussianity and the usual inflationary scenarios lead to
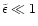 .
.
Here it is interesting to consider the linear regime, that is the statistics of the linear density field. Then, we have
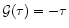 and
and
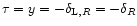 ,
so that
,
so that
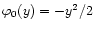 .
This yields from Eq. (129):
.
This yields from Eq. (129):
![\begin{displaymath}%
\psi_{\rm L}(y) = {\rm e}^{y^2 \sigma_0^2/2} \; \left[ 1 - \tilde{\epsilon} \; y^3 \sigma_0^3 \right]
\end{displaymath}](/articles/aa/full/2002/05/aa1670/img420.gif) |
(139) |
where the subscript "L'' refers to the "linearly evolved'' density field. Then, from the expansion (4) we obtain for the third-order moment of the linear density field
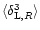 and for the skewness D3:
and for the skewness D3:
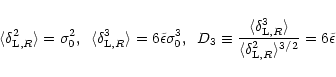 |
(140) |
at first-order in
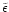 .
Thus, we see that the parameter
.
Thus, we see that the parameter
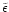 is directly related to the skewness of the linear density field on the scale of interest, due to the slight non-Gaussianity of the primordial density field.
is directly related to the skewness of the linear density field on the scale of interest, due to the slight non-Gaussianity of the primordial density field.
5.4 The pdf of the density contrast
From the rescaled Laplace transform
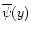 obtained in Eq. (129) we can derive the pdf
obtained in Eq. (129) we can derive the pdf
 ,
using the inverse Laplace transform (3). This yields:
,
using the inverse Laplace transform (3). This yields:
![\begin{displaymath}%
{\cal P}(\delta_{R}) = \int_{-i\infty}^{+i\infty}\frac{{\rm...
...eft[ 1 - \tilde{\epsilon} \; \frac{\tau^3}{\sigma_0^3} \right]
\end{displaymath}](/articles/aa/full/2002/05/aa1670/img423.gif) |
(141) |
where the function 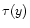 is given by Eq. (128). The pdf
is given by Eq. (128). The pdf
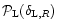 of the linearly evolved density field is obtained from Eq. (141) by using
of the linearly evolved density field is obtained from Eq. (141) by using
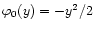 and
and 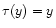 which gives:
which gives:
![\begin{displaymath}%
{\cal P}_{\rm L}(\delta_{{\rm L},R}) = \int_{-i\infty}^{+i\...
...t[ 1 - \tilde{\epsilon} \; \frac{y^3}{\sigma_0^3} \right]\cdot
\end{displaymath}](/articles/aa/full/2002/05/aa1670/img426.gif) |
(142) |
Then we can perform the Gaussian integration over y in Eq. (142) which yields (see Gradshteyn & Ryzhik 1965, Sect. 3.462.4):
![\begin{displaymath}%
{\cal P}_{\rm L}(\delta_{{\rm L},R}) = \frac{{\rm e}^{-\del...
...( \frac{\delta_{{\rm L},R}}{\sqrt{2} \sigma_0} \right) \right]
\end{displaymath}](/articles/aa/full/2002/05/aa1670/img427.gif) |
(143) |
where H3(x) is the Hermite polynomial of order 3 defined by:
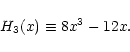 |
(144) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS1670f3.eps}\end{figure}](/articles/aa/full/2002/05/aa1670/Timg431.gif) |
Figure 3:
The pdf
 for n=-1 and
for n=-1 and
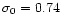 ,
for slightly non-Gaussian initial conditions: ,
for slightly non-Gaussian initial conditions:
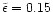 .
The solid line shows the prediction of Eq. (141) for the non-linear pdf .
The solid line shows the prediction of Eq. (141) for the non-linear pdf
 while the dashed-curve shows the pdf
while the dashed-curve shows the pdf
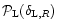 of the linearly evolved density field from Eq. (143). The dotted lines display the results obtained with
of the linearly evolved density field from Eq. (143). The dotted lines display the results obtained with
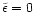 ,
i.e. for Gaussian initial conditions. ,
i.e. for Gaussian initial conditions. |
| Open with DEXTER |
Finally, we display in Fig. 3 our results for slightly non-Gaussian initial conditions:
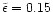 .
In order to compare the pdf with the case of Gaussian initial conditions we also show the results obtained for
.
In order to compare the pdf with the case of Gaussian initial conditions we also show the results obtained for
 (dotted curves). Let us recall that Eq. (142) for the pdf of the linearly evolved density field is exact to first-order in
(dotted curves). Let us recall that Eq. (142) for the pdf of the linearly evolved density field is exact to first-order in
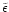 .
In agreement with Eq. (140) we can check that
.
In agreement with Eq. (140) we can check that
 leads to a small positive skewness for the linear density field. In particular, the high-density tail of the pdf is slightly enhanced. We can see that this feature remains valid for the non-linear pdf
leads to a small positive skewness for the linear density field. In particular, the high-density tail of the pdf is slightly enhanced. We can see that this feature remains valid for the non-linear pdf
 .
However, as gravitational clustering proceeds the deviations from Gaussianity become dominated by the non-linear dynamics over the slight primordial non-Gaussianity. More precisely, we can obtain the low-order moments of the density field through the expansion (4). At the lowest order in y we have
.
However, as gravitational clustering proceeds the deviations from Gaussianity become dominated by the non-linear dynamics over the slight primordial non-Gaussianity. More precisely, we can obtain the low-order moments of the density field through the expansion (4). At the lowest order in y we have
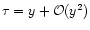 and
and
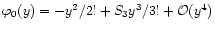 where the parameter S3 is given by the standard result (e.g., Bernardeau 1994a):
where the parameter S3 is given by the standard result (e.g., Bernardeau 1994a):
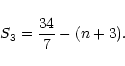 |
(145) |
Then, we obtain from Eq. (129) the expansion:
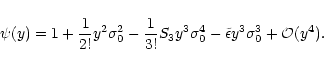 |
(146) |
This yields for the lowest order moments:
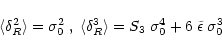 |
(147) |
and for the skewness D3:
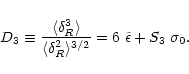 |
(148) |
This relation clearly shows that the relative importance of the primordial deviation from Gaussianity is greater at earlier times before gravitational clustering builds up, as could be expected. Note that in Fig. 3 we used the generating function
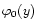 defined by the branch of Eq. (128) which is regular at the origin y=0. Since here we considered the case n=-1 this function actually shows a branch cut along the real negative axis for
defined by the branch of Eq. (128) which is regular at the origin y=0. Since here we considered the case n=-1 this function actually shows a branch cut along the real negative axis for
 (with
(with
 ). Then, for large density contrasts one needs to take into account the second branch of
). Then, for large density contrasts one needs to take into account the second branch of
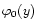 defined over the range
defined over the range
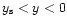 which is singular at the origin. However, as shown in Fig. 6 in Paper II this is irrelevant for the case displayed in Fig. 3 for
which is singular at the origin. However, as shown in Fig. 6 in Paper II this is irrelevant for the case displayed in Fig. 3 for
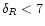 .
We refer the reader to Paper II for a detailed discussion of this point. Of course, for the non-Gaussian model we study here one simply needs to follow the procedure outlined in Paper II for Gaussian initial conditions and to add to the relevant expressions the term in the brackets in Eq. (141) which describes the effects due to the small primordial deviation from Gaussianity (to first order in
.
We refer the reader to Paper II for a detailed discussion of this point. Of course, for the non-Gaussian model we study here one simply needs to follow the procedure outlined in Paper II for Gaussian initial conditions and to add to the relevant expressions the term in the brackets in Eq. (141) which describes the effects due to the small primordial deviation from Gaussianity (to first order in
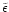 ).
).
Thus, using a non-perturbative method developed in a previous work (Paper II), we have described in details how to obtain the pdf
 of the density contrast within spherical cells in the quasi-linear regime for three specific non-Gaussian models.
of the density contrast within spherical cells in the quasi-linear regime for three specific non-Gaussian models.
The first case is a straightforward generalization of the Gaussian scenario and it can be seen as a phenomenological description of a density field where the tails of the linear pdf are of the form
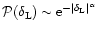 ,
where
,
where  is no longer required to be equal to two (as in the Gaussian case). Then, we have shown that the derivation of the pdf presented for the Gaussian case can be directly extended to this model. This provides again exact results for the pdf in the quasi-linear limit.
is no longer required to be equal to two (as in the Gaussian case). Then, we have shown that the derivation of the pdf presented for the Gaussian case can be directly extended to this model. This provides again exact results for the pdf in the quasi-linear limit.
The second scenario is a physically motivated model of isocurvature cold dark matter presented in Peebles (1999a). It arises from an inflationary scenario with three scalar fields. This case is slightly more difficult as one needs to adapt the method to this specific model. Moreover, in order to get simple analytical results one must introduce a simple approximation (which is not related to the gravitational dynamics but to the non-Gaussian properties of the initial conditions). However, we have shown that even with this approximation we get good results for the linear pdf
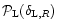 for
for
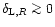 by comparison with numerical simulations. For lack of data we could not check our prediction for the non-linear pdf
by comparison with numerical simulations. For lack of data we could not check our prediction for the non-linear pdf
 but we can expect a good agreement of the same accuracy.
but we can expect a good agreement of the same accuracy.
Finally, the third scenario corresponds to the small primordial deviations from Gaussianity which arise in standard slow-roll inflation. We obtained exact results for the pdf of the density field in the quasi-linear limit, to first-order over the primordial deviations from Gaussianity.
This study shows that our approach is powerful enough to be applied to a large variety of initial conditions. Note that our predictions for the linear pdf
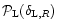 for such non-Gaussian scenarios may be used to estimate the mass function of just-collapsed objects, using a straightforward extension of the Press-Schechter recipe. Note that we shall discuss the Press-Schechter prescription in the light of the formalism developed in Paper II and used in this work in a companion article (Paper IV).
for such non-Gaussian scenarios may be used to estimate the mass function of just-collapsed objects, using a straightforward extension of the Press-Schechter recipe. Note that we shall discuss the Press-Schechter prescription in the light of the formalism developed in Paper II and used in this work in a companion article (Paper IV).
To conclude, we note that our approach being non-perturbative it can in principle be applied to the non-linear regime. Indeed, it does not rely either on the hydrodynamical description. We shall present a study of this non-linear regime in a future work, see Paper IV, for Gaussian initial conditions. However, it is clear that this can be extended to the non-Gaussian models described here.
Appendix A: Isocurvature scenario. Reduction to ordinary integrals
In this appendix we show how to derive the expression (79) from Eq. (58). We first consider the linear regime where Eq. (79) is exact. The path-integral (58) involves the functional measure
![$[{\rm d}\delta_{\rm L}({\vec x})]$](/articles/aa/full/2002/05/aa1670/img445.gif) .
The latter can be defined from a discretization procedure (i.e. a spatial grid for the coordinate
.
The latter can be defined from a discretization procedure (i.e. a spatial grid for the coordinate 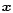 with an infinitesimal spacing) but an equivalent formulation (e.g., Zinn-Justin 1989) is to expand the function
with an infinitesimal spacing) but an equivalent formulation (e.g., Zinn-Justin 1989) is to expand the function
 on a complete set of real orthonormal functions fq (in the Hilbert space
on a complete set of real orthonormal functions fq (in the Hilbert space
 ):
):
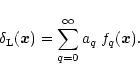 |
(A.1) |
The vectors fq obey the relation:
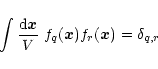 |
(A.2) |
which expresses the fact that they form an orthonormal basis. Here
 is the usual Kronecker symbol. We introduced a factor 1/V in the scalar product (A.2) so that the functions fq are dimensionless, but this is not essential (here V is a constant). Then, the functional measure
is the usual Kronecker symbol. We introduced a factor 1/V in the scalar product (A.2) so that the functions fq are dimensionless, but this is not essential (here V is a constant). Then, the functional measure
![$[{\rm d}\delta_{\rm L}({\vec x})]$](/articles/aa/full/2002/05/aa1670/img445.gif) can be defined as (e.g., Zinn-Justin 1989):
can be defined as (e.g., Zinn-Justin 1989):
![\begin{displaymath}%
[{\rm d}\delta_{\rm L}({\vec x})] \equiv {\cal N}\prod_{q=0}^{\infty} {\rm d}a_q
\end{displaymath}](/articles/aa/full/2002/05/aa1670/img450.gif) |
(A.3) |
where  is a normalization constant. In order to get a discrete basis in Eq. (A.1) we restricted the density field to a large finite volume
is a normalization constant. In order to get a discrete basis in Eq. (A.1) we restricted the density field to a large finite volume  .
However, this is not essential: we choose
.
However, this is not essential: we choose 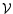 to be much larger than any relevant length scale and we can eventually take the limit
to be much larger than any relevant length scale and we can eventually take the limit
 .
Next, we can choose for the first basis vector f0 the top-hat of radius R:
.
Next, we can choose for the first basis vector f0 the top-hat of radius R:
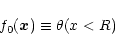 |
(A.4) |
where
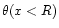 is the usual top-hat with obvious notations. Then, from Eqs. (A.1) and (A.2) we have:
is the usual top-hat with obvious notations. Then, from Eqs. (A.1) and (A.2) we have:
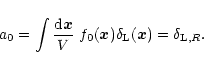 |
(A.5) |
We can expand the auxiliary field
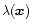 on the same basis:
on the same basis:
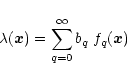 |
(A.6) |
so that the path-integral (58) now writes:
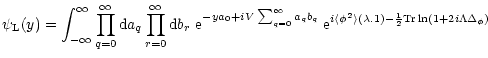 |
|
|
(A.7) |
where the subscript "L'' refers to the "linearly evolved'' density field (so that
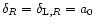 )
and we did not write the normalization constant of the integrals. Then, the integration over the variables aq with
)
and we did not write the normalization constant of the integrals. Then, the integration over the variables aq with  yields the Dirac functions
yields the Dirac functions
 .
The integration over br is now straightforward for
.
The integration over br is now straightforward for  and we obtain:
and we obtain:
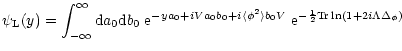 |
|
|
(A.8) |
where the matrix  is obtained from
is obtained from
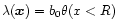 .
Then, using
.
Then, using
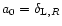 from Eq. (A.5) and making the change of variable
from Eq. (A.5) and making the change of variable
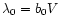 we obtain Eq. (79) in the linear regime (i.e.
we obtain Eq. (79) in the linear regime (i.e.
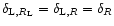 and
and
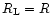 ).
).
Now, we investigate how the previous derivation is modified when we study the non-linear density field
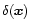 .
We can again define the functional measure
.
We can again define the functional measure
![$[{\rm d}\delta_{\rm L}({\vec x})]$](/articles/aa/full/2002/05/aa1670/img445.gif) (and
(and
![$[{\rm d}\lambda({\vec x})]$](/articles/aa/full/2002/05/aa1670/img467.gif) )
by Eq. (A.3). However, we now introduce the new variable
)
by Eq. (A.3). However, we now introduce the new variable
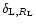 ,
which also defines
,
which also defines
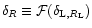 and
and
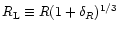 .
Then, we define the functions
.
Then, we define the functions
 by:
by:
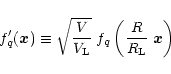 |
(A.9) |
so that we still have the orthonormalization property:
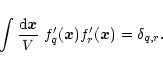 |
(A.10) |
Then, we write the linear density field
 as:
as:
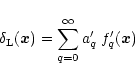 |
(A.11) |
which also implies:
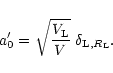 |
(A.12) |
This yields:
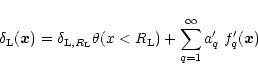 |
(A.13) |
while we write the auxiliary field
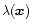 as:
as:
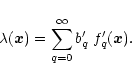 |
(A.14) |
Then, the path-integral (58) now writes:
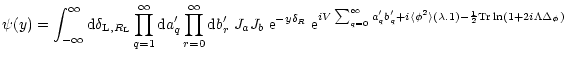 |
|
|
(A.15) |
where we made the changes of variables
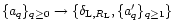 and
and
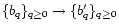 .
In Eq. (A.15) the Jacobians Ja and Jb of these transformations are given by the determinants:
.
In Eq. (A.15) the Jacobians Ja and Jb of these transformations are given by the determinants:
![\begin{displaymath}%
J_a \equiv \left\vert {\rm Det}\left[ \frac{\partial a_i}{\...
...t[ \frac{\partial b_i}{\partial b_j'} \right] \right\vert\cdot
\end{displaymath}](/articles/aa/full/2002/05/aa1670/img480.gif) |
(A.16) |
These Jacobians do not depend on the amplitude  of the density fluctuations. On the other hand, the quasi-linear regime corresponds to the limit
of the density fluctuations. On the other hand, the quasi-linear regime corresponds to the limit
 for a fixed finite y (which leads to finite
for a fixed finite y (which leads to finite
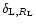 and
and
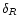 ,
as shown in the Gaussian case in Paper II). In this limit, the generating function
,
as shown in the Gaussian case in Paper II). In this limit, the generating function  is governed by the exponent in Eq. (A.15) which depends on
is governed by the exponent in Eq. (A.15) which depends on 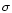 and sets the cutoffs of order
and sets the cutoffs of order 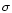 for the density contrast
for the density contrast
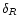 .
Then, we can neglect the Jacobians in Eq. (A.15): they do not contribute to
.
Then, we can neglect the Jacobians in Eq. (A.15): they do not contribute to 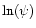 at leading order for
at leading order for
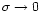 (however, they give a
(however, they give a  -independent prefactor which appears in
-independent prefactor which appears in 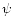 ,
see the discussion below). Moreover, if we make the approximation
,
see the discussion below). Moreover, if we make the approximation
![$\delta_{R}[\delta_{\rm L}] \simeq {\cal F}(\delta_{{\rm L},R_{\rm L}})$](/articles/aa/full/2002/05/aa1670/img483.gif) we can again integrate over aq' for
we can again integrate over aq' for 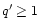 ,
which gives the Dirac functions
,
which gives the Dirac functions
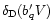 ,
and we eventually recover Eq. (79).
,
and we eventually recover Eq. (79).
Let us now discuss the approximation
![$\delta_{R}[\delta_{\rm L}] \simeq {\cal F}(\delta_{{\rm L},R_{\rm L}})$](/articles/aa/full/2002/05/aa1670/img483.gif) used above. The point is that in the limit
used above. The point is that in the limit
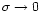 the path-integral (58) and the ordinary integrals (A.15) are dominated by the saddle-points of the exponent. As discussed in Sect. 4.3, because of the spherical symmetry of the physics we investigate there exist some spherical saddle-points, of the form (70). Then, if there are no other saddle-points (or if some other saddle-points exist but they yield a lower contribution to integral, which will vanish in the limit
the path-integral (58) and the ordinary integrals (A.15) are dominated by the saddle-points of the exponent. As discussed in Sect. 4.3, because of the spherical symmetry of the physics we investigate there exist some spherical saddle-points, of the form (70). Then, if there are no other saddle-points (or if some other saddle-points exist but they yield a lower contribution to integral, which will vanish in the limit
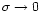 )
the path-integral is given at leading-order by its value for these spherical saddle-points. Note that the case of Gaussian initial conditions studied in Paper II exhibits the same behaviour in a simpler manner. Indeed, in this case there exists only one spherical saddle-point for both the linear and non-linear generating functions
)
the path-integral is given at leading-order by its value for these spherical saddle-points. Note that the case of Gaussian initial conditions studied in Paper II exhibits the same behaviour in a simpler manner. Indeed, in this case there exists only one spherical saddle-point for both the linear and non-linear generating functions
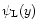 and
and  .
Then, in order to keep only the leading order for
.
Then, in order to keep only the leading order for
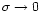 one defines the rescaled generating function
one defines the rescaled generating function
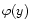 by:
by:
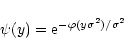 |
(A.17) |
as in Eq. (19), which can be expressed through the path-integral:
![\begin{displaymath}%
{\rm e}^{-\varphi(y)/\sigma^2} = \int [{\rm d}\delta_{\rm L}({\vec x})] \; {\rm e}^{- S[\delta_{\rm L}]/\sigma^2}
\end{displaymath}](/articles/aa/full/2002/05/aa1670/img487.gif) |
(A.18) |
in a fashion similar to Eq. (20). Next, in the quasi-linear limit
 the path-integral in the r.h.s. in Eq. (A.18) is dominated by one saddle-point and taking the logarithm of both sides in Eq. (A.18) one obtains in this limit:
the path-integral in the r.h.s. in Eq. (A.18) is dominated by one saddle-point and taking the logarithm of both sides in Eq. (A.18) one obtains in this limit:
![\begin{displaymath}%
\varphi(y) = \min_{\delta_{\rm L}({\vec x})} S[\delta_{\rm L}]
\end{displaymath}](/articles/aa/full/2002/05/aa1670/img488.gif) |
(A.19) |
as described in Paper II (see also Sect. 3.2). Going back to  this means that in the quasi-linear limit the generating function
this means that in the quasi-linear limit the generating function  is given by the maximum of the exponent which appears in the relevant path-integral. This corresponds to the procedure we described above for the isocurvature CDM scenario in order to get Eq. (79). However, the difference is that in this non-Gaussian case there exists an infinite number of spherical saddle-points with respect to
is given by the maximum of the exponent which appears in the relevant path-integral. This corresponds to the procedure we described above for the isocurvature CDM scenario in order to get Eq. (79). However, the difference is that in this non-Gaussian case there exists an infinite number of spherical saddle-points with respect to
 .
Therefore, at leading order the generating function
.
Therefore, at leading order the generating function  is not given by a unique contribution but rather by the sum of all contributions due to these saddle-points which are parameterized by the variables
is not given by a unique contribution but rather by the sum of all contributions due to these saddle-points which are parameterized by the variables
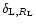 and
and 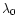 .
.
Finally, we note that the minimum of the action
![$S[\delta_{\rm L}]$](/articles/aa/full/2002/05/aa1670/img383.gif) ,
or the value of the exponent in Eq. (A.15), only provides the leading order contribution to
,
or the value of the exponent in Eq. (A.15), only provides the leading order contribution to 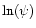 in the limit
in the limit
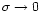 .
This means that it yields the exact exponential
.
This means that it yields the exact exponential 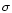 -dependent term of the pdf
-dependent term of the pdf
 which describes the cutoffs of the pdf for density contrasts which are large relative to
which describes the cutoffs of the pdf for density contrasts which are large relative to 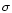 .
In our case, this is the factor
.
In our case, this is the factor
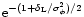 which appears in Eq. (92). However, it does not give the exact multiplicative prefactor of the generating function
which appears in Eq. (92). However, it does not give the exact multiplicative prefactor of the generating function  and of the pdf
and of the pdf
 .
Indeed, the Jacobians Ja and Jb in Eq. (A.15) (or the Gaussian integration around the saddle-point in the Gaussian case) contribute to this term. In the case we study here, this means that Eq. (79) differs from the exact result by a multiplicative factor which may depend on
.
Indeed, the Jacobians Ja and Jb in Eq. (A.15) (or the Gaussian integration around the saddle-point in the Gaussian case) contribute to this term. In the case we study here, this means that Eq. (79) differs from the exact result by a multiplicative factor which may depend on
 and
and  .
Therefore, the expression (92) obtained for the pdf is correct up to a multiplicative factor which may depend on
.
Therefore, the expression (92) obtained for the pdf is correct up to a multiplicative factor which may depend on
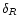 but not on
but not on 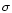 .
This point is also discussed in Sect. 4.4 where we compare Eq. (92) with the result (102) of a simple spherical model. The latter can be seen as an attempt to model this prefactor. Note that for the pdf of the linear density field we do not encounter this difficulty since, as shown above, Eq. (A.8) is actually exact.
.
This point is also discussed in Sect. 4.4 where we compare Eq. (92) with the result (102) of a simple spherical model. The latter can be seen as an attempt to model this prefactor. Note that for the pdf of the linear density field we do not encounter this difficulty since, as shown above, Eq. (A.8) is actually exact.
- Bernardeau, F. 1992, ApJ, 392, 1
In the text
NASA ADS
- Bernardeau, F. 1994a, A&A, 291, 697
In the text
NASA ADS
- Bernardeau, F. 1994b, ApJ, 427, 51
In the text
NASA ADS
- Cramer, H. 1946, Mathematical methods of statistics (Princeton University Press)
In the text
- Falk, T., Rangarajan, R., & Srednicki, M. 1993, ApJ, 403, L1
In the text
NASA ADS
- Gangui, A., Lucchin, F., Matarrese, S., & Mollerach, S. 1994, ApJ, 430, 447
In the text
NASA ADS
- Gradshteyn, I. S., & Ryzhik, I. M. 1965, Table of integrals, series and products, fourth edition (Academic Press)
In the text
- Matarrese, S., Verde, L., & Jimenez, R. 2000, ApJ, 541, 10
In the text
NASA ADS
- Peebles, P. J. E., & Groth, E. J. 1976, A&A, 53, 131
In the text
NASA ADS
- Peebles, P. J. E. 1980, The large scale structure of the universe (Princeton University Press)
In the text
- Peebles, P. J. E. 1999a, ApJ, 510, 523
In the text
NASA ADS
- Peebles, P. J. E. 1999b, ApJ, 510, 531
In the text
NASA ADS
- Press, W. H., & Schechter, P. 1974, ApJ, 187, 425
In the text
NASA ADS
- Robinson, J., & Baker, J. E. 2000, MNRAS, 311, 781
In the text
NASA ADS
- Valageas, P. 1998, A&A, 337, 655
In the text
NASA ADS
- Valageas, P. 2001, A&A, 379, 8 (Paper I)
NASA ADS
- Valageas, P. 2002, A&A, 382, 412 (Paper II)
- Valageas, P. 2002, A&A, 382, 450 (Paper IV)
- Valageas, P. 2002, A&A, 382, 477 (Paper V)
- Verde, L., Jimenez, R., Kamionkowski, M., & Matarrese, S. 2001, MNRAS, 325, 412
In the text
NASA ADS
- Zinn-Justin, J. 1989, Quantum Field Theory and Critical Phenomena (Clarendon Press, Oxford)
In the text
Copyright ESO 2002
![]() of the density contrast within spherical cells in the quasi-linear regime for some non-Gaussian initial conditions. We describe three such models. The first one is a straightforward generalization of the Gaussian scenario. It can be seen as a phenomenological description of a density field where the tails of the linear density contrast distribution would be of the form
of the density contrast within spherical cells in the quasi-linear regime for some non-Gaussian initial conditions. We describe three such models. The first one is a straightforward generalization of the Gaussian scenario. It can be seen as a phenomenological description of a density field where the tails of the linear density contrast distribution would be of the form
![]() ,
where
,
where ![]() is no longer restricted to 2 (as in the Gaussian case). We derive exact results for
is no longer restricted to 2 (as in the Gaussian case). We derive exact results for
![]() in the quasi-linear limit. The second model is a physically motivated isocurvature CDM scenario. Our approach needs to be adapted to this specific case and in order to get convenient analytical results we introduce a simple approximation (which is not related to the gravitational dynamics but to the initial conditions). Then, we find a good agreement with the available results from numerical simulations for the pdf of the linear density contrast for
in the quasi-linear limit. The second model is a physically motivated isocurvature CDM scenario. Our approach needs to be adapted to this specific case and in order to get convenient analytical results we introduce a simple approximation (which is not related to the gravitational dynamics but to the initial conditions). Then, we find a good agreement with the available results from numerical simulations for the pdf of the linear density contrast for
![]() .
We can expect a similar accuracy for the non-linear pdf
.
We can expect a similar accuracy for the non-linear pdf
![]() .
Finally, the third model corresponds to the small deviations from Gaussianity which arise in standard slow-roll inflation. We obtain exact results for the pdf of the density field in the quasi-linear limit, to first-order over the primordial deviations from Gaussianity.
.
Finally, the third model corresponds to the small deviations from Gaussianity which arise in standard slow-roll inflation. We obtain exact results for the pdf of the density field in the quasi-linear limit, to first-order over the primordial deviations from Gaussianity.
![]() (where
(where ![]() is the rms density fluctuation) to obtain all order cumulants. This yields the probability distribution function (pdf)
is the rms density fluctuation) to obtain all order cumulants. This yields the probability distribution function (pdf)
![]() of the density contrast within spherical cells. However, this method only applies to Gaussian initial conditions. Moreover, it may miss some non-perturbative effects.
of the density contrast within spherical cells. However, this method only applies to Gaussian initial conditions. Moreover, it may miss some non-perturbative effects.
![]() in this quasi-linear regime. It is based on a steepest-descent approximation which yields asymptotically exact results in this limit. This allowed us to justify the results obtained by perturbative means and to correct some misconceptions related to non-perturbative effects. Another advantage of our approach is that in principle it can also be applied to non-Gaussian primordial density fluctuations. However, the determination of the relevant saddle-points needed in order to get simple analytic results may then be more difficult. In particular, the method may need to be adapted to specific cases.
in this quasi-linear regime. It is based on a steepest-descent approximation which yields asymptotically exact results in this limit. This allowed us to justify the results obtained by perturbative means and to correct some misconceptions related to non-perturbative effects. Another advantage of our approach is that in principle it can also be applied to non-Gaussian primordial density fluctuations. However, the determination of the relevant saddle-points needed in order to get simple analytic results may then be more difficult. In particular, the method may need to be adapted to specific cases.
![]() for three specific non-Gaussian models, in the quasi-linear regime. Indeed, although observations are consistent with Gaussian initial conditions so far, it is of interest to investigate a broader class of models until any non-Gaussianity is definitely ruled out. Moreover, there exist some reasonable physical scenarios (though somewhat more contrived than the standard CDM model) which give rise to non-Gaussian primordial fluctuations. Finally, even standard inflationary scenarios lead to small deviations from Gaussianity for the primordial density fluctuations.
for three specific non-Gaussian models, in the quasi-linear regime. Indeed, although observations are consistent with Gaussian initial conditions so far, it is of interest to investigate a broader class of models until any non-Gaussianity is definitely ruled out. Moreover, there exist some reasonable physical scenarios (though somewhat more contrived than the standard CDM model) which give rise to non-Gaussian primordial fluctuations. Finally, even standard inflationary scenarios lead to small deviations from Gaussianity for the primordial density fluctuations.
![]() in terms of initial conditions. Then, in Sect. 3 we apply our method to a non-Gaussian model which is a straightforward generalization of the Gaussian case and could be used as a phenomenological tool to reproduce observations in case some departure from Gaussianity would be measured (e.g., in the CMB data). Then, in Sect. 4 we investigate a physically motivated model which describes an isocurvature cold dark matter scenario (Peebles 1999a). In particular, we obtain a good agreement with the available results from numerical simulations for the pdf of the linearly evolved density field. Finally, in Sect. 5 we consider the small primordial deviations from Gaussianity which arise in standard slow-roll inflation.
in terms of initial conditions. Then, in Sect. 3 we apply our method to a non-Gaussian model which is a straightforward generalization of the Gaussian case and could be used as a phenomenological tool to reproduce observations in case some departure from Gaussianity would be measured (e.g., in the CMB data). Then, in Sect. 4 we investigate a physically motivated model which describes an isocurvature cold dark matter scenario (Peebles 1999a). In particular, we obtain a good agreement with the available results from numerical simulations for the pdf of the linearly evolved density field. Finally, in Sect. 5 we consider the small primordial deviations from Gaussianity which arise in standard slow-roll inflation.
![]() of the density contrast
of the density contrast
![]() within a spherical cell of comoving radius R, volume V:
within a spherical cell of comoving radius R, volume V:
![]() given by:
given by:
![]() are fully defined by the two-point correlation:
are fully defined by the two-point correlation:
![]() are determined by the kernel
are determined by the kernel
![]() given in Eq. (10) (or equivalently by
given in Eq. (10) (or equivalently by
![]() given in Eq. (12)). In particular, the average over the initial conditions in Eq. (2) can be written as the path-integral:
given in Eq. (12)). In particular, the average over the initial conditions in Eq. (2) can be written as the path-integral:
![]() of the density field are of the form
of the density field are of the form
![]() ,
where
,
where ![]() is no longer restricted to 2 (as in the Gaussian case). In addition, it allows us to show on a simple example the power of the method we developed in Paper II and how it can be applied to non-Gaussian initial conditions.
is no longer restricted to 2 (as in the Gaussian case). In addition, it allows us to show on a simple example the power of the method we developed in Paper II and how it can be applied to non-Gaussian initial conditions.
![]() (i.e. the Laplace transform of the pdf
(i.e. the Laplace transform of the pdf
![]() )
is simply given by the Gaussian weight
)
is simply given by the Gaussian weight
![]() in the path-integral (14) which takes the average of
in the path-integral (14) which takes the average of
![]() over all possible initial states, as we recalled in the previous section. A straightforward generalization of the Gaussian case (14) is to modify this weight. Thus, one can consider the case where the average over the field
over all possible initial states, as we recalled in the previous section. A straightforward generalization of the Gaussian case (14) is to modify this weight. Thus, one can consider the case where the average over the field
![]() is given by:
is given by:
![]() we simply follow the steps of the calculation developed in Paper II. Thus, we first define a new generating function
we simply follow the steps of the calculation developed in Paper II. Thus, we first define a new generating function
![]() through:
through:
![]() is independent of the normalization of the kernel
is independent of the normalization of the kernel
![]() .
Thus, as in Paper II we can apply the steepest-descent method in the limit
.
Thus, as in Paper II we can apply the steepest-descent method in the limit
![]() .
Indeed, it is clear than in this limit the path-integral (20) is dominated by the global minimum of the action
.
Indeed, it is clear than in this limit the path-integral (20) is dominated by the global minimum of the action
![]() while the contributions from other points
while the contributions from other points
![]() are exponentially damped. Then, the steepest-descent method yields asymptotically exact results in this limit. We briefly describe below the main steps of this steepest-descent method. Since the derivation is very close to the one performed in Paper II for the Gaussian case we refer the reader to that paper for the details of the calculation. Note that the Gaussian case actually corresponds to
are exponentially damped. Then, the steepest-descent method yields asymptotically exact results in this limit. We briefly describe below the main steps of this steepest-descent method. Since the derivation is very close to the one performed in Paper II for the Gaussian case we refer the reader to that paper for the details of the calculation. Note that the Gaussian case actually corresponds to ![]() .
.
![]() .
The condition which expresses that the point
.
The condition which expresses that the point
![]() is an extremum (or a saddle-point) is:
is an extremum (or a saddle-point) is:
![]() is described by the well-known spherical collapse solution of the gravitational dynamics. This reads:
is described by the well-known spherical collapse solution of the gravitational dynamics. This reads:
![]() defined by
defined by
![]() is given by the value of the action
is given by the value of the action
![]() at this minimum which yields the implicit system:
at this minimum which yields the implicit system:
![]() in the quasi-linear regime through Eq. (32) which yields
in the quasi-linear regime through Eq. (32) which yields ![]() as in Eq. (19). This will give the pdf
as in Eq. (19). This will give the pdf
![]() through Eq. (3). However, we first need to check that the spherical saddle-point defined by Eq. (26) and Eq. (27) is the global minimum of the action
through Eq. (3). However, we first need to check that the spherical saddle-point defined by Eq. (26) and Eq. (27) is the global minimum of the action
![]() .
For small positive y this can be rigorously proved as for the Gaussian case, using the fact that the kernel
.
For small positive y this can be rigorously proved as for the Gaussian case, using the fact that the kernel
![]() is positive definite. We shall not repeat this discussion here (see Sect. 3.4 in Paper II). For negative y this cannot be proved as it may actually happen that the spherical saddle-point is only a local minimum. This also occurs in the Gaussian case for a power-spectrum with n<0. This case is discussed in great details in Paper II where we show that the steepest-descent method remains useful but requires a careful justification. Since the same discussion can be applied to the non-Gaussian model we investigate here we refer the reader to Paper II for a description of such cases and we shall only give a brief comment on this point in the next section.
is positive definite. We shall not repeat this discussion here (see Sect. 3.4 in Paper II). For negative y this cannot be proved as it may actually happen that the spherical saddle-point is only a local minimum. This also occurs in the Gaussian case for a power-spectrum with n<0. This case is discussed in great details in Paper II where we show that the steepest-descent method remains useful but requires a careful justification. Since the same discussion can be applied to the non-Gaussian model we investigate here we refer the reader to Paper II for a description of such cases and we shall only give a brief comment on this point in the next section.
![]() defined by Eq. (32). Indeed, this latter expression can also be written:
defined by Eq. (32). Indeed, this latter expression can also be written:
![]() are replaced by the curves
are replaced by the curves
![]() .
That is, the minimum point
.
That is, the minimum point ![]() which yields
which yields
![]() in Eq. (33) is given by the first contact of the curve
in Eq. (33) is given by the first contact of the curve
![]() with the curves
with the curves
![]() of varying height h. For y>0 we start from below at
of varying height h. For y>0 we start from below at ![]() while for y<0 we start from above at
while for y<0 we start from above at ![]() .
.
![]() has no global minimum. This can be seen from the geometrical construction shown in Fig. 4 or simply from Eq. (33). Indeed, as noticed in Paper II from Eq. (31) we have the following asymptotic behaviour for
has no global minimum. This can be seen from the geometrical construction shown in Fig. 4 or simply from Eq. (33). Indeed, as noticed in Paper II from Eq. (31) we have the following asymptotic behaviour for
![]() :
:
![]() itself from the results obtained in Sect. 3.2. We consider the case n=-1 and
itself from the results obtained in Sect. 3.2. We consider the case n=-1 and ![]() where the action
where the action
![]() always shows a global minimum. Then, the Laplace transform
always shows a global minimum. Then, the Laplace transform ![]() is fully defined by the generating function
is fully defined by the generating function
![]() given by Eq. (32).
given by Eq. (32).
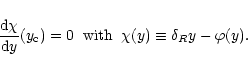
![]() .
It is given by the constraint
.
It is given by the constraint
![]() and it is orthogonal to the real axis at the point
and it is orthogonal to the real axis at the point ![]() .
This path is also symmetric about the real axis which implies that the result for
.
This path is also symmetric about the real axis which implies that the result for
![]() is real. Note that in the quasi-linear limit
is real. Note that in the quasi-linear limit
![]() the contributions to the integral (35) only come from an infinitesimal neighbourhood of the saddle-point
the contributions to the integral (35) only come from an infinitesimal neighbourhood of the saddle-point
![]() around the real axis.
around the real axis.
![]() is not regular at the origin since we have
is not regular at the origin since we have
![]() for small real y. Then, the pdf
for small real y. Then, the pdf
![]() is not analytic at
is not analytic at
![]() and the moments of the pdf cannot be recovered from the expansion (4). This is not the case for Gaussian initial conditions where both
and the moments of the pdf cannot be recovered from the expansion (4). This is not the case for Gaussian initial conditions where both
![]() and
and
![]() are regular at the origin.
are regular at the origin.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{MS1670f1.eps}\end{figure}](/articles/aa/full/2002/05/aa1670/Timg148.gif)
![]() for the case
for the case ![]() and n=-1 (solid line). We also have
and n=-1 (solid line). We also have
![]() where
where
![]() is the rms density fluctuation. Since
is the rms density fluctuation. Since
![]() we numerically compute
we numerically compute ![]() from the second moment of the linear pdf
from the second moment of the linear pdf
![]() .
Indeed, the steepest-descent method developed in Sect. 3.2 also yields the linear pdf
.
Indeed, the steepest-descent method developed in Sect. 3.2 also yields the linear pdf
![]() of the linearly-evolved density field. In this case we have
of the linearly-evolved density field. In this case we have
![]() and
and
![]() ,
hence we simply need to take
,
hence we simply need to take
![]() in Eq. (32) (of course, for
in Eq. (32) (of course, for ![]() this gives back the Gaussian). The non-linear evolution of the density field increases the value of
this gives back the Gaussian). The non-linear evolution of the density field increases the value of
![]() at large positive
at large positive
![]() (it actually spreads the linear pdf towards larger value of the density) as in the Gaussian case but the cutoff remains much sharper. It also induces a cutoff at low densities
(it actually spreads the linear pdf towards larger value of the density) as in the Gaussian case but the cutoff remains much sharper. It also induces a cutoff at low densities
![]() which expresses the fact that the actual density
which expresses the fact that the actual density ![]() is positive.
is positive.
![]() (dotted lines). These curves were derived in Paper II. As could be anticipated from Eq. (15) the large density contrast cutoff of the linear pdf is much sharper than for the Gaussian case: it goes as
(dotted lines). These curves were derived in Paper II. As could be anticipated from Eq. (15) the large density contrast cutoff of the linear pdf is much sharper than for the Gaussian case: it goes as
![]() since here we take
since here we take ![]() .
Moreover, we can check that for the actual non-linear pdfs this trend remains valid. More precisely, as shown in Paper II the high-density tail of the non-linear pdf for Gaussian initial conditions is of the form:
.
Moreover, we can check that for the actual non-linear pdfs this trend remains valid. More precisely, as shown in Paper II the high-density tail of the non-linear pdf for Gaussian initial conditions is of the form:
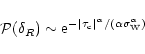
![]() at large densities, whatever the details of the model. In fact, we have shown that in the quasi-linear regime the tail (39) (actually the generating function
at large densities, whatever the details of the model. In fact, we have shown that in the quasi-linear regime the tail (39) (actually the generating function
![]() itself !) is common to all models of the class described by Eq. (16) with
itself !) is common to all models of the class described by Eq. (16) with
![]() .
.
![]() is constrained to be close to 2 (the Gaussian value). Note that this family of models presents the advantage of containing the usual Gaussian scenario as a particular case.
is constrained to be close to 2 (the Gaussian value). Note that this family of models presents the advantage of containing the usual Gaussian scenario as a particular case.
![]() )
the CDM mass distribution is (Peebles 1999a):
)
the CDM mass distribution is (Peebles 1999a):
![]() as in Eq. (2) but the Gaussian average over
as in Eq. (2) but the Gaussian average over
![]() which appeared in Eq. (14) must now be replaced by a Gaussian average over
which appeared in Eq. (14) must now be replaced by a Gaussian average over
![]() :
:
![]() no longer yields a Dirac functional. Besides, even for the linear density field the expression (63) is not very convenient since it is not obvious to compute the logarithm. Thus, for practical purposes it only provides the first few cumulants of
no longer yields a Dirac functional. Besides, even for the linear density field the expression (63) is not very convenient since it is not obvious to compute the logarithm. Thus, for practical purposes it only provides the first few cumulants of
![]() ,
which can be obtained by expanding the logarithm as a series over y and computing the trace of each power of
,
which can be obtained by expanding the logarithm as a series over y and computing the trace of each power of
![]() .
Hence we can try a steepest-descent approximation to the path-integral (58), in the spirit of the calculations presented in Paper II for the Gaussian case or in Sect. 3 for a simple non-Gaussian model. More precisely, we may try to evaluate the contributions of all possible saddle-points to the path-integral (58).
.
Hence we can try a steepest-descent approximation to the path-integral (58), in the spirit of the calculations presented in Paper II for the Gaussian case or in Sect. 3 for a simple non-Gaussian model. More precisely, we may try to evaluate the contributions of all possible saddle-points to the path-integral (58).
![]() .
This yields:
.
This yields:
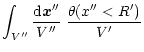
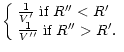
![]() we can estimate the trace which appeared in Eq. (58) as follows. Let us note this trace as
we can estimate the trace which appeared in Eq. (58) as follows. Let us note this trace as
![]() .
Then, we have:
.
Then, we have:
![]() is not very convenient for practical calculations hence it is natural to use the approximation (78) which was derived for such spherical fields
is not very convenient for practical calculations hence it is natural to use the approximation (78) which was derived for such spherical fields
![]() .
This yields:
.
This yields:
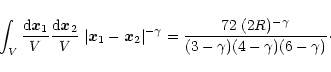
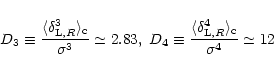
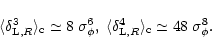
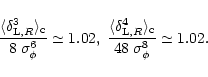
![]() which yields:
which yields:
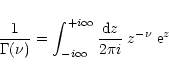
![]() using the inverse Laplace transform (3). Indeed, the integration over y simply gives the Dirac function
using the inverse Laplace transform (3). Indeed, the integration over y simply gives the Dirac function
![]() .
After a trivial integration over
.
After a trivial integration over ![]() we obtain:
we obtain:
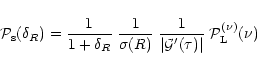
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS1670f2.eps}\end{figure}](/articles/aa/full/2002/05/aa1670/Timg313.gif)
![]() and
and
![]() .
The dashed-line shows the pdf
.
The dashed-line shows the pdf
![]() of the linearly evolved density field, from Eq. (93). As could be seen from Eq. (93) it is strongly non-Gaussian, whatever the value of
of the linearly evolved density field, from Eq. (93). As could be seen from Eq. (93) it is strongly non-Gaussian, whatever the value of
![]() .
In particular, for large overdensities
.
In particular, for large overdensities
![]() the pdf exhibits a simple exponential cutoff (multiplied by a power
the pdf exhibits a simple exponential cutoff (multiplied by a power
![]() )
which is much smoother than a Gaussian cutoff. Hence the number of extreme events (i.e.
)
which is much smoother than a Gaussian cutoff. Hence the number of extreme events (i.e.
![]() )
is much larger than for the Gaussian case, as can be checked by comparison with the lower dotted curve in Fig. 1. We can see that for
)
is much larger than for the Gaussian case, as can be checked by comparison with the lower dotted curve in Fig. 1. We can see that for
![]() our predictions agree very well with the results of numerical simulations from Robinson & Baker (2000) for the linear density field (shown by the histogram). Note that for the theoretical curve we used the exact value of
our predictions agree very well with the results of numerical simulations from Robinson & Baker (2000) for the linear density field (shown by the histogram). Note that for the theoretical curve we used the exact value of
![]() obtained from Eq. (83) in order to get a meaningful comparison. Hence the variance of the approximate pdf (93) underestimates the exact result by a factor
obtained from Eq. (83) in order to get a meaningful comparison. Hence the variance of the approximate pdf (93) underestimates the exact result by a factor
![]() .
However, we can check that the agreement is quite good for
.
However, we can check that the agreement is quite good for
![]() so that for practical purposes one can directly use Eq. (93). For instance, Robinson & Baker (2000) actually use the linear pdf to apply the usual Press-Schechter recipe (Press & Schechter 1974) in order to estimate the mass function of just-collapsed objects.
so that for practical purposes one can directly use Eq. (93). For instance, Robinson & Baker (2000) actually use the linear pdf to apply the usual Press-Schechter recipe (Press & Schechter 1974) in order to estimate the mass function of just-collapsed objects.
![]() .
In particular, we see that the pdf vanishes for
.
In particular, we see that the pdf vanishes for
![]() ,
that is the exact lower bound
,
that is the exact lower bound
![]() has been replaced by
has been replaced by
![]() .
This is due to the approximation (76). Indeed, the exact linear pdf obtained from Eqs. (3) and (60) is:
.
This is due to the approximation (76). Indeed, the exact linear pdf obtained from Eqs. (3) and (60) is:
![]() defined in Eq. (94), as in the usual Gaussian case. This scaling property was actually used in order to obtain
defined in Eq. (94), as in the usual Gaussian case. This scaling property was actually used in order to obtain
![]() from the numerical simulations. However, this property is not exact and it fails for underdensities since as noticed above the linear density contrast also satisfies the lower bound
from the numerical simulations. However, this property is not exact and it fails for underdensities since as noticed above the linear density contrast also satisfies the lower bound
![]() which does not scale as
which does not scale as ![]() (e.g., contrary to
(e.g., contrary to ![]() it is independent of scale).
it is independent of scale).
![]() from Eq. (92) (dotted line) and from Eq. (102) (solid line) from the spherical model (97) for the actual non-linear density field. In Fig. 2 we used the approximation:
from Eq. (92) (dotted line) and from Eq. (102) (solid line) from the spherical model (97) for the actual non-linear density field. In Fig. 2 we used the approximation:
![]() in the first case) and they apply to "non-standard'' scenarios for the generation of primordial density fluctuations. For instance, the second model is based on a multifield inflationary scenario. By contrast, in standard slow-roll inflation the primordial density perturbations should be very close to Gaussian. Nevertheless, they may still show some small deviations from Gaussianity. In particular, one is led to consider models where the perturbed primordial gravitational potential
in the first case) and they apply to "non-standard'' scenarios for the generation of primordial density fluctuations. For instance, the second model is based on a multifield inflationary scenario. By contrast, in standard slow-roll inflation the primordial density perturbations should be very close to Gaussian. Nevertheless, they may still show some small deviations from Gaussianity. In particular, one is led to consider models where the perturbed primordial gravitational potential
![]() is given by:
is given by:
![]() of the linearly evolved density field was already studied in Matarrese et al. (2000) using path-integral methods like those described in Sect. 5.2 below. However, they did not investigate the effects of the non-linear dynamics. On the other hand, Verde et al. (2000) studied the observational tests which may constrain such deviations from Gaussian initial conditions.
of the linearly evolved density field was already studied in Matarrese et al. (2000) using path-integral methods like those described in Sect. 5.2 below. However, they did not investigate the effects of the non-linear dynamics. On the other hand, Verde et al. (2000) studied the observational tests which may constrain such deviations from Gaussian initial conditions.
![]() we again introduce the Laplace transform
we again introduce the Laplace transform ![]() as in Eq. (2), which yields again Eq. (52). Next, we introduce the linear density field through the Dirac functional
as in Eq. (2), which yields again Eq. (52). Next, we introduce the linear density field through the Dirac functional
![]() .
This Dirac functional can again be expressed through an auxiliary real field
.
This Dirac functional can again be expressed through an auxiliary real field
![]() so that the analog of Eq. (54) now reads:
so that the analog of Eq. (54) now reads:
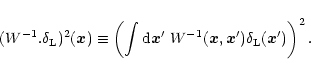
![]() by:
by:
![]() and
and
![]() ,
so that
,
so that
![]() .
This yields from Eq. (129):
.
This yields from Eq. (129):
![]() obtained in Eq. (129) we can derive the pdf
obtained in Eq. (129) we can derive the pdf
![]() ,
using the inverse Laplace transform (3). This yields:
,
using the inverse Laplace transform (3). This yields:
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS1670f3.eps}\end{figure}](/articles/aa/full/2002/05/aa1670/Timg431.gif)
![]() .
In order to compare the pdf with the case of Gaussian initial conditions we also show the results obtained for
.
In order to compare the pdf with the case of Gaussian initial conditions we also show the results obtained for
![]() (dotted curves). Let us recall that Eq. (142) for the pdf of the linearly evolved density field is exact to first-order in
(dotted curves). Let us recall that Eq. (142) for the pdf of the linearly evolved density field is exact to first-order in
![]() .
In agreement with Eq. (140) we can check that
.
In agreement with Eq. (140) we can check that
![]() leads to a small positive skewness for the linear density field. In particular, the high-density tail of the pdf is slightly enhanced. We can see that this feature remains valid for the non-linear pdf
leads to a small positive skewness for the linear density field. In particular, the high-density tail of the pdf is slightly enhanced. We can see that this feature remains valid for the non-linear pdf
![]() .
However, as gravitational clustering proceeds the deviations from Gaussianity become dominated by the non-linear dynamics over the slight primordial non-Gaussianity. More precisely, we can obtain the low-order moments of the density field through the expansion (4). At the lowest order in y we have
.
However, as gravitational clustering proceeds the deviations from Gaussianity become dominated by the non-linear dynamics over the slight primordial non-Gaussianity. More precisely, we can obtain the low-order moments of the density field through the expansion (4). At the lowest order in y we have
![]() and
and
![]() where the parameter S3 is given by the standard result (e.g., Bernardeau 1994a):
where the parameter S3 is given by the standard result (e.g., Bernardeau 1994a):
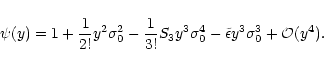
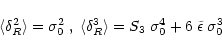
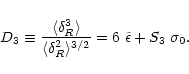
![]() of the density contrast within spherical cells in the quasi-linear regime for three specific non-Gaussian models.
of the density contrast within spherical cells in the quasi-linear regime for three specific non-Gaussian models.
![]() ,
where
,
where ![]() is no longer required to be equal to two (as in the Gaussian case). Then, we have shown that the derivation of the pdf presented for the Gaussian case can be directly extended to this model. This provides again exact results for the pdf in the quasi-linear limit.
is no longer required to be equal to two (as in the Gaussian case). Then, we have shown that the derivation of the pdf presented for the Gaussian case can be directly extended to this model. This provides again exact results for the pdf in the quasi-linear limit.
![]() for
for
![]() by comparison with numerical simulations. For lack of data we could not check our prediction for the non-linear pdf
by comparison with numerical simulations. For lack of data we could not check our prediction for the non-linear pdf
![]() but we can expect a good agreement of the same accuracy.
but we can expect a good agreement of the same accuracy.
![]() for such non-Gaussian scenarios may be used to estimate the mass function of just-collapsed objects, using a straightforward extension of the Press-Schechter recipe. Note that we shall discuss the Press-Schechter prescription in the light of the formalism developed in Paper II and used in this work in a companion article (Paper IV).
for such non-Gaussian scenarios may be used to estimate the mass function of just-collapsed objects, using a straightforward extension of the Press-Schechter recipe. Note that we shall discuss the Press-Schechter prescription in the light of the formalism developed in Paper II and used in this work in a companion article (Paper IV).
![]() .
The latter can be defined from a discretization procedure (i.e. a spatial grid for the coordinate
.
The latter can be defined from a discretization procedure (i.e. a spatial grid for the coordinate ![]() with an infinitesimal spacing) but an equivalent formulation (e.g., Zinn-Justin 1989) is to expand the function
with an infinitesimal spacing) but an equivalent formulation (e.g., Zinn-Justin 1989) is to expand the function
![]() on a complete set of real orthonormal functions fq (in the Hilbert space
on a complete set of real orthonormal functions fq (in the Hilbert space
![]() ):
):
![]() .
We can again define the functional measure
.
We can again define the functional measure
![]() (and
(and
![]() )
by Eq. (A.3). However, we now introduce the new variable
)
by Eq. (A.3). However, we now introduce the new variable
![]() ,
which also defines
,
which also defines
![]() and
and
![]() .
Then, we define the functions
.
Then, we define the functions
![]() by:
by:
![]() used above. The point is that in the limit
used above. The point is that in the limit
![]() the path-integral (58) and the ordinary integrals (A.15) are dominated by the saddle-points of the exponent. As discussed in Sect. 4.3, because of the spherical symmetry of the physics we investigate there exist some spherical saddle-points, of the form (70). Then, if there are no other saddle-points (or if some other saddle-points exist but they yield a lower contribution to integral, which will vanish in the limit
the path-integral (58) and the ordinary integrals (A.15) are dominated by the saddle-points of the exponent. As discussed in Sect. 4.3, because of the spherical symmetry of the physics we investigate there exist some spherical saddle-points, of the form (70). Then, if there are no other saddle-points (or if some other saddle-points exist but they yield a lower contribution to integral, which will vanish in the limit
![]() )
the path-integral is given at leading-order by its value for these spherical saddle-points. Note that the case of Gaussian initial conditions studied in Paper II exhibits the same behaviour in a simpler manner. Indeed, in this case there exists only one spherical saddle-point for both the linear and non-linear generating functions
)
the path-integral is given at leading-order by its value for these spherical saddle-points. Note that the case of Gaussian initial conditions studied in Paper II exhibits the same behaviour in a simpler manner. Indeed, in this case there exists only one spherical saddle-point for both the linear and non-linear generating functions
![]() and
and ![]() .
Then, in order to keep only the leading order for
.
Then, in order to keep only the leading order for
![]() one defines the rescaled generating function
one defines the rescaled generating function
![]() by:
by:
![]() ,
or the value of the exponent in Eq. (A.15), only provides the leading order contribution to
,
or the value of the exponent in Eq. (A.15), only provides the leading order contribution to ![]() in the limit
in the limit
![]() .
This means that it yields the exact exponential
.
This means that it yields the exact exponential ![]() -dependent term of the pdf
-dependent term of the pdf
![]() which describes the cutoffs of the pdf for density contrasts which are large relative to
which describes the cutoffs of the pdf for density contrasts which are large relative to ![]() .
In our case, this is the factor
.
In our case, this is the factor
![]() which appears in Eq. (92). However, it does not give the exact multiplicative prefactor of the generating function
which appears in Eq. (92). However, it does not give the exact multiplicative prefactor of the generating function ![]() and of the pdf
and of the pdf
![]() .
Indeed, the Jacobians Ja and Jb in Eq. (A.15) (or the Gaussian integration around the saddle-point in the Gaussian case) contribute to this term. In the case we study here, this means that Eq. (79) differs from the exact result by a multiplicative factor which may depend on
.
Indeed, the Jacobians Ja and Jb in Eq. (A.15) (or the Gaussian integration around the saddle-point in the Gaussian case) contribute to this term. In the case we study here, this means that Eq. (79) differs from the exact result by a multiplicative factor which may depend on
![]() and
and ![]() .
Therefore, the expression (92) obtained for the pdf is correct up to a multiplicative factor which may depend on
.
Therefore, the expression (92) obtained for the pdf is correct up to a multiplicative factor which may depend on
![]() but not on
but not on ![]() .
This point is also discussed in Sect. 4.4 where we compare Eq. (92) with the result (102) of a simple spherical model. The latter can be seen as an attempt to model this prefactor. Note that for the pdf of the linear density field we do not encounter this difficulty since, as shown above, Eq. (A.8) is actually exact.
.
This point is also discussed in Sect. 4.4 where we compare Eq. (92) with the result (102) of a simple spherical model. The latter can be seen as an attempt to model this prefactor. Note that for the pdf of the linear density field we do not encounter this difficulty since, as shown above, Eq. (A.8) is actually exact.