A&A 382, 722-729 (2002)
DOI: 10.1051/0004-6361:20011664
Radiative processes in the intracluster plasma
N. Itoh1 - T. Sakamoto1
- S. Kusano1 - Y. Kawana1
- S. Nozawa2
1 - Department of Physics, Sophia University, 7-1 Kioi-cho, Chiyoda-ku, Tokyo, 102-8554, Japan
2 -
Josai Junior College for Women, 1-1 Keyakidai, Sakado-shi, Saitama,
350-0290, Japan
Received 6 June 2001 / Accepted 7 November 2001
Abstract
We present useful analytic fitting formulae for the study of the radiative processes which take place in the hot intracluster plasma (the plasma which exists in the clusters of galaxies). The first is for the frequency-integrated emissivity of the relativistic thermal bremsstrahlung. The Gaunt factor for the relativistic thermal bremsstrahlung as a function of the ionic charge 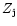 ,
the electron temperature
,
the electron temperature 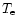 ,
and the photon frequency
,
and the photon frequency 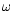 has been recently calculated by us and its analytic fitting formula has been presented. In this paper we will integrate this Gaunt factor over the photon frequency
has been recently calculated by us and its analytic fitting formula has been presented. In this paper we will integrate this Gaunt factor over the photon frequency 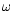 and express the results by accurate analytic fitting formulae. These results will be useful when one wishes to evaluate the total amount of energy emitted by the hot intracluster plasma as well as other hot plasmas that exist in supernova remnants. The present results for the frequency-integrated emissivity of the thermal bremsstrahlung generally have accuracy of the order of 0.1%, thus making the present results the most accurate to date that calculate the thermal bremsstrahlung due to electron-ion scattering. The present accurate results will be especially useful for the analysis of the precision data taken by the Chandra X-Ray Observatory and XMM-Newton. The second analytic fitting formula that we will present in this paper is for the thermal Sunyaev-Zeldovich effect for clusters of galaxies. The thermal Sunyaev-Zeldovich effect for clusters of galaxies has been recently calculated with high precision by the present authors as well as by other groups. We have, in particular, presented an analytic fitting formula for this effect. In this paper we will present an analytic fitting formula which has still higher accuracy. The present fitting formula will be particularly suited for the forthcoming measurements of the kinematical Sunyaev-Zeldovich effect such as the BOLOCAM project that will be carried out in the crossover frequency region where the thermal Sunyaev-Zeldovich signal changes from negative to positive sign.
and express the results by accurate analytic fitting formulae. These results will be useful when one wishes to evaluate the total amount of energy emitted by the hot intracluster plasma as well as other hot plasmas that exist in supernova remnants. The present results for the frequency-integrated emissivity of the thermal bremsstrahlung generally have accuracy of the order of 0.1%, thus making the present results the most accurate to date that calculate the thermal bremsstrahlung due to electron-ion scattering. The present accurate results will be especially useful for the analysis of the precision data taken by the Chandra X-Ray Observatory and XMM-Newton. The second analytic fitting formula that we will present in this paper is for the thermal Sunyaev-Zeldovich effect for clusters of galaxies. The thermal Sunyaev-Zeldovich effect for clusters of galaxies has been recently calculated with high precision by the present authors as well as by other groups. We have, in particular, presented an analytic fitting formula for this effect. In this paper we will present an analytic fitting formula which has still higher accuracy. The present fitting formula will be particularly suited for the forthcoming measurements of the kinematical Sunyaev-Zeldovich effect such as the BOLOCAM project that will be carried out in the crossover frequency region where the thermal Sunyaev-Zeldovich signal changes from negative to positive sign.
Key words: galaxies: clusters: general - plasmas - radiation mechanisms thermal - relativity - cosmic microwave background - cosmology: theory
In recent years we have published two series of papers aimed at laying accurate theoretical foundations for the study of high-temperature plasmas that exist in clusters of galaxies. The first series of papers is concerned with accurate calculations of the relativistic thermal bremsstrahlung Gaunt factor for the intracluster plasma (Nozawa et al. 1998a; Itoh et al. 2000b). The relativistic thermal bremsstrahlung Gaunt factor is an essential physical quantity for the determination of the electron temperature of the hot intracluster plasma from the analysis of the X-ray observational data. Their calculation is based on the method of Itoh and collaborators (Itoh et al. 1985; Nakagawa et al. 1987; Itoh et al. 1990; Itoh et al. 1991, 1997). In calculating the relativistic thermal bremsstrahlung Gaunt factor for the high-temperature, low-density plasma, Nozawa et al. (1998a) have made use of the Bethe-Heitler cross section (Bethe & Heitler 1934) corrected by the Elwert factor (Elwert 1939). They have also calculated the Gaunt factor using the Coulomb-distorted wave functions for nonrelativistic electrons following the method of Karzas & Latter (1961). The Bethe-Heitler-Elwert method gives accurate results at high temperatures, whereas the Karzas-Latter method gives exact results at low temperatures (nonrelativistic limit). Nozawa et al. (1998a) have confirmed that the two methods give almost identical results at intermediate temperatures, thereby proving the validity of the two methods. Other references on the calculation of the thermal bremsstrahlung Gaunt factor include Culhane (1969), Culhane & Acton (1970), Raymond & Smith (1977), Gronenschild & Mewe (1978), Gould (1980), Svensson (1982), Dermer (1986), Mewe et al. (1986), and Carson (1988). Svensson (1982), Haug (1985) and Dermer (1986), in particular, have carried out extremely detailed calculations including the electron-electron bremsstrahlung contribution. They have found that the contribution of the electron-electron bremsstrahlung at the electron temperature of 108 K is about 1% of that of the electron-ion bremsstrahlung. In this paper we will restrict ourselves to the electron-ion bremsstrahlung contribution and calculate this process accurately. We will report on an accurate calculation of the electron-electron bremsstrahlung in a future paper.
In this paper, we will consider the optically thin case. Therefore the radiation field is not in equilibrium with the matter. Hence we assume that no positrons exist. As far as the intracluster plasma is concerned, this assumption is justified, thereby making the positron contribution entirely negligible. The contributions of the positrons in the optically thick plasma have been discussed by Svensson (1982), Haug (1985) and Dermer (1986) as well as by our group (Itoh et al. 1985; Nakagawa et al. 1987; Itoh et al. 1990; Itoh et al. 1991, 1997). In this paper we will assume that the electrons are in complete thermal equilibrium. Under certain conditions the electron thermalization will be incomplete because of the bremsstrahlung process. This subject has been fully discussed by Dermer & Liang (1989). The recent discovery of the hard X-ray emission from some galaxy clusters (Fusco-Femiano et al. 1999; Fusco-Femiano et al. 2000; Fusco-Femiano et al. 2001) suggests the existence of a nonthermal component in the X-ray emission from some galaxy clusters. This nonthermal emission requires special treatment. In this paper we will restrict ourselves to the case of pure thermal emission. We also restrict ourselves to the calculation of the single-photon bremsstrahlung process. Our aim is to produce the most accurate results for the single-photon electron-ion bremsstrahlung process in the semirelativistic regime.
Nozawa et al. (1998a) have presented the results of the numerical calculations in the form of extensive numerical tables. The grid of their numerical table is made fine enough so that smooth interpolations can be carried out for the applications of the results to the analyses of various astrophysical observational data. In order to facilitate the application of the numerical results further, Itoh et al. (2000b) have smoothly combined the two results, employing the Bethe-Heitler-Elwert Gaunt factor at high temperatures and the nonrelativistic exact Gaunt factor at low temperatures. They have expressed the results in the form of accurate analytic fitting formulae. These Gaunt factors are the most accurate Gaunt factors currently available.
In this paper we will integrate these Gaunt factors over the photon frequency 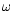 ,
and present accurate analytic fitting formulae for the frequency-integrated Gaunt factors for relativistic thermal bremsstrahlung. These frequency-integrated Gaunt factors will be useful when one wishes to evaluate the total amount of energy emitted by the hot intracluster plasma as well as other hot plasmas that exist in supernova remnants. The present results for the frequency-integrated emissivity of the thermal bremsstrahlung generally have accuracy of the order of 0.1%, thereby making the present results the most accurate to date that calculate the thermal bremsstrahlung due to electron-ion scattering. The present accurate results will be ideally suited for the analysis of the precision data obtained by the Chandra X-Ray Observatory and XMM-Newton.
,
and present accurate analytic fitting formulae for the frequency-integrated Gaunt factors for relativistic thermal bremsstrahlung. These frequency-integrated Gaunt factors will be useful when one wishes to evaluate the total amount of energy emitted by the hot intracluster plasma as well as other hot plasmas that exist in supernova remnants. The present results for the frequency-integrated emissivity of the thermal bremsstrahlung generally have accuracy of the order of 0.1%, thereby making the present results the most accurate to date that calculate the thermal bremsstrahlung due to electron-ion scattering. The present accurate results will be ideally suited for the analysis of the precision data obtained by the Chandra X-Ray Observatory and XMM-Newton.
The second series of papers is concerned with accurate relativistic calculations of the Sunyaev-Zeldovich effects for clusters of galaxies (Itoh et al. 1998; Nozawa et al. 1998b; Itoh et al. 2000a; Nozawa et al. 2000). The original Sunyaev-Zeldovich formula (Zeldovich & Sunyaev 1969; Sunyaev & Zeldovich 1972, 1980a, 1980b, 1981) has been derived from a kinetic equation for the photon distribution function taking into account the Compton scattering by electrons: the Kompaneets equation (Kompaneets 1957; Weymann 1965). The original Kompaneets equation has been derived with a nonrelativistic approximation for the electron. However, recent X-ray observations have revealed the existence of many high-temperature galaxy clusters (David et al. 1993; Arnaud et al. 1994; Markevitch et al. 1994; Markevitch et al. 1996; Holzapfel et al. 1997; Mushotzky & Scharf 1997; Markevitch 1998). In particular, Tucker et al. (1998) reported the discovery of a galaxy cluster with the electron temperature
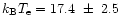 keV. Rephaeli and his collaborator (Rephaeli 1995; Rephaeli & Yankovitch 1997) have emphasized the need to take into account the relativistic corrections to the Sunyaev-Zeldovich effect for clusters of galaxies.
keV. Rephaeli and his collaborator (Rephaeli 1995; Rephaeli & Yankovitch 1997) have emphasized the need to take into account the relativistic corrections to the Sunyaev-Zeldovich effect for clusters of galaxies.
In recent years remarkable progress has been achieved in the theoretical studies of the relativistic corrections to the Sunyaev-Zeldovich effects for clusters of galaxies. Stebbins (1997) generalized the Kompaneets equation. Itoh et al. (1998) have adopted a relativistically covariant formalism to describe the Compton scattering process (Berestetskii et al. 1982; Buchler & Yueh 1976), thereby obtaining higher-order relativistic corrections to the thermal Sunyaev-Zeldovich effect in the form of the Fokker-Planck expansion. In their derivation, the scheme to conserve the photon number at every stage of the expansion that has been proposed by Challinor & Lasenby (1998) played an essential role. The results of Challinor & Lasenby (1998) are in agreement with those of Itoh et al. (1998). The latter results include higher-order expansions. Itoh et al. (1998) have also calculated the collision integral of the Boltzmann equation numerically and have compared the results with those obtained by the Fokker-Planck expansion method. They have confirmed that the Fokker-Planck expansion method gives an excellent result for
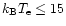 keV, where
keV, where 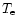 is the electron temperature. For
is the electron temperature. For
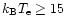 keV, however, the Fokker-Planck expansion results show non-negligible deviations from the results obtained by the numerical integration of the collision term of the Boltzmann equation.
keV, however, the Fokker-Planck expansion results show non-negligible deviations from the results obtained by the numerical integration of the collision term of the Boltzmann equation.
Nozawa et al. (1998b) have extended their method to the case where the galaxy cluster is moving with a peculiar velocity with respect to CMB. They have thereby obtained the relativistic corrections to the kinematical Sunyaev-Zeldovich effect. Challinor & Lasenby (1999) have confirmed the correctness of the result obtained by Nozawa et al. (1998b). Sazonov & Sunyaev (1998a, 1998b) have calculated the kinematical Sunyaev-Zeldovich effect by a different method. Their results are in agreement with those of Nozawa et al. (1998b). The latter authors have given the results of the higher-order expansions.
Itoh et al. (2000a) have also applied their method to the calculation of the relativistic corrections to the polarization Sunyaev-Zeldovich effect (Sunyaev & Zeldovich 1980b, 1981). They have thereby confirmed the result of Challinor et al. (2000) which has been obtained with a completely different method. Recent works on the polarization Sunyaev-Zeldovich effect include Audit & Simons (1999), Hansen & Lilje (1999), and Sazonov & Sunyaev (1999).
In the present paper we address ourselves to the numerical calculation of the relativistic corrections to the thermal Sunyaev-Zeldovich effect. As stated above, Itoh et al. (1998) have carried out the numerical integration of the collision term of the Boltzmann equation. This method produces the exact results without the power series expansion approximation. Sazonov & Sunyaev (1998a, 1998b) have reported the results of the Monte Carlo calculations on the relativistic corrections to the Sunyaev-Zeldovich effect. In Sazonov & Sunyaev (1998b), a numerical table that summarizes the results of the Monte Carlo calculations has been presented. This table is of great value when one wishes to calculate the relativistic corrections to the Sunyaev-Zeldovich effect for galaxy clusters of extremely high temperatures. Accurate analytic fitting formulae would be still more convenient to use for the observers who wish to analyze the galaxy clusters with extremely high temperatures.
Nozawa et al. (2000) have presented an accurate analytic fitting formula which summarizes the results of the numerical integration of the collision term of the Boltzmann equation for the relativistic thermal Sunyaev-Zeldovich effect. The fitting has been carried out for the ranges
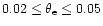 and
and
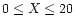 ,
where
,
where
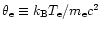 ,
,
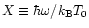 ,
,
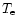 is the electron temperature,
is the electron temperature, 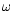 is the angular frequency of the photon, and T0 is the temperature of the cosmic microwave background radiation. The accuracy of the fitting is better than 0.1% for most of the parameter region. However, the fitting for the crossover frequency region where the thermal Sunyaev-Zeldovich signal changes from negative to positive sign was extremely difficult, and the accuracy in this region was much poorer, amounting to a few tens % in some cases. In view of the forthcoming measurements of the kinematical Sunyaev-Zeldovich effect such as the BOLOCAM project (Bock et al. 1996) which will be carried out by tuning at the crossover frequency region (Mauskopf et al. 2000), it is extremely important to improve upon our previous fitting formula (Nozawa et al. 2000) and obtain an analytic fitting formula that has high accuracy even for the crossover frequency region. This is the task to which we will address ourselves in this paper.
is the angular frequency of the photon, and T0 is the temperature of the cosmic microwave background radiation. The accuracy of the fitting is better than 0.1% for most of the parameter region. However, the fitting for the crossover frequency region where the thermal Sunyaev-Zeldovich signal changes from negative to positive sign was extremely difficult, and the accuracy in this region was much poorer, amounting to a few tens % in some cases. In view of the forthcoming measurements of the kinematical Sunyaev-Zeldovich effect such as the BOLOCAM project (Bock et al. 1996) which will be carried out by tuning at the crossover frequency region (Mauskopf et al. 2000), it is extremely important to improve upon our previous fitting formula (Nozawa et al. 2000) and obtain an analytic fitting formula that has high accuracy even for the crossover frequency region. This is the task to which we will address ourselves in this paper.
The present authors (Itoh et al. 2001) have recently calculated the relativistic corrections to the multiple scattering effect on the Sunyaev-Zeldovich effect in the isotropic approximation. They have found that the multiple scattering effects are at most 0.2% for the observed galaxy clusters thereby showing that the multiple scattering effects can be safely neglected for the observed galaxy clusters. By combining the recent works of the present authors including the present paper, X-ray astronomers and radio astronomers working on the galaxy clusters will be provided with accurate basic physical data in order to analyze their observational data. The present paper is organized as follows. In Sect. 2 we calculate the frequency-integrated Gaunt factor for the relativistic thermal bremsstrahlung. In Sect. 3 we calculate the frequency-integrated Gaunt factor for the nonrelativistic thermal bremsstrahlung. In Sect. 4 we present an analytic fitting formula for thermal Sunyaev-Zeldovich effect which has high accuracy even for the crossover frequency region. Concluding remarks will be given in Sect. 5.
The thermal bremsstrahlung emissivity is expressed in terms of the thermally averaged relativistic Gaunt factor
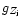 (Nozawa et al. 1998a) by
(Nozawa et al. 1998a) by
where 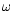 is the angular frequency of the emitted photon,
is the angular frequency of the emitted photon, 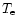 is the temperature of the electrons (in kelvins),
is the temperature of the electrons (in kelvins), 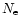 is the number density of the electrons (in cm-3), and
is the number density of the electrons (in cm-3), and 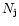 is the number density of the ions with the charge
is the number density of the ions with the charge 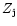 (in cm-3). In Nozawa et al. (1998a), the nonrelativistic Gaunt factor
(in cm-3). In Nozawa et al. (1998a), the nonrelativistic Gaunt factor
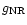 has also been calculated. This Gaunt factor is exact in the low-temperature limit. At intermediate temperatures, it has been confirmed by Nozawa et al. (1998a) that the relativistic Gaunt factor that has been calculated with the use of the Bethe-Heitler crosssection corrected by the Elwert factor shows excellent agreement with the nonrelativistic exact Gaunt factor. At higher temperatures, the nonrelativistic Gaunt factor deviates from the relativistic Gaunt factor because of the insufficiency of the nonrelativistic approximation. These two Gaunt factors have been tabulated in Nozawa et al. (1998a).
has also been calculated. This Gaunt factor is exact in the low-temperature limit. At intermediate temperatures, it has been confirmed by Nozawa et al. (1998a) that the relativistic Gaunt factor that has been calculated with the use of the Bethe-Heitler crosssection corrected by the Elwert factor shows excellent agreement with the nonrelativistic exact Gaunt factor. At higher temperatures, the nonrelativistic Gaunt factor deviates from the relativistic Gaunt factor because of the insufficiency of the nonrelativistic approximation. These two Gaunt factors have been tabulated in Nozawa et al. (1998a).
At sufficiently high temperatures, we adopt the relativistic Gaunt factor. At sufficiently low temperatures, we adopt the nonrelativistic exact Gaunt factor.
At intermediate temperatures, these two Gaunt factors coincide with each other for small values of 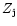 .
For larger values of
.
For larger values of 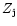 ,
the two Gaunt factors show small discrepancies even at intermediate temperatures. Therefore, we generally interpolate between the two Gaunt factors smoothly at intermediate temperatures. To be more precise, we find the point at which the discrepancy between the two Gaunt factors (for fixed values of
,
the two Gaunt factors show small discrepancies even at intermediate temperatures. Therefore, we generally interpolate between the two Gaunt factors smoothly at intermediate temperatures. To be more precise, we find the point at which the discrepancy between the two Gaunt factors (for fixed values of 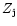 and u) is the smallest as a function of the temperature. Then we interpolate between the two Gaunt factors smoothly using a sine function. The temperature range for the interpolation is
and u) is the smallest as a function of the temperature. Then we interpolate between the two Gaunt factors smoothly using a sine function. The temperature range for the interpolation is 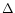
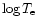 =
= 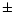 0.1 to
0.1 to 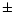 0.5 with respect to the central temperature at which the discrepancy is the smallest depending on the minimum value of the discrepancy. The analytic fitting formulae of
0.5 with respect to the central temperature at which the discrepancy is the smallest depending on the minimum value of the discrepancy. The analytic fitting formulae of
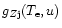 for
for
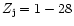 ,
,
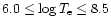 ,
,
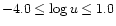 have been presented in Itoh et al. (2000b).
have been presented in Itoh et al. (2000b).
Now we will integrate the emissivity over the whole frequency range. Thus we obtain
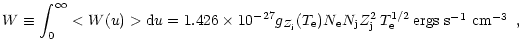 |
|
|
(3) |
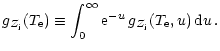 |
|
|
(4) |
In Fig. 1 we show the frequency integrated Gaunt factor
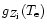 as a function of temperature for various values of
as a function of temperature for various values of 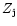 .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms1552fig1.eps} \end{figure}](/articles/aa/full/2002/05/aa1552/Timg33.gif) |
Figure 1:
Frequency integrated Gaunt factor
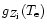 for relativistic thermal bremsstrahlung as a function of temperature for
various values of
for relativistic thermal bremsstrahlung as a function of temperature for
various values of 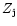 . . |
| Open with DEXTER |
We give an analytic fitting formula for
 .
The range of the fitting is
.
The range of the fitting is
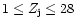 ,
,
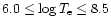 .
We express the frequency integrated Gaunt factor by
.
We express the frequency integrated Gaunt factor by
The coefficients
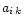 are presented in Table 1. The accuracy of the fitting is generally better than 0.1%. This analytic fitting formula will be extremely useful for the analysis of the precision data taken by the Chandra X-Ray Observatory and XMM-Newton. The present results which calculate thermal bremsstrahlung due to electron-ion scattering generally have accuracy of the order of 0.1%, thereby making the present results the most accurate electron-ion thermal bremsstrahlung bolometric emissivity to date. With the present results we believe the basic physics data for the analysis of the X-ray data taken by the Chandra X-Ray Observatory and XMM-Newton are afforded about 1% accuracy. The remaining 1% accuracy is due to the contribution of the electron-electron thermal bremsstrahlung (Svensson 1982; Haug 1985; Dermer 1986). We wish to report on an accurate calculation of the electron-electron thermal bremsstrahlung in a forthcoming publication.
are presented in Table 1. The accuracy of the fitting is generally better than 0.1%. This analytic fitting formula will be extremely useful for the analysis of the precision data taken by the Chandra X-Ray Observatory and XMM-Newton. The present results which calculate thermal bremsstrahlung due to electron-ion scattering generally have accuracy of the order of 0.1%, thereby making the present results the most accurate electron-ion thermal bremsstrahlung bolometric emissivity to date. With the present results we believe the basic physics data for the analysis of the X-ray data taken by the Chandra X-Ray Observatory and XMM-Newton are afforded about 1% accuracy. The remaining 1% accuracy is due to the contribution of the electron-electron thermal bremsstrahlung (Svensson 1982; Haug 1985; Dermer 1986). We wish to report on an accurate calculation of the electron-electron thermal bremsstrahlung in a forthcoming publication.
Table 1:
Coefficients aik.
| |
k = 0 |
k = 1 |
k = 2 |
k = 3 |
k = 4 |
k = 5 |
| i |
|
|
|
|
|
|
| 0 |
1.40092E+0 |
1.54638E-1 |
-1.23959E-1 |
-1.16975E-1 |
2.14395E-2 |
2.34238E-2 |
| 1 |
-1.00893E-1 |
1.58466E-1 |
2.46348E-1 |
-2.86550E-2 |
-2.24939E-1 |
2.62997E-2 |
| 2 |
-2.40128E-3 |
-2.25452E-1 |
-1.00552E-1 |
2.16833E-1 |
3.13853E-2 |
1.08847E-1 |
| 3 |
6.27343E-2 |
1.90501E-1 |
-2.32050E-1 |
-2.37181E-1 |
3.66311E-1 |
8.57778E-2 |
| 4 |
-9.06484E-2 |
-9.96615E-2 |
4.23102E-1 |
2.43977E-1 |
-3.11848E-1 |
-7.75490E-1 |
| 5 |
9.79512E-3 |
-4.34963E-2 |
2.84554E-1 |
-2.53216E-1 |
-5.57177E-1 |
-7.76022E-1 |
| 6 |
4.41703E-2 |
7.85887E-2 |
-5.65980E-1 |
-8.74859E-2 |
8.92841E-1 |
1.89781E+0 |
| 7 |
1.23203E-1 |
3.35024E-2 |
-1.09511E+0 |
7.33247E-1 |
1.05388E+0 |
1.63143E+0 |
| 8 |
-1.58523E-1 |
3.03478E-2 |
1.19685E+0 |
-5.57371E-1 |
-1.54700E+0 |
-2.48868E+0 |
| 9 |
-4.10980E-2 |
-1.73758E-1 |
7.58040E-1 |
-2.36066E-1 |
-6.52591E-1 |
-9.86901E-1 |
| 10 |
6.81836E-2 |
9.49741E-2 |
-7.80917E-1 |
2.65356E-1 |
8.72583E-1 |
1.25501E+0 |
|
k = 6 |
k = 7 |
k = 8 |
k = 9 |
k = 10 |
i |
|
|
|
|
|
0 |
-5.89208E-2 |
3.92687E-2 |
1.06170E-1 |
-1.47162E-2 |
-4.37176E-2 |
1 |
1.93223E-1 |
-1.74988E-1 |
-2.47926E-1 |
1.20553E-1 |
1.36623E-1 |
2 |
5.05110E-1 |
-2.81975E-1 |
-7.95224E-1 |
1.14518E-1 |
3.42773E-1 |
3 |
-1.02700E+0 |
2.46117E-1 |
1.39771E+0 |
-1.87375E-1 |
-6.23280E-1 |
4 |
7.70985E-3 |
7.80591E-1 |
2.70056E-1 |
-3.03752E-1 |
-2.05378E-1 |
5 |
2.01951E+0 |
1.60661E+0 |
-2.26472E+0 |
-7.94442E-1 |
7.62416E-1 |
6 |
-2.76644E+0 |
-2.75074E+0 |
2.75232E+0 |
1.34593E+0 |
-6.86149E-1 |
7 |
-1.38406E+0 |
-3.84191E+0 |
6.90910E-1 |
1.94313E+0 |
1.00617E-1 |
8 |
3.74683E+0 |
4.67373E+0 |
-3.33774E+0 |
-2.39266E+0 |
6.80864E-1 |
9 |
2.07710E-1 |
2.16066E+0 |
4.09320E-1 |
-1.07379E+0 |
-3.66206E-1 |
10 |
-1.40357E+0 |
-2.48054E+0 |
9.72879E-1 |
1.26406E+0 |
-7.12021E-2 |
The thermal bremsstrahlung emissivity in the nonrelativistic limit is expressed in terms of the nonrelativistic exact Gaunt factor
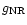 (Nozawa et al. 1998a) by
(Nozawa et al. 1998a) by
where 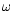 is the angular frequency of the emitted photon,
is the angular frequency of the emitted photon, 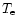 is the temperature of the electrons (in kelvins),
is the temperature of the electrons (in kelvins), 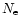 is the number density of the electrons (in cm-3), and
is the number density of the electrons (in cm-3), and 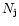 is the number density of the ions with the charge
is the number density of the ions with the charge 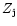 (in cm-3). It should be noted that the thermal bremsstrahlung emissivity in the nonrelativistic limit is a function of
(in cm-3). It should be noted that the thermal bremsstrahlung emissivity in the nonrelativistic limit is a function of 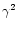 and u only. It does not depend on
and u only. It does not depend on 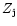 and
and 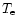 separately, but on the ratio
separately, but on the ratio
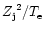 .
This is a remarkable fact for nonrelativistic electrons.
.
This is a remarkable fact for nonrelativistic electrons.
The analytic fitting formula for the nonrelativistic exact Gaunt factor
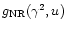 for the ranges
for the ranges
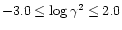 ,
,
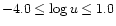 has been presented in Itoh et al. (2000b).
has been presented in Itoh et al. (2000b).
Now we will integrate the nonrelativistic emissivity over the whole frequency range. Thus we obtain
In Fig. 2 we show the frequency integrated nonrelativistic Gaunt factor
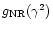 as a function of
as a function of
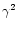 .
A similar graph has been shown in Karzas & Latter (1961).
.
A similar graph has been shown in Karzas & Latter (1961).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms1552fig2.eps} \end{figure}](/articles/aa/full/2002/05/aa1552/Timg54.gif) |
Figure 2:
Frequency integrated Gaunt factor
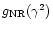 for nonrelativistic thermal bremsstrahlung as a function of
for nonrelativistic thermal bremsstrahlung as a function of
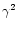 . . |
| Open with DEXTER |
We give an analytic fitting formula for
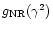 .
The range of the fitting is
.
The range of the fitting is
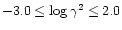 .
We express the frequency integrated nonrelativistic Gaunt factor by
.
We express the frequency integrated nonrelativistic Gaunt factor by
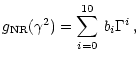 |
|
|
(13) |
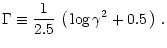 |
|
|
(14) |
The coefficients bi are presented in Table 2. The accuracy of the fitting is generally better than 0.1%. This analytic fitting formula will be useful for the plasma where relativistic effects can be neglected, say
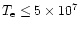 K. This is also useful when one wishes to obtain a simple expression for the bolometric emissivity of thermal bremsstrahlung which is valid for the general chemical element
K. This is also useful when one wishes to obtain a simple expression for the bolometric emissivity of thermal bremsstrahlung which is valid for the general chemical element 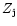 .
.
Table 2:
Coefficients bi.
| i |
bi |
| 0 |
1.42752E+0 |
| 1 |
1.70677E-1 |
| 2 |
-8.13616E-1 |
| 3 |
-4.88059E-1 |
| 4 |
1.33141E+0 |
| 5 |
7.27788E-1 |
| 6 |
-1.50917E+0 |
| 7 |
-5.99317E-1 |
| 8 |
9.86146E-1 |
| 9 |
1.99586E-1 |
| 10 |
-2.72392E-1 |
Itoh et al. (1998) have calculated the fractional distortion of the photon distribution function caused by the thermal Sunyaev-Zeldovich effect
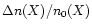 by numerical integration of the collision term of the Boltzmann equation:
by numerical integration of the collision term of the Boltzmann equation:
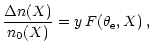 |
|
|
(15) |
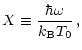 |
|
|
(16) |
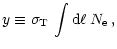 |
|
|
(17) |
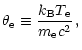 |
|
|
(18) |
where 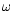 is the angular frequency of the photon (here
is the angular frequency of the photon (here 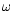 denotes a different quantity from that in Sect. 2 and Sect. 3), and T0 is the temperature of the cosmic microwave background radiation,
denotes a different quantity from that in Sect. 2 and Sect. 3), and T0 is the temperature of the cosmic microwave background radiation,
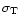 is the Thomson scattering cross section,
is the Thomson scattering cross section, 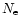 is the electron number density,
is the electron number density, 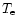 is the electron temperature, and the integral in equation (17) is over the path length of the galaxy cluster. Nozawa et al. (2000) have presented an analytic fitting formula for
is the electron temperature, and the integral in equation (17) is over the path length of the galaxy cluster. Nozawa et al. (2000) have presented an analytic fitting formula for
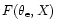 .
Since
.
Since
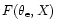 is a rapidly varying function of X, it was extremely difficult to obtain an excellent overall fitting. Nozawa et al.'s (2000) fitting formula has a general accuracy of 0.1%. However, in the crossover frequency region where
is a rapidly varying function of X, it was extremely difficult to obtain an excellent overall fitting. Nozawa et al.'s (2000) fitting formula has a general accuracy of 0.1%. However, in the crossover frequency region where
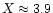 ,
the relative error in some cases amounted to a few tens %. In view of the forthcoming measurements of the kinematical Sunyaev-Zeldovich effect such as BOLOCAM project (Bock et al. 1996) which will be made by tuning at the crossover frequency region (Mauskopf et al. 2000), it is extremely important to improve upon our previous fitting formula (Nozawa et al. 2000) and obtain an analytic fitting formula which has high accuracy even for the crossover frequency region.
,
the relative error in some cases amounted to a few tens %. In view of the forthcoming measurements of the kinematical Sunyaev-Zeldovich effect such as BOLOCAM project (Bock et al. 1996) which will be made by tuning at the crossover frequency region (Mauskopf et al. 2000), it is extremely important to improve upon our previous fitting formula (Nozawa et al. 2000) and obtain an analytic fitting formula which has high accuracy even for the crossover frequency region.
In the observation of the thermal Sunyaev-Zeldovich effect, the directly observed quantity corresponds to the distortion of the spectral intensity
In this paper we will present an analytic fitting formula for 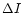 instead of
instead of
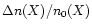 .
.
We express the fitting formula for
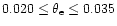 ,
,
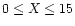 as follows:
as follows:
The functions Y0, Y1, Y2, Y3, and Y4 have been obtained by Itoh et al. (1998) with the Fokker-Planck expansion method, and their explicit expressions have been given. The graph of the exact residual function R is shown in Fig. 3. We take the fitting formula for R as
| R |
= |
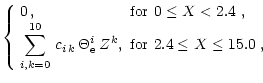 |
(21) |
where
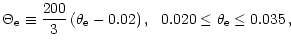 |
|
|
(22) |
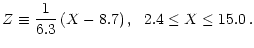 |
|
|
(23) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms1552fig3.eps} \end{figure}](/articles/aa/full/2002/05/aa1552/Timg79.gif) |
Figure 3:
The exact residual function R in Eq. (20) as
a function of X for
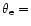 0.02, 0.03.
0.02, 0.03. |
| Open with DEXTER |
Table 3:
Coefficients ci k.
| |
k = 0 |
k = 1 |
k = 2 |
k = 3 |
k = 4 |
k = 5 |
| i |
|
|
|
|
|
|
| 0 |
2.38348E-4 |
-5.55171E-4 |
-4.87242E-3 |
3.15750E-3 |
1.82590E-2 |
-9.21742E-3 |
| 1 |
7.70060E-4 |
-9.02681E-3 |
-1.28519E-2 |
4.58081E-2 |
1.83934E-2 |
-9.91460E-2 |
| 2 |
7.61858E-3 |
1.78164E-1 |
-1.87023E-1 |
-7.16782E-1 |
1.23170E+0 |
1.04791E+0 |
| 3 |
-5.11946E-2 |
-1.94593E+0 |
1.05512E+0 |
6.63376E+0 |
-7.78160E+0 |
-7.79860E+0 |
| 4 |
2.46541E-1 |
1.08690E+1 |
-3.55801E+0 |
-3.08818E+1 |
2.76593E+1 |
2.53107E+1 |
| 5 |
-6.55886E-1 |
-3.59915E+1 |
4.42411E+0 |
8.52378E+1 |
-4.88313E+1 |
-4.01387E+1 |
| 6 |
1.04523E+0 |
7.42310E+1 |
3.94568E+0 |
-1.46255E+2 |
3.29857E+1 |
1.82737E+1 |
| 7 |
-9.82508E-1 |
-9.64435E+1 |
-1.99013E+1 |
1.57577E+2 |
2.49955E+1 |
3.43644E+1 |
| 8 |
5.03123E-1 |
7.67639E+1 |
2.61111E+1 |
-1.03418E+2 |
-6.15775E+1 |
-5.81462E+1 |
| 9 |
-1.08542E-1 |
-3.41927E+1 |
-1.56504E+1 |
3.76441E+1 |
4.18075E+1 |
3.44306E+1 |
| 10 |
2.26789E-4 |
6.52867E+0 |
3.66727E+0 |
-5.79648E+0 |
-1.01200E+1 |
-7.45573E+0 |
| |
k = 6 |
k = 7 |
k = 8 |
k = 9 |
k = 10 |
| i |
|
|
|
|
|
| 0 |
-2.83553E-2 |
1.18551E-2 |
2.03055E-2 |
-5.19957E-3 |
-5.51710E-3 |
| 1 |
3.02605E-2 |
9.94126E-2 |
-6.51622E-2 |
-3.55883E-2 |
2.89212E-2 |
| 2 |
-2.84910E+0 |
-6.72433E-1 |
2.56521E+0 |
1.27246E-1 |
-7.71024E-1 |
| 3 |
1.79093E+1 |
4.20865E+0 |
-1.45222E+1 |
-7.18783E-1 |
3.43548E+0 |
| 4 |
-6.14780E+1 |
-9.40878E+0 |
4.18355E+1 |
2.08060E+0 |
-5.04902E+0 |
| 5 |
1.13587E+2 |
1.00474E+1 |
-6.01877E+1 |
-1.28611E+1 |
-6.82987E+0 |
| 6 |
-1.14236E+2 |
-1.44360E+1 |
4.52390E+1 |
5.62636E+1 |
2.70797E+1 |
| 7 |
5.43853E+1 |
4.60361E+1 |
-3.22989E+1 |
-1.27553E+2 |
-1.99352E+1 |
| 8 |
-4.15730E+0 |
-7.82655E+1 |
4.68655E+1 |
1.53193E+2 |
-1.36621E+1 |
| 9 |
-4.21105E+0 |
5.95121E+1 |
-4.31270E+1 |
-9.35633E+1 |
2.43417E+1 |
| 10 |
4.33807E-1 |
-1.68492E+1 |
1.41021E+1 |
2.29488E+1 |
-8.74479E+0 |
The coefficients
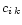 are presented in Table 3. The accuracy of the fitting formula (20), (21) is generally better than 0.5%. The fitting formula has about 1% accuracy in the crossover frequency region where
are presented in Table 3. The accuracy of the fitting formula (20), (21) is generally better than 0.5%. The fitting formula has about 1% accuracy in the crossover frequency region where
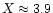 except for the narrow region where the thermal Sunyaev-Zeldovich signal almost exactly vanishes. For
except for the narrow region where the thermal Sunyaev-Zeldovich signal almost exactly vanishes. For
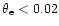 ,
the results of Itoh et al. (1998) give sufficiently accurate results (the accuracy is generally better than 1% for
,
the results of Itoh et al. (1998) give sufficiently accurate results (the accuracy is generally better than 1% for
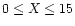 ). The accuracy of the previous (Nozawa et al. 2000) and the present fitting formulae is shown in Figs. 4, 5, respectively.
). The accuracy of the previous (Nozawa et al. 2000) and the present fitting formulae is shown in Figs. 4, 5, respectively.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms1552fig4.eps} \end{figure}](/articles/aa/full/2002/05/aa1552/Timg82.gif) |
Figure 4:
The accuracy of the fitting formula of Nozawa et al. (2000) for various values of
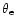 .
The dotted, dashed, dash-dotted and solid curves correspond to .
The dotted, dashed, dash-dotted and solid curves correspond to
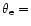 0.020, 0.025, 0.030 and 0.035, respectively. 0.020, 0.025, 0.030 and 0.035, respectively. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms1552fig5.eps} \end{figure}](/articles/aa/full/2002/05/aa1552/Timg83.gif) |
Figure 5:
The accuracy of the present fitting formula (20), (21) for various values of
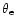 .
The dotted, dashed, dash-dotted and solid curves correspond to .
The dotted, dashed, dash-dotted and solid curves correspond to
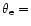 0.020, 0.025, 0.030 and 0.035, respectively. 0.020, 0.025, 0.030 and 0.035, respectively. |
| Open with DEXTER |
We have presented accurate analytic fitting formulae for the frequency-integrated Gaunt factors for relativistic as well as nonrelativistic thermal bremsstrahlung for high temperature plasmas which exist in galaxy clusters and supernova remnants. The accuracy of the fitting formula is generally better than 0.1%. These fitting formulae will be useful when one wishes to evaluate the total amount of energy emitted by the hot intracluster plasma as well as other hot plasmas that exist in supernova remnants. These thermal bremsstrahlung Gaunt factors are the most accurate Gaunt factors currently available. The present results will be extremely useful for the analysis of the precision data taken by the Chandra X-Ray Observatory and XMM-Newton. With the publication of the present results the basic physics data for the analysis of the X-ray observational data are afforded about 1% accuracy. The remaining 1% accuracy is due to the contribution of the electron-electron thermal bremsstrahlung. We will report on the results of the accurate calculation of the electron-electron bremsstrahlung in a forthcoming publication.
We have also succeeded in obtaining an analytic fitting formula for the thermal Sunyaev-Zeldovich effect which has generally about 1% accuracy even for the crossover frequency region where the thermal Sunyaev-Zeldovich signal changes from negative to positive sign. At a frequency where the thermal Sunyaev-Zeldovich signal almost exactly vanishes, the accuracy of the fitting formula becomes poorer than 1%. It is of course impossible to avoid this situation as long as one defines the relative accuracy by the formula
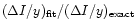 .
In practice, the present fitting formula will be useful for the forthcoming measurements of the kinematical Sunyaev-Zeldvich effect such as the BOLOCAM project which will be carried out by tuning at the crossover frequency region.
.
In practice, the present fitting formula will be useful for the forthcoming measurements of the kinematical Sunyaev-Zeldvich effect such as the BOLOCAM project which will be carried out by tuning at the crossover frequency region.
Acknowledgements
We are most indebted to our referee for many useful suggestions which have helped us tremendously in revising the original manuscript. We thank Professor Y. Oyanagi for allowing us to use the least square fitting program SALS. This work is financially supported in part by the Grant-in-Aid of Japanese Ministry of Education, Science, Sports, and Culture under the contract #10640289, #13640245.
- Arnaud, K. A., Mushotzky, R. F., Ezawa, H., et al. 1994, ApJ, 436, L67
In the text
NASA ADS
- Audit, E., & Simmons, J. F. L. 1999, MNRAS, 305, L27
In the text
NASA ADS
- Berestetskii, V. B., Lifshitz, E. M., & Pitaevskii, L. P. 1982, Quantum Electrodynamics (Oxford: Pergamon)
In the text
- Bethe, H. A., & Heitler, W. 1934, Proc. R. Soc. London A, 146, 83
In the text
- Bock, J. J., DelCastillo, H. M., Turner, A. D., et al. 1996, in Submillimetre and Far-Infrared Space Instrumentation (ESTEC, Noordwijk, Netherlands)
In the text
- Buchler, J. R., & Yueh, W. R. 1976, ApJ, 210, 440
In the text
NASA ADS
- Carson, T. R. 1988, A&A, 189, 319
In the text
NASA ADS
- Challinor, A., Ford, M., & Lasenby, A. 2000, MNRAS, 312, 159
In the text
NASA ADS
- Challinor, A., & Lasenby, A. 1998, ApJ, 499, 1
In the text
NASA ADS
- Challinor, A., & Lasenby, A. 1999, ApJ, 510, 930
In the text
NASA ADS
- Culhane, J. L. 1969, MNRAS, 144, 375
In the text
NASA ADS
- Culhane, J. L., & Acton, L. W. 1970, MNRAS, 151, 141
In the text
NASA ADS
- David, L. P., Slyz, A., Jones, C., Forman, W., & Vrtilek, S. D. 1993, ApJ, 412, 479
In the text
NASA ADS
- Dermer, C. D. 1986, ApJ, 307, 47
In the text
NASA ADS
- Dermer, C. D., & Liang, E. P. 1989, ApJ, 339, 512
In the text
NASA ADS
- Elwert, G. 1939, Ann. Phys., 34, 178
In the text
- Fusco-Femiano, R., Dal Fiume, D., Feretti, L., et al. 1999, ApJ, 513, L21
In the text
NASA ADS
- Fusco-Femiano, R., Dal Fiume, D., De Grandi, S., et al. 2000, ApJ, 534, L7
In the text
NASA ADS
- Fusco-Femiano, R., Dal Fiume, D., Orlandini, M., et al. 2001, ApJ, 552, L97
In the text
NASA ADS
- Gould, R. J. 1980, ApJ, 238, 1026
In the text
NASA ADS
- Gronenschild, E. H. B., & Mewe, R. 1978, A&AS, 32, 283
In the text
NASA ADS
- Hansen, E., & Lilje, P. B. 1999, MNRAS, 306, 153
In the text
NASA ADS
- Haug, E. 1985, A&A, 148, 386
In the text
NASA ADS
- Holzapfel, W. L., Arnaud, M., Ade, P. A. R., et al. 1997, ApJ, 480, 449
In the text
NASA ADS
- Itoh, N., Kawana, Y., Nozawa, S., & Kohyama, Y. 2001, MNRAS, in press
In the text
- Itoh, N., Kohyama, Y., & Nozawa, S. 1998, ApJ, 502, 7
In the text
NASA ADS
- Itoh, N., Kojo, K., & Nakagawa, M. 1990, ApJS, 74, 291
In the text
NASA ADS
- Itoh, N., Kojo, K., Nakagawa, M., et al. 1997, in AAS CD-ROM Series, Astrophysics on Discs, vol. 9 (Washington, D.C.: AAS)
In the text
- Itoh, N., Kuwashima, F., Ichihashi, K., & Mutoh, H. 1991, ApJ, 382, 636
In the text
NASA ADS
- Itoh, N., Nakagawa, M., & Kohyama, Y. 1985, ApJ, 294, 17
In the text
NASA ADS
- Itoh, N., Nozawa, S., & Kohyama, Y. 2000a, ApJ, 533, 588
In the text
NASA ADS
- Itoh, N., Sakamoto, T., Kusano, S., Nozawa, S., & Kohyama, Y. 2000b, ApJS, 128, 125
In the text
NASA ADS
- Karzas, W. J., & Latter, R. 1961, ApJS, 6, 167
In the text
NASA ADS
- Kompaneets, A. S. 1957, Soviet Phys. - JETP Lett., 4, 730
In the text
- Markevitch, M. 1998, ApJ, 504, 27
In the text
NASA ADS
- Markevitch, M., Mushotzky, R., Inoue, H., et al. 1996, ApJ, 456, 437
In the text
NASA ADS
- Markevitch, M., Yamashita, K., Furuzawa, A., & Tawara, Y. 1994, ApJ, 436, L71
In the text
NASA ADS
- Mauskopf, P. D., Ade, P. A. R., Allen, S. W., et al. 2000, ApJ, 538, 505
In the text
NASA ADS
- Mewe, R., Lemen, J. R., & van den Oord, G. H. J. 1986, A&AS, 65, 511
In the text
NASA ADS
- Mushotzky, R. F., & Scharf, C. A. 1997, ApJ, 482, L13
In the text
NASA ADS
- Nakagawa, M., Kohyama, Y., & Itoh, N. 1987, ApJS, 63, 661
In the text
NASA ADS
- Nozawa, S., Itoh, N., Kawana, Y., & Kohyama, Y. 2000, ApJ, 536, 31
In the text
NASA ADS
- Nozawa, S., Itoh, N., & Kohyama, Y. 1998a, ApJ, 507, 530
In the text
NASA ADS
- Nozawa, S., Itoh, N., & Kohyama, Y. 1998b, ApJ, 508, 17
In the text
NASA ADS
- Raymond, J. C., & Smith, B. W. 1977, ApJS, 35, 419
In the text
NASA ADS
- Rephaeli, Y. 1995, ApJ, 445, 33
In the text
NASA ADS
- Rephaeli, Y., & Yankovitch, D. 1997, ApJ, 481, L55
In the text
NASA ADS
- Sazonov, S. Y., & Sunyaev, R. A. 1998a, ApJ, 508, 1
In the text
NASA ADS
- Sazonov, S. Y., & Sunyaev, R. A. 1998b, Astron. Lett., 24, 553
In the text
NASA ADS
- Sazonov, S. Y., & Sunyaev, R. A. 1999, MNRAS, 310, 765
In the text
NASA ADS
- Stebbins, A. 1997, preprint [astro-ph/9705178]
In the text
- Sunyaev, R. A., & Zeldovich, Ya. B. 1972, Comments Astrophys. Space Sci., 4, 173
In the text
- Sunyaev, R. A., & Zeldovich, Ya. B. 1980a, ARA&A, 18, 537
In the text
NASA ADS
- Sunyaev, R. A., & Zeldovich, Ya. B. 1980b, MNRAS, 190, 413
In the text
NASA ADS
- Sunyaev, R. A., & Zeldovich, Ya. B. 1981, Astrophys. Space Phys. Rev., 1, 1
In the text
- Svensson, R. 1982, ApJ, 258, 335
In the text
NASA ADS
- Tucker, W., Blanco, P., Rappoport, S., et al. 1998, ApJ, 496, L5
In the text
NASA ADS
- Weymann, R. 1965, Phys. Fluids, 8, 2112
In the text
- Zeldovich, Ya. B., & Sunyaev, R. A. 1969, Ap&SS, 4, 301
In the text
NASA ADS
Copyright ESO 2002
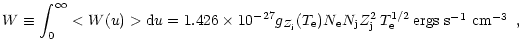
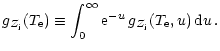
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms1552fig1.eps} \end{figure}](/articles/aa/full/2002/05/aa1552/Timg33.gif)
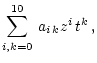
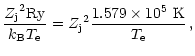
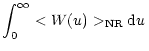
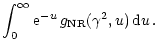
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms1552fig2.eps} \end{figure}](/articles/aa/full/2002/05/aa1552/Timg54.gif)
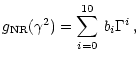
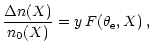
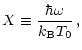
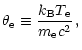
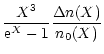
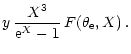
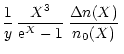
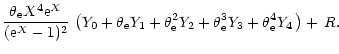
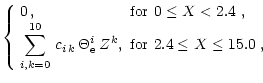
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms1552fig3.eps} \end{figure}](/articles/aa/full/2002/05/aa1552/Timg79.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms1552fig4.eps} \end{figure}](/articles/aa/full/2002/05/aa1552/Timg82.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms1552fig5.eps} \end{figure}](/articles/aa/full/2002/05/aa1552/Timg83.gif)