We analyse the consequences of the recently measured parallax of SSCygni (Harrison et al. 1999) on the accretion disc limit cycle model. Using the observed long term light curve of SSCyg and
A&A 382, 124-129 (2002)
DOI: 10.1051/0004-6361:20011627
M. R. Schreiber 1,2 - B. T. Gänsicke 1
1 - Universitäts-Sternwarte, Geismarlandstr. 11, 37083 Göttingen,
Germany
2 - Department of Astronomy, University of Cape Town, Private Bag,
Rondebosch 7700, Cape Town, South Africa
Received 2 November 2001 / Accepted 6 November 2001
Abstract
We analyse the consequences of the recently measured
parallax of SSCygni (Harrison et al. 1999) on the accretion disc
limit cycle model. Using the observed long term light curve of
SSCyg and
![]() ,
we obtain for the mean mass
transfer rate
,
we obtain for the mean mass
transfer rate
![]() .
In addition, we calculate the vertical structure of the accretion disc
taking into account heating of the outer disc by the stream impact.
Comparing the mean accretion rate derived from the observations with
the calculated critical mass transfer rate, we
find that the disc instability model disagrees with the observed long
term light curve of SSCyg as
.
In addition, we calculate the vertical structure of the accretion disc
taking into account heating of the outer disc by the stream impact.
Comparing the mean accretion rate derived from the observations with
the calculated critical mass transfer rate, we
find that the disc instability model disagrees with the observed long
term light curve of SSCyg as
![]() is greater or similar to the critical mass
transfer rate.
The failure of the model indicated by this result can be confirmed by
considering that the accretion rate at the onset of the decline should
be exactly equal to the value critical for stability. In contrast to
this prediction of the model, we find that the accretion rate required
to explain the observed visual magnitude at the onset of the decline must be significantly higher than the critical mass transfer rate.
Our results strongly suggest that either the usually assumed temperature
dependence of the viscosity parameter
is greater or similar to the critical mass
transfer rate.
The failure of the model indicated by this result can be confirmed by
considering that the accretion rate at the onset of the decline should
be exactly equal to the value critical for stability. In contrast to
this prediction of the model, we find that the accretion rate required
to explain the observed visual magnitude at the onset of the decline must be significantly higher than the critical mass transfer rate.
Our results strongly suggest that either the usually assumed temperature
dependence of the viscosity parameter ![]() is not a realistic description
of the disc viscosity,
that the mass transfer rate in SSCyg noticeably
increases during the outbursts or, finally, that the HST distance of
is not a realistic description
of the disc viscosity,
that the mass transfer rate in SSCyg noticeably
increases during the outbursts or, finally, that the HST distance of
![]() pc, is too high.
pc, is too high.
Key words: accretion, accretion discs - binaries: close - stars: individual: SSCygni - novae, cataclysmic variables
The dwarf nova SSCyg is among the visually brightest CVs and has a
detailed long term light curve covering more than a century. SSCyg
has, therefore, become the reference object for accretion
disc instability analyses, and its observed light curve has been used
to calibrate the viscosity parameter ![]() .
Cannizzo & Mattei
(1992) examined the long term light curve of
SSCyg (Fig. 1) in detail in order to test the limit
cycle model (Cannizzo 1993a) and found a mean outburst duration
of
.
Cannizzo & Mattei
(1992) examined the long term light curve of
SSCyg (Fig. 1) in detail in order to test the limit
cycle model (Cannizzo 1993a) and found a mean outburst duration
of
![]() d and a mean quiescence time of
d and a mean quiescence time of
![]() d (corresponding to a mean cycle duration of
d (corresponding to a mean cycle duration of
![]() d). In a later paper, Cannizzo & Mattei
(1998) again examined the light curve of
SSCyg, deriving the rise and decay times. Only the mean values are
important in the context of our analysis:
d). In a later paper, Cannizzo & Mattei
(1998) again examined the light curve of
SSCyg, deriving the rise and decay times. Only the mean values are
important in the context of our analysis:
![]() d,
d,
![]() d. These values are obtained using a
conservatively low estimate of the outburst magnitude of mv=8.5.
d. These values are obtained using a
conservatively low estimate of the outburst magnitude of mv=8.5.
![\begin{figure}
\par\includegraphics[width=8.8cm]{H3263_f1.ps}\end{figure}](/articles/aa/full/2002/04/aah3263/Timg27.gif) |
Figure 1: The visual long term light curve of SSCyg compiled from observations made by members of the Association Francaise des Observateurs d'Étoiles Variables. |
| Open with DEXTER | |
However, even though the brightness variation of SSCyg has been
monitored to a high level of precision, its distance has been
highly uncertain. As a consequence, the absolute
magnitude and the accretion rate,
have also been ill-defined. Recently, a high-quality parallax of
SSCyg was obtained using the Hubble Space Telescope (HST) Fine
Guidance Sensor (FGS), which moves the system to a distance 1.5-2 times
larger than previously thought (Harrison et al. 1999). The
HST/FGS distance of ![]() pc is confirmed by
Beuermann (2000), who showed that the accretion disc in SSCyg
contributes significantly to the observed K band flux.
As a consequence of the now firmly established (larger) distance, the
absolute magnitude of SSCyg in outburst increased, too.
Figure 2 shows the absolute visual magnitudes of dwarf
novae at outburst maximum as a function of their orbital period,
adapted from Warner (1987). The arrow displays the impact
of the HST/FGS parallax on SSCyg: the system is now the
absolute brightest dwarf nova in outburst and its maximum absolute magnitude
is brighter than one would expect from its orbital period (Cannizzo 1998).
pc is confirmed by
Beuermann (2000), who showed that the accretion disc in SSCyg
contributes significantly to the observed K band flux.
As a consequence of the now firmly established (larger) distance, the
absolute magnitude of SSCyg in outburst increased, too.
Figure 2 shows the absolute visual magnitudes of dwarf
novae at outburst maximum as a function of their orbital period,
adapted from Warner (1987). The arrow displays the impact
of the HST/FGS parallax on SSCyg: the system is now the
absolute brightest dwarf nova in outburst and its maximum absolute magnitude
is brighter than one would expect from its orbital period (Cannizzo 1998).
The mean accretion rate in SSCyg inferred from its long term
light curve depends, in addition to the absolute magnitude, on the
inclination i of the accretion disc. This system parameter is
somewhat uncertain, most studies of SSCyg suggest
![]() (Ritter & Kolb 1998). A significantly
higher value of
(Ritter & Kolb 1998). A significantly
higher value of
![]() was derived by
Voloshina & Khruzina (1997), but, throughout this paper we assume
the lower value. To account for the influence of the inclination on
the absolute magnitude we follow
Paczynski & Schwarzenberg-Czerny (1980):
was derived by
Voloshina & Khruzina (1997), but, throughout this paper we assume
the lower value. To account for the influence of the inclination on
the absolute magnitude we follow
Paczynski & Schwarzenberg-Czerny (1980):
![\begin{displaymath}\Delta\,M_{v}(i)=-2.5\log\left[\frac{(0.4+0.6\cos\,i)\cos\,i}{0.4}\right],
\end{displaymath}](/articles/aa/full/2002/04/aah3263/img30.gif) |
(1) |
Throughout this paper we use the system parameters of SSCyg
given in the literature, i.e.
the primary mass
![]() (Ritter & Kolb 1998; van Teeseling 1997),
secondary mass
(Ritter & Kolb 1998; van Teeseling 1997),
secondary mass
![]() ,
and orbital period in hours
,
and orbital period in hours
![]() (Ritter & Kolb 1998).
(Ritter & Kolb 1998).
The goal of this section is to check if the "standard'' disc instability model can reproduce the absolute magnitude of the outbursts of SSCyg, taking into account the larger HST/FGS distance, the inclination, and the mean outburst time scales derived from the long term light curve.
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm]{H3263_f2.ps}\end{figure}](/articles/aa/full/2002/04/aah3263/Timg35.gif) |
Figure 2:
The absolute magnitudes of dwarf novae adapted from
Warner (1987) corrected to a mean inclination of
|
| Open with DEXTER | |
Figure 3 shows a light curve computed with the FE/FD DIM code used for the first time in Schreiber & Hessman (1998) and described in detail in Schreiber et al. (2000b). We adapted the parameters suggested by Ludwig et al. (1994) and two different values for the mass transfer rate.
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm]{H3263_f3.ps}\end{figure}](/articles/aa/full/2002/04/aah3263/Timg38.gif) |
Figure 3:
Simulated light curves using the orbital parameters of SSCyg,
|
| Open with DEXTER | |
During an outburst cycle the disc subsequently goes through a
phase of quiescence, rise, adjustment, quasi-stationary outburst
state, and decay. After the heating front has brought the entire disc
into the hot state (rise), the disc redistributes its mass
(adjustment) until it accretes without radial variations of the
accretion rate (quasi-stationary state). Almost all the mass accreted
during an outburst cycle is transferred onto the white dwarf during
this quasi-stationary outburst state (Fig. 3). Thus, to derive a
lower limit for the mass accreted during a mean outburst cycle, one
simply has to multiply the accretion rate of a stationary standard
disc which reaches
![]() with the mean
quasi-steady state duration,
with the mean
quasi-steady state duration,
![]() d
d![]() . Throughout this paper we assume a very
large disc for SSCyg during outburst, i.e.
. Throughout this paper we assume a very
large disc for SSCyg during outburst, i.e. ![]() % of the
primary's Roche radius
% of the
primary's Roche radius
![]() .
(Ritter 1980; Harrop-Allin & Warner 1996)
(
.
(Ritter 1980; Harrop-Allin & Warner 1996)
(
![]() cm for the binary parameter of
SSCyg). Following Buat-Ménard et al. (2001),
we describe the
additional heating of the outer disc due to the stream disc impact
with
cm for the binary parameter of
SSCyg). Following Buat-Ménard et al. (2001),
we describe the
additional heating of the outer disc due to the stream disc impact
with
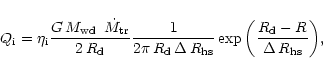 |
(2) |
The accretion rate necessary to reproduce the observed visual
flux during the outburst can be described with a power-law:
| = | 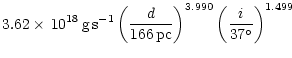 |
||
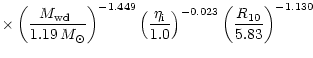 |
|||
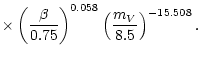 |
(3) |
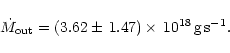 |
(4) |
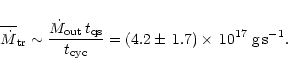 |
(5) |
In the absence of stream impact heating the critical accretion rate is given
by the accretion rate at the upper turning point of the
S-curve
![]() and
can be approximated by a power-law, i.e.
and
can be approximated by a power-law, i.e.
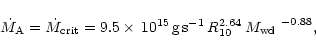 |
(6) |
Taking into account heating of the outer edge of the disc by the
impact of the stream, the critical mass transfer rate is given by an
implicit equation as the turning point of the modified S-curve
![]() depends on the mass transfer rate
itself;
depends on the mass transfer rate
itself;
![]() .
The critical mass transfer rate is then given by a solution of
.
The critical mass transfer rate is then given by a solution of
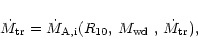 |
(7) |
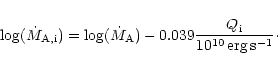 |
(8) |
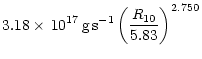 |
|
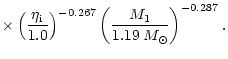 |
(9) |
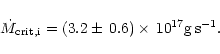 |
(10) |
| + | |||
![$\displaystyle \times\left[1+\left(\displaystyle{\frac{2.5\times\,10^4\,{\rm K}}{T_{{\rm c}}}}\right)^8\right]^{-1},$](/articles/aa/full/2002/04/aah3263/img76.gif) |
(11) |
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm]{H3263_f4.ps}\end{figure}](/articles/aa/full/2002/04/aah3263/Timg80.gif) |
Figure 4:
S-curves for outer radii [in units of
1010cm,
|
| Open with DEXTER | |
For the mean mass transfer rate we obtain
![]() (Fig. 4), which would lead to steady disc accretion. Considering the uncertainties of the involved
parameters, we find
(Fig. 4), which would lead to steady disc accretion. Considering the uncertainties of the involved
parameters, we find
![]() .
.
The critical and the mean mass transfer rate derived in the previous
section are sensitive to the uncertainties in the binary
parameters and the assumed efficiency of stream impact heating
![]() as the additional heating can significantly reduce the
critical mass transfer rate.
Thus, while our results
presented in Sect.3 suggest that the DIM fails in describing the
observations of SSCyg, they do not allow to categorically
exclude the validity of the DIM.
as the additional heating can significantly reduce the
critical mass transfer rate.
Thus, while our results
presented in Sect.3 suggest that the DIM fails in describing the
observations of SSCyg, they do not allow to categorically
exclude the validity of the DIM.
However, in this section we show in an independent way that the observed light
curve of SSCyg provides additional evidence for the failure of the DIM,
independent from the details of stream impact heating or the uncertainties
in the system parameters.
For the mass accretion rate at the onset of the decline
![]() the DIM
predicts
an essentially lower value than required by the
observations as, (a) the DIM predicts that the start of the cooling
front at the outer edge
of the disc defines the onset of the decline in the outburst light curve.
The cooling front starts when the
accretion rate of the quasi stationary disc is exactly equal to the
critical rate, thus,
the DIM
predicts
an essentially lower value than required by the
observations as, (a) the DIM predicts that the start of the cooling
front at the outer edge
of the disc defines the onset of the decline in the outburst light curve.
The cooling front starts when the
accretion rate of the quasi stationary disc is exactly equal to the
critical rate, thus,
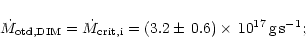 |
(12) |
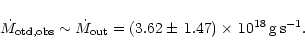 |
(13) |
It is worth noting that even if we completely neglect stream impact heating
the DIM cannot explain the observations. Then, the critical mass transfer rate
can be approximated by
Eq.(6) and the accretion rate necessary to reach the visual flux
during outburst somewhat increases:
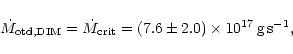 |
(14) |
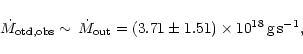 |
(15) |
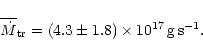 |
(16) |
Considering the "larger'' distance of SSCyg and the observed long
term light curve, we calculated the mean mass transfer rate
![]() .
Taking into account stream
impact heating of the outer disc we find
.
Taking into account stream
impact heating of the outer disc we find
![]() (Fig. 4) which contrasts with the predictions of the DIM: with such a
high mean mass transfer rate, SSCyg should not be a dwarf nova at
all, but a novalike variable with a stationary hot accretion disc.
This result is, however, sensitive to the assumed efficiencies of
stream heating and disk irradiation
and the uncertainties of the binary parameters, the
inclination, and the distance.
While this result on its own is not sufficient to proclaim a
general failure of the DIM, an independent suggestion for a major
problem with the DIM comes from comparing the accretion rate predicted
by the DIM at the onset of the decline with the accretion rate
required by the observed visual magnitude at this point (see
Sect.4). Hence, the conclusion from both these results must
be: the current DIM cannot explain the observations of SSCyg for
a distance of
(Fig. 4) which contrasts with the predictions of the DIM: with such a
high mean mass transfer rate, SSCyg should not be a dwarf nova at
all, but a novalike variable with a stationary hot accretion disc.
This result is, however, sensitive to the assumed efficiencies of
stream heating and disk irradiation
and the uncertainties of the binary parameters, the
inclination, and the distance.
While this result on its own is not sufficient to proclaim a
general failure of the DIM, an independent suggestion for a major
problem with the DIM comes from comparing the accretion rate predicted
by the DIM at the onset of the decline with the accretion rate
required by the observed visual magnitude at this point (see
Sect.4). Hence, the conclusion from both these results must
be: the current DIM cannot explain the observations of SSCyg for
a distance of
![]() pc.
pc.
There are three possibilities that may resolve this problem:
(a) the temperature dependence of ![]() ,
the key ingredient in the
accretion disc limit cycle model, has to be modified, (b) increased
mass transfer during the outburst plays an important rôle, or
finally (c) the HST/FGS distance of 166pc and/or the assumed
inclination are wrong.
,
the key ingredient in the
accretion disc limit cycle model, has to be modified, (b) increased
mass transfer during the outburst plays an important rôle, or
finally (c) the HST/FGS distance of 166pc and/or the assumed
inclination are wrong.
Considering (a), it seems that we do not yet have an adequate
understanding of the viscosity in accretion discs. The instability
necessary to obtain the limit cycle behaviour appears mainly due to an
artificial change of ![]() ,
given by Eq.(11), at the point where
the small "natural'', i.e. without a change of
,
given by Eq.(11), at the point where
the small "natural'', i.e. without a change of ![]() ,
ionisation
instability has been found in the S-curves. There is no physical
reason for this assumption and it might be the case that
,
ionisation
instability has been found in the S-curves. There is no physical
reason for this assumption and it might be the case that ![]() starts to change at higher temperatures than previously assumed.
This would lead to a higher value of the critical mass transfer
rate. As such a modification would affect the dividing line between
dwarf novae and nova likes, one should carefully consider the
consequences for other dwarf nova before changing Eq.(11).
starts to change at higher temperatures than previously assumed.
This would lead to a higher value of the critical mass transfer
rate. As such a modification would affect the dividing line between
dwarf novae and nova likes, one should carefully consider the
consequences for other dwarf nova before changing Eq.(11).
With respect to (b), we point out that another possibility to solve
the problem obtained in Sects. 2-4 is to assume that the mass transfer
increases during the outbursts, e.g. due to irradiation of the
secondary star. Assuming a mean mass transfer rate of
![]() gs-1during quiescence, rise, and decay, the mean mass transfer rate during
the outburst state should be
gs-1during quiescence, rise, and decay, the mean mass transfer rate during
the outburst state should be
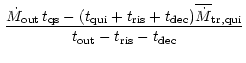 |
|||
| = | (17) |
Finally, considering (c), we can only note that at least one of the
additional CV parallaxes measured with HST, namely UGem, agrees very
well with previous distance estimates (Harrison et al. 1999).
UGem has a noticeably lower accretion rate than SSCyg, therefore
the distance estimated based on K band magnitude and/or spectroscopy
of the secondary star is much less affected by emission from the disc
than in SSCyg. Thus, at least for UGem an error in the HST/FGS
parallax appears extremely unlikely.
However, assuming
![]() and demanding
and demanding
![]() gs-1 for SSCyg
leads to
gs-1 for SSCyg
leads to
![]() gs-1and requires
gs-1and requires
![]() pc for agreement with the DIM.
pc for agreement with the DIM.
Acknowledgements
This research has made use of the AFOEV database, operated at CDS, France. Special thanks are extended to Jean-Marie Hameury, Hans Ritter and Rick Hessman for interesting discussions at the CV-Conference in Göttingen (2001). We also wish to thank an anonymous referee for helpful comments. MRS thanks the Astronomy Department of the UCT for the warm hospitality during a nice and productive stay in March-May 2001 and the DAAD (PKZ:D/01/05718) for financial support. BTG thanks for support from the DLR under grant 50OR99036.