A&A 382, 342-358 (2002)
DOI: 10.1051/0004-6361:20011592
A photometric-dynamic model to simulate coma and jets from a comet
Application to comet Hale-Bopp (C/1995 O1)
R. Vasundhara
Indian Institute of Astrophysics, Bangalore 560034, India
Received 29 December 1998 / Accepted 5 November 2001
Abstract
A model to compute the trajectories of dust grains ejected by comets
to simulate intensity and polarization maps on the sky plane is presented.
The model is used to constrain the silicate to organic mass ratio,
porosity and size distribution of the grains
in the shells and coma of comet Hale-Bopp to explain
1) the published polarizations at three continuum wavelengths at
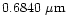 ,
,
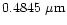 and
and
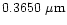 at different phase angles,
2) higher polarization and bluer colour of the shells compared to the coma,
3) the intensity variation and rapid decline of polarization on the
sunward side and 4) higher polarization on the anti-sunward direction.
The present results obtained using Mie theory in the model indicate that although
it is impossible to determine the nature of the silicate
(pyroxenes/olivines or amorphous/crystalline) using the present technique,
the porosity, organic fraction and size distribution of the grains can be
constrained.
The fit to the data set indicates an ensemble of grains in which
at different phase angles,
2) higher polarization and bluer colour of the shells compared to the coma,
3) the intensity variation and rapid decline of polarization on the
sunward side and 4) higher polarization on the anti-sunward direction.
The present results obtained using Mie theory in the model indicate that although
it is impossible to determine the nature of the silicate
(pyroxenes/olivines or amorphous/crystalline) using the present technique,
the porosity, organic fraction and size distribution of the grains can be
constrained.
The fit to the data set indicates an ensemble of grains in which
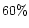 are silicate grains
with a range in silicate to organic mass ratio
are silicate grains
with a range in silicate to organic mass ratio 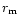 between 1 and 2 and
of medium
porosity <
between 1 and 2 and
of medium
porosity <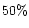 .
A higher silicate content of
.
A higher silicate content of
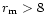 on the
shells can explain their bluer colour.
A narrow size distribution
between
on the
shells can explain their bluer colour.
A narrow size distribution
between
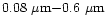 is inferred for
is inferred for  of the grains in
the coma and shell.
These small
grains may not be individual grains but part of loosely bound grains in which
larger grains may also be present which may control the dynamics.
The narrow size distribution may therefore represent statistically the
size range of individual subunits of larger highly porous aggregates of fractal
dimension close to two. The polarizations in JHK bands also support the
aggregate structure.
Despite the availability of an extensive and wide range of
data set on this comet, the inclusion of a large parameter space, lack of
knowledge on the nature of organic material found in comets and use of
Mie theory, which does not adequately represent the polarization phase curves
of natural grains, set limitations in getting a unique solution in the present work.
The results presented here are open to improvements when more realistic
light scattering theories are used in the model and our understanding on the
nature of the organic content of the grains improves. However,
visibility of up to 8-10 shells in well exposed images implies
of the grains in
the coma and shell.
These small
grains may not be individual grains but part of loosely bound grains in which
larger grains may also be present which may control the dynamics.
The narrow size distribution may therefore represent statistically the
size range of individual subunits of larger highly porous aggregates of fractal
dimension close to two. The polarizations in JHK bands also support the
aggregate structure.
Despite the availability of an extensive and wide range of
data set on this comet, the inclusion of a large parameter space, lack of
knowledge on the nature of organic material found in comets and use of
Mie theory, which does not adequately represent the polarization phase curves
of natural grains, set limitations in getting a unique solution in the present work.
The results presented here are open to improvements when more realistic
light scattering theories are used in the model and our understanding on the
nature of the organic content of the grains improves. However,
visibility of up to 8-10 shells in well exposed images implies 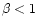 for these grains. As a result of this dynamical constraint which is independent of
the assumptions on the scattering characteristics of the grains, the results
for the dust grains in the shell may be more robust compared to that of the coma.
for these grains. As a result of this dynamical constraint which is independent of
the assumptions on the scattering characteristics of the grains, the results
for the dust grains in the shell may be more robust compared to that of the coma.
Key words: comets - Hale-Bopp: scattering - polarization - colour
Compositions of the silicate grains in the coma of comet
Hale-Bopp have been derived from the spectral emission signatures in the
10 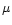 m region by
Crovisier et al. (1997),
Hayward & Hanner (1997)
and Wooden et al. (1999).
Hayward et al. (2000) from their thermal infrared
imaging and spectroscopy of Comet Hale-Bopp found that the silicate features
were up to
m region by
Crovisier et al. (1997),
Hayward & Hanner (1997)
and Wooden et al. (1999).
Hayward et al. (2000) from their thermal infrared
imaging and spectroscopy of Comet Hale-Bopp found that the silicate features
were up to 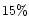 stronger in the jets and halos compared to regions between the
halos. Further, the leading edge of the shells were found by these authors
to have higher color temperature and silicate/continuum flux ratio.
Variation of the silicate features
from central coma to the first two shells has been reported by
Galdemard et al. (1997).
stronger in the jets and halos compared to regions between the
halos. Further, the leading edge of the shells were found by these authors
to have higher color temperature and silicate/continuum flux ratio.
Variation of the silicate features
from central coma to the first two shells has been reported by
Galdemard et al. (1997).
In the optical and near IR regions,
extensive polarization observations at a range of solar phase angles
have been reported by Ganesh et al. (1998),
Hadamcik et al. (1997),
Hasegawa et al. (1999),
Jockers et al. (1997), Jones & Gehrz (2000),
Manset & Bastien (1998) and
Tanga et al. (1997).
Use of the technique of imaging polarimetry by most of these
groups yielded valuable information on the spatial variation of polarization.
Polarization was found to be high in the anti-sunward direction and in
the new shells but rapidly declined
in the older shells in the sunward direction.
Information on the colour of the grains has been reported by
Kiselev & Velichko (1997), Kolokolova et al. (2001)
and Bellucci (1998).
The full potential of these
spatially resolved infrared, colour and polarimetric observational data
can be harvested to investigate the
porosity p,
silicate to organic mass ratio
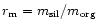 of the grains
and their size distributions separately in the coma and the shells.
The present work describes a photometric model
to map the trajectory of the grains
and to compute the theoretical brightness distribution, colour and polarization
in the coma and the shells for comparison with these reported observations.
of the grains
and their size distributions separately in the coma and the shells.
The present work describes a photometric model
to map the trajectory of the grains
and to compute the theoretical brightness distribution, colour and polarization
in the coma and the shells for comparison with these reported observations.
The computer simulations are based on the basic concepts introduced
by Sekanina (1981, 1991)
and Sekanina & Larson (1984). Except for the outburst
events during 1995, which were sporadic activities, the dust grains are assumed
to be ejected continuously from the sources
radially outwards, from local sunrise to sunset.
The ejected grains are subjected
to the gravitational attraction of the Sun and the Solar radiation pressure
force in the opposite direction. In the present work, since we study the
shells which are close to the nucleus within a distance of 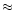
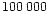 km, it is assumed that
dust grains follow the same Keplerian motion as that of the comet due to solar
gravity. Thus, relative to the
comet, the position of the dust grain can be calculated from its
initial velocity,
the radiation pressure force and the ejection geometry.
km, it is assumed that
dust grains follow the same Keplerian motion as that of the comet due to solar
gravity. Thus, relative to the
comet, the position of the dust grain can be calculated from its
initial velocity,
the radiation pressure force and the ejection geometry.
The velocity
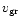 attained by the grains
due to gas drag (Probstein 1969) can be calculated
using the relation by Sekanina (1981):
attained by the grains
due to gas drag (Probstein 1969) can be calculated
using the relation by Sekanina (1981):
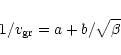 |
(1) |
and also the following equation by Fulle (1987)
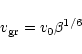 |
(2) |
where  is the ratio of the force due to solar radiation
pressure on the grain to the gravitational force.
Sekanina & Larson (1984) have used Eq. (1) successfully for emission from
discrete sources, and pointed out that it is valid for slightly absorbing
grains with
is the ratio of the force due to solar radiation
pressure on the grain to the gravitational force.
Sekanina & Larson (1984) have used Eq. (1) successfully for emission from
discrete sources, and pointed out that it is valid for slightly absorbing
grains with
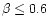 .
The acceleration
.
The acceleration  due to solar
radiation pressure depends on the nature of the grain and the heliocentric
distance. Using the definition of
due to solar
radiation pressure depends on the nature of the grain and the heliocentric
distance. Using the definition of  ,
,
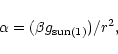 |
(3) |
where
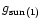 is the acceleration due to solar gravity at one
AU (
is the acceleration due to solar gravity at one
AU (
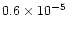 kms-2) and
r the heliocentric distance of the comet.
The value of
kms-2) and
r the heliocentric distance of the comet.
The value of  can be calculated
for a grain of given size and composition
using the relation by Finson & Probstein (1968):
can be calculated
for a grain of given size and composition
using the relation by Finson & Probstein (1968):
where
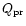 is the scattering efficiency for radiation pressure
of the grain, s its radius and
is the scattering efficiency for radiation pressure
of the grain, s its radius and 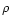 its density.
its density.
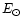 is the total solar radiation per second, c the velocity
of light,
is the total solar radiation per second, c the velocity
of light, 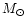 the mass of the Sun and G the universal gravitational
constant.
In the present investigation, the grain size is allowed to vary from
the mass of the Sun and G the universal gravitational
constant.
In the present investigation, the grain size is allowed to vary from
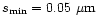 to
to
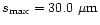 with Hanner (1985)
size distribution law.
Since
the radiation pressure parameter
with Hanner (1985)
size distribution law.
Since
the radiation pressure parameter
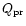 of a
grain material depends both on its size and
the wavelength of radiation,
the value of
of a
grain material depends both on its size and
the wavelength of radiation,
the value of  for a grain of radius s was calculated using the more
precise relation
for a grain of radius s was calculated using the more
precise relation
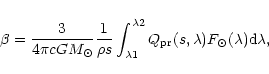 |
(6) |
where,
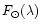 is the mean total solar radiation from the sun per second
per Angstrom at the wavelength
is the mean total solar radiation from the sun per second
per Angstrom at the wavelength 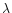 .
The above integration was carried out from
.
The above integration was carried out from
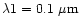 to
to
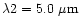 .
.
In the simulation, the path of the dust grain
ejected radially from an active region at a comet-o-centric longitude u, latitude 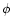 and the nuclear radius R is calculated as a function of time.
Figure 1 shows the ideal case of a spherically symmetric nucleus centered at C.
and the nuclear radius R is calculated as a function of time.
Figure 1 shows the ideal case of a spherically symmetric nucleus centered at C.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms8445f1.eps}\end{figure}](/articles/aa/full/2002/04/aa8445/Timg74.gif) |
Figure 1:
A model to compute the sky plane coordinates of the ejected dust grains.
The comet centered at C is assumed to be spherically symmetric. The grain from the
source at G is ejected with velocity
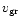 .
The north pole of the comet is
at .
The north pole of the comet is
at 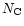 ,
CPE is the direction of Earth's celestial pole, E and S are the
sub-Earth and sub-Sun points respectively. See text for more details. ,
CPE is the direction of Earth's celestial pole, E and S are the
sub-Earth and sub-Sun points respectively. See text for more details. |
| Open with DEXTER |
The sub-Sun and sub-Earth points are S and E respectively and 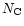 is the North pole of the comet.
The direction of the Earth's north pole is along
is the North pole of the comet.
The direction of the Earth's north pole is along
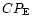 .
The ascending node of the comet's equator on the Earth's equator
is
.
The ascending node of the comet's equator on the Earth's equator
is
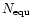 and that on the ecliptic is indicated by
and that on the ecliptic is indicated by
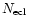 .
Components of
.
Components of 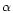 parallel to the plane of the comet's equator and
perpendicular to it
are
parallel to the plane of the comet's equator and
perpendicular to it
are
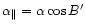 parallel to SF and
parallel to SF and
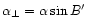 parallel to ST respectively where
parallel to ST respectively where
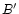 is the comet-o-centric latitude of the Sun.
The longitude of the source and the dust grains are measured from
is the comet-o-centric latitude of the Sun.
The longitude of the source and the dust grains are measured from
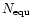 along the direction of rotation of the comet. The longitude of the sub-Earth
point E is
along the direction of rotation of the comet. The longitude of the sub-Earth
point E is 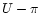 and the angle
and the angle
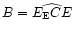 is its latitude.
Dust grains are ejected radially outwards with the velocity
is its latitude.
Dust grains are ejected radially outwards with the velocity
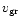 from an
active source
from an
active source
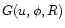 ,
where
,
where
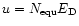 and
and
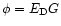 .
Strictly speaking, the grain attains this velocity
after it is dragged by the subliming gas to a few nuclear radii.
However, considering the vast spatial extent of the shell and jet structures
of several rotations which are being modeled, this distance can be ignored.
Relative to the comet, during time t, the dust traverses a
distance
.
Strictly speaking, the grain attains this velocity
after it is dragged by the subliming gas to a few nuclear radii.
However, considering the vast spatial extent of the shell and jet structures
of several rotations which are being modeled, this distance can be ignored.
Relative to the comet, during time t, the dust traverses a
distance
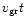 in the radial direction and
a distance
in the radial direction and
a distance
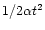 along the Sun - comet direction due to
solar radiation pressure.
along the Sun - comet direction due to
solar radiation pressure.
The position (
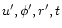 )
of the grain at time t reckoned after ejection is given by:
)
of the grain at time t reckoned after ejection is given by:
where
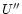 ,
the longitude of the sub-Sun point is given by
,
the longitude of the sub-Sun point is given by
The expressions in Eq. (7) are valid provided the direction and magnitude
of 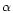 is constant. For the observations during February-May 1997, since we model only up
to a maximum of 8 shells,
a constant value for
is constant. For the observations during February-May 1997, since we model only up
to a maximum of 8 shells,
a constant value for 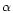 during the period of 8 rotations
may be a valid assumption for comet Hale-Bopp with a period of
11.34 hr (Jorda et al. 1997; Licandro et al. 1998). For
the 1995-96 images, slow apparent
motion of the comet again justifies such an assumption.
during the period of 8 rotations
may be a valid assumption for comet Hale-Bopp with a period of
11.34 hr (Jorda et al. 1997; Licandro et al. 1998). For
the 1995-96 images, slow apparent
motion of the comet again justifies such an assumption.
The angles
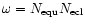 ,
,
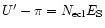 can be calculated from the following relations:
can be calculated from the following relations:
where i is the inclination of the comet's equator to the ecliptic.
The angles
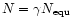 and J, the inclination of the comet's equator to the Earth's
equator are related to the right ascension and declination of the comet's pole:
and J, the inclination of the comet's equator to the Earth's
equator are related to the right ascension and declination of the comet's pole:
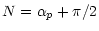 |
|
|
|
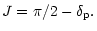 |
|
|
(9) |
The angles U,
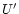 ,
B,
,
B,
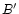 and the position angle Pof the north pole of the comet projected on the sky plane were
calculated using the equations used for calculating the planet-o-centric
positions of the satellite with respect to the planets
(Rhode & Sinclair 1992):
and the position angle Pof the north pole of the comet projected on the sky plane were
calculated using the equations used for calculating the planet-o-centric
positions of the satellite with respect to the planets
(Rhode & Sinclair 1992):
where 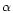 ,
,
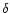 ,
l and b are the geocentric right ascension,
declination, heliocentric ecliptic longitude and latitude of the comet
respectively. The angle
,
l and b are the geocentric right ascension,
declination, heliocentric ecliptic longitude and latitude of the comet
respectively. The angle
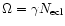 can be calculated using the following relations:
can be calculated using the following relations:
The angles U, P and B are not directly needed for calculating the trajectory of
the dust grain. These are nevertheless useful to visualize the defect of
solar illumination on the comet, the orientation and
aspect angle of the dust jet and shell patterns.
The comet-o-centric coordinates
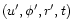 referred to the comet's equator were
calculated using Eq. (7).
These were transformed to the comet-o-centric Earth's equatorial coordinates
referred to the comet's equator were
calculated using Eq. (7).
These were transformed to the comet-o-centric Earth's equatorial coordinates
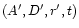 of the grain using the following
equations:
of the grain using the following
equations:
The comet-o-centric equatorial coordinate of the source at
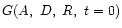 is shown in Fig. 1.
is shown in Fig. 1.
The projected location of the grain on the sky plane with respect to the
comet center is obtained by computing its differential Earth's equatorial
co-ordinates using the following equations (Gurnette & Woolley 1960):
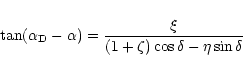 |
(13) |
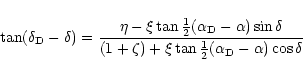 |
(14) |
where
where
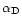 and
and
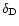 are the geocentric right ascension and declination
of the grain and
are the geocentric right ascension and declination
of the grain and 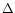 its geocentric distance.
These rigorous expressions in Eqs. (13)-(17) are actually used for
calculating the differential coordinates of satellites with respect to the
primary without any assumptions regarding their latitudes. These are therefore
applicable in the present case of the comet-dust geometry.
its geocentric distance.
These rigorous expressions in Eqs. (13)-(17) are actually used for
calculating the differential coordinates of satellites with respect to the
primary without any assumptions regarding their latitudes. These are therefore
applicable in the present case of the comet-dust geometry.
The intensity of light
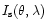 and polarization
and polarization
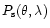 scattered by the grain towards
the observer are given by (Krishnaswamy & Shah 1987):
scattered by the grain towards
the observer are given by (Krishnaswamy & Shah 1987):
where 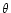 is the scattering angle and
is the scattering angle and
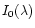 is the solar intensity at
1 AU. The intensity scattering functions
is the solar intensity at
1 AU. The intensity scattering functions
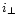 &
&
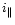 polarized perpendicular and parallel to the scattering plane,
and the scattering efficiency for
radiation pressure
polarized perpendicular and parallel to the scattering plane,
and the scattering efficiency for
radiation pressure
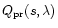 of the grain of radius s at the
wavelength of radiation
of the grain of radius s at the
wavelength of radiation 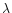 (Eq. (6))
were estimated using Mie scattering using the code
BHMIE by Bohren & Huffman (1983).
(Eq. (6))
were estimated using Mie scattering using the code
BHMIE by Bohren & Huffman (1983).
The position of the grain in the shell projected on the sky plane at a given
time was thus calculated using Eqs. (13) and (14) and the intensity and
polarization of light
scattered by it was computed using the Eqs. (18) and (19).
The colour is calculated following the definition by Jewitt & Meech
(1986) as the normalized reflectivity gradient expressed in 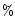 ,
,
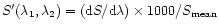 between
wavelengths
between
wavelengths 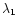 and
and 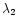 ,
where dS/d
,
where dS/d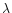 is the rate
of change of reflectivity with wavelength and
is the rate
of change of reflectivity with wavelength and
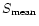 is the mean
reflectivity.
is the mean
reflectivity.
- 1.
- Image of comet Hale-Bopp on 10 April, 1997 in R filter
obtained from the Vainu Bappu observatory was used to investigate the
intensity variations in the shells and the coma.
- 2.
- Published polarizations on 10 June, 1996, 30 September, 1996,
and 9th April, 1997 separately in the coma and bright regions
by Hadamcik et al. (1997) were used to
investigate the nature of the grains in the coma.
- 3.
- As the colour of the grains do not change drastically with phase angle,
we set a conservative limit of
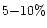 per 1000 Å on the
shells and
per 1000 Å on the
shells and
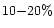 per 1000 Å on the regions between the shells representing
the coma based on the colour reported by
Bellucci (1998),
Furusho et al. (1999),
Kiselev & Velichko (1997) and
Kolokolova et al. (2001).
per 1000 Å on the regions between the shells representing
the coma based on the colour reported by
Bellucci (1998),
Furusho et al. (1999),
Kiselev & Velichko (1997) and
Kolokolova et al. (2001).
- 4.
- Published aperture polarimetric observations at a range of
phase angles by several groups (Sect. 1 and references therein).
Cometary grains are known to be porous and contain an organic component
(Greenberg & Hage 1990; Hage & Greenberg 1990;
Krishnaswamy et al. 1988; Xing & Hanner 1997).
The dynamics as well as the scattering properties of the grains are
affected by porosity and organic content, as both these factors
modify the complex refractive indices of the grains significantly.
The silicaceous components in the grain have been identified from
their emission signatures in the IR spectra in the
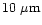 region by Hayward et al. (2000) and
Wooden et al. (1999). In the visible and near IR regions,
it is futile to identify the Mg rich
silicates either in glassy or crystalline form in the composite
grains using their
scattered radiation, as presence of
even a small amount of organic content of 1/12 by weight
will be sufficient to significantly
alter the refractive index of the composite grain.
Hence silicates were sub grouped
into three classes depending on the absorption index k:
region by Hayward et al. (2000) and
Wooden et al. (1999). In the visible and near IR regions,
it is futile to identify the Mg rich
silicates either in glassy or crystalline form in the composite
grains using their
scattered radiation, as presence of
even a small amount of organic content of 1/12 by weight
will be sufficient to significantly
alter the refractive index of the composite grain.
Hence silicates were sub grouped
into three classes depending on the absorption index k:
- 1.
- Mg rich silicates with
0.0001<k<0.001, we
refer to this group as SiX.
Forsterite, with the optical constants by Scott & Duley (1996)
was taken as the sample representative of this class (class 1).
- 2.
- Astronomical
silicate (Draine 1985; Draine & Lee 1984)
with
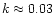 (SiA). The present study uses
the constants of crystalline olivine constructed by Li & Greenberg (1997)
which uses the absorptive index of SiA in the visible region.
Since polarization mainly depends on the
absorptive index, we refer to this sample also as SiA (class 2).
(SiA). The present study uses
the constants of crystalline olivine constructed by Li & Greenberg (1997)
which uses the absorptive index of SiA in the visible region.
Since polarization mainly depends on the
absorptive index, we refer to this sample also as SiA (class 2).
- 3.
- Mg poor silicates characterized by an absorption at wavelengths
shortward of 0.5
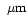 and with k > 0.03. Amorphous olivine (Aol)
and pyroxene (Apy)
with Mg number of 0.5 (Dorschner et al. 1995) were taken as
representatives of this class (class 3).
and with k > 0.03. Amorphous olivine (Aol)
and pyroxene (Apy)
with Mg number of 0.5 (Dorschner et al. 1995) were taken as
representatives of this class (class 3).
At
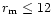 ,
distinction between
SiA and SiX almost vanishes.
Following Li & Greenberg (1998), the organic refractory component was
assumed to be a composite of interstellar refractory (Li & Greenberg 1997)
and amorphous carbon (Rouleau & Martin 1991) of equal mass.
Effective refractive indices of the composite grains were determined using
Bruggmann's mixing rule.
Collections of individual grains of these silicates
with the organic refractory component in the mass ratios
,
distinction between
SiA and SiX almost vanishes.
Following Li & Greenberg (1998), the organic refractory component was
assumed to be a composite of interstellar refractory (Li & Greenberg 1997)
and amorphous carbon (Rouleau & Martin 1991) of equal mass.
Effective refractive indices of the composite grains were determined using
Bruggmann's mixing rule.
Collections of individual grains of these silicates
with the organic refractory component in the mass ratios
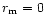 ,
1, 2, 8, 12 and
,
1, 2, 8, 12 and 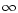 and
the porosities
and
the porosities 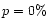 ,
,
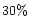 ,
,
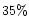 ,
,
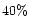 ,
,
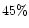 ,
,
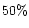 ,
,
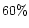 ,
,
 ,
,
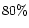 and
and 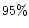 were considered.
were considered.
Phase dependence of polarization carries valuable information on the
interaction between the reflected and refracted components from the grain
along different scattering directions. The fraction of the refracted component
depends on
the optical properties of the grain, its size and shape.
Polarization of light scattered by an ensemble of spherical grains at the three
continuum
wavelengths 0.6840 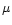 m, 0.4845
m, 0.4845 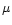 m and
0.3650
m and
0.3650 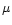 m corresponding to aperture polarimetry observations by
Ganesh et al. (1998) and Manset & Bastien (1998) were
computed.
For a proper match with these observations over the entire range of
phase angles, combinations of grain types and
proper choice of their size distribution are essential.
Hanner size distribution (Hanner 1985)
m corresponding to aperture polarimetry observations by
Ganesh et al. (1998) and Manset & Bastien (1998) were
computed.
For a proper match with these observations over the entire range of
phase angles, combinations of grain types and
proper choice of their size distribution are essential.
Hanner size distribution (Hanner 1985)
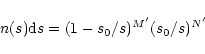 |
(20) |
was used.
The constants s0,
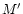 and
and
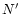 determine the
slopes at the lower and upper size domains and the
radius
determine the
slopes at the lower and upper size domains and the
radius 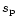 at which n(s) is maximum.
As a first guess, four component equal weight
inter-combinations of the three classes of silicates, each with 30 different combinations of p and
at which n(s) is maximum.
As a first guess, four component equal weight
inter-combinations of the three classes of silicates, each with 30 different combinations of p and 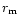 were considered.
A total of
810000 combinations were compared in the least square sense
with the observed phase curves of Ganesh et al. (1998).
The size distribution parameters were varied to improve the
were considered.
A total of
810000 combinations were compared in the least square sense
with the observed phase curves of Ganesh et al. (1998).
The size distribution parameters were varied to improve the 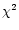 values.
The constants in set 'a' in Table 1 yielded best fit.
values.
The constants in set 'a' in Table 1 yielded best fit.
The intensity contribution
I(s)n(s)ds for this distribution at a mean wavelength of
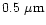 is shown as the solid line in Fig. 2.
is shown as the solid line in Fig. 2.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms8445f2.eps}\end{figure}](/articles/aa/full/2002/04/aa8445/Timg174.gif) |
Figure 2:
Intensity contribution of grains of sizes between
s and
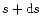 ,
along the scattering
angle of ,
along the scattering
angle of  and at a wavelength of
and at a wavelength of
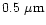 for the
size distribution constants in Table 1. All the three curves have been normalized
to enable a direct comparison. The solid vertical line indicates the lower limit
of 0.05
for the
size distribution constants in Table 1. All the three curves have been normalized
to enable a direct comparison. The solid vertical line indicates the lower limit
of 0.05
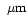 on the grain size used in the present investigation.
on the grain size used in the present investigation. |
| Open with DEXTER |
Table 2 gives the grain types which were common in the first 100 best fitting
combinations.
It is striking to note that except for the highly porous grains,
all grain types have porosities in the range between 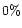 (compact)
and
(compact)
and 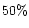 .
.
The size distribution
'a' represents the combined grain population in the coma and shell
which are sampled in the aperture of
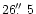 .
In the present work it is attempted to investigate
the relative fraction
of the grain type and their size distributions
separately in the coma and the shells.
.
In the present work it is attempted to investigate
the relative fraction
of the grain type and their size distributions
separately in the coma and the shells.
The simulations of the intensity, colour and polarization maps
of comet Hale-Bopp were carried out for
the geometry on 10 April, 1997, in the
wavelength band corresponding to the cometary continuum wavelengths
at
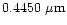 and
and
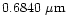 for the grain types in Table 2.
The pole positions and latitude of the
sources are adapted from Paper II.
The grain velocities computed using Eq. (2)
with
v0 = 0.63 kms-1 were found to be within
for the grain types in Table 2.
The pole positions and latitude of the
sources are adapted from Paper II.
The grain velocities computed using Eq. (2)
with
v0 = 0.63 kms-1 were found to be within
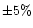 -
-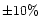 to the values computed using Eq. (1). The latter was used
in the simulations.
The coma was simulated by considering emission from a grid on the
comet at intervals of
to the values computed using Eq. (1). The latter was used
in the simulations.
The coma was simulated by considering emission from a grid on the
comet at intervals of 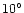 in latitude and
in latitude and
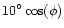 in longitude,
where
in longitude,
where 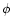 is the latitude of the point on the grid.
The sources are assumed to be active when sunlit.
The trajectories
of the dust grains are computed assuming collimated emissions. In
reality, the emission may be spread over a cone. Further, the velocity
of the grains will have a spread due to deviation from their assumed
sphericity, finite size of the active
regions and possible irregular local terrain. Their cumulative effect
will produce a broadening of the shells. As it is difficult to model each
of these effects, the sky plane position of the grains
were convolved
with a Gaussian-random profile with a sigma of 1
is the latitude of the point on the grid.
The sources are assumed to be active when sunlit.
The trajectories
of the dust grains are computed assuming collimated emissions. In
reality, the emission may be spread over a cone. Further, the velocity
of the grains will have a spread due to deviation from their assumed
sphericity, finite size of the active
regions and possible irregular local terrain. Their cumulative effect
will produce a broadening of the shells. As it is difficult to model each
of these effects, the sky plane position of the grains
were convolved
with a Gaussian-random profile with a sigma of 1
 5.
To include the effect of spreading with time,
the sigma was allowed to increase by 0
5.
To include the effect of spreading with time,
the sigma was allowed to increase by 0
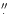 25 per day.
Due to rotation of the nucleus, grains in the expanding jets are swept
along the azimuth of the comet giving the appearance of a set of shells,
one shell per rotation.
The simulated images contain 8 shells and coma
dust ejected between 0 - 150 hr.
25 per day.
Due to rotation of the nucleus, grains in the expanding jets are swept
along the azimuth of the comet giving the appearance of a set of shells,
one shell per rotation.
The simulated images contain 8 shells and coma
dust ejected between 0 - 150 hr.
Larger grains in the coma compared to the shells
or a different grain composition for the two regions
have been inferred by
Hadamcik et al. (1997),
Jockers et al. (1997) and
Tanga et al. (1997).
High polarization
and high silicate IR emission (Sect. 1 and references therein) in the shells
suggest predominance of smaller grains in these regions.
The size distribution 'a' obtained by overall fit to coma and
the shells may represent a distribution which is the average
of a larger grain population for the coma and finer grains in the shells.
The simulations were carried out for the distribution
'b' (Table 1),
used by Hayward et al. (2000) to include
larger grains. The dot dashed line in Fig. 2 shows this distribution.
The size distribution of the smaller set of grains should be such that
the total ensemble should
produce the observed trend of
increase of polarization with wavelength.
As shown in the next section, the distribution 'c' with the coefficients
given in Table 1 and the intensity distribution curve shown as
the "dashed'' line in Fig. 2 produces this trend.
Effects of variation of porosity, organic fraction and size distributions
are demonstrated in the left, middle and right columns of Fig. 3 for
distributions 'c',
![\begin{figure}
\par\includegraphics[width=16cm,clip]{ms8445f3.eps}\end{figure}](/articles/aa/full/2002/04/aa8445/Timg186.gif) |
Figure 3:
Effects of grain size distribution ('c': left, 'a': middle,
'b': right) and organic content
on the spatial
variation of intensity (lower panel, superposed on the observations), colour (middle panel),
polarizations 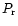 and
and 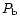 ( solid and dashed lines in top panel),
across the coma
along the sunward - anti sunward direction for the geometry on April 10, 1997.
The horizontal line at
( solid and dashed lines in top panel),
across the coma
along the sunward - anti sunward direction for the geometry on April 10, 1997.
The horizontal line at 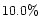 polarization represents
polarization represents 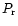 in the dark regions
(Hadamcik et al. 1997). The lower horizontal
line at in the dark regions
(Hadamcik et al. 1997). The lower horizontal
line at 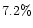 represents the expected value of
represents the expected value of 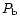 . . |
| Open with DEXTER |
'a' and 'b' respectively
for a few sample grain types in Table 2.
Variation of intensity, colour and polarizations
along the solar - anti-solar direction across
the simulated comae are shown in the
lower, middle and top sections respectively. For distribution 'c',
at porosities less than 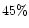 ,
the polarization in
,
the polarization in
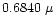 ,
,
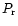 (solid line) is larger compared to
that in
(solid line) is larger compared to
that in
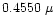 ,
,
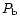 (dashed line).
The horizontal line at
(dashed line).
The horizontal line at 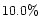 polarization level indicates
the reported value in dark regions by
Hadamcik et al. (1997) in red. The lower horizontal
line at
polarization level indicates
the reported value in dark regions by
Hadamcik et al. (1997) in red. The lower horizontal
line at 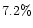 is the expected polarization in
is the expected polarization in
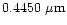 based on the
based on the
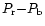 values from published
aperture photometry.
The error bars in the observed intensity cuts represent the uncertainty in the determination of sky
background which is the largest source of error in the image.
The upper and
lower limits correspond to sky fluxes which were
values from published
aperture photometry.
The error bars in the observed intensity cuts represent the uncertainty in the determination of sky
background which is the largest source of error in the image.
The upper and
lower limits correspond to sky fluxes which were 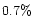 and
and 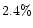 of
the central flux. The solid curve in the middle section of this panel shows the
simulated colour variation.
The steep fall in intensity
and polarization beyond
of
the central flux. The solid curve in the middle section of this panel shows the
simulated colour variation.
The steep fall in intensity
and polarization beyond 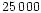 km on the sunward side
in the coma of grains with
km on the sunward side
in the coma of grains with
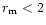 and distributions 'a' and 'c'
occurs because of their large
and distributions 'a' and 'c'
occurs because of their large  (Eqs. (4) and (5)) values.
The increase in
polarization beyond
(Eqs. (4) and (5)) values.
The increase in
polarization beyond 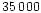 km in the sunward direction has opposite polarization colour
as this is caused by the larger grains in the tail end of distribution.
km in the sunward direction has opposite polarization colour
as this is caused by the larger grains in the tail end of distribution.
Figure 3 illustrates clearly the effect of size distribution
on the colour and polarization. For grains of medium porosity (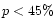 ),
),
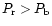 for distribution 'c',
for distribution 'c',
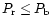 for 'a' and
for 'a' and
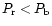 for 'b'. The anti-correlation in colour and polarization
as pointed out by Kolokolova et al. (2001)
is clearly noticeable for 'a' and 'b': the collection
'b' (right) which has larger grains has lower polarization but larger colour
than the distribution 'a' (middle). Contrary to scattering behavior of
sub-micron sized grains,
the absorptive grains in population 'c' are redder compared to that in 'a'which contains additional larger grains. The reddening is found to increase
with the refractive index of the grain either due to increase of organic
fraction or reduction in porosity. It is marginally higher for Aol
compared to the less absorptive SiA. As pointed out by
Kolokolova et al. (2001), a grain may be redder if its
size parameter x is just beyond the scattering peak. The scattering peak
occurs at
for 'b'. The anti-correlation in colour and polarization
as pointed out by Kolokolova et al. (2001)
is clearly noticeable for 'a' and 'b': the collection
'b' (right) which has larger grains has lower polarization but larger colour
than the distribution 'a' (middle). Contrary to scattering behavior of
sub-micron sized grains,
the absorptive grains in population 'c' are redder compared to that in 'a'which contains additional larger grains. The reddening is found to increase
with the refractive index of the grain either due to increase of organic
fraction or reduction in porosity. It is marginally higher for Aol
compared to the less absorptive SiA. As pointed out by
Kolokolova et al. (2001), a grain may be redder if its
size parameter x is just beyond the scattering peak. The scattering peak
occurs at
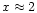 for absorptive grains with
an effective refractive index of
for absorptive grains with
an effective refractive index of 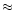
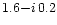 corresponding to
corresponding to
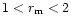 and
and
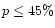 .
For less absorptive grains of pure silicates
of effective refractive index
.
For less absorptive grains of pure silicates
of effective refractive index 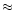
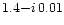 corresponding to
corresponding to
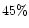 porosity,
the peak occurs
at
porosity,
the peak occurs
at
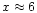 (Wickramasinghe 1973).
For the average grain size of
(Wickramasinghe 1973).
For the average grain size of
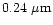 at the broad peak in Fig. 2
for distribution 'c', the size parameters at
at the broad peak in Fig. 2
for distribution 'c', the size parameters at
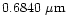 and
and
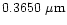 are 2.2 and 4.4 respectively. This range in size parameter is beyond the
scattering peak for absorptive grains and before for the pure silicates.
This explains the red colour of the absorptive grains and the blue colour
of the less absorptive ones.
Further, for this distribution
are 2.2 and 4.4 respectively. This range in size parameter is beyond the
scattering peak for absorptive grains and before for the pure silicates.
This explains the red colour of the absorptive grains and the blue colour
of the less absorptive ones.
Further, for this distribution
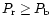 ,
the reason for this large polarization colour is that
in this domain of
,
the reason for this large polarization colour is that
in this domain of
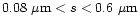 ,
the grain becomes increasingly forward
scattering with
increase in its size parameter.
Blue light is therefore more forward scattered than the red. With increase in the transmitted
part of blue light
which is parallelly polarized (negative polarization) the resultant
polarization is lower compared to that in red.
On the other hand, for the large grain population 'b',
,
the grain becomes increasingly forward
scattering with
increase in its size parameter.
Blue light is therefore more forward scattered than the red. With increase in the transmitted
part of blue light
which is parallelly polarized (negative polarization) the resultant
polarization is lower compared to that in red.
On the other hand, for the large grain population 'b',
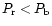 ,
which is opposite to the observed trend for comets. Therefore, the difference
in the grain populations in the coma and shells may in most part be due to difference
in the silicate to organic ratio rather than difference in grain sizes.
,
which is opposite to the observed trend for comets. Therefore, the difference
in the grain populations in the coma and shells may in most part be due to difference
in the silicate to organic ratio rather than difference in grain sizes.
The selected
grain types should also explain the phase dependent polarization in
various colours.
Figure 4 shows the phase dependence of the polarization produced by the same
grain types as in Fig. 3
at seven continuum wavelengths
for distributions c (left),
![\begin{figure}
\par\includegraphics[width=15cm,clip]{ms8445f4.eps}\end{figure}](/articles/aa/full/2002/04/aa8445/Timg207.gif) |
Figure 4:
Effects of grain size distribution and organic content
on the phase dependence of polarization for the same
sample grain types as in Fig. 3. Details of the computed curves and the data are same as for
Fig. 6. |
| Open with DEXTER |
a (middle) and b (right) respectively.
The polarizations
at
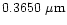 (short dashed line),
(short dashed line),
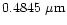 (dotted line),
(dotted line),
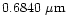 (solid line),
(solid line),
 (short dash - dot),
(short dash - dot),
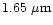 (short dash - dot, thick line)
and
(short dash - dot, thick line)
and
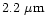 (short dash - long dash) show different trends for the three
distributions. The observed polarizations in the optical by
Ganesh et al. (1998), Hadamcik et al. (1997),
Kiselev & Velichko (1997) and Manset & Bastien (1998)
and the infrared observations by Hasegawa (1999)
are over plotted.
The phase dependence and colour of polarization again critically depend
on the size distribution. The relative polarization colour
represented by (
(short dash - long dash) show different trends for the three
distributions. The observed polarizations in the optical by
Ganesh et al. (1998), Hadamcik et al. (1997),
Kiselev & Velichko (1997) and Manset & Bastien (1998)
and the infrared observations by Hasegawa (1999)
are over plotted.
The phase dependence and colour of polarization again critically depend
on the size distribution. The relative polarization colour
represented by (
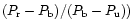 matches with the observed
ratio for grains of distribution 'c' with
matches with the observed
ratio for grains of distribution 'c' with
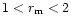 and
and 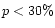 ,
where
,
where 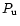 is polarization in
is polarization in
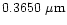 .
Organic refractory component has increased absorption in blue and UV.
Comparing SiA grains of
.
Organic refractory component has increased absorption in blue and UV.
Comparing SiA grains of 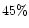 porosity of
porosity of
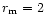 (SiA0245) and
(SiA0245) and
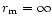 (SiA
(SiA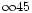 ), in this grain size domain,
polarizations in
), in this grain size domain,
polarizations in
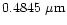 and 0.3650 are therefore lower in the latter compared to the former
because of lesser attenuation of the refracted component.
Grains of Aol
and 0.3650 are therefore lower in the latter compared to the former
because of lesser attenuation of the refracted component.
Grains of Aol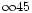 show their characteristic signature. The absorption
in blue causes higher positive polarization in all size domains.
The fluctuations in the large pure silicate grains are caused by the interference
between the refracted and reflected components of light (Kolokolova et al.
1997).
show their characteristic signature. The absorption
in blue causes higher positive polarization in all size domains.
The fluctuations in the large pure silicate grains are caused by the interference
between the refracted and reflected components of light (Kolokolova et al.
1997).
Figures 3 and 4 clearly demonstrate that porosity, organic fraction and
the size distribution of grains in the coma and shells
play an important role in controlling the phase dependence of polarization,
colour of polarization, photometric colour and spatial variation
of intensity in a comet. We exploit this to investigate the
composition of grains in the coma and shell separately.
Synthetic comae were constructed by combining the grain types in
Table 2.
The relative weights were adjusted to fulfill the following four observational
constrains:
- 1.
- The published values of red polarization between the shells (dark regions)
of
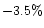 ,
,
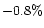 and
and 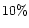 at phase angles of
at phase angles of
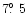 ,
,
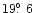 and
and
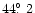 respectively by Hadamcik et al. (1997),
and blue polarizations
deduced from the published aperture photometry;
respectively by Hadamcik et al. (1997),
and blue polarizations
deduced from the published aperture photometry;
- 2.
- Colour of the coma in the range
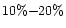 ;
;
- 3.
- Higher polarization on the anti-sunward direction.
All the three size distributions were considered for each grain type.
The weights and the size distributions which met this test are given in
Table 3.
These
weights correspond to the relative contribution to the red intensity rather
than the number of grains.
Thus the coma may contain a large fraction of grains with distribution 'c'.
However such grains will produce a very flattened coma. Hence these grains
may be part of larger fluffy grains some of which may also be
physically associated with grains of distribution 'b'. The dynamics will then
be controlled by an average value of  and the coma profile will
follow the observed coma (regions between
the shells). Alternatively, some of the grains may
have distributed sources and hence have a synthetic radial
profile mimicking the grains of distribution 'b'.
and the coma profile will
follow the observed coma (regions between
the shells). Alternatively, some of the grains may
have distributed sources and hence have a synthetic radial
profile mimicking the grains of distribution 'b'.
The weights of the grain types in the shells were adjusted so that the
simulated shells have the following attributes reported by
Hadamcik et al. (1997),
Jockers et al. (1997) and Tanga et al. (1997):
- 1.
- High polarization on the shells;
- 2.
- Bluer colour of the shells by
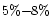 ;
;
- 3.
- Rapid decline of polarization of the shells on the
sunward side;
- 4.
- Intensity contrast between the shells and the underlying coma.
Figure 5 shows the simulations of shells
made up of grain types which produce polarizations larger than the published
aperture polarization measurements.
![\begin{figure}
\par\includegraphics[width=16cm,clip]{ms8445f5.eps} .\end{figure}](/articles/aa/full/2002/04/aa8445/Timg237.gif) |
Figure 5:
Column 1: observed processed image from VBO  (projected
cometocentric distance)-1.
North is top and East is left.
The sets of shells expanding from the nucleus in the direction of N-W, S-W and
S-E are from the sources at
(projected
cometocentric distance)-1.
North is top and East is left.
The sets of shells expanding from the nucleus in the direction of N-W, S-W and
S-E are from the sources at 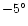 , ,
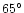 and
and 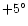 respectively.
Columns 2 and 3: simulated intensity (shell) and polarization (shell + coma) maps.
Column 4: intensity scans of the shells superposed on the
coma (lower panel), colour in % (middle panel),
respectively.
Columns 2 and 3: simulated intensity (shell) and polarization (shell + coma) maps.
Column 4: intensity scans of the shells superposed on the
coma (lower panel), colour in % (middle panel), 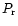 (solid line in top panel),
(solid line in top panel),
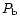 (short dashed line in top panel) and
(short dashed line in top panel) and
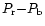 (long dashed line in
top panel).
(long dashed line in
top panel). |
| Open with DEXTER |
The first column shows the observed processed image from VBO.
The shell structures are enhanced by
dividing by a synthetic image of a coma (Chakraborty 2001) in which
the intensity declines
as the inverse of projected cometocentric distance. The coma image was
scaled so that the resultant normalized flux
in the N-E edge of the image which is devoid of shells, was unity.
The sets of shells expanding from the nucleus in the direction of N-W, S-W and
S-E are from the sources at 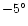 ,
,
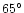 and
and 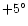 respectively (Papers I and II).
The simulated intensity map of the shells and polarization map of the
shells superposed on the coma are shown in second
and third columns respectively.
Each simulated image is divided into
respectively (Papers I and II).
The simulated intensity map of the shells and polarization map of the
shells superposed on the coma are shown in second
and third columns respectively.
Each simulated image is divided into
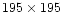 square pixels of
size 0
square pixels of
size 0
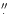 5 on a side.
The number density of the grains in the jets were adjusted to
match the intensity variation in the shells.
The fourth column shows the intensity scans of the shells superposed on the
coma (lower panel), colour in % (middle panel),
5 on a side.
The number density of the grains in the jets were adjusted to
match the intensity variation in the shells.
The fourth column shows the intensity scans of the shells superposed on the
coma (lower panel), colour in % (middle panel), 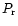 (solid line in top panel),
(solid line in top panel),
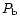 (short dashed line in top panel)
and
(short dashed line in top panel)
and
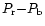 (long dashed line in
top panel).
Each grain type has its
characteristic signature in the intensity, colour and polarization map.
(long dashed line in
top panel).
Each grain type has its
characteristic signature in the intensity, colour and polarization map.
- 1.
- Row 1 (starting from below):
grains of the type "Si
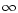 45'' with distribution 'a'produce shells that resemble the observed ones. The shells are bluer
but the polarization is only marginally higher than the ambient coma.
45'' with distribution 'a'produce shells that resemble the observed ones. The shells are bluer
but the polarization is only marginally higher than the ambient coma.
- 2.
- Row 2:
grains of the type "Si
 45'' but with distribution 'c'appear to be likely candidate as
45'' but with distribution 'c'appear to be likely candidate as  is larger on the shell compared to coma.
However neither is there a rapid fall in polarization in the sun ward
direction nor an increase in polarization in the anti sunward direction.
is larger on the shell compared to coma.
However neither is there a rapid fall in polarization in the sun ward
direction nor an increase in polarization in the anti sunward direction.
- 3.
- Row 3 & 4:
increasing the organic fraction to
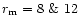 causes the older shells
to be depleted of finer grains as these are blown away towards the
anti-sunward direction. The shells are compressed and
a piling up of shells older than four rotations causes a "shell pause''
like structure in the polarization map and
an abrupt decline in polarization. In the intensity map, the pile up of matter
merges with the coma. This region appears bluer in the colour map because of
the shell material. For a detailed comparison with observed colour and
polarization maps, shells ejected over a larger numbers of the nuclear rotations
(>8) and coma ejections over an extended duration (t > 150 hr)
are required.
causes the older shells
to be depleted of finer grains as these are blown away towards the
anti-sunward direction. The shells are compressed and
a piling up of shells older than four rotations causes a "shell pause''
like structure in the polarization map and
an abrupt decline in polarization. In the intensity map, the pile up of matter
merges with the coma. This region appears bluer in the colour map because of
the shell material. For a detailed comparison with observed colour and
polarization maps, shells ejected over a larger numbers of the nuclear rotations
(>8) and coma ejections over an extended duration (t > 150 hr)
are required.
- 4.
- Row 5 & 6:
with increase in the organic fraction to
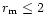 ,
the radiation pressure
blows out grains from the shells older than two rotations and produces
a very steep increase in polarization in the anti-sunward direction and
an abrupt fall in the sunward direction.
The contrast in colour between the coma and the shells disappears
The effect is pronounced for
,
the radiation pressure
blows out grains from the shells older than two rotations and produces
a very steep increase in polarization in the anti-sunward direction and
an abrupt fall in the sunward direction.
The contrast in colour between the coma and the shells disappears
The effect is pronounced for
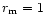 .
.
- 5.
- Row 7: porous grains are known to produce
large polarizations. Hence we considered a collection of highly porous
grains
with distribution 'a' which are assumed to be homogeneous in the
Rayleigh limit. This set produces well constrained
shells which survive several rotation periods.
This is because of
lower
 values which vary slowly with the grain size.
Although the present approach of EMT + Mie theory
is known to have serious limitations for porous grains,
these simulations help to visualize the signature of highly porous homogeneous
grains.
The streaks in the polarization map streaming away in the anti-sun direction represent
the small grains in the population.
values which vary slowly with the grain size.
Although the present approach of EMT + Mie theory
is known to have serious limitations for porous grains,
these simulations help to visualize the signature of highly porous homogeneous
grains.
The streaks in the polarization map streaming away in the anti-sun direction represent
the small grains in the population.
From Fig. 5, it is apparent that larger polarization and bluer colour
on the shells are produced by grains of SiA with
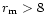 .
However, not more than 3 shells survive the radiation pressure forces while
the observed image after careful evaluation and removal of the
underlying coma
shows up to 8 shells (Chakraborty 2001). Therefore a population
of grains with high polarization but low
.
However, not more than 3 shells survive the radiation pressure forces while
the observed image after careful evaluation and removal of the
underlying coma
shows up to 8 shells (Chakraborty 2001). Therefore a population
of grains with high polarization but low  ,
similar to the over simplified
example of a uniform porous grain in Row 7 in Fig. 5 also appear to be
needed to explain the survival of older shells.
A reliable estimate of the fractional weights of these grain types can
only be made by a quantitative comparison of the polarization maps.
In the absence of availability of such a data set, we make use of the
aperture polarimetry observations.
As the aperture photometry represents combined contribution of coma and shells,
the grains which may explain the polarization
on the shell, when added in the same proportion to the selected
combination representing the coma should explain
the aperture polarimetric data. The best fitting weights for the shells
which fitted polarization vs. phase curves
are given in Table 3. Figure 6 shows the resultant simulated polarization vs. phase
curves.
,
similar to the over simplified
example of a uniform porous grain in Row 7 in Fig. 5 also appear to be
needed to explain the survival of older shells.
A reliable estimate of the fractional weights of these grain types can
only be made by a quantitative comparison of the polarization maps.
In the absence of availability of such a data set, we make use of the
aperture polarimetry observations.
As the aperture photometry represents combined contribution of coma and shells,
the grains which may explain the polarization
on the shell, when added in the same proportion to the selected
combination representing the coma should explain
the aperture polarimetric data. The best fitting weights for the shells
which fitted polarization vs. phase curves
are given in Table 3. Figure 6 shows the resultant simulated polarization vs. phase
curves.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{ms8445f6.eps}\end{figure}](/articles/aa/full/2002/04/aa8445/Timg244.gif) |
Figure 6:
Fitted polarization vs. phase angle curves for comet Hale-Bopp:
computed curves:
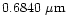 (solid line),
(solid line),
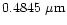 (dotted line),
(dotted line),
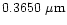 (dashed line),
(dashed line),
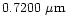 (long
dashed line),
(long
dashed line),
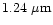 (short dash - dot, thin line),
(short dash - dot, thin line),
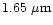 (short dash - dot, thick line) and
(short dash - dot, thick line) and
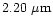 (long dash - short dash).
(long dash - short dash). |
| Open with DEXTER |
At phase angles larger than 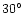 ,
the fits were better if the relative
fraction of Mg poor silicate grains
with distribution b were increased gradually with heliocentric distance.
A possible explanation for this is given in Sect. 6.
,
the fits were better if the relative
fraction of Mg poor silicate grains
with distribution b were increased gradually with heliocentric distance.
A possible explanation for this is given in Sect. 6.
The resultant simulated intensity maps of the shells and polarization maps of
shells and coma using weights in Table 3 are shown in the top, middle and right
panels of Fig. 7.
![\begin{figure}
\par\includegraphics[width=14.5cm,clip]{ms8445f7.eps}\end{figure}](/articles/aa/full/2002/04/aa8445/Timg246.gif) |
Figure 7:
Top left: the processed observed image as in Fig. 5.
Top middle and right: simulated intensity maps of the shells and
polarization maps of
shells+coma using weights in Table 3.
The lower panel shows
the intensity, colour and polarization scans
in the sun-ward - anti-sun-ward direction. |
| Open with DEXTER |
The first
panel is the processed observed image as in Fig. 5.
Separation of the high  (
(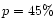 )
grains and low
)
grains and low  grains
(
grains
(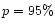 )
components produces the splitting of the shells in the N-W and S-E
region of the simulated image (Table 3).
)
components produces the splitting of the shells in the N-W and S-E
region of the simulated image (Table 3).
The lower panel of Fig. 7 shows
the intensity, colour and polarization scans
in the sunward - anti-sunward direction.
In order to reduce the fluctuations arising due to discretization of
cometary longitudes and latitudes, the scans
have been averaged over 9 pixels (
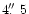 ). The polarization
contrast between the coma and the shells are therefore reduced in these plots.
The maximum and minimum value of polarization in the map however correspond to
). The polarization
contrast between the coma and the shells are therefore reduced in these plots.
The maximum and minimum value of polarization in the map however correspond to
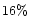 in the bright regions and
in the bright regions and 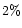 beyond the 4th shell in the sunward
direction.
beyond the 4th shell in the sunward
direction.
The width
and separation of the shells depend
on the pole position,
velocity
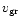 and the acceleration
and the acceleration 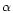 of the grains.
The later two quantities depend on the size distribution and the nature
of the grains.
For the geometry on 10 April, 1997, the uncertainty
in the computed separation of the shells from the source at
of the grains.
The later two quantities depend on the size distribution and the nature
of the grains.
For the geometry on 10 April, 1997, the uncertainty
in the computed separation of the shells from the source at 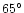 ,
is found to be
,
is found to be
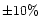 along the projected sunward direction for a change in
along the projected sunward direction for a change in
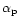 by
by
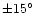 and
and
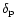 by
by
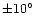 .
The model thus reproduces the shells
within an accuracy of
.
The model thus reproduces the shells
within an accuracy of 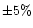 in the shell separation corresponding
to the uncertainty of
in the shell separation corresponding
to the uncertainty of
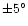 in
the pole position used in the present study following Paper II. The grain
velocities cannot therefore be constrained better than
in
the pole position used in the present study following Paper II. The grain
velocities cannot therefore be constrained better than 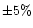 .
For a more rigorous check on the derived pole positions and the grain velocities,
intensity scans across the observed image along the directions
.
For a more rigorous check on the derived pole positions and the grain velocities,
intensity scans across the observed image along the directions
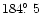 (b),
(b),
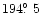 (c),
(c),
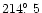 (d),
(d),
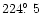 (e, the sunward direction),
(e, the sunward direction),
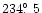 (f),
(f),
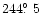 (g) and
(g) and
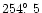 (h),
divided by the scans along the
same directions across the simulated coma of composition in Table 3
are compared with the simulated scans in Fig. 8 (lower panel).
(h),
divided by the scans along the
same directions across the simulated coma of composition in Table 3
are compared with the simulated scans in Fig. 8 (lower panel).
![\begin{figure}
\par\includegraphics[width=5.4cm,clip]{ms8445f8.eps}\end{figure}](/articles/aa/full/2002/04/aa8445/Timg265.gif) |
Figure 8:
Top: the processed observed image as in Fig. 5 showing the directions of scans.
Lower panel:
intensity scans across the observed (dashed line) and simulated
(solid line) images along directions
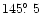 a),
a),
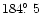 b),
b),
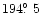 c),
c),
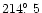 d),
d),
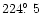 e), e),
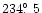 f),
f),
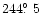 g),
g),
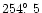 h) and
h) and
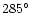 i), divided by the scans along the
same directions across the simulated coma of composition in Table 3.
i), divided by the scans along the
same directions across the simulated coma of composition in Table 3. |
| Open with DEXTER |
The directions are marked on the observed image in the top panel.
The nucleus rotated by
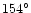 during the interval of time between the
ejections of the two extreme sections of the shells.
The cuts along the directions
during the interval of time between the
ejections of the two extreme sections of the shells.
The cuts along the directions
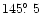 (a) and
(a) and
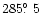 (i) are across the equatorial shells. The location and width
of the shells
match reasonably well over a range of hour angle of the Sun spanning
(i) are across the equatorial shells. The location and width
of the shells
match reasonably well over a range of hour angle of the Sun spanning
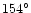 for the high latitude shells as well as the two cuts
across the equatorial shells.
The cuts along the directions 'b', 'c' and 'h' are contaminated by
the equatorial shells.
For all the cuts, at distances larger than
for the high latitude shells as well as the two cuts
across the equatorial shells.
The cuts along the directions 'b', 'c' and 'h' are contaminated by
the equatorial shells.
For all the cuts, at distances larger than
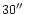 -
-
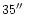 ,
deviations
between the observed and simulated cuts become noticeable. This may be
attributed to low intensity level of the observed image at these distances
as a result of which the errors associated with improper sky subtraction increase rapidly,
as indicated by the large error bars in Figs. 5 and 7.
The simulated image also suffers from limitations due to under-sampling
of the shells of only 8 rotations and coma of 13 rotations.
The deviations may also be due to the simplicity of the model which
does not take into
account the grain evolution processes like evaporation or splitting. These
processes alter
,
deviations
between the observed and simulated cuts become noticeable. This may be
attributed to low intensity level of the observed image at these distances
as a result of which the errors associated with improper sky subtraction increase rapidly,
as indicated by the large error bars in Figs. 5 and 7.
The simulated image also suffers from limitations due to under-sampling
of the shells of only 8 rotations and coma of 13 rotations.
The deviations may also be due to the simplicity of the model which
does not take into
account the grain evolution processes like evaporation or splitting. These
processes alter  of the grains and hence their dynamics.
There is also a gradual increase in the intensity of the first shell
from morning till evening (a-i). This may be due to the assumption
of uniform dust emission from dawn till dusk made in the simulation of
the coma, which is used to normalize the intensity. The simulated "shell+coma''
profile may be unaffected because of similar assumptions for simulating
the shells. The local E-W asymmetry appears to smoothen out in the outer
regions.
In any case, inferring the grain composition by matching the observed separation and width
of the first few shells alone
will be questionable because a variety of factors such as
grain size distribution, spread in porosity and organic content of the grains
determine the average value and spread in
of the grains and hence their dynamics.
There is also a gradual increase in the intensity of the first shell
from morning till evening (a-i). This may be due to the assumption
of uniform dust emission from dawn till dusk made in the simulation of
the coma, which is used to normalize the intensity. The simulated "shell+coma''
profile may be unaffected because of similar assumptions for simulating
the shells. The local E-W asymmetry appears to smoothen out in the outer
regions.
In any case, inferring the grain composition by matching the observed separation and width
of the first few shells alone
will be questionable because a variety of factors such as
grain size distribution, spread in porosity and organic content of the grains
determine the average value and spread in
 of the ensemble. Fortunately, these factors influence
the colour and the phase dependence of
polarization at different wavelengths in different ways (Figs. 3 and 4).
Hence as attempted in the present investigation, the
spatial match must be accompanied by comparisons of (1)
colour and (2) polarization of the observed and
simulated shells (Figs. 3 and 5). The derived range in porosity and organic
fraction must
explain the published phase curves in three colours (Fig. 6). This places
further constraints on the derived values of p and
of the ensemble. Fortunately, these factors influence
the colour and the phase dependence of
polarization at different wavelengths in different ways (Figs. 3 and 4).
Hence as attempted in the present investigation, the
spatial match must be accompanied by comparisons of (1)
colour and (2) polarization of the observed and
simulated shells (Figs. 3 and 5). The derived range in porosity and organic
fraction must
explain the published phase curves in three colours (Fig. 6). This places
further constraints on the derived values of p and 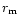 .
However, there are limitations
in the present model which should not be overlooked. As explained in
the following sections, Mie theory does not accurately
predict the polarization vs. phase curves of porous grains
which are not homogeneous. Lack of our understanding
of the nature of the organic component limits the reliability of the
derived compositions. If the composition of
the organic material assumed in Sect. 4.2 is changed by including
the extremely reddish material inferred by Tegler and Romanishin (2000)
in the Kuiper-belt objects, the fitted fraction of Aol will be modified.
This may also change the best fitting size distribution as this parameter
was constrained to explain the colour of the grains. Further,
despite the availability of an extensive and wide range of
data set on this comet, the inclusion of a large parameter space will
hinder in getting a unique solution due to cross talk between the effects
of different parameters.
.
However, there are limitations
in the present model which should not be overlooked. As explained in
the following sections, Mie theory does not accurately
predict the polarization vs. phase curves of porous grains
which are not homogeneous. Lack of our understanding
of the nature of the organic component limits the reliability of the
derived compositions. If the composition of
the organic material assumed in Sect. 4.2 is changed by including
the extremely reddish material inferred by Tegler and Romanishin (2000)
in the Kuiper-belt objects, the fitted fraction of Aol will be modified.
This may also change the best fitting size distribution as this parameter
was constrained to explain the colour of the grains. Further,
despite the availability of an extensive and wide range of
data set on this comet, the inclusion of a large parameter space will
hinder in getting a unique solution due to cross talk between the effects
of different parameters.
For reasons explained in Sect. 4.2,
the present technique cannot be used to identify the mineralogy of the
silicates in the grains although distinction can be made between the low and high Mg content
silicates based on the photometric and polarization colours (Figs. 3 and 4). Such investigations
are best made using IR spectroscopy
(Hayward et al. 2000; Wooden et al. 1999).
However, the derived porosities and organic contents
in the present work can help in constraining the IR continuum, and hence the
two techniques are complementary to one another.
The simulations at
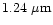 ,
,
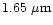 and
and
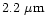 are shown in Fig. 6 along with the observations
by Hasegawa et al. (1999) and Jones & Gehrz (2000).
Except near
are shown in Fig. 6 along with the observations
by Hasegawa et al. (1999) and Jones & Gehrz (2000).
Except near 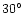 phase, the fitted curves do not match very well with these high
quality observations.
The possible reasons could be any of the following:
the narrow size range population of grains in Table 3
which comprise of
phase, the fitted curves do not match very well with these high
quality observations.
The possible reasons could be any of the following:
the narrow size range population of grains in Table 3
which comprise of 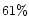 in the coma and
in the coma and 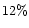 in the shell sampled by
the aperture
may not be isolated but may be sub units of highly porous larger
grains with porosity
in the shell sampled by
the aperture
may not be isolated but may be sub units of highly porous larger
grains with porosity
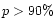 as suggested by Kolokolova et al. (2001), Levasseur-Regourd
et al. (1997) and
Xing & Hanner (1997). Such a grain model is similar to the ballistic
cluster aggregation (BCCA) investigated by Mukai et al. (1992).
At these porosities, the individual units will
interact independently with the incoming visible light and will act as isolated
scatterers (Xing & Hanner 1997). However, at infrared wavelengths,
the separation between the sub units becomes significant and the porous
grain should be treated as an aggregate with non Rayleigh inclusions of
these sub units. For such a study the present method of EMT and Mie theory
is inadequate and the more elegant technique
of Discrete Dipole Approximation (DDA)
using the code DDSCAT by Draine & Flatau (1994)
will be appropriate.
Wolf et al. (1998)
compared the results using different EMT rules along with Mie scattering
with that using
the technique of Discrete Dipole Approximation and
showed that significant differences are noticed
for grains with non Rayleigh inclusions. In particular, these authors point out
that for such grains, computations using DDA reduce forward
scattering and the polarization phase function becomes distinctively positive
compared to Rayleigh inclusions and the EMT solutions.
Large negative polarization at low phase angles in Fig. 6 may significantly
reduce if DDA is used.
Further, the present method treats the small grain population
as individual grains. In the
as suggested by Kolokolova et al. (2001), Levasseur-Regourd
et al. (1997) and
Xing & Hanner (1997). Such a grain model is similar to the ballistic
cluster aggregation (BCCA) investigated by Mukai et al. (1992).
At these porosities, the individual units will
interact independently with the incoming visible light and will act as isolated
scatterers (Xing & Hanner 1997). However, at infrared wavelengths,
the separation between the sub units becomes significant and the porous
grain should be treated as an aggregate with non Rayleigh inclusions of
these sub units. For such a study the present method of EMT and Mie theory
is inadequate and the more elegant technique
of Discrete Dipole Approximation (DDA)
using the code DDSCAT by Draine & Flatau (1994)
will be appropriate.
Wolf et al. (1998)
compared the results using different EMT rules along with Mie scattering
with that using
the technique of Discrete Dipole Approximation and
showed that significant differences are noticed
for grains with non Rayleigh inclusions. In particular, these authors point out
that for such grains, computations using DDA reduce forward
scattering and the polarization phase function becomes distinctively positive
compared to Rayleigh inclusions and the EMT solutions.
Large negative polarization at low phase angles in Fig. 6 may significantly
reduce if DDA is used.
Further, the present method treats the small grain population
as individual grains. In the
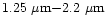 region, these will scatter
poorly and the signature of the larger grain population 'b' dictates
the resultant polarization at these wavelengths.
The present investigation restricted the fit to polarization in the optical
region only. Extension to polarization in the JHK bands
are important because it will help in investigating
the crystal field band of Fe2+ in the
region, these will scatter
poorly and the signature of the larger grain population 'b' dictates
the resultant polarization at these wavelengths.
The present investigation restricted the fit to polarization in the optical
region only. Extension to polarization in the JHK bands
are important because it will help in investigating
the crystal field band of Fe2+ in the
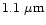 region of Fe rich
olivines.
(Dorschner et al. 1995). This band is week in Mg poor pyroxene.
The effect of this band which is spread over the JHK bands will be to
increase the opacity of the grains and hence the polarization. A detailed
fit from UV to JHK using DDA is planned as the next phase of investigations.
region of Fe rich
olivines.
(Dorschner et al. 1995). This band is week in Mg poor pyroxene.
The effect of this band which is spread over the JHK bands will be to
increase the opacity of the grains and hence the polarization. A detailed
fit from UV to JHK using DDA is planned as the next phase of investigations.
The relative
fraction of Mg poor silicate grains
needed to be increased gradually with heliocentric distance/solar
phase angle in order to match the polarization colour at phase angles
larger than 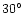 .
Presence of the component Aol with size distribution b in the
ensemble causes an increased absorption (Dorschner et al. 1995)
and hence an increase in positive polarization at 0.3650
.
Presence of the component Aol with size distribution b in the
ensemble causes an increased absorption (Dorschner et al. 1995)
and hence an increase in positive polarization at 0.3650 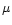 m compared to
m compared to
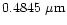 and longer wavelengths (Fig. 4). The same effect can be mimicked if
the organic part of the grain resembles the very red material found
in the Kuiper-belt objects (Tegler & Romanishin 2000) instead
of the composition of organic refractory and amorphous carbon of equal
mass assumed in the present work (Sect. 4.2).
Organic refractory (Li & Greenberg 1997) has a
gradual increase in k with decreasing wavelength in the optical region,
while for amorphous carbon (Rouleau & Martin 1991) k although
large, decreases with decreasing wavelength. As very
little is known about the nature of cometary organics, any change
in the assumed composition of the organic component
may also alter the shape of the polarization curve and hence the derived
compositions. Caution is also needed
in interpreting the required change in the composition of
Aol (or grains with enhanced blue absorption) with heliocentric
distance/phase angles for a good fit, as a real effect.
This unreliability arises due to the use of Mie scattering
and Effective Medium Theory in our model which has been shown to be
inadequate in reproducing the polarization vs. phase curves for
porous grains of non Rayleigh inclusions (Wolf et al.
1998). As naturally occurring composite grains are more likely to
have non Rayleigh inclusions than to be of homogeneous composition,
the results presented here may be substantially improved if DDA is
used. On the other hand, due to changes in solar illumination
geometry during the apparition of the comet, there is also reason to suspect
that the requirement of change in composition may at least be partially real
due to possible dichotomy in the surface composition in the northern and
southern regions of comet Hale-Bopp. The latter regions
being sunlit during and prior to 1996 and the former regions in 1997.
The porcupine like
appearance of the jets (O'Meara et al. 1996) have been explained due to
dust emission from discrete southern sources at latitudes
of
and longer wavelengths (Fig. 4). The same effect can be mimicked if
the organic part of the grain resembles the very red material found
in the Kuiper-belt objects (Tegler & Romanishin 2000) instead
of the composition of organic refractory and amorphous carbon of equal
mass assumed in the present work (Sect. 4.2).
Organic refractory (Li & Greenberg 1997) has a
gradual increase in k with decreasing wavelength in the optical region,
while for amorphous carbon (Rouleau & Martin 1991) k although
large, decreases with decreasing wavelength. As very
little is known about the nature of cometary organics, any change
in the assumed composition of the organic component
may also alter the shape of the polarization curve and hence the derived
compositions. Caution is also needed
in interpreting the required change in the composition of
Aol (or grains with enhanced blue absorption) with heliocentric
distance/phase angles for a good fit, as a real effect.
This unreliability arises due to the use of Mie scattering
and Effective Medium Theory in our model which has been shown to be
inadequate in reproducing the polarization vs. phase curves for
porous grains of non Rayleigh inclusions (Wolf et al.
1998). As naturally occurring composite grains are more likely to
have non Rayleigh inclusions than to be of homogeneous composition,
the results presented here may be substantially improved if DDA is
used. On the other hand, due to changes in solar illumination
geometry during the apparition of the comet, there is also reason to suspect
that the requirement of change in composition may at least be partially real
due to possible dichotomy in the surface composition in the northern and
southern regions of comet Hale-Bopp. The latter regions
being sunlit during and prior to 1996 and the former regions in 1997.
The porcupine like
appearance of the jets (O'Meara et al. 1996) have been explained due to
dust emission from discrete southern sources at latitudes
of
 ,
,
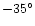 and
and 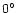 by Sekanina & Boehnhardt (1998) and
of
by Sekanina & Boehnhardt (1998) and
of
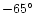 ,
,
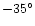 and
and
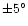 by Vasundhara & Chakraborty (1998).
The prominent shell structures near perihelion have been attributed by
these authors to a source near
by Vasundhara & Chakraborty (1998).
The prominent shell structures near perihelion have been attributed by
these authors to a source near 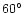 latitude.
As shown in the top panel of Fig. 9,
the solar phase angle while oscillating
between oppositions steadily increased with heliocentric distance.
The dates of the available polarimetric observations in red are marked with the
same symbols as in Figs. 4 and 6.
Variation of the angle
latitude.
As shown in the top panel of Fig. 9,
the solar phase angle while oscillating
between oppositions steadily increased with heliocentric distance.
The dates of the available polarimetric observations in red are marked with the
same symbols as in Figs. 4 and 6.
Variation of the angle
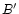 (Sect. 2.2) with heliocentric distance
is shown in the middle panel.
(Sect. 2.2) with heliocentric distance
is shown in the middle panel.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms8445f9.eps}\end{figure}](/articles/aa/full/2002/04/aa8445/Timg280.gif) |
Figure 9:
Top panel: variation of the solar phase angle with heliocentric distance.
The dates of the available polarimetric observations in red are marked with the
same symbols as in Fig. 6.
Middle panel: variation of the angle
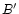 (Sect. 2.2) with heliocentric distance.
Lower panel: the activity of the sources near
(Sect. 2.2) with heliocentric distance.
Lower panel: the activity of the sources near 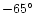 (solid line) and
(solid line) and 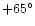 (dashed line)
as determined by the average value of the cosine of the local zenith
distance of the Sun over a rotation period of the comet,
(dashed line)
as determined by the average value of the cosine of the local zenith
distance of the Sun over a rotation period of the comet,
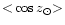 . . |
| Open with DEXTER |
The activity of the sources near
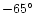 and
and
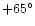 as determined by the average value of the cosine of the local zenith
distance of the Sun over a rotation period of the comet,
as determined by the average value of the cosine of the local zenith
distance of the Sun over a rotation period of the comet,
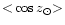 ,
at different heliocentric distances are shown as solid and dashed lines
respectively in the lower most
panel.
The activity of the latter
source increased steeply during February 1997.
The best fit to polarization vs. phase curves corresponds to a 15 fold
increase in the relative number of Mg poor grains at the phase angle of
,
at different heliocentric distances are shown as solid and dashed lines
respectively in the lower most
panel.
The activity of the latter
source increased steeply during February 1997.
The best fit to polarization vs. phase curves corresponds to a 15 fold
increase in the relative number of Mg poor grains at the phase angle of
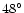 compared to
their composition at <
compared to
their composition at <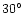 .
.
The proposed dichotomy may also explain the presence of the most volatile gaseous species
to be more abundant at large heliocentric distances before perihelion reported
by Biver et al. (1997). The stalling or reduction of production rates
between 3 and 1.6 AU before perihelion reported by them coincides with the epoch
when the solar illumination in the southern regions started decreasing rapidly.
Wooden et al. (1999) note that the
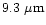 shoulder in the
7.5-13.4 IR spectra of the comet is present only in the images when the heliocentric
distances were less than 1.2 AU. From Fig. 9 it is seen that
the activity of the source at
shoulder in the
7.5-13.4 IR spectra of the comet is present only in the images when the heliocentric
distances were less than 1.2 AU. From Fig. 9 it is seen that
the activity of the source at
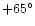 increased steeply at heliocentric distances closer than
increased steeply at heliocentric distances closer than 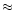 1.2 AU,
hence the extra feature at
1.2 AU,
hence the extra feature at
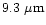 may have come from the northern region
of the comet.
may have come from the northern region
of the comet.
A model has been described to obtain intensity and polarization maps of
coma and shell (jet) of comets. The intensity profile across the simulated
coma and shells for the geometry on 10 April, 1997 of comet Hale-Bopp
is compared with the observed profile.
Published values of polarization and colour
in the coma and shells of comet Hale-Bopp on a close by date are used
to investigate the nature of the
grains, their organic content and porosity.
Published aperture photometry
at
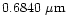 ,
,
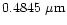 and
and
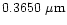 are initially used
to short-list the possible range in porosities and the silicate to
organic mass ratio. The relative weights of grain types in the coma and shell are
further constrained such that the combined coma and shell population
1) reproduces the polarization vs. phase curve, 2) explains
the high polarization on
the shells and 3) their bluer colour (compared to coma).
The results indicate that although
it is impossible to determine the nature of the silicate
(pyroxenes/olivines or amorphous/crystalline) using the present technique,
the porosity, organic fraction and size distribution of the grains can be
constrained.
The scattered light from coma has polarization and colour
characteristics which point to presence of at least
are initially used
to short-list the possible range in porosities and the silicate to
organic mass ratio. The relative weights of grain types in the coma and shell are
further constrained such that the combined coma and shell population
1) reproduces the polarization vs. phase curve, 2) explains
the high polarization on
the shells and 3) their bluer colour (compared to coma).
The results indicate that although
it is impossible to determine the nature of the silicate
(pyroxenes/olivines or amorphous/crystalline) using the present technique,
the porosity, organic fraction and size distribution of the grains can be
constrained.
The scattered light from coma has polarization and colour
characteristics which point to presence of at least
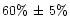 of
grains with
of
grains with
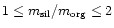 and of medium porosity in the range
and of medium porosity in the range
 .
A narrow size distribution
between
.
A narrow size distribution
between
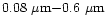 is inferred for
is inferred for  of the grains in
the coma and shell.
These grains could be the building blocks of larger fluffy grains
of porosity larger than
of the grains in
the coma and shell.
These grains could be the building blocks of larger fluffy grains
of porosity larger than 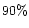 .
At these porosities the individual units will
interact independently with the incoming light and will act as isolated
scatterers (Xing & Hanner 1997).
The silicate in these grains could be Astronomical silicate (SiA) or a combination
of Mg poor and Mg rich olivines or pyroxenes in crystalline or amorphous state.
The shells of comet Hale-Bopp which produce larger
polarization and are bluer compared to the coma appear to contain
grains of silicate
with lower
organic fraction (
.
At these porosities the individual units will
interact independently with the incoming light and will act as isolated
scatterers (Xing & Hanner 1997).
The silicate in these grains could be Astronomical silicate (SiA) or a combination
of Mg poor and Mg rich olivines or pyroxenes in crystalline or amorphous state.
The shells of comet Hale-Bopp which produce larger
polarization and are bluer compared to the coma appear to contain
grains of silicate
with lower
organic fraction (
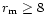 )
and of moderate porosity (
)
and of moderate porosity (
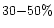 ).
In order to explain the presence of as many as 8-10 shells in well processed images,
the fit using the present dynamical model imposes the condition that
the shells must contain grains of
).
In order to explain the presence of as many as 8-10 shells in well processed images,
the fit using the present dynamical model imposes the condition that
the shells must contain grains of 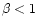 .
This is independent of detailed
assumptions on the optical properties of the grains or the scattering theory.
Our Mie scattering calculations using Effective Median Theory to calculate the
overall optical properties suggest that highly porous grains with
.
This is independent of detailed
assumptions on the optical properties of the grains or the scattering theory.
Our Mie scattering calculations using Effective Median Theory to calculate the
overall optical properties suggest that highly porous grains with
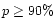 made up
of sub units in the form of Rayleigh inclusions (uniform density) have this property.
This inference can be tested or further refined by using more elegant light scattering
theories or techniques as mentioned below.
Alternatively, the fluffy grains made of sub micron grains as sub units
may also contain
larger grains which may control the dynamics by reducing the effective
made up
of sub units in the form of Rayleigh inclusions (uniform density) have this property.
This inference can be tested or further refined by using more elegant light scattering
theories or techniques as mentioned below.
Alternatively, the fluffy grains made of sub micron grains as sub units
may also contain
larger grains which may control the dynamics by reducing the effective  .
The change in slope of the polarization vs phase curves at
high phase angles which occurred at closer heliocentric distances and when the
northern region of the comet was sunlit, could be better explained by increasing the
fraction of the Mg poor olivine grains with
.
The change in slope of the polarization vs phase curves at
high phase angles which occurred at closer heliocentric distances and when the
northern region of the comet was sunlit, could be better explained by increasing the
fraction of the Mg poor olivine grains with
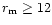 at these epochs.
This may be due to the limitations of the Mie theory in constructing
the phase vs. polarization of natural grains. Considering the geometry of
the apparition of the comet,
a dichotomy in the surface composition of the comet may also be
responsible to some extent
for such an enhancement of these grain types required to fit the data set
near perihelion.
at these epochs.
This may be due to the limitations of the Mie theory in constructing
the phase vs. polarization of natural grains. Considering the geometry of
the apparition of the comet,
a dichotomy in the surface composition of the comet may also be
responsible to some extent
for such an enhancement of these grain types required to fit the data set
near perihelion.
In spite of the limitations of EMT theory with Mie solutions,
the present results which indicate predominance of grains in the size
range
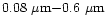 ,
and porosity in the range
,
and porosity in the range
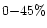 are similar to that suggested by
Xing & Hanner (1997)
using DDSCAT. They find that a mixture of aggregates of
carbonaceous and silicate monomers of a tenth of micron in size and of intermediate
porosity of
are similar to that suggested by
Xing & Hanner (1997)
using DDSCAT. They find that a mixture of aggregates of
carbonaceous and silicate monomers of a tenth of micron in size and of intermediate
porosity of 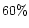 resembles the observed phase dependence of polarization of comets.
For this intermediate porosity, it therefore appears that, at least for
the polydisperse grains, EMT solutions may approximate
the real scattering solutions.
The DDA technique and
assuming the grains to be made up of organic coated silicate
monomers (Greenberg & Hage 1990) will
be attempted as the next step to match the polarizations in the range
from
resembles the observed phase dependence of polarization of comets.
For this intermediate porosity, it therefore appears that, at least for
the polydisperse grains, EMT solutions may approximate
the real scattering solutions.
The DDA technique and
assuming the grains to be made up of organic coated silicate
monomers (Greenberg & Hage 1990) will
be attempted as the next step to match the polarizations in the range
from
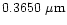 to
to
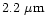 .
The use of computational techniques
can be dispensed with and one
could directly use (1) the microwave and laser facilities to determine
scattering and colour signatures related to the physical properties
of dust grains (Weiss-Wrana et al. 1985a, 1985b), (2) the database created by Gustafson et al. (1999)
using microwave analogues of complex grain systems
or (3) the data from the scattering experiments (PROGRA) conducted under
micro gravity conditions on
fluffy grains (Levasseur-Regourd et al. 1998; Worms et al. 1999)
with optical
constants similar to Astronomical silicate. In any case,
by adapting a superior light scattering theory or using results
of laboratory simulations, the present model can be used to fully extract
the information available from polarization and intensity maps of cometary shells
and coma.
.
The use of computational techniques
can be dispensed with and one
could directly use (1) the microwave and laser facilities to determine
scattering and colour signatures related to the physical properties
of dust grains (Weiss-Wrana et al. 1985a, 1985b), (2) the database created by Gustafson et al. (1999)
using microwave analogues of complex grain systems
or (3) the data from the scattering experiments (PROGRA) conducted under
micro gravity conditions on
fluffy grains (Levasseur-Regourd et al. 1998; Worms et al. 1999)
with optical
constants similar to Astronomical silicate. In any case,
by adapting a superior light scattering theory or using results
of laboratory simulations, the present model can be used to fully extract
the information available from polarization and intensity maps of cometary shells
and coma.
Acknowledgements
I am grateful to Dr. P. Chakraborty of the Indian Institute
of Astrophysics for the processed image of 10 April, 1997 and access to his
software to convert the simulated images to IRAF images. I am also grateful to
Dr. A. Li for the optical constants of the silicates.
I am indebted to the referee for the valuable comments.
-
Bellucci, G. 1998, , 333, 369
In the text
NASA ADS
-
Biver, N., Bockelée-Morvan, D., Calon, P., et al. 1997,
Earth, Moon, and Planets, 78, 5
In the text
-
Bohren, C. F., & Huffman, D. R. 1983, Absorption and scattering of light
by small Particles (John Willey & Sons Inc)
In the text
-
Chakraborty, P. 2001, Ph.D. Thesis
In the text
-
Crovisier, J., Leech, K., Bockelée-Morvan, D., et al. 1997, Science, 275, 1904
In the text
NASA ADS
-
Dorschner, J., Begemann, B., Henning, et al. 1995, , 300, 503
In the text
NASA ADS
-
Draine, B. T. 1985, , 57, 587
In the text
NASA ADS
-
Draine, B. T., & Flatau, P. J. 1994, J. Opt. Soc. Am. A, 22, 1491
In the text
-
Draine, B. T., & Lee, H. M. 1984, , 285, 89
In the text
NASA ADS
-
Finson, M. L., & Probstein, R. F. 1968, , 154, 327
In the text
NASA ADS
-
Fulle, M. 1987, , 171, 327
NASA ADS
-
Furusho, R., Suzuki, B., Yamamoto, N., et al. 1999, , 51, 367
In the text
-
Galdemard, P., Lagage, P. O., Dubreuil, D., et al. 1997, Earth, Moon, and Planets, 78, 271
In the text
-
Ganesh, S., Joshi, U. C., Baliyan, K. S., & Deshpande, M. R. 1998, , 129, 489
In the text
-
Greenberg, J. M., & Hage, J. I. 1990, , 361, 260
In the text
NASA ADS
-
Gurnette, B. L., & Woolley, R. v. d. R. (eds.) 1960, in Explanatory
Supplement
to the Astronomical Ephemeris and The American Ephemeris & Nautical
Almanac, prepared by the Nautical Almanac Offices, UK
& USA, 342
In the text
-
Gustafson, B. A. S. 1999, in Formation and Evolution of Solids in Space,
ed. J. Mayo Greenberg, & Li. Aigen (Kluwer Academic Publishers), 535
In the text
-
Hadamcik, E., Levasseur-Regourd, A. C., & Renard, J. B. 1997,
Earth, Moon, and Planets, 78, 365
In the text
-
Hage, J. I., & Greenberg, J. M. 1990, , 361, 251
In the text
NASA ADS
-
Hanner, M. S. 1985, Adv. Space. Res., 4(9), 189
In the text
-
Hasegawa, H., Ichikawa, T., Abe, S., et al. 1997,
Earth, Moon, and Planets, 78, 353
In the text
-
Hayward, T. L., & Hanner 1997, Earth, Moon, and Planets, 78, 265
In the text
-
Hayward, T. L., Hanner, M. S., & Sekanina, Z. 2000, , 538, 428
In the text
NASA ADS
-
Jewitt, D., & Meech, K. J. 1986, , 310, 937
In the text
NASA ADS
-
Jockers, K., Rosenbush, V. K., Bonev, T., & Credner, T.
1997, Earth, Moon, and Planets, 78, 373
In the text
-
Jones, T. J., & Gehrz, R. D. 2000, Icarus, 143, 338
In the text
NASA ADS
-
Jorda, L., Rembor, K., Lecacheux, J., et al. 1997-1999, Earth, Moon, and Planets, 77, 167
In the text
-
Kiselev, N. N., & Velichko, F. P. 1997, Earth, Moon, and Planets, 78, 347
In the text
-
Kolokolova, L., Jockers, K., & Chernova, G. 1997, Icarus, 126, 351
In the text
NASA ADS
-
Kolokolova, L., Gustafson, B. A. S., Jockers, K., & Lichtenberg, G.
2001, , 106, 10113
In the text
-
Krishna Swamy, K. S., & Shah, G. A. 1987, Earth, Moon, and Planets, 38, 273
In the text
-
Krishna Swamy, K. S., Sandford, S. A., Allamandola, L. J., Witteborn, F. C.,
& Bregman, J. D. 1988, Icarus, 75, 351
In the text
NASA ADS
-
Levasseur-Regourd, A. C., Cabane, M., Haudebourg, V., & Worms, J. C.
1998, Earth, Moon and Planets, 80, 343
In the text
-
Levasseur-Regourd, A. C., Cabane, M., Worms, J. C., et al. 1997,
Adv. Space Res., 20, 1585
In the text
NASA ADS
-
Li, A., & Greengerg, M. 1997, , 323, 566
In the text
NASA ADS
-
Li, A., & Greengerg, M. 1998, , 498, L83
In the text
NASA ADS
-
Licandro, J., Rubio, L. R. B., Boehnhardt, H., et al. 1998, , 501, L221-225
In the text
-
Manset, N. H., & Bastien, P. 2000, Icarus, 105, 203
In the text
-
O'Meara, S. J., Bortle, J. E., Birkle, K., et al. 1996, 1996 August 28,
ed. B. G. Marsden, IAUC, 6463
-
Mukai, T., Ishimoto, H., Kozasa, T., Blum, J., & Greenberg, J. M.
1992, , 262, 315
In the text
NASA ADS
-
Probstein, R. F. 1969, in Problems of Hydrodynamics and Continuum
Mechanics, Soc. Industr. Appl. Math., ed. F. Bisshopp et al., 568
In the text
-
Rhode, J. R., & Sinclair, A. 1992, in Explanatory Supplement
to the Astronomical Almanac, Prepared by the Nautical Almanac Offices, UK
& USA, Jet Propulsion Laboratory,
Bureau des Longitudes and the Time
Service
& Astrometry departments, U.S. Naval Observatory, ed. P. K. Seidelmann, 325
In the text
-
Rouleau, F., & Martin, P. G. 1991, , 377, 526
In the text
NASA ADS
-
Scott, A., & Duley, W. W. 1996, , 105, 401
In the text
-
Sekanina, Z. 1981, , 86, 1741
In the text
NASA ADS
-
Sekanina, Z. 1991, in Comets in the Post-Halley Era,
ed. R. L. Newburn Jr., M. Neugebauer, & J. Rahe
(Kluwer, Dordrecht), 769
In the text
-
Sekanina, Z., & Boehnhardt, H. 1998, Earth, Moon, and Planets, 78, 313
In the text
-
Sekanina, Z., & Larson, S. M. 1984, , 89, 1408
In the text
NASA ADS
-
Tanga, P., Cellino, A., & Di Martino, M. 1997, Earth, Moon, and Planets, 78, 359
In the text
-
Tegler, S. C., & Romanishin, W. 2000, , 407, 979
In the text
NASA ADS
-
Vasundhara, R., Chakraborty, P., Hänel, A., et al. 1997,
Earth, Moon, and Planets, 78, 321, Paper I
-
Vasundhara, R., & Chakraborty, P. 1998, Icarus, 140, 221, Paper II
In the text
-
Weiss-Wrana, K., Giese, R. H., & Zerull, R. H. 1985a, in Properties and
Interactions of Interplanetary Dust, Proc. of the 85th IAU Colloq.,
Marseille, France, July 9-12, 1984, ed. R. H. Giese, & P. Lamy, 219
In the text
-
Weiss-Wrana, K., Giese, R. H., & Zerull, R. H. 1985b, in Properties and
Interactions of Interplanetary Dust, Proc. of the 85th IAU Colloq.,
Marseille, France, July 9-12, 1984, ed. R. H. Giese, & P. Lamy, 223
In the text
-
Wickramasinghe, N. C. 1973, in Light scattering functions for small particles,
Produced and published by Adam Hilger Ltd, Ch. 5
In the text
-
Wolf, M. J., Clayton, G. C., & Gibson, S. J. 1998, , 503, 815
In the text
NASA ADS
-
Wooden, D. H., Harker, D. E., Woodward, C. E., et al. 1999, , 517, 1034
In the text
NASA ADS
-
Worms J. C., Renard, J. B., Hadamcik, E.,
Levasseur-Regourd, A. C., & Gayet, J. F. 1999, Icarus, 142, 281
In the text
NASA ADS
-
Xing, Z., & Hanner, M. S. 1997, A&A, 324, 805
In the text
NASA ADS
Copyright ESO 2002
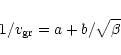
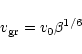
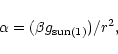
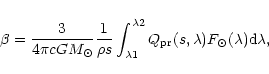
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms8445f1.eps}\end{figure}](/articles/aa/full/2002/04/aa8445/Timg74.gif)
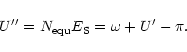
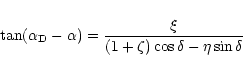
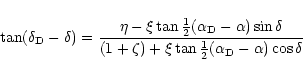
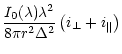
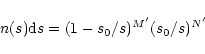
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms8445f2.eps}\end{figure}](/articles/aa/full/2002/04/aa8445/Timg174.gif)
![\begin{figure}
\par\includegraphics[width=16cm,clip]{ms8445f3.eps}\end{figure}](/articles/aa/full/2002/04/aa8445/Timg186.gif)
![\begin{figure}
\par\includegraphics[width=15cm,clip]{ms8445f4.eps}\end{figure}](/articles/aa/full/2002/04/aa8445/Timg207.gif)
![\begin{figure}
\par\includegraphics[width=16cm,clip]{ms8445f5.eps} .\end{figure}](/articles/aa/full/2002/04/aa8445/Timg237.gif)
![\begin{figure}
\par\includegraphics[width=14cm,clip]{ms8445f6.eps}\end{figure}](/articles/aa/full/2002/04/aa8445/Timg244.gif)
![\begin{figure}
\par\includegraphics[width=14.5cm,clip]{ms8445f7.eps}\end{figure}](/articles/aa/full/2002/04/aa8445/Timg246.gif)
![\begin{figure}
\par\includegraphics[width=5.4cm,clip]{ms8445f8.eps}\end{figure}](/articles/aa/full/2002/04/aa8445/Timg265.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms8445f9.eps}\end{figure}](/articles/aa/full/2002/04/aa8445/Timg280.gif)