3 The model

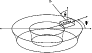
Figure 2: Flux tube embedded in the sunspot penumbra.

For the computation of synthetic Stokes profiles, we rely on the moving tube model of SJS98. For our calculations, we use a typical model snapshot with a flux tube breaking through the photosphere in the inner penumbra from where it bends outwards horizontally. An upflow of hot optically thick plasma enters the photosphere along the tube from below. As it flows outwards horizontally, with a flow speed of up to 14 km s^-1, it radiatively cools. In this paper, we concentrate on one specific radial position in the outer penumbra where the outflowing plasma has cooled off and the tube is in temperature equilibrium with the background model and has essentially the same magnetic field strength. At that location, at a radial distance of 12000 km from spot center, the background magnetic field has an inclination of $\gamma'_{\rm b}=65^\circ$, while the tube is horizontal, $\gamma'_{\rm t}=90^\circ$. Since we assume an axially symmetric model sunspot that has no azimuthal component, the azimuth of the magnetic field, $\phi '$, equals the azimuthal location in the spot, $\psi$, i.e., $\phi' = \psi$. Along the LOS ( $\theta =15^\circ$ in our calculations), the Unno-Rachkovsky-equations for polarized light are integrated numerically for the iron lines at 1564.8 nm and 630.2 nm (details are given in Müller 2001; Müller et al. 2001). The geometry of the tube for a certain $\psi$ within the sunspot is sketched in Fig. 2.

The presence of a tube embedded in a penumbral background atmosphere causes discontinuities along a line-of-sight transversing it: (1) $\triangle v$, the LOS component of the flow velocity (flow channel embedded in a background at rest), (2) $\triangle \gamma$, the inclination of the magnetic field vector (horizontal flux tube in an inclined background magnetic field), and (3) $\triangle \phi$, the azimuth of the magnetic field vector w.r.t. the LOS. The discontinuity in azimuth, $\triangle \phi$, needs clarification: Although the azimuth of the tube, $\phi'_{\rm t}$ and of the background, $\phi'_{\rm b}$, are the same w.r.t. the local system, $\triangle \phi=\phi_{\rm t} - \phi_{\rm b}$ is non-zero (except for $\theta=0^\circ$ or $\psi=0^\circ$, $180^\circ$) as a consequence of $\gamma'_{\rm t} \neq \gamma'_{\rm b}$ (cf. Eq. (2)).

Our model shares common features with the models of Solanki & Montavon (1993), Sanchez Almeida et al. (1996), and Martínez Pillet (2000), but in our case, the background is at rest and the field strength of the tube is the same as in the background model. Moreover, we concentrate on the dependence of N along an azimuthal section, i.e., along the circumference of a spot-centered circle within the penumbra at a given heliocentric angle, while the mentioned works have focussed on the center-to-limb variation of N.