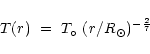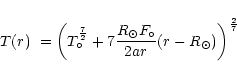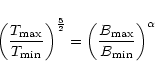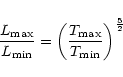A&A 381, 1049-1058 (2002)
DOI: 10.1051/0004-6361:20011563
Solar cycle variation of the temperature structure
within the cores of coronal streamers
C. R. Foley1 -
S. Patsourakos1 -
J. L. Culhane1 -
D. MacKay2
1 - Mullard Space Science Laboratory, University College London,
Holmbury St Mary, Dorking, Surrey RH5 6NT, UK
2 -
Department of Mathematical and Physical Sciences,
St Andrews University, Scotland, UK
Received 30 July 2001 / Accepted 8 November 2001
Abstract
We use the Coronal Diagnostic Spectrometer onboard the Solar and Heliospheric
Observatory (SOHO) to analyze conditions in coronal streamer structures
observed close to solar minimum (1996 July 8) and near maximum (1999 August 5). We measured the intensities of emission lines from Fe IX-XV ions and found
the most intense emission to be from Fe XI at solar minimum and from Fe XV at
solar maximum. We then used the line ratio method with transitions in
selected ions to extract the radial temperature behavior in the
structures. The solar minimum peak values were about 1.4 MK at 1.3 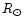 ,
while values derived close to
solar maximum were consistent with the Yohkoh observations at the last
maximum, displaying an apparently asymptotic temperature of around 2.2 MK
above 1.2
,
while values derived close to
solar maximum were consistent with the Yohkoh observations at the last
maximum, displaying an apparently asymptotic temperature of around 2.2 MK
above 1.2 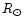 .
We discuss the observations in relation to possible
mechanisms for energy deposition in large coronal structures at different
phases of the solar cycle.
.
We discuss the observations in relation to possible
mechanisms for energy deposition in large coronal structures at different
phases of the solar cycle.
Key words: Sun: corona - Sun: activity - Sun: X-rays, gamma rays - stars: coronae
Knowledge of the electron temperature in the corona and its variation with
height in different regions forms an integral part of our understanding of
coronal heating and solar wind acceleration. Recently the coronal temperature has been successfully measured at significant heights above the limb using the
broadband filter ratio technique (Foley et al. 1996; Sturrock et al. 1996; Wheatland et al. 1997; Foley 1998; Priest et al. 1998, 2000). In these papers the radial temperature structure,
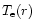 ,
has been used in an attempt to determine the heating function of the Sun's Corona. This work has generally found that temperature is an increasing function of
height above the limb, and this result has subsequently been used to demonstrate a requirement for
heating up to and including the maximum observed height range of almost 2 solar
radii. Analysis of the broadband data obtained with the Yohkoh Soft X-ray
Telescope, has required an isothermal assumption which may not
be realized in practice. Using this method, positive temperature gradients have been consistently
reported for the quiescent regions, overlying neutral lines located in the
high latitude regions.
,
has been used in an attempt to determine the heating function of the Sun's Corona. This work has generally found that temperature is an increasing function of
height above the limb, and this result has subsequently been used to demonstrate a requirement for
heating up to and including the maximum observed height range of almost 2 solar
radii. Analysis of the broadband data obtained with the Yohkoh Soft X-ray
Telescope, has required an isothermal assumption which may not
be realized in practice. Using this method, positive temperature gradients have been consistently
reported for the quiescent regions, overlying neutral lines located in the
high latitude regions.
The SOHO Coronal Diagnostic Spectrometer (CDS, Harrison et al. 1995)
allows us to view the relative distribution of individual ions as function of
height. Consequently, we now have the ability to examine the true distribution of
plasma in many regions of the corona. In this work we evaluate the relative abundance
of Fe IX through Fe XV ions for coronal streamers observed close to the solar
minimum and maximum of the current solar cycle (23), on 1996 July 8 and
1999 August 5 respectively. The most abundant (adjacent in 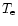 )
ions were then used to establish
the best representation of the apparent temperature profile with height.
The derived temperature profile and its variation from solar minimum to
maximum are used to infer how the corona evolves and its associated energy requirements. For comparison we have also included solar maximum data
for cycle 22 (1992, October 3) obtained from Yohkoh observations using the filter ratio method (Tsuneta et al. 1991).
)
ions were then used to establish
the best representation of the apparent temperature profile with height.
The derived temperature profile and its variation from solar minimum to
maximum are used to infer how the corona evolves and its associated energy requirements. For comparison we have also included solar maximum data
for cycle 22 (1992, October 3) obtained from Yohkoh observations using the filter ratio method (Tsuneta et al. 1991).
In the following section we describe the instrumentation. In
Sect. 3, we discuss the principles behind our analysis method.
Section 4 treats the observations which we obtained for solar maximum and
minimum. The paper concludes with a discussion of the implications for
coronal structure and heating through the solar cycle in Sect. 5, and
concluding remarks in Sect. 6.
The Coronal Diagnostic Spectrometer (CDS) on SOHO consists of two complementary
spectrometers which make use of a common grazing incidence telescope: a Grazing
Incidence Spectrometer (GIS); and a Normal Incidence Spectrometer
(NIS). Together, GIS and NIS cover most of the wavelength range from 150 Å to 785 Å (Harrison et al. 1995). The GIS system has four detectors,
with spectral ranges 151-221 Å, 256-341 Å, 393-492 Å and 656-785 Å, while the NIS covers two ranges: 308-381 Å and 513-633 Å.
The NIS uses for its detector an intensified CCD camera. This makes use of a
micro-channel plate with a phosphor converter which intensifies and converts
the incident EUV to visible light. This is then focussed by a lens onto a CCD.
The GIS detectors (Breeveld et al. 1992) are open-faced microchannel
plate (MCP) detectors in a Z stack configuration with the output
charge of the MCP directed on to a charge division read-out. The
detectors operate in photon counting mode, and this allows events to
be discriminated by pulse height, thereby allowing cosmic ray hits to
be excluded from the accumulated spectra. The GIS is therefore able to
obtain deep exposures relatively free of cosmic ray background.
The Yohkoh Soft X-ray Telescope (SXT, Tsuneta et al. 1991) provides
full-Sun images in the range 4-60 Å. Use of pairs of filters allows the
estimation of electron temperature assuming that the plasma sampled is isothermal.
Coronagraphic images of the streamers that were observed were obtained with the SOHO Large Angle Solar Coronagraph (LASCO, Brueckner et al. 1995) and with the ground-based instrument on Mauna Loa (Fisher et al. 1981).
In this work we use the intensities of individual emission lines in the
EUV regime to determine the properties of the Sun's corona to over one
solar radius above the solar limb. Assuming optically thin radiation the
intensity of an emission line which we observe can be represented by
(Mason & Fossi 1994)
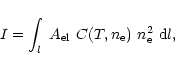 |
(1) |
where the integral is over the line of sight (l);
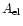 is the absolute
abundance of the element and
is the absolute
abundance of the element and
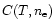 is the contribution function of the
emitting line at electron density
is the contribution function of the
emitting line at electron density 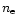 .
We used the CHIANTI spectral
package (Dere et al. 1997) for calculating the contribution functions
.
We used the CHIANTI spectral
package (Dere et al. 1997) for calculating the contribution functions
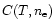 ,
adopting Grevesse & Sauval (1998) coronal
abundance values and Mazzotta et al. (1998) ionization equilibria.
,
adopting Grevesse & Sauval (1998) coronal
abundance values and Mazzotta et al. (1998) ionization equilibria.
As mentioned in the introduction, observations of the temperature profile in
the corona have been obtained with the Yohkoh SXT near the maximum of cycle 22
(1992, October 3). These observations use the ratio of the signal recorded in
two broadband filter images to determine the weighted isothermal temperature
of the observed region. By taking the calculated intensity ratios
using emission lines from the same element (e.g. Fe, see Fig. 1),
![\begin{figure}
\par\includegraphics[width=9.3cm,clip]{MS1748f1.eps}\end{figure}](/articles/aa/full/2002/03/aa1748/Timg12.gif) |
Figure 1:
a) Line ratios and Yohkoh SXT filter ratio used for the diagnostics
in this paper. b) The contribution functions
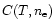 for Fe XI, XIV, XV lines
and the Yohkoh SXT thin aluminum filter. These have each been normalized
to their peak value.
for Fe XI, XIV, XV lines
and the Yohkoh SXT thin aluminum filter. These have each been normalized
to their peak value. |
| Open with DEXTER |
we can estimate 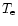 values which are free from
uncertainty in
values which are free from
uncertainty in
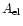 but do rely on the accuracy of the ionization
equilibrium calculation.
The strength of using this spectroscopic technique as compared to the filter ratio method
is highlighted in Fig. 1. In
this figure we plot as a function of temperature (a) several line and filter intensity
ratios for CDS and SXT respectively and (b) the normalized (to their peak value)
temperature responses for several CDS spectral lines and an SXT filter.
The line ratios are
but do rely on the accuracy of the ionization
equilibrium calculation.
The strength of using this spectroscopic technique as compared to the filter ratio method
is highlighted in Fig. 1. In
this figure we plot as a function of temperature (a) several line and filter intensity
ratios for CDS and SXT respectively and (b) the normalized (to their peak value)
temperature responses for several CDS spectral lines and an SXT filter.
The line ratios are 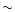 1000 times more sensitive to temperature change than are
the broadband filter ratio observations of the Yohkoh SXT.
An additional benefit of using emission line diagnostics in this region is
that the contribution functions are more constrained in temperature. This
allows the average emission measure for a range of temperatures to be
estimated. Although this is an average emission measure, it does indicate
the approximate amount of material at each temperature which would produce
the observed emission line intensities (e.g. see Griffiths & Jordan 1998).
1000 times more sensitive to temperature change than are
the broadband filter ratio observations of the Yohkoh SXT.
An additional benefit of using emission line diagnostics in this region is
that the contribution functions are more constrained in temperature. This
allows the average emission measure for a range of temperatures to be
estimated. Although this is an average emission measure, it does indicate
the approximate amount of material at each temperature which would produce
the observed emission line intensities (e.g. see Griffiths & Jordan 1998).
Our derivation of electron temperatures will be made with the assumption
of ionization-equilibrium. However, since mass flows take place in streamers,
these may induce some departures from the ionization-equilibrium due to slow
solar wind flow. Therefore the transit times
 associated
with mass flows should be considered as they may induce some departures from the ionization-equilibrium
(e.g., Dupree et al. 1979). The
ionization time
associated
with mass flows should be considered as they may induce some departures from the ionization-equilibrium
(e.g., Dupree et al. 1979). The
ionization time
 is a function of both the electron
temperature and density. We have used here the analytic fits given in Shull
& Van Steenberg (1982). The transit times
is a function of both the electron
temperature and density. We have used here the analytic fits given in Shull
& Van Steenberg (1982). The transit times
 associated with
mass flows may be defined as:
associated with
mass flows may be defined as:
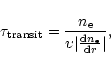 |
(2) |
where
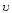 is the flow speed of the solar wind and
is the flow speed of the solar wind and
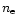 the electron density.
the electron density.
 is essentially the time
taken for the flowing plasma to traverse a density scale-height.
is essentially the time
taken for the flowing plasma to traverse a density scale-height.
The slow solar wind radial velocity 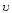 was determined by assuming
mass flux conservation between the inner corona and 1 AU. We
used the standard form of the cross-sectional area of a flux tube given by
Kopp & Holtzer (1976) and adapted it for slow speed wind emanating from
streamers by using the parameters given in Withbroe (1988). We used the
value of
was determined by assuming
mass flux conservation between the inner corona and 1 AU. We
used the standard form of the cross-sectional area of a flux tube given by
Kopp & Holtzer (1976) and adapted it for slow speed wind emanating from
streamers by using the parameters given in Withbroe (1988). We used the
value of
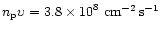 measured
in-situ by Ulysses in the ecliptic plane (Goldstein et al. 1996).
For the
measured
in-situ by Ulysses in the ecliptic plane (Goldstein et al. 1996).
For the 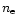 radial profile, we used the corresponding relation for streamers
given by Guhathakurta et al. (1996). We finally assumed a fully-ionized
plasma with 10
radial profile, we used the corresponding relation for streamers
given by Guhathakurta et al. (1996). We finally assumed a fully-ionized
plasma with 10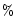 helium which results in
helium which results in
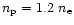 .
We found a
slow solar wind velocity that does not exceed 20 kms-1 at 2
.
We found a
slow solar wind velocity that does not exceed 20 kms-1 at 2
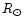 .
.
The results for the calculated
 and
and
 for
the distance range 1-2
for
the distance range 1-2
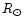 and for four different values of
the temperature, which was assumed to be constant in the above region,
are shown in Fig. 2.
and for four different values of
the temperature, which was assumed to be constant in the above region,
are shown in Fig. 2.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{MS1748f2.eps}\end{figure}](/articles/aa/full/2002/03/aa1748/Timg21.gif) |
Figure 2:
Transit (in thick lines) and ionization times
(in dashes-dots) as a function of the solar distance for
Fe IX to Fe XVI. The ionization times were calculated by assuming
a constant temperature which is indicated in each panel. Ionization
times for Fe IX to Fe XVI run from the bottom to the top in the figure. |
| Open with DEXTER |
Ionization times tend to increase with
distance due to the decrease of electron density, while transit times
decrease with distance as a consequence of the solar wind acceleration.
Ionization times are smaller than transit times for the lower ionization
stages of iron (Fe IX-Fe XIII) and for all the distances considered.
However we find, for Fe XIV, Fe XV and Fe XVI
at T < 2 MK, that
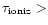
 for most of the distances covered by our observations.
Therefore under the above conditions non-ionization equilibrium
effects could be relevant for the above Fe ions.
On the other hand, for temperatures greater that 2 MK, ionization times begin to
exceed the transit times beyond a distance of about 1.7-1.8
for most of the distances covered by our observations.
Therefore under the above conditions non-ionization equilibrium
effects could be relevant for the above Fe ions.
On the other hand, for temperatures greater that 2 MK, ionization times begin to
exceed the transit times beyond a distance of about 1.7-1.8
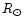 ,
which is the largest radial distance of our solar maximum
observations. Therefore, since the I(Fe XV)/I(Fe XIV)
and I(Fe XVI)/I(Fe XIV) ratios lead to temperatures larger than
1.9 MK, (see Sect. 4.3), we can assert that ionization equilibrium
exists for these ions under solar maximum conditions. We have also calculated the recombination
times and find that even at 2
,
which is the largest radial distance of our solar maximum
observations. Therefore, since the I(Fe XV)/I(Fe XIV)
and I(Fe XVI)/I(Fe XIV) ratios lead to temperatures larger than
1.9 MK, (see Sect. 4.3), we can assert that ionization equilibrium
exists for these ions under solar maximum conditions. We have also calculated the recombination
times and find that even at 2 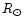 where the lowest density plasma
to be encountered in this work is found, the recombination time is at
least a factor ten below the transit time for the entire temperature range
being considered.
where the lowest density plasma
to be encountered in this work is found, the recombination time is at
least a factor ten below the transit time for the entire temperature range
being considered.
During the middle part of 1996 the solar cycle reached its minimum phase of
activity. The corona was dominated by two large polar coronal holes, with a
relatively simple large-scale coronal streamer extending between them.
We constructed a synoptic map using LASCO C2 data at a height of 2.2 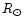 which we present in Fig. 3.
which we present in Fig. 3.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS1748f3.eps}\end{figure}](/articles/aa/full/2002/03/aa1748/Timg23.gif) |
Figure 3:
Lasco C2 synoptic map generated by extracting and averaging the
daily signal at a height of 2.2 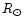 ,
between ,
between 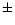
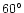 . . |
| Open with DEXTER |
This is centered on
the simple streamer, observations of which we obtained using the
Grazing Incidence Spectrometer (GIS) on SOHO on 1999 July 8. The synoptic
map demonstrates that the quiescent streamer was symmetric about the limb
in longitude at the time of our observations, and that there are no other structures
contributing to or biasing our measurements.
In Fig. 4 we have illustrated the region as it appeared in
one of these images.
![\begin{figure}
\par\includegraphics[width=10cm,clip]{MS1748f4.eps}\end{figure}](/articles/aa/full/2002/03/aa1748/Timg24.gif) |
Figure 4:
Composite image of the Sun that was obtained on 1996 July 8.
The central part is an EIT 284 Å image, outside that is a Mauna Loa
coronagraph image, and the outermost region a LASCO C2 image. |
| Open with DEXTER |
We have filled the occulted region with an image
obtained from the Mauna Loa MK3 Coronagraph, while the disc region is used
to display an EIT 284 Å image. The area which our observations cover
is delineated by the rectangle and was stable for a few Carrington rotations.
For some of these it has already been studied by others (Raymond et al. 1997;
Gibson et al. 1999; Li et al. 1998).
The observational sequence which we used to study the region is summarized
in Table 1.
This was performed using the
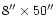 slit and produced five
rasters of size 240
slit and produced five
rasters of size 240
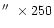
 .
We used the standard procedures
(gis_smooth, ghost_buster, and gis_calib) which are distributed
as part of the CDS software, to correct and intensity calibrate the data. These
routines use the results of the laboratory calibration of the CDS which
is described by Lang et al. (2000). This calibration confirms the flux of
any detected emission line to an accuracy of 30% which applies to all the
observations we describe from the CDS instrument here. These calibrations
have been confirmed in-flight by Landi et al. (1999).
.
We used the standard procedures
(gis_smooth, ghost_buster, and gis_calib) which are distributed
as part of the CDS software, to correct and intensity calibrate the data. These
routines use the results of the laboratory calibration of the CDS which
is described by Lang et al. (2000). This calibration confirms the flux of
any detected emission line to an accuracy of 30% which applies to all the
observations we describe from the CDS instrument here. These calibrations
have been confirmed in-flight by Landi et al. (1999).
We have summed data from each of the five rasters to produce an average count rate for
each radial position. We fitted selected regions using the cfit
routine which is distributed as part of the Solarsoft package. This allows
a structure to be defined which contains the lines and the allowed range of
parameters of the fit, such as width, position and intensity. The results
of these fits for each of the raster positions are presented in Table 2.
In order to understand the distribution of plasma we have plotted the loci of the emission
measure (see e.g. Griffiths & Jordan 1998) for each ion from Table 2 as a function of temperature in Fig. 5.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{MS1748f5.eps}\end{figure}](/articles/aa/full/2002/03/aa1748/Timg30.gif) |
Figure 5:
Emission measure loci of each Fe ion from Table 2 for
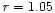 -1.3 -1.3 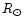 .
The hatched region represents the probable distribution of plasma in
the observed region. .
The hatched region represents the probable distribution of plasma in
the observed region. |
| Open with DEXTER |
These loci represent from left to right, the emission measure which would
reproduce our observed flux for Fe IX-Fe XV within the height range 1.05-1.3  .
If the plasma was isothermal, all the curves should intersect at the
correct single value of emission measure. It is clear from the figure that
this is not the case which suggests that the plasma located in the height range
is distributed in temperature between 1-1.5 MK.
.
If the plasma was isothermal, all the curves should intersect at the
correct single value of emission measure. It is clear from the figure that
this is not the case which suggests that the plasma located in the height range
is distributed in temperature between 1-1.5 MK.
To investigate the variation of temperature as a function of height we have used the line
intensity ratio which is most sensitive to temperature changes for the bulk
of the plasma in this temperature regime namely I(Fe IX)/I(Fe XI). We present the results of
this analysis in Sect. 4.3 along with similar calculations for the solar maximum.
Solar maximum of the current solar cycle was characterized by
the appearance of bright coronal streamers located close to the poles.
These structures appear to have evolved from the decaying magnetic field
from the first high latitude spots of the cycle. During 1999 August 5,
we performed observations of such a compact streamer.
In Fig. 6 we show a composite view using
an enhanced SXT image and a MK4 coronagraph image which was obtained from
the Mauna Loa solar observatory.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{MS1748f6.eps}\end{figure}](/articles/aa/full/2002/03/aa1748/Timg31.gif) |
Figure 6:
Composite view of the corona formed from an enhanced
composite Yohkoh SXT image (central region) and a Mauna Loa MK4
coronagraph image (outer region) on 1999 August 5. The streamer which we observed
is indicated by the arrow was centered at a Carrington longitude of
80 of rotation 1952.
of rotation 1952. |
| Open with DEXTER |
The streamer was observed to have evolved
directly from active region AR 8657, and remained connected via an extended
arcade which can be seen to increase in altitude away from the active region center.
To study this region we constructed an observing sequence which rastered over the
whole streamer and included data from both the NIS and GIS.
The observational sequence used for each detector is summarized in Table 3.
Table 3:
Study summary for solar maximum observations obtained on 1999
August 5. The upper part of the table refers to the GIS observations
whilst those below the dividing line represent the NIS observations.
The NIS was used to cover the lower corona and Limb.
| Coordinates |
Height |
Exposure |
Raster |
| |
|
|
positions (spacing) |
| |
(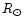 ) ) |
(s) |
solar-x |
solar-y |
| -920, -1170 |
1.55 |
50 |
30 (32
 ) ) |
4 (61
 ) ) |
| -920, -1020 |
1.43 |
20 |
30 (8
 ) ) |
5 (51
 ) ) |
| -920, -780 |
1.26 |
10 |
30 (8
 ) ) |
5 (51
 ) ) |
| -680, -1383 |
1.60 |
50 |
8 (32
 ) ) |
4 (61
 ) ) |
| -680, -1215 |
1.45 |
20 |
30 (8
 ) ) |
5 (51
 ) ) |
| -680, -975 |
1.24 |
10 |
30 (8
 ) ) |
5 (51
 ) ) |
| -440, -1535 |
1.66 |
50 |
8 (32
 ) ) |
4 (61
 ) ) |
| -440, -1335 |
1.46 |
20 |
30 (8
 ) ) |
5 (51
 ) ) |
| -440, -1095 |
1.23 |
10 |
30 (8
 ) ) |
5 (51
 ) ) |
| -200, 1375 |
1.45 |
20 |
30 (8
 ) ) |
5 (51
 ) ) |
| -200, -1135 |
1.20 |
10 |
30 (8
 ) ) |
5 (51
 ) ) |
| -680, -975 |
1.24 |
50 |
30 (8
 ) ) |
18 (13
 ) ) |
| -680, -735 |
1.04 |
50 |
30 (8
 ) ) |
18 (13
 ) ) |
| -440, -1095 |
1.23 |
50 |
30 (8
 ) ) |
18 (13
 ) ) |
| -440, -855 |
1.00 |
50 |
30 (8
 ) ) |
18 (13
 ) ) |
The NIS as mentioned earlier, covers a complementary wavelength range and
has the ability to image a region. We coarsely sampled the region (as
indicated in the bottom section of Table 3) with slit 5 (
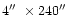 )
along which we summed every 8 pixels, to produce a macropixel. We
did this to reduce the required telemetry transmission bandwidth and thus
allow the complete spectra of NIS 1 and NIS 2 to be returned within a
reasonable time and without additional telemetry overheads. The NIS
observations allow us to check the calibration of our lines and to observe
the emission variation all the way to the limb, where the intensity would
normally exceed threshold limits of the GIS detectors.
)
along which we summed every 8 pixels, to produce a macropixel. We
did this to reduce the required telemetry transmission bandwidth and thus
allow the complete spectra of NIS 1 and NIS 2 to be returned within a
reasonable time and without additional telemetry overheads. The NIS
observations allow us to check the calibration of our lines and to observe
the emission variation all the way to the limb, where the intensity would
normally exceed threshold limits of the GIS detectors.
We corrected the data using the same procedure which we described in the
preceding section. There is no evidence for significant aging of the GIS
detectors over the course of mission, and we have therefore used the preflight flat
field for the GIS. This is not the case for the NIS which requires a flat field to
correct for the Long Term Gain Depression (LTGD). We thus use the NIS to
check the intensities of the lines in the overlap region (1.05-1.20 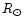 ), and to confirm the absolute intensity
calibration of similar lines found in both the NIS (Fe XIV 334.17 Å, Fe XV 327.06 Å) and GIS (Fe XIV 211.32 Å, Fe XV 417.75) detectors.
), and to confirm the absolute intensity
calibration of similar lines found in both the NIS (Fe XIV 334.17 Å, Fe XV 327.06 Å) and GIS (Fe XIV 211.32 Å, Fe XV 417.75) detectors.
The brightest lines we observed and for which we could obtain fits, are summarized in
Table 4.
These included lines which appeared in GIS detectors 1 and 3,
Fe XIV and Fe XV located at 211.3 Å and 417.75 Å respectively. In
Fig. 7 we plot loci of the emission measure for each ion
from Table 2
as a function of temperature as we did for the solar minimum observation.
![\begin{figure}
\includegraphics[width=8.6cm,clip]{MS1748f7.eps}\end{figure}](/articles/aa/full/2002/03/aa1748/Timg33.gif) |
Figure 7:
Emission measure loci for solar maximum data of each Fe ion from
Table 4 for
r=1.05-1.3 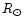 and latitude = -60
and latitude = -60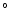 to
-70
to
-70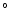 .
The hatched region represents the probable
plasma distribution within the observed region. This distribution is both
hotter and denser than that presented in Fig. 7 for solar
minimum. The Fe XIII, XIV, and XV all intersect close to 2.1 MK. .
The hatched region represents the probable
plasma distribution within the observed region. This distribution is both
hotter and denser than that presented in Fig. 7 for solar
minimum. The Fe XIII, XIV, and XV all intersect close to 2.1 MK. |
| Open with DEXTER |
The difference in the streamer temperature is striking in the plot.
The emission is dominated by plasma in the region of 2 MK; in fact this
component is enhanced by an order of magnitude compared to the solar minimum
values, while the cooler component (Fe IX, XI 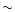 1 MK) in this region is
effectively halved.
1 MK) in this region is
effectively halved.
The origin of the different plasma components is illustrated in
Fig. 8.
![\begin{figure}
\par\includegraphics[width=10cm,clip]{MS1748f8.eps}\end{figure}](/articles/aa/full/2002/03/aa1748/Timg34.gif) |
Figure 8:
Monochromatic images constructed of the observed region. The
upper panel corresponds to the NIS observations, and the lower panel
corresponds to the GIS observations as summarized in Table 3. In the top
left hand panel we have indicated the location of the solar limb. It is
interesting to note that the Fe XI emission appears to dominate at the
edge of the streamer where the field is expected to be open (arrowed). |
| Open with DEXTER |
In this figure the streamer is bright and easily
resolved in the hotter emission lines Fe XIV-XVI, and faintly in Fe
XIII. Fe XI is enhanced at the boundary to the streamer which we have
indicated by the arrow in the figure. There appears to be
no Fe XI plasma within the streamer which demonstrates that the
streamer is hotter than 1.3 MK, the peak temperature of formation for this
ion.
To investigate the variation of temperature as a function of height
through the core (-60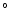 to -70
to -70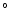 latitude) of this solar
maximum streamer we have used the line intensity ratio which is most sensitive to temperature changes
for the bulk of the plasma in this temperature regime namely I(Fe XV)/I(Fe
XIV) and I(Fe XVI)/I(Fe XIV)
for the GIS and NIS respectively. We present the results of this analysis in the following section
along with similar calculations for the solar minimum.
latitude) of this solar
maximum streamer we have used the line intensity ratio which is most sensitive to temperature changes
for the bulk of the plasma in this temperature regime namely I(Fe XV)/I(Fe
XIV) and I(Fe XVI)/I(Fe XIV)
for the GIS and NIS respectively. We present the results of this analysis in the following section
along with similar calculations for the solar minimum.
In Fig. 9 we present the temperature estimates that
result from the CDS line fits and line ratios.
![\begin{figure}
\par\includegraphics[width=13cm,clip]{MS1748f9.eps}\end{figure}](/articles/aa/full/2002/03/aa1748/Timg35.gif) |
Figure 9:
The radial temperature structure determined for solar maximum
(1999 August 5, triangles - NIS; squares - GIS) and solar minimum (1996
July 8, asterisks). The values from Foley (1998) are over plotted as
diamonds in the inset panel and were determined through a similar region
at the last solar maximum. The similarity between the two maximums is
surprising given the degree of systematic uncertainty associated with each
plot. The error bars of each point represent the statistical error of the
measurements. The standard error is associated with the uncertainty in
the relative calibration of each emission line/passband. In the case of CDS the
absolute calibration this is approximately 30% for the GIS and equates to
approximately 1 MK. We have overplotted a conserved heat flux model from
Sturrock et al. (1996), with the fitted values
indicated. For solar minimum this includes an outward heat flux from
Owocki et al. (1983). |
| Open with DEXTER |
We also plot the radial
temperature structure from the SXT filter ratios which were presented in Foley
(1998). We note the excellent agreement between values obtained
using the broadband filter ratio technique for the solar maximum (cycle 22)
and the observations we have presented here from the current maximum
(cycle 23) using CDS. In evaluating the line ratio I(Fe XV)/I(Fe XIV) from
the GIS we found the temperatures in fact were in the region of 2.5 MK. We
attributed this to the calibration of the detectors and adopted the NIS
calibration by normalizing our ratio to that observed with the NIS.
The radial temperature structure we derive here agrees
well with typical values which were found during the last solar
maximum which are summarized in Foley (1998).
This suggests that the assumptions which were used in deriving the
temperatures from the Yohkoh SXT filter ratio data were valid during the
solar maximum. These assumptions were associated with the use of
two broadband filters which limit the analysis to a weighted isothermal
approximation for each position.
Our other finding of an increase in the coronal temperature from
solar minimum to maximum, is broadly consistent with electron density
distributions obtained from eclipse observations during solar minimum
and maximum periods (e.g., Gabryl et al. 1999). These authors found
that when moving from solar minimum to maximum the slope of the electron
density radial distribution in streamers flattens. This would imply, by
assuming hydrostatic equilibrium, that the electron temperature (assumed
equal to the ion temperature) should increase from solar minimum to solar
maximum. This is exactly what we observe.
Gibson et al. (1999) reports the densities and temperatures of the same
coronal streamer observed 1.5 Carrington rotations later on 1996 August 17.
This was determined from the density gradients found from the
LASCO C2 and Mauna Loa MK 3 Coronameter data. They found temperatures
which peaked at 1.5 MK and a location 1.3 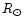 .
These results are consistent
with those we have found here spectroscopically. This suggests that the cores of
solar minimum quiescent streamers are in hydrostatic equilibrium.
.
These results are consistent
with those we have found here spectroscopically. This suggests that the cores of
solar minimum quiescent streamers are in hydrostatic equilibrium.
Departure from hydrostatic equilibrium is something which is
often cited as a reason why soft X-ray emission gradients cannot
be fitted for coronal streamer data. However, it is noted that solar
minimum streamers may be considered to be in hydrostatic equilibrium from
the work here. It is interesting to note that in Sturrock et al. (1996) that the
analysis of a structure which appears to be a leg of a large scale loop
was consistent with a hydrostatic barometric atmosphere.
In Fig. 10 we present a potential field extrapolation of the magnetic field
in the region of interest as would be seen when viewed on the limb.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{MS1748f10.eps}\end{figure}](/articles/aa/full/2002/03/aa1748/Timg36.gif) |
Figure 10:
Potential field extrapolation of the magnetic field in the region
of interest on 1996, July 8. |
| Open with DEXTER |
To obtain the
extrapolation, the synoptic magnetogram CR 1911 was taken from the NSO/Kitt Peak database
and a potential field (
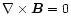 )
deduced. A source surface is placed
at 2.5
)
deduced. A source surface is placed
at 2.5 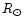 where the field is assumed to become radial. This in a crude manner
simulates the effect of the solar wind opening up the field which then extends into
interplanetary space. From the image it can be seen that near the equator at low heights
there are many loops that lie along the line of sight. With increasing
height, until about
where the field is assumed to become radial. This in a crude manner
simulates the effect of the solar wind opening up the field which then extends into
interplanetary space. From the image it can be seen that near the equator at low heights
there are many loops that lie along the line of sight. With increasing
height, until about
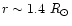 ,
the loops become more
concentrated, longer and extend from the higher latitudes of each
hemisphere. We can see from Fig. 9 that our temperature maximum is located around
the tops of these larger loops, and declines
at greater heights.
,
the loops become more
concentrated, longer and extend from the higher latitudes of each
hemisphere. We can see from Fig. 9 that our temperature maximum is located around
the tops of these larger loops, and declines
at greater heights.
We have over-plotted in Fig. 9 (dashed curve) the temperature profile anticipated if the decline from this height
was that expected for outward conserved conductive loss (see Owocki et al. 1983)
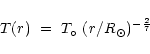 |
(3) |
where 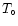 is the electron temperature at the base
of the corona. We also have over-plotted in
Fig. 9 (dashed-dots curve) the temperature which corresponds to a
conserved inward heat flux (such as that proposed by Sturrock et al. 1996) namely,
is the electron temperature at the base
of the corona. We also have over-plotted in
Fig. 9 (dashed-dots curve) the temperature which corresponds to a
conserved inward heat flux (such as that proposed by Sturrock et al. 1996) namely,
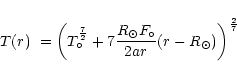 |
(4) |
where 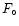 is the heat flux at the base of the corona
and a is the coefficient of thermal conductivity (Spitzer 1962).
is the heat flux at the base of the corona
and a is the coefficient of thermal conductivity (Spitzer 1962).
Measurements of the plasma beta value in the cores of streamers
have been performed by Li et al. (1998). They found that the plasma
pressure was the dominant force in streamer cores. In light of this
and our outwardly declining temperature gradient, it would seem probable that we are viewing
the initiation of the slow speed wind from the tops of loops. The fact that we observe a
temperature increase within the cores of coronal streamers would imply
that the heating source for the streamer must lie at or above the
location of the temperature maximum e.g. at the tops of the large
transequatorial loops that comprise the large scale structure of
the streamers.
Raymond et al. (1997), Raymond et al. (1998) and Feldman et al. (1999) report a depletion
of high FIP elements at solar minimum within quiescent streamers. They
attribute this to a gravitational settling. This is consistent with the
view drawn in the previous paragraph, where the principal energy source is
from the heating of the loops embedded within streamers. The material which
fills coronal streamers may also originate within these loops.
This may account for the often reported departure from normal hydrostatic
equilibrium for coronal streamer structures (e.g. see Aschwanden & Nitta
2000). Although this may also be directly related to the geometry.
The role of coronal magnetic field in coronal heating is well established with
many different heating mechanisms being distinguished by their scaling with
the field strength (Priest et al. 1998, 2000). In such models the coronal heating
rate is proportional to
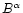 ,
with
,
with 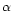 being a function of
the specific mechanism of magnetic energy build-up, release and dissipation.
These mechanisms were recently reviewed by Mandrini et al.
(2000), who compiled the values of
being a function of
the specific mechanism of magnetic energy build-up, release and dissipation.
These mechanisms were recently reviewed by Mandrini et al.
(2000), who compiled the values of 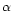 expected
for different magnetic-based heating scenarios.
Our aim here is to calculate an approximate value for
expected
for different magnetic-based heating scenarios.
Our aim here is to calculate an approximate value for 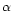 so as to
gain insights on which magnetic heating models may be more relevant.
By assuming that the heating sets up a conductive flux in the corona and by noting from Fig. 9 that the temperature scale heights are more or less identical for solar minimum and maximum,
we can write, to first order, that
so as to
gain insights on which magnetic heating models may be more relevant.
By assuming that the heating sets up a conductive flux in the corona and by noting from Fig. 9 that the temperature scale heights are more or less identical for solar minimum and maximum,
we can write, to first order, that
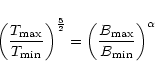 |
(5) |
where 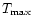 ,
,
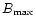 and
and
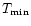 ,
,
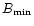 are the maximum coronal temperature and the magnetic field
strength for solar maximum and minimum respectively.
By assuming
are the maximum coronal temperature and the magnetic field
strength for solar maximum and minimum respectively.
By assuming
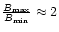 (e.g. Pevtsov & Acton
2001) and
(e.g. Pevtsov & Acton
2001) and
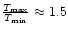 from Fig. 9, we find that
from Fig. 9, we find that
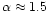 .
This value of
.
This value of 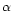 compares well with
the
compares well with
the 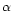 predicted by "direct current'' stressing models based on reconnection
and turbulence with constant dissipation coefficients (cf. models 5 and 11 in the
Mandrini et al. 2000 compilation).
predicted by "direct current'' stressing models based on reconnection
and turbulence with constant dissipation coefficients (cf. models 5 and 11 in the
Mandrini et al. 2000 compilation).
In a recent paper Schühle et al. (2000), found by using
SUMER data, an increase in the transition region (TR)
emission of up to a factor of 2 from solar minimum to solar maximum.
This behavior could be related to the observed increase
of the coronal temperature demonstrated in the previous sections.
Transition region models for the quiet Sun (e.g., Gabriel 1976)
indicate that TR radiative losses are powered from the
coronal conductive flux. By noting from Fig. 9 that the
temperature scale heights are more or less identical in solar minimum and maximum,
we can make the approximation that the TR radiative losses
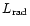 would scale as
would scale as
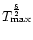 where
where 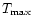 is the maximum coronal
temperature. Therefore, we have (Withbroe 1988)
is the maximum coronal
temperature. Therefore, we have (Withbroe 1988)
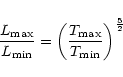 |
(6) |
where 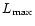 ,
,
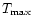 and
and 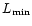 ,
,
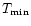 are
the TR radiative losses and coronal maximum temperature
for solar maximum and minimum respectively
(see for example Withbroe 1988).
From Fig. 9 it is clear that
are
the TR radiative losses and coronal maximum temperature
for solar maximum and minimum respectively
(see for example Withbroe 1988).
From Fig. 9 it is clear that
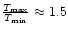 which means that
which means that
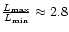 .
It is thus possible
that the coronal temperature increase from solar minimum to maximum
could have a bearing on the observed solar cycle modulation of TR emission.
.
It is thus possible
that the coronal temperature increase from solar minimum to maximum
could have a bearing on the observed solar cycle modulation of TR emission.
We have observed fundamental elements of the quiet solar corona, namely coronal streamers
at solar minimum and solar maximum using the CDS instrument on SOHO. From these observations
we have determined the distribution of Fe IX-XV as a function of height out to 2.3 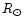 (1.8
(1.8 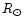 )
at solar minimum (maximum). We find that the solar minimum emission is
dominated by Fe XI while at solar maximum the emission is dominated by Fe
XV. This comes about due to an order of magnitude increase in the emission measure of Fe XV,
while the Fe XI decreases by about half.
)
at solar minimum (maximum). We find that the solar minimum emission is
dominated by Fe XI while at solar maximum the emission is dominated by Fe
XV. This comes about due to an order of magnitude increase in the emission measure of Fe XV,
while the Fe XI decreases by about half.
We have used the ratio of the most abundant ions to determine the vertical temperature
structure at solar minimum and maximum. We find that the temperature increases as a
function of height to a peak of about 1.4 MK at 1.3 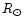 at solar minimum. This
is reduced by around 0.7 MK compared to temperatures determined by both
the SOHO CDS and the Yohkoh SXT at solar maximum 22 (see Foley 1998); and the measurements
which we present here using CDS for the current maximum 23.
at solar minimum. This
is reduced by around 0.7 MK compared to temperatures determined by both
the SOHO CDS and the Yohkoh SXT at solar maximum 22 (see Foley 1998); and the measurements
which we present here using CDS for the current maximum 23.
The location of the temperature maximum is coincident with the tops of
loops which comprised the regions observed. The temperature declines below
and above these loops suggesting they are the focus of energy deposition
within coronal streamers. The magnetic field extrapolation suggests that, above the temperature
maximum, the field may progressively open with the falling temperature
suggesting outflow that may be related to the slow solar wind.
We find that the modulation of coronal electron temperature through the
decline and rise of a solar cycle is consistent with a scaling with
magnetic field of the order of B1.5. This from current theory is
consistent with uniform heating by current dissipation and turbulence.
We have also shown that this temperature increase could be responsible
for the observed solar cycle enhancement of the transition region emission.
We plan to investigate these ideas in the future using further observations
from the instruments on the SOHO spacecraft.
Acknowledgements
We are grateful to the UK Particle Physics and Astronomy Research Council
for financial support. We acknowledge the Solar UK Research Facility (SURF
- http://surfwww.mssl.ucl.ac.uk/surf/) for providing data
for use in this publication. SOHO is a project of international cooperation between
ESA and NASA. The Yohkoh soft X-ray telescope is a collaborative project of the
Lockheed Palo Alto Research Laboratory, the National Astronomical Observatory of
Japan, and the University of Tokyo, supported by NASA and ISAS. The Mauna
Loa MK3 and MK4 Coronagraph data was provided courtesy, High Altitude Observatory,
National Center for Atmospheric Research (NCAR), Boulder, Colorado, USA. NCAR
is sponsored by the National Science Foundation.
We would like to thank Terry Kucera, Ron Yurow, Eddie Breeveld, Dave Pike and Stein Vider Haugan for help
coordinating and monitoring some of our observations. We would also like to thank Matt Wyndham, Ben Sanderson, Jon Lappington, Alec McCalden, and
Alice Breeveld for helpful discussion regarding the way in which the GIS
operates, and making this work possible. This research has made use of
NASA's Astrophysics Data System Abstract Service. The CHIANTI database is a collaborative project
involving the Naval Research Laboratory (Washington DC, USA), the Arcetri Observatory (Firenze, Italy), and
Cambridge University (UK). We would also like to thank the
anonymous referee for useful comments which improved the clarity of this
paper.
- Aschwanden, M. J., & Nitta, N. 2000, ApJ, 535, L59 In the text
NASA ADS
- Breeveld, A. A., Edgar, M. L., Lappington,
J. S., & Smith, A. 1992, SPIE, 1743, 315
In the text
- Brueckner, G. E., Howard, R. A., Koomen, M. J., et al. 1995, Sol. Phys., 162, 357
In the text
NASA ADS
- Dere, K. P., Landi, E., Mason, H. E., Monsignori Fossi, B. C., & Young, P. R. 1997, A&AS,
125, 149
In the text
NASA ADS
- Dupree, A. K., Moore, R. T., & Shapiro, P. R. 1979, ApJ, 229, L101
In the text
NASA ADS
- Feldman, U., Doschek, G. A., Schühle, U., & Wilhelm, K. 1999, ApJ, 518, 500
In the text
NASA ADS
- Fisher, R. R., Lee, R. H., MacQueen, M. R., & Poland. A. I. 1981, Appl. Opt., 20, 1094
In the text
NASA ADS
-
Foley, C. R. 1998, Ph.D. Thesis, University of London In the text
http://www.mssl.ucl.ac.uk/www_solar/publications/foleydiss.zip
-
Foley, C. R., Culhane, J. L., Acton, L. W., & Lemen, J. 1996, in Proc. of the IAU, 153 (held in Makuhari)
In the text
- Gabriel, A. H. 1976, Phil. Trans. Roy. Lond. A, 28l, 575
In the text
- Gabryl, J.-R., Cugnon, P., & Clette, F. 1999, C. Ska, 28, 216
In the text
NASA ADS
- Gibson S. E., Fludra, A., Bagnal, F., et al. JGR, 104, A5, 9691, 1999
In the text
-
Goldstein, B. E., Neugebauer, M., Phillips, J. L., et al. 1996, A&A, 316, 296
In the text
NASA ADS
-
Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161
In the text
NASA ADS
- Griffiths, N. W., & Jordan, C. 1998, ApJ, 497, 883
In the text
NASA ADS
-
Guhathakurta, M., Holtzer, T. E., & MacQueen, R. M. 1996, ApJ, 458, 817
In the text
NASA ADS
-
Harrison, R. A., Sawyer, E. C., Carter, M. K., et al. 1995, Sol. Phys., 162, 233
In the text
NASA ADS
- Kopp, R. A., & Holtzer, T. E. 1976, Sol. Phys., 49, 43 In the text
NASA ADS
- Lang, J., Kent, B. J., Breeveld, A. A., et al. 2000, J. Opt. A: Pure Appl. Opt., vol. 2(2), 88
In the text
- Landi, E., Del Zanna, G., Breeveld, E. R., et al. 1999, A&AS, 135, 171
In the text
NASA ADS
- Li, J., Raymond, J. C., Acton, L. W., et al. 1998, ApJ, 506, 431
In the text
NASA ADS
- Mazzotta, P., Mazzitelli, G., Colafrancesco, S., & Vittorio, N. 1998, A&AS, 133, 403
In the text
NASA ADS
- Mandrini, C. H., D
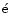 moulin, P., &
Klimchuk, J. A. 2000, ApJ, 530, 999
In the text
NASA ADS
moulin, P., &
Klimchuk, J. A. 2000, ApJ, 530, 999
In the text
NASA ADS
- Mason, H. E., & Fossi, B. C. M. 1994, A&AR, 6, 123
In the text
- Owocki, S. P., Holzer,
T. E., & Haundhausen, A. J. 1983, ApJ, 275, 354
In the text
NASA ADS
- Pevtsov, A. A., & Acton, L. W. 2001, ApJ, 554, 416
In the text
NASA ADS
-
Priest, E. R., Foley, C. R., Heyvaerts, J., et al. 1998, Nature, 393, 545
In the text
-
Priest, E. R., Foley, C. R., Heyvaerts, J., et al. 2000, ApJ, 539, 1002
In the text
NASA ADS
-
Raymond, J. C., Kohl, J. L., Noci, G., et al. 1997, Sol. Phys., 175, 645
In the text
NASA ADS
- Raymond, J. C., Suleiman, R., & Kohl, J. L. 1998, Space Sci. Rev., 85, 283
In the text
NASA ADS
- Shull, J. M., & Van Steenberg, M. 1982,
ApJS, 48, 95
In the text
NASA ADS
- Schühle, U., Wilhelm, K., Hollandt, J., Lemaire, P., & Pauluhn, A. 2000, A&A, 354, L71
In the text
NASA ADS
- Spitzer, L. 1962, Physics of Fully Ionized Gases (New York: Interscience)
In the text
-
Sturrock, P. A., Wheatland, M. S., & Acton, L. W. 1996, ApJ, 461, 115
In the text
NASA ADS
- Tsuneta, S., Acton, L., Bruner, M., et al. 1991, Sol. Phys., 136, 37
In the text
NASA ADS
-
Wheatland, M. S., Sturrock, P. A., & Acton, L. W. 1997, ApJ, 482, 510
In the text
NASA ADS
- Withbroe, G. L. 1988, ApJ, 325, 442
In the text
NASA ADS
Copyright ESO 2002
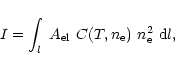
![\begin{figure}
\par\includegraphics[width=9.3cm,clip]{MS1748f1.eps}\end{figure}](/articles/aa/full/2002/03/aa1748/Timg12.gif)
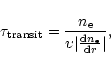
![\begin{figure}
\par\includegraphics[width=7cm,clip]{MS1748f2.eps}\end{figure}](/articles/aa/full/2002/03/aa1748/Timg21.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS1748f3.eps}\end{figure}](/articles/aa/full/2002/03/aa1748/Timg23.gif)
![\begin{figure}
\par\includegraphics[width=10cm,clip]{MS1748f4.eps}\end{figure}](/articles/aa/full/2002/03/aa1748/Timg24.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{MS1748f5.eps}\end{figure}](/articles/aa/full/2002/03/aa1748/Timg30.gif)
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{MS1748f6.eps}\end{figure}](/articles/aa/full/2002/03/aa1748/Timg31.gif)
![\begin{figure}
\includegraphics[width=8.6cm,clip]{MS1748f7.eps}\end{figure}](/articles/aa/full/2002/03/aa1748/Timg33.gif)
![\begin{figure}
\par\includegraphics[width=10cm,clip]{MS1748f8.eps}\end{figure}](/articles/aa/full/2002/03/aa1748/Timg34.gif)
![\begin{figure}
\par\includegraphics[width=13cm,clip]{MS1748f9.eps}\end{figure}](/articles/aa/full/2002/03/aa1748/Timg35.gif)
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{MS1748f10.eps}\end{figure}](/articles/aa/full/2002/03/aa1748/Timg36.gif)