A&A 381, 884-893 (2002)
DOI: 10.1051/0004-6361:20011633
E. E. Giorgi1, 2 - R. A. Vàzquez1 - G. Baume1, 3 - W. Seggewiss4 - J.-M. Will4
1 - Facultad de Ciencias Astronómicas y Geofísicas,
UNLP, and IALP (UNLP-CONICET),
Paseo del Bosque s/n, 1900, La Plata, Argentina
2 -
Fellow of Comisión de Investigaciones Científicas de la
Provincia de Buenos Aires, Argentina
3 -
Post-doctoral fellow of CONICET
4 -
Sternwarte der Universität Bonn,
Auf dem Hügel 71, 53121 Bonn, Germany
Received 3 August 2001 / Accepted 18 October 2001
Abstract
CCD UBVI imaging photometry was carried out in the field of
the open cluster NGC 2571. From the analysis of our data
we state the cluster is at a distance of 1380 ![]() 130 pc and its age
is
130 pc and its age
is
![]() yr. The cluster mass function has
a slope larger than a typical Salpeter's law. There are two notorious
features in NGC 2571: the cluster contains a high proportion of stars
located below the reference line that are serious candidates
to be metallic line stars (probably Am-Fm), and shows
also a sharp gap along its main sequence that cannot be
explained by a random process nor by a biased rejection of cluster
members. A striking blue object was detected in the cluster
field that could be a white dwarf candidate.
yr. The cluster mass function has
a slope larger than a typical Salpeter's law. There are two notorious
features in NGC 2571: the cluster contains a high proportion of stars
located below the reference line that are serious candidates
to be metallic line stars (probably Am-Fm), and shows
also a sharp gap along its main sequence that cannot be
explained by a random process nor by a biased rejection of cluster
members. A striking blue object was detected in the cluster
field that could be a white dwarf candidate.
Key words: open clusters and associations: individual: NGC 2571 - stars: luminosity function, mass function - H-R diagrams - stars: chemically peculiar - stars: blue stragglers
The open cluster NGC 2571 (C0816-295,
![]() is located in the direction of
the Vela-Puppis spur, at
is located in the direction of
the Vela-Puppis spur, at
![]() and
and
![]() ,
in a region of nearly constant
interstellar absorption,
,
in a region of nearly constant
interstellar absorption,
![]() from 1 to 4 kpc from
the Sun (Vogt & Moffat 1972;
Neckel & Klare 1980).
Three attempts have been made to determine
the distance of NGC~2571 using UBV photometry:
Lindoff (1968, pg photometry) derives
a distance of 2.05kpc and a colour excess of
from 1 to 4 kpc from
the Sun (Vogt & Moffat 1972;
Neckel & Klare 1980).
Three attempts have been made to determine
the distance of NGC~2571 using UBV photometry:
Lindoff (1968, pg photometry) derives
a distance of 2.05kpc and a colour excess of
![]() .
But Clariá (1976, pe) and
Kilambi (1978, pg) place the cluster at a distance of
1.25kpc only under
.
But Clariá (1976, pe) and
Kilambi (1978, pg) place the cluster at a distance of
1.25kpc only under
![]() .
.
On the other hand, Lindoff (1968) and Clariá (1976) agree
on the cluster's age, about
![]() yr based
on an absolute magnitude
yr based
on an absolute magnitude
![]() of the turn-off point (TO).
Kilambi (1978) reduces the TO to
of the turn-off point (TO).
Kilambi (1978) reduces the TO to
![]() thus increasing the age to
thus increasing the age to
![]() yr.
yr.
As a consequence, subsequent interpreters of the foregoing
photometric papers arrived at different conclusions on the nature
of the brightest stars of the cluster: HD70058 (B3/5) and
HD70078 (B2V), spectral types from Houk (1982).
Mermilliod (1981) and Mermilliod & Maeder (1986) considered them
as genuine cluster main-sequence stars and attributed NGC~2571 to
their "NGC~3766 age-group'' for which they derive the
young age of
![]() yr. On the other hand, Kilambi's
(1978) faint TO and higher age led Ahumada
& Lapasset (1995) to the conclusion that the two brightest
stars must be blue stragglers.
yr. On the other hand, Kilambi's
(1978) faint TO and higher age led Ahumada
& Lapasset (1995) to the conclusion that the two brightest
stars must be blue stragglers.
The extensive photographic photometry carried out by Kilambi
(1978) shows several interesting features in NGC 2571
which deserve further study:
(1) The cluster shows a pronounced gap in the stellar distribution
along the main sequence (MS) at
![]() .
(2) The cluster contains several variable stars that have been identified
by comparing photoelectric and photographic photometry.
(3) There is an unusual number of stars placed below the
reference line in Kilambi's colour-colour diagram, which he attributed
to a non-linearity effect in the (U-B) transformations.
Unfortunately, the photoelectric photometry performed by Clariá
(1976), although more precise, is not deep enough to detect
this feature revealed by Kilambi's work.
.
(2) The cluster contains several variable stars that have been identified
by comparing photoelectric and photographic photometry.
(3) There is an unusual number of stars placed below the
reference line in Kilambi's colour-colour diagram, which he attributed
to a non-linearity effect in the (U-B) transformations.
Unfortunately, the photoelectric photometry performed by Clariá
(1976), although more precise, is not deep enough to detect
this feature revealed by Kilambi's work.
![\begin{figure}
\par\includegraphics[width=10cm,clip]{MS1675f1.eps}\end{figure}](/articles/aa/full/2002/03/aa1675/Timg21.gif) |
Figure 1: Finding chart of NGC 2571. North and East are indicated. The arrow gives the position of star No. 1357, a White Dwarf candidate (see Sect. 3.6). |
| Open with DEXTER | |
The present work is therefore aimed to re-examine the reliability of Kilambi's findings with a deeper CCD photometry. In Sect. 2 we describe the observational procedure and the photometric reduction techniques. Section 3 contains the cluster data analysis including a discussion on distance and age, on cluster membership, variable stars, peculiar star candidates, and on the main-sequence gap. In addition, we describe briefly the luminosity function (LF) and mass function (MF) of NGC 2571. Section 4 contains our conclusions.
We carried out CCD imaging photometry in the Kron-Cousins UBVI
system on April 27 and 29, 1994 using
a
![]() pxl CCD
with a scale of
pxl CCD
with a scale of
![]() /pxl
and a field of view of
/pxl
and a field of view of
![]() attached to the 1.54-m Danish
telescope at ESO, La Silla, Chile. Figure 1 shows the two overlapping
fields that were observed for the cluster NGC 2571.
They cover an effective area of
attached to the 1.54-m Danish
telescope at ESO, La Silla, Chile. Figure 1 shows the two overlapping
fields that were observed for the cluster NGC 2571.
They cover an effective area of
![]() .
Whenever possible, the statistics of the faintest stars was
maximized taking long frames of same exposure time and
combining them. In addition, very short exposures were needed
to obtain reliable photometric data for the two brightest stars
in the field. However,
in this case, it was necessary to apply a shutter timing correction.
Details of the exposure times and the number of observations
can be found in Table 1. The mean seeing on the
entire run was
.
Whenever possible, the statistics of the faintest stars was
maximized taking long frames of same exposure time and
combining them. In addition, very short exposures were needed
to obtain reliable photometric data for the two brightest stars
in the field. However,
in this case, it was necessary to apply a shutter timing correction.
Details of the exposure times and the number of observations
can be found in Table 1. The mean seeing on the
entire run was
![]() and the quality of both nights was
photometric.
and the quality of both nights was
photometric.
| Passband | U | B | V | I | |
| Night 1 | short | 4 | 1 | 1 | 1 |
| medium | 10 | 10 | 60 | 20 | |
| long | 600 (2) | 600 (4) | 300 (4) | 300 (4) | |
| Night 2 | short | 15 | 3 | 1 | 1 |
| medium | 300 | 120 | 30 | 20 | |
| long | 900 | 600 (4) | 300 (4) | 300 (4) |
Instrumental magnitudes were obtained by point spread function (PSF) fitting using the DAOPHOT package (Stetson 1987) running within IRAF. More than fifteen stars from two standard fields of Landolt (1992) have been observed each night to convert the instrumental magnitudes into the standard system via transformation equations of the following form:
|
|
u2=0.397 |
|
|
| Night 1 |
|
b2=0.245 |
|
|
|
v2=0.137 |
|
|
|
|
i2=0.052 |
|
|
|
|
u2=0.425 |
|
|
| Night 2 |
|
b2=0.251 |
|
|
|
v2=0.142 |
|
|
|
|
i2=0.052 |
|
The final photometric catalogue for 1575 stars is given
in self-explanatory format in Table 3; it also includes a cross
correlation with other authors and additional information
from different sources. The precision of our data is depicted
in Fig. 2 that shows the photometric errors from DAOPHOT
against the visual magnitude; even at very faint magnitudes
the errors of our photometry are quite small. The final errors for
stars with
![]() (including fitting and calibration) are:
(including fitting and calibration) are:
![]() .
The mean values and standard
deviations of the internal errors of our photometry,
obtained by comparison of stars observed in both nights are:
.
The mean values and standard
deviations of the internal errors of our photometry,
obtained by comparison of stars observed in both nights are:
![]() .
.
To estimate the angular diameter of NGC 2571, we computed
the surface stellar density using an image
of
![]() retrieved from the Digitized Sky
Survey 2-Red (DSS2-Red), centred on NGC 2571. The counts were
performed in concentric rings around star No. 1 up to
retrieved from the Digitized Sky
Survey 2-Red (DSS2-Red), centred on NGC 2571. The counts were
performed in concentric rings around star No. 1 up to
![]() mag and then divided by their respective surfaces. The final
density profile and the respective error bars are depicted in Fig. 3.
The surface density decreases with radius
up to
mag and then divided by their respective surfaces. The final
density profile and the respective error bars are depicted in Fig. 3.
The surface density decreases with radius
up to ![]()
![]() from the cluster
centre where it merges into the background stellar density
indicated by the dashed line, obtained as the mean of the stellar density
outside the apparent boundaries of the cluster. It is quite obvious that
the cluster is mostly evident because of its few moderately
bright stars instead of having a high stellar density.
Within the unavoidable uncertainty we adopt
from the cluster
centre where it merges into the background stellar density
indicated by the dashed line, obtained as the mean of the stellar density
outside the apparent boundaries of the cluster. It is quite obvious that
the cluster is mostly evident because of its few moderately
bright stars instead of having a high stellar density.
Within the unavoidable uncertainty we adopt
![]() as the angular radius of NGC 2571 (see also Lindoff 1968).
When comparing with the area covered in our survey we conclude
that our observations comprise very well the core of
the cluster and more than 60% of its total area. But we note
that the bright red star, CD
as the angular radius of NGC 2571 (see also Lindoff 1968).
When comparing with the area covered in our survey we conclude
that our observations comprise very well the core of
the cluster and more than 60% of its total area. But we note
that the bright red star, CD
![]() (= Clariá No. 3) classified as non cluster member
by Clariá (1976), is not in our field.
(= Clariá No. 3) classified as non cluster member
by Clariá (1976), is not in our field.
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{MS1675f2.eps}\end{figure}](/articles/aa/full/2002/03/aa1675/Timg55.gif) |
Figure 2: Photometric errors in colour and magnitude vs. V magnitude as given by DAOPHOT. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS1675f3.eps}
\end{figure}](/articles/aa/full/2002/03/aa1675/Timg56.gif) |
Figure 3: Density of stars in NGC 2571 as a function of radius. The line is the mean field stellar density. |
| Open with DEXTER | |
| No. | Lind | Clar | Kila | Sp.Type | Ref. | Rem. | X | Y | V | (B - V) | (U - B) | (V - I) |
| 1 | 10 | 1 | 1 | B2V | 1 | 422.56 | 495.72 | 8.85 | -0.07 | -0.76 | -0.15 | |
| 2 | 16 | 2 | 2 | B3/5, B8 | 1.3 | 544.73 | 588.43 | 9.00 | -0.09 | -0.67 | -0.11 | |
| 3 | 12 | 5 | 5 | B4 | 2 | 216.93 | 657.26 | 10.38 | -0.07 | -0.28 | 0.00 | |
| 4 | 24 | 7 | 7 | B5 | 2 | 845.34 | 532.86 | 10.83 | -0.02 | -0.39 | -0.13 | |
| 5 | 75 | 6 | 6 | K0 | 2 | var? | 829.68 | 968.29 | 10.90 | 1.12 | 1.29 | 1.36 |
| 6 | 8 | 8 | 1540.64 | 988.93 | 11.15 | 0.04 | -0.02 | 0.02 | ||||
| 7 | 68 | 9 | 9 | B5 | 2 | 1055.79 | 774.39 | 11.16 | -0.01 | -0.24 | 0.00 | |
| 8 | 25 | 13 | 13 | B5 | 2 | 750.39 | 504.01 | 11.42 | 0.04 | -0.21 | -0.10 | |
| 9 | 11 | 16 | 16 | B8 | 2 | 237.46 | 530.24 | 11.72 | 0.01 | -0.08 | -0.08 | |
| 10 | 18 | 17 | 17 | A0 | 2 | 683.93 | 436.88 | 11.72 | 0.13 | 0.09 | 0.05 | |
| 11 | 19 | 19 | 1160.40 | 698.73 | 11.76 | 1.04 | 0.66 | 1.03 | ||||
| 12 | 23 | 23 | 1407.14 | 945.06 | 11.90 | 0.07 | 0.00 | 0.05 | ||||
| 13 | 22 | 22 | B6 | 2 | 388.32 | 466.69 | 11.91 | 0.04 | -0.08 | -0.03 | ||
| 14 | 25 | 25 | 560.67 | 684.72 | 12.00 | 0.04 | 0.08 | 0.01 | ||||
| 15 | 19 | 26 | 26 | 736.00 | 338.99 | 12.13 | 0.06 | 0.04 | 0.02 | |||
| 16 | 27 | 27 | B9 | 2 | 1203.26 | 61.27 | 12.28 | 0.11 | 0.16 | 0.12 | ||
| 17 | 148 | 110 | 1529.70 | 244.12 | 12.29 | 1.68 | 1.87 | 1.68 | ||||
| 18 | 28 | 28 | B9 | 2 | 1272.94 | 561.11 | 12.33 | 0.13 | 0.14 | 0.11 | ||
| 19 | 20 | 29 | 29 | A1 | 2 | 790.28 | 335.75 | 12.37 | 0.09 | 0.16 | 0.07 | |
| 20 | 14 | 32 | 32 | 470.12 | 637.68 | 12.51 | 0.29 | 0.19 | 0.38 | |||
| 21 | 69 | 33 | 33 | A0 | 2 | pec, var | 1012.53 | 793.81 | 12.56 | 0.08 | 0.23 | 0.16 |
| 22 | 22 | 31 | 31 | var | 911.28 | 414.62 | 12.57 | 1.05 | 0.89 | 1.19 | ||
| 23 | 74 | 36 | 36 | pec, var | 871.26 | 985.17 | 12.77 | 0.11 | 0.26 | 0.22 |
As mentioned above, previous studies of NGC 2571 are reported
in the literature. The photometric works of Lindoff,
Clariá and Kilambi provide the most extended data sets to carry
out a straight comparison of our photometry with theirs.
Table 4 shows the mean differences in V, (B-V),
and (U-B) computed in the sense "our values minus others''.
As it is expected, larger differences are found
with the photographic data sets of Lindoff and Kilambi,
especially for the (U-B) index. However, what surprises
most are the large standard deviations found in ![]() for all
three sets. Even with the more accurate photoelectric
photometry of Clariá (1976) the V deviation is so large that
we conclude the cluster
may contain several variable stars or photometrically
unresolved stars. This was first mentioned by Kilambi (1978)
who compared his photographic observations to those of Clariá
and published a list of variable stars. Here, we search for
variable stars by comparing our CCD observations with
Clariá's photoelectric photometry. We call a star
"variable'' if the differences with Clariá's data are larger
than 0.1 in magnitude V and in at least one colour.
A candidate star is called "probable variable''
if it shows differences larger than 0.1mag in V or one
colour alone.
Therefore, we state that star No. 5 is a "probable variable''
and stars Nos. 21, 22, 24, 27, 30, 33, and 38 are "variable stars''.
Table 3 includes details on variability in NGC 2571.
Just when this article was submitted, Moitinho (2001)
kindly provided us with his unpublished data on NGC 2571 for comparison
purposes (as shown in Table 4). Although there is a very good agreement
of both CCD data sets, some of our variable stars were found to show
V and colour differences.
for all
three sets. Even with the more accurate photoelectric
photometry of Clariá (1976) the V deviation is so large that
we conclude the cluster
may contain several variable stars or photometrically
unresolved stars. This was first mentioned by Kilambi (1978)
who compared his photographic observations to those of Clariá
and published a list of variable stars. Here, we search for
variable stars by comparing our CCD observations with
Clariá's photoelectric photometry. We call a star
"variable'' if the differences with Clariá's data are larger
than 0.1 in magnitude V and in at least one colour.
A candidate star is called "probable variable''
if it shows differences larger than 0.1mag in V or one
colour alone.
Therefore, we state that star No. 5 is a "probable variable''
and stars Nos. 21, 22, 24, 27, 30, 33, and 38 are "variable stars''.
Table 3 includes details on variability in NGC 2571.
Just when this article was submitted, Moitinho (2001)
kindly provided us with his unpublished data on NGC 2571 for comparison
purposes (as shown in Table 4). Although there is a very good agreement
of both CCD data sets, some of our variable stars were found to show
V and colour differences.
Some astrometric data for NGC 2571 stars can be found in the Hipparcos and Tycho Catalogues (ESA 1997): proper motions are available for ten stars, and four stars also have parallax measures (see also Baumgardt et al. 2000). Unfortunately, these data have such large errors that they cannot be used to derive membership probability and cluster distance. Therefore, we have to rely on photometric data alone.
There is some discussion in the literature on the question of
membership in star clusters. Abt (1979) claims that
proper motions constitute the basic criterion
for reliable cluster membership. However,
as stated by Turner (1993) and emphasized
by Forbes (1996), photometric membership
is good enough when it relies on a careful inspection of
the two-colour (TCD) and colour-magnitude diagram (CMD)
and on a consistent reddening solution.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{MS1675f4.eps}\end{figure}](/articles/aa/full/2002/03/aa1675/Timg58.gif) |
Figure 4:
Two-colour diagram (TCD) [(U-B) vs. (B-V)]
of stars in the field of
NGC 2571. Symbols are:
|
| Open with DEXTER | |
| Author |
|
|
|
N | |
| Lindoff (1968) |
|
|
|
51 | |
| Clariá (1976) |
|
|
|
30 | |
| Kilambi (1978) |
|
|
|
44 | |
| Moitinho (2001) |
|
|
|
|
919 |
![\begin{figure}
\par\includegraphics[width=6cm,clip]{MS1675f5.eps}\end{figure}](/articles/aa/full/2002/03/aa1675/Timg79.gif) |
Figure 5: Colour-magnitude diagram (CMD) [V vs. (B-V)] of stars in the field of NGC 2571. Symbols as in Fig. 4. The solid line represents the Schmidt-Kaler (1982) ZAMS. The dotted lines show the position of the gap (see Sect. 3.7). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6cm,clip]{MS1675f6.eps}
\end{figure}](/articles/aa/full/2002/03/aa1675/Timg80.gif) |
Figure 6: CMD [V vs. (U-B)] of stars in the field of NGC 2571. Symbols as in Fig. 4. The solid line represents the Schmidt-Kaler (1982) ZAMS. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6cm,clip]{MS1675f7.eps}\end{figure}](/articles/aa/full/2002/03/aa1675/Timg81.gif) |
Figure 7:
TCD [(B-V) vs. (V-I)] of stars in the field of
NGC 2571. The dashed lines represents
the intrinsic location of stars of luminosity classes V and III from
Cousins (1978). The solid line represent the reddening line
|
| Open with DEXTER | |
To get the intrinsic colours of the cluster members
we applied the well-known relations
![]() and
and
![]() (Golay 1974; Feinstein et al. 1986) to the eleven
bluest members, with
(B-V)<0.20, that have a unique reddening solution.
As an average we get
(Golay 1974; Feinstein et al. 1986) to the eleven
bluest members, with
(B-V)<0.20, that have a unique reddening solution.
As an average we get
![]() (s.d.)
and
(s.d.)
and
![]() (s.d.) in complete agreement
with previous values found by Clariá (1976) and Kilambi (1978),
respectively. These mean values were used to correct the colours
of the rest of the cluster members.
(s.d.) in complete agreement
with previous values found by Clariá (1976) and Kilambi (1978),
respectively. These mean values were used to correct the colours
of the rest of the cluster members.
Concerning the reddening law towards NGC 2571, we show in
Fig. 7 the TCD [(B-V) vs. (V-I)] with
the intrinsic lines of stars of luminosity classes V and III
from Cousins (1978) and the path of normal reddening
E(V-I)/E(B-V)=1.244 from Dean et al. (1978).
The coincidence between the bulk of our data with this reddening
line suggests that R=3.1 holds in this region. Knowing now that
the reddening law is normal in this site, we decided to calculate
the absorption-corrected magnitudes through the standard
expression
![]() .
.
To derive the distance modulus of NGC 2571 we fitted
the Schmidt-Kaler (1982) ZAMS to the de-reddened MS.
The best fits in both, the V0 vs. (B-V)0 and
V0 vs. (U-B)0 planes,
were achieved for a distance modulus of
![]() mag (error from best-eye inspection),
corresponding to a distance of
mag (error from best-eye inspection),
corresponding to a distance of
![]() pc.
Our distance is thus larger than the previous values derived
by Clariá and Kilambi (
pc.
Our distance is thus larger than the previous values derived
by Clariá and Kilambi (
![]() and
and
![]() ,
respectively).
This is probably caused by the fact that we fitted the ZAMS to
the lower envelope of stars in the corrected CMDs.
,
respectively).
This is probably caused by the fact that we fitted the ZAMS to
the lower envelope of stars in the corrected CMDs.
The age of NGC 2571 was estimated through a set of isochrones
obtained from evolutionary models of Girardi et al. (2000) which were
computed with mass loss and overshooting.
Figure 8 shows the isochrones superimposed on the corrected
CMD (a similar age is obtained when using Schaller et al.'s (1992) isochrones).
The two isochrones of 39 and 63 Myr,
respectively, permit the best fit of the upper part of NGC 2571.
Another age estimation can be obtained from the relation
between the observed position of the blue TO and
log(age) as given by Meynet et al. (1993).
With the TO
at
![]() ,
NGC 2571 is 80 Myr old.
Since the location of the TO is highly uncertain
(as it depends on the way the ZAMS is fitted)
and for the sake of coherence with our previous works,
we prefer an average age obtained through isochrone fitting.
Therefore, we adopt 50 Myr as the mean age estimate
for NGC 2571. This age disagrees with previous
values of 27 and 175 Myr given by Clariá and Kilambi, respectively.
Ahumada & Lapasset (1995) suggest that the two brightest
stars are blue stragglers, as they are located far above
the cluster TO if an age
of 175 Myr is adopted. With the age obtained here
(and, of course, also with Clariá's value) these
two stars are not blue stragglers.
,
NGC 2571 is 80 Myr old.
Since the location of the TO is highly uncertain
(as it depends on the way the ZAMS is fitted)
and for the sake of coherence with our previous works,
we prefer an average age obtained through isochrone fitting.
Therefore, we adopt 50 Myr as the mean age estimate
for NGC 2571. This age disagrees with previous
values of 27 and 175 Myr given by Clariá and Kilambi, respectively.
Ahumada & Lapasset (1995) suggest that the two brightest
stars are blue stragglers, as they are located far above
the cluster TO if an age
of 175 Myr is adopted. With the age obtained here
(and, of course, also with Clariá's value) these
two stars are not blue stragglers.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{MS1675f8.eps}\end{figure}](/articles/aa/full/2002/03/aa1675/Timg93.gif) |
Figure 8:
CMD [MV vs. (B-V)0] of NGC 2571. The solid line is
the Schmidt-Kaler (1982) ZAMS fitted to a corrected distance
modulus of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6cm,clip]{MS1675f9.eps}\end{figure}](/articles/aa/full/2002/03/aa1675/Timg94.gif) |
Figure 9: TCD [(U-V) vs. (V-I)] of NGC 2571. Symbols as in Fig. 4. The intrinsic location of stars of luminosity class V is indicated. |
| Open with DEXTER | |
The TCD of NGC 2571 displays a striking feature:
13 stars are situated below the reference line at
![]() (Fig. 4) and,
simultaneously, fall below the reddening line of an A0V-type
star as shown in the insert of Fig. 4.
Such a location would indicate that
they are A/F-type stars with anomalous colours. The same feature is
noticed in Kilambi's (1978) Fig. 2.
(Fig. 4) and,
simultaneously, fall below the reddening line of an A0V-type
star as shown in the insert of Fig. 4.
Such a location would indicate that
they are A/F-type stars with anomalous colours. The same feature is
noticed in Kilambi's (1978) Fig. 2.
Feinstein (1974) demonstrated with a sample of 103 stars of type Am and Ap that the TCD [(U-V) vs. (V-I)] segregates very well the normal from peculiar stars of this kind (see his Fig. 3). This is exactly what we see in our Fig. 9, where these "peculiar stars'' show, in general, quite different locations compared to the supposedly normal stars. One is tempted to conclude that these stars are metallic line stars, namely Am stars.
In fact, the Am phenomenon (i.e. strong metallic lines
but extremely weak calcium lines) is explained by the radiative diffusion
theory and makes a star lie below the MS in the TCD
because the metallic lines block the star's continuum radiation,
especially in the U band.
Besides, most of the Am stars (![]()
![]() )
belong to binary systems (Berthet 1992), so that light variations could be
expected among our "candidates''. In particular five of them
are variable and three of them lie on or above the ZAMS in the CMD
(Fig. 5). One should be cautious in these cases as the
Delta Scuti stars are also variables of spectral types A-F but
more evolved than Am stars (Eggen 1976; Breger 1979).
)
belong to binary systems (Berthet 1992), so that light variations could be
expected among our "candidates''. In particular five of them
are variable and three of them lie on or above the ZAMS in the CMD
(Fig. 5). One should be cautious in these cases as the
Delta Scuti stars are also variables of spectral types A-F but
more evolved than Am stars (Eggen 1976; Breger 1979).
Am/Ap stars are also frequent members of open
cluster and associations with ages
106-108 yr (see Abt
1979 and references therein). If our Am candidates are cluster
members their absolute magnitudes go from +1.5 down to +5mag, as shown in
Fig. 8, becoming thus fainter than the lower limit given
by Abt (1979): ![]() +3mag. This would be a valid argument to
reject the faintest of them as cluster members. However,
even these faintest stars still could be late Am, viz. Fm-type,
stars, if we really see a descending sequence of metallic line stars
belonging to the cluster. Malaroda (1973) lists
metallic line stars as late as F8. That would
explain the faintness of some of our candidates. Unfortunately,
there is no way, photometrically speaking, to address this subject;
spectroscopy is clearly needed.
+3mag. This would be a valid argument to
reject the faintest of them as cluster members. However,
even these faintest stars still could be late Am, viz. Fm-type,
stars, if we really see a descending sequence of metallic line stars
belonging to the cluster. Malaroda (1973) lists
metallic line stars as late as F8. That would
explain the faintness of some of our candidates. Unfortunately,
there is no way, photometrically speaking, to address this subject;
spectroscopy is clearly needed.
The filled triangle in Fig. 4 shows a blue star
(No. 1357 indicated by the arrow in Fig. 1)
which is very faint as seen in Figs. 5 and 6
(V=20.9).
The position of this object in the diagrams led us to think of
it as a White Dwarf (WD) candidate. The discovery of WDs in the
70 Myr clusters, Pleiades and NGC 2422 (Luyten & Herbig 1960), allows us to
speculate that WD can descend from intermediate massive
stars (Romanishin & Angel 1980). Using Bergeron et al.'s (1995) tables
that provide relations between absolute magnitudes, colour indices, temperatures
and cooling ages for pure helium and pure hydrogen WDs [log g = 8], we shall
derive the parameters of star No. 1357. If our candidate were a cluster member
and if we account for the fitting error in the distance
modulus of NGC 2571 and the mean cluster excess E(B-V),
its absolute magnitude would be
![]() .
Such an absolute
magnitude prevents this star from being a pure helium WD member because
it should be fainter.
It is, however, completely concordant with a pure hydrogen WD member
having a temperature of
.
Such an absolute
magnitude prevents this star from being a pure helium WD member because
it should be fainter.
It is, however, completely concordant with a pure hydrogen WD member
having a temperature of ![]()
![]() K, proper for
a "young'' WD with a cooling age from
11-3+10 Myr. If instead
of using the star magnitude we use the (B-V) colour index (including its error),
Bergeron et al.'s Table 3 gives a lower temperature, of
K, proper for
a "young'' WD with a cooling age from
11-3+10 Myr. If instead
of using the star magnitude we use the (B-V) colour index (including its error),
Bergeron et al.'s Table 3 gives a lower temperature, of
![]() K, and
accordingly a larger cooling age of
74-30+50 Myr, for a pure hydrogen WD.
If star No. 1357 is a field WD we can still estimate its distance and
temperature with Bergeron et al.'s tables. We first derive the temperature from
the observed (B-V) colour (assuming no reddening or a maximum reddening of
E(B-V) = 0.1) and then the corresponding WD's absolute magnitude MV. We
found that if star No. 1357 is a pure hydrogen WD, its distance would range from
800 to 1000 pc and its temperature from 15000 to 23000 K; if it is a pure helium
WD, the distance would range from 600 to 900 pc with temperature values
from 10000 to 20000 K.
K, and
accordingly a larger cooling age of
74-30+50 Myr, for a pure hydrogen WD.
If star No. 1357 is a field WD we can still estimate its distance and
temperature with Bergeron et al.'s tables. We first derive the temperature from
the observed (B-V) colour (assuming no reddening or a maximum reddening of
E(B-V) = 0.1) and then the corresponding WD's absolute magnitude MV. We
found that if star No. 1357 is a pure hydrogen WD, its distance would range from
800 to 1000 pc and its temperature from 15000 to 23000 K; if it is a pure helium
WD, the distance would range from 600 to 900 pc with temperature values
from 10000 to 20000 K.
As already noticed by Kilambi (1978), there is a notorious
gap along the MS of NGC 2571 centred at
![]() and
and
![]() with sizes of
with sizes of
![]() and
and
![]() ,
respectively
(see Figs. 5 and 8). Our photometry
comprises many more stars than any previous work in this
area of the CMD so that no incompleteness
effect can be invoked to explain the gap. The literature
reports the existence of gaps in several open clusters:
,
respectively
(see Figs. 5 and 8). Our photometry
comprises many more stars than any previous work in this
area of the CMD so that no incompleteness
effect can be invoked to explain the gap. The literature
reports the existence of gaps in several open clusters:
- Mermilliod (1976) found "hot'' gaps between
spectral types B7 and B8 (
![]() )
in young
open clusters having ages lesser than the Pleiades;
)
in young
open clusters having ages lesser than the Pleiades;
- Phelps & Janes (1993) found this feature in Berkeley7
in the mass range 3...4
![]() ,
in NGC 637 (8...12
,
in NGC 637 (8...12
![]() ), and in Berkeley62
(5...8
), and in Berkeley62
(5...8
![]() );
);
- Forbes (1996) found a gap between
![]() in NGC 6531;
in NGC 6531;
- A gap (not so obvious) can be observed, too, in NGC 3293
(Herbst & Miller 1982);
- High-precision astrometry and photometry of the Hyades
reveal two gaps along the cluster´s MS
(de Bruijne et al. 2000);
- A detailed description of gaps in several other open clusters
has recently been given by Rachford & Canterna (2000).
The attempts to explain the gaps found in open clusters range from the onset of convection in the stellar envelopes (Böhm-Vitense & Canterna 1974) to peculiarities in the Balmer jump and Balmer lines as suggested by Mermilliod (1976). Ulrich (1971a, 1971b) has proposed that gaps in some open cluster might be produced by the presence of 3He isotopes that halt the gravitational contraction 1...2 mag above the MS. While Mermilliod's gaps occur in the range of B-type stars, Böhm-Vitense & Canterna's (and also Ulrich's) gaps are found at less massive stars.
Apparently, the NGC 2571 gap is not
produced by a biased estimate of membership: the gap is evident
in Fig. 5 even without subtracting any star so that a wrong
rejection of members in our analysis is unlikely.
Following Scalo's (1986) discussion of
the statistical nature of the initial mass function (IMF),
we can compute the probability of finding a gap in
the MS: if the cluster has a continuous
mass distribution from small masses up to a mass m1,
no stars from m1 to m2, and N stars more massive than m2,
then the probability that this lack of stars is caused by a
random process is
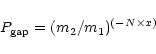 |
(1) |
The luminosity function LF of a star sample is defined
by
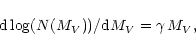 |
(2) |
| LF | MF | ||||||
| M V bins | N |
|
|
|
|||
|
|
2 | ||||||
|
|
0 | ||||||
|
|
2 | 7.85 | 0.90 | 2 | 0.89 | ||
|
|
8 | 3.41 | 0.53 | 4 | 1.26 | ||
|
|
8 | 2.33 | 0.37 | 13 | 1.87 | ||
|
|
8 | 1.40 | 0.15 | 62 | 2.31 | ||
|
|
21 | 0.86 | -0.06 | 61 | 2.31 | ||
|
|
33 | ||||||
|
|
38 | ||||||
|
|
22 | ||||||
|
|
1 |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS1675f10.eps}\end{figure}](/articles/aa/full/2002/03/aa1675/Timg134.gif) |
Figure 10: The LF of NGC 2571 constructed with likely and probably members (cleaned columns). Kilambi's (1978) data are superimposed (shaded columns). Errors bars are indicated. |
| Open with DEXTER | |
Figure 10 also shows for comparison the luminosity function given by Kilambi (1978). Because our cluster distance is slightly larger than that found by Kilambi, the two brightest stars are less bright in his histogram than in ours. No noticeable differences can be seen except that our photometry allows us to define very well the LF down to dwarf stars of spectral-type G and K.
The cluster's MF describes the distribution
of stars over mass intervals. In particular,
if such a description is referred to the moment of the cluster
formation, it is called the initial mass function IMF.
NGC 2571 is an intermediate-age cluster and, as a consequence, there is
a possibility that evolutionary effects
have introduced some distortion in its star distribution due
to the loss of massive stars.
Assuming a power law (see e.g. Scalo 1986), the slope of the
MF is given by
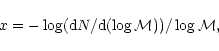 |
(3) |
To estimate the MF, we first transformed
the corrected data of the member stars from the
(MV vs. (B-V)0) plane to the (
![]() vs.
log
vs.
log
![]() )
plane, where the bolometric corrections were taken from
Schmidt-Kaler (1982). The ZAMS's masses of each stars are obtained using an
interpolation procedure between the two closest evolutionary tracks of
Schaller et al. (1992).
The two brightest stars, having spectroscopic classification,
were transformed using the spectral information instead of
their colour indices. Because of the gap, once all the stellar masses were
obtained, we scaled bin sizes arbitrarily to avoid empty bins. As
cluster members go down to
)
plane, where the bolometric corrections were taken from
Schmidt-Kaler (1982). The ZAMS's masses of each stars are obtained using an
interpolation procedure between the two closest evolutionary tracks of
Schaller et al. (1992).
The two brightest stars, having spectroscopic classification,
were transformed using the spectral information instead of
their colour indices. Because of the gap, once all the stellar masses were
obtained, we scaled bin sizes arbitrarily to avoid empty bins. As
cluster members go down to
![]() while our magnitude limit
is
while our magnitude limit
is ![]()
![]() ,
we are relatively
free from incompleteness effects in the low mass bin. By fitting the five mass
points of Table 5 using an un-weighted least squares method, we obtain
,
we are relatively
free from incompleteness effects in the low mass bin. By fitting the five mass
points of Table 5 using an un-weighted least squares method, we obtain
![]() but if we neglect the most massive bin, the fitting
yields
but if we neglect the most massive bin, the fitting
yields
![]() ,
representing thus the MF of the cluster MS stars.
These two values are larger than the typical slope of x=1.35 given
by Salpeter (1955) for field stars.
Tarrab (1982) placed this cluster in the age group of
NGC 3766 (
,
representing thus the MF of the cluster MS stars.
These two values are larger than the typical slope of x=1.35 given
by Salpeter (1955) for field stars.
Tarrab (1982) placed this cluster in the age group of
NGC 3766 (
![]() yrs) whose mean slope
is x=1.58. The slope she assigned to NGC 2571, with
yrs) whose mean slope
is x=1.58. The slope she assigned to NGC 2571, with
![]() even larger than ours, was obtained using only 20 stars
in the mass range 2.2 to 10
even larger than ours, was obtained using only 20 stars
in the mass range 2.2 to 10
![]() which is unrealistic in view of the mass values and star
numbers given in Table 5.
The actual age of NGC 2571 indicates that the cluster must be placed
in Tarrab's (1982) age group of the
which is unrealistic in view of the mass values and star
numbers given in Table 5.
The actual age of NGC 2571 indicates that the cluster must be placed
in Tarrab's (1982) age group of the ![]() Persei
cluster (
Persei
cluster (
![]() yrs)
characterized by a mean slope of x = 1.65.
yrs)
characterized by a mean slope of x = 1.65.
![]() NGC 2571 is a moderate young open cluster of
50 Myr, located in the association Vela-Puppis at a distance of
1380
NGC 2571 is a moderate young open cluster of
50 Myr, located in the association Vela-Puppis at a distance of
1380 ![]() 130 pc in a low absorption zone, AV = 0.3.
130 pc in a low absorption zone, AV = 0.3.
![]() The present work confirms earlier investigations that a
number of cluster members are indeed variable stars: a comparison of
magnitudes and colours of 30 stars in common between our CCD photometry
and the photoelectric photometry of Clariá (1976) reveals that
7 stars are definitely variable and one star is probably variable,
i.e. about 30% of all stars in this sample.
The present work confirms earlier investigations that a
number of cluster members are indeed variable stars: a comparison of
magnitudes and colours of 30 stars in common between our CCD photometry
and the photoelectric photometry of Clariá (1976) reveals that
7 stars are definitely variable and one star is probably variable,
i.e. about 30% of all stars in this sample.
![]() The cluster has an unusual high number
of stars with "peculiar colours'' which are candidates for
metallic line stars, probably constituting a sequence of Am
to Fm. It is a known fact that peculiar A-type stars
are frequently found in open clusters with ages
from 106 to 108 yr. All our stars with "peculiar colours''
exhibit photometric characteristics that are typical
for Am stars: they lie below the
[(U-B)/(B-V)] intrinsic line in
the two-colour diagram (Fig. 4); they mainly have
absolute magnitudes in the required range as found by Abt
(1979) for open cluster Am-type stars; some of these potential
Am stars are variable as well.
The cluster has an unusual high number
of stars with "peculiar colours'' which are candidates for
metallic line stars, probably constituting a sequence of Am
to Fm. It is a known fact that peculiar A-type stars
are frequently found in open clusters with ages
from 106 to 108 yr. All our stars with "peculiar colours''
exhibit photometric characteristics that are typical
for Am stars: they lie below the
[(U-B)/(B-V)] intrinsic line in
the two-colour diagram (Fig. 4); they mainly have
absolute magnitudes in the required range as found by Abt
(1979) for open cluster Am-type stars; some of these potential
Am stars are variable as well.
![]() Kilambi (1978) noticed the presence of a gap in the
stellar distribution along the cluster's MS. We
demonstrated that this gap is not produced by a random process
but is a real lack of stars in a given magnitude interval.
Kilambi (1978) noticed the presence of a gap in the
stellar distribution along the cluster's MS. We
demonstrated that this gap is not produced by a random process
but is a real lack of stars in a given magnitude interval.
It is worth mentioning that not only open clusters show gaps but also field star distributions. Mermilliod (1976) noticed that two gaps start at the limit where the Ap and the Am stars appear, i.e. near spectral types B7V and A7V, respectively. In NGC 2571 the gap is closely connected to the position of the probable Am-type stars. Furthermore, it occupies the same location that the gap found in NGC 6531 (Forbes 1996), a young cluster of 8 Myr only, i.e. about 40 Myr younger than NGC 2571. We conclude that different mechanisms of gap production are at work for clusters of different age: the gaps in the MSs of intermediate-age clusters are likely the consequence of the onset of convection in the stellar envelopes (Böhm-Vitense & Canterna (1974), whereas in young clusters the gaps may be produced by the "burn-off'' of 3He in stars contracting to the MS (Ulrich 1971b).
![]() WDs in old open clusters have been successfully searched for
(e.g. von Hippel et al. 1995); but, as far as we know, for intermediate-age
clusters the results were not always convincing or even negative
(Anthony-Twarog 1981; Romanishin & Angel 1980). Using the absolute
magnitude of the candidate star No. 1357 as the most secure parameter,
we find no contradiction in considering this star to be a cluster WD
in the intermediate-age cluster NGC 2571.
WDs in old open clusters have been successfully searched for
(e.g. von Hippel et al. 1995); but, as far as we know, for intermediate-age
clusters the results were not always convincing or even negative
(Anthony-Twarog 1981; Romanishin & Angel 1980). Using the absolute
magnitude of the candidate star No. 1357 as the most secure parameter,
we find no contradiction in considering this star to be a cluster WD
in the intermediate-age cluster NGC 2571.
A strong criterium for a WD to be a cluster member is that the sum of the
evolutionary time of its progenitor, t(evolution), and its
cooling age, t(cooling), is of the order of the cluster's age.
The mass distribution of NGC 2571 (Table 5)
gives a mean mass at the TO of ![]()
![]() ,
thus allowing us to consider star No. 1357 as the remnant of
the evolution of an even more massive star, say about
,
thus allowing us to consider star No. 1357 as the remnant of
the evolution of an even more massive star, say about
![]() (i.e.
(i.e.
![]() ,
conservatively, above the cluster TO).
[We note that progenitors of WDs may have masses up to the order
of
,
conservatively, above the cluster TO).
[We note that progenitors of WDs may have masses up to the order
of
![]() that had suffered strong mass loss
D'Antonna & Mazzitelli 1990; Weidemann & Koester 1983; Weidemann 1990.
We know that a WD progenitor of
that had suffered strong mass loss
D'Antonna & Mazzitelli 1990; Weidemann & Koester 1983; Weidemann 1990.
We know that a WD progenitor of
![]() spends about 30 Myr to
completely exhaust its nuclear helium (Schaller et al. 1992) while, on
the other hand star No. 1357 as WD may be as young
as
11-3+10 Myr (Sect. 3.6). Thus, the sum t(evolution)
+ t(cooling) is smaller than the cluster age favouring
its membership. Even the less favourable case, where temperature
and age of the WD candidate are derived from the (B-V) index,
indicates that the WD (if cluster member) is
74-30+50 Myr old -
showing still a weak agreement between the stellar evolutionary time
spent prior to the WD phase plus the cooling age of the WD with
the cluster age.
spends about 30 Myr to
completely exhaust its nuclear helium (Schaller et al. 1992) while, on
the other hand star No. 1357 as WD may be as young
as
11-3+10 Myr (Sect. 3.6). Thus, the sum t(evolution)
+ t(cooling) is smaller than the cluster age favouring
its membership. Even the less favourable case, where temperature
and age of the WD candidate are derived from the (B-V) index,
indicates that the WD (if cluster member) is
74-30+50 Myr old -
showing still a weak agreement between the stellar evolutionary time
spent prior to the WD phase plus the cooling age of the WD with
the cluster age.
![]() The MF of NGC 2571 was investigated in the mass range from
The MF of NGC 2571 was investigated in the mass range from
![]() to
to ![]()
![]() .
The slope of the
cluster MF varies from 1.66 to 1.74, depending on whether the most massive
bin is included or not; but, on average, it is larger than the
Salpeter's (1955) one. It is worth mentioning that with Scalo's (1986)
relations (1.7 and 1.8) and a cluster MF's slope x = 1.74, the expected
number of stars more massive than
.
The slope of the
cluster MF varies from 1.66 to 1.74, depending on whether the most massive
bin is included or not; but, on average, it is larger than the
Salpeter's (1955) one. It is worth mentioning that with Scalo's (1986)
relations (1.7 and 1.8) and a cluster MF's slope x = 1.74, the expected
number of stars more massive than
![]() in NGC 2571 is 2.1. That
strongly increases the chance that the WD candidate star No. 1357 is the
result of the evolution of a massive cluster member.
in NGC 2571 is 2.1. That
strongly increases the chance that the WD candidate star No. 1357 is the
result of the evolution of a massive cluster member.
Acknowledgements
The authors are gateful to the referee Dr. G. Carraro for carefully reading their manuscript and for valuable comments. We also thank Dr. H. Levato for helpful discussions on peculiar stars. J.-M.W. wishes to thank ESO for granting observing time and the kind hospitality at La Silla mountain.This article is partially based in the "Second Epoch Survey'' of the southern sky that was made by the Anglo-Australian Observatory (AAO) with the UK Schmidt Telescope. Plates from this survey have been digitized and compressed by the STScI. The digitized images are copyright (c) 1993-7 by the Anglo-Australian Observatory Board.