A&A 381, 440-445 (2002)
DOI: 10.1051/0004-6361:20011528
M. Salaris1,2 - M. A. T. Groenewegen3,4
1 -
Astrophysics Research Institute, Liverpool John Moores
University, Twelve Quays House, Egerton Wharf, Birkenhead CH41 1LD, UK
2 -
Max-Planck-Institut für Astrophysik,
Karl-Schwarzschild-Straße 1, 85748 Garching, Germany
3 -
Instituut voor Sterrenkunde, PACS-ICC,
Celestijnenlaan 200B, 3001 Heverlee, Belgium
4 -
European Southern Observatory, EIS-team,
Karl-Schwarzschild-Straße 2, 85740 Garching, Germany
Received 22 August 2001 / Accepted 29 October 2001
Abstract
We present a new method to determine the distance to
B-stars in eclipsing binary systems. The method is completely empirical,
and it is based on the existence of a very tight linear relationship
between the V-band "zero magnitude angular diameter'' and the Strömgren
colour index c1 for B-stars; we have empirically calibrated
this relationship using local single B-stars with accurate angular
diameters, and B-stars in eclipsing binaries with precise radii and parallax
determinations. By studying the differential behaviour of this
relationship as predicted by theoretical stellar evolution models, we
find that it is independent of the stellar metallicities for a range
of [Fe/H] values between the solar one and that of young
stars in the Magellanic Clouds. The method, which also provides the
value of the reddening to the system, is discussed in detail, together
with a thorough estimate of the associated errors. We conclude that
accurate Strömgren photometry obtainable with 1.5 m-class telescopes
of the LMC eclipsing binaries HV 2274 and HV 982 will allow
to obtain an empirical
LMC distance with an accuracy of the order of 0.13 mag.
Key words: binaries: eclipsing - stars: distances - stars: individual: HD 24909, HD 161783, HD 218066, HV 982, HV 2274 - stars: fundamental parameters - Magellanic Clouds - distance scale
The distance to the large Magellanic Cloud is the cornerstone of the
extragalactic distance scale, since the zero point of both the
Cepheids and Type Ia supernovae distances is tied to the LMC
distance. Disappointingly enough, existing determinations of this
fundamental quantity span a wide range, comprising both "short''
(
![]() - e.g. Udalski 2000) and "long'' (
- e.g. Udalski 2000) and "long'' (
![]() - e.g. Feast & Catchpole 1997) values.
- e.g. Feast & Catchpole 1997) values.
In the last few years well-detached main sequence B type eclipsing
binary (EB) systems have been proposed as virtually ideal standard
candles, and employed by Guinan et al. (1998) and Fitzpatrick et
al. (2001 - F01) to derive the distance to two EB systems in the LMC
(HV 2274 and HV 982). From an observational point of view, what is
required is the monitoring of the light curve (preferably in several
filters) and of the radial velocity. Analysing this data gives the
orbital elements, the masses and radii of both components. In
addition to that, UV/optical spectra are necessary; once obtained, a
multi-parametric fit of theoretical spectra to the observed spectrum
and the broadband data is performed, in order to simultaneously derive
the effective temperature of both components, reddening, metallicity,
micro-turbulent velocity, the distance and 5 parameters describing the
UV/optical extinction curve. When applying this method to HV2274,
Guinan et al. (1998) and F01 found, respectively,
(m-M)0 = 18.30 and
(m-M)0 = 18.36, with an error on the
individual determinations of the order of 0.10 mag; F01 obtained
![]() for HV982. As shown
by Groenewegen & Salaris (2001 - GS01) for the case of HV 2274, this
method heavily relies on the absolute value of the fluxes predicted by
the theory, which, given the current uncertainty of stellar
atmospheres modelling (see GS01 for more details), can introduce large
systematic errors. Moreover, GS01 have shown that the resulting
distance is also dependent on what broadband colours are included in
the fitting procedure, so that, even if a formal error of the order of
0.10 mag can be derived from the fitting procedure, the real
uncertainty is probably much larger.
for HV982. As shown
by Groenewegen & Salaris (2001 - GS01) for the case of HV 2274, this
method heavily relies on the absolute value of the fluxes predicted by
the theory, which, given the current uncertainty of stellar
atmospheres modelling (see GS01 for more details), can introduce large
systematic errors. Moreover, GS01 have shown that the resulting
distance is also dependent on what broadband colours are included in
the fitting procedure, so that, even if a formal error of the order of
0.10 mag can be derived from the fitting procedure, the real
uncertainty is probably much larger.
An alternative method to use EB systems as distance indicators is
based on empirical relationships linking colours to surface brightness
(see, e.g., Barnes & Evans 1976; Lacy 1977; Di Benedetto 1998 and
references therein). Once the colours of the individual components of
the system are known from the light curve analysis (e.g. Lacy 1977),
these relationships provide the apparent radii; since the true radii
are also known from the analysis of the radial velocity curve, the
distance to the system is derived straightforwardly. This method has
been applied recently by Thompson et al. (2001) to one EB system in
the turn-off region of the Colour-Magnitude-Diagram of the globular
cluster ![]() Centauri. They made use of surface brightness (in the
V-band) versus colour relationships in
(V-K), (V-H), (V-J),
calibrated on the stellar sample by Di Benedetto (1998), for A, F, G, K
dwarfs and giants. This method is very much appealing, since it
avoids the use of the still uncertain model atmospheres. One drawback
is that it is necessary to know in advance the reddening of the
system, which is not an easy task if one wants to apply this technique
to LMC objects. Moreover a calibration for B-stars - like the stars
in the LMC EB systems previously discussed - does not exist yet.
Centauri. They made use of surface brightness (in the
V-band) versus colour relationships in
(V-K), (V-H), (V-J),
calibrated on the stellar sample by Di Benedetto (1998), for A, F, G, K
dwarfs and giants. This method is very much appealing, since it
avoids the use of the still uncertain model atmospheres. One drawback
is that it is necessary to know in advance the reddening of the
system, which is not an easy task if one wants to apply this technique
to LMC objects. Moreover a calibration for B-stars - like the stars
in the LMC EB systems previously discussed - does not exist yet.
In this paper we propose a variant of this surface brightness technique using Strömgren colours, suited to determine the distance of B-stars in EB systems. This method turns out to be largely independent of the metallicity of the components and, moreover, working with the Strömgren filters one can easily derive the reddening of B-stars from the c1-(b-y) diagram (see, e.g., Larsen et al. 2000 - LCS00).
In Sect. 2 we discuss the theoretical background of the method, while in Sect. 3 we present our calibration and use for B-stars. Section 4 discusses the errors associated with the method through an application to some Galactic EB systems and the LMC system HV 982. Conclusions follow in Sect. 5.
The surface brightness (S) of a star is classically defined as:
| (1) |
A slightly alternative concept, but essentially equivalent, is used by
van Belle (1999) to define the angular diameter a star would have if
its magnitude (in a given passband) were zero (zero magnitude angular
diameter):
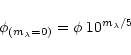 |
(2) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3098f1.ps}\end{figure}](/articles/aa/full/2002/02/aah3098/Timg13.gif) |
Figure 1: Standard sequence for B-stars. The arrow shows the direction of the reddening vector. |
| Open with DEXTER | |
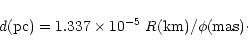 |
(3) |
When trying to apply surface brightness techniques one must face the problem of reddening. The reddening in, e.g., the LMC is strongly variable on very short spatial scales (see, e.g., Romaniello et al. 2000, LCS00), and the ideal way to proceed is to determine it on a star-by-star basis. Strömgren uvby photometry provides the tool to do this, at least for B-stars, by employing the c1-(b-y)diagram (we briefly recall that c1=(u-v)-(v-b)). As discussed by Larsen et al. (2000), in this plane luminosity class IV and V B-stars are located on a standard sequence (see Table 1) which is largely independent of the star metallicity (LCS00). In Fig. 1 we show the standard sequence by Perry et al. (1987), and the direction of the reddening vector, which is nearly horizontal, since (c1)0=c1-0.20 E(b-y). To first order, the reddening E(b-y)can be estimated as simply being the difference between the observed (b-y) and the intrinsic value (b-y)0 corresponding to the observed c1. We recall that E(B-V)=1.4 E(b-y).
To confirm the independence of this standard sequence on metallicity,
we show in Fig. 2 the
c1-(b-y) relationship for B-stars between
the zero age main sequence and the turn off (luminosity classes IV and
V) with ages between 10 and 50 Myr (the precise age range is not
relevant), from the theoretical models by Bertelli et al. (1994),
transformed to the Strömgren filters by means of the Kurucz (1992)
colour transformations. In the [Fe/H] range displayed - [Fe/H]
between 0.0 and -0.7, which covers the metallicity range of B-stars
in the Milky Way, LMC and SMC (see, e.g., the discussion in GC01) -
the standard sequence of B-stars is practically unaffected by the
stellar chemical composition. The maximum difference is less
than 0.01 mag in (b-y) at a given value of c1 between the
![]() and 0.0 sequence.
and 0.0 sequence.
Therefore, as a first step, after the radial velocity and light curve analysis (from Strömgren filter observations) of a given EB system with B main sequence star components, one can derive the reddening of the two objects by simply using the c1-(b-y) diagram and the sequence provided in Table 1.
| (b-y) | c1 | (b-y) | c1 |
| -0.134 | -0.250 | -0.050 | 0.578 |
| -0.126 | -0.128 | -0.046 | 0.619 |
| -0.120 | -0.075 | -0.044 | 0.656 |
| -0.118 | -0.025 | -0.042 | 0.693 |
| -0.114 | 0.022 | -0.041 | 0.724 |
| -0.109 | 0.065 | -0.040 | 0.755 |
| -0.105 | 0.108 | -0.039 | 0.785 |
| -0.100 | 0.150 | -0.038 | 0.811 |
| -0.096 | 0.192 | -0.037 | 0.833 |
| -0.091 | 0.235 | -0.035 | 0.856 |
| -0.086 | 0.278 | -0.034 | 0.878 |
| -0.080 | 0.321 | -0.032 | 0.900 |
| -0.075 | 0.362 | -0.029 | 0.925 |
| -0.070 | 0.404 | -0.026 | 0.950 |
| -0.065 | 0.448 | -0.023 | 0.975 |
| -0.061 | 0.491 | -0.020 | 1.000 |
| -0.055 | 0.535 |
|
|
c1 | (b-y) | V | E(b-y) | name |
|
|
|
|
|
0.00 | HD 35468 |
|
|
|
|
|
0.00 | HD 6882A |
|
|
|
|
|
0.00 | HD 6882B |
|
|
|
|
|
0.00 | HD 87901 |
|
|
|
|
|
0.01 | HD 135876A |
|
|
|
|
|
0.01 | HD 135876B |
|
|
|
|
|
0.10 | HD 143275 |
|
|
|
|
|
0.00 | HD 193924 |
|
|
|
|
|
0.00 | HD 209952 |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3098f2.ps}\end{figure}](/articles/aa/full/2002/02/aah3098/Timg53.gif) |
Figure 2:
Theoretical sequences for main sequence B-stars
with ages between 10 and 50 Myr and
|
| Open with DEXTER | |
As a second step, one needs a relationship between the surface brightness or zero magnitude angular diameter, and a de-reddened colour. The following precepts have guided our choice:
In Fig. 3 we show the calibration of the empirical
![]() relationship using the data in Table 2,
which is given by
relationship using the data in Table 2,
which is given by
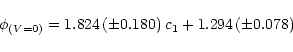 |
(4) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3098f3.ps}\end{figure}](/articles/aa/full/2002/02/aah3098/Timg58.gif) |
Figure 3:
Calibration of the
|
| Open with DEXTER | |
| name | V | (b-y) | c1 | radius | E(b-y) | (m-M)0 |
|
| HD 24909A |
|
|
|
|
|
|
|
| HD 161783A |
|
|
|
|
|
|
|
| HD 218066A |
|
|
|
|
|
|
|
| HD 218066B |
|
|
|
|
|
|
|
At present there are no calibrations of the relationship between zero magnitude angular diameter (or surface brightness) and colours, spanning the entire main sequence B star range, other than the one we obtained. Since there are essentially no infrared colours available for our calibrating objects, neither the Di Benedetto (1998), nor the van Belle (1999) calibrations cover this range. It would be very interesting, when data will be available in the future, to compare our result with equivalent calibrations using, e.g., (V-K).
An important issue is the dependence of Eq. (4) on the
stellar metal content, since the calibrators are local stars of
presumably solar-like metallicity, while the B-stars in the LMC are
more metal poor. The only way to assess this dependence, due to the
lack of appropriate data for more metal poor stars, is - as in the
case of the
c1-(b-y) standard sequence - to use the differential
(not the absolute quantities) behaviour of theoretical models.
Figure 4 shows in the
![]() plane the same models
displayed in Fig. 2.
plane the same models
displayed in Fig. 2.
For B-stars of luminosity class IV and V one expects that the
![]() relationship is negligibly affected by the
metallicity for [Fe/H] between 0.0 and -0.7. In the case of
relationship is negligibly affected by the
metallicity for [Fe/H] between 0.0 and -0.7. In the case of
![]() (typical metallicity of SMC young stars) the difference
with respect to the solar case is small for late type B-stars (higher
values of c1), causing a systematic underestimate of the
distance (when using the local calibration) of the order of only 0.05 mag,
and completely vanishing for earlier types. It is therefore possible to
apply Eq. (4) with confidence also to stars in the Magellanic Clouds.
(typical metallicity of SMC young stars) the difference
with respect to the solar case is small for late type B-stars (higher
values of c1), causing a systematic underestimate of the
distance (when using the local calibration) of the order of only 0.05 mag,
and completely vanishing for earlier types. It is therefore possible to
apply Eq. (4) with confidence also to stars in the Magellanic Clouds.
Summarizing, from the Johnson V and Strömgren uvby light curves of B-stars in well-detached EB systems, one can derive the individual V magnitude and Strömgren colour of the single components. Using the standard relationship in Table 1, the reddening of the system can be easily estimated. Once the de-reddened c1 values of the 2 components are at hand, one can employ Eq. (4) to derive the corresponding zero magnitude angular diameters in V, which can be transformed to true angular diameters using Eq. (2). At this stage, since the angular diameters and the physical radii (derived from the analysis of the radial velocity curve) are known, one can finally use Eq. (3) to obtain the distance of the individual stars. As a check for the consistency of the results, one has to ensure that the distances of the two components are in agreement within the errors, or, equivalently, that the ratio of the derived angular diameters agrees with the observed radii ratio.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3098f4.ps}\end{figure}](/articles/aa/full/2002/02/aah3098/Timg98.gif) |
Figure 4:
Theoretical
|
| Open with DEXTER | |
In this section we will apply the previously outlined method to some B-stars in Galactic EB systems, in order to estimate the associated errors. We have considered 3 EB systems spanning the entire spectral range of B main sequence stars; the data about these systems are displayed in Table 3. Observed magnitudes and colours (Cols. 2, 3 and 4) come from the compilation by Jordi et al. (1997), with the exception of the error bars on the Strömgren data for HD 161783, which we have computed from the original paper by Clausen (1996); radii (Col. 5) come from the compilation by Andersen (1991), while Cols. 6 and 7 show reddenings and distance moduli obtained with our technique. Finally, Col. 8 displays the distance according to the Hipparcos parallax. For HD 24909 and HD 161783 we considered just one component, since for the former system the secondary star is an A-star, while for the latter one the secondary star is variable. All 3 systems have parallaxes with large error bars; otherwise, we would have included them in our empirical calibration of Eq. (4). We want also to mention the fact that the c1 values for both components of HD 218066, once de-reddened, are slightly outside the range of validity of our calibration (by less than 0.02 mag). The stars in Table 3 are ordered according to their spectral type; HD 24909A is a late type B-star, while the components of the HD 218066 system are both early type B-stars. Notice the good agreement between the distances derived for the components of this system.
The errors on the distances have been derived by adding in quadrature
the contributions of the errors on V, (b-y), c1, the
individual radii and the coefficients of Eq. (4). The largest component
of the total error comes from the errors on the coefficients of Eq. (4);
they alone provide an uncertainty of about 0.10-0.12 mag on the final
error on the distance modulus. Errors on the photometry and on the
radii are of much less importance, as long as they are within
![]() 0.02 mag and 3%, respectively.
0.02 mag and 3%, respectively.
To summarize the results of these error estimates, our empirical method to derive distances to individual B-stars in EB systems provides distance moduli with errors of the order of 0.12-0.16 mag, when applied to systems with photometry and radius determinations precise at the level discussed before.
In case of the LMC, HV 2274 and HV 982 are EB systems with early type B-stars, for which radius determinations and V photometry have a high enough precision (errors of the order of 3% on the radii and 0.02 mag on V) to make the error on the distance dominated only by the dispersion associated to Eq. (4). Unfortunately, Strömgren data for HV 2274 are not available in the literature, while for HV982 the Strömgren photometry by Pritchard et al. (1998 - P98) has large errors of the order of 0.04-0.05 mag in (b-y) and c1. Nevertheless, as an exercise, we derive the distance to HV 982 following our method. In Table 4 we present the observational data for this system (Strömgren data are from P98, V-band data and radii are from F01) and the derived reddening and distance modulus of both components.
The derived reddening is in agreement with the estimate for B-stars in
a field around HV 982 derived by LCS00 using the (b-y) and c1indices; they find an average
E(b-y) = 0.10 with values ranging
between ![]() 0.04 and
0.04 and ![]() 0.25 mag. FP01 derive a reddening of
0.25 mag. FP01 derive a reddening of
![]() from their multidimensional spectral
fitting method, consistent with the value derived here.
The distances
we obtain,
from their multidimensional spectral
fitting method, consistent with the value derived here.
The distances
we obtain,
![]() and
and
![]() ,
do not put very strong constraints on the LMC distance, given the
large error bar.
However, it is feasible to get Strömgren photometry accurate to
0.02-0.03 mag in (b-y) and c1 with only 1.5 m-class telescopes
(see, e.g., the data by LCS00); already with these errors one could
get the distance to HV 982, for example, with an accuracy of 0.17-0.18 mag, equivalent to a parallax error of about 8%. Since both
HV 982 and HV 2274 lie near the LMC center (van der Marel & Cioni
2001), if Strömgren data of the same precision were available also
for HV 2274, it would be possible to combine both distances and obtain
an empirical LMC distance accurate to 0.13 mag.
,
do not put very strong constraints on the LMC distance, given the
large error bar.
However, it is feasible to get Strömgren photometry accurate to
0.02-0.03 mag in (b-y) and c1 with only 1.5 m-class telescopes
(see, e.g., the data by LCS00); already with these errors one could
get the distance to HV 982, for example, with an accuracy of 0.17-0.18 mag, equivalent to a parallax error of about 8%. Since both
HV 982 and HV 2274 lie near the LMC center (van der Marel & Cioni
2001), if Strömgren data of the same precision were available also
for HV 2274, it would be possible to combine both distances and obtain
an empirical LMC distance accurate to 0.13 mag.
We have presented a new technique to estimate reddening and distance
moduli to B-stars in EB systems. It is based on the observation of
the Vuvby light curve and the consequent determination of V,
c1 and (b-y) magnitudes for the individual components of the
binary. A comparison of the stars' positions on the
c1-(b-y)plane with respect to the local sequence of Table 1 permits to derive
the reddening to the system. After de-reddening the individual Vand c1 values, the use of an empirically calibrated
![]() relationship (Eq. (4)) allows one to derive the
apparent diameter of the objects; this apparent diameter, coupled with
the knowledge of the physical radius from the radial velocity
analysis, provides straightforwardly the distance to the system
(Eq. (3)). These two empirical relationships used to derive reddening
and distance are expected to be basically independent of the stellar
metallicities in the [Fe/H] range covered by young stars in the solar
neighborood, LMC and SMC. Photometric errors within
relationship (Eq. (4)) allows one to derive the
apparent diameter of the objects; this apparent diameter, coupled with
the knowledge of the physical radius from the radial velocity
analysis, provides straightforwardly the distance to the system
(Eq. (3)). These two empirical relationships used to derive reddening
and distance are expected to be basically independent of the stellar
metallicities in the [Fe/H] range covered by young stars in the solar
neighborood, LMC and SMC. Photometric errors within ![]() 0.02 mag
and radius uncertainties up to 3% allow to determine distances to
individual systems with an error bar of 0.12-0.17 mag. If this
photometric accuracy is obtained for the photometry of the two LMC
systems HV 2274 and HV 982 - which have both precise radius
determinations and lie close to the LMC center - one can derive an
empirical estimate of the LMC distance with an accuracy of the order
of 0.13 mag.
0.02 mag
and radius uncertainties up to 3% allow to determine distances to
individual systems with an error bar of 0.12-0.17 mag. If this
photometric accuracy is obtained for the photometry of the two LMC
systems HV 2274 and HV 982 - which have both precise radius
determinations and lie close to the LMC center - one can derive an
empirical estimate of the LMC distance with an accuracy of the order
of 0.13 mag.
Acknowledgements
M.S. wishes to thank the Max-Planck-Institut für Astrophysik for the kind hospitality during the completion of this work. We thank Phil James for comments on a preliminary version of the manuscript. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France.