A&A 381, 606-627 (2002)
DOI: 10.1051/0004-6361:20011504
N. L. Martín-Hernández1 - E. Peeters2,1 - C. Morisset3 - A. G. G. M. Tielens1,2 - P. Cox4 - P. R. Roelfsema2 - J.-P. Baluteau3 - D. Schaerer5 - J. S. Mathis6 - F. Damour3 - E. Churchwell6 - M. F. Kessler7
1 -
Kapteyn Institute, PO Box 800, 9700 AV Groningen, The Netherlands
2 - SRON, National Institute for Space Reasearch, PO Box 800,
9700 AV Groningen, The Netherlands
3 - Institut d'Astrophysique de Marseille, CNRS & Univ. de
Provence, BP 8, 13376 Marseille Cedex 12, France
4 - Institut d'Astrophysique Spatiale, Bât. 121,
Université de Paris XI, 91405 Orsay, France
5 - Laboratoire d'Astrophysique, Observatoire
Midi-Pyrénées, 14, Av. E. Belin, 31400 Toulouse, France
6 - Department of Astronomy, 475 North Charter Street,
University of Wisconsin, Madison, WI 53706, USA
- ISO Data Centre, Astrophysics Division, ESA, Villafranca, Spain
Received 3 August 2001 / Accepted 18 October 2001
Abstract
Based on the ISO spectral catalogue of compact H II regions by Peeters et al. (2002), we present a first analysis of the
hydrogen recombination and atomic fine-structure lines originated in
the ionized gas. The sample consists of 34 H II regions located at
galactocentric distances between
![]() = 0 and 15 kpc. The SWS H I recombination lines between 2 and 8
= 0 and 15 kpc. The SWS H I recombination lines between 2 and 8
![]() are used to estimate the
extinction law at these wavelengths for 14 H II regions. An
extinction in the K band between 0 and
are used to estimate the
extinction law at these wavelengths for 14 H II regions. An
extinction in the K band between 0 and ![]() 3 mag has been derived.
The fine-structure lines of N, O, Ne, S and Ar are detected in most of
the sources. Most of these elements are observed in two different
ionization stages probing a range in ionization potential up to 41 eV.
The ISO data, by itself or combined with radio data taken from the
literature, is used to derive the elemental abundances relative to
hydrogen. The present data thus allow us to describe for each source
its elemental abundance, its state of ionization and to constrain the
properties of the ionizing star(s). The main results of this study
are as follows. The ionization ratios Ar++/Ar+, N++/N+, S+3/S++ and
Ne++/Ne+, which measure the degree of ionization and to first order,
the hardness of the stellar radiation, seem to increase with
3 mag has been derived.
The fine-structure lines of N, O, Ne, S and Ar are detected in most of
the sources. Most of these elements are observed in two different
ionization stages probing a range in ionization potential up to 41 eV.
The ISO data, by itself or combined with radio data taken from the
literature, is used to derive the elemental abundances relative to
hydrogen. The present data thus allow us to describe for each source
its elemental abundance, its state of ionization and to constrain the
properties of the ionizing star(s). The main results of this study
are as follows. The ionization ratios Ar++/Ar+, N++/N+, S+3/S++ and
Ne++/Ne+, which measure the degree of ionization and to first order,
the hardness of the stellar radiation, seem to increase with
![]() .
These ionization ratios correlate well with each other, implying that
the spectral hardening affects equally the full range of ionizing
energies. A Galactocentric gradient of N/O (
.
These ionization ratios correlate well with each other, implying that
the spectral hardening affects equally the full range of ionizing
energies. A Galactocentric gradient of N/O (
![]() )
is observed in the sense of a
decreasing abundance ratio with
)
is observed in the sense of a
decreasing abundance ratio with
![]() in agreement with previous
studies. Abundance gradients for neon and argon are derived of the
form
in agreement with previous
studies. Abundance gradients for neon and argon are derived of the
form
![]() and
and
![]() .
These elemental gradients could be enlarged by the existing Galactic
.
These elemental gradients could be enlarged by the existing Galactic
![]() gradient. Adopting a
gradient. Adopting a ![]() gradient of approximately 330
K kpc-1, the slopes in the Ne/H and Ar/H gradients become
-0.06 and -0.07 dex kpc-1, respectively. Lower limits for
the sulphur and oxygen abundances are derived. Nitrogen abundances are
derived for 16 sources.
gradient of approximately 330
K kpc-1, the slopes in the Ne/H and Ar/H gradients become
-0.06 and -0.07 dex kpc-1, respectively. Lower limits for
the sulphur and oxygen abundances are derived. Nitrogen abundances are
derived for 16 sources.
Key words: ISM: abundances - ISM: dust, extinction - ISM: H II regions - galaxy: abundances - infrared: ISM: lines - atomic data
The distribution of Galactic elemental abundances is central to study the chemical evolution of the Milky Way. The relative abundances of the elements are sensitive to the star formation history, the number of massive stars, the relative yield of the elements, and the exchange of matter between the disk and the halo through infall or ejection. Measurements of elemental abundances throughout the Galactic disk thus provide vital inputs to model the formation and evolution of the Galaxy.
H II regions are prime targets to derive the present-day elemental abundances. These objects consist of gas which is ionized and heated by the radiation of massive stars. When the massive ionizing star is newly formed, it is still embedded in its natal molecular cloud and the resulting H II, region is a young, bright and compact nebula. Measuring the elemental abundances of the ionized gas in H II regions allows us to probe the interstellar medium (ISM) in the vicinity of massive stars and to trace the present composition of the ISM in the Galaxy.
Abundance determination methods based on infrared observations present clear advantages over optical studies because the infrared fine-structure lines are not very sensitive to changes in the electron temperature and do not suffer from high extinction. Infrared measurements can thus trace the elemental abundances in the central regions of the Galaxy. The infrared is also the only wavelength regime to measure the N++ ion, the dominant form of nitrogen in highly ionized H II regions.
Previous determinations of the Galactic distribution of elemental
abundances based on the study of H II regions have been performed in
the optical (Shaver et al. 1983; Fich & Silkey 1991; Deharveng et al. 2000)
and in the infrared, based on IRAS (Simpson & Rubin 1990)
and Kuiper Airborne Observatory (KAO) observations
(Lester et al. 1987; Rubin et al. 1988; Simpson et al. 1995b; Afflerbach et al. 1997; Rudolph et al. 1997).
These studies resulted in a series of
firm results concerning the variation of elemental abundances across
the Galaxy: the electron temperature (![]() )
of the H II regions
increases with
)
of the H II regions
increases with
![]() ;
the abundance ratio N/O decreases with
;
the abundance ratio N/O decreases with
![]() ;
the abundances of the heavy elements N, O, Ne, S, and Ar decrease with
;
the abundances of the heavy elements N, O, Ne, S, and Ar decrease with
![]() .
Additional optical studies are based on photospheric emission
lines from B stars
(Fitzsimmons et al. 1992; Smartt & Rolleston 1997; Gummersbach et al. 1998; Rolleston et al. 2000; Smartt et al. 2001)
and on planetary nebulae (Maciel & Koppen 1994; Maciel & Quireza 1999). Similar results and
gradients have been derived towards other
galaxies (e.g. Vila-Costas & Edmunds 1992; Zaritsky et al. 1994).
.
Additional optical studies are based on photospheric emission
lines from B stars
(Fitzsimmons et al. 1992; Smartt & Rolleston 1997; Gummersbach et al. 1998; Rolleston et al. 2000; Smartt et al. 2001)
and on planetary nebulae (Maciel & Koppen 1994; Maciel & Quireza 1999). Similar results and
gradients have been derived towards other
galaxies (e.g. Vila-Costas & Edmunds 1992; Zaritsky et al. 1994).
The Infrared Space Observatory (ISO) spectral catalogue of compact
H II regions (Peeters et al. 2002, hereafter Paper I) presents the
combined Short Wavelength Spectrometer (SWS) and Long Wavelength
Spectrometer (LWS) grating spectra from 2.3 to 196
![]() for 43
nebulae. The catalogue tabulates the fluxes for the hydrogen
recombination and atomic fine-structure lines. A detailed explanation
on the error of these line fluxes, which will be used in the present
paper, is given in Sect. 4 of the catalogue. The spectral coverage gives
access to nearly all the atomic fine-structure lines in the infrared
range. Lines from the elements C, O, N, S, Ne, Si and Ar are present
in most of the sources. This paper will concentrate on the lines
emitted by the ionized gas in the H II region. The [C II], [O I] and
[Si II] lines, produced by ions with ionization potentials lower than
13.6 eV, are expected to be mostly emitted in the Photodissociation
Region (PDR) and will be analyzed by Damour et al. (in prep.). For
some of the ions (O++, Ne++ and S++) two lines are
present providing, in principle, an estimate of the electron density.
All the elements except for oxygen (note that O0, as mentioned
above, is produced in the PDR) are observed in two ionization stages
(see Fig. 1), which alleviates the problem of applying
ionization correction factors for unseen ions (especially for S, Ne
and Ar). Finally, the range of ionization potential covered by this
set of data (up to 41 eV) allows us to examine the ionization state of
the H II regions and to constrain the properties of the ionizing
star(s). From the whole sample, 34 H II regions present enough
emission lines to determine their elemental abundances and ionization
properties. This subsample covers the Galactic plane from the centre
to a galactocentric distance,
for 43
nebulae. The catalogue tabulates the fluxes for the hydrogen
recombination and atomic fine-structure lines. A detailed explanation
on the error of these line fluxes, which will be used in the present
paper, is given in Sect. 4 of the catalogue. The spectral coverage gives
access to nearly all the atomic fine-structure lines in the infrared
range. Lines from the elements C, O, N, S, Ne, Si and Ar are present
in most of the sources. This paper will concentrate on the lines
emitted by the ionized gas in the H II region. The [C II], [O I] and
[Si II] lines, produced by ions with ionization potentials lower than
13.6 eV, are expected to be mostly emitted in the Photodissociation
Region (PDR) and will be analyzed by Damour et al. (in prep.). For
some of the ions (O++, Ne++ and S++) two lines are
present providing, in principle, an estimate of the electron density.
All the elements except for oxygen (note that O0, as mentioned
above, is produced in the PDR) are observed in two ionization stages
(see Fig. 1), which alleviates the problem of applying
ionization correction factors for unseen ions (especially for S, Ne
and Ar). Finally, the range of ionization potential covered by this
set of data (up to 41 eV) allows us to examine the ionization state of
the H II regions and to constrain the properties of the ionizing
star(s). From the whole sample, 34 H II regions present enough
emission lines to determine their elemental abundances and ionization
properties. This subsample covers the Galactic plane from the centre
to a galactocentric distance,
![]() ,
of 15 kpc. It is thus possible to
investigate trends of the ionization conditions in H II regions and
of relative and absolute abundances across a large part of the
Galactic disk. Atomic parameters are crucial in order to interpret
correctly the strengths of the different lines. The latest
transition probabilities and collisional strengths have been compiled
(cf. Table 1) and used throughout this paper.
,
of 15 kpc. It is thus possible to
investigate trends of the ionization conditions in H II regions and
of relative and absolute abundances across a large part of the
Galactic disk. Atomic parameters are crucial in order to interpret
correctly the strengths of the different lines. The latest
transition probabilities and collisional strengths have been compiled
(cf. Table 1) and used throughout this paper.
This paper is structured as follows. Section 2 describes
the kinematic distances and radio properties of the H II regions;
Sect. 3 discusses the problem of extinction; a discussion
of the densities of the H II regions is given in Sect. 4;
Sect. 5 gives an outline of the methodology used to
derive elemental abundances with a particular emphasis on the
advantages/disadvantages of the present data; Sect. 6
presents the results for the ionization state and its variation with
galactocentric distance. The ionic and elemental abundances, and
their variation with
![]() ,
are presented in Sect. 7;
finally, Sect. 8 discusses and summarizes the results of
this paper.
,
are presented in Sect. 7;
finally, Sect. 8 discusses and summarizes the results of
this paper.
![\begin{figure}
\par\includegraphics[width=10cm,clip]{h3072f1.ps} \end{figure}](/articles/aa/full/2002/02/aah3072/Timg30.gif) |
Figure 1:
The fine-structure atomic lines observed in the
combined ISO SWS/LWS spectra of compact H II regions are
shown as a function of the ionization potential. The
electron critical
densities, indicated for every line in italic, are
given in units of cm-3 and are expressed as
|
| Species | Reference | |
| N II | A: | Galavís et al. 1997 (IP XXII) |
| Lennon & Burke 1994 (IP II) | ||
| N III | A: | Galavís et al. 1998a (IP XXIX) |
| Blum & Pradhan 1992 | ||
| O III | A: | Galavís et al. 1997 (IP XXII) |
| Lennon & Burke 1994 (IP II) | ||
| Ne II | A: | Mendoza 1983 |
| Saraph & Tully 1994 (IP IV) | ||
| Ne III | A: | Galavís et al. 1997 (IP XXII) |
| Butler & Zeipen 1994 (IP V) | ||
| S III | A: | Biemont & Bromage 1983 |
| Tayal & Gupta 1999 | ||
| S IV | A: | Mendoza 1983 |
| Saraph & Storey 1999 (IP XXX) | ||
| Ar II | A: | Mendoza 1983 |
| Pelan & Berrington 1995 (IP IX) | ||
| Ar III | A: | Mendoza 1983 |
| Galavis et al. 1995 (IP X) | ||
| Galavis et al. 1998b (IP XXXII) |
| Source |
|
Size | EM |
|
| Ref. | ||||||
| (kpc) | (kpc) | (cm) | (mJy) | (
|
(106 pc cm-6) | (103 cm-3) | (s-1) | |||||
| IR01045 | 13.8 | 7.0 | 6 | 290 | 3 | 14.5 | 11.9 | 47.9 | 1,2 | |||
| IR02219 | 11.0 | 3.3 | 6 | 25000 | 35 | 9.2 | 4.0 | 49.2 | 3,4 | |||
| IR10589 | 9.5 | 8.0 | - | - | - | - | - | - | - | |||
| IR11143 | 9.7 | 8.8 | - | - | - | - | - | - | - | |||
| IR12063 | 9.3 | 9.5 | - | - | - | - | - | - | - | |||
| IR12073 | 10.1 | 10.8 | - | - | - | - | - | - | - | |||
| IR12331 | 6.9 | 4.5 | - | - | - | - | - | - | - | |||
| IR15384 | 6.4 | 2.7 | (11.5) | - | - | - | - | - | - | - | ||
| IR15502 | 4.6 | 6.0 | (8.4) | - | - | - | - | - | - | - | ||
| IR16128 | 5.5 | 3.7 | (11.4) | - | - | - | - | - | - | - | ||
| IR17160 | 3.0 | 5.7 | (11.0) | 6 | 1300 | 12 | 4.0 | 3.5 | (2.5) | 48.4 | (48.9) | 5 |
| IR17221 | 5.2 | 3.4 | (13.4) | - | - | - | - | - | - | - | ||
| IR17279 | 3.4 | 5.1 | (11.8) | 6 | 161 | 10 | 0.7 | 1.7 | (1.1) | 47.3 | (48.1) | 5 |
| SgrC | 0.3 | 8.2 | (8.8) | 21 | 6400 | 120 | 0.2 | 0.2 | (0.2) | 49.3 | (49.4) | 6 |
| IR17455 | 0.5 | 8.0 | (9.0) | 6 | 1600 | 14 | 3.7 | 2.6 | (2.4) | 48.7 | (48.8) | 5,7 |
| IR17591 | 5.5 | 3.0 | (13.8) | 6 | 1310 | 8 | 9.2 | 8.9 | (4.1) | 47.8 | (49.1) | 7 |
| IR18032 | 7.6 | 1.0 | (15.8) | 6 | 640 | 15 | 1.3 | 4.2 | (1.1) | 46.5 | (48.9) | 7 |
| IR18116 | 4.3 | 4.5 | (12.0) | 6 | 3860 | 20 | 4.3 | 3.1 | (1.9) | 48.6 | (49.5) | 7 |
| IR18162 | 6.6 | 1.9 | (14.7) | 6 | 4 | 5 | 0.07 | 1.3 | (0.5) | 44.9 | (46.7) | 1 |
| IR18317 | 4.5 | 4.9 | (10.6) | 6 | 1290 | 13 | 3.4 | 3.3 | (2.3) | 48.2 | (48.9) | 5 |
| IR18434 | 4.6 | 5.7 | (9.0) | 6 | 2280 | 7 | 20.9 | 10.4 | (8.3) | 48.6 | (49.0) | 5 |
| IR18469 | 4.8 | 5.3 | (9.2) | 6 | 102 | 13 | 0.3 | 0.9 | (0.7) | 47.2 | (47.7) | 5 |
| IR18479 | 7.5 | 1.2 | (13.1) | 6 | 2030 | 7 | 18.6 | 21.4 | (6.5) | 47.2 | (49.3) | 5 |
| IR18502 | 4.7 | 7.1 | 6 | 1090 | 6 | 13.6 | 8.1 | (2.2) | 48.5 | (50.8) | 7 | |
| IR19207 | 6.1 | 5.7 | 21 | 13700 | 140 | 0.3 | 0.3 | (0.1) | 49.3 | (51.8) | 8 | |
| IR19442 | 7.6 | 2.5 | (5.8) | 6 | 23 | 1 | 10.3 | 29.2 | (19.2) | 45.9 | (46.6) | 9 |
| IR19598 | 9.8 | 8.5 | 3.6 | 3475 | 6 | 45.6 | 13.6 | 49.1 | 10 | |||
| DR21 | 8.6 | 2.8 | 6 | 17500 | 20 | 19.6 | 8.5 | 48.9 | 11 | |||
| IR21190 | 12.7 | 8.9 | 6 | 906 | 4 | 25.4 | 12.1 | 48.6 | 12 | |||
| IR21270 | 14.8 | 11.3 | 6 | 563 | 120 | 0.02 | 0.1 | 48.6 | 13 | |||
| IR21306 | 12.6 | 8.3 | - | - | - | - | - | - | - | |||
| IR22308 | 11.3 | 5.5 | 6 | 554 | 90 | 0.03 | 0.1 | 48.0 | 13 | |||
| IR23030 | 11.4 | 5.2 | 6 | 1900 | 40 | 0.5 | 0.7 | 48.4 | 14 | |||
| IR23133 | 11.7 | 5.5 | 6 | 1048 | 15 | 2.1 | 2.3 | 48.2 | 14 | |||
The study of the elemental abundance variation from atomic fine-structure lines emitted by H II regions relies on proper determinations of the galactic distances to the H II regions and in this sense, a detailed literature study has been done in order to get the most accurate distances to the program sources.
The determination of the distances to the H II regions of the ISO
sample has been discussed in Paper I and the reader is referred to
this paper for detailed information. Table 2 lists in
Cols. 2 and 3 the adopted distances
![]() and
and ![]() (including in the latter the near and far solar distances).
(including in the latter the near and far solar distances).
Radio continuum measurements allow one to derive various properties of
the H II regions such as the emission measure (EM), rms electron
density (
![]() )
and the Lyman continuum photon flux (
)
and the Lyman continuum photon flux (
![]() ). These parameters can be derived for spherical sources if the
radio flux density and the source size are known. For non-spherical
sources, the geometrical average of the major and minor axes can be
taken as a representative size.
). These parameters can be derived for spherical sources if the
radio flux density and the source size are known. For non-spherical
sources, the geometrical average of the major and minor axes can be
taken as a representative size.
In the Rayleigh-Jeans limit, the brightness temperature, ![]() ,
can be estimated from:
,
can be estimated from:
where ![]() is the integrated flux density in Jy,
is the integrated flux density in Jy,
![]() is the frequency in Hz and
is the frequency in Hz and ![]() is the source solid angle in sr. The optical depth for an ionized, optically
thin gas at a temperature
is the source solid angle in sr. The optical depth for an ionized, optically
thin gas at a temperature ![]() is given by:
is given by:
where a![]() is a correction factor close to unity
(Mezger & Henderson 1967).
is a correction factor close to unity
(Mezger & Henderson 1967).
To estimate the rms electron density we used the formalism explained by Wood & Churchwell (1989):
where ![]() s is the path length of the emitting region
(taken as the source size). Finally,
the photon flux of the Lyman continuum can be determined from:
s is the path length of the emitting region
(taken as the source size). Finally,
the photon flux of the Lyman continuum can be determined from:
where
![]() cm3 s-1
(Hummer & Storey 1987) is the case
B recombination coefficient of hydrogen to all levels
cm3 s-1
(Hummer & Storey 1987) is the case
B recombination coefficient of hydrogen to all levels ![]() (for
(for
![]() = 7500 K).
= 7500 K).
Flux densities and source sizes were taken from the literature
selecting observations made at frequencies larger than 5 GHz. This
ensures that the emission is optically thin. In addition, care was
taken to select observations with a spatial resolution of the order
of a few arcseconds to avoid structures larger than 10
![]() to be
resolved out. Radio properties derived using the above equations are
listed in Table 2 for those sources with published
observations satisfying the above requirements.
to be
resolved out. Radio properties derived using the above equations are
listed in Table 2 for those sources with published
observations satisfying the above requirements.
Compact H II regions are heavily embedded in dust and gas and suffer a dimming of their radiation by dust located either within the ionized gas or in the neutral foreground material. The term "extinction'' usually refers to the dimming of starlight, for which scattering from the beam contributes as much as true absorption because the star is effectively a point source. For extended objects, the scattering is less effective in attenuating the radiation because photons can be scattered into the beam as well as out of it. The effectiveness of scattering depends upon the geometry of the sources relative to the dust. In our objects, this is unknown. Hence, we will refer to the dimming of our objects due to dust absorption as "extinction'' throughout this paper.
The extinction towards compact H II regions is generally high with
values of AV ranging from ![]() 10 to hundreds of magnitudes -
corresponding to extinction of
10 to hundreds of magnitudes -
corresponding to extinction of ![]() 1 to a few 10 mag at near- and
mid-infrared wavelengths. The extinction in the far-infrared is
generally negligible. For a number of H II regions, the ISO SWS
spectra show a series of H I recombination lines which can be used
to derive the extinction curve characterizing the dust absorption
towards these sources. Radio continuum emission can also be used to
derive the expected flux at any H I recombination line to provide an
alternative estimate of the extinction when comparing with the
observed line flux.
1 to a few 10 mag at near- and
mid-infrared wavelengths. The extinction in the far-infrared is
generally negligible. For a number of H II regions, the ISO SWS
spectra show a series of H I recombination lines which can be used
to derive the extinction curve characterizing the dust absorption
towards these sources. Radio continuum emission can also be used to
derive the expected flux at any H I recombination line to provide an
alternative estimate of the extinction when comparing with the
observed line flux.
![\begin{figure}
\par\includegraphics[width=13.7cm,clip]{h3072f2.ps} \end{figure}](/articles/aa/full/2002/02/aah3072/Timg50.gif) |
Figure 2: Near- and mid-infrared extinction curves as derived from the H I recombination lines. Each panel is labeled by the name of the H II region and the derived extinction AK. The solid lines show the extinction law (see Sect. 3.1). |
The mid-infrared H I recombination lines from the Brackett
(
![]() ), Pfund (
), Pfund (
![]() )
and Humpreys
(
)
and Humpreys
(
![]() )
series between 2 and 8
)
series between 2 and 8
![]() can be used to derive
the extinction law at these wavelengths by comparing the ratio of
observed line strengths to the predictions of recombination theory
assuming a nebular electron density,
can be used to derive
the extinction law at these wavelengths by comparing the ratio of
observed line strengths to the predictions of recombination theory
assuming a nebular electron density, ![]() ,
and temperature,
,
and temperature, ![]() .
The
ratio of the hydrogen emission coefficients is not very sensitive to
.
The
ratio of the hydrogen emission coefficients is not very sensitive to
![]() or
or ![]() .
Therefore, we have adopted
.
Therefore, we have adopted ![]() = 1000 3 and
= 1000 3 and
![]() = 7500 K, which are typical values for H II regions. In the
following, we will consider the standard case B treatment, ie. where
the nebula is optically thick to the Lyman series photons but
optically thin to all other series photons (see, e.g., Osterbrock 1989).
The observed line flux,
= 7500 K, which are typical values for H II regions. In the
following, we will consider the standard case B treatment, ie. where
the nebula is optically thick to the Lyman series photons but
optically thin to all other series photons (see, e.g., Osterbrock 1989).
The observed line flux,
![]() ,
can then be expressed as:
,
can then be expressed as:
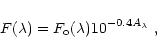 |
(6) |
where
![]() is the non-extincted line flux, given by
case B theory, and
is the non-extincted line flux, given by
case B theory, and
![]() is the extinction at the wavelength
is the extinction at the wavelength ![]() .
The relative extinction
to a reference line (e.g. Br
.
The relative extinction
to a reference line (e.g. Br![]() at 4.05
at 4.05
![]() ) is:
) is:
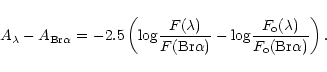 |
(7) |
The theoretical ratios are taken from Hummer & Storey (1987).
Figure 2 shows the relative extinction
![]() derived for the H II regions which
have at least 3 H I recombination lines (14 sources in total) within
the SWS range. The line fluxes are taken from Tables 7 and 8 in
Paper I.
derived for the H II regions which
have at least 3 H I recombination lines (14 sources in total) within
the SWS range. The line fluxes are taken from Tables 7 and 8 in
Paper I.
At infrared wavelengths longward of 1.25
![]() ,
the extinction law, as
based on JHK photometry, appears to be independent of the line of
sight and consistent with a simple power law
,
the extinction law, as
based on JHK photometry, appears to be independent of the line of
sight and consistent with a simple power law
![]() (Mathis 1990; Martin & Whittet 1990),
were AK is the extinction in the K band (2.2
(Mathis 1990; Martin & Whittet 1990),
were AK is the extinction in the K band (2.2
![]() ). For all the 14
sources we could derive an AK for which this power law satisfies
both the relative extinction at 2.62
). For all the 14
sources we could derive an AK for which this power law satisfies
both the relative extinction at 2.62
![]() (Br
(Br![]() )
and 4.05
)
and 4.05
![]() (Br
(Br![]() ). The solid lines in Fig. 2 show this
power law for the corresponding AK. Note that the curves generally
fit the relative extinction at the other wavelengths nicely. The
derived extinction values (AK) are listed in Table 3.
). The solid lines in Fig. 2 show this
power law for the corresponding AK. Note that the curves generally
fit the relative extinction at the other wavelengths nicely. The
derived extinction values (AK) are listed in Table 3.
| Line |
|
Line |
|
||
| Br |
2.6 | 0.741 | [Ne II] | 12.8 | 0.165 |
| Br |
4.0 | 0.354 | [Ne III] | 15.5 | 0.156 |
| 7.0 | 0.140 | [S III] | 18.7 | 0.217 | |
| 9.0 | 0.429 | [S III] | 33.5 | 0.069 | |
| 10.5 | 0.429 | [Ne III] | 36.0 | 0.060 |
From the computed AK one can derive the extinction at other
wavelengths using the results tabulated in Mathis (1990), namely
A9.7/AK=0.544 for the 9.7
![]() silicate feature and
A18/AK=0.217 for the 18
silicate feature and
A18/AK=0.217 for the 18
![]() silicate, in combination
with the astronomical silicate profile of Draine (1985) and a
silicate, in combination
with the astronomical silicate profile of Draine (1985) and a
![]() power law for
power law for
![]()
![]() .
Using this
"standard'' extinction law, the extinction
.
Using this
"standard'' extinction law, the extinction
![]() /AK to apply to
the near- and mid-infrared line fluxes is shown in
Table 4. In contrast to the extinction between 2
and 7
/AK to apply to
the near- and mid-infrared line fluxes is shown in
Table 4. In contrast to the extinction between 2
and 7
![]() ,
the extinction due to the silicate absorption at 9.7 and
18
,
the extinction due to the silicate absorption at 9.7 and
18
![]() depends on the line-of-sight (Draine 1989) and still both
the shape and strength of these features remain controversial.
Therefore, the "standard'' extinctions for wavelengths longer than 7
depends on the line-of-sight (Draine 1989) and still both
the shape and strength of these features remain controversial.
Therefore, the "standard'' extinctions for wavelengths longer than 7
![]() given in Table 4 are merely illustrative and
may not be applicable to all the H II regions.
given in Table 4 are merely illustrative and
may not be applicable to all the H II regions.
Because of the lack of information on the extinction for most of the
sample sources (extinction could only be derived for 14 sources out of
34) and the difficulties explained above in correcting the lines
beyond 7
![]() ,
the line fluxes will not be corrected for
extinction in the analysis presented in this paper and instead the
effect of the extinction will be indicated.
,
the line fluxes will not be corrected for
extinction in the analysis presented in this paper and instead the
effect of the extinction will be indicated.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{h3072f3.ps} \end{figure}](/articles/aa/full/2002/02/aah3072/Timg63.gif) |
Figure 3:
Comparison between the Br |
The intrinsic flux of any H I recombination line can be determined
if both ![]() and the emission measure, EM, in the nebula are
known. Radio continuum observations can provide this information (see
Sect. 2). The intrinsic flux of Br
and the emission measure, EM, in the nebula are
known. Radio continuum observations can provide this information (see
Sect. 2). The intrinsic flux of Br![]() can be
determined using:
can be
determined using:
where
![]() is the emissivity of
is the emissivity of
![]() and
and ![]() is the solid angle of the source.
Using Eqs. (1)-(3) and
(8), the ratio
of protons to electrons
is the solid angle of the source.
Using Eqs. (1)-(3) and
(8), the ratio
of protons to electrons
![]() ,
,
![]() = 7500 K and
= 7500 K and
![]() erg s-1 cm3(Hummer & Storey 1987), we obtain:
erg s-1 cm3(Hummer & Storey 1987), we obtain:
where the flux densities, S![]() ,
from Table 2 can
be used. Figure 3 compares these predicted fluxes for
Br
,
from Table 2 can
be used. Figure 3 compares these predicted fluxes for
Br![]() with the fluxes observed by SWS corrected using the
extinction derived in Sect. 3.1. The radio flux
densities and
with the fluxes observed by SWS corrected using the
extinction derived in Sect. 3.1. The radio flux
densities and
![]() are considered to have a nominal 20%
uncertainty. In general, the radio Br
are considered to have a nominal 20%
uncertainty. In general, the radio Br![]() fluxes are larger than
the extinction-corrected SWS fluxes, especially for IR 02219 and
IR 23030. These two sources are much more extended in radio than the
SWS beam (see Table 2). On the other hand, the
predicted radio line flux for IR 18434 is slightly smaller. This
source lies in a region of extended emission of up to a few
arc-minutes (Kim & Koo 2001) which is observed by SWS and it is not
included in the quoted radio flux density. This is probably the reason
why the radio prediction leads to a lower line flux.
fluxes are larger than
the extinction-corrected SWS fluxes, especially for IR 02219 and
IR 23030. These two sources are much more extended in radio than the
SWS beam (see Table 2). On the other hand, the
predicted radio line flux for IR 18434 is slightly smaller. This
source lies in a region of extended emission of up to a few
arc-minutes (Kim & Koo 2001) which is observed by SWS and it is not
included in the quoted radio flux density. This is probably the reason
why the radio prediction leads to a lower line flux.
The application of predictions from radio continuum observations to our ISO data depends on the source geometry at both radio and infrared wavelengths and on the knowledge of the radio emission corresponding to the infrared emission observed by ISO.
In the following, we comment on the extinction determination in individual H II regions from which previous studies are available.
It is a very bright H II region located in a
large 4![]() by 3
by 3![]() (Dickel et al. 1980) complex of H II regions, infrared
sources and molecular clouds. Hayward et al. (1989) studied the
extinction to W3 A by comparing the 5 GHz map by Harris & Wynn-Williams (1976)
with their infrared (H and K) observations. They
found that the extinction varies from AK
(Dickel et al. 1980) complex of H II regions, infrared
sources and molecular clouds. Hayward et al. (1989) studied the
extinction to W3 A by comparing the 5 GHz map by Harris & Wynn-Williams (1976)
with their infrared (H and K) observations. They
found that the extinction varies from AK ![]() 1.0 to 1.7, in
agreement with our computed extinction (AK = 1.5). The 9.7
1.0 to 1.7, in
agreement with our computed extinction (AK = 1.5). The 9.7
![]() extinction was studied by Hackwell et al. (1978), who found
extinction was studied by Hackwell et al. (1978), who found
![]() to
vary from
to
vary from ![]() 2.0 at the position of W3 A to
2.0 at the position of W3 A to ![]() 4.0 at the
perimeter of the W3 complex. This extinction due to the 9.7
4.0 at the
perimeter of the W3 complex. This extinction due to the 9.7
![]() silicate absorption is much larger than the
silicate absorption is much larger than the
![]() = 0.8 derived from
our AK when the "standard'' extinction law described in
Sect. 3.1 is used.
= 0.8 derived from
our AK when the "standard'' extinction law described in
Sect. 3.1 is used.
Near-infrared slit observations by Armand et al. (1996) mapped the
variation of several H I recombination lines across
IRAS 12073-6233 and found AK to vary from 1.2 to 1.7. We derive
an extinction of AK = 0.8 mag. The discrepancy in ![]() 0.4-0.9 mag. can be caused by the fact that we have observed the
integrated H I emission in a
0.4-0.9 mag. can be caused by the fact that we have observed the
integrated H I emission in a
![]() beam, which
may lead to a lower hydrogen density column because of the
contribution of extended emission around the nebula and thus, to the
lower extinction we obtain.
beam, which
may lead to a lower hydrogen density column because of the
contribution of extended emission around the nebula and thus, to the
lower extinction we obtain.
It is one of the best studied ultracompact H II
regions and classified as cometary (Wood & Churchwell 1989). By
comparing images of the 2.17
![]() Br
Br![]() recombination line and
2 cm radio continuum emission (Fey et al. 1995), Watson et al. (1997)
derived a map of the extinction towards this H II region. They found
that the apparent extinction to the nebula is not uniform, with AK varying from 2.2 to 2.6 mag. They give a mean value AK =
recombination line and
2 cm radio continuum emission (Fey et al. 1995), Watson et al. (1997)
derived a map of the extinction towards this H II region. They found
that the apparent extinction to the nebula is not uniform, with AK varying from 2.2 to 2.6 mag. They give a mean value AK =
![]() .
Pratap et al. (1999) estimated AK =
.
Pratap et al. (1999) estimated AK =
![]() towards the ionizing
star based on its H-K colour. As discussed above in the case of
IRAS 12073-6233, the contribution of the extended envelope around
the compact H II region (Kim & Koo 2001) to the SWS aperture may
cause ISO to observe a lower hydrogen column density than the ones
observed by the high
towards the ionizing
star based on its H-K colour. As discussed above in the case of
IRAS 12073-6233, the contribution of the extended envelope around
the compact H II region (Kim & Koo 2001) to the SWS aperture may
cause ISO to observe a lower hydrogen column density than the ones
observed by the high ![]() 1
1
![]() resolution observations of
Watson et al. (1997) and Pratap et al. (1999). This could explain our lower
AK = 1.6 mag.
resolution observations of
Watson et al. (1997) and Pratap et al. (1999). This could explain our lower
AK = 1.6 mag.
It is the only H II region in the sample
for which the SWS spectrum was also taken at speed 4, yielding a
resolving power of ![]() 1500 (see Paper I). In total, 20 H I recombination lines were detected (Tables 7 and 8 in Paper I)
allowing us to derive a better sampled extinction curve in K3-50 A than
for the other nebulae of the catalogue, especially in the region from
2 to 5
1500 (see Paper I). In total, 20 H I recombination lines were detected (Tables 7 and 8 in Paper I)
allowing us to derive a better sampled extinction curve in K3-50 A than
for the other nebulae of the catalogue, especially in the region from
2 to 5
![]() (Fig. 2). Note that the points
around 3
(Fig. 2). Note that the points
around 3
![]() seem to be slightly above the standard extinction
curve, which could be due to the 3
seem to be slightly above the standard extinction
curve, which could be due to the 3
![]() O-H stretching mode seen in
the spectrum (see Paper I).
The extinction to K3-50 A has been studied in detail by Howard et al. (1996)
using both high-resolution near-infrared and radio images. They
found variations in the extinction across the nebula. They reported
an extinction at 4.05
O-H stretching mode seen in
the spectrum (see Paper I).
The extinction to K3-50 A has been studied in detail by Howard et al. (1996)
using both high-resolution near-infrared and radio images. They
found variations in the extinction across the nebula. They reported
an extinction at 4.05
![]() (Br
(Br![]() )
varying from 0 to 3 mag, with
an averaged value of 1.6 in the central 2.7
)
varying from 0 to 3 mag, with
an averaged value of 1.6 in the central 2.7
![]() region. This is
the same value we get from the H I recombination lines analysis.
region. This is
the same value we get from the H I recombination lines analysis.
The electron density (![]() )
can be determined from the ratio of two
atomic fine-structure lines of the same ionic species when they are
emitted from levels with nearly the same excitation energy
(e.g. Rubin et al. 1994). This ratio is sensitive to gas densities
approximately
in between the critical densities of each line (see
Fig. 1). A good indicator of gas with densities lower
than a few thousands particles/cm3 is the ratio of the [O III] lines at 52 and 88
)
can be determined from the ratio of two
atomic fine-structure lines of the same ionic species when they are
emitted from levels with nearly the same excitation energy
(e.g. Rubin et al. 1994). This ratio is sensitive to gas densities
approximately
in between the critical densities of each line (see
Fig. 1). A good indicator of gas with densities lower
than a few thousands particles/cm3 is the ratio of the [O III] lines at 52 and 88 ![]() m. Higher density gas can be probed using
line ratios with higher critical densities such as [S III] 33/19
m. Higher density gas can be probed using
line ratios with higher critical densities such as [S III] 33/19
![]() and [Ne III] 36/15
and [Ne III] 36/15
![]() .
.
The densities derived from the [O III] line ratio for the ISO sample of
H II regions are in the range from ![]() 100 to 3000 cm-3(see Table 5). No dependence of the density on
galactocentric distance is found (see Fig. 4), in
agreement with previous studies (e.g. Simpson et al. 1995b; Afflerbach et al. 1997).
100 to 3000 cm-3(see Table 5). No dependence of the density on
galactocentric distance is found (see Fig. 4), in
agreement with previous studies (e.g. Simpson et al. 1995b; Afflerbach et al. 1997).
The derived [O III] densities, ![]() ([O III]), are compared to the rms
densities,
([O III]), are compared to the rms
densities,
![]() ,
calculated from the radio continuum observations
(see Table 2) in Fig. 5. In general,
the rms densities are larger than the [O III] densities, except for
three sources (IR 19207, IR 21270 and IR 22308), which are more
extended (their radio sizes are 140, 120 and 90
,
calculated from the radio continuum observations
(see Table 2) in Fig. 5. In general,
the rms densities are larger than the [O III] densities, except for
three sources (IR 19207, IR 21270 and IR 22308), which are more
extended (their radio sizes are 140, 120 and 90
![]() ,
respectively)
than the LWS aperture.
,
respectively)
than the LWS aperture.
| Source | Source | ||||||
| (cm-3) | (cm-3) | ||||||
| IR02219 | 2834 | + 1225 - 680 | IR18116 | 753 | + 224 - 152 | ||
| IR10589 | 645 | + 194 - 132 | IR18317 | 1543 | + 738 - 397 | ||
| IR11143 | 290 | + 103 - 71 | IR18434 | 817 | + 260 - 171 | ||
| IR12063 | 1335 | + 454 - 284 | IR18469 | 146 | + 65 - 46 | ||
| IR12073 | 962 | + 295 - 195 | IR18479 | 836 | + 268 - 175 | ||
| IR12331 | 623 | + 181 - 125 | IR18502 | 1181 | + 411 - 257 | ||
| IR15384 | 1224 | + 390 - 251 | IR19207 | 485 | + 152 - 104 | ||
| IR15502 | 452 | + 178 - 114 | IR19598 | 484 | + 154 - 105 | ||
| IR16128 | 891 | + 271 - 180 | DR21 | 320 | + 139 - 90 | ||
| IR17160 | 476 | + 144 - 100 | IR21190 | 2882 | + 1987 - 871 | ||
| IR17221 | 594 | + 182 - 124 | IR21270 | 186 | + 74 - 52 | ||
| IR17279 | 127 | + 61 - 44 | IR21306 | 214 | + 109 - 70 | ||
| SgrC | 107 | + 66 - 45 | IR22308 | 768 | + 366 - 207 | ||
| IR17455 | 548 | + 181 - 121 | IR23030 | 806 | + 246 - 164 | ||
| IR17591 | 462 | + 143 - 99 | IR23133 | <478 | |||
| IR18032 | 512 | + 274 - 154 | |||||
If the radio and ISO sample the same gas and there is no collisional
de-excitation, ![]() ([O III]) reflects the mean of the local density
and must always be of the same order or greater than
([O III]) reflects the mean of the local density
and must always be of the same order or greater than
![]() ,
which is derived assuming that the emission is spread uniformly along
the line of sight. The ratio of both densities is the filling factor,
which has been found to be typically of the order of
,
which is derived assuming that the emission is spread uniformly along
the line of sight. The ratio of both densities is the filling factor,
which has been found to be typically of the order of ![]() 0.1 for
many H II regions (Copetti et al. 2000). The sources with
0.1 for
many H II regions (Copetti et al. 2000). The sources with
![]() <
<![]() ([O III]) likely contain high density clumps embedded in a hot, low
density gas from stellar winds. However, Fig. 5 shows
that
([O III]) likely contain high density clumps embedded in a hot, low
density gas from stellar winds. However, Fig. 5 shows
that ![]() ([O III]) is much too low for most of the sources. At the
densities implied by the radio continuum observations, the [O III] line
at 88
([O III]) is much too low for most of the sources. At the
densities implied by the radio continuum observations, the [O III] line
at 88
![]() (with
(with
![]() )
is collisionally
de-excited in the ultracompact core of the H II region. Considering
that the real densities of these cores are probably even higher than
our derived rms densities, even the [O III] line at 52
)
is collisionally
de-excited in the ultracompact core of the H II region. Considering
that the real densities of these cores are probably even higher than
our derived rms densities, even the [O III] line at 52
![]() (
(
![]() )
could also well be collisionaly
de-excited. Therefore, the density derived from the [O III] lines is
likely representative of a dilute shell surrounding the ultracompact
core. This low density gas at high excitation (note that O++ is
produced by ionizing photons with
)
could also well be collisionaly
de-excited. Therefore, the density derived from the [O III] lines is
likely representative of a dilute shell surrounding the ultracompact
core. This low density gas at high excitation (note that O++ is
produced by ionizing photons with ![]() eV) could be produced by
leakage of radiation from the core. Recent radio observations
(Kurtz et al. 1999; Kim & Koo 2001) have shown that the presence of
physically related envelopes around ultracompact H II regions is the
usual case rather than the exception.
eV) could be produced by
leakage of radiation from the core. Recent radio observations
(Kurtz et al. 1999; Kim & Koo 2001) have shown that the presence of
physically related envelopes around ultracompact H II regions is the
usual case rather than the exception.
The derivation of electron densities using the [S III] and [Ne III] line
ratios from the ISO data yielded inconsistent results.
Figure 6 compares the observed line ratios of these
ions with their expected values for uniform electron densities
between 102 and 106 3, plotted as a solid line. The assumed
![]() of 7500 K has almost no effect on the plot. Meaningful [S III] and [Ne III] line ratios should lie below their expected values at low
densities, but we see that almost all points for the [Ne III] line
ratio, and many for [S III], lie above these limits by up to a factor
of 3. This problem has also been recognized for the [Ne III] line
ratio in some planetary nebula (Rubin et al. 2000). However, in that
case the observed ratio is only 10% larger than what theory predicts
for the low density limit. Possible causes of this discrepancy
between observations and theory are:
of 7500 K has almost no effect on the plot. Meaningful [S III] and [Ne III] line ratios should lie below their expected values at low
densities, but we see that almost all points for the [Ne III] line
ratio, and many for [S III], lie above these limits by up to a factor
of 3. This problem has also been recognized for the [Ne III] line
ratio in some planetary nebula (Rubin et al. 2000). However, in that
case the observed ratio is only 10% larger than what theory predicts
for the low density limit. Possible causes of this discrepancy
between observations and theory are:
![\begin{figure}
\par\includegraphics[width=8cm,clip]{h3072f4.ps} \end{figure}](/articles/aa/full/2002/02/aah3072/Timg80.gif) |
Figure 4:
Electron densities of the compact H II regions derived from
the [O III] 88/52
|
The lines involved in both [S III] and [Ne III] ratios have been
observed in different apertures (
![]() and
and
![]() ,
respectively for the short and long
wavelength lines). The black, large arrows in the bottom right corner
of Fig. 6 indicate the shift in both line ratios that
might be caused by aperture effect if the emitting region is larger
than the SWS band 4 (
,
respectively for the short and long
wavelength lines). The black, large arrows in the bottom right corner
of Fig. 6 indicate the shift in both line ratios that
might be caused by aperture effect if the emitting region is larger
than the SWS band 4 (
![]() )
and has an uniform
brightness. Aperture effects may have affected the sources which
cluster around a [S III] ratio of unity. Actually, this correction
would bring these sources within the expected [S III] and [Ne III] ranges at densities of about
103-104 3, the rms density range.
However, this aperture correction is not large enough to bring the
most-offending sources (IR 16128, IR 17160, IR 17279, IR 17591,
IR 18469 and IR 19207), with a [S III] ratio
)
and has an uniform
brightness. Aperture effects may have affected the sources which
cluster around a [S III] ratio of unity. Actually, this correction
would bring these sources within the expected [S III] and [Ne III] ranges at densities of about
103-104 3, the rms density range.
However, this aperture correction is not large enough to bring the
most-offending sources (IR 16128, IR 17160, IR 17279, IR 17591,
IR 18469 and IR 19207), with a [S III] ratio ![]() 3, into the
theoretical limits. Instead, these sources are undoubtedly off
because only part of these sources were included in the SWS
beam. Specifically, recent 6 cm ATCA maps of IR 16128, IR 17160 and
IR 17279 (Martín-Hernández et al. 2002, in prep.) show that
SWS was pointing at the edge of these sources and more of the source
was included in the larger aperture of the longer wavelength lines
than in that of the shorter wavelength lines. Likewise, radio maps of
the sources IR 17591 (Garay et al. 1993), IR 18469 (Kurtz et al. 1994)
and IR 19207 (Mehringer 1994) reveal complex structure
- core halo or multiple components - part of which was not included
in the short wavelength, smaller aperture.
3, into the
theoretical limits. Instead, these sources are undoubtedly off
because only part of these sources were included in the SWS
beam. Specifically, recent 6 cm ATCA maps of IR 16128, IR 17160 and
IR 17279 (Martín-Hernández et al. 2002, in prep.) show that
SWS was pointing at the edge of these sources and more of the source
was included in the larger aperture of the longer wavelength lines
than in that of the shorter wavelength lines. Likewise, radio maps of
the sources IR 17591 (Garay et al. 1993), IR 18469 (Kurtz et al. 1994)
and IR 19207 (Mehringer 1994) reveal complex structure
- core halo or multiple components - part of which was not included
in the short wavelength, smaller aperture.
The lines at the longest wavelengths, [S III] 33 and [Ne III] 36
![]() ,
are
located in the SWS band 4. Band 4 detectors suffer strongly from
memory effects, are very sensitive to cosmic particle hits and their
responsivity curve is still unsatisfactory and based on pre-flight
ground based tests (see Paper I). Therefore, these lines are affected
by large calibration errors (an official
,
are
located in the SWS band 4. Band 4 detectors suffer strongly from
memory effects, are very sensitive to cosmic particle hits and their
responsivity curve is still unsatisfactory and based on pre-flight
ground based tests (see Paper I). Therefore, these lines are affected
by large calibration errors (an official ![]() 25% calibration
error is quoted in Paper I and used in Fig. 6).
However, this calibration uncertainty is not enough to explain the
discrepancy between the observed and the predicted line ratios.
25% calibration
error is quoted in Paper I and used in Fig. 6).
However, this calibration uncertainty is not enough to explain the
discrepancy between the observed and the predicted line ratios.
The most recent theoretical calculations (McLaughlin & Bell 2000) of the collisional strengths for the [Ne III] levels differ from earlier studies (Butler & Zeippen 1994) by only a few percent. Hence, we consider it unlikely that the observed factor 2-3 discrepancy in the [Ne III] line ratios of H II regions results from errors in the theoretical collisional strengths.
The lines involved in both [S III] and [Ne III] ratios suffer also from
differential extinction. The color excesses between the [S III] lines
and the [Ne III] lines are
![]() AK and
AK and
![]() AK (cf. Table 4), respectively. For the
nominal AK
AK (cf. Table 4), respectively. For the
nominal AK ![]() mag. derived from the H I recombination lines
(cf. Table 3), these extinction corrections (indicated
in Fig. 6 by the grey arrows in the bottom right
corner) are, however, quite small.
mag. derived from the H I recombination lines
(cf. Table 3), these extinction corrections (indicated
in Fig. 6 by the grey arrows in the bottom right
corner) are, however, quite small.
We conclude that the present [S III] and [Ne III] line ratio
observations are unreliable as density indicators largely due to
aperture differences. The sources above mentioned (IR 16128,
IR 17160, IR 17279, IR 17591, IR 18469 and IR 19207),
together with IR 21270 and IR 21306, which, although not present
in Fig. 6 are known to be mispointed (see
Paper I), will be
excluded from the analysis involving any SWS line. Moreover, the
[S III] 33 and [Ne III] 36
![]() lines will not be used in the data
analysis.
lines will not be used in the data
analysis.
The object IR 21190, identified in Fig. 6, is of
special interest. It is a very compact H II region (and thus
point-like for the SWS; see its spectrum in Fig. 8, Paper I, which
does not present jumps between the different apertures) and has an
AK = 0 (see Table 3). Thus, it should not be affected by
aperture changes or extinction. Indeed, the [S III] and [Ne III] ratios
for this source are well inside the theoretical limits. However, the
densities derived from these two indicators (![]() <104 3 and
>105 3, respectively for the [S III] and [Ne III] ratios) do not
agree. IRAS 21190 presents a complex density morphology (Peeters et al. 2002, in prep.) and it is therefore not surprising that the
tracer of lower density and lower ionization state material yields a
lower density than the tracer of higher density and higher ionization
state material.
<104 3 and
>105 3, respectively for the [S III] and [Ne III] ratios) do not
agree. IRAS 21190 presents a complex density morphology (Peeters et al. 2002, in prep.) and it is therefore not surprising that the
tracer of lower density and lower ionization state material yields a
lower density than the tracer of higher density and higher ionization
state material.
Ionic abundances can be determined from the measured strengths of the
lines when a specific model for the structure of the H II region is
assumed. The simplest model is to assume that the nebula is
homogeneous with constant ![]() and
and ![]() .
If one also assumes that all
the line photons emitted in the nebula escape without absorption and
therefore without causing further upward transitions, the calculation
of the ionic abundances is straightforward (e.g. Rubin et al. 1988).
.
If one also assumes that all
the line photons emitted in the nebula escape without absorption and
therefore without causing further upward transitions, the calculation
of the ionic abundances is straightforward (e.g. Rubin et al. 1988).
Considering two ions X+i and Y+j, the ratio of their ionic abundances is given by:
where
FX+i and
FY+j are the fluxes corrected from
extinction corresponding to any line produced by the ions X+i and
Y+j, and
![]() and
and
![]() are their
respective emission coefficients. This equation assumes that the
volume occupied by both ionic gases and the solid angles included in
the fluxes are the same. Because the beam sizes of ISO differ
significantly with wavelength (see Paper I), the
distribution of the emission over the beam becomes important in
determining abundances for some of the elements.
are their
respective emission coefficients. This equation assumes that the
volume occupied by both ionic gases and the solid angles included in
the fluxes are the same. Because the beam sizes of ISO differ
significantly with wavelength (see Paper I), the
distribution of the emission over the beam becomes important in
determining abundances for some of the elements.
The emission coefficients depend on ![]() ,
,
![]() and the relevant
atomic parameters (transition probabilities, A, and collisional
strengths,
and the relevant
atomic parameters (transition probabilities, A, and collisional
strengths, ![]() ). They are computed using a 5-level atom (or a
2-level atom for ions with a 2P ground term) in statistical
equilibrium (Kafatos & Lynch 1980). The references for the atomic
parameters used in this paper are given in Table 1.
Fortunately, the emissivities of the fine-structure lines show only a
very slight dependence on
). They are computed using a 5-level atom (or a
2-level atom for ions with a 2P ground term) in statistical
equilibrium (Kafatos & Lynch 1980). The references for the atomic
parameters used in this paper are given in Table 1.
Fortunately, the emissivities of the fine-structure lines show only a
very slight dependence on ![]() because these lines are emitted from
levels with excitation energies much lower than the mean colliding
electron energy. Thus, we will use an electron temperature of 7500 K,
typical for galactic H II regions
(Shaver et al. 1983; Afflerbach et al. 1996; Afflerbach et al. 1997),
to evaluate these emissivities.
However, the dependence of the fine-structure emission coefficients on
because these lines are emitted from
levels with excitation energies much lower than the mean colliding
electron energy. Thus, we will use an electron temperature of 7500 K,
typical for galactic H II regions
(Shaver et al. 1983; Afflerbach et al. 1996; Afflerbach et al. 1997),
to evaluate these emissivities.
However, the dependence of the fine-structure emission coefficients on
![]() is particularly important when the density of the emitting
region is comparable to the critical density of the levels involved.
It is illustrative to consider the
is particularly important when the density of the emitting
region is comparable to the critical density of the levels involved.
It is illustrative to consider the ![]() correction factor,
correction factor,
![]() ,
needed to apply to the
abundance ratio of sequential ionic ionization states (Ne++/Ne+,
calculated from [Ne II] 12.8 and [Ne III] 15.5
,
needed to apply to the
abundance ratio of sequential ionic ionization states (Ne++/Ne+,
calculated from [Ne II] 12.8 and [Ne III] 15.5
![]() ,
Ar++/Ar+, from
[Ar II] 7.0 and [Ar III] 9.0
,
Ar++/Ar+, from
[Ar II] 7.0 and [Ar III] 9.0
![]() ,
S+3/S++ from [S III] 18.7 and [S IV] 10.5
,
S+3/S++ from [S III] 18.7 and [S IV] 10.5
![]() ,
and N++/N+, from [N II] 122 and [N III] 57
,
and N++/N+, from [N II] 122 and [N III] 57
![]() )
when the
respective line emissivities are evaluated in the low density limit
(cf. Fig. 7). This correction factor is,
basically, the quotient between the ratio of the respective
emissivities evaluated at a density
)
when the
respective line emissivities are evaluated in the low density limit
(cf. Fig. 7). This correction factor is,
basically, the quotient between the ratio of the respective
emissivities evaluated at a density ![]() and in the low density
limit. Over most of our parameter space (ie.
and in the low density
limit. Over most of our parameter space (ie. ![]()
![]() 3, cf. Fig. 5), Ne++/Ne+ and Ar++/Ar+ can be
considered in the low density
limit. The correction factor for S+3/S++ is not larger than 1.35.
N++/N+ can be overestimated by up to a factor of 3. However, the
strong dependence of N++/N+ on
3, cf. Fig. 5), Ne++/Ne+ and Ar++/Ar+ can be
considered in the low density
limit. The correction factor for S+3/S++ is not larger than 1.35.
N++/N+ can be overestimated by up to a factor of 3. However, the
strong dependence of N++/N+ on ![]() can be circumvented by the use
of the LWS [O III] densities, which characterize the ionic gas in the
same region where the nitrogen lines are produced.
can be circumvented by the use
of the LWS [O III] densities, which characterize the ionic gas in the
same region where the nitrogen lines are produced.
To derive the ionic abundances with respect to hydrogen, one needs the
H+ emission associated with the nebula. These can be derived from
a near-infrared H I recombination line, for instance Br![]() ,
which is detected in most of the sources, using
Eq. (10) as follows:
,
which is detected in most of the sources, using
Eq. (10) as follows:
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{h3072f7.ps} \end{figure}](/articles/aa/full/2002/02/aah3072/Timg100.gif) |
Figure 7:
The |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{h3072f8.ps} \end{figure}](/articles/aa/full/2002/02/aah3072/Timg101.gif) |
Figure 8:
The |
The H+ emission can also be derived from optically thin, radio
continuum observations. Combining Eqs. (9) and (11):
where
FX+i is in units of erg s-1 cm-2,
![]() in erg s-1 cm3,
in erg s-1 cm3, ![]() in K,
in K, ![]() in
GHz and
in
GHz and ![]() in Jy. The ratio of electrons to protons,
in Jy. The ratio of electrons to protons,
![]() ,
differs from unity because of the contribution of
singly ionized He to the total number of electrons. This can be
included by using
,
differs from unity because of the contribution of
singly ionized He to the total number of electrons. This can be
included by using
![]() .
As can be seen from
equation 12, this method shows a small
dependence on
.
As can be seen from
equation 12, this method shows a small
dependence on ![]() and the assumption of a single
and the assumption of a single ![]() = 7500 K gives
correction factors of the order of 15% at most.
= 7500 K gives
correction factors of the order of 15% at most.
The dependence on ![]() of the fine-structure emission coefficients
can also produce systematic uncertainties in the derived ionic
abundances with respect to H+. Figure 8
illustrates the case of the neon, argon and sulphur ionic abundances
(calculated using the lines [Ne II] 12.8, [Ne III] 15.5, [Ar II] 7.0,
[Ar III] 9.0, [S III] 18.7 and [S IV] 10.5
of the fine-structure emission coefficients
can also produce systematic uncertainties in the derived ionic
abundances with respect to H+. Figure 8
illustrates the case of the neon, argon and sulphur ionic abundances
(calculated using the lines [Ne II] 12.8, [Ne III] 15.5, [Ar II] 7.0,
[Ar III] 9.0, [S III] 18.7 and [S IV] 10.5
![]() )
and plots the
)
and plots the ![]() correction factor,
correction factor,
![]() ,
needed to apply
when the low density limit is assumed. This correction becomes larger
than 1 when
,
needed to apply
when the low density limit is assumed. This correction becomes larger
than 1 when ![]()
![]() .
For the neon and argon abundances,
this correction only becomes important for
.
For the neon and argon abundances,
this correction only becomes important for ![]() > 104 3. More
critical is the case of the sulphur abundances because of the lower
critical densities of the [S III] 18.7
> 104 3. More
critical is the case of the sulphur abundances because of the lower
critical densities of the [S III] 18.7
![]() (104 3) and [S IV] 10.5
(104 3) and [S IV] 10.5
![]() (
(
![]() 3) lines. At densities around 1043, the sulphur abundance will be underestimated by a factor of 2.
Even more dramatic, although not shown in
Fig. 8, is the case of N+/H+, N++/H+and O++/H+. As in the case of N++/N+, their strong
3) lines. At densities around 1043, the sulphur abundance will be underestimated by a factor of 2.
Even more dramatic, although not shown in
Fig. 8, is the case of N+/H+, N++/H+and O++/H+. As in the case of N++/N+, their strong ![]() dependence can be circumvented by the use of the LWS [O III] densities.
dependence can be circumvented by the use of the LWS [O III] densities.
The total abundance of a given element is calculated by adding the
contributions of the different ionic species of that element. However,
ionization correction factors (ICFs) must be applied when some of the
ionic species are not observed. The nebular abundances are then
determined by:
 |
(13) |
In order to evaluate in detail the dependence of the atomic
fine-structure line flux ratios of the H II regions on the physical
conditions (stellar and nebular properties), a set of photoionization
models based on the code NEBU (Morisset & Pequignot 1996) was
performed. For the stellar spectral energy distribution (SED), the
CoStar atmosphere models of Schaerer & de Koter (1997) were
used. These non-LTE stellar models include the effects of stellar wind
and line blanketing, important for massive stars. A total of 26
CoStar models are available with effective temperatures ranging from
22 to 55 kK and luminosities from
![]() to
to
![]() .
For each stellar atmosphere model, a
series of photoionization models was build for nebular densities of
.
For each stellar atmosphere model, a
series of photoionization models was build for nebular densities of
![]() ,
103,
,
103,
![]() ,
104,
,
104,
![]() and
105 3, which cover the density range probed by the atomic
fine-structure lines detected in the ISO spectra. The nebulae are
assumed to be spherically symmetric. The nebular abundances are solar
(Grevesse & Sauval 1998), the distance between the star and the
nebula is taken to be
and
105 3, which cover the density range probed by the atomic
fine-structure lines detected in the ISO spectra. The nebulae are
assumed to be spherically symmetric. The nebular abundances are solar
(Grevesse & Sauval 1998), the distance between the star and the
nebula is taken to be
![]() and the
filling factor of the gas is supposed to be unity. In total, 156
nebular models were calculated spanning a wide range in stellar
properties (one order of magnitude in luminosity) and nebular
densities (two orders of magnitude), corresponding to a range in the
ionization parameter of more than 3 orders of magnitude. This large
range in ionization parameter combined with the effective stellar
temperatures is likely to describe the physical conditions of the
sample of H II regions. Since the main results deal with the
predictions of line flux ratios, the distances to the objects are not
relevant. A detailed comparison of the predictions of such a model
with the ISO spectrum of the compact H II region IRAS 18434-0242
(G29.96-0.02) is given in Morisset et al. (2001) - hereafter
Paper III.
and the
filling factor of the gas is supposed to be unity. In total, 156
nebular models were calculated spanning a wide range in stellar
properties (one order of magnitude in luminosity) and nebular
densities (two orders of magnitude), corresponding to a range in the
ionization parameter of more than 3 orders of magnitude. This large
range in ionization parameter combined with the effective stellar
temperatures is likely to describe the physical conditions of the
sample of H II regions. Since the main results deal with the
predictions of line flux ratios, the distances to the objects are not
relevant. A detailed comparison of the predictions of such a model
with the ISO spectrum of the compact H II region IRAS 18434-0242
(G29.96-0.02) is given in Morisset et al. (2001) - hereafter
Paper III.
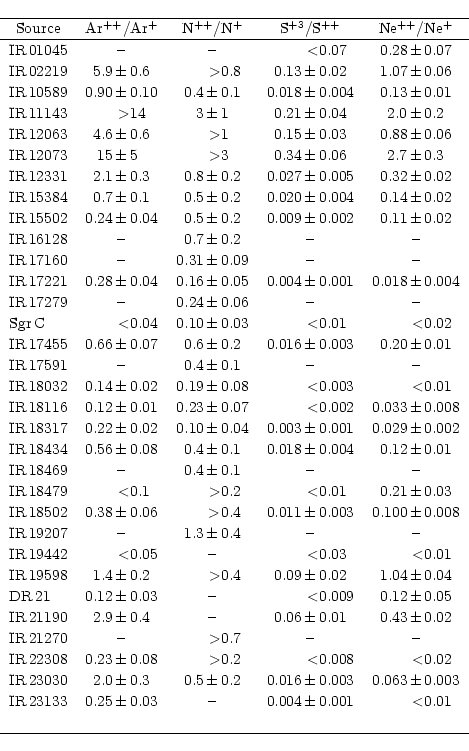
Any two successive stages of ionization i and i+1 of a
given element can be used as a measure of the state of ionization of
the nebula. The line ratios [Ar III]/[Ar II] 9.0/7.0, [N III]/[N II] 57.3/121.7, [S IV]/[S III] 10.5/18.7 and [Ne III]/[Ne II] 15.5/12.8
![]() can be used to determine (cf. equation 10) the
relative ionic abundance ratios Ar++/Ar+, N++/N+, S+3/S++ and
Ne++/Ne+, respectively. A single
can be used to determine (cf. equation 10) the
relative ionic abundance ratios Ar++/Ar+, N++/N+, S+3/S++ and
Ne++/Ne+, respectively. A single ![]() = 7500 K and the low density
limit (except for N++/N+, which was evaluated using the [O III] densities calculated in Sect. 4) are assumed in the
derivation. The results are presented in
Table 6, assuming no correction for beam
differences or for differential extinction. As mentioned in
Sect. 5, the low density limit is valid for Ne++/Ne+ and
Ar++/Ar+ over the range of the derived
= 7500 K and the low density
limit (except for N++/N+, which was evaluated using the [O III] densities calculated in Sect. 4) are assumed in the
derivation. The results are presented in
Table 6, assuming no correction for beam
differences or for differential extinction. As mentioned in
Sect. 5, the low density limit is valid for Ne++/Ne+ and
Ar++/Ar+ over the range of the derived ![]() ([O III]) and
([O III]) and
![]() (
(![]()
![]() 3), while S+3/S++ may be affected by up to a 35%
uncertainty. The errors listed in Table 6
stem from the direct propagation of the line flux uncertainties (the
N++/N+ analysis includes also the uncertainties in the [O III] density). [Ne III]/[Ne II] is not affected by calibration errors because the
lines involved in the ratio are measured in the same spectral band
(see Paper I), resulting in smaller errors.
3), while S+3/S++ may be affected by up to a 35%
uncertainty. The errors listed in Table 6
stem from the direct propagation of the line flux uncertainties (the
N++/N+ analysis includes also the uncertainties in the [O III] density). [Ne III]/[Ne II] is not affected by calibration errors because the
lines involved in the ratio are measured in the same spectral band
(see Paper I), resulting in smaller errors.
|
Successive stages of ionization X+i and X+i+1 of a given
element indicate the state of ionization of the nebula, which depends
only, in first approximation, on the ionization parameter, U, and
the hardness of the ionizing radiation (Vílchez & Pagel 1988):
where ![]() is the mean intensity of the radiation. Therefore, a
ratio
X+i+1/X+i is, to first order and for a given U,
proportional to the relative number of photons able to ionize
X+i, ie. above
is the mean intensity of the radiation. Therefore, a
ratio
X+i+1/X+i is, to first order and for a given U,
proportional to the relative number of photons able to ionize
X+i, ie. above
![]() ,
as compared to that of Lyman
continuum photons (above 13.6 eV). Hence, Ar++/Ar+, N++/N+, S+3/S++ and Ne++/Ne+ probe the hardness of the stellar radiation between
13.6 eV and 28, 30, 35 and 41 eV, respectively (see
Fig. 1).
,
as compared to that of Lyman
continuum photons (above 13.6 eV). Hence, Ar++/Ar+, N++/N+, S+3/S++ and Ne++/Ne+ probe the hardness of the stellar radiation between
13.6 eV and 28, 30, 35 and 41 eV, respectively (see
Fig. 1).
The behaviour of these "hardness'' indicators with galactocentric
distance (cf. Fig. 9) shows that the highest ionized
H II regions are located at the highest galactocentric
distances. Assuming no systematic variations of U with
![]() ,
Fig. 9 indicates, consequently, a hardening of the
radiation field towards large galactocentric distances.
,
Fig. 9 indicates, consequently, a hardening of the
radiation field towards large galactocentric distances.
A ratio
(Xi+1/X+i)/(Yi+1/Y+i) involving two different
elements X and Y measures to first order, according to
Eq. (14), the relative number of ionizing photons
in the respective ionizing continua (e.g. Vílchez & Pagel 1988),
ie. above
![]() and
and
![]() ,
respectively.
Figure 10 shows the correlations between the 4
"hardness'' indicators, i.e. log(Ar++/Ar+) vs. log(N++/N+),
log(N++/N+) vs. log(S+3/S++), log(S+3/S++) vs. log(Ne++/Ne+) and
log(Ne++/Ne+) vs. log(Ar++/Ar+). The arrows indicate the extinction
correction to be applied if the "standard'' extinction law (see
Sect. 3.1) is assumed. The extinction correction for the
neon and nitrogen line ratios is negligible. The dotted line in every
panel represents a straight line fit to the data and is a fairly good
representation of the data behaviour. The slopes obtained from a
least squares fit are very close to one:
,
respectively.
Figure 10 shows the correlations between the 4
"hardness'' indicators, i.e. log(Ar++/Ar+) vs. log(N++/N+),
log(N++/N+) vs. log(S+3/S++), log(S+3/S++) vs. log(Ne++/Ne+) and
log(Ne++/Ne+) vs. log(Ar++/Ar+). The arrows indicate the extinction
correction to be applied if the "standard'' extinction law (see
Sect. 3.1) is assumed. The extinction correction for the
neon and nitrogen line ratios is negligible. The dotted line in every
panel represents a straight line fit to the data and is a fairly good
representation of the data behaviour. The slopes obtained from a
least squares fit are very close to one:
![]() ,
,
![]() ,
,
![]() and
and ![]() ,
respectively for panels a, b, c and d. Because these ionic pairs probe the ionizing
energies up to 41 eV, Fig. 10 shows that the
hardening of the radiation field affects equally the full range of
the ionizing spectra.
,
respectively for panels a, b, c and d. Because these ionic pairs probe the ionizing
energies up to 41 eV, Fig. 10 shows that the
hardening of the radiation field affects equally the full range of
the ionizing spectra.
Photoionization models, however, show an additional dependence of
(X+i+1/X+i)/(Y+i+1/Y+i) on U (Stasinska & Schaerer 1997, Paper III)
rendering the interpretation more complex and
probably producing part of the scatter in Figs. 9
and 10. The set of photoionization models
described in Sect. 5.2 allows us to study the influence of the
ionization parameter U and the stellar effective temperature
![]() (ie. the shape of the ionizing spectrum) on the ionization state of
the gas, traced by any of the ratios
X+i+1/X+i, for instance
Ne++/Ne+. The variation of Ne++/Ne+ is shown as a function of
(ie. the shape of the ionizing spectrum) on the ionization state of
the gas, traced by any of the ratios
X+i+1/X+i, for instance
Ne++/Ne+. The variation of Ne++/Ne+ is shown as a function of
![]() in Fig. 11. For a given stellar atmosphere
model or
in Fig. 11. For a given stellar atmosphere
model or
![]() ,
this ratio decreases with increasing electron
density. The observed Ne++/Ne+ ranges from
,
this ratio decreases with increasing electron
density. The observed Ne++/Ne+ ranges from ![]() 0.01 to 3, a range
predicted by the models for values of
0.01 to 3, a range
predicted by the models for values of
![]() between 31 and 38 kK
(Fig. 11). Similar variations are predicted for the
other ionization ratios (N++/N+, Ar++/Ar+ and S+3/S++). Changing
U at a given
between 31 and 38 kK
(Fig. 11). Similar variations are predicted for the
other ionization ratios (N++/N+, Ar++/Ar+ and S+3/S++). Changing
U at a given
![]() (by changing the stellar luminosity and/or the
gas density) can change Ne++/Ne+ by a factor of 10 or more. An
estimate of the
(by changing the stellar luminosity and/or the
gas density) can change Ne++/Ne+ by a factor of 10 or more. An
estimate of the
![]() of the ionizing star is therefore only possible
if robust constraints on U are available. A detailed study of the
relations between the ionization diagnostics and the stellar
atmosphere models is postponed to a future paper (Morisset et al. in
prep.).
of the ionizing star is therefore only possible
if robust constraints on U are available. A detailed study of the
relations between the ionization diagnostics and the stellar
atmosphere models is postponed to a future paper (Morisset et al. in
prep.).
![\begin{figure}
\par\includegraphics[width=9cm]{h3072f10.ps} \end{figure}](/articles/aa/full/2002/02/aah3072/Timg123.gif) |
Figure 10:
Correlations between
the ionic abundance ratios
tracing the degree of ionization of the compact H II regions:
a) Ar++/Ar+ vs. N++/N+, b) N++/N+ vs. S+3/S++
c) S+3/S++ vs. Ne++/Ne+ and d) Ne++/Ne+ vs.
Ar++/Ar+. Upper/lower limits are indicated by short
arrows. The long arrows
indicate the direction of extinction correction. If using
the "standard'' extinction quoted in
Table 4, the extinction corrections to
apply are: a) 0.12 |
However, as tracers of the ionization state, the ionic abundance ratios X+i+1/X+i are sensitive indicators of the ionization correction factors. Figure 12 shows the ICFs for N, O, Ne, S and Ar derived from the grid of photoionization models as a function of Ne++/Ne+. The scatter in the calculated ionization correction factors is low, indicating that the use of the ionic abundance ratios X+i+1/X+i to constrain the ICFs is a robust method. In other words, even if U and the SED of the ionizing star are poorly known, the knowledge of the ionization state of the gas through the ionization ratios is enough to determine reliable ICFs. This conclusion does not strongly depend on the stellar atmosphere models as shown by comparing the results of a photoionization code using other atmosphere models (e.g. CMFGEN - Bourret, private communication).
The observed values of the ionization ratios can therefore be used to
correct the elemental abundances for the unseen ions. As shown in
Fig. 12, the effects are rather small, except for oxygen.
The effect on the Ne abundance is negligible. In the case of sulphur,
the abundance is always underestimated by typically ![]() 15%. For
high ionization conditions, the abundances of N and Ar can be
underestimated by up to 10 and 30%, respectively, because of the
missing N+3 and Ar+3. For O, only O++ is available and
thus, we are missing the low ionization state O+. The ICF for O is
very large, between 1.5 and 100.
15%. For
high ionization conditions, the abundances of N and Ar can be
underestimated by up to 10 and 30%, respectively, because of the
missing N+3 and Ar+3. For O, only O++ is available and
thus, we are missing the low ionization state O+. The ICF for O is
very large, between 1.5 and 100.
The N++/O++ abundance ratio is straightforward to derive from
equation 10 using the [N III] 57
![]() and [O III] 52+88
and [O III] 52+88
![]() line fluxes together with the densities derived from
the [O III] 88/52 line ratio (Table 5), which are well
adapted because both the N and O lines are emitted by low density
gas. All three lines are observed with LWS and consequently, beam
differences and differential extinction are negligible. Finally, the
use of both [O III] lines minimizes considerably the dependence of the
ionic abundance on
line fluxes together with the densities derived from
the [O III] 88/52 line ratio (Table 5), which are well
adapted because both the N and O lines are emitted by low density
gas. All three lines are observed with LWS and consequently, beam
differences and differential extinction are negligible. Finally, the
use of both [O III] lines minimizes considerably the dependence of the
ionic abundance on ![]() .
The resulting N++/O++ ionic abundance
ratios are listed in Table 7 (the quoted
uncertainties come from the error propagation of the line fluxes).
The ionic abundance ratio
.
The resulting N++/O++ ionic abundance
ratios are listed in Table 7 (the quoted
uncertainties come from the error propagation of the line fluxes).
The ionic abundance ratio
![]() is found to decrease
with galactocentric distance (Fig. 13).
is found to decrease
with galactocentric distance (Fig. 13).
| Source | N++/O++ | Source | N++/O++ | ||||
| IR02219 | 0.16 | 0.04 | IR18032 | 0.6 | 0.1 | ||
| IR10589 | 0.24 | 0.04 | IR18116 | 0.50 | 0.08 | ||
| IR11143 | 0.14 | 0.02 | IR18317 | 0.8 | 0.1 | ||
| IR12063 | 0.18 | 0.03 | IR18434 | 0.49 | 0.07 | ||
| IR12073 | 0.13 | 0.02 | IR18469 | 0.43 | 0.07 | ||
| IR12331 | 0.30 | 0.04 | IR18479 | 0.15 | 0.04 | ||
| IR15384 | 0.41 | 0.06 | IR18502 | 0.39 | 0.07 | ||
| IR15502 | 0.47 | 0.08 | IR19207 | 0.24 | 0.04 | ||
| IR16128 | 0.38 | 0.06 | IR19598 | 0.10 | 0.02 | ||
| IR17160 | 0.50 | 0.07 | DR21 | 0.21 | |||
| IR17221 | 0.7 | 0.1 | IR21190 | 0.33 | |||
| IR17279 | 0.7 | 0.1 | IR21270 | 0.17 | 0.03 | ||
| SgrC | 0.7 | 0.1 | IR21306 | 0.13 | |||
| IR17455 | 0.44 | 0.07 | IR22566 | 0.2 | 0.1 | ||
| IR17591 | 0.12 | 0.02 | IR23030 | 0.33 | 0.05 | ||
| IR18032 | 0.6 | 0.1 | |||||
The significance of N++/O++ and its dependence on
![]() has been
discussed in detail in previous studies (e.g. Rubin et al. 1988, and
references therein). N++/O++ is a function of both the ionization
state of the nebula (the ionization potentials of N+ and O+are 29.6 and 35.1 eV, respectively) as well as of abundance, and one
has to disentangle their effects to derive the N/O elemental
abundance ratio. Figure 14 presents the
correlation between N++/O++ and Ne++/Ne+ (note that the spectral
"hardness'' indicators are inter-correlated and thus, they all
correlate with N++/O++). As can be seen in
Figs. 13 and 14, N++/O++ is inversely proportional to the degree of ionization (ie. low
ionized nebulae have high N++/O++ ionic abundances) and this
dependence is connected to the location in the Galaxy (ie. nebulae
with high N++/O++ are preferentially located in the inner Galaxy).
For these inner nebulae, N+ and O+ are probably the
dominant ionic species over N++ and O++ and therefore, the
ionization correction needed to get N/O from N++/O++ could be
rather large (N++/O++ will be then overestimating N/O). In contrast,
N++/O++ must be close to N/O for the nebulae in the outer Galaxy.
has been
discussed in detail in previous studies (e.g. Rubin et al. 1988, and
references therein). N++/O++ is a function of both the ionization
state of the nebula (the ionization potentials of N+ and O+are 29.6 and 35.1 eV, respectively) as well as of abundance, and one
has to disentangle their effects to derive the N/O elemental
abundance ratio. Figure 14 presents the
correlation between N++/O++ and Ne++/Ne+ (note that the spectral
"hardness'' indicators are inter-correlated and thus, they all
correlate with N++/O++). As can be seen in
Figs. 13 and 14, N++/O++ is inversely proportional to the degree of ionization (ie. low
ionized nebulae have high N++/O++ ionic abundances) and this
dependence is connected to the location in the Galaxy (ie. nebulae
with high N++/O++ are preferentially located in the inner Galaxy).
For these inner nebulae, N+ and O+ are probably the
dominant ionic species over N++ and O++ and therefore, the
ionization correction needed to get N/O from N++/O++ could be
rather large (N++/O++ will be then overestimating N/O). In contrast,
N++/O++ must be close to N/O for the nebulae in the outer Galaxy.
The predictions of the photoionization models are useful to quantify the effects of ionization conditions on N++/O++. In particular, one can estimate the ionization correction factor which has to be applied by using one of the ionization diagnostic X+i+1/X+i. Based on the model results, an empirical method can be determined to derive the elemental abundance ratio N/O from the observed [N III] and [O III] line fluxes. The N/O abundance ratio can be expressed as follows:
where the first term on the right side is the ratio of the [N III] and
[O III] line fluxes, the second term is the ratio of the emissivities
of these lines (taking into account the density effect leading to
collisional de-excitation) and the third term is the ratio of the ICFs
which have to be applied to N and O. ![]() [O III] is the sum
of the two [O III] lines, ie. [O III] 52+88
[O III] is the sum
of the two [O III] lines, ie. [O III] 52+88
![]() .
.
The second and third member of the Eq. (15) can be
empirically determined by the use of appropriate observables and the
grid of models leading to the following relation:
where r[O III] is the ratio [O III] 88/52
![]() .
The density correction
via r[O III], which transforms [N III]/
.
The density correction
via r[O III], which transforms [N III]/![]() [O III]
into N++/O++, yields N++/O++ ratios on average 10% lower than the
N++/O++ derived from Eq. (10), mainly due to
slight differences between the atomic constants used in the code NEBU
and the ones used in this work.
[O III]
into N++/O++, yields N++/O++ ratios on average 10% lower than the
N++/O++ derived from Eq. (10), mainly due to
slight differences between the atomic constants used in the code NEBU
and the ones used in this work.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{h3072f13.ps} \end{figure}](/articles/aa/full/2002/02/aah3072/Timg130.gif) |
Figure 13:
Plot of the ionic abundance ratio N++/O++ versus
the galactocentric distance
|
The photoionization model predictions of these successive ratios are
shown in Fig. 15 as a function of degree of
ionization (as measured by the ionic abundance ratio Ne++/Ne+): the
line flux ratio [N III]/![]() [O III] (plus signs),
the ionic abundance ratio N++/O++ (diamonds) and the elemental
abundance ratio N/O after correcting for the density and the unseen
ions (stars). The dotted horizontal line indicates the input value of N/O of
the model, ie. the solar ratio of 0.123 (Grevesse & Sauval 1998).
As can be seen, when no ICF corrections are applied, the N++/O++ ratio overestimates the N/O abundance ratio for low ionization
conditions and slightly underestimates the N/O ratio for high
ionization conditions. Finally, the results for the N/O abundance
ratio after correcting for the density and the ICF dependence (stars
in Fig. 15) agree very well with the input solar
value of 0.123.
[O III] (plus signs),
the ionic abundance ratio N++/O++ (diamonds) and the elemental
abundance ratio N/O after correcting for the density and the unseen
ions (stars). The dotted horizontal line indicates the input value of N/O of
the model, ie. the solar ratio of 0.123 (Grevesse & Sauval 1998).
As can be seen, when no ICF corrections are applied, the N++/O++ ratio overestimates the N/O abundance ratio for low ionization
conditions and slightly underestimates the N/O ratio for high
ionization conditions. Finally, the results for the N/O abundance
ratio after correcting for the density and the ICF dependence (stars
in Fig. 15) agree very well with the input solar
value of 0.123.
Equation (16) provides a useful empirical law to derive
the N/O abundance ratio from the observed [O III], [N III] and neon line
fluxes. Any deviation from the solar N/O abundance after applying this
law to the observed [N III]/![]() [O III] indicates
intrinsic variations in the N/O abundance ratio. Similar empirical
laws can be derived for the [Ar III]/[Ar II] and [S IV]/[S III] ionization
diagnostics. However, we prefer the method based on the neon lines,
whose ratio is hardly affected by differential extinction and
aperture differences. Note that the [N III]/[N II] has an extra dependence
on density and is, therefore, less appropriate.
[O III] indicates
intrinsic variations in the N/O abundance ratio. Similar empirical
laws can be derived for the [Ar III]/[Ar II] and [S IV]/[S III] ionization
diagnostics. However, we prefer the method based on the neon lines,
whose ratio is hardly affected by differential extinction and
aperture differences. Note that the [N III]/[N II] has an extra dependence
on density and is, therefore, less appropriate.
Figure 16 shows the N/O abundance ratio as a function of
galactocentric distance after applying the corrections described above
by using the neon lines. Note that there are only 25 sources for which
the corrections could be applied. Whereas the slope of the variation
is not as steep as that for
![]() (see
Fig. 13), a gradient of N/O with galactocentric
distance is clearly present in the sense of a decreasing ratio with
(see
Fig. 13), a gradient of N/O with galactocentric
distance is clearly present in the sense of a decreasing ratio with
![]() :
:
![\begin{figure}
\par\includegraphics[width=8cm,clip]{h3072f16.ps} \end{figure}](/articles/aa/full/2002/02/aah3072/Timg133.gif) |
Figure 16:
Plot of the elemental abundance ratio
N/O versus galactocentric distance
|
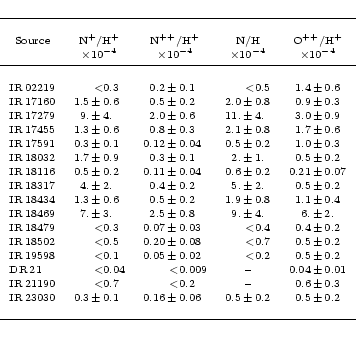
|
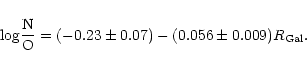 |
(17) |
Because of the large difference between the SWS and LWS apertures and
the fact that many sources are more extended than the SWS aperture,
the hydrogen line flux corresponding to the gas where the nitrogen
and oxygen lines are formed will be underestimated if a SWS H I recombination line is used. Thus, the resulting abundances of N and O
will be overestimated. Hence, the radio continuum measurements are
thought to be more appropriate to evaluate H+ and
Eq. (12) is used to calculate N+/H+,
N++/H+ and O++/H+ via the lines [N II] 122, [N III] 57 and [O III] 52+88
![]() .
The radio flux densities from
Table 2 are used and the sources which are more
extended than the LWS aperture (Sgr C, IR 19207, IR 21270 and
IR 22308) are excluded. [O III] densities
(cf. Table 5) are used to evaluate the line
emissivities involved.
.
The radio flux densities from
Table 2 are used and the sources which are more
extended than the LWS aperture (Sgr C, IR 19207, IR 21270 and
IR 22308) are excluded. [O III] densities
(cf. Table 5) are used to evaluate the line
emissivities involved.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{h3072f17.ps} \end{figure}](/articles/aa/full/2002/02/aah3072/Timg136.gif) |
Figure 17:
a) N/H and b) O++/H+ as a function of
|
For nitrogen, both ions N+ and N++ are
measured. Figure 9 shows that N+ is the dominant
species over N++ and therefore, N+3 is not expected to
contribute significantly to the total abundance of nitrogen. Indeed,
the grid of photoionization models (cf. Fig. 12) shows that
the contribution of N+3 for the highest ionized sources is only
at the 10% level. Hence, the total nitrogen abundance N/H is
calculated by adding the ionic abundances N+/H+ and
N++/H+. The calculated N+/H+, N++/H+and N/H are given in
Table 8. Figure 17a represents
N/H versus
![]() .
An attempt to fit a straight line was made, but no
statistically significant fit was possible because of the few
points and the large scatter. We note that sources in the inner 5 kpc
have supersolar nitrogen abundances, in agreement with determinations
using B stars (Smartt et al. e.g. 2001).
.
An attempt to fit a straight line was made, but no
statistically significant fit was possible because of the few
points and the large scatter. We note that sources in the inner 5 kpc
have supersolar nitrogen abundances, in agreement with determinations
using B stars (Smartt et al. e.g. 2001).
For oxygen, only O++ is available and thus, we are missing
O+. We have used the grid of photoionization models to estimate
the effect of the missing O+ abundance. These models show that the
ionization correction factor is very large, between 1.5 and 100
depending on the degree of ionization (cf. Fig. 12).
Therefore, the derived O++/H+ listed in
Table 8 can only be interpreted as a lower limit
for the total O/H abundance. Figure 17b plots
O++/H+ versus
![]() .
Clearly, the derived O++/H+abundances are much lower than the solar log(O/H)=-3.2 (Grevesse & Sauval 1998).
.
Clearly, the derived O++/H+abundances are much lower than the solar log(O/H)=-3.2 (Grevesse & Sauval 1998).
A note of caution must be brought concerning the nitrogen and oxygen
abundances. In most cases, the ISO [O III] 88/52
![]() line ratio give
densities which are far below those required to produce the
ultracompact H II emission observed at radio wavelengths (
line ratio give
densities which are far below those required to produce the
ultracompact H II emission observed at radio wavelengths (
![]() )
(see Fig. 5). This suggests that the
ultracompact H II regions are surrounded by a tenuous shell of
O++ (and probably also N++). If this is the case, both N and
O++ abundances will not be the true nebular abundances as the
H+ emission associated with the shell will not be the one given by
the radio observations.
)
(see Fig. 5). This suggests that the
ultracompact H II regions are surrounded by a tenuous shell of
O++ (and probably also N++). If this is the case, both N and
O++ abundances will not be the true nebular abundances as the
H+ emission associated with the shell will not be the one given by
the radio observations.
Despite the inherent uncertainty associated with the H I recombination line method concerning ![]() (cf. Sect. 5), we will use the Br
(cf. Sect. 5), we will use the Br![]() line fluxes
observed with ISO/SWS in analyzing all the SWS fine-structure lines of
neon, sulphur and argon because the beams are well matched. As the
lines of [Ne II] 12.8 and [Ne III] 15.5, [S III] 18.7 and [S IV] 10.5, and
[Ar II] 7.0 and [Ar III] 9.0, used to determine the abundances of neon,
sulphur and argon, respectively, are observed by a beam comparable to
Br
line fluxes
observed with ISO/SWS in analyzing all the SWS fine-structure lines of
neon, sulphur and argon because the beams are well matched. As the
lines of [Ne II] 12.8 and [Ne III] 15.5, [S III] 18.7 and [S IV] 10.5, and
[Ar II] 7.0 and [Ar III] 9.0, used to determine the abundances of neon,
sulphur and argon, respectively, are observed by a beam comparable to
Br![]() ,
the use of Eq. (11) is straightforward. The fine-structure lines
and H I recombination line emissivities involved in the calculation
were evaluated in the low density limit and considering a single
,
the use of Eq. (11) is straightforward. The fine-structure lines
and H I recombination line emissivities involved in the calculation
were evaluated in the low density limit and considering a single
![]() = 7500 K. The lines in the SWS band 4, [S III] 33.4 and [Ne III] 36.0
= 7500 K. The lines in the SWS band 4, [S III] 33.4 and [Ne III] 36.0
![]() ,
which are observed in a larger aperture and are affected
by large calibration uncertainties, are not included in the
determination (see discussion in Sect. 4).
,
which are observed in a larger aperture and are affected
by large calibration uncertainties, are not included in the
determination (see discussion in Sect. 4).
The absolute abundances for neon, sulphur and argon were calculated adding the contribution from the different ionization stages available:
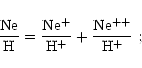 |
(18) |
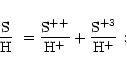 |
(19) |
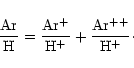 |
(20) |
Figure 18 shows Ne/H and Ar/H as a function of
![]() .
Clear
gradients with galactocentric distance can be observed for both
species. Linear least squares fits to the neon and argon abundances,
displayed as solid lines in Fig. 18, are:
.
Clear
gradients with galactocentric distance can be observed for both
species. Linear least squares fits to the neon and argon abundances,
displayed as solid lines in Fig. 18, are:
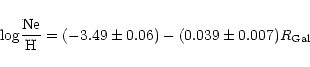 |
(21) |
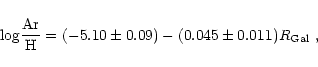 |
(22) |
with correlation coefficients r=-0.76 and -0.66, respectively.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{h3072f18.ps} \end{figure}](/articles/aa/full/2002/02/aah3072/Timg143.gif) |
Figure 18:
Total abundances of a) neon and b) argon as a
function of
|
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{h3072f19.ps} \end{figure}](/articles/aa/full/2002/02/aah3072/Timg144.gif) |
Figure 19:
S/H abundance as a function of
|
We note that an electron temperature gradient in the Galaxy may
systematically enlarge the above derived elemental abundance
gradients. Specifically, if we correct for a ![]() gradient given by
gradient given by
![]()
![]() (
(
![]() (kpc)/15), based on the
(kpc)/15), based on the ![]() gradients
derived by Shaver et al. (1983), Afflerbach et al. (1996) and Deharveng et al. (2000),
the slopes in the Ne/H and Ar/H gradients
become -0.06 and -0.07 dex kpc-1, respectively.
gradients
derived by Shaver et al. (1983), Afflerbach et al. (1996) and Deharveng et al. (2000),
the slopes in the Ne/H and Ar/H gradients
become -0.06 and -0.07 dex kpc-1, respectively.
While Ar/H and Ne/H are ![]() -dependent through the Br
-dependent through the Br![]() line
emissivity, the ratio Ar/Ne is practically insensitive to changes in
line
emissivity, the ratio Ar/Ne is practically insensitive to changes in
![]() .
An approximately constant Ar/Ne close to solar is found,
contrary to the tentative Ar/Ne galactic gradient derived from a
small sample of KAO observations (Simpson et al. 1995a).
.
An approximately constant Ar/Ne close to solar is found,
contrary to the tentative Ar/Ne galactic gradient derived from a
small sample of KAO observations (Simpson et al. 1995a).
S/H abundances are plotted in Fig. 19. No meaningful
Galactic gradient is seen for S/H and a very large dispersion is
found at any given
![]() ,
unlike the smaller dispersion in the Ar/H or
Ne/H Galactic abundances. The absolute abundances are also improbably
low compared to the solar and interstellar abundances - on average 2 times lower that the IS sulphur abundance by Snow & Witt (1996); a
factor of 5 for the extreme cases -, since sulphur is not expected to
be strongly depleted into grains. However, the quoted sulphur
abundances do not include the systematic uncertainties due to the
effect of electron temperature and density
(cf. Sect. 5). In view of the rms densities derived from
the radio observations (we note that the sources with the lower S/H
abundances also have very high
,
unlike the smaller dispersion in the Ar/H or
Ne/H Galactic abundances. The absolute abundances are also improbably
low compared to the solar and interstellar abundances - on average 2 times lower that the IS sulphur abundance by Snow & Witt (1996); a
factor of 5 for the extreme cases -, since sulphur is not expected to
be strongly depleted into grains. However, the quoted sulphur
abundances do not include the systematic uncertainties due to the
effect of electron temperature and density
(cf. Sect. 5). In view of the rms densities derived from
the radio observations (we note that the sources with the lower S/H
abundances also have very high
![]() > 104 3) and the
> 104 3) and the ![]() gradient in the Galaxy, we estimate that the S abundances are
underestimated by up to a factor 4.
gradient in the Galaxy, we estimate that the S abundances are
underestimated by up to a factor 4.
Figure 20 compares the gradient slopes derived for
N/O, Ne/H and Ar/H with previous determinations using H II regions -
optical (Shaver et al. 1983), IRAS (Simpson & Rubin 1990), KAO (Simpson et al. 1995b) -,
disk planetary nebulae of type II (Maciel & Quireza 1999) and B stars
(Smartt et al. 2001).
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{h3072f20.ps} \end{figure}](/articles/aa/full/2002/02/aah3072/Timg146.gif) |
Figure 20:
Comparison of the derived gradient slopes for N/O,
Ne/H and Ar/H with previous determinations using H II regions - optical (Shaver et al. 1983), IRAS (Simpson & Rubin 1990),
KAO (Simpson et al. 1995b) -, disk planetary nebulae of type II
(Maciel & Quireza 1999) and B stars (Smartt et al. 2001).
The open stars indicate the slopes obtained
when a Galactic |
Good agreement is found for N/O and Ar/H. Our Ne/H gradient matches
the one found from planetary nebula, but is flatter than the previous
infrared determinations using IRAS and KAO. Both IRAS and KAO
determinations agree, however. We note that both relied on radio data
to derive the abundances and therefore, did not suffer much from the
systematic electron temperature uncertainty, while our gradients have
been probably depressed because of the assumption of a single
![]() = 7500 K. Indeed, if we correct our derived Ne/H gradient from the
= 7500 K. Indeed, if we correct our derived Ne/H gradient from the ![]() gradient in the Galaxy (the open stars in
Fig. 20), then we are in reasonable agreement with
both IRAS and KAO.
gradient in the Galaxy (the open stars in
Fig. 20), then we are in reasonable agreement with
both IRAS and KAO.
|
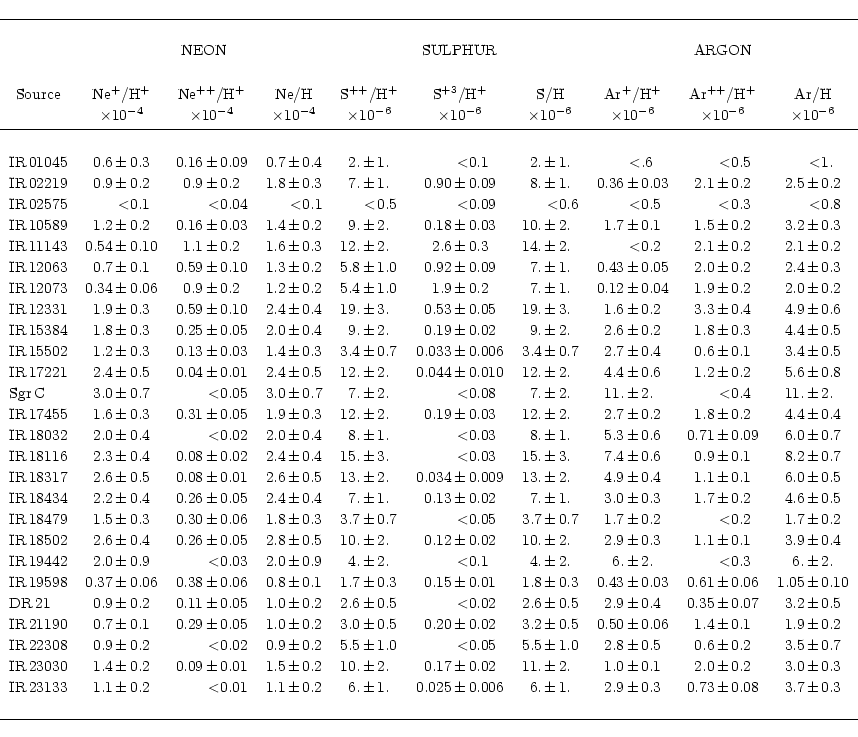
|
Based on the ISO spectral catalogue of compact H II regions by Peeters et al. (2002), a first analysis of the hydrogen recombination and atomic fine-structure lines originated in the ionized gas has been presented. The main results of this study are:
The complete infrared spectra from 2.3 to 196
![]() provided by the
ISO catalogue of galactic H II regions (Peeters et al. 2002)
has allowed us to study the ionizing conditions in these
sources and derive relative and absolute elemental abundances across
the Galactic disk. The first analysis presented in this paper has
shown that useful conclusions can be drawn from these data. However,
there are still open issues and to improve on the present results
additional information is required. In particular, the detailed
knowledge of the extent and relative spatial distributions of the
fine-structure atomic lines is lacking for almost all the compact
H II regions.
The knowledge of the electron temperature is also
critical in refining the elemental abundances. Observations of radio
recombinations lines will be helpful to estimate
provided by the
ISO catalogue of galactic H II regions (Peeters et al. 2002)
has allowed us to study the ionizing conditions in these
sources and derive relative and absolute elemental abundances across
the Galactic disk. The first analysis presented in this paper has
shown that useful conclusions can be drawn from these data. However,
there are still open issues and to improve on the present results
additional information is required. In particular, the detailed
knowledge of the extent and relative spatial distributions of the
fine-structure atomic lines is lacking for almost all the compact
H II regions.
The knowledge of the electron temperature is also
critical in refining the elemental abundances. Observations of radio
recombinations lines will be helpful to estimate ![]() for all the
sources discussed in this paper and to correct for the
for all the
sources discussed in this paper and to correct for the ![]() dependence.
dependence.