A&A 381, 428-439 (2002)
DOI: 10.1051/0004-6361:20011523

The Double Quasar HE 1104-1805: A case study for time delay determination with poorly sampled lightcurves

R. Gil-Merino - L. Wisotzki - J. Wambsganss

Universität Potsdam, Am Neuen Palais 10, 14469 Potsdam, Germany

Received 27 July 2001 / Accepted 25 October 2001

Abstract
We present a new determination of the time delay of the gravitational lens system HE 1104-1805 ("Double Hamburger'') based on a previously unpublished dataset. We argue that the previously published value of $\Delta t_{{\rm A}-{\rm B}}=0.73$ years was affected by a bias of the employed method. We determine a new value of $\Delta t_{{\rm A}-{\rm B}}=0.85\pm0.05$ years (2$\sigma$ confidence level), using six different techniques based on non interpolation methods in the time domain. The result demonstrates that even in the case of poorly sampled lightcurves, useful information can be obtained with regard to the time delay. The error estimates were calculated through Monte Carlo simulations. With two already existing models for the lens and using its recently determined redshift, we infer a range of values of the Hubble parameter: $H_0=48\pm4~{\rm km}~{\rm s}^{-1}~{\rm Mpc}^{-1}$ (2$\sigma$) for a singular isothermal ellipsoid (SIE) and $H_0=62\pm4~{\rm km}~{\rm s}^{-1}~{\rm Mpc}^{-1}$ (2$\sigma$) for a constant mass-to-light ratio plus shear model ( $M/L+\gamma$). The possibly much larger errors due to systematic uncertainties in modeling the lens potential are not included in this error estimate.

Key words: gravitational lensing - time delays - quasars: HE 1104-1805 - general: data analysis


1 Introduction

The double quasar HE 1104-1805 at a redshift of $z_{\rm Q} = 2.319$ was originally discovered by Wisotzki et al. (1993). The two images with (original) B magnitudes of 16.70 and 18.64 are separated by $3\hbox{$.\!\!^{\prime\prime}$ }195$ (Kochanek et al. 1998). The spectral line ratios and profiles turned out to be almost identical between the two images, but image A has a distinctly harder continuum. Wisotzki et al. (1995) report about a dimming of both components over about 20 months, accompanied by a softening of the continuum slope of both images. The lensing galaxy was discovered by Courbin et al. (1998) in the NIR and by Remy et al. (1998) with HST. The authors tentatively identified the lensing galaxy with a previously detected damped Lyman alpha system at z=1.66 (Wisotzki et al. 1993; Smette et al. 1995; Lopez et al. 1999). This identification, however, was disputed by Wisotzki et al. (1998). Using FORS2 at the VLT, Lidman et al. (2000) finally determined the redshift of the lensing galaxy to $z_{\rm G} = 0.729\pm0.001$.

A first determination of the time delay in this system was published by Wisotzki et al. (1998), based on five years of spectrophotometric monitoring of HE 1104-1805, in which the quasar images varied significantly, while the emission line fluxes appear to have remained constant. The Wisotzki et al. (1998) value for the time delay was $\Delta t_{{\rm A}-{\rm B}}=0.73$ years (no formal error bars were reported), but they cautioned that a value as small as 0.3 years could not be excluded.

HE 1104-1805 shows strong and clear indications of gravitational microlensing, in particular based on the continuum variability with the line fluxes almost unaffected (Wisotzki et al. 1993; Courbin et al. 2000).

Here we present an analysis of previously unpublished photometric monitoring data of HE 1104-1805. First the data and light curves are presented (Sect. 2), then a number of numerically techniques are described and discussed and, as the scope of this paper is a comparison of different techniques in the case of poorly sampled data, we finally applied to this data set, in order to determine the time delay (Sect. 3). A discussion of the results and the implications for the value of the Hubble constant based on this new value of the time delay and on previously avalaible lens models are given in Sect. 4. In Sect. 5 we present our conclusions.

2 Data acquisition and reduction

Between 1993 and 1998, we obtained a B band lightcurve of HE 1104-1805 at 19 independent epochs, mostly in the course of a monitoring campaign conducted at the ESO 3.6 m telescope in service mode. The main intention of the programme was to follow the spectral variations by means of relative spectrophotometry, but at each occasion also at least one frame in the B band was taken. A continuum lightcurve, derived from the spectrophotometry, and a first estimate of the time delay were presented by Wisotzki et al. (1998, hereafter W98); details of the monitoring will be given in a forthcoming paper (Wisotzki & López, in preparation). Here we concentrate on the broad band photometric data which have not been published to date. Images were taken typically once a month during the visibility period. The instrument used was EFOSC1 with 512$\times$512 pixels Tektronix CCD until June 1997, and EFOSC2 with a 2K$\times$2K Loral/Lesser chip afterwards. The B band frames (which were also used as acquisition images for the spectroscopy) were always exposed for 30 s, which ensured that also the main comparison stars were unsaturated at the best recorded seeing of $1\hbox{$^{\prime\prime}$ }$. Sometimes more than one exposure was made, enabling us to make independent estimates of the photometric uncertainties. A journal of the observations is presented together with the measured lightcurve in Table 1.

 

 
Table 1: B band lightcurve data for HE 1104-1805. The first measurement of component A has arbitrarily been set to zero. The error estimates include shot noise, PSF fitting uncertainties, and also standard deviations in case of multiple images at a given epoch.

Epoch [yrs]		 $\Delta B_{\rm A}$ $\sigma_{B_{\rm A}}$ $\Delta B_{\rm B}$ $\sigma_{B_{\rm B}}$

1993.19		 0.000 0.009 1.920 0.022
1994.82 0.397 0.009 2.282 0.019
1995.16 0.529 0.008 2.236 0.028
1995.96 0.399 0.012 2.140 0.014
1996.11 0.436 0.008 2.207 0.017
1996.23 0.454 0.005 2.176 0.013
1996.30 0.486 0.009 2.171 0.023
1996.45 0.500 0.008 2.115 0.019
1996.88 0.383 0.007 2.074 0.012
1997.04 0.389 0.007 2.054 0.016
1997.12 0.533 0.009 2.031 0.013
1997.21 0.428 0.016 2.007 0.015
1997.27 0.392 0.007 2.055 0.012
1997.33 0.403 0.008 2.089 0.014
1998.00 0.252 0.017 2.029 0.018
1998.08 0.279 0.004 2.006 0.011
1998.16 0.292 0.004 2.004 0.011
1998.33 0.531 0.006 2.100 0.011
1998.40 0.441 0.007 2.054 0.030


The CCD frames were reduced in a homogeneous way following standard procedures. After debiasing and flatfielding, photometry of all sources in the field was conducted using the DAOPHOT II package (Stetson et al. 1987) as implemented into ESO-MIDAS. The instrumental magnitudes of the QSO components and reference stars 1-5 (following the nomenclature of Wisotzki et al. 1995) were recorded and placed on a homogeneous relative magnitude scale defined by the variance-weighted averages over all comparison stars. In Fig. 1 we show the resulting QSO lightcurves, together with the two brightest comparison stars.
  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H3051F1.ps} \end{figure} Figure 1: The new photometric dataset running from 1993 to 1998. The zero point for the relative photometry of HE 1104-1805 is the first data point of component A (see Table 1 for error estimates).
Open with DEXTER

The variability of both QSO components is highly significant, including strong fluctuations on the barely sampled timescales of months. This behaviour is stronger in component A, while component B leads the variability. The error estimates include shot noise, PSF fitting uncertainties and standard deviations in case of multiple images at a given epoch. Note the similarity of these B band data with the completely independently calibrated continuum lightcurves of W98.

3 Time delay determination

3.1 Dispersion spectra method

A first estimation for the time delay in this system resulted in a value of $\Delta t_{{\rm B}-{\rm A}}=-0.73$ years (W98), using the dispersion spectra method developed by Pelt et al. (1994, 1996; hereafter P94 and P96, respectly). Note that we will express the time delay as $\Delta t_{{\rm B}-{\rm A}}$ (instead of $\Delta t_{{\rm A}-{\rm B}}$), since B leads the variability (see Fig. 1), and thus there appears a minus sign in the result. We shall demonstrate below that the dispersion spectra method is not bias-free. To facility a better understanding of this claim, we first briefly describe the method in the following: the two time series Ai and Bj can be expressed, using the P96 notation, as

    $\displaystyle A_i=q(t_i)+\epsilon_{\rm A}(t_i), i=1,...,N_{\rm A}$ (1)
    $\displaystyle B_j=q(t_j-\tau)+l(t_j)+\epsilon_{\rm B}(t_j), j=1,...,N_{\rm B}$ (2)

q(t) being the intrinsic variability of the quasar, $\tau$ the time delay and l(t) the magnification ratio plus another possible noise component (this could be pure noise or microlensing). Both lightcurves Ai and Bj are combined into a new one, Ck, for each value of the pair $(\tau, l(t))$, ``correcting'' Bj serie by l(t) in magnitudes and by $\tau$ in time

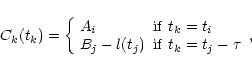\begin{displaymath}C_k(t_k)=\left \{\begin{array}{ll} A_i & {\rm if}\ t_k=t_i \\ B_j-l(t_j) & {\rm if}\ t_k=t_j-\tau \end{array} \right., \end{displaymath} (3)

with k=1,...,N and $N=N_{\rm A}+N_{\rm B}$. Then the dispersion spectrum is calculated analytically by the expression

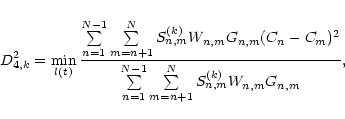\begin{displaymath}D^2_{4,k}=\min_{l(t)}\frac{\sum\limits^{N-1}_{n=1}\sum\limits... ...{N-1}_{n=1} \sum\limits^N_{m=n+1}S^{(k)}_{n,m}W_{n,m}G_{n,m}}, \end{displaymath} (4)

where Wn,m are the statistical weights; Gn,m=1 if the points Cn and Cm come from different time series, Ai or Bj, and is 0 otherwise; and S(k)n,m is a function that weights each difference (Cn-Cm) depending on the distance between the points. In P96 they show three possible definitions for this function, here we have selected

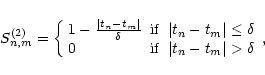\begin{displaymath}S^{(2)}_{n,m}=\left \{\begin{array}{ll} 1-\frac{\left\vert t... ... \left\vert t_n-t_m\right\vert > \delta \end{array} \right., \end{displaymath} (5)

which includes those pairs for which the distance between two observations is less than a certain decorrelation length $\delta$. More details can be found in P94 and P96. The definition of this function here is slightly different from the one used in W98. We have two reasons to do so: first, we will demonstrate that the selection of one or another definition does not play a crucial role in this case; second, the function S(3)n,m used in W98 is supposed to avoid the problem of having big gaps between the observational points in the lightcurves, but we will try to solve this problem in a different way.

The new dataset used here has the same sampling as the one used for the first estimation of the time delay in W98. As the errorbars for individual points are also very similar, one should expect to obtain a similar time delay. And in fact this is exactly what happens when applying the dispersion spectra method as described above. The original dataset is plotted in Fig. 1. There are 19 observational points for each component. We apply the dispersion spectra method (P94, P96): the result is $\Delta t_{{\rm B}-{\rm A}}=-0.73$ years, i.e., the same value as the first published estimation.

Since W98 did not provide a formal error estimate, we now investigate the goodness of this value and try to estimate the uncertainty, and we also want to check the self-consistency of the method in this case. For this purpose we do a test based on an iterative procedure: after having applied the dispersion spectra method to the whole data set, we make a selection of the data trying to avoid big gaps between the epochs and considering points in both lightcurves that fall in the same time interval once one has corrected the time shift with the derived time delay. This will avoid the so-called border effects, and a time delay close to the initial one should result when the dispersion spectra are recalculated for the selected data. We do this in the next subsection.

   
3.2 Borders and gaps

We first consider $\Delta t_{{\rm B}-{\rm A}}=-0.73$ years as a first rough estimate of the time delay, in agreement with W98. It is obvious that using this time delay, the first point of the whole dataset (epoch 1993.19) of component B has no close partner in component A. Eliminating this point means avoiding the big gap of almost two years at the beginning of the lightcurves. Once this is done, the last five points of the lightcurve B and the first two ones of A (after eliminating the epoch 1993.19) are not useful anymore for a time delay determination since they do not cover the same intrinsic time interval. We also eliminate these points. Now we have a "clean'' dataset with 16 points from component A and 13 points from component B. The situation is illustrated in Fig. 2,

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H3051F2.ps} \end{figure} Figure 2: The first point of the whole dataset has been removed and then the points that do not fall in the same time interval once we have shifted the A lightcurve with the value of the first time delay estimation, $\Delta t_{{\rm B}-{\rm A}}=-0.73$ years. Thus component A has now 16 points and the component B 13 points. If the procedure were self-consistent and the first time delay estimation right, we would naturaly expect a confirmation of this value in a second measurement of the delay by using the new dataset.
Open with DEXTER

where only the epochs inside the time interval [1994.5, 1998.0] are plotted. This is the time interval for which the two lightcurves overlap after the -0.73 years correction for component A.

Now we again apply the dispersion spectra method to the "clean'' data set, i.e. a second iteration is made. The result is surprising: $\Delta t_{{\rm B}-{\rm A}}=-0.38$ years. The technique should converge to a value near to that of the first result, if the previous estimation was correct and the technique is self-consistent. For consistency, we repeat this analysis assuming a time delay of -0.38 years, i.e., a third iteration. The result is again unexpected: we recover the previous value of -0.73 years. These results can be seen in Fig. 3,

  \begin{figure} \par\includegraphics[angle=-90,width=8.8cm,clip]{H3051F3_upper.ps... ...m] \includegraphics[angle=-90,width=8.8cm,clip]{H3051F3_bottom.ps} \end{figure} Figure 3: Dispersion spectra: the upper panel shows the result when all the points are taken into account. In the middle panel, the result after correcting borders with the first estimation of the time delay, i.e. $\Delta t_{{\rm B}-{\rm A}}=-0.73$ years. In the bottom panel we use a correction of -0.38 years obtained in the middle panel. We recover the previous value for the time delay of $\Delta t_{{\rm B}-{\rm A}}=-0.73$ years, showing the inconsistency of the method. In each subfigure, two curves are plotted for two different values of the decorrelation length: solid for $\delta _1=0.3$ years and broken for $\delta _2=0.4$ years.
Open with DEXTER

upper panel (dispersion with all points), middle panel (borders and gap corrected around 1 year) and bottom panel (borders and gap corrected around half a year) where the minimum of the function gives the time delay. The solid and broken lines in each figure correspond to two slightly different decorrelation lengths ( $\delta _1=0.3$ years, $\delta _2=0.4$ years).

This clearly means that the method is not self-consistent when applying it to the current data set. The dispersion spectra method is very sensitive to individual points, and in poorly sampled sets such as this one, these points are critical. It is obvious that we need better techniques for the determination of the time delay. But these techniques must not be interpolating ones because the lightcurves have lots of variability and wide gaps, and any simple interpolation scheme might introduce spurious signals.

3.3 Techniques based on the discrete correlation function (DCF)

3.3.1 Reasons for "clean'' datasets

Many authors have applied different versions of the DCF since it was introduced by Edelson & Krolik (1988, hereafter EK88). Here we have selected five of them. These techniques take into account the global behavior of the curves, rather than "critical points''. But in order to well apply all these methods one has to eliminate border effects and gaps as described previously. If one does not do this, one will lose signal in the peak of the DCF and secondary peaks could appear, which can bias the final result. We will demonstrate this last point later (Fig. 7, described in Sect. 3.3.4, is used for this purpose).

   
3.3.2 Standard DCF plus a parabolic fit

First we apply the usual form of the DCF to the data set. We briefly recall the expression, following EK88:

 \begin{displaymath} DCF(\tau)=\frac{1}{M}\sum_{ij}\frac{(a_i-\bar{a})(b_j-\bar{b})}{\sqrt{ (\sigma^2_a-\epsilon^2_a)(\sigma^2_b-\epsilon^2_b)}}, \end{displaymath} (6)

where M is the number of data pairs (aj, bj) in the bin associated with the lag $\tau$, $\epsilon_x$ the measurement error, $\sigma_x$ the standard deviation and $\bar{x}$ the mean of x. It gives the cross correlation between both components at lag $\tau$ by considering bins that include all pairs of points (aj, bj) verifying $\tau-\alpha\leq(t_j-t_i)<\tau+\alpha$, where $\alpha $ is the bin semisize. In DCF-based techniques, one always needs to find a compromise between the bin size and the error for each bin: increasing the former decreases the latter, but resolution with respect to $\tau$ is lost. The result of applying this procedure to the HE 1104-1805 data is a function with a few points and without a prominent feature around the peak, because of our sparse sampling. The position of the peak gives the time delay: $\Delta t_{{\rm B}-{\rm A}}=-0.91$ years.

A modification of this method was suggested by Lehár et al. (1992). A parabolic fit to the peak of the function was proposed to solve the problem of not resolving the peak. Doing this fit, we obtain a time delay of $\Delta t_{{\rm B}-{\rm A}}=-0.89$ years. These results are shown in Fig. 4.

  \begin{figure} \par\includegraphics[angle=-90,width=8.8cm,clip]{H3051F4.ps} \end{figure} Figure 4: The standard DCF and an added fit are shown in this figure. The peak is located at -0.89 years (-0.91 without fit) using a bin semisize 0.07 years. The continuous lines are the noise levels and the zero level is also plotted. Only two points defining the peak are outside the noise band.
Open with DEXTER

The noise level is computed as $\sqrt{M}$, M being the number of pairs in each bin. The problem in this case is that the peak of the function is defined with only two points above the noise level. We used a bin semisize of $\alpha=0.07$ years. Increasing the bin semisize to $\alpha =0.14$ years the result is not better in the sense that the peak is defined by only one point, and the fit does not modify the location of this peak. The obtained value for the time delay in this case ( $\alpha =0.14$ years) is $\Delta t_{{\rm B}-{\rm A}}=-0.84$ years.

3.3.3 Locally normalized discrete correlation function (LNDCF): Averaging in each bin

The locally normalized discrete correlation function was also proposed by Lehár et al. (1992). Its main difference to the simple DCF is that it computes the means and variances locally (i.e. in each bin):

 \begin{displaymath} LNDCF(\tau)=\frac{1}{M}\sum_{ij}\frac{(a_i-\bar{a}_\ast)(b_j... ..._\ast}-\epsilon^2_a)(\sigma^2_{b_\ast}-\epsilon^2_b)]^{1/2)}}, \end{displaymath} (7)

computing the sum over all pairs where $\tau-\alpha\leq(t_j-t_i)<\tau+\alpha$. The mean, $\bar{x}_\ast$, and the standard deviation, $\sigma^2_{a_\ast}$, are calculated for each bin. Again a parabolic fit is needed for a more accurate value of the peak, which then gives the time delay. For the same reasons as in Sect. 3.3.2 we choose a bin semisize $\alpha=0.07$ years. The result is shown in Fig. 5.
  \begin{figure} \par\includegraphics[angle=-90,width=8.6cm,clip]{H3051F5.ps} \end{figure} Figure 5: The LNDCF is evaluated with a 0.07 years bin semisize and the peak is fitted with a parabolic law. The result is a time delay $\Delta t_{{\rm B}-{\rm A}}=-0.87$ years (-0.91 years without the fit). A secondary peak appears at -0.35 years, although with larger error bars. This peak was the feature that "confused" the dispersion spectra.
Open with DEXTER

As in the case of the standard DCF, the peak is just defined by two points. The obtained time delay in this case is $\Delta t_{{\rm B}-{\rm A}}=-0.87$ years (the value without the fit is -0.91 years). Furthermore, a secondary competing peak appears at -0.35 years, with more points, although these points have larger errorbars. This is an interesting aspect, because it was this secondary peak which "confused'' the dispersion spectra technique and it may suggest a close relation between these two techniques (both favour "local'' behaviour of the signals, rather than "global'' ones). We will investigate this possible relation in a future, more general paper.

In any case, the poorly defined peak means the technique is again quite sensitive to our poor sampling. We look for a method less sensitive to this problem. The two following techniques are two different ways of trying to solve the problem of not having many points around the prominent peak.

   
3.3.4 Continuously evaluated discrete correlation function (CEDCF): Overlapping bins in the DCF

The continuously evaluated bins discrete correlation function was introduced by Goicoechea et al. (1998a). The difference to the standard way of computing the DCF in this method is that the bins are non disjoint (i.e. each bin ovelaps with other adjacent bins, see Sect. 3.3.2 where the bins do not overlap each other). One has to fix the distance between the centers of the bins in addition to their width. In this way it is possible to evaluate the DCF in more points, having a more continuously distributed curve. We will have also more significant points around the peak, i.e. above the noise level, and there is no need for fitting.

Selecting the distance between the centers of the bins is again a matter of compromise: increasing the distance means needing wider bins and, thus, losing resolution. The adopted time resolution should depend on the sampling; it seems reasonable to select a value slightly less then the inverse of the highest frequency of sampling ( $1/f\simeq0.1$ years). We choose 0.05 years as the best value for the distance between bin centers and two values for bin semisizes: $\alpha =0.14$ and $\alpha =0.21$ years. The overlapping between bins allows us to consider slightly wider bin sizes. We plot the results in Fig. 6,

  \begin{figure} \par\includegraphics[angle=-90,width=8.8cm,clip]{H3051F6_top.ps}\... ...m] \includegraphics[angle=-90,width=8.8cm,clip]{H3051F6_bottom.ps} \end{figure} Figure 6: The CEDCF is a DCF more continuously evaluated. Top panel: using a bin semize of $\alpha =0.14$ years we obtain a peak at -0.85 years with a good signal-to-noise ratio equal to 3.9. Bottom panel: with a bin semisize equal to $\alpha =0.21$ years, the peak is at -0.80 years. Although it seems that the function is better defined, i.e. with more points, the signal-to-noise ratio at the peak is 3.8. The continuous lines are the noise levels in both panels (cf. also Fig. 7).
Open with DEXTER

upper and lower panel, respectively. The continuous lines are the noise levels. The $\alpha =0.14$ years semisize shows a peak at -0.85 years, whereas with the $\alpha =0.21$ years semisize the peak is at -0.80 years.

Now we need a good reason for preferring one over the other bin size. This reason could be the signal-to-noise ratio of the peak: in the first case $\alpha =0.14$ years, S/N = 3.9, and in the second $\alpha =0.21$ yrs, S/N=3.8. Clearly, the difference of these two values is not high enough to conclude that one of them is the best.

In spite of the insignificant difference in this case, we notice that the signal-to-noise ratio is an important aspect and it is here where we justify the need for using "clean'' data sets, i.e. border effects and gaps corrected. In Fig. 7 we plot the CEDCF for the original dataset (without any correction):

  \begin{figure} \par\includegraphics[angle=-90,width=8.8cm,clip]{H3051F7.ps} \end{figure} Figure 7: Not eliminating borders can be crucial in DCF-based methods. Here the CEDCF has been computed with the original data set, i.e. using all points. There is a peak at -0.90 years, with a signal-to-noise value of 1.95. Other points around a secondary peak located at time zero describe another feature. The great amount of information lost in the main peak is obvious.
Open with DEXTER

the peak is located at -0.90 years, but the signal-to-noise is 1.95! The main peak loses signal recovered by a secondary competing peak around lag zero and by the wings. Although this secondary peak is very unlikely to be the delay peak, Fig. 7 cannot solve this ambiguity, which demonstrate that border effects can be dramatic in some cases. In Sect. 3.4 we will discuss the criteria to select a particular bin size.

   
3.3.5 Continously evaluated bins and locally normalized discrete correlation function (CELNDCF): Overlapping bins in the LNDCF

To our knowledge, this technique has not been applied before, but it seems a natural step as a combination of the two former techniques (i.e., the LNDCF and the CEDCF). From the one side, we use Eq. (7) for computing the DCF, i.e., it is a locally normalized discrete correlation function. From the other side, we use the idea of overlapping bins described in Sect. 3.3.4. Thus, the final result is a "continuously evaluated bins and locally normalized discrete correlation function'' (CELNDCF). Again, we fix the distances between the bins and also their width. The result will be a function similar in shape to the LNDCF in Fig. 5 but with more points evaluated.

The method was applied for three different values of the bin semisize: 0.07, 0.14 and 0.21 years. The first value is not a good choice, it gives relatively large errorbars for the points of the CELNDCF, since the number of points per bin is low. Selecting the last two values, i.e. $\alpha =0.14$ yrs and $\alpha =0.21$ yrs, we obtain Fig. 8.

  \begin{figure} \par\includegraphics[angle=-90,width=8.6cm,clip]{H3051F8_top.ps} \includegraphics[angle=-90,width=8.6cm,clip]{H3051F8_bottom.ps} \end{figure} Figure 8: Top panel: the CELNDCF is evaluated with $\alpha =0.14$ years bin semisize and a distance between bin centers of 0.05 years. The result is a time delay $\Delta t_{{\rm B}-{\rm A}}=-0.85$ years. Bottom panel: the CELNDCF computed with $\alpha =0.21$ years bin semisize. The distances between the bin centers is also 0.05 years. The peak is obtained at -0.75 years where it is assumed to be the time delay.
Open with DEXTER

The first one gives a time delay of $\Delta t_{{\rm B}-{\rm A}}=-0.85$ years and the second one a value of $\Delta t_{{\rm B}-{\rm A}}=-0.75$ years. This second result is very close to the first estimation in W98. The reader can easily compare the results with and without overlapping bins (Figs. 8 and 5, respectively) and clearly see the advantages of this second procedure. Nevertheless, there is a relatively large difference between selecting one or the other value of the bin semisize (i.e. $\alpha =0.14$ years vs. $\alpha =0.21$ years). This means the technique is also very sensitive to the poor sampling. The next and final technique will clarify which is the best bin size selection.

   
3.4 The $\delta ^{2}$ technique: A comparison between the cross correlation function and the autocorrelation function

The following method, called $\delta ^{2}$, was introduced by Goicoechea et al. (1998b) and Serra-Ricart et al. (1999). Its expression is

\begin{displaymath}\delta^2(\theta)=\frac{1}{N}\sum^N_{i=1}S_i[DCC(\tau_i)-DAC(\tau_i-\theta)]^2 \end{displaymath} (8)

where Si=1 if $DCC(\tau)$ and $DAC(\tau_i-\theta)$ are both defined and Si=0 otherwise. The DCC is the continuously evaluated discrete correlation function, and the DAC is the discrete autocorrelation function. The method uses the DCC and the DAC of one of the components, and tries to get the best match between them by minimizing its difference. If one has two equal signals, these functions must be identical. The $\delta ^{2}$ function reaches its minimum $\theta_0=\Delta t_{{\rm B}-{\rm A}}$ at the time delay. We note that the match of both functions is not a match between their peaks, but rather a global match.

We have selected component B for computing the DAC, because component A has more variability (presumably due to microlensing). We compute $\delta ^{2}$ for different values of the bin semisize. Adopting a bin semisize $\alpha =0.14$, the function shows some features and reaches its minimum at -0.85 years (see Fig. 9, solid line).

  \begin{figure} \par\includegraphics[width=8.6cm,clip]{H3051F9.ps} \end{figure} Figure 9: The $\delta ^{2}$ function for three different values of the bin semisize $\alpha $: solid line 0.14 years, short dashed 0.21 years and long dashed 0.28 years. Since $\delta^2_{\min}(\alpha=0.28) <\delta^2_{\min}(\alpha=0.21)<\delta^2_{\min}(\alpha=0.14)$, the features in $\delta ^{2}$ for $\alpha =0.14$ years is unlikely to be an artifact (see text for more details).
Open with DEXTER

Now we compute $\delta ^{2}$ for a bin semisize $\alpha =0.21$ years, which yields a minimum at -0.90 years (Fig. 9, long dashed line). The question now is: are we loosing resolution using this last bin semisize ( $\alpha =0.21$ years) or is this minimum at -0.90 years a better estimate? The reader could argue that $\delta^2_{\min}(\alpha=0.21)<\delta^2_{\min}(\alpha=0.14)$, so that the agreement between DAC and DCC is better for $\alpha =0.21$. This is not so. Consider a bin semisize $\alpha =0.28$ years (Fig. 9, short dashed line): we obtain a minimum at -0.85 years while again $\delta^2_{\min}(\alpha=0.28)<\delta^2_{\min}(\alpha=0.21)$. This indicates that the minimum located at -0.85 years with $\alpha =0.14$ years was not an artifact of some noise features, but that these features are real. To clarify this, Fig. 10 shows the comparison between the DCC and DAC function for the three different values of the bin semisize $\alpha $ (0.14, 0.21 and 0.28 years in the upper panel, middle panel and bottom panel, respectively).
  \begin{figure} \par\includegraphics[angle=-90,width=8.8cm,clip]{H3051F10_upper.p... ...] \includegraphics[angle=-90,width=8.8cm,clip]{H3051F10_bottom.ps} \end{figure} Figure 10: Upper panel: both DCC (filled circles) and DAC (open circles) are plotted. The bin semisize is $\alpha =0.14$ years and the DAC has been shifted by -0.85 years, which is the value for the time delay obtained with the $\delta ^{2}$ technique. Middle panel: the bin semisize is now $\alpha =0.21$ years. DAC (open circles) has now been shifted by -0.80 years, which is the value obtained with the $\delta ^{2}$ technique. The bin semisize is now $\alpha =0.21$ years. Bottom panel: for $\alpha =0.28$, $\delta^2_{\min}=-0.85$ again, so the DCC (filled circles) is shifted by that value. In the three subfigures the solid lines indicate the noise levels. The best agreement between DCC and DAC is for $\alpha =0.14$ years (upper pannel).
Open with DEXTER

Accordingly, we consider the $\alpha =0.14$ years the best bin semisize and we analyse $\delta ^{2}$ for that value.

In order to better study the features in the $\delta ^{2}$ function, we plot it normalized to its minimum in Fig. 11.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H3051F11.ps} \end{figure} Figure 11: The minimum of the $\delta ^{2}$ function gives the time delay between the components. We have normalized it with its minimum. A secondary peak is present around -0.55, a value also considered by W98. The trend of the main feature is asymmetric, favoring values in the range [-0.9, -0.7], including several best estimates of the time delay from other techniques or binning.
Open with DEXTER

This figure is quite illustrative: (i) the minimum is reached at -0.85 years. (ii) the trend of the main feature is asymmetric, with a relatively slow rise at the right hand side, favoring values in the range [-0.9, -0.7], including most of the estimates from other techniques or binning. (iii) a "secondary minimum'' is present at -0.55years. This may be due to the fact remarked already by W98: for such a lag, the observing periods of one component coincides with the seasonal gaps in the lightcurve of the other. (iv) the feature in the range [-0.3, -0.4] is not present, meanning that this value is very unlikely (this was the value that appeared with dispersion spectra, LNDCF and CELNDCF methods).

To obtain an estimate for the formal error of this method, we used 1000 Monte Carlo simulations. For each simulation we did the following: for each epoch ti we associated a value in magnitudes $x_{i}+\Delta x_{i}$, where xi is the observed value and $\Delta x_{i}$ is a Gaussian random variable with zero mean and variance equal to the estimated measurement error. The histogram is presented in Fig. 12.

  \begin{figure} \par\includegraphics[angle=-90,width=8.8cm,clip]{H3051F12.ps} \end{figure} Figure 12: Histogram of time delays obtained in 1000 Monte Carlo simulations, using the $\delta ^{2}$ technique.
Open with DEXTER

As it can be seen, the simulations reproduce all the information contained in the $\delta ^{2}$ function in Fig. 11: the most probable value is -0.85 years (599 simulations); it also appears in a number of simulations around -0.90 years (57 simulations), -0.80 years (285 simulations), -0.75 years (5 simulations) and around -0.70 years (20 simulations). A few simulations (36) are also located around -0.55 years, which is very close to the one considered in W98 as spurious (a value around half a year). In any case, the simulations are in very good agreement with the information contained in the $\delta ^{2}$ function. As 95% of the simulations claim a time delay in the interval [-0.90, -0.80], we can adopt a value of $\Delta t_{{\rm B}-{\rm A}}=-0.85 \pm 0.05$ for the time delay of this system, with a 2$\sigma$ confidence level (formal or internal error). Figure 13 shows the lightcurves with component A shifted the adopted time delay.
  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H3051F13.ps} \end{figure} Figure 13: The original dataset with the component A shifted by the new adopted time delay, $\Delta t_{{\rm B}-{\rm A}}=-0.85$ years.
Open with DEXTER

4 Discussion

4.1 Comparison of the different techniques

From the tour through the different techniques we can learn several useful things. First of all, when only one technique is selected for deriving a time delay between two signals, it is important to check the internal consistency of the method and its behaviour with a given data set. We have demonstrated in Sect. 3.2 that dispersion spectra does not pass this test at least in this case (see Fig. 3). We have then applied and discussed the discrete correlation function and several of its modifications. The standard DCF (Fig. 4) had problems to properly define the peak in the case of very poorly sampled lightcurves; although a fit was proposed to solve this problem, there were only two points above the noise level in the best case and the fit was not very plausible. The LNDCF (Fig. 5), based on locally normalized bins, had a similar behaviour and although the error bars of each point are smaller, the peak is not well defined either. The CEDCF (Fig. 6) and the CELNDCF (Fig. 8) worked better under these circunstances, but we found the problem of selecting the bin size; in the case of the CEDCF the difference between the two selected bin sizes was smaller than in the case of the CELNDCF. Finally applying the $\delta ^{2}$ technique, we found a good reason for selecting one bin size: the match between the DAC and the DCC. The resulting estimate and its uncertainty include, as a "byproduct'', the results of the rest of the techniques for the same bin size (except the dispersion spectra method which was not self-consistent). This fact is not the same as computing all the techniques and doing some statistics to obtain an uncertainty. This frequently appears in the time delay determination literature, although it is not at all clear which was the weight of each technique when computing the final result. We note that for consistency we should apply a correction to the original data set with the final adopted time delay of -0.85 years. Due to the (very) sparse sampling of our data set, this correction gives a reduced data set identical to the previous "clean'' data set obtained with a correction of -0.73 years, so we do not need to repeat the whole process. The procedure is self-consistent.

It is important to notice that we have not meant to establish any general hierarchy between all these techniques. The hierarchy is valid in our particular case study. Nevertheless, the idea, not new, of correcting border effects in the signals with first estimations has been proved to be a good procedure in DCF based techniques.

4.2 Investigation of secondary minima/maxima

In some of the techniques we have discussed and applied here for the data of HE 1104-1805, there appear secondary peaks/dips located at different values for the time lags (see Figs. 5, 8 and 11). Here we investigate two obvious effects that might cause such behaviour, namely microlensing and sampling. We do this only as a case study for the $\delta ^{2}$ technique, but assume that our conclusions can be generalized to the other methods as well.

4.2.1 Microlensing

Microlensing affects the two quasar lightcurves differently. That means that the two lightcurves will not be identical copies of each other (modulo offsets in magnitude and time), but there can be minor or major deviations between them. On the other hand, experience from other multiple quasar systems tells us that microlensing cannot dominate the variability, because otherwise there would be no way to determine a time delay at all. In any case, microlensing is a possible source of "noise'' with respect to the determination of the time delay.

A complete analysis of microlensing on this system is beyond the scope of this article, and will be addressed in a forthcoming paper. Here we present a simple, but illustrative, approach to the way microlensing can effect the determination of the time delay, and in particular its effect on the $\delta ^{2}$ technique. An "extreme'' view of microlensing was investigated by Falco et al. (1991), who showed for the Q0957+561 system that it is very unlikely that microlensing can mimic "parallel'' intrinsic fluctuations causing completely wrong values for the time delay correlations. But strong microlensing clearly affects the features of the cross-correlation function (Goicoechea et al. 1998a). Depending on the exact amplitude and shape of the microlensing event, the main and secondary peaks of this function can be distorted, possibly inducing wrong interpretations.

In order to study this effect here, we do the following: we consider the lightcurve of component B (assumed to reflect only intrinsic quasar variability) and a copy of it, shifted by 0.85 years, which we shall call B'. Obviously, any technique will give a time delay value of $\Delta t_{{\rm B}-{\rm B}'}=-0.85$ years between B and B'. In the case of the $\delta ^{2}$ technique, a very sharp minimum is located at this lag. Now we introduce artificial "microlensing'' as a kind of Gaussian random process with zero mean and a certain standard deviation $\sigma_{\rm ML}$ to the lightcurve B'. We consider three cases: $\sigma_{\rm ML} = 0.050$ mag, 0.075 mag and 0.100 mag. Although microlensing is in general obviously not a random process (it depends a bit on the sampling), we use this simple approximation in order to study whether and how secondary peaks can appear in time delay determinations. The resulting $\delta ^{2}$-functions can be seen in Fig. 14,

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H3051F14.ps} \end{figure} Figure 14: We calculate the time delay between the lightcurves B and B' with the $\delta ^{2}$ technique. B' is a copy of B, shifted 0.85 years and with a Gaussian random process added. Thin solid line: the Gaussian random process has a standard deviation of 0.05 mag. There are no secondary peaks. Dashed line: if the standard deviation of the Gaussian random process is 0.075 mag, some secondary features appear. Thick solid line: the $\delta ^{2}$ normalized function is much more distorted, but the technique can calculate the shifted value of 0.85 years.
Open with DEXTER

which can be compared to Fig. 11. It is very obvious that for the "smallest'' microlensing contribution ( $\sigma_{\rm ML} = 0.050$ mag, thin solid line) the minimum of the $\delta ^{2}$ normalized function is still a very sharp feature. For the next case ( $\sigma_{\rm ML} = 0.075$ mag, dashed line) the $\delta ^{2}$ function gets wider and "noisier'', and for the strongest influence of microlensing ( $\sigma_{\rm ML} = 0.1$ mag, thick solid line) a secondary features appears. But in no case the distortion prohibits a clear and correct time delay determination, the primary minimum is still clearly identifiable (as will be demonstrated by Wisotzki & López 2001, in preparation, microlensing fluctuations during the period covered by our monitoring are of the order of 0.07 mag rms).

To make sure that this is not a chance observational effect of this particular selected lag, we repeat this exercise for an assumed shift of -0.5 years between the observed lightcurve and its shifted copy, plus added "artificial microlensing'' with $\sigma_{\rm ML} = 0.1$ mag. Again, the correct value is clearly recovered in all realisations. This is particularly convincing because a lag of 0.5 years is the "worst case scenario'' with minimal overlap between the two lightcurves. To summarize, moderate microlensing can be a cause of distortions of the time delay determination function, but it is unlikely that microlensing dominates it completely.

4.2.2 Sampling

In order to study the effect of sampling on the shape of the $\delta ^{2}$ function, we proceed as follows: again, we consider the lightcurve of component B and an identical copy of it shifted by 0.85 years, lightcurve B'. Now we remove some points from lightcurve B'. Resulting $\delta ^{2}$ functions are shown in Fig. 15 for three cases.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H3051F15.ps} \end{figure} Figure 15: We analyse the sampling effect in the $\delta ^{2}$ technique. We use lightcurves B and B', being B' a copy of B shifted 0.85 years and removing a number of points. Thin solid line: we remove 2 random points in the component B'. Dashed line: when removing 4 random points, it appears secondary structure in the $\delta ^{2}$ function. Thick solid line: if 3 selected points are remove, the $\delta ^{2}$ normalized function is very similar to the one computed with lightcurves A and B (see Fig. 11).
Open with DEXTER

The thin solid line is a case in which 2 random points have been removed from B. The minimum of the $\delta ^{2}$ normalized function is still well defined, with no secondary structure. For the dashed curve in Fig. 15, 4 random points were taken away. The shape of the function is distorted and a secondary dip appears. For the thick solid line, 3 adjacent hand-picked points (epochs 1997.12, 1997.21, 1997.27) were excluded. Surprisingly, although all the remaining data points have identical spacing in B' as in B, the removal of the 3 points causes a secondary minimum in the $\delta ^{2}$ function, which is very similar to the one obtained for the real data, using the observed lightcurves A and B (Fig. 11). This case is very illustrative: it suggest that the sampling alone could be responsible for the secondary minimum found in the real data (Fig. 11). This effect certainly deserves more study. From this preliminary analysis it appears that better and denser sampling of quasar lightcurves could be much more important for time delay studies than fewer data points with higher photometric precision.

As above, we also want to check whether the particular value of the time lag plays an important role, and we again repeat the simulation exercise with an assumed lag of -0.5 years, and 4 randomly selected points removed. The result is again $\Delta t_{{\rm B}-{\rm B}'} = -0.5$ years, recovering the assumed lag in all cases.

4.2.3 Summary of microlensing/sampling effects

Summarizing, we can state that both microlensing and sampling differences affect the shape of the time delay determination function. However, moderate microlensing will have only small effects on these curves, whereas moderate (and unavoidable!) differences in the sampling for the two lightcurves can easily introduce effects like secondary minima. The primary minimum of the $\delta ^{2}$ method in all cases considered was still clearly representing the actual value of the time delay. Applied to HE 1104-1805, this means that most likely microlensing does not affect much the time delay determination, the features in the time delay determination function can be easily explained by the sampling differences, and the primary minimum appears to be a good representation of the real time delay.

4.3 Implications for H0 determination

If one wants to use the time delay to estimate the Hubble parameter H0, one needs to know the geometry and mass distribution of the system. Accurate astrometry is available from HST images presented by Lehár et al. (2000). There are also several models for the lens in the literature. In W98, two models are described: a singular isothermal sphere with external shear and a singular isothermal ellipsoid without external shear. The first model is similar to Remy et al. (1998) and Lehár et al. (2000). Courbin et al. 2000 also present two models: a singular ellipsoid without external shear and a singular isothermal ellipsoid plus an extended component representing a galaxy cluster centered on the lens galaxy.

The redshift of the lens in this system has been establish by Lidman et al. (2000) to be $z_{\rm d}=0.729$. Note that HE 1104-1805 is somehow atypical, in the sense that the brightest component is closer to the lens galaxy. We use the most recents models by the CASTLES group (Lehár et al. 2000), described by a singular isothermal ellipsoid (SIE) and a constant mass-to-light ratio plus shear model ( $M/L+\gamma$). The derived value for the Hubble constant using the first model (SIE) is $H_0=48\pm4~{\rm km}~{\rm s}^{-1}~{\rm Mpc}^{-1}$ with $2\sigma$ confidence level. A ( $M/L+\gamma$) model gives $H_0=62\pm4~{\rm km}~{\rm s}^{-1}~{\rm Mpc}^{-1}$ ($2\sigma$), both for $\Omega_0=1$. The formal uncertainty in these values are very low, due to the low formal uncertainties both in the time delay estimation and in the models. Nevertheless, the mass distribution is not well constrained, since a sequence of models can fit the images positions (Zhao & Pronk 2000). We note that other models in Lehár et al. (2000) will give very different results for H0, but we did not use them because no error estimate was reported for them. Moreover, the angular separation is big enough to expect an additional contribution to the potential from a group or cluster of galaxies (Muñoz 2001, priv. comm.).

5 Conclusions

We have shown that the existing data allow us to constrain the time delay of HE 1104-1805 with high confidence between 0.8 and 0.9 years, slightly higher than the one available previous estimate. We have demonstrated that the six different techniques employed in this study were not equally suited for the available dataset. In fact, this case study has demonstrated that a very careful analysis of each technique is needed when applying it to a certain set of observations. Such an analysis becomes even more important in the case of poorly sample lightcurves. In this sense, the $\delta ^{2}$ technique showed the best behaviour against the poor sampling: unless the lack of information due to sampling is so severe that it prevents the determination of a well defined DAC and DCC, the minimum of the $\delta ^{2}$ function will be a robust estimator for the time delay.

Our improved time delay estimate yields a value of the Hubble parameter which now depends mostly on the uncertainties of the mass model. The degeneracies inherent to a simple 2-image lens system such as HE 1104-1805 currently preclude to derive very tight limits on H0. We note, however, that there are prospects to improve the constraints on the model e.g. by using the lensed arclet features visible from the QSO host galaxy. Even now, there seems to be a remarkable trend in favour of a relatively low value of H0, consistent with other recent lensing-based estimates (Schechter 2000).

Acknowledgements

We are especially grateful to Dr. L. J. Goicoechea (Universidad de Cantabria, Spain) for indicating us the best way of applying the $\delta ^{2}$ technique and for many comments to a first version of this paper. We also thank Dr. L. Tenorio (MINES, USA) for his useful comments on Monte Carlo and bootstrap simulations and Dr. J. A. Muñoz (IAC, Spain) for enlightening our understanding of lens modeling.

References

 

Copyright ESO 2002