A&A 381, 694-702 (2002)
DOI: 10.1051/0004-6361:20011556

First detection of the impulsive and extended phases of a solar radio burst above 200 GHz

G. Trottet 1 - J.-P. Raulin 2 - P. Kaufmann 2 - M. Siarkowski 3 - K.-L. Klein 1 - D. E. Gary 4


1 - DASOP, CNRS-UMR 8645, Observatoire de Paris, Section de Meudon, 92195 Meudon, France
2 - CRAAE/CRAAM, Instituto Presbiteriano Mackenzie, Rua da Consolação 896, 01302-907 São Paulo, Brazil
3 - Space Research Center, Polish Academy of Sciences, ul. Kopernika 11, 51-622 Wroclaw, Poland
4 - NJIT, Center for Solar Research, 323 M L King Blvd., Newark, NJ 07102, USA

Received 20 September 2001 / Accepted 24 October 2001

Abstract
We present a detailed analysis of radio observations obtained at 212 and 405 GHz during the 2000 March 22 H$\alpha$ 2N flare that occured in AR8910 at $\sim$1834 UT. These data are compared with microwave, soft X-ray and hard X-ray measurements of this flare. While the flare emission is not clearly detected at 405 GHz, the time profile of the 212 GHz emission exhibits an impulsive burst, associated in time with the 1-18 GHz impulsive microwave burst and a long-lasting thermal burst which finishes at about the same time as the soft X-ray emission but reaches its maximum later. The 212 GHz impulsive emission and the lack of detection at 405 GHz are consistent with synchrotron radiation from a population of ultrarelativistic electrons in an average magnetic field of 400-600 G. This radiating population of electrons has a hard energy spectrum (power law index $\approx$2.7). The expected >1 MeV gamma-ray continuum emission from the radio emitting electrons is comparable to that detected for mid-size electron-dominated events and the hard X-ray flux they would produce at 100 keV is consistently lower than the upper limit inferred from the observations. It is shown that the 212 GHz thermal source has to be different from that radiating the soft X-ray and microwave thermal emission. The present observations of a solar burst provide the first evidence of the extension of the gyrosynchrotron spectrum of an impulsive radio burst in the synchrotron domain above 200 GHz.

Key words: Sun: activity - flares - particle emission - radio radiation


1 Introduction

Solar flares are fundamentally high energy phenomena (Ramaty & Mandzhavidze 1993) that produce highly accelerated electrons and ions which contain a large fraction, if not most, of the released energy. The understanding of particle acceleration is thus a key issue to establish the physics of flares. While the knowledge of the low energy electron and ion distribution functions is a basic ingredient to study the flare energetics, the characteristics (energy spectrum, upper energy cut-off, ...) of the most energetic particles provide among the strongest constraints to acceleration models. The most direct diagnostics of high energy electrons are: (i) the high energy ( $\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle ...1 MeV) gamma-ray (GR) continuum from e-p and e-e bremsstrahlung (e.g. Chupp 1984; Rieger et al. 1998) and (ii) the radio emission from gyrosynchrotron radiation in coronal magnetic field structures (see Pick et al. 1990; Bastian et al. 1998 and references therein). High energy GR continua of electronic origin have been detected for a few tens of flares. In particular the observations show that: (i) for some flares the >1 MeV GR continuum from electron bremsstrahlung shows a high energy rollover in the 50-60 MeV energy range (Rieger & Marschhäuser 1990; Trottet et al. 1998) while, for other events, there is no rollover up to 100 MeV (the upper energy limit of solar dedicated instruments) and even up to $\sim$300 MeV (Vilmer et al. 1994, 1999; Leikov et al. 1993) and (ii) the spectrum of >0.5-1 MeV GR-producing electrons is harder than that of lower energy hard X-ray (HXR) producing electrons (e.g. Vestrand 1988; Rieger et al. 1998; Trottet et al. 1998; Vilmer et al. 1999). However, due to the sensitivity of GR detectors, high energy GR observations have only been obtained for large flares. The radio emission in the centimeter-millimeter domain provides of more sensitive diagnostics which, in principle allow us to investigate if electron acceleration up to relativistic energies also occurs in weak flares. Short millimeter wave observations obtained at 86 GHz have indeed revealed that energetic electrons with hard spectra, like those of GR-producing electrons, may be accelerated in weak flares that would not produce detectable GR emission (e.g. Kundu et al. 1994). Nevertheless, at 86 GHz, the characteristic energy of radiating electrons is of the order of a few MeV for magnetic fiels of a few 100 G (e.g. Dulk 1985; Ramaty et al. 1994). Radio observations at higher frequencies are thus needed to probe higher energy electrons. This is achieved by the Solar Sub-millimeter Telescope (SST) installed at the El Leoncito Astronomical Complex in the argentinean Andes which started solar observations at 212 and 405 GHz mid-1999 (Kaufmann et al. 2000a). First SST observations of a solar flare that occured on 2000 March 22 at $\sim$1834 UT have been described in Kaufmann et al. (2001). This study emphasizes the detection of numerous 100-300 ms duration spikes at both observing frequencies but did not provide clear evidence that the time evolution of 212 and 405 GHz emission exhibits a counterpart to the gyrosynchrotron microwave burst observed up to 18 GHz.

In this paper we show that the time evolution of the 212 GHz radio emission detected by SST during the 2000 March 22 flare exhibits a short ($\sim$3 min) impulsive burst which is the short-millimeter counterpart of the impulsive microwave burst, followed by a long-lasting ($\sim$60 min) thermal emission. Both components are below the noise level at 405 Ghz. These findings are discussed in Sect. 3 and a summary of the main results is given in Sect. 4.

2 Observations and data analysis


 \begin{figure} \par\includegraphics[clip, width=10cm]{fig1_ms1925.eps} \end{figure} Figure 1: From top to bottom, time evolution of: the 1.5-12 keV soft X-ray flux observed by GOES, the 15-30 keV and 120-240 keV hard X-ray emission observed by RF15-I on Interball, the 15.4 GHz radio flux density measured by RSTN and the 212 GHz flux density detected by SST. The data gap in the 212 GHz time profile is due to calibration
Open with DEXTER

The 2000 March 22 H$\alpha$ 2N (GOES X1.1) flare occurred in active region NOAA 8910 (N14 W57) at $\sim$1834 UT. The present multi-wavelength study of this flare combines mm and sub-mm radio observations with microwave and X-ray measurements. Figure 1 displays the time evolution of these different emissions from 1820 UT to 2000 UT.

The soft X-ray emission (SXR) in the 1.5-12 keV and 3-24 keV energy bands was obtained by GOES with a time resolution of 3 s. Assuming an iso-thermal source, these data allow us to estimate the temporal evolution of the temperature T and emission measure EM of the hot flare plasma as a function of time by using the method given in Thomas et al. (1985). The results are discussed in Sect. 3.2.

The hard X-ray (HXR) data were obtained by the RF15-I soft/hard X-ray photometer aboard the Interball Tail Probe satellite (Sylvester et al. 2000; Siarkowski et al. 1999). HXR measurements are performed by a NaI (T1) sintillator in five energy channels in the 10-240 keV energy range. Figure 1 shows the time evolution of the 15-30 keV and 120-240 keV count rates (1 s averaged) obtained after dead time and counter wrapping corrections (Sylvester et al. 2000). Due to the high flux of low energy HXR photons all channels are strongly affected by pile-up during the whole observation period. After $\sim$1844 UT, around the maximum of the 15.4 GHz and 212 GHz burst (see Fig. 1), pile-up, effects are so strong that they dominate the count rates shown in Fig. 1. Thus: (i) the time evolution of the measured 120-240 keV HXR rate (the less affected by pile up) is not the actual one and (ii) the data cannot be used for spectral analysis. However we consider that before $\sim$1844 UT the HXR rates in the 60-120 keV and 120-240 keV channels provide an upper limit of the actual rates. Therefore an upper limit $\Phi^{\rm max}_{100}$ of the 100 keV photon flux can be estimated by normalizing the 120-240 keV count rate expected from an incident photon energy spectrum, taken as a power law of index $\gamma$, to the observed count rate. Moreover, because pile-up effects are expected to be less important at higher energies, the actual value of the photon spectral index is expected to be lower than that obtained from the two highest energy channels. Thus around 1844 UT (maximum of the microwave and 212 GHz impulsive burst), it is found that $\gamma$ $\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle ... 5.4 and that $\Phi^{\rm max}_{100}$ ranges from 3 to 13 photons cm-2s-1keV-1 for $\gamma$ ranging from 1.5 to 5.4.

Microwave total flux measurements were obtained by the Owens Valley Solar Array (OVSA) in the frequency range 1.2-18 GHz, and with the Radio Solar Telescope Network (RSTN) in the frequency range 1.4-15.4 GHz, with time resolutions of 10 s and 1 s respectively. The time evolution of the 15.4 GHz flux density from RSTN is shown in Fig. 1. In the following this frequency will be used for timing considerations whereas the spectrum of the radio emission will be taken from OVSA observations.

The SST provides observations at 212 and 405 GHz with a time resolution of 1 ms. The multiple-receiver focal array produces 6 beams (1-4 at 212 GHz and 5-6 at 405 GHz), allowing us to estimate the burst location (Giménez de Castro et al. 1999). During the 2000 March 22 flare observations, the projection on the sky of beam 5 is centered on and tracks AR 8910, while those of beams 2-4 vary with time but always cover the active region, and those of beams 1 and 6 are away from AR 8910 (see Fig. 1 in Kaufmann et al. 2001). The half power beamwidths were 7.5 $\hbox{$^\prime$ }$ for beams 2, 3, 4, 5 and 10 $\hbox{$^\prime$ }$ for beams 1 and 6. In order to, as much as possible, get rid of non-solar temporal variations (due to e.g. atmospheric opacity, a hot calibration source within the receiver system), the signal S1 from beam 1 (away from AR 8910) has been subtracted from the signal S3 of beam 3 (always on the solar disk). This difference is referred to as S31 in the following. This procedure also removes the contribution of the quiet Sun which, at a given frequency, is expected to be similar in the different beams. Thus S31 will represent the actual signal from an optically thin source but will underestimate the signal from an optically thick source. In addition, the smooth decrease of S3-S1 due to the progressive entry of beam 1 onto the solar disk during the flare observation has been removed from S31(t). S31 has been calibrated by setting S31 = 0 for sky observations. Because beams 2 and 4 projected partly onto the sky, it was not possible to derive S21 and S41 in a similar way to S31.

The flux density F212 (in units of 10-22 Wm-2Hz-1 = 1 sfu), which is displayed in Fig. 1, is related to S31 by:

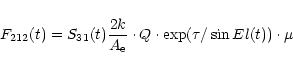\begin{displaymath}F_{212}(t) = S_{31}(t) \frac{2k}{A_{\rm e}} \cdot Q \cdot \exp(\tau/\sin El(t)) \cdot \mu \end{displaymath} (1)

where $k = 1.38 \times 10^{-23}$ J/K is the Boltzmann constant, $A_{\rm e} = 0.09$ m2 is the antenna effective area, Q = 0.37 K/(analog-digital conversion units), $\tau = 0.15$ for the present observations is the opacity at zenith and El is the Sun's elevation angle. $\mu = 1.2$ is a correcting factor that accounts for the position of the burst within beam 3. Taking into account the uncertainties affecting the different parameters in Eq. (1), we estimated that F212 is known to within $\pm 40$%. Because the receivers associated with beams 5 and 6 have different bandwidths, it is not possible to derive F405 in a similar way to F212 so that only the signal received by beam 5 should be considered. Unfortunately this signal shows variations due to changes in the atmospheric opacity which are much stronger than those expected from the flare emission. This is mainly due to the low values of aperture efficiencies at the epoch of the event. Since then, the latter have been improved by a factor of $\sim$10, and so too, the sensitivity (e.g. Kaufmann et al. 2001). We thus consider that, at 405 GHz, the flux density increase from the flare was lower than 90 sfu, the estimated noise level from beam 5.

3 Results and discussion

Figure 1 shows that the 212 GHz radio burst exhibits two components: (i) an impulsive burst B1 ($\sim$1843-1846 UT), which is the counterpart of the impulsive microwave burst, and (ii) a more intense and time-extended emission B2 ($\sim$1846-2000 UT). While B2 and the 1.5-12 keV SXR emission vanish roughly at the same time, B2 reaches its maximum during the decay of the SXR emission. Such a B1-B2 time sequence has been already observed for a few events detected at 86 GHz (e.g. Kundu et al. 1994; Raulin et al. 1999). In the following, B1 and B2 are discussed separately.


 \begin{figure} \par\includegraphics[clip, width=10cm]{fig2_ms1925.eps} \end{figure} Figure 2: From top to bottom, time evolution of: the 120-240 keV hard X-ray emission, the time derivative of the 1.5-12 keV soft X-ray intensity, the 15.4 GHz and 212 GH radio flux density and the radio spectral index (see text) during the impulsive burst B1. The vertical dashed lines indicate the onset and the maximum of the 212 GHz burst.
Open with DEXTER

3.1 The impulsive component B1

Figure 2 shows the time evolution of the 120-240 keV HXR rate, of the time derivative of the 1.5-12 keV SXR emission, of the 15.4 GHz and 212 GHz radio flux densities and of the radio spectral index during B1. The spectral index has been obtained by assuming that the the radio spectrum is represented by a power law between 15.4 and 212 GHz. Because the 120-240 keV rate is strongly affected by pile-up (see Sect. 2), the SXR time derivative is used as a proxy of the HXR rate (e.g. Neupert 1968; Dennis & Zarro 1993).

Figure 2 shows that, although the 212 GHz and 15.4 GHz bursts are globally time-associated, the onset and the main peak at 212 GHz are delayed ($\sim$12 s for the peak) with respect to those at 15.4 GHz. Previous comparisons between the millimeter, microwave and HXR emission indicate that the 86 GHz emission onset appears sometimes to be delayed with respect to the microwave and HXR onset (e.g. Kundu et al. 1994; Lim et al. 1992). Such delays have been taken as evidence that the acceleration time of relativistic (a few MeV) electrons, which radiate the millimeter emission, is longer than that of a few tens to a few hundreds keV electrons which produce the HXR and microwave emission. Such an interpretation is not consistent with the observation of fast correlated time variations of radiative signatures due to a large range of electron energies, i.e. (i) HXR and GR from $\sim$100 keV to >10 MeV, which are found to co-evolve within the 1-2 s time resolution of GR detectors (Forrest & Chupp 1983; Talon et al. 1993) and (ii) HXR and millimeter waves where common features were reported on sub-second time scales (Kaufmann et al. 2000b and references therein). Indeed, such findings likely support the idea that the acceleration of electrons up to sub-relativistic and relativistic energies is simultaneous within $\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle ...1 s.

For the present burst, the time evolution of the main 15.4 GHz emission ($\sim$1842 UT to $\sim$1846 UT) is not simple but comprises several secondary maxima or changes of slope (during both the rise and the decay of the burst) which reveal successive episodes of acceleration and injection of electrons in the radio emitting region. Multiple energy releases are also supported by the fact that the evolution of the SXR time derivative exhibits numerous time structures. Although it is not possible to estimate how well this time derivative reproduces the actual HXR time evolution, we note that most of these time structures find counterparts at 15.4 GHz and at 212 GHz after the maximum. Due to energy dependent transport effects (energy losses, pitch angle diffusion, partial trapping) the HXR and radio burst will last longer than the associated injection of electrons, so that successive injections may lead to HXR and microwave bursts which overlap in time (see discussion in Kaufmann et al. 2000b). This may explain why the maximum of the 15.4 GHz emission falls between two maxima of the SXR time derivative and why some of the injections show up as a change of slope of the microwave time profile. Although this precludes an estimate of the actual start, maximum time and duration of a given injection, the data suggest that the 212 GHz burst starts during one of the electron injections which constitute the rise of the main peak at 15.4 GHz (see Fig. 2). Figure 2 also shows that the radio spectral index increases smoothly from the beginning of the main rise till the maximum of the 212 GHz emission. Thus a plausible, though not unique, interpretation of the delays between the 212 GHz and 15.4 GHz onsets and maxima, is that significant 212 GHz emission is only observed for an injection with a hard electron spectrum and that such an injection overlaps with a previous injection of a softer electron spectrum (in the same magnetic structure or a neighboring one). This is in line with results of multi-wavelength studies of HXR/GR bursts which revealed that these events exhibit sucessive injections of electrons and ions and that noticeable changes in the electron spectrum and in the electron to ion ratio occur from one injection to the other (Chupp et al. 1993; Trottet et al. 1994; Trottet el al. 1998). This interpretation is also consistent with the observations by White (1999), Kundu et al. (1994) and Lim et al. (1992). Indeed a careful examination of the hard X-ray, microwave and 86 GHz time profiles shows, for those events where the 86 GHz onsets are delayed, that these onsets occur when a new electron injection shows up in the HXR/microwave time profiles.

 \begin{figure} \par\includegraphics[clip, width=8.8cm]{fig3_ms1925.eps} \end{figure} Figure 3: The radio spectrum measused over a 10 s time interval at the maximum of the B1 burst (triangles). The solid lines are theoretical spectra computed for magnetic fields of 300 G, 500 G and 700 G (see text).
Open with DEXTER

Figure 3 displays the radio spectrum measured over the 10 s interval which covers the maximum of B1. The shape of this spectrum is as expected for gyrosynchrotron/synchrotron emission generated by relativistic/ultra relativistic electrons in coronal magnetic fields. It exhibits a turnover frequency $\nu_{\rm max}$ between $\sim$9 and 11 GHz, an optically thick rising part up to $\sim$8 GHz and an optically thin decreasing part above 15-18 GHz. Due to lack of radio observations between 18 GHz and 212 GHz, the optically thin part of the spectrum is poorly defined. As a first approximation the radio spectrum is assumed to decrease monotonously above 18 GHz. The solid lines in Fig. 3 are gyrosynchrotron spectra calculated for different values of a uniform magnetic field B ranging from 300 G to 700 G by using exact gyrosynchrotron codes developed by Ramaty (1969) and corrected by Ramaty et al. (1994). These calculations have been performed for: (i) a radio source size of 10 $\hbox {$^{\prime \prime }$ }$ (typical size for millimeter sources, e.g. Raulin et al. 1999 and references therein); (ii) a viewing angle $\theta=45\hbox{$^\circ$ }$ and (iii) an instantaneous isotropic distribution of radiating electrons with an energy spectrum taken as: $N(E)=KE^{-\delta}$ (electrons MeV-1). The ratio $3\nu_{B}/2\nu_{\rm p}$ (where $\nu_{\rm p}$ is the plasma frequency and $\nu_{B}$ gyrofrequency) that governs the level of the Razin-Tsytovich suppression below $\nu_{\rm max}$ has been set to 1 for all values of B. This choice does not affect the results below because they are related to the spectrum above $\nu_{\rm max}$. For a given value of B, the free parameters K and $\delta$ have been estimated by using a minimum $\chi^2$ algorithm which provides the computed spectrum which best fits the observed one above 10-14 GHz. The comparison between the observed and computed radio spectra (respectively, triangles and solid lines in Fig. 3) results in the following comments:

-
Below $\sim$8 GHz (optically thick emission), the measured spectrum rises as $\nu^{0.7-1.2}$. This is much flatter than the computed spectrum which rises as $\nu^{3.5}$ due to Razin suppression for the chosen value of $\nu_{B}$/ $\nu_{\rm p}$. This is even flatter than $\nu^{2.5}$ (resp. $\nu^{2.9}$ ), expected for an emission from relativistic (resp. midly-relativistic) electrons with a power law energy spectrum when the low frequency part of the spectrum is dominated by self absoption (e.g. Dulk & Marsh 1982). Only a highly inhomogeneous radio emitting region (e.g. several loops of different sizes) can provide such a flat spectrum below $\nu_{\rm max}$ (e.g. Dulk 1985; Klein et al. 1986). The fact that $\nu_{\rm max}$ is not sharply defined provides a further indication for an inhomogeneous radio source (e.g. Klein & Trottet 1984). An inhomogeneous radio source is also consistent with TRACE images of this flare that reveal that the flare occured in a complex of highly dynamic loops. The microwave spectral data provide thus further support to our interpretation of the delay between the optically thin microwave emission and the 212 GHz emission.
-
Above $\sim$15-18 GHz (optically thin emission) a reasonable fit of the spectrum is obtained for $\delta = 2.7 \pm 0.2$. Although the radio emitting region is most likely very inhomogeneous the radio spectral slope and thus the deduced value of $\delta$ is quite independent of B (e.g. Dulk 1985; Klein & Trottet 1984; Klein et al. 1986). Therefore, calculations for a uniform magnetic field allow us to estimate K for B averaged over the radio emitting region. Figure 3 shows that $\nu_{\rm max}$ is close to the optically thin part of the observed spectrum for B = 700 G. Thus the average magnetic field in the radio source region should not be much higher than 600 G. Because microwave and short mm-wave emission are radiated by electrons with energies ranging from a few hundred of keV to a few tens of MeV (e.g. Dulk 1985; Ramaty et al. 1994) the electron spectrum inferred fron the present radio obsevations is essentially valid for $\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle ...1 MeV electrons. The total number of >1 MeV electrons N(>1 MeV) is found to be (9.0 $\pm$ 0.1) $\times$ 1030 to (2.4 $\pm$ 0.3) $\times$ 1030 electrons for B = 300 G and B = 600 G respectively.
It is of interest to estimate F(>1 MeV) and F(>10 MeV) GR fluences as well as the >100 keV HXR thick taget flux $\Phi_{100}$ produced by the radio emitting electrons in order to compare with GR fluences observed for other flares and with the upper limit $\Phi^{\rm max}_{100}$ obtained from the RF15-I observations (see Sect. 2). For that, the electron spectrum deduced from radio observations is extrapolated down to 100 keV and it is assumed that: (i) the distribution of electrons in the radio emitting region is isotropic and (ii) electrons propagate freely across the radio source.

Because the effect of partial trapping of electrons within the radio emitting region is ignored, the electron flux $F_{\rm e}$ entering the thick-target HXR/GR emitting source may be overestimated. This leads to $F_{\rm e}$ $\approx$ $N(E)v(E)/L\cos\alpha$ (electrons keV-1 s-1), where L is the radio source scale length (10 $\hbox {$^{\prime \prime }$ }$), v(E)the electron speed and $\alpha$ the mean electron pitch angle (taken as 45 $\hbox{$^\circ$ }$ for the assumed isotropic distribution). Thick target calculations taking into acount both e-p and e-e bremsstrahlung (Vilmer, private communication) are then performed to comptute $\Phi_{100}$, F(>1 MeV) and F(>10 MeV). The obtained HXR/GR spectrum is well represented by a single power law of index $\gamma$ $\approx$ 1.5 in the 100 keV-100 MeV photon energy range. Such a hard spectrum is characteristic of that measured for electron-dominated events above 1 MeV (Rieger et al. 1998; Trottet et al. 1998; Vilmer et al. 1999). In Fig. 4 (top panel) F(>10 MeV) is plotted as a function of F(>1 MeV) for the events reported by Rieger et al. The rectangle shows the domain of values of F(>1 MeV) and F(>10 MeV) estimated for the present event and for B ranging from 300 G to 600 G. Figure 4 indicates that the present event should correspond to a mid-size electron-dominated event. Figure 4 (bottom panel) displays $\Phi^{\rm max}_{100}$ for $\gamma$ ranging from 1.5 to 5.4 (solid line) and the estimated values of $\Phi_{100}$ obtained for $\gamma$ = 1.5 and B ranging from 300 G to 600 G. Except for B = 300 G and $\gamma$ = 1.5, $\Phi_{100}$ is always lower than $\Phi^{\rm max}_{100}$ as it should be. In fact the photon spectrum below 0.5-1 MeV is generally steeper than above 1 MeV (e.g. Rieger et al. 1998; Trottet et al. 1998 and references therein). Thus it would be more relevant to compare the value of $\Phi_{100}$ obtained for $\gamma$ = 1.5 to that of $\Phi^{\rm max}_{100}$ obtained for $\gamma > $ 1.5, so that B = 300 G cannot be fully excluded.

In summary, the microwave and short mm-wave impulsive burst emission observed during the 2000 March 22 X1.1 flare is consistent with gyrosynchrotron radiation from an inhomogenous source with an average magnetic field strength in the 400-600 G range. The characteristic energy of electrons radiating synchrotron emission at a given frequency $\nu$ in a magnetic field B is (e.g. Dulk 1985): E(MeV) $\approx$ [( $\nu/\nu_{\rm b}\sin(\theta/2))^{1/2}-1] \times 0.511$, where $\theta$ is the viewing angle. For B $\sim$ 400-600 G, the 212 GHz emission is produced by synchrotron radiation from ultra-relativistic electrons with E in the 12-15 MeV range.

3.2 The time extended component B2


 \begin{figure} \par\includegraphics[clip, width=8.8cm]{fig4_ms1925.eps} \end{figure} Figure 4: Top panel: the >10 MeV GR continuum fluence as a function of the >1 MeV GR continuum fluence for the electron-dominated events reported in Rieger et al. (1998) (triangles); the solid rectangle shows the domain of values deduced from the present radio observations for a magnetic field ranging from 300 G to 600 G (see text). Bottom panel: the upper limit of the photon flux at 100 keV estimated, as a function of the hard X-ray spectral index, from the RF15-I HXR measurements (solid line); the triangles show the photon flux at 100 keV for a spectral index of 1.5 deduced from the radio observations and for different values of the magnetic field strength.
Open with DEXTER


 \begin{figure} \par\includegraphics[clip, width=8.8 cm]{fig5_ms1925.eps} \end{figure} Figure 5: Top panel: time evolution of the 14.8 GHz flux density observed by OVSA during the decay of the microwave emission and comptuted for a 30 $\hbox {$^{\prime \prime }$ }$ and a 45 $\hbox {$^{\prime \prime }$ }$ isothermal source, the emission measure and temperature of which have been derived from the GOES SXR observations. Bottom panel: observed (error bars) and computed (solid line) radio spectra when the microwave emission is predominently produced by free-free emission.
Open with DEXTER

The radio spectra measured by OVSA during B2 indicate that both non thermal gyrosynchrotron and thermal bremsstrahlung radiation contribute to the observed 1-18 GHz microwave emission. Assuming that the microwave thermal source is the same as the SXR source the values of EM and T obtained from the GOES observations (see Sect. 2) are used to compute the expected microwave free-free emission for a source diameter ranging from 30 $\hbox {$^{\prime \prime }$ }$ to 45 $\hbox {$^{\prime \prime }$ }$ (typical sizes for 17 GHz thermal sources; e.g. Raulin et al. 1999). The top panel of Fig. 5 shows the time evolution of the observed and expected 14.8 GHz flux density during the decay of the microwave emission after 1850 UT. The contribution of free-free emission to the total 14.8 GHz emission increases with time and becomes dominant after $\sim$1900 UT. As an example, in the bottom panel of Fig. 5, the thermal spectrum (solid lines) derived from GOES SXR observations ( $EM = 2.5 \times 10^{49}$ cm-3 and $T = 9 \times 10^6$ K) at 1910:50 UT, when free-free emission is dominant, is overplotted on the observed one (error bars). The observed and computed spectra agree reasonably well and exhibit a turnover frequency around 10 GHz below (above) which free-free emission is optically thick (thin). As expected, in the optically thin regime the computed flux density does not depend on the cross section of the source for a given value of EM (i.e. at a given time; see e.g. Dulk 1985). Below $\sim$10 GHz (optically thick emission), a slightly better agreement is obtained for a source diameter of 30 $\hbox {$^{\prime \prime }$ }$. The good agreement between observed and computed spectra is consistent with the assumption that the SXR and microwave thermal sources are similar.

The smooth time profile of the 212 GHz flux density during B2 suggests that this radio emission is predominantly of thermal origin. Indeed, after $\sim$1846 UT, the OVSA spectra indicate that the contribution of gyrosynchrotron radiation to the 212 GHz emission is negligeable. However, the 212 GHz flux density expected from the microwave thermal source ($\sim$20 sfu) is much lower than the observed one ($\sim$190 sfu; see Fig. 2, bottom). This is in agreement with the suggestion by Kaufmann et al. (2001) that the SXR and 212 GHz emission arise from different regions. Kaufmann et al. also proposed that the short mm-wave emission might be produced deep in the chromosphere.

The investigation of such a possibility is beyond the scope of the present study, since it would require a realistic and time dependant flare model of the deep atmosphere, which is poorly constrained by the present observations.

4 Summary

In this paper we have reported and analysed observations of a radio burst at frequencies larger than 100 GHz. These observations were obtained at 212 and 405 GHz by the SST during the 2000 March 22 H$\alpha$ 2N (GOES X1.1) flare at $\sim$1834 UT. At 212 GHz the radio event comprises an impulsive part B1 which lasts for $\sim$3 min and a time extended burst B2 which lasts for $\sim$60 min. Neither B1 nor B2 produced a significant signal at 405 GHz, most probably because of the low level of aperture efficiency of the SST at that frequency during the considered observing period (see Sect. 2). The time evolution of the 212 GHz radiation has been compared with that of the 1.5-24 keV SXR, 120-240 keV HXR and 1-18 GHz microwave emission and radio frequency spectra have been analysed. The main results can be summarized as follows:

-
B1 is produced by synchrotron radiation from $\approx$10-15 MeV ultra relativistic electrons in an average magnetic field of $\sim$400-600 G.

-
At 212 GHz, B1 is the high frequency counterpart of the 1-18 GHz microwave burst radiated by gyrosynchrotron emission from lower energy (>a few $\times$ 100 keV) electrons. However, the onset and the maximum of B1 occur later at 212 GHz than at optically thin microwave frequencies. Such delays do not necessarily imply that the electron acceleration timescale increases with energy. Indeed the present observations indicate that B1 is the result of successive injections of electrons in a highly inhomogeneous radio-emitting region and that significant 212 GHz emission is detected only when electrons are injected with a hard spectrum. Observations at several frequencies above $\sim$80 GHz would provide a crucial test of these alternatives: delays due to energy-dependent acceleration times will grow with increasing frequency, while injections with different spectra will give simultaneous burst onsets.

-
The electron population producing such a synchrotron burst has a hard spectrum (power law index $\sim$2.7). The 100 keV HXR flux expected from these electrons is consistently lower than the observed upper limit. The spectral slope and the >1 MeV (or >10 MeV) GR continuum fluence, estimated from the spectral characteristics of the radio emitting electrons, are comparable to those measured for mid-size electron-dominated GR events.

-
During B2 the microwave emission is produced by both gyrosynchrotron and free-free emission. In the late part of B2, when free-free emission is the dominant process, the microwave source is consistent with an isothermal coronal region which also radiates the SXR emission. The 212 GHz radiation during B2 is also consistent with thermal emission. However, this short mm-wave thermal source is found to be different from the coronal source radiating SXR and thermal microwaves.

It is obvious that synchrotron emission from ultra relativistic electrons is expected for GR flares with significant electron bremsstrahlung emission above 10 MeV. The present observations constitute the first detection of such a synchrotron component above 200 GHz and demonstrate the ability of the SST to measure it. Kaufmann et al. (2001) reported that numerous fast subsecond time structures were detected at 212 and 405 GHz during both B1 and B2. Although the physics of such fast time variations is not yet understood, the fact that their flux density increases with frequency provides a clear indication that their origin is different from that of the synchrotron impulsive burst analysed in the present study. The high-energy bremsstrahlung continuum expected from the electrons radiating this synchrotron burst could have been detected by present GR detectors. However, it is obvious that the sensitivity of the SST, which has been substantially improved since the observations discussed in this paper, should allow us to detect much weaker flares than the one studied here and thus to investigate if the acceleration of ultra relativistic electrons occurs only during large (GOES M and X) flares.

Acknowledgements
GOES data were provided by the Solar Data Analysis Center at NASA/GSFC. RSTN data have been retrieved from the National Geophysical Data Center homepage with the assistance of H. Coffey and TRACE images were visualized from the instrument homepage. One of the authors (PK) is also part time with CCS, Unicamp, Campinas, SP, Brazil. The present work was supported by the French-Bresilian program of exchange of scientists (CNRS-CNPq contract 8810 and 910089/99-0) and by FAPESP under grants No 99/06126-7 and 01/03791-1. The OVSA instrument and data analysis were supported through NSF grant AST-9987366 and NASA grant NAG5-9682 to NJIT.

References

 

Copyright ESO 2002