A&A 381, 420-427 (2002)
DOI: 10.1051/0004-6361:20011561
Group analysis in the SSRS2 catalog
C. Adami - A. Mazure
LAM, Traverse du Siphon, 13012 Marseille, France
Received 31 July 2001 / Accepted 24 October 2001
Abstract
We present an automated method to detect populations of groups in galaxy
redshift catalogs. This method uses both analysis of the redshift distribution
along lines of sight in
fixed cells to detect elementary structures and a friend-of-friend algorithm
to merge these elementary structures into physical structures. We apply this
method to the SSRS2 galaxy redshift catalog. The groups detected with our
method are similar to group catalogs detected with pure friend-of-friend
algorithms. They have similar mass distribution, similar abundance versus
redshift, a similar 2-point correlation function (modeled by a power law:
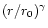 with
with
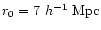 and
and
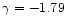 )
and the same
redshift completeness limit, close to 5000 kms-1. If instead of SSRS2, we use
catalogs of the new generation (deep redshift surveys obtained with 10 m class telescopes), it would lead to a completeness limit of
)
and the same
redshift completeness limit, close to 5000 kms-1. If instead of SSRS2, we use
catalogs of the new generation (deep redshift surveys obtained with 10 m class telescopes), it would lead to a completeness limit of 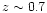 .
We model the luminosity function for nearby galaxy groups by a Schechter
function with parameters
.
We model the luminosity function for nearby galaxy groups by a Schechter
function with parameters
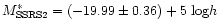 and
and
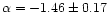 to compute the mass to light ratio. The median value of the mass to light ratio is 360
to compute the mass to light ratio. The median value of the mass to light ratio is 360
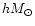 /
/
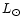 (in the SSRS2 band, close to a B band magnitude) and we deduce a relation
between mass to light ratio and velocity dispersion
(in the SSRS2 band, close to a B band magnitude) and we deduce a relation
between mass to light ratio and velocity dispersion 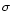 (
(
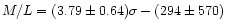 ). The more massive the group, the
higher the mass to light ratio, and therefore, the larger the amount of dark
matter inside the group. Another explanation is a significant stripping of
the gas of the galaxies in massive groups as opposed to low mass groups.
This extends to groups of galaxies the mild tendency already detected for
rich clusters of galaxies. Finally, we detect a barely significant
fundamental plane for these groups (
). The more massive the group, the
higher the mass to light ratio, and therefore, the larger the amount of dark
matter inside the group. Another explanation is a significant stripping of
the gas of the galaxies in massive groups as opposed to low mass groups.
This extends to groups of galaxies the mild tendency already detected for
rich clusters of galaxies. Finally, we detect a barely significant
fundamental plane for these groups (
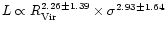 for groups with more than 8 galaxies) but it is much less
narrow than for clusters of galaxies.
for groups with more than 8 galaxies) but it is much less
narrow than for clusters of galaxies.
Key words: galaxies: clusters: general - cosmology: large-scale structure of Universe
The abundance evolution of galaxy structures is a major prediction of
cosmological models (e.g. Oukbir & Blanchard 1992, 1997; Romer et al.
2001). The more distant the structure, the stronger the constraint. Until
now, however, we are limited to the study of the most massive distant
structures. This is because these structures are the easiest to detect at
high redshift using for example X-ray selected samples (e.g. Borgani et al.
1999; Burke et al. 1997; Ebeling et al. 2000; Gioia et al. 1990; Romer et al. 2000; Vikhlinin et al. 1998). These distant massive structures are the progenitors of the most massive 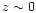 clusters. The hierarchical models predict, however, that nearby intermediate-mass clusters have formed from
low mass high redshift systems as groups of galaxies. The new generation of
deep galaxy surveys (VLT and Keck surveys) will be able to detect such high
redshift low mass structures. This will add an element to the large-scale
structure formation models.
clusters. The hierarchical models predict, however, that nearby intermediate-mass clusters have formed from
low mass high redshift systems as groups of galaxies. The new generation of
deep galaxy surveys (VLT and Keck surveys) will be able to detect such high
redshift low mass structures. This will add an element to the large-scale
structure formation models.
We present in this paper a new efficient method to detect and study such
structures in very large galaxy redshift samples (Sect. 2). We applied
this method to the SSRS2 (da Costa et al. 1998) galaxy redshift catalog in
order to quantify our detection efficiency at low redshift. We have created
a catalog of groups from this survey and we have studied the properties of
these structures (Sect. 3), comparing our results to literature studies
(Carlberg et al. 2001; Girardi et al. 2000; Merchan et al. 2000). We conclude in Sect. 4.
The structure detection we used is an hybrid method derived from the method
used for the ENACS sample of galaxy clusters (e.g. Katgert et al. 1996) and
from classical friend-of-friend detection methods (e.g. Huchra & Geller
1982). The friend-of-friend algorithm is applied to a preprocessed catalog
of elementary galaxy associations and not to individual galaxies. In this way we
reduce the computation time by a large factor (see Sect. 3.3). The procedure
consists of four steps:
- We apply a running window (with an overlap of half of the window
size) to the original catalog of galaxies to divide the total area covered
by the survey in several elementary lines of sight. The angular size
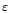 of the running window is chosen as a function of the kind of
structures we are trying to detect (
of the running window is chosen as a function of the kind of
structures we are trying to detect (
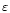 has to be close to the
typical size of the structures) and as a function of the redshift of these
structures;
has to be close to the
typical size of the structures) and as a function of the redshift of these
structures;
- We search for compact galaxy redshift associations in each of these
elementary beams by using a technique similar to Katgert et al. (1996).
This technique is basically detecting gaps (fixed redshift separations
between successive galaxies) greater than a given value (noted "gap analysis'' in
the following). This value is given by the typical maximal
velocity dispersion of the structures we try to detect. For groups, we
searched galaxies separated by more than 600 kms-1 in each elementary beam.
If two galaxies are separated by more than this value, these galaxies belong
to different structures. An elementary structure has more than 2 galaxies;
- We apply a friend-of-friend algorithm to merge the elementary
structures into larger real structures. Two elementary structures were
assumed to be connected if they were closer than
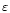 .
This value
is an approximation of the maximal diameter of a group in real space. This
allows us to generate a preliminary catalog of interesting regions with
potential structures inside;
.
This value
is an approximation of the maximal diameter of a group in real space. This
allows us to generate a preliminary catalog of interesting regions with
potential structures inside;
- Finally, we re-apply the gap method for each of these regions in
order to detect real structures in the catalog.
The SSRS2 catalog is a sample of 5369 galaxies, covering a region of 1.70 sr
of the southern sky (
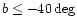 and
and
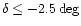 for the
southern galactic cap and
for the
southern galactic cap and
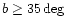 and
and
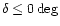 for the
northern galactic cap). This catalog is 99% complete down to
for the
northern galactic cap). This catalog is 99% complete down to
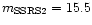 .
The
.
The
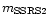 magnitude is close to a B magnitude (see da Costa et al. 1998). The precision of the individual galaxy redshift measurements is
magnitude is close to a B magnitude (see da Costa et al. 1998). The precision of the individual galaxy redshift measurements is  40 kms-1. Detailed information on this catalog can be found in da Costa et al. (1998). We limited our analysis to the
40 kms-1. Detailed information on this catalog can be found in da Costa et al. (1998). We limited our analysis to the
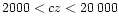 kms-1 range. To detect groups, we used
kms-1 range. To detect groups, we used
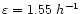 Mpc. This value is an approximation of the maximal diameter of a
group and gives the most similar results compared to the SSRS2 group
analysis by Merchan et al. (2000). We kept only the structures with more
than 4 galaxies and less than 40 galaxies (to be consistent with Merchan et al. 2000). Structures with less than or with 3 galaxies are possibly close
superposition effects and not real dynamical structures (Ramella et al.
1997). Structures with more than 40 galaxies are likely to be rich clusters
or diffuse elongated filaments of galaxies.
Mpc. This value is an approximation of the maximal diameter of a
group and gives the most similar results compared to the SSRS2 group
analysis by Merchan et al. (2000). We kept only the structures with more
than 4 galaxies and less than 40 galaxies (to be consistent with Merchan et al. 2000). Structures with less than or with 3 galaxies are possibly close
superposition effects and not real dynamical structures (Ramella et al.
1997). Structures with more than 40 galaxies are likely to be rich clusters
or diffuse elongated filaments of galaxies.
The detected structures are described in Tables 1 and 2. The mean number of
galaxies per structure is 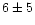 and 90% of the structures have less than
11 galaxies. The largest group has 32 galaxies. The richest groups are the
closer ones, in agreement with the detection of a uniform richness class of
groups. This is because, due to apparent limiting magnitude, the closest
groups have more galaxies brighter than the SSRS2 catalog magnitude limit.
and 90% of the structures have less than
11 galaxies. The largest group has 32 galaxies. The richest groups are the
closer ones, in agreement with the detection of a uniform richness class of
groups. This is because, due to apparent limiting magnitude, the closest
groups have more galaxies brighter than the SSRS2 catalog magnitude limit.
The groups are more or less circular: they have the same angular extension
in 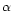 (right ascension) and
(right ascension) and 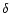 (declination). We have
(declination). We have
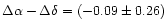 arcmin (computed with 80 groups).
This means that we are not detecting systematically elongated structures
such as poor filaments. The mean extension of the detected groups (computed
as the dispersion of the coordinates of the galaxies of a given group) is
arcmin (computed with 80 groups).
This means that we are not detecting systematically elongated structures
such as poor filaments. The mean extension of the detected groups (computed
as the dispersion of the coordinates of the galaxies of a given group) is
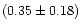 h-1 Mpc. We have no variation
of the group size as a function of the redshift, but the richest groups are
also the larger ones. The groups with more than 10 galaxies have a size in
the range [0.45; 0.8] h-1 Mpc. The groups with less than 10 galaxies have
a size in the range [0.05; 0.65] h-1 Mpc. Finally, the mean virial radius
h-1 Mpc. We have no variation
of the group size as a function of the redshift, but the richest groups are
also the larger ones. The groups with more than 10 galaxies have a size in
the range [0.45; 0.8] h-1 Mpc. The groups with less than 10 galaxies have
a size in the range [0.05; 0.65] h-1 Mpc. Finally, the mean virial radius
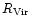 of the groups is
of the groups is
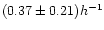 Mpc (in the range
[0.06; 0.87] h-1 Mpc, see Tables 1 and 2).
Mpc (in the range
[0.06; 0.87] h-1 Mpc, see Tables 1 and 2).
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{fig_sig2.ps}\end{figure}](/articles/aa/full/2002/02/aa1761/Timg32.gif) |
Figure 1:
Histogram of the group velocity dispersions (in kms-1). |
| Open with DEXTER |
We computed velocity dispersions using a robust estimator (Beers et al.
1990). This gives a more realistic estimate of the velocity dispersion for
groups with more than 10 galaxies, but still a low number, compared to
classical estimators. For groups with less than 10 galaxies, there is no
significant difference between this robust estimator and the classical
estimator of the velocity dispersion (Lax 1985).
The mean velocity dispersion of the groups is
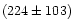 kms-1. None of
them has a velocity dispersion greater than 500 kms-1 (see Fig. 1). These
values are consistent with several other computations for groups (e.g.
Carlberg et al. 2001 with a median velocity dispersion of 200 kms-1). This
means that we detected no rich clusters. The groups with the highest
velocity dispersions are also the richest (see Fig. 2) but we have no
significant relation between the group mean redshift and velocity
dispersion. This is, one more time, in favor of a uniform detection of
groups as a function of redshift.
kms-1. None of
them has a velocity dispersion greater than 500 kms-1 (see Fig. 1). These
values are consistent with several other computations for groups (e.g.
Carlberg et al. 2001 with a median velocity dispersion of 200 kms-1). This
means that we detected no rich clusters. The groups with the highest
velocity dispersions are also the richest (see Fig. 2) but we have no
significant relation between the group mean redshift and velocity
dispersion. This is, one more time, in favor of a uniform detection of
groups as a function of redshift.
In order to check how many spurious groups we are detecting (groups with a
large velocity dispersion, but a low number of galaxies: chance alignments),
we plotted the velocity dispersion as a function of the number of galaxies
inside the groups (Fig. 2). Only 10% of the groups have less than 5 galaxies
and a velocity dispersion greater than 300 kms-1. This can be assumed to be
the contamination rate of our catalog.
Combining the virial radius and the velocity dispersion, we computed the
mass using the standard virial mass estimator (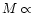 virial radius
virial radius
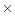 (velocity dispersion)2) (e.g. Ramella et al. 1997). About 85%
of the sample has a mass in the range [
(velocity dispersion)2) (e.g. Ramella et al. 1997). About 85%
of the sample has a mass in the range [
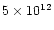 ;
;
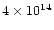 ]
solar
masses and 97.5% has a mass in the range [1012;
]
solar
masses and 97.5% has a mass in the range [1012;
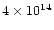 ]
solar
masses. None of the groups has a mass greater than
]
solar
masses. None of the groups has a mass greater than
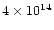 solar masses.
The mean mass is (
solar masses.
The mean mass is (
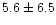 )
)
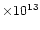 solar masses. All the masses
computed by Merchan et al. (2000) are in the range [
solar masses. All the masses
computed by Merchan et al. (2000) are in the range [
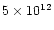 ;
;
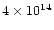 ] solar masses. This means that we have slightly lower masses in the sample
(for 15% of the sample). This is probably due to the fact that we are using
robust estimators to compute velocity dispersions. Such estimators are less
biased toward high values for small samples of galaxies. The velocity
dispersions and masses are given in Tables 1 and 2.
] solar masses. This means that we have slightly lower masses in the sample
(for 15% of the sample). This is probably due to the fact that we are using
robust estimators to compute velocity dispersions. Such estimators are less
biased toward high values for small samples of galaxies. The velocity
dispersions and masses are given in Tables 1 and 2.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{fig_interlop.ps}\end{figure}](/articles/aa/full/2002/02/aa1761/Timg40.gif) |
Figure 2:
Number of galaxies inside each group as a function of the velocity dispersion of the group. The stars are the groups with too low a richness compared to the velocity dispersion. |
| Open with DEXTER |
In order to estimate the mass uncertainty, we used galaxy groups with more
than 10 galaxies. For these groups, a reliable error can be computed for
velocity dispersion using 100 bootstrap resamplings. This is obviously a
lower limit of the velocity dispersion uncertainty as this uncertainty is
probably larger for smaller groups. The 1-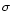 uncertainty is:
uncertainty is:
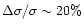 .
The mass uncertainty can be written as:
.
The mass uncertainty can be written as:
Assuming that the velocity dispersion uncertainty is the dominant factor, we
have the 1-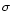 error on the mass:
error on the mass:
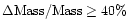 .
This
large error raises the question of the validity of virial mass estimates for
groups of galaxies as these structures are probably not all in equilibrium
(e.g. Dos Santos & Mamon 1999).
.
This
large error raises the question of the validity of virial mass estimates for
groups of galaxies as these structures are probably not all in equilibrium
(e.g. Dos Santos & Mamon 1999).
Table 1:
Group sample: Col. 1 (N): number of galaxies inside groups, Col. 2 (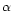 ): right ascension (in degrees), Col. 3 (
): right ascension (in degrees), Col. 3 (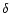 ): declination (degrees), Col. 4 (z): mean redshift, Col. 5 (Obs. Lum.): observed group luminosity (luminosity before corrections: in unit of solar luminosity), Col. 6: E(B-V) from Schlegel et al. (1998) at the group coordinates, Col. 7 (Ext.): extinction correction factor, Col. 8 (Comp.): completeness correction factor, Col. 9 (Tot. Lum.): group total luminosity (in unit of solar luminosity), Col. 10 (Mass): virial mass (in unit of solar mass), Col. 11 (M/L): mass to light ratio in the SSRS2 magnitude passband, Col. 12 (
): declination (degrees), Col. 4 (z): mean redshift, Col. 5 (Obs. Lum.): observed group luminosity (luminosity before corrections: in unit of solar luminosity), Col. 6: E(B-V) from Schlegel et al. (1998) at the group coordinates, Col. 7 (Ext.): extinction correction factor, Col. 8 (Comp.): completeness correction factor, Col. 9 (Tot. Lum.): group total luminosity (in unit of solar luminosity), Col. 10 (Mass): virial mass (in unit of solar mass), Col. 11 (M/L): mass to light ratio in the SSRS2 magnitude passband, Col. 12 (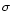 ): velocity dispersion in kms-1, Col. 13 (Rvir): virial radius in h-1 Mpc.
): velocity dispersion in kms-1, Col. 13 (Rvir): virial radius in h-1 Mpc.
| N |
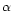 |
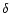 |
z |
Obs. Lum. |
E(B-V) |
Ext. |
Comp. |
Tot. Lum. |
Mass |
M/L |
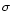 |
Rvir |
| 5 |
3.2488 |
-24.3504 |
0.0255 |
5.33E+10 |
0.02220 |
1.09 |
3.20 |
1.86E+11 |
1.90E+12 |
10.2 |
82 |
0.13 |
| 4 |
3.2868 |
-7.4360 |
0.0181 |
4.54E+10 |
0.03389 |
1.14 |
1.94 |
1.01E+11 |
4.91E+13 |
486.9 |
286 |
0.27 |
| 4 |
5.5908 |
-4.3517 |
0.0138 |
1.13E+10 |
0.03145 |
1.13 |
1.60 |
2.04E+11 |
2.13E+14 |
1043.7 |
401 |
0.6 |
| 5 |
6.8999 |
-9.0373 |
0.0192 |
2.99E+10 |
0.03553 |
1.15 |
2.19 |
7.56E+10 |
1.44E+14 |
1905.7 |
359 |
0.51 |
| 4 |
7.0446 |
-37.3208 |
0.0245 |
3.91E+10 |
0.02375 |
1.10 |
3.13 |
1.34E+11 |
4.04E+12 |
30.1 |
86 |
0.25 |
| 4 |
7.1985 |
-22.9825 |
0.0268 |
7.17E+10 |
0.01305 |
1.05 |
3.06 |
2.31E+11 |
4.44E+12 |
19.2 |
113 |
0.16 |
| 5 |
7.3508 |
-10.9007 |
0.0122 |
5.79E+10 |
0.03334 |
1.14 |
2.15 |
1.42E+11 |
2.45E+13 |
172.4 |
189 |
0.31 |
| 5 |
8.0602 |
-3.3412 |
0.0196 |
3.70E+10 |
0.03581 |
1.15 |
2.23 |
9.51E+10 |
1.98E+13 |
208.3 |
215 |
0.2 |
| 4 |
8.4047 |
-28.5031 |
0.0234 |
3.47E+10 |
0.02017 |
1.08 |
2.62 |
9.86E+10 |
2.45E+13 |
248.4 |
149 |
0.5 |
| 4 |
8.8372 |
-23.7145 |
0.0128 |
1.90E+10 |
0.01679 |
1.07 |
1.80 |
3.65E+10 |
3.89E+12 |
106.5 |
99 |
0.18 |
| 7 |
10.6675 |
-9.3056 |
0.0197 |
4.22E+10 |
0.03604 |
1.15 |
1.89 |
9.20E+10 |
6.88E+13 |
747.4 |
281 |
0.4 |
| 4 |
12.7327 |
-13.4234 |
0.0376 |
9.85E+10 |
0.02390 |
1.10 |
7.94 |
8.60E+11 |
2.06E+13 |
24.0 |
286 |
0.12 |
| 4 |
14.2872 |
-9.1834 |
0.0150 |
2.88E+10 |
0.08095 |
1.38 |
2.07 |
8.22E+10 |
1.35E+13 |
164.2 |
113 |
0.48 |
| 9 |
18.0011 |
-32.3378 |
0.0192 |
1.25E+11 |
0.02365 |
1.10 |
2.18 |
3.00E+11 |
5.37E+13 |
179.0 |
346 |
0.2 |
| 4 |
18.0096 |
-6.6967 |
0.0204 |
2.76E+10 |
0.11385 |
1.57 |
2.37 |
1.03E+11 |
1.10E+13 |
107.0 |
285 |
0.06 |
| 14 |
20.7478 |
-35.3655 |
0.0193 |
1.23E+11 |
0.01880 |
1.08 |
2.17 |
2.88E+11 |
5.47E+13 |
190.1 |
212 |
0.56 |
| 5 |
20.7672 |
-38.5622 |
0.0205 |
4.90E+10 |
0.01960 |
1.08 |
2.18 |
1.15E+11 |
7.60E+12 |
65.8 |
159 |
0.14 |
| 4 |
25.2701 |
-34.4858 |
0.0128 |
1.14E+10 |
0.01997 |
1.08 |
1.57 |
1.93E+10 |
4.52E+12 |
233.7 |
190 |
0.06 |
| 5 |
25.3051 |
-4.2930 |
0.0180 |
3.59E+10 |
0.02266 |
1.09 |
2.05 |
8.05E+10 |
1.92E+13 |
238.4 |
157 |
0.36 |
| 5 |
26.2856 |
-13.8575 |
0.0181 |
2.74E+10 |
0.01640 |
1.07 |
2.08 |
6.09E+10 |
1.94E+13 |
318.4 |
175 |
0.29 |
| 4 |
28.2577 |
-4.2047 |
0.0164 |
2.91E+10 |
0.02386 |
1.10 |
1.85 |
5.92E+10 |
1.25E+14 |
2110.9 |
331 |
0.52 |
| 4 |
28.7924 |
-9.3172 |
0.0173 |
1.91E+10 |
0.02394 |
1.10 |
1.95 |
4.10E+10 |
1.08E+14 |
2635.4 |
265 |
0.7 |
| 4 |
29.5184 |
-25.5656 |
0.0144 |
3.66E+10 |
0.01053 |
1.04 |
1.98 |
7.56E+10 |
2.34E+13 |
309.5 |
256 |
0.16 |
| 5 |
30.2063 |
-32.1871 |
0.0183 |
4.08E+10 |
0.01977 |
1.08 |
2.33 |
1.03E+11 |
1.17E+14 |
1138.0 |
288 |
0.64 |
| 4 |
30.6148 |
-29.3072 |
0.0169 |
3.96E+10 |
0.01656 |
1.07 |
2.15 |
9.10E+10 |
1.34E+14 |
1471.9 |
289 |
0.73 |
| 4 |
31.4930 |
-6.8843 |
0.0169 |
1.60E+10 |
0.01961 |
1.08 |
1.83 |
3.16E+10 |
3.71E+13 |
1172.2 |
271 |
0.23 |
| 4 |
31.5281 |
-23.1068 |
0.0178 |
5.10E+10 |
0.01674 |
1.07 |
2.12 |
1.16E+11 |
9.35E+13 |
808.6 |
316 |
0.43 |
| 4 |
34.8054 |
-38.3532 |
0.0167 |
2.95E+10 |
0.02016 |
1.08 |
1.83 |
5.85E+10 |
4.24E+12 |
72.4 |
55 |
0.64 |
| 7 |
36.4329 |
-11.4888 |
0.0153 |
3.37E+10 |
0.02209 |
1.09 |
1.75 |
6.44E+10 |
6.41E+12 |
99.6 |
181 |
0.09 |
| 9 |
39.0671 |
-13.1909 |
0.0150 |
5.33E+10 |
0.03001 |
1.13 |
1.68 |
1.01E+11 |
4.99E+13 |
494.9 |
243 |
0.39 |
| 9 |
40.8864 |
-25.7116 |
0.0229 |
1.15E+11 |
0.01903 |
1.08 |
3.60 |
4.45E+11 |
8.34E+13 |
187.4 |
219 |
0.79 |
| 8 |
41.4914 |
-31.8348 |
0.0221 |
1.13E+11 |
0.02305 |
1.10 |
2.55 |
3.17E+11 |
1.66E+14 |
523.7 |
393 |
0.49 |
| 5 |
42.5306 |
-8.9778 |
0.0178 |
2.59E+10 |
0.02907 |
1.12 |
2.04 |
5.93E+10 |
9.15E+13 |
1542.9 |
274 |
0.56 |
| 14 |
46.6818 |
-10.4633 |
0.0155 |
8.66E+10 |
0.07630 |
1.36 |
1.67 |
1.96E+11 |
1.17E+14 |
597.3 |
422 |
0.3 |
| 5 |
47.4664 |
-25.3934 |
0.0212 |
2.99E+10 |
0.01680 |
1.07 |
2.33 |
7.45E+10 |
3.07E+12 |
41.2 |
113 |
0.11 |
| 4 |
48.1498 |
-7.5486 |
0.0177 |
3.10E+10 |
0.06842 |
1.31 |
2.15 |
8.76E+10 |
7.86E+13 |
896.8 |
203 |
0.87 |
| 10 |
49.0948 |
-4.7276 |
0.0079 |
2.40E+10 |
0.06228 |
1.28 |
1.26 |
3.87E+10 |
8.08E+13 |
2087.3 |
387 |
0.25 |
| 4 |
52.7168 |
-4.8493 |
0.0198 |
3.00E+10 |
0.04634 |
1.20 |
2.24 |
8.10E+10 |
8.13E+13 |
1004.3 |
235 |
0.07 |
| 4 |
53.8719 |
-18.4927 |
0.0142 |
2.26E+10 |
0.06259 |
1.28 |
2.06 |
5.97E+10 |
1.94E+12 |
32.5 |
67 |
0.2 |
| 11 |
55.2961 |
-4.5489 |
0.0138 |
1.01E+11 |
0.06435 |
1.29 |
1.58 |
2.07E+11 |
3.45E+13 |
166.7 |
216 |
0.34 |
| 5 |
149.4540 |
-2.7081 |
0.0210 |
5.70E+10 |
0.04201 |
1.18 |
2.13 |
1.43E+11 |
2.49E+13 |
173.6 |
308 |
0.12 |
| 7 |
150.3229 |
-6.2040 |
0.0164 |
4.93E+10 |
0.03796 |
1.16 |
1.78 |
1.02E+11 |
3.36E+13 |
329.0 |
249 |
0.25 |
| 5 |
151.6062 |
-2.4202 |
0.0202 |
3.65E+10 |
0.04465 |
1.19 |
2.37 |
1.03E+11 |
2.66E+12 |
25.8 |
58 |
0.36 |
| 5 |
155.7194 |
-2.3807 |
0.0186 |
5.69E+10 |
0.04830 |
1.21 |
1.93 |
1.33E+11 |
4.88E+13 |
366.3 |
218 |
0.47 |
| 6 |
160.6563 |
-10.2180 |
0.0077 |
1.29E+10 |
0.00910 |
1.04 |
1.38 |
1.77E+10 |
6.25E+13 |
3522.1 |
245 |
0.48 |
| 4 |
162.5583 |
-12.2600 |
0.0154 |
1.79E+10 |
0.03559 |
1.15 |
1.86 |
3.84E+10 |
2.77E+13 |
721.7 |
248 |
0.21 |
| 4 |
164.2253 |
-9.5503 |
0.0270 |
6.25E+10 |
0.03783 |
1.16 |
3.15 |
2.29E+11 |
2.44E+13 |
106.6 |
191 |
0.31 |
| 17 |
165.7276 |
-14.5042 |
0.0144 |
1.09E+11 |
0.00944 |
1.04 |
1.52 |
1.66E+11 |
2.97E+14 |
1787.6 |
475 |
0.6 |
| 5 |
168.0586 |
-13.6485 |
0.0171 |
3.23E+10 |
0.07506 |
1.35 |
1.93 |
8.42E+10 |
1.25E+14 |
1484.7 |
351 |
0.46 |
| 4 |
170.6570 |
-13.4858 |
0.0173 |
5.77E+10 |
0.03418 |
1.15 |
1.85 |
1.22E+11 |
7.72E+13 |
630.9 |
244 |
0.59 |
We compared our catalog with that one of Merchan et al. (2000) that used the
same galaxy sample. Figure 3 shows the group redshift distribution of the two
catalogs. We detect similar numbers of groups up to
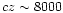 kms-1. The mean difference per bin is 5% (with redshift bins of 1250 kms-1 width). Merchan et al. detect more groups at higher redshift. However, their catalog begins to be incomplete above 5000 kms-1. This means
that we have the same detection completeness level, in agreement with Press
& Schechter (1974) predictions (Merchan et al. 2000). Finally, we estimated
the 2-point correlation function for the sample. Using a power law
approximation of the form
kms-1. The mean difference per bin is 5% (with redshift bins of 1250 kms-1 width). Merchan et al. detect more groups at higher redshift. However, their catalog begins to be incomplete above 5000 kms-1. This means
that we have the same detection completeness level, in agreement with Press
& Schechter (1974) predictions (Merchan et al. 2000). Finally, we estimated
the 2-point correlation function for the sample. Using a power law
approximation of the form
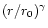 ,
we have
r0=7.0 h-1 Mpc and
,
we have
r0=7.0 h-1 Mpc and
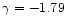 .
This is consistent at the 1
.
This is consistent at the 1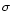 level with the values of
Merchan et al. (2000):
level with the values of
Merchan et al. (2000):
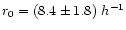 Mpc and
Mpc and
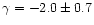 ,
Girardi et al. (2000):
,
Girardi et al. (2000):
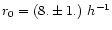 Mpc and
Mpc and
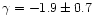 or Carlberg et al. (2001):
or Carlberg et al. (2001):
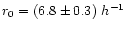 Mpc and
Mpc and
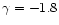 (fixed). We detect a positive signal up to
(fixed). We detect a positive signal up to 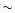 90 h-1 Mpc (similar to
the values of Merchan et al. 2000). These estimates are all in good
agreement and give confidence in the detection method. The only significant
difference is a lower group detection rate at the faint end of the galaxy
catalog. However, this does not affect the completeness level of our group
sample as we detect the same number of groups up to
90 h-1 Mpc (similar to
the values of Merchan et al. 2000). These estimates are all in good
agreement and give confidence in the detection method. The only significant
difference is a lower group detection rate at the faint end of the galaxy
catalog. However, this does not affect the completeness level of our group
sample as we detect the same number of groups up to
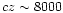 kms-1(assuming that the Merchan et al. completeness limit is correct).
kms-1(assuming that the Merchan et al. completeness limit is correct).
The redshift completeness limit close to 5000 kms-1 is directly related to
the magnitude limit of the catalog:
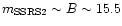 .
It gives an
absolute magnitude of -18+5 logh. This is the magnitude limit for the
galaxies lying inside groups before the completeness limit. We can
extrapolate this redshift completeness limit assuming the typical depth of
the new generation of redshift surveys using 10 meter class telescopes
(Keck and VLT). For example, the deep part of the Virmos survey should
provide a redshift survey 80% complete down to
.
It gives an
absolute magnitude of -18+5 logh. This is the magnitude limit for the
galaxies lying inside groups before the completeness limit. We can
extrapolate this redshift completeness limit assuming the typical depth of
the new generation of redshift surveys using 10 meter class telescopes
(Keck and VLT). For example, the deep part of the Virmos survey should
provide a redshift survey 80% complete down to 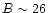 ,
and the shallow
part of this survey a 50% complete redshift catalog down to
,
and the shallow
part of this survey a 50% complete redshift catalog down to 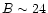 .
Assuming a k-correction proportional to the redshift, it should provide a
catalog of groups complete up to
.
Assuming a k-correction proportional to the redshift, it should provide a
catalog of groups complete up to 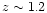 for the deep catalog and
for the deep catalog and 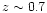 for the shallow catalog. This is enough to sample nearly all classes of
galaxy structures up to
for the shallow catalog. This is enough to sample nearly all classes of
galaxy structures up to 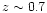 .
This will allow one to put strong
constraints on cosmological models (e.g. Romer et al. 2001) as well as
sampling the internal structure evolution of groups (and more massive
clusters) up to these redshifts.
.
This will allow one to put strong
constraints on cosmological models (e.g. Romer et al. 2001) as well as
sampling the internal structure evolution of groups (and more massive
clusters) up to these redshifts.
The time required to treat these future samples with our method
is very short. We used the simulations of Steve Hatton (private communication)
in order to estimate these times. These simulations cover 1 deg2 and
reproduce an
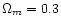 and
and
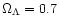 Universe, including
several structures as clusters or groups. We used a single 6' running window
for simplicity and we selected randomly different sub-samples of galaxies in
this catalog. The computation times are given in Fig. 4. We see that a catalog
of 150000 galaxies, comparable to the spectroscopic catalogs which will be
produced by the VLT and Keck surveys, is completely analyzed in about 2 min (using an ES40 Compaq, processor EB67 at 600 Mhz).
Universe, including
several structures as clusters or groups. We used a single 6' running window
for simplicity and we selected randomly different sub-samples of galaxies in
this catalog. The computation times are given in Fig. 4. We see that a catalog
of 150000 galaxies, comparable to the spectroscopic catalogs which will be
produced by the VLT and Keck surveys, is completely analyzed in about 2 min (using an ES40 Compaq, processor EB67 at 600 Mhz).
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{fig_comp2.ps}\end{figure}](/articles/aa/full/2002/02/aa1761/Timg57.gif) |
Figure 3:
Number of detected groups as a function of redshift by Merchan et al. (circles) and with our method (solid line). |
| Open with DEXTER |
We computed the luminosity function of the group galaxies of the detected
sample. The galaxy catalog is complete down to
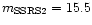 with groups
up to 8000 kms-1. Limiting ourselves to groups with velocity lower than 6000 kms-1 (this velocity limit is close to the completeness limit of the group
sample), we have a galaxy catalog complete down to
with groups
up to 8000 kms-1. Limiting ourselves to groups with velocity lower than 6000 kms-1 (this velocity limit is close to the completeness limit of the group
sample), we have a galaxy catalog complete down to
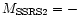
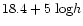 .
Using the estimate of Zabludoff & Mulchaey (2000), this corresponds to
about M*+1.5. We fitted a Schechter function on the magnitude
distribution down to
.
Using the estimate of Zabludoff & Mulchaey (2000), this corresponds to
about M*+1.5. We fitted a Schechter function on the magnitude
distribution down to
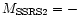
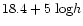 and for groups with
and for groups with
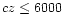 kms-1 using a maximum likelihood technique (e.g. Lobo et al. 1997).
kms-1 using a maximum likelihood technique (e.g. Lobo et al. 1997).
The absolute magnitudes were k-corrected (but this is a minor correction due
to the low redshift of the sample: see Tables 1 and 2) using the k-correction
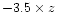 (Rauzy et al. 1998). We also corrected for galactic extinction
using the work by Schlegel et al. (1998). The correction we applied for the
magnitudes was
(Rauzy et al. 1998). We also corrected for galactic extinction
using the work by Schlegel et al. (1998). The correction we applied for the
magnitudes was
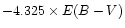 .
The mean correction was 16% of the
luminosity (but up to 60% for the worse cases: see Tables 1 and 2).
.
The mean correction was 16% of the
luminosity (but up to 60% for the worse cases: see Tables 1 and 2).
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{fig_perf.ps}\end{figure}](/articles/aa/full/2002/02/aa1761/Timg63.gif) |
Figure 4:
Computation time (in s) for a simulated catalog of galaxies
including groups and clusters, as a function of the number of galaxies inside
the catalog. |
| Open with DEXTER |
The best fit parameters of a Schechter function are
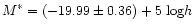 and
and
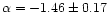 (estimates with 1-
(estimates with 1-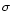 error). This is consistent at the 1-
error). This is consistent at the 1-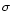 level with the estimates of Zabludoff & Mulchaey (2000):
level with the estimates of Zabludoff & Mulchaey (2000):
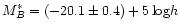 (assuming
(assuming
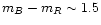 )
and
)
and
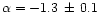 for groups in
2800<cz<7700 kms-1. These values are also similar at the 1-
for groups in
2800<cz<7700 kms-1. These values are also similar at the 1-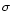 level
with the estimates of Rauzy et al. (1998) for rich clusters of galaxies.
level
with the estimates of Rauzy et al. (1998) for rich clusters of galaxies.
In order to check the robustness of our estimates, we split the sample in
two parts: the northern and the southern galactic cap. The southern cap
gives
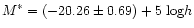 and
and
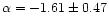 and the
northern cap gives
and the
northern cap gives
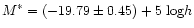 and
and
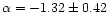 .
Despite the larger uncertainty, these values are still consistent, with, however, a mild tendency to have more faint galaxies in the southern galactic cap.
.
Despite the larger uncertainty, these values are still consistent, with, however, a mild tendency to have more faint galaxies in the southern galactic cap.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{fig_m_l_sig.ps}\end{figure}](/articles/aa/full/2002/02/aa1761/Timg72.gif) |
Figure 5:
Mass to light ratio as a function of the velocity dispersion for
groups of galaxies detected by our method in the SSRS2 galaxy catalog. The
circles are the groups with more than 8 galaxies. |
| Open with DEXTER |
We computed the total luminosity of each group summing up all the individual
magnitudes (see Tables 1 and 2). We used
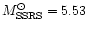 (approximation of
(approximation of
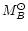 ). We corrected these values for incompleteness due to galaxy
catalog magnitude limit by using the ratio between the luminosity function
integrated from
). We corrected these values for incompleteness due to galaxy
catalog magnitude limit by using the ratio between the luminosity function
integrated from
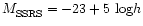 to
to
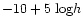 and integrated between
the faintest magnitude of each group and
and integrated between
the faintest magnitude of each group and
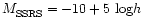 .
This is
because we assumed that the faintest galaxies were not fainter than
.
This is
because we assumed that the faintest galaxies were not fainter than
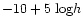 .
This limit has, however, a moderate influence on this correction
factor. We used the luminosity function computed in the previous section
with
.
This limit has, however, a moderate influence on this correction
factor. We used the luminosity function computed in the previous section
with
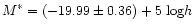 and
and
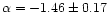 .
The
mean correction was 135% of the raw group luminosity. The total
luminosities and the individual completeness corrections are given in Tables 1 and 2.
.
The
mean correction was 135% of the raw group luminosity. The total
luminosities and the individual completeness corrections are given in Tables 1 and 2.
Combining estimates of the mass and of the luminosity, we computed the mass
to light ratio (see Tables 1 and 2). The mean value is 550
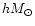 /
/
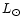 and the median is 250
and the median is 250
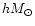 /
/
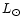 .
We compared
these estimates with those of Carlberg et al. (2001). In the R band, they
computed median values in the range [150; 250]
.
We compared
these estimates with those of Carlberg et al. (2001). In the R band, they
computed median values in the range [150; 250]
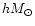 /
/
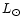 .
Assuming
.
Assuming
 (Allen 1973) and
(Allen 1973) and
 for galaxies in nearby structures (e.g. Katgert et al. 1998),
it corresponds to median values in the range [204; 340]
for galaxies in nearby structures (e.g. Katgert et al. 1998),
it corresponds to median values in the range [204; 340]
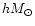 /
/
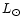 in the SSRS2 magnitude passband (multiplication factor of 10
0.4(1.5-1.17)). This is in good agreement with our estimates. We found a relation between the mass to light ratio and the velocity dispersion
in the SSRS2 magnitude passband (multiplication factor of 10
0.4(1.5-1.17)). This is in good agreement with our estimates. We found a relation between the mass to light ratio and the velocity dispersion 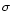 for our sample (see Fig. 5 and Table 3).
for our sample (see Fig. 5 and Table 3).
These relations are qualitatively similar to the relation we found between
rich cluster velocity dispersion and cluster mass to light ratio (Adami et al. 1998):
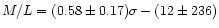 .
The slope is,
however, significantly steeper for groups than for clusters. The slope of
these relations is also similar to that of Carlberg et al. (2001) which is
close to 3.5. The more massive the group (or the cluster), the higher the
mass to light ratio, and therefore, the larger the amount of dark matter
inside the group (or cluster). Another explanation would be a very efficient
stripping of the gas of the galaxies in rich groups (as opposed to very low
mass groups). This would be due to a denser intra group medium or a more
efficient tidal stripping due to the higher number of galaxies (e.g. Dos Santos & Mamon 1999) in rich groups. It would lower the star formation rate in galaxies, inducing a higher mass to light ratio for the richest groups (see also Carlberg et al. 2001). The dispersion of the relation is also smaller for richer groups. This is probably due to a better computation of
the velocity dispersion due to the larger number of available galaxies.
.
The slope is,
however, significantly steeper for groups than for clusters. The slope of
these relations is also similar to that of Carlberg et al. (2001) which is
close to 3.5. The more massive the group (or the cluster), the higher the
mass to light ratio, and therefore, the larger the amount of dark matter
inside the group (or cluster). Another explanation would be a very efficient
stripping of the gas of the galaxies in rich groups (as opposed to very low
mass groups). This would be due to a denser intra group medium or a more
efficient tidal stripping due to the higher number of galaxies (e.g. Dos Santos & Mamon 1999) in rich groups. It would lower the star formation rate in galaxies, inducing a higher mass to light ratio for the richest groups (see also Carlberg et al. 2001). The dispersion of the relation is also smaller for richer groups. This is probably due to a better computation of
the velocity dispersion due to the larger number of available galaxies.
Schaeffer et al. (1993) or Adami et al. (1998) have shown, using optical
data, that clusters of galaxies populate a well defined area in the [total
luminosity: L, characteristic radius of a beta profile: 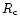 ,
velocity
dispersion:
,
velocity
dispersion: 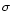 ]
space. Adami et al. (1998) found the following
relation:
]
space. Adami et al. (1998) found the following
relation:
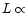
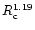
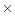
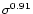 with a dispersion of the
relation of 5
with a dispersion of the
relation of 5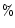 .
.
Using the virial radius instead of the characteristic radius of a beta
profile would give:
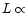
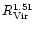
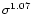 .
.
This relation, called the fundamental plane, is also detected for elliptical
galaxies, but with different coefficients (see Adami et al. 1998 for a
comparison). This is interpreted as the different relaxation state of
elliptical galaxies and clusters of galaxies. We searched for the same kind
of relation in the groups we detected. Using all the groups, we found no
relation between L,
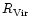 and
and 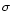 .
Using only
groups with more than 8 galaxies, we found:
.
Using only
groups with more than 8 galaxies, we found:
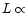
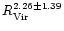
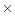
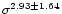 with a
dispersion of 58
with a
dispersion of 58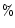 .
.
The coefficients are consistent with those of clusters of galaxies, but the
uncertainties are very large, and the intrinsic dispersion of the relation
is 10 times larger than for clusters. We conclude that a mean relation
between L,
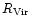 and
and 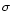 probably exists for groups, but this
relation is much less well defined than for rich clusters. Moreover, poor
groups (less than 7 galaxies) probably have too large a velocity dispersion
uncertainty to allow any detection of this relation.
probably exists for groups, but this
relation is much less well defined than for rich clusters. Moreover, poor
groups (less than 7 galaxies) probably have too large a velocity dispersion
uncertainty to allow any detection of this relation.
We demonstrated that we are able to detect similar populations of groups
with our method compared to classical friend-of-friend algorithms. The
groups detected with our method have the same physical properties as those
detected by Merchan et al. (2000): nearly the same mass distribution (most of
our groups are in the range [
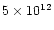 ;
;
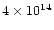 ]
solar masses),
same abundances up to
]
solar masses),
same abundances up to
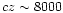 kms-1 (and, therefore, same completeness
limit:
kms-1 (and, therefore, same completeness
limit: 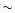 5000 kms-1 and abundances in agreement with Press & Schechter
models), and same 2-point correlation function (modeled by a power law:
5000 kms-1 and abundances in agreement with Press & Schechter
models), and same 2-point correlation function (modeled by a power law:
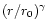 with
r0=7 h-1 Mpc and
with
r0=7 h-1 Mpc and
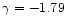 ).
).
This redshift completeness limit close to 5000 kms-1 is directly related to
the magnitude limit of the catalog:
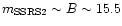 .
Extrapolating these limits assuming the typical depth of the new generation
of redshift surveys using 10 meter class telescopes (Keck and VLT) leads to
a redshift completeness limit of
.
Extrapolating these limits assuming the typical depth of the new generation
of redshift surveys using 10 meter class telescopes (Keck and VLT) leads to
a redshift completeness limit of 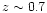 for the groups in these
samples.
for the groups in these
samples.
We found for the SSRS2 catalog a similar luminosity function for nearby group
galaxies to that of Zabludoff et al. (2000):
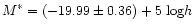 and
and
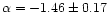 .
We computed a similar mass to light ratio compared to Carlberg
et al. (2001) (median value of 250
.
We computed a similar mass to light ratio compared to Carlberg
et al. (2001) (median value of 250
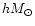 /
/
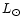 in the B
SSRS2 magnitude passband) and we deduced a similar relation between the mass
to light ratio and velocity dispersion (
in the B
SSRS2 magnitude passband) and we deduced a similar relation between the mass
to light ratio and velocity dispersion (
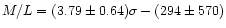 ). This relation is qualitatively similar to that detected for
rich clusters of galaxies (Adami et al. 1998), but with a significantly
steeper slope. The more massive the group (or the cluster), the higher the
mass to light ratio, and therefore, the larger the amount of dark matter
inside the group (and cluster). Another explanation is a significant stripping
of the gas of the galaxies in rich groups as opposed to poorer groups.
Finally, we detected a fundamental plane for these groups (
). This relation is qualitatively similar to that detected for
rich clusters of galaxies (Adami et al. 1998), but with a significantly
steeper slope. The more massive the group (or the cluster), the higher the
mass to light ratio, and therefore, the larger the amount of dark matter
inside the group (and cluster). Another explanation is a significant stripping
of the gas of the galaxies in rich groups as opposed to poorer groups.
Finally, we detected a fundamental plane for these groups (
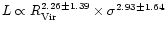 for groups with more
than 8 galaxies) but that is much less narrow and barely significant compared to
clusters of galaxies. We conclude that a mean relation between L,
for groups with more
than 8 galaxies) but that is much less narrow and barely significant compared to
clusters of galaxies. We conclude that a mean relation between L,
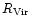 and
and 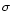 probably exists for groups, but this relation is much less
well defined compared to clusters.
probably exists for groups, but this relation is much less
well defined compared to clusters.
Acknowledgements
The authors thank the referee for useful comments, all the VIRMOS team
in France and Italy for help and F. Durret for a careful reading of the
manuscript.
- Adami, C., Mazure, A., Biviano, A., et al. 1998, A&A, 331, 493
In the text
NASA ADS
- Allen, C. 1973, Astrophysical Quantities, University of London (the Athlone Press)
In the text
- Beers, T., Flyn, K., & Gebhardt, K. 1990, AJ, 100, 32
In the text
NASA ADS
- Borgani, S., Rosati, P., Tozzi, P., & Norman, C. 1999, ApJ, 517, 40
In the text
NASA ADS
- Burke, D., Collins, C., Sharples, R., et al. 1997, ApJ, 488, L83
In the text
NASA ADS
- Carlberg, R., Yee, H., Morris, S., et al. 2001, ApJ, 552, 427
In the text
NASA ADS
- da Costa, L., Willmer, C., Pellegrini, P., et al. 1998, AJ, 116, 1
NASA ADS
- Ebeling, H., Jones, L., Perlman, E., et al. 2000, ApJ, 534, 133
In the text
NASA ADS
- Gioia, I., Henry, J., Maccacaro, T., et al. 1990, ApJ, 356, L35
In the text
NASA ADS
- Girardi, M., Boschin, W., & da Costa, L. 2000, A&A, 353, 57
In the text
NASA ADS
- Huchra, J., & Geller, M. 1982, ApJ, 257, 423
In the text
NASA ADS
- Katgert, P., Mazure, A., den Hartog, R., et al. 1998, A&AS, 129, 399
In the text
NASA ADS
- Katgert, P., Mazure, A., Perea, J., et al. 1996, A&A, 310, 8
In the text
NASA ADS
- Lax, D. 1985, J. Am. Stat. Assoc., 80, 736
In the text
- Lobo, C., Biviano, A., Durret, F., et al. 1997, A&A, 317, 385
In the text
NASA ADS
- Merchan, M., Maia, M., & Lambas, D. 2000, ApJ, 545, 26
In the text
NASA ADS
- Oukbir, J., & Blanchard, A. 1997, A&A, 317, 1
In the text
NASA ADS
- Oukbir, J., & Blanchard, A. 1992, A&A, 262, L21
In the text
NASA ADS
- Press, W., & Schechter, P. 1974, ApJ, 187, 425
In the text
NASA ADS
- Ramella, M., Pisani, A., & Geller, M. 1997, AJ, 113, 483
In the text
NASA ADS
- Rauzy, S., Adami, C., & Mazure, A. 1998, A&A, 337, 31
In the text
NASA ADS
- Romer, A., Viana, P., Liddle, A., & Mann, R. 2001, ApJ, 547, 594
In the text
NASA ADS
- Romer, A., Nichol, R., Holden, B., et al. 2000, ApJS, 126, 209
In the text
NASA ADS
- Dos Santos, S., & Mamon, G. 1999, A&A, 352, 1
NASA ADS
- Schaeffer, R., Maurogordato, S., Cappi, A., & Bernardeau, F. 1993,
MNRAS, 263, L21
In the text
NASA ADS
- Schlegel, D., Finkbeiner, D., & Davis, M. 1998, ApJ, 500, 525
In the text
NASA ADS
- Vikhlinin, A., Mc Namara, B., Forman, W., et al. 1998, ApJ 498, L21
In the text
NASA ADS
- Zabludoff, A., & Mulchaey, J. 2000, A&A, 331, 493
In the text
NASA ADS
Copyright ESO 2002
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{fig_sig2.ps}\end{figure}](/articles/aa/full/2002/02/aa1761/Timg32.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{fig_interlop.ps}\end{figure}](/articles/aa/full/2002/02/aa1761/Timg40.gif)
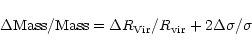
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{fig_comp2.ps}\end{figure}](/articles/aa/full/2002/02/aa1761/Timg57.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{fig_perf.ps}\end{figure}](/articles/aa/full/2002/02/aa1761/Timg63.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{fig_m_l_sig.ps}\end{figure}](/articles/aa/full/2002/02/aa1761/Timg72.gif)