A&A 381, 560-565 (2002)
DOI: 10.1051/0004-6361:20011381

CH2DCCH along the TMC-1 ridge

A. J. Markwick1 - T. J. Millar1 - S. B. Charnley2


1 - Department of Physics, UMIST, PO Box 88, Manchester M60 1QD, UK
2 - Space Science Division, NASA Ames Research Center, MS 245-3, Moffett Field, CA 94035, USA

Received 9 May 2001 / Accepted 2 October 2001

Abstract
In this paper we present measurements of the ${\rm CH_2DCCH}/{\rm CH_3CCH}$ ratio along the TMC-1 ridge. The level of deuterium fractionation in this molecule is found to be larger than previously thought, but more significantly, the fractionation increases as one moves from the cyanopolyyne peak to the ammonia peak, as is the case with measurements of other molecules in TMC-1. This confirms the prediction of our recent chemical/dynamical model of TMC-1 and supports the hypothesis that the chemical evolution of TMC-1 has been affected by Alfvén waves.

Key words: MHD: waves - ISM: abundances - ISM: molecules - ISM: individual (Taurus Molecular Cloud) - molecular processes


1 Introduction

The small, dark interstellar cloud TMC-1 is a dense, quiescent ridge of gas which runs southeast to northwest in the Heiles Cloud 2 complex of dark interstellar dust clouds, at a distance of 140 pc. It contains an embedded protostellar source, IRAS 04381+2540 towards the northwestern end. When the ridge was mapped in HC7N and NH3, the distributions of these molecules were found to differ - the HC7N emission peaks near the southeastern end of the ridge, but ammonia peaks further to the northwest (Olano et al. 1988). These regions have become known as the CP (cyanopolyyne peak) and the AP (ammonia peak). A comprehensive study by Pratap et al. (1997), in which abundances are measured relative to HCO+, shows abundance gradients for several molecules, the most pronounced being for CS, SO, HCN, HNC, C2H, HC3N.

Studies of deuterated species have also shown spatial gradients to exist along the ridge, this time in the level of fractionation. Observations show that the fractionation in the molecules HCO+, C3H2, HC3N and HNC increases from the CP to the AP (Guélin et al. 1982; Butner & Charnley 1997, 2001; Bell et al. 1988; Howe et al. 1994; Hirota & Yamamoto 1998; Hirota et al. 2001).

In Markwick et al. (2000), we presented a model which produces the molecular abundance gradients and explains the organic diversity in the CP region. The model is based on the assumption that shear Alfvén waves are propagating in TMC-1, perhaps from the embedded protostellar source IRAS 04381+2540. In Markwick et al. (2000), Alfvén waves are shown to be capable of desorbing grain ice mantles, releasing the carbonaceous species C2H2, C2H4 and CH4 into the gas phase, which then react in a complex chemistry to enhance the abundances of other organic compounds. After some time, the carbon chain species are destroyed and molecules like ammonia begin to be formed. If the waves propagate along the ridge from the IRAS source through AP to CP, releasing mantles as they go, the CP region will be younger than the AP in chemical terms, and the observed gradients in molecular abundance are reproduced. There is circumstantial evidence for the propagation of MHD waves in TMC-1. Firstly, they could be responsible for the observed superthermal molecular line widths (Arons & Max 1975), and furthermore, the dissipation length of the waves, which is the length over which chemistry is affected, is similar to the clump sizes observed in CCS by Peng et al. (1998).

Recently, the model was augmented to include deuterium chemistry to address the fractionation gradient issue, and to treat more completely the effect of the wave on the cloud chemistry (Markwick et al. 2001, hereafter Paper I). In particular, the small ion-neutral drift induced by the passing wave enhances the rates of ion-neutral reactions, enabling small energy barriers to be overcome (Charnley 1998). Some of the most affected reactions are fundamental to molecular deuteration, for example the reaction $\rm {H_2D^+} + \rm {H_2} \longrightarrow \rm {H_3^+} + \rm {HD}$. This reaction is usually ineffective at 10 K, but becomes around 106 times faster as the wave passes, effectively switching off deuteration for a time. This has a devastating effect on the fractionation ratios of the major deuterating ions, thereby affecting the fractionation of all species. After the wave passes, the above reaction switches off and deuteration proceeds normally, ultimately recovering to its pre-wave value. In Paper I, the passage of the Alfvén wave was shown to be capable of causing the molecular abundance and the fractionation gradients.

Previously, however, the comparison of the model with observations was limited to the molecules for which spatial information was available at the time; DCO+, C3HD, DC3N and DNC. Here, we present measurements of the ${\rm CH_2DCCH}/{\rm CH_3CCH}$ ratio at various positions along the ridge between the cyanopolyyne peak and the ammonia peak for comparison with the model.

2 Observations

The observations were made in December 2000 with the Onsala 20 m Space Observatory in Sweden. The lines we observed are shown in Table 1. CH2DCCH has been observed previously at TMC-1:CP by Gerin et al. (1992), and we chose to observe one of the same lines, namely the 606-505 line at 97.081 GHz. For ${\rm CH_3CCH}$, we chose the lines observed by Pratap et al. (1997) in their comprehensive study of TMC-1. These are the 60-50 and 61-51 lines at 102.548 and 102.546 GHz respectively. Because of the long integration times involved to observe ${\rm CH_2DCCH}$ (around 6 hours per point), we were only able to obtain column densities for ${\rm CH_2DCCH}$ at three positions. We obtained column densities for ${\rm CH_3CCH}$ at 6 positions. The observations were made with the SIS 100 GHz receiver. The beam size is 40''. The backend was the low resolution correlator (LRC) with a bandwith of 20 MHz and 1600 channels, giving a spectral resolution of 12.5 kHz. For the ${\rm CH_3CCH}$ observations, we used frequency switching with a throw of 4 MHz and for ${\rm CH_2DCCH}$ we used beam switching, where the throw is 11'. The pointing errors were typically 2'' rms on each axis, determined by observing the IK Tau SiO maser emission. The system temperature was 400 K on average, although on 2 nights the weather was too bad to observe. We had enough time to determine the fractionation of ${\rm CH_3CCH}$ in 3 positions; TMC-1:CP and two further points, the most distant from CP being about 60% of the way towards the ammonia peak.


 

 
Table 1: Molecular line data.
Species Transition $\nu_{\rm rest}$ (GHz) $E_{\rm u}$ (K) Q(10) $S_{\rm ul}g_Kg_I$ f(T)
CH2DCCH 606-505 97.080695 16.3 62.56 6.000 1.467
CH3CCH 60-50 102.547983 17.2 38.01 6.001 1.477
CH3CCH 61-51 102.546023 24.4 38.01 5.834 1.477



 

 
Table 2: Observational data. The offsets are in seconds of arc relative to TMC-1:CP. N is the total column density in each molecule, assuming the statistical ortho/para ratio of 3:1.
Position Species $T_{\rm mb}$ $\Delta v$ $T_{\rm mb}\Delta v$ N
    (K) (km s-1) (K km s-1) (1013 cm-2)
(0, 0) CH2DCCH 0.20 0.41 0.087 $1.61\pm 0.30$
  CH3CCH K=0 1.35 0.44 0.640 $7.39\pm 0.70$
  CH3CCH K=1 1.25 0.45 0.600 $14.6\pm 1.37$
(-40, +90) CH3CCH K=0 1.42 0.32 0.484 $5.59\pm 0.57$
  CH3CCH K=1 1.31 0.31 0.427 $10.4\pm 1.26$
(-80, +150) CH2DCCH 0.34 0.25 0.091 $1.68\pm 0.30$
  CH3CCH K=0 1.32 0.32 0.453 $5.23\pm 0.60$
  CH3CCH K=1 1.25 0.36 0.484 $11.8\pm 1.19$
(-120, +200) CH3CCH K=0 1.71 0.26 0.474 $5.47\pm 0.57$
  CH3CCH K=1 1.73 0.25 0.456 $11.1\pm 1.17$
(-160, +240) CH2DCCH 0.34 0.24 0.088 $1.63\pm 0.35$
  CH3CCH K=0 1.21 0.27 0.415 $4.79\pm 0.59$
  CH3CCH K=1 1.23 0.23 0.305 $7.44\pm 1.19$
(-200, +310) CH3CCH K=0 0.67 0.34 0.242 $2.79\pm 0.39$
  CH3CCH K=1 0.64 0.26 0.181 $4.41\pm 0.80$



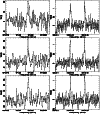  \begin{figure} \hbox{\psfig{figure=ms1456f1.ps,width=9cm,height=6.825cm}\psfig{f... ...ght=6.825cm}\psfig{figure=ms1456f6.ps,width=9cm,height=6.825cm} } \end{figure} Figure 1: Observed spectra at offsets (0, 0), (-80, +150) and (-160, +240) from TMC-1:CP (top to bottom). The left panels show ${\rm CH_2DCCH}\ 6_{06}{-}5_{05}$ and the right panels ${\rm CH_3CCH}\ 6_{0}{-}5_{0}$ and 61-51. The spectra are unsmoothed, and linear baselines have been removed.
Open with DEXTER

3 Data analysis

The observed spectra for three positions are shown in Fig. 1. In the data reduction, we averaged the individual scans over position, weighting them according to system temperature. We have removed only linear baselines, and the spectra are shown unsmoothed.

Deriving column densities from these observations requires knowledge of the rotational temperature of the molecules. For this, we use the estimates given in Pratap et al. (1997), which were derived from methyl acetylene, and which were shown to be consistent with adopting a temperature of 10 K along the ridge from CP to AP. We therefore take the rotational temperature as 10 K at all positions. In practice, the ${\rm CH_2DCCH}/{\rm CH_3CCH}$ abundance ratio is not sensitive to the assumed temperature (Gerin et al. 1992).

For an optically thin line, the relationship between its integrated area $T_{\rm b}\Delta$v and the total column density N is

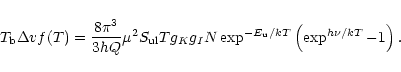
\begin{displaymath}T_{\rm b}\Delta{v}f(T)=\frac{8\pi^3}{3hQ}\mu^2S_{\rm ul}Tg_Kg_IN\exp ^{-E_{\rm u}/kT}\left(\exp^{h\nu/kT}-1\right).\end{displaymath}

Here, $\mu$ is the electric dipole moment, gK and gI are the state degeneracies and Q is the partition function. We took $\mu=0.78$D, and obtained the quantities Q and $S_{\rm ul}g_Kg_I$ from tabulated data in the JPL catalogue (Pickett et al. 1998). The factor f(T) is given by

\begin{displaymath}f(T)=\frac{kT}{h\nu}\left[\left({\rm e}^{h\nu /kT}-1\right)^{-1}-\left({\rm e}^{h\nu /kT_{\rm bg}}-1\right)^{-1}\right]^{-1}\end{displaymath}

where $T_{\rm bg}=2.73$ K. The values of the molecular line parameters are given in Table 1. The column densities derived for each line at each position we observed are shown in Table 2, along with the integrated intensities and other observational data.

3.1 Ortho/para ratios

Both the species we observed exist in ortho and para forms. For ${\rm CH_3CCH}$, we have observed lines with K=0 (A symmetry state) and K=1 (E symmetry state), which correspond to ortho and para respectively. Column 6 in Table 2 lists the total column densities in each molecule assuming the statistical ortho/para ratio of 3:1. The fact that these numbers are different for the two lines of ${\rm CH_3CCH}$ is indicative of the actual ortho/para ratio being different from this. Therefore, we have used the observations of the two ${\rm CH_3CCH}$ lines to determine the ortho/para ratio in this species at the various positions observed. This is presented in Table 3. The ratio is found to vary between 4:3 and 2:1. For ${\rm CH_2DCCH}$, Table 2 also shows the total column density assuming 3:1. Since we have observed only the K=0 (para) line, we have assumed the ortho/para ratio for this species to be the same as that of CH3CCH at the same position. The result of this adjustment is shown in Table 4.


 

 
Table 3: Ortho/para ratios, determined from the CH3CCH data. The offsets are in seconds of arc relative to TMC-1:CP.
Offset ('') o/p ratio
(0, 0) 1.52
(-40, +90) 1.61
(-80, +150) 1.33
(-120, +200) 1.48
(-160, +240) 1.93
(-200, +310) 1.90


   
4 Discussion

CH2DCCH has been observed previously at TMC-1:CP by Gerin et al. (1992), who obtained a fractionation ratio of between 0.05 and 0.06 depending on the kinetic temperature used - a relatively high ratio (compare DCO $^+ \sim 0.013$). In Paper I, we presented predictions for the spatial variation of the fractionation ratio of several molecules, including methyl acetlyene, which was found to rise quite steeply along the ridge compared to other species (see Paper I, Table 7), a prediction confirmed by the observations presented here. Table 4 shows the total column densities, adjusted for the derived ortho/para ratio, and the calculated ${\rm CH_2DCCH}/{\rm CH_3CCH}$ abundance ratios. The ratio we obtained at TMC-1:CP is 0.11, a factor of 2 higher the ratio obtained by Gerin et al. (1992). A comparison of the derived column densities at TMC-1:CP in each case shows that for a rotational temperature of 10 K, Gerin et al. found $1.7\times 10^{14}$ and $9.2\times 10^{12}$ cm-2 for ${\rm CH_3CCH}$ and ${\rm CH_2DCCH}$ respectively, giving a ratio of 0.054. On the other hand, we find column densities of $9.18\times 10^{13}$ and $1.01\times 10^{13}$ cm-2 respectively, giving 0.110. The column density of ${\rm CH_3CCH}$ observed recently at TMC-1:CP by Pratap et al. (1997) is $8.1\times 10^{13}$ cm-2. The level of fractionation we find in ${\rm CH_2DCCH}$ is the largest observed at TMC-1:CP.


 

 
Table 4: Column density determinations and levels of fractionation observed. The offsets are in seconds of arc relative to TMC-1:CP.
Offset ('') R $N_{{\rm CH_2DCCH}}$ $N_{{\rm CH_3CCH}}$
    (1013 cm-2) (1013 cm-2)
(0, 0) $0.11\pm 0.03$ $1.01\pm 0.19$ $9.18\pm 0.87$
(-40, +90) - - $6.80\pm 0.69$
(-80, +150) $0.14\pm 0.05$ $0.98\pm 0.17$ $6.87\pm 0.79$
(-120, +200) - - $6.87\pm 0.72$
(-160, +240) $0.22\pm 0.04$ $1.19\pm 0.26$ $5.45\pm 0.67$
(-200, +310) - - $3.19\pm 0.45$


Gerin et al. also placed an upper limit on the column density of CH3CCD. We chose not to observe this molecule, due to the long integration times we estimated based on this previous search. However, in light of the results presented here, it appears that another search for this molecule is necessary.

4.1 Chemistry of CH2DCCH


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms1456f7.ps} \end{figure} Figure 2: Observed spatial variations of the fractionation in DC3N (triangles; Howe et al. 1994), C3HD (squares; Bell et al. 1988), DCO+ (stars; Butner & Charnley 1997, 2001), DNC (crosses; Hirota et al. 2001) and CH2DCCH (diamonds; this work) along the TMC-1 ridge. The vertical lines mark the positions of the CP and AP.
Open with DEXTER

Theoretical models of deuterium fractionation form ${\rm CH_2DCCH}$ through the CH2D+ ion, by dissociative recombination of CH2DC2H2+ or CH2DC3H2+ ions, which are themselves formed from CH2D+ by ion-neutral reactions with smaller hydrocarbon species like methane or acetylene. ${\rm CH_2DCCH}$ is destroyed by atomic and molecular ions, primarily H3+ and He+. Since experimental data is scarce for deuterium reactions of importance in the ISM, a deuterium chemistry is usually constructed with statistical analogues. There are two assumptions in this method which are important for the abundance of ${\rm CH_2DCCH}$. First, a deuteron cannot change site in the same molecule in the same reaction, e.g. the reaction

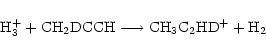
\begin{displaymath}{\rm H_3^+} + {\rm CH_2DCCH} \longrightarrow {\rm CH_3C_2HD^+} + {\rm H_2} \end{displaymath}

is not allowed. Second, any branching ratios are statistical, that is, the reactions

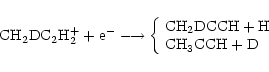
\begin{displaymath}\rm {CH_2DC_2H_2^+} + \rm {e^-} \longrightarrow \left\{ \begi... ...DCCH} + \rm {H} \\ \rm {CH_3CCH} + \rm {D} \end{array} \right. \end{displaymath}

will have rates $\frac{3}{5}k$ and $\frac{2}{5}k$ respectively, where the analogue reaction rate is k.

If either of these assumptions are wrong, the amount of ${\rm CH_2DCCH}$ produced in the models will change. There is already some evidence from storage ring experiments that dissociative recombination reactions preferentially form deuterated species (Jensen et al. 2000). Where experimental data exists, it is put into the reaction schemes, but there are still many reactions (like those above) which are assumed to have statistical branching ratios and as such are possible sources of error. In this case, the ratio ${\rm CH_2DCCH}/{\rm CH_3CCH}$ will be enhanced if dissociative recombination prefers to form ${\rm CH_2DCCH}$.

Current gas-phase deuterium chemistries place the ratio ${\rm CH_2DCCH}/{\rm CH_3CCH}$ at 0.070 (Markwick et al. 2001). Roberts & Millar (2000) get 0.099, but their model excludes CH3CCD as a separate species, so this is an overestimate of the true ratio. These numbers are in reasonably good agreement with the observed ratio of 0.11 at the CP, but are in worse agreement as we move away from this point. There are now a few species whose observed fractionation ratios are higher than gas-phase models can predict, the others being C3HD and DC3N. While there has been considerable interest recently in the detection of doubly deuterated species and their production in chemical models, it is worth noting that there remain species for which the level of single deuteration remains unexplained by these models.

4.2 Fractionation gradients

Since in this paper we are primarily interested in the spatial variations of the fractionation, we plot in Fig. 2 the fractionation ratios of a number of molecules as a function of position along the ridge. In Paper I, we noted that while we could explain the spatial increase in fractionation along the ridge between the CP and AP, we generally underestimated the size of each increase. Again, we find this to be the case for ${\rm CH_3CCH}$. The observations presented here give us a value of 0.28 for the increase in log fractionation along the ridge. The value predicted in Paper I is 0.27, which is almost the same as the observed value, but this prediction is for the whole CP-AP distance, whereas we have observed to a point roughly 60% of the way (see Fig. 2). If the fractionation keeps increasing towards the AP, as it does for the other observed molecules, then our predicted value is an underestimate of the true gradient. We found this to be the case for the previously observed species as well, and therefore it appears that our model is neglecting a process or suppressing a mechanism which could increase the fractionation further. In Paper I we speculated that this could be the accretion of gas phase species back onto grain surfaces. As the timescale for accretion is comparable to our assumed age difference between the CP and AP ($\sim$ $2 \times 10^5$ yr), we might expect to see the effects of accretion between the peaks. Another more interesting possibility that we have not considered yet is periodic MHD waves sweeping the gas in TMC-1. It is not obvious what effect this will have on the deuterium chemistry. These topics will therefore be the subject of a future paper.

4.3 Why this model?

In Paper I we noted that there are different ways to increase the level of fractionation in a chemical model - differences in the density of the gas or differential accretion, for example. Why is this model to be preferred over the other, simpler solutions? To answer this question, consider Fig. 2, which shows the spatial position along the TMC-1 ridge of measurements of deuterated molecular species. The curious thing here is that between TMC-1:CP and AP, the level of fractionation increases monotonically. Taking DC3N as an example, there are two points away from TMC-1:CP where the fractionation is greater. For DCO+ there are 3. In this work, we show that for CH2DCCH there are 2. For the other species observed (C3HD, DNC), there is 1. With two exceptions, none of these observations are at the same position. On the basis of the available data, one is forced to conclude that deuterium fractionation increases monotonically from TMC-1:CP to AP.

Now if we wanted to use a different argument to explain the existence of monotonic fractionation gradients, say, differential depletion due to density differences, we would then have to explain why the density varies monotonically along the ridge. Alternatively, if we assume that we actually have a distribution of densities and have just happened to observe monotonic gradients by chance, we find that there is a less than one percent chance of getting Fig. 2.

The monotonic fractionation gradients produced by our model are a natural consequence of the Alfvén wave traversing the ridge and resetting the clock, making TMC-1:CP less advanced chemically than AP. Without this feature, it is difficult to see how the spatial variations could be systematic.

We note also that there are other recent observations of TMC-1 which are being interpreted as due to Alfvén wave activity (Dickens et al. 2000).

5 Conclusion

We have determined the level of deuterium fractionation in ${\rm CH_3CCH}$ at three positions along the TMC-1 ridge between the cyanopolyyne peak and ammonia peak. We find that the fractionation ratio is large, from 0.11 to 0.22 in the three positions observed. Gas-phase models predict a ${\rm CH_2DCCH}/{\rm CH_3CCH}$ ratio of between 0.07 and 0.10 at TMC-1:CP, in reasonable agreement with our observation. These models will, however, fail to produce the higher ratios we find away from the CP, a discrepancy which could possibly due to the assumption of statistical branching ratios in deuterium fractionation chemical modelling. The high level of fractionation in CH2DCCH also suggests that another search for CH3CCD would be successful.

The observations show that there is a positive gradient in ${\rm CH_2DCCH}/{\rm CH_3CCH}$ along the TMC-1 ridge from CP to AP, as predicted in Paper I, and therefore support the hypothesis that the chemical evolution of molecular gas in TMC-1 has been affected by Alfvén waves.

Acknowledgements

Research in Astrophysics at UMIST is supported by PPARC. Theoretical astrochemistry at NASA Ames is supported by NASA's Origins of Solar Systems and Exobiology Programs through NASA Ames Interchange NCC2-1162.

References

 

Copyright ESO 2002