We built K band extinction maps in the area of two candidate low-extinction windows in the inner Bulge: W0.2-2.1 at (
A&A 381, 219-226 (2002)
DOI: 10.1051/0004-6361:20011541
C. M. Dutra1,2 - B. X. Santiago1 - E. Bica1
1 - Universidade Federal do Rio Grande do Sul, IF,
CP15051, Porto Alegre 91501-970, RS, Brazil
2 -
Instituto Astronomico e Geofisico da USP, CP 3386, São Paulo 01060-970, SP,
Brazil
Received 9 March 2001 / Accepted 30 October 2001
Abstract
We built K band extinction maps in the area of two candidate
low-extinction windows in the inner Bulge: W0.2-2.1 at
(![]() )
= (0.25
)
= (0.25![]() ,
-2.15
,
-2.15![]() ), and W359.4-3.1 at
(
), and W359.4-3.1 at
(![]() )
= (359.40
)
= (359.40![]() ,
-3.10
,
-3.10![]() ). We employed
). We employed
![]() photometry from the 2MASS Point Source Catalog.
Extinction values were determined by fitting the upper giant branch found
in the present 2MASS
photometry from the 2MASS Point Source Catalog.
Extinction values were determined by fitting the upper giant branch found
in the present 2MASS ![]() (
(
![]() )
diagrams to a de-reddened
bulge stellar population reference giant branch. We tested
the method on the well known Baade's and Sgr I windows: the 2MASS
mean extinction values in these fields agreed well with those of
previous studies.
We confirm the existence of low-extinction windows in the regions studied,
as local minima in the AK maps reaching AK values about 2 standard deviations below
the mean values found in the neighbouring areas. Schlegel et al.'s (1998) FIR extinction maps, which integrate dust
contributions throughout the Galaxy, are structurally similar to
those derived with 2MASS
photometry in the two studied windows. We thus conclude that
the dust clouds affecting the 2MASS and FIR maps in these directions
are basically the same and are located
on foreground of the bulk of bulge stars. However, the AK
absolute values differ significantly. In particular, the
FIR extinction values for W359.4-3.1 are a factor
)
diagrams to a de-reddened
bulge stellar population reference giant branch. We tested
the method on the well known Baade's and Sgr I windows: the 2MASS
mean extinction values in these fields agreed well with those of
previous studies.
We confirm the existence of low-extinction windows in the regions studied,
as local minima in the AK maps reaching AK values about 2 standard deviations below
the mean values found in the neighbouring areas. Schlegel et al.'s (1998) FIR extinction maps, which integrate dust
contributions throughout the Galaxy, are structurally similar to
those derived with 2MASS
photometry in the two studied windows. We thus conclude that
the dust clouds affecting the 2MASS and FIR maps in these directions
are basically the same and are located
on foreground of the bulk of bulge stars. However, the AK
absolute values differ significantly. In particular, the
FIR extinction values for W359.4-3.1 are a factor ![]() 1.45 larger
than those derived from
the 2MASS photometry. Possible explanations of this effect are discussed.
The lower Galactic latitudes of the low-extinction
windows W359.4-3.1 and W0.2-2.1, as compared to Baade's Window, make
them promising targets for detailed studies of more central bulge regions.
1.45 larger
than those derived from
the 2MASS photometry. Possible explanations of this effect are discussed.
The lower Galactic latitudes of the low-extinction
windows W359.4-3.1 and W0.2-2.1, as compared to Baade's Window, make
them promising targets for detailed studies of more central bulge regions.
Key words: Galaxy: interstellar medium: dust
Most of the Bulge stellar population is still largely unstudied due to the combined effects of large distances and high extinction. The information on Bulge stellar populations comes mainly from either globular clusters or from its M and K field giant stars. Yet, the study of the age and metallicity distribution in this region is of considerable importance, since a comprehensive study of the resolved Galactic Bulge allows us to better understand the bulge of external early and late type galaxies. Furthermore, inferring the main properties of the Bulge and comparing them to those of other components of the Galaxy is likely to provide clues to unveiling the process of galaxy formation (Aguerri et al. 2001; Wyse et al. 2000).
During the last years the Galactic Bulge stellar population has been studied mainly in the direction of low-extinction regions (Lloyd Evans 1976; Whitford 1978; Terndrup 1988; Tiede et al. 1995; Alard et al. 2001). Baade (1963) identified the windows Sgr I, Sgr II, and the NGC 6522 field; this latter has been widely referred to as Baade's Window in subsequent studies. Stanek (1996) studied the extinction distribution in Baade's Window using the OGLE photometry of red clump stars, obtaining values from AV = 1.26 up to AV = 2.79. Frogel et al. (1999, hereafter FTK99) determined the extinction for 11 inner Bulge fields using Baade's Window red giant branch as a reference, yielding values in the range AV = 2.41 up to 19.20.
Recently, wide-angle near infrared (NIR) surveys such as the
Two Micron All Sky Survey (hereafter, 2MASS;
Skrutskie et al. 1997) and the Deep NIR Southern Sky Survey (DENIS;
Epchtein et al. 1997) have
allowed investigations of the stellar population
(Unavane et al. 1998) and reddening (Schultheis et al. 1999) in
the inner Bulge. Schultheis et al. (1999) mapped the extinction in the inner
Bulge for ![]() < 8
< 8![]() and |b| < 1.5
and |b| < 1.5![]() (with a resolution of 4
(with a resolution of 4![]() )
using isochrone fitting to the
colour-magnitude diagrams (CMDs) obtained from DENIS
J,
)
using isochrone fitting to the
colour-magnitude diagrams (CMDs) obtained from DENIS
J, ![]() observations. The extinction varies from AV
observations. The extinction varies from AV ![]() 6 up to AV
6 up to AV ![]() 37.
They showed that the extinction and, as a consequence, the dust clouds
in the inner Bulge, present a very patchy distribution.
37.
They showed that the extinction and, as a consequence, the dust clouds
in the inner Bulge, present a very patchy distribution.
In the present study we use the 2MASS survey in the J (1.25 ![]() m),
H (1.65
m),
H (1.65 ![]() m) and
m) and ![]() (2.17
(2.17 ![]() m) bands to identify low-extinction windows in the inner
Galactic Bulge. In Sect. 2
we discuss the process to select low-extinction candidate regions in the
inner Galactic Bulge. In Sect. 3 we discuss
the method of deriving extinction values throughout these regions,
provide a reddening
distribution map for them and analyse the results. Finally, the concluding
remarks are given in Sect. 4.
m) bands to identify low-extinction windows in the inner
Galactic Bulge. In Sect. 2
we discuss the process to select low-extinction candidate regions in the
inner Galactic Bulge. In Sect. 3 we discuss
the method of deriving extinction values throughout these regions,
provide a reddening
distribution map for them and analyse the results. Finally, the concluding
remarks are given in Sect. 4.
In search for candidate low-extinction regions we
used the DIRBE/IRAS dust emission redddening map from Schlegel et al.
(1998, hereafter SFD98), which is available
in Web Interface http://astro.berkeley.edu/dust. The extinction
maps derived from these far infra-red
observations will be referred to as "FIR extinction maps'' throughout
the present work. Analogously, we will use the notation AK,FIR to
denote the K band extinction derived from SFD98 data.
Stanek (1998) identified two
low-extinction windows
on the FIR extinction maps, centred at (![]() , b) =
(0
, b) =
(0![]() ,
-2
,
-2![]() )
and (
)
and (![]() , b) = (4
, b) = (4![]() ,
-3
,
-3![]() ).
Although the FIR extinction corresponds to the contribution of the
entire dust column
throughout the Galaxy (Dutra & Bica 2000), its angular distribution
can help with the selection of potentially interesting areas of
low-extinction towards the Bulge. We obtained
).
Although the FIR extinction corresponds to the contribution of the
entire dust column
throughout the Galaxy (Dutra & Bica 2000), its angular distribution
can help with the selection of potentially interesting areas of
low-extinction towards the Bulge. We obtained
![]() values
in the field of 10
values
in the field of 10![]()
![]() 10
10![]() around the Galactic
Centre from the original overall FIR map in SFD98, using an
extraction tool thereby provided. Figure 1 shows the resulting AK,FIR extinction map, where the positions of the
three low-reddening regions from Baade (1963), two from Stanek (1998), and
a newly identified one, are indicated.
The transformation from
around the Galactic
Centre from the original overall FIR map in SFD98, using an
extraction tool thereby provided. Figure 1 shows the resulting AK,FIR extinction map, where the positions of the
three low-reddening regions from Baade (1963), two from Stanek (1998), and
a newly identified one, are indicated.
The transformation from
![]() to AK,FIR
assumed AK = 0.112 AV and
RV = AV/E(B-V) = 3.1 (Cardelli et al. 1989).
to AK,FIR
assumed AK = 0.112 AV and
RV = AV/E(B-V) = 3.1 (Cardelli et al. 1989).
In Table 1 we condense the basic information on the mentioned bulge windows. By columns: (1) adopted designation throughout the present study (a practical way to refer to the windows is "W'' followed by its values of galactic coordinates), (2) other designations, (3) and (4) galactic coordinates, (5) approximate angular dimensions, (6) reference for window identification, and (7) extinction map and photometric source.
| Name | Other Designation |
|
b( |
d( |
Reference | Photometry |
| W359.4-3.1 | ---- | 359.40 | -3.10 | 40 |
present study | 2MASS (present study) |
| W0.2-2.1 | (l, b)= (0, -2) Window | 0.24 | -2.14 | 60 |
Stanek (1998) | 2MASS (present study) |
| Baade's Window | NGC6522 field,W1.0-3.9 | 1.04 | -3.88 | 60 | Baade (1963) | OGLE (Stanek 1996) |
| Sgr I Window | W1.4-2.6 | 1.44 | -2.64 | 60 | Baade (1963) | ----- |
| W4.0+3.0 | (l, b)= (4, 3) Window | 4.00 | 3.00 | 180 |
Stanek (1998) | ----- |
| Sgr II Window | W4.2-5.1 | 4.15 | -5.14 | 85 | Baade (1963) | ----- |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2738f1.ps}\end{figure}](/articles/aa/full/2002/01/aah2738/Timg25.gif) |
Figure 1:
10
|
| Open with DEXTER | |
Figure 2 shows the
![]() maps within 2
maps within 2![]()
![]() 2
2![]() around (
around (![]() , b) = (0
, b) = (0![]() ,
-2
,
-2![]() ).
This region should contain W0.2-2.1, listed in Table 1 and which was
originally identified by Stanek (1998).
In fact, we can more precisely locate this window at
(
).
This region should contain W0.2-2.1, listed in Table 1 and which was
originally identified by Stanek (1998).
In fact, we can more precisely locate this window at
(![]() , b) = (0.25
, b) = (0.25![]() ,
-2.15
,
-2.15![]() ), with
dimensions
), with
dimensions ![]()
![]() .
This is a
nearly closed region in Fig. 2 where
.
This is a
nearly closed region in Fig. 2 where
![]() values
are systematically below
the average value in the map,
values
are systematically below
the average value in the map,
![]() = 0.41.
The lowest
= 0.41.
The lowest
![]() values within W0.2-2.1 reach down to
values within W0.2-2.1 reach down to
![]() ,
which corresponds
to about 2 standard deviations (std) below the mean. Therefore, there is
a well defined local
,
which corresponds
to about 2 standard deviations (std) below the mean. Therefore, there is
a well defined local
![]() minimum in this area.
minimum in this area.
Figure 3 shows a similar map centred at (![]() , b) =
(0
, b) =
(0![]() ,
-2
,
-2![]() ),
close to the new candidate low-extinction region proposed in this work,
W359.4-3.1.
A distinct region with lower than average
),
close to the new candidate low-extinction region proposed in this work,
W359.4-3.1.
A distinct region with lower than average
![]() values is again visible;
it is centred at (
values is again visible;
it is centred at (![]() , b) = (359.40
, b) = (359.40![]() ,
-3.10
,
-3.10![]() ), with
), with
![]() in size. This region has a deeper minimum,
reaching
in size. This region has a deeper minimum,
reaching
![]() ,
which is 2.5 std below the average map value
of
,
which is 2.5 std below the average map value
of
![]() = 0.42. It is also more circular in shape and completely
encircled by areas of larger
= 0.42. It is also more circular in shape and completely
encircled by areas of larger
![]() values.
We should point out that, by inspection of the FIR extincion map in Fig. 1,
one notices that even the average
values.
We should point out that, by inspection of the FIR extincion map in Fig. 1,
one notices that even the average
![]() values in Figs. 2 and 3 are
very atypical for their (
values in Figs. 2 and 3 are
very atypical for their (![]() , b) location.
, b) location.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2738f2.ps}\end{figure}](/articles/aa/full/2002/01/aah2738/Timg32.gif) |
Figure 2:
FIR extinction map of window W0.2-2.1.
Contour levels correspond to
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2738f3.ps}\end{figure}](/articles/aa/full/2002/01/aah2738/Timg33.gif) |
Figure 3:
FIR extinction map of window W359.4-3.1.
The contour levels correspond to
|
| Open with DEXTER | |
An alternative way to obtain K band extinction values and to
build extinction maps for W0.2-2.1 and W359.4-3.1 is to use
the 2MASS JK![]() photometry available in
Web Interface
photometry available in
Web Interface
http://irsa.ipac.caltech.edu/applications/Gator/.
2MASS also provides H band data, but
we prefer not to use them, since the (J-K![]() )
colours
appear to be more sensitive to extinction variations than the
(H-K
)
colours
appear to be more sensitive to extinction variations than the
(H-K![]() )
ones; this is probably due to the larger wavelength interval.
)
ones; this is probably due to the larger wavelength interval.
We extracted the 2MASS data for stars with 8.0 ![]() K
K![]()
![]() 11.5
within 1
11.5
within 1![]() radius centred on the Galactic coordinates
(
radius centred on the Galactic coordinates
(![]() , b) = (0.0
, b) = (0.0![]() ,
-2.0
,
-2.0![]() )
and (
)
and (![]() , b) =
(359.0
, b) =
(359.0![]() ,
-3.0
,
-3.0![]() ).
These are the same centers as in the FIR extinction maps discussed in
the previous subsection.
The choice of K
).
These are the same centers as in the FIR extinction maps discussed in
the previous subsection.
The choice of K![]() magnitude range for data extraction is motivated
by the fact that the upper giant branch is as well defined and linear
in this range as in Baade's window. The total number of extracted stars
from the 2MASS database were 90407 in the W0.2-2.1 region and
69286 in the W359.4-3.1 region. For comparison, we also extracted
2MASS data from regions at (
magnitude range for data extraction is motivated
by the fact that the upper giant branch is as well defined and linear
in this range as in Baade's window. The total number of extracted stars
from the 2MASS database were 90407 in the W0.2-2.1 region and
69286 in the W359.4-3.1 region. For comparison, we also extracted
2MASS data from regions at (![]() , b) = (1.0
, b) = (1.0![]() ,
-3.0
,
-3.0![]() )
and (
)
and (![]() , b) = (1.0
, b) = (1.0![]() ,
-4.0
,
-4.0![]() ), which include the
Sgr I (48040 stars) and Baade's (20358 stars) windows, respectively (see
Table 1). We note, however, that the 2MASS archive data do not
yet provide complete coverage of these two comparison fields.
The mean magnitude errors from the extracted 2MASS data are
), which include the
Sgr I (48040 stars) and Baade's (20358 stars) windows, respectively (see
Table 1). We note, however, that the 2MASS archive data do not
yet provide complete coverage of these two comparison fields.
The mean magnitude errors from the extracted 2MASS data are
![]() = 0.04
= 0.04 ![]() 0.01 and
0.01 and
![]() = 0.04
= 0.04 ![]() 0.01. These photometric errors
bracket 95% and 92% of all extracted stars, respectively for J and
0.01. These photometric errors
bracket 95% and 92% of all extracted stars, respectively for J and ![]() .
.
In order to map the selected low-extinction regions in AK, we define
small square cells with
![]() .
The extinction in each cell
was determined by upper
giant branch fitting to its observed CMD, similar to the FTK99 extinction
determination method.
FTK99 derived AK values for their fields using the upper giant
branch of Baade's window (Tiede et al. 1995) as reference.
Our reference upper giant branch was defined from that of FTK99.
We proceeded as follows: we first extracted 2MASS photometry for
seven fields from FTK99. These fields are g0-1.8a, g0-2.3a, g0-2.8a,
g1-1.3a, g2-1.3a, g3-1.3a and g4-1.3a, where the field designation
incorporates its position in Galactic coordinates. We used the K and
.
The extinction in each cell
was determined by upper
giant branch fitting to its observed CMD, similar to the FTK99 extinction
determination method.
FTK99 derived AK values for their fields using the upper giant
branch of Baade's window (Tiede et al. 1995) as reference.
Our reference upper giant branch was defined from that of FTK99.
We proceeded as follows: we first extracted 2MASS photometry for
seven fields from FTK99. These fields are g0-1.8a, g0-2.3a, g0-2.8a,
g1-1.3a, g2-1.3a, g3-1.3a and g4-1.3a, where the field designation
incorporates its position in Galactic coordinates. We used the K and ![]() filter transmission curves given in
Persson et al. (1998) and the extinction curve of Cardelli et al. (1989) to obtain the ratios
filter transmission curves given in
Persson et al. (1998) and the extinction curve of Cardelli et al. (1989) to obtain the ratios
![]() ,
,
![]() and
and
![]() .
These ratios allow us to transform from
.
These ratios allow us to transform from
![]() to AK. The
relation between
extinction and reddening
to AK. The
relation between
extinction and reddening
![]() (Mathis 1990)
was used to derive the relation
(Mathis 1990)
was used to derive the relation
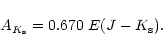 |
(1) |
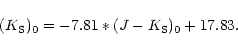 |
(2) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2738f4.ps}\end{figure}](/articles/aa/full/2002/01/aah2738/Timg47.gif) |
Figure 4: Determination of the upper giant branch mean locus from the combined CMD of the fields in Frogel et al. (1999). |
| Open with DEXTER | |
In panels (5a) and (5c)
we show extinction-corrected (![]() )0, (
)0, (
![]() )0 CMDs
for stars of typical cells in the W0.2-2.1 and W359.4-3.1 maps,
respectively.
Each CMD was corrected by the median extinction derived
from the histograms of AK values in each cell.
These histograms are shown
in panels (5b) and (5d) for the cells in W0.2-2.1 and W359.4-3.1 maps, respectively,
their median values being
)0 CMDs
for stars of typical cells in the W0.2-2.1 and W359.4-3.1 maps,
respectively.
Each CMD was corrected by the median extinction derived
from the histograms of AK values in each cell.
These histograms are shown
in panels (5b) and (5d) for the cells in W0.2-2.1 and W359.4-3.1 maps, respectively,
their median values being
![]() = 0.54
= 0.54 ![]() 0.16 and
0.16 and
![]() = 0.33
= 0.33 ![]() 0.10.
We note that there are secondary upper giant branches in the CMDs
and consequently a second peak in AK distribution for the two cells
(at <AK> = 0.14 and
0.02 for the chosen cells in W0.2-2.1 and W359.4-3.1, respectively).
These are probably caused
by a secondary dust layer or to a dust cloud variation scale smaller than
4 arcmin along the lines of sight considered.
0.10.
We note that there are secondary upper giant branches in the CMDs
and consequently a second peak in AK distribution for the two cells
(at <AK> = 0.14 and
0.02 for the chosen cells in W0.2-2.1 and W359.4-3.1, respectively).
These are probably caused
by a secondary dust layer or to a dust cloud variation scale smaller than
4 arcmin along the lines of sight considered.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2738f5.ps}\end{figure}](/articles/aa/full/2002/01/aah2738/Timg49.gif) |
Figure 5:
a) (K |
| Open with DEXTER | |
For the comparison regions, which include the
low-extinction Sgr I and Baade's windows, we
obtain
![]() = 0.23
= 0.23 ![]() 0.05 and
0.05 and
![]() =
0.18
=
0.18 ![]() 0.04, respectively, using the same method described above.
Glass et al. (1995) studied variable stars
in the Sgr I window and adopted AK= 0.21. For Baade's Window,
considering the extinction map obtained by Stanek (1996) and zero-point
calibrations (Gould et al. 1998; Alcock et al. 1998), the mean extinction
is <AK> = 0.17
0.04, respectively, using the same method described above.
Glass et al. (1995) studied variable stars
in the Sgr I window and adopted AK= 0.21. For Baade's Window,
considering the extinction map obtained by Stanek (1996) and zero-point
calibrations (Gould et al. 1998; Alcock et al. 1998), the mean extinction
is <AK> = 0.17 ![]() 0.03. The adopted extinction determination method
and the 2MASS photometry produce results compatible to those found in the
literature. Thus, they are certainly
useful to map the extinction in the inner Galactic Bulge, although one
has to keep in mind that
regions much closer to the Galactic Centre are more affected by crowding
and highly variable
extinction, which may in turn have an impact on photometric precision and
on the applicability of the method.
Another issue is the possible existence of metallicity gradients in the stellar
content of the inner Bulge, which may result in systematic errors in
the inferred extinction values (Schultheis et al. 1999). However, there
is some recent evidence,
based on spectroscopy of M giants, against significant metallicity variations
in that region (Ramírez et al. 2000).
0.03. The adopted extinction determination method
and the 2MASS photometry produce results compatible to those found in the
literature. Thus, they are certainly
useful to map the extinction in the inner Galactic Bulge, although one
has to keep in mind that
regions much closer to the Galactic Centre are more affected by crowding
and highly variable
extinction, which may in turn have an impact on photometric precision and
on the applicability of the method.
Another issue is the possible existence of metallicity gradients in the stellar
content of the inner Bulge, which may result in systematic errors in
the inferred extinction values (Schultheis et al. 1999). However, there
is some recent evidence,
based on spectroscopy of M giants, against significant metallicity variations
in that region (Ramírez et al. 2000).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2738f6.ps}\end{figure}](/articles/aa/full/2002/01/aah2738/Timg50.gif) |
Figure 6:
2MASS extinction map of window W0.2-2.1. Contour
levels correspond to
|
| Open with DEXTER | |
Figures 6 and 7 show the
![]() maps for the W0.2-2.1 and
W359.4-3.1 regions, respectively. These contour maps are similar in shape
to those shown in Figs. 2 and 3. In both figures we see nearly
closed regions with
maps for the W0.2-2.1 and
W359.4-3.1 regions, respectively. These contour maps are similar in shape
to those shown in Figs. 2 and 3. In both figures we see nearly
closed regions with
![]() .
The mean extinction values
are
.
The mean extinction values
are
![]() in W0.2-2.1 and
in W0.2-2.1 and
![]() in W359.4-3.1. Therefore, some cells
within the low-extinction windows have
in W359.4-3.1. Therefore, some cells
within the low-extinction windows have
![]() value about 2 std below the mean map values.
Note that the lack of contours
in the corners of the figures just reflects the circular areas used for
the 2MASS extractions.
value about 2 std below the mean map values.
Note that the lack of contours
in the corners of the figures just reflects the circular areas used for
the 2MASS extractions.
Panels a) and c) of Fig. 8 show the histograms
of
![]() values for all
the cells in the W0.2-2.1 and W359.4-3.1 maps.
In W0.2-2.1 there is a larger number
of cells with high
values for all
the cells in the W0.2-2.1 and W359.4-3.1 maps.
In W0.2-2.1 there is a larger number
of cells with high
![]() values than in W359.4-3.1.
This reflects the closer proximity of the former field to
the Galactic Centre.
Panels b) and d) of the same figure show
the internal errors in
the determination of the
values than in W359.4-3.1.
This reflects the closer proximity of the former field to
the Galactic Centre.
Panels b) and d) of the same figure show
the internal errors in
the determination of the
![]() values as a function
of
values as a function
of
![]() itself.
These errors correspond to the std of the final, sigma-clipped,
histogram of
itself.
These errors correspond to the std of the final, sigma-clipped,
histogram of
![]() values in each cell.
We notice that in W0.2-2.1 the internal errors have a larger
dispersion with
values in each cell.
We notice that in W0.2-2.1 the internal errors have a larger
dispersion with
![]() .
Such behaviour was also found
by FTK99 and is due to the small scale variations of
the dust distribution in the region. The mean internal errors
are
.
Such behaviour was also found
by FTK99 and is due to the small scale variations of
the dust distribution in the region. The mean internal errors
are ![]() = 0.09
= 0.09 ![]() 0.03
in W0.2-2.1 and
0.03
in W0.2-2.1 and ![]() = 0.08
= 0.08 ![]() 0.03 in W359.4-3.1.
These errors are somewhat higher than
those estimated by FTK99 in their Bulge fields. The reason is that
that our 4
0.03 in W359.4-3.1.
These errors are somewhat higher than
those estimated by FTK99 in their Bulge fields. The reason is that
that our 4
![]() 4
4![]() cells
are larger than those used by FTK99 (1.5
cells
are larger than those used by FTK99 (1.5
![]() 1.5
1.5![]() )
and should, therefore, include a larger dispersion by dust gradients.
)
and should, therefore, include a larger dispersion by dust gradients.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2738f7.ps}\end{figure}](/articles/aa/full/2002/01/aah2738/Timg56.gif) |
Figure 7:
2MASS extinction map of window W359.4-3.1. Contour
levels correspond to
|
| Open with DEXTER | |
The bulge windows W0.2-2.1 and W359.4-3.1 are relatively closer to the Galactic Centre than Sgr I, Sgr II and Baade's windows and are located in a hole surrounded by the dark clouds LDN48, LND43, LDN1801, LDN1769, LDN1783, LDN3, LDN1795, LDN1788 from the Lynds' (1962) catalogue and FSDN435, FSDN431, FSDN430, FSDN444 from the Feitzinger & Stüwe's (1984) catalogue.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2738f8.ps}\end{figure}](/articles/aa/full/2002/01/aah2738/Timg57.gif) |
Figure 8:
2MASS extinction histogram for window W0.2-2.1 in panel a),
and for W359.4-3.1 in panel c). Extinction internal errors
as a function of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2738f9.ps}\end{figure}](/articles/aa/full/2002/01/aah2738/Timg59.gif) |
Figure 9:
Comparison of FIR and 2MASS extinction values for cells in windows W0.2-2.1 (panel a)) and W359.4-3.1 (panel b)). The identity function is indicated as a straight line. The function
|
| Open with DEXTER | |
As mentioned previously, the 2MASS extinction maps of Figs. 6 and 7
show essentially the same features as the FIR extinction maps
(Figs. 2 and 3). In order to investigate this similarity in a more
quantitative manner, we convolve the 2MASS AK extinction maps with
a ![]() = 4.5
= 4.5![]() Gaussian, obtaining a resolution
of approximately 6
Gaussian, obtaining a resolution
of approximately 6![]() FWHM, which
is compatible with that of SFD98's extinction maps (6.1
FWHM, which
is compatible with that of SFD98's extinction maps (6.1![]() ).
Figure 9 shows the comparison between the
).
Figure 9 shows the comparison between the
![]() and
and
![]() values for both low-extinction windows.
values for both low-extinction windows.
In both panels we see a clear correlation between
![]() and
and
![]() ,
quantitatively confirming the similarities between the two extinction maps.
The relation between the two AK estimates, however, has a much more complex
pattern in W0.2-2.1 (Panel 9a) than in W359.4-3.1 (Panel 9b). We see several branches
in panel 9a, some above the identity line, some lying below it.
We verify that the cells that form these
particular structures in the AK scatter plot correspond to
specific spatial regions in the extinction map.
These may correspond to lines of sight crossing specific dust clouds whose
physical characteristics, most specially dust temperature and density, could
yield distinct signatures in their emission and absorption properties.
As mentioned in the end of the previous section, several individual
dark clouds lying close to and around our two low-extinction regions have
been catalogued.
,
quantitatively confirming the similarities between the two extinction maps.
The relation between the two AK estimates, however, has a much more complex
pattern in W0.2-2.1 (Panel 9a) than in W359.4-3.1 (Panel 9b). We see several branches
in panel 9a, some above the identity line, some lying below it.
We verify that the cells that form these
particular structures in the AK scatter plot correspond to
specific spatial regions in the extinction map.
These may correspond to lines of sight crossing specific dust clouds whose
physical characteristics, most specially dust temperature and density, could
yield distinct signatures in their emission and absorption properties.
As mentioned in the end of the previous section, several individual
dark clouds lying close to and around our two low-extinction regions have
been catalogued.
In the W359.4-3.1 region (panel 9b), there is a distribution much closer to
linear relation between
![]() and
and
![]() .
The slope in this relation, however,
is larger than unity:
.
The slope in this relation, however,
is larger than unity:
![]() .
Arce & Goodman (1999) obtained a similar result in their analysis of the
Taurus dark cloud complex (
.
Arce & Goodman (1999) obtained a similar result in their analysis of the
Taurus dark cloud complex (
![]() 15
15![]() );
by comparing the dust emission values derived by SFD98
to those derived from four other methods,
including a dust emission extinction derived directly from 100
);
by comparing the dust emission values derived by SFD98
to those derived from four other methods,
including a dust emission extinction derived directly from 100 ![]() m
flux with temperature corrections.
They concluded that SFD98 may be overestimating extinction
by a factor varying from 1.3 to 1.5.
They also pointed out that this factor could not be due to overestimation of
the ratio of total-to-selective extinction RV,
because several studies (Kenyon et al. 1994; Vrba & Rydgren 1985; and
recently Whittet et al. 2001) suggested that the RV = 3.1 in
most parts of the Taurus dark cloud complex, in regions where the visual extinction is lower than AV < 3.0.
This systematic effect in
m
flux with temperature corrections.
They concluded that SFD98 may be overestimating extinction
by a factor varying from 1.3 to 1.5.
They also pointed out that this factor could not be due to overestimation of
the ratio of total-to-selective extinction RV,
because several studies (Kenyon et al. 1994; Vrba & Rydgren 1985; and
recently Whittet et al. 2001) suggested that the RV = 3.1 in
most parts of the Taurus dark cloud complex, in regions where the visual extinction is lower than AV < 3.0.
This systematic effect in
![]() may originate
from SFD98's calibration of the dust
column density
may originate
from SFD98's calibration of the dust
column density ![]() reddening relation, which was derived
in regions of low to moderate extinction (
reddening relation, which was derived
in regions of low to moderate extinction (
![]() ), but
may not apply equally well to the high extinction regime.
), but
may not apply equally well to the high extinction regime.
As a helping tool in understanding the differences in
the
![]() and
and
![]() values, we have considered the amount of dust expected to
lie beyond the inner Galactic Bulge, therefore being located
behind most of the stars measured by 2MASS. This dust located on the far
side of the Galaxy will have an obvious influence
over the
values, we have considered the amount of dust expected to
lie beyond the inner Galactic Bulge, therefore being located
behind most of the stars measured by 2MASS. This dust located on the far
side of the Galaxy will have an obvious influence
over the
![]()
![]()
![]() correlation,
since it is expected to
affect the first but not the second extinction value.
A simple model of dust distributed on
a plane with an exponential drop both along and perpendicular
to this plane has been used to predict the relative contribution
of the material
on the far side of the Galaxy. We thus consider a model of linear absorption
coefficient given by:
correlation,
since it is expected to
affect the first but not the second extinction value.
A simple model of dust distributed on
a plane with an exponential drop both along and perpendicular
to this plane has been used to predict the relative contribution
of the material
on the far side of the Galaxy. We thus consider a model of linear absorption
coefficient given by:
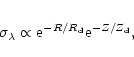
Temperature effects may play a role in explaining the observed features,
since dust clouds in the direction of the Galactic Centre may be warmer on
average than elsewhere. In addition, the low resolution
(![]() 1
1![]() )
of SFD98's temperature maps increases the
uncertainties in the
)
of SFD98's temperature maps increases the
uncertainties in the
![]() temperature corrections, especially in
zones of large temperature gradients.
Figure 10 shows SFD98's temperature map in the central 10
temperature corrections, especially in
zones of large temperature gradients.
Figure 10 shows SFD98's temperature map in the central 10![]() of the Galaxy. Despite the low
resolution, we notice that W0.2-2.1 is much closer to a local peak
in the dust temperature map than W359.4-3.1.
This adds support to the idea of temperature gradients
contributing to the complexity of Panel 9a as compared to Panel 9b.
of the Galaxy. Despite the low
resolution, we notice that W0.2-2.1 is much closer to a local peak
in the dust temperature map than W359.4-3.1.
This adds support to the idea of temperature gradients
contributing to the complexity of Panel 9a as compared to Panel 9b.
Additional sources of scatter in the
![]() relation are possible contamination effects in both datasets.
As pointed out by SFD98, extragalactic and unresolved Galactic
sources at low Galactic latitudes (|b| < 5
relation are possible contamination effects in both datasets.
As pointed out by SFD98, extragalactic and unresolved Galactic
sources at low Galactic latitudes (|b| < 5![]() )
have not been
removed from the dust maps. They could be an important
contribution to increase
)
have not been
removed from the dust maps. They could be an important
contribution to increase
![]() values in very low latitudes,
in particular in the
Bulge window closer the Galactic Plane, W0.2-2.1. Concerning the 2MASS data,
apart from applying the
values in very low latitudes,
in particular in the
Bulge window closer the Galactic Plane, W0.2-2.1. Concerning the 2MASS data,
apart from applying the ![]() clipping of the AK distribution in
each cell, we did not attempt any further correction for contaminating
foreground disk stars.
clipping of the AK distribution in
each cell, we did not attempt any further correction for contaminating
foreground disk stars.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2738f10.ps}\end{figure}](/articles/aa/full/2002/01/aah2738/Timg70.gif) |
Figure 10:
10
|
| Open with DEXTER | |
We identified a new low-extinction window towards the Galactic Bulge,
W359.4-3.1, located at (![]() , b) = (359.40
, b) = (359.40![]() ,
-3.10
,
-3.10![]() )
and
of size
)
and
of size
![]() ,
using a
10
,
using a
10![]()
![]() 10
10![]() map around the Galactic Centre
extracted from Schlegel et al.'s (1998) FIR emission reddening database.
map around the Galactic Centre
extracted from Schlegel et al.'s (1998) FIR emission reddening database.
Using the infrared photometry available from the 2MASS JHK![]() survey
archive, we built
survey
archive, we built
![]() extinction maps for
W359.4-3.1 and for W0.2-2.1, this latter
window previously identified by Stanek (1998). The extinction values were
determined by means of upper giant branch fitting, using as a reference
the upper giant branch of fields previously studied by
Frogel et al. (1999). The extinction determination method and the 2MASS
photometry were tested on fields with well known low-extinction values:
Sgr I and Baade's Window (Baade 1963). Our
derived extinction values for these windows agree well with previous values
quoted in the literature, indicating that the present method is a useful
tool for the study of the bulge windows.
extinction maps for
W359.4-3.1 and for W0.2-2.1, this latter
window previously identified by Stanek (1998). The extinction values were
determined by means of upper giant branch fitting, using as a reference
the upper giant branch of fields previously studied by
Frogel et al. (1999). The extinction determination method and the 2MASS
photometry were tested on fields with well known low-extinction values:
Sgr I and Baade's Window (Baade 1963). Our
derived extinction values for these windows agree well with previous values
quoted in the literature, indicating that the present method is a useful
tool for the study of the bulge windows.
The
![]() maps confirmed the existence of the two bulge windows.
The mean extinction in the field around W0.2-2.1 is
maps confirmed the existence of the two bulge windows.
The mean extinction in the field around W0.2-2.1 is
![]() = 0.29
= 0.29
![]() 0.05, whereas in the field around W359.4-3.1 we obtained
0.05, whereas in the field around W359.4-3.1 we obtained
![]() = 0.28
= 0.28 ![]() 0.04.
In both cases we find an area of systematically lower than average
0.04.
In both cases we find an area of systematically lower than average
![]() values, with minima around
values, with minima around
![]() .
These windows are located very close to the Galactic Centre, through a
hole in the distribution of known dark clouds.
The extinction maps obtained with 2MASS data show very similar features
to those based on FIR dust emission data.
However, some systematic effects, usually
in the sense that
.
These windows are located very close to the Galactic Centre, through a
hole in the distribution of known dark clouds.
The extinction maps obtained with 2MASS data show very similar features
to those based on FIR dust emission data.
However, some systematic effects, usually
in the sense that
![]() ,
are seen
when a direct comparison of the two extinction estimates is made.
In particular, for the W359.4-3.1 region,
,
are seen
when a direct comparison of the two extinction estimates is made.
In particular, for the W359.4-3.1 region,
![]() with a small scatter. For W0.2-2.1, which lies closer to
the Galactic Centre, the situation is more complex, with several structures
with distinct correlations between dust emission and absorption being present.
with a small scatter. For W0.2-2.1, which lies closer to
the Galactic Centre, the situation is more complex, with several structures
with distinct correlations between dust emission and absorption being present.
The qualitative agreement suggests that the dust clouds that
redden the bulk of Bulge stars
are the main contributors to the dust emission in the region. Indeed,
a simple model for the distribution of dust shows that
most of the dust clouds
in the line of sight towards the low-extinction windows should be located
on the near side of the Galaxy. The amount of dust expected to lie
beyond the Galactic Centre does not alone explain the quantitative
differences between
![]() and
and
![]() .
These may be caused by temperature
variations as a function of distance from the centre of the Galaxy or
from one individual dust cloud to another. Alternatively, systematic effects
in the conversion of DIRBE/IRAS maps into extinction measures might explain
the observed differences. It is not possible to
disentangle these effects using only the data shown here.
.
These may be caused by temperature
variations as a function of distance from the centre of the Galaxy or
from one individual dust cloud to another. Alternatively, systematic effects
in the conversion of DIRBE/IRAS maps into extinction measures might explain
the observed differences. It is not possible to
disentangle these effects using only the data shown here.
These low-extinction windows are interesting new targets to studies of the properties of the Bulge stellar population, especially considering their location closer to the Galactic Centre than Baade's Window.
Acknowledgements
We thank Dr. D. Schlegel for pointing out to us the availability of a new version of his software dust-getval for reading the temperature maps. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. We also have made use of the NASA/IPAC Infrared Science Archive, which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the NASA. We acknowledge support from the Brazilian institutions FAPESP and CNPq. CD acknowledges the FAPESP pos-doc fellowship Proc. 00/11864-6.