A&A 381, 311-323 (2002)
DOI: 10.1051/0004-6361:20011659
Coronal seismology through wavelet analysis
I. De Moortel 1 - A. W. Hood 1 - J. Ireland 2
1 - School of Mathematics and Statistics, University of St
Andrews, North Haugh, St Andrews,
Fife KY16 9SS, UK
2 - Osservatorio Astronomica de Capodimonte, via Moiariello 16, 80131 Napoli, Italy
Received 10 September 2001 / Accepted 18 October 2001
Abstract
This paper expands on the suggestion of De Moortel & Hood (2000) that it will be possible to infer coronal plasma properties by making a detailed study of the wavelet transform of observed oscillations. TRACE observations, taken on 14 July 1998, of a flare-excited, decaying coronal loop oscillation are used to illustrate the possible applications of wavelet analysis. It is found that a decay exponent
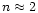 gives the best fit to the double logarithm of the wavelet power, thus suggesting an e
gives the best fit to the double logarithm of the wavelet power, thus suggesting an e
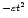 damping profile for the observed oscillation. Additional examples of transversal loop oscillations, observed by TRACE on 25 October 1999 and 21 March 2001, are analysed and a damping profile of the form e
damping profile for the observed oscillation. Additional examples of transversal loop oscillations, observed by TRACE on 25 October 1999 and 21 March 2001, are analysed and a damping profile of the form e
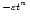 ,
with
,
with
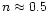 and
and
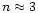 respectively, is suggested. It is demonstrated that an e
respectively, is suggested. It is demonstrated that an e
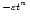 damping profile of a decaying oscillation survives the wavelet transform, and that the value of both the decay coefficient
damping profile of a decaying oscillation survives the wavelet transform, and that the value of both the decay coefficient
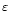 and the exponent n can be extracted by taking a double logarithm of the normalised wavelet power at a given scale. By calculating the wavelet power analytically, it is shown that a sufficient number of oscillations have to be present in the analysed time series to be able to extract the period of the time series and to determine correct values for both the damping coefficient and the decay exponent from the wavelet transform.
and the exponent n can be extracted by taking a double logarithm of the normalised wavelet power at a given scale. By calculating the wavelet power analytically, it is shown that a sufficient number of oscillations have to be present in the analysed time series to be able to extract the period of the time series and to determine correct values for both the damping coefficient and the decay exponent from the wavelet transform.
Key words: MHD - Sun - corona - activity
For several decades, the mechanism(s) by which the solar corona is heated has proved to be a major challenge for solar physicists and it remains yet to be fully understood. An important class of proposed mechanisms are the so called MHD wave heating mechanisms, which rely on the dissipation of wave energy to provide the necessary heating. Although the existence of MHD waves in the corona is widely accepted on theoretical grounds, there is still very little consensus on the direct observation of oscillatory phenomena in the solar atmosphere. Obviously, the detection of oscillations in the corona is a crucial step in determining the presence and relevance of MHD wave heating mechanisms. For a long time, observations were often used in support of a suggested mechanism but were not sufficiently detailed to provide direct evidence of any coronal heating mechanism. Extended reviews of observations of various periodic and quasi-periodic oscillations in the solar atmosphere can be found in e.g. Aschwanden (1987), Tsubaki (1988), Aschwanden et al. (1999) and Roberts (2000). Due to the increased spatial and temporal resolution of current satellite missions such as SOHO and TRACE, recent observations of the solar corona have clearly demonstrated the existence of wave-like motions. For example, Ofman et al. (1997) were first to report quasi-periodic compressive waves in solar polar plumes, using the UVCS (SOHO) white light channel data. DeForest & Gurman (1998) also reported on quasi-periodic compressive waves in plumes, which Ofman et al. (1999) consider to be slow magneto-acoustic waves. Berghmans & Clette (1999) and Robbrecht et al. (2001) found propagating disturbances in coronal loops, observed on 13th May 1998, in the TRACE 171 Å and EIT (SOHO) 195 Å passband. De Moortel et al. (2000) reported on the detection of similar propagating oscillations observed on 23rd March 1999 in the TRACE 171 Å passband, which they suggest to be propagating slow magneto-acoustic waves. A totally different class of oscillatory phenomena, namely flare-excited, transversal oscillations of coronal loops were first discussed by Schrijver et al. (1999), and subsequently by Aschwanden et al. (1999), Nakariakov et al. (1999) and Schrijver & Brown (2000).
As solar observations continue to get better, the idea of coronal seismology, i.e. using observed oscillations as a diagnostic tool to provide information on the plasma supporting the oscillations, is rapidly gaining popularity. From an analysis of a flare-induced, transverse loop oscillation observed by TRACE, Nakariakov et al. (1999) estimated that the coronal dissipation coefficient could be as much as eight or nine orders of magnitude larger than the theoretically predicted classical value. More recently, Nakariakov & Ofman (2001) discuss the possibility of determining the Alfvén speed and magnetic field strength in coronal loops, again using observations of flare-generated loop oscillations. However, in almost all cases, the observed wave motions are not steady harmonic waves but tend to be waves with only a few periods and either are of finite lifetime or are damped. Wavelet analysis is a powerful technique which allows a local decomposition of timescales in the time series and therefore is ideal for analysing non-stationary time series or time series where one expects localised variations of power. In the last few years, wavelet analysis has been used more and more frequently for analysing solar observations. To give a few recent examples, Ofman et al. (2000) found good agreement between the Fourier and wavelet transform methods, used to analyse quasi-periodic oscillations in the south polar coronal hole, observed by the UVCS (SOHO) white light channel. Banerjee et al. (2000) again used both Fourier and wavelet transforms to analyse spectral times series obtained by CDS and reported the existence of oscillations with periods of 20-25 min in polar plumes. Giménez de Castro et al. (2001) identify and characterise the different time scales observed in the different phases of solar bursts at millimeter wavelength, using a wavelet representation of multi-resolution analysis. From high cadence CDS (SOHO) observations, O'Shea et al. (2001) investigate high frequency oscillations in active regions and using the technique of wavelet analysis conclude that certain frequencies are favoured in different spectral lines.
De Moortel & Hood (2000) (Paper I) introduce a method to combine both wavelet analysis and coronal seismology, using wavelet analysis to find out more about the coronal plasma through which observed wave-like oscillations are propagating. It was demonstrated that certain characteristics of, for example, Alfvén wave propagation are present in the wavelet transform and from this it was pointed out that a detailed use of wavelet transforms can provide valuable diagnostic information through coronal seismology. Here we expand further on this idea and in Sect. 2, we consider observed, flare-excited, coronal loop oscillations and, assuming an e
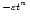 damping profile, use the wavelet transform to obtain estimates for the decay exponent
damping profile, use the wavelet transform to obtain estimates for the decay exponent
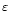 and power n. In Sect. 3, we investigate the effect of the exponential decay on the wavelet transform and how the number of oscillations in the time series affects the values of the period, the damping coefficient and exponent that can be obtained from the wavelet transform. Additionally, the effect of the temporal resolution of a time series on its wavelet transform is examined. Section 4 contains the discussion and conclusions.
and power n. In Sect. 3, we investigate the effect of the exponential decay on the wavelet transform and how the number of oscillations in the time series affects the values of the period, the damping coefficient and exponent that can be obtained from the wavelet transform. Additionally, the effect of the temporal resolution of a time series on its wavelet transform is examined. Section 4 contains the discussion and conclusions.
2 Transverse loop oscillations
In Paper I, it was shown that a detailed study of the wavelet transform can provide information on the damping profile of the analysed time series. However the method was demonstrated for simple harmonic oscillations and we now want to apply the analysis approach described in Paper I on "real'' data. Due to the high spatial and temporal resolution of TRACE (Transition Region and Coronal Explorer) there recently have been a number of observations of flare-excited, transversal oscillations of coronal loops. Schrijver et al. (1999) reported the first detection of such oscillating displacements of coronal loops and a more detailed study was carried out by Aschwanden et al. (1999). From an analysis of the damping of these loop oscillations, Nakariakov et al. (1999) estimated that the coronal dissipation coefficient could be as much as eight or nine orders of magnitude larger than the theoretically predicted classical value. Schrijver & Brown (2000) discuss a different set of flare-excited loop oscillations but also argue that rocking motions of the photosphere (associated with a flare) could cause loops to oscillate. If this is the case, the period and decay rate of the oscillations will be largely determined by the characteristics of the photosphere, saying very little about the properties of the corona. Recently, a database of coronal loop oscillations has been published on the TRACE website
(http:// vestige.lmsal.com/TRACE/POD/looposcillations/ paperI/SchrijverAschwandenTitle.html). The oscillations were analysed by Schrijver et al. (2001) and Aschwanden et al. (2001), and many parameters of the oscillations loops were obtained. We will concentrate our proposed wavelet analysis on the data analysed by Nakariakov et al. (1999) as this is one of the clearest examples of a damped coronal oscillation observed so far.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1907f1.ps}\end{figure}](/articles/aa/full/2002/01/aa1907/Timg30.gif) |
Figure 1:
A
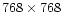 image of active region AR 8270, taken at 13:03 UT on 14 July 1998. The analysed loop is outlined and the box across the loop indicates the location where the loop displacement is determined.
image of active region AR 8270, taken at 13:03 UT on 14 July 1998. The analysed loop is outlined and the box across the loop indicates the location where the loop displacement is determined. |
| Open with DEXTER |
The data is part of observations of active region AR8270, taken by TRACE in the 171 Å bandpass on 14 July 1998. The flare that occurred in this active region at 12:55 UT caused a large adjacent set of loops to oscillate but we will only analyse the isolated, thin, bright loop that was chosen by Nakariakov et al. (1999). These authors fitted the observed loop displacement with a harmonic oscillation with period
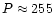 s, multiplied with an e
s, multiplied with an e
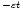 damping profile. The analysed sequence consists of 18 images with a pixel size of 0.5'', starting at 13:08 UT with a nearly constant cadence of about 75 s. Figure 1 shows an
damping profile. The analysed sequence consists of 18 images with a pixel size of 0.5'', starting at 13:08 UT with a nearly constant cadence of about 75 s. Figure 1 shows an
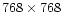 image of active region AR 8270, taken at 13:03 UT. The analysed loop is outlined by the solid, white lines.
image of active region AR 8270, taken at 13:03 UT. The analysed loop is outlined by the solid, white lines.
To determine the loop displacement, we follow the method used by Nakariakov et al. (1999). A 4-pixel-wide slit is taken near the loop apex, roughly perpendicular to the loop axis, as indicated in Fig. 1. For each of the 18 frames in the sequence, the average intensity along this slit is plotted in Fig. 2a. The maximum of this average intensity along the slit is then taken to be the position of the loop at each time step. The loop positions along the slit are plotted as a function of the frame number (from 0 to 17) in Fig. 2b. A displacement of 1 pixel corresponds to 0.5'', which is approximately 360 km. As the original data was not corrected for solar rotation, we have to take this into account when determining the loop oscillation. As a first approximation to correcting for solar rotation, we have just subtracted a linear fit (dashed line) from the intensity maxima. The resulting loop displacement is plotted in Fig. 3a as a function of elapsed time in seconds. This figure is identical to Fig. 2 of Nakariakov et al. (1999). It is clear that there is a decaying oscillation present and in the next section we will use a wavelet analysis to try and determine the characteristics of the damping profile.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1907f2a.ps}\hspace*{4mm}\includegraphics[width=8cm,clip]{1907f2b.ps}\end{figure}](/articles/aa/full/2002/01/aa1907/Timg33.gif) |
Figure 2:
a) The average intensity along the slit for each of the 18 frames in the sequence. b) The position of the maximum of the average intensity along the slit as a function of frame number and a linear fit to these positions (dashed line). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1907f3a.ps}\hspace*{4mm}\includegraphics[width=8cm,clip]{1907f3b.ps}\end{figure}](/articles/aa/full/2002/01/aa1907/Timg34.gif) |
Figure 3:
a) The loop displacement in pixels as a function of elapsed time in seconds. The solid line just connects the actual data points (diamonds). b) The corresponding wavelet transform (99.0% confidence level) where the dashed line indicates the COI. |
| Open with DEXTER |
The wavelet transform of the oscillating loop positions is displayed in Fig. 3b, again as a function of elapsed time in seconds. For the entire length of the time series, there is strong wavelet power present above the 99.0% confidence level. At the start, the wavelet power is concentrated around 260 s and then decreases to about 200 s, which is of the same order as the period found by Nakariakov et al. (1999). Unfortunately, these periods are rather long compared to the length of the time series so that there are only about 4 clear oscillations present and with a cadence of roughly 75 s, the temporal resolution is quite low.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1907f4a.ps}\hspace*{4mm}\includegraphics[width=8cm,clip]{1907f4b.ps}\end{figure}](/articles/aa/full/2002/01/aa1907/Timg35.gif) |
Figure 4:
a) A logarithmic plot of the square-root of the normalised wavelet power, following the maximum of the wavelet power in time, plotted against time in minutes. Again the solid line only connects the actual data points (diamonds) and the dashed lines indicate the COI. The dot-dashed line corresponds to
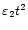 with
with
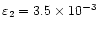 .
b) A close-up of the transform inside the COI. The dot-dot-dashed line and long-dashed line correspond to .
b) A close-up of the transform inside the COI. The dot-dot-dashed line and long-dashed line correspond to
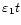 and
and
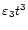 respectively, with
respectively, with
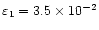 and
and
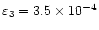 . . |
| Open with DEXTER |
In Fig. 4a we plotted the logarithm of the square-root of the normalised wavelet power on a logarithmic scale. However, as there is a clear change in the period in time, we follow the maximum power at each time step rather than taking a cross-section at a constant period. We have also over plotted where the cone of influence (COI-dashed lines) intersects the wavelet power at the respective periods, so we can get an idea of where our results will be relevant. From Paper I, we know that if the cross-section of the wavelet power tends to a straight line inside the COI, this corresponds to an exponential damping of the original time series. The gradient of the straight line, will give the power of the exponential decay. As the main aim of this paper is to show the potential and limitations of coronal seismology through wavelet analysis, we limit ourselves in this first study to simple, exponential damping profiles. From Fig. 4a, we see that the last section of the wavelet transform inside the COI indeed tends to a straight line and the dot-dashed line is the closest fit using a
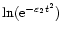 damping profile where t is the time in minutes and
damping profile where t is the time in minutes and
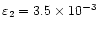 .
The agreement between the fitted profile and the wavelet power is remarkably good, which suggests that the analysed time series has an e
.
The agreement between the fitted profile and the wavelet power is remarkably good, which suggests that the analysed time series has an e
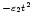 damping profile. Figure 4b is a close-up of the cross-section of the transform inside the COI. To make a comparison, we have now over plotted
damping profile. Figure 4b is a close-up of the cross-section of the transform inside the COI. To make a comparison, we have now over plotted
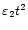 (dot-dashed line),
(dot-dashed line),
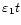 (dot-dot-dashed line) with
(dot-dot-dashed line) with
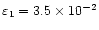 and
and
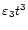 (long-dashed line) with
(long-dashed line) with
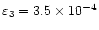 .
It is clear that out of these three fits,
.
It is clear that out of these three fits,
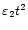 is the better one, fitting the largest number of actual data points. The
is the better one, fitting the largest number of actual data points. The
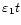 fit, which could have indicated straightforward magnetic damping, is too shallow, whereas the
fit, which could have indicated straightforward magnetic damping, is too shallow, whereas the
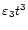 fit, which could have indicated that phase mixing might be responsible for the damping, is too steep.
fit, which could have indicated that phase mixing might be responsible for the damping, is too steep.
Although the identification of these fits has just been done by eye, it gives us a rough estimate of the gradient of the damping profile and the wavelet analysis suggests an exponent close to 2, rather than 1 or 3. Using a least-square (polynomial) fitting routine, the best fit to the straight section of the double logarithm of the wavelet transform is given by
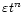 ,
thus implying that the observed oscillation decays as e
,
thus implying that the observed oscillation decays as e
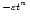 ,
with
,
with
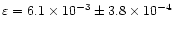 and
and
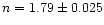 .
.
We now analyse two additional examples, taken from the set of transverse loop oscillations described by Schrijver et al. (2001). The first oscillating time series (Fig. 5a) we consider is associated with an M1.7 flare that occured on 25 October 1999, in active region AR8741. The second loop oscillation (Fig. 6a) was triggered by an M1.8 flare on 21 March 2001, in AR9373. We will here only concentrate on a wavelet analysis of the resulting loop oscillations and refer the reader to Schrijver et al. (2001) and Aschwanden et al. (2001) for more details on the respective events and the method used to determine the loop displacements.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1907f5a.ps}\hspace*{4mm}\includegraphics[width=8cm,clip]{1907f5b.ps}\end{figure}](/articles/aa/full/2002/01/aa1907/Timg39.gif) |
Figure 5:
a) The loop displacement of the 25 October 1999 event (event 5c in Schrijver et al. 2001 & Aschwanden et al. 2001) in pixels as a function of elapsed time in seconds. b) A close-up inside the COI (dashed lines) of the logarithmic plot of the square-root of the normalised wavelet power, following the maximum of the wavelet power in time, plotted against time in seconds. The dot-dashed line corresponds to
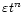 with
with
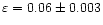 and
and
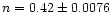 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1907f6a.ps}\hspace*{4mm}\includegraphics[width=8cm,clip]{1907f6b.ps}\end{figure}](/articles/aa/full/2002/01/aa1907/Timg40.gif) |
Figure 6:
a) The loop displacement of the 21 March 2001 event (event 10a in Schrijver et al. 2001 and Aschwanden et al. 2001) in pixels as a function of elapsed time in seconds. b) A close-up inside the COI (dashed lines) of the logarithmic plot of the square-root of the normalised wavelet power, following the maximum of the wavelet power in time, plotted against time in seconds. The dot-dashed line corresponds to
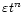 with
with
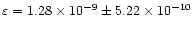 and
and
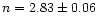 . . |
| Open with DEXTER |
In Fig. 5b we plotted the logarithm of the square-root of the normalised wavelet power of the 25 October 1999 event, on a logarithmic scale. As the period of the oscillation changes in time, we again followed the maximum wavelet power at each time step. The positions where the COI intersects with the wavelet power are marked by dashed line. From a least-squares fit (dot-dashed line) to the final, linear part of the wavelet transform inside the COI we obtained an e
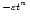 damping profile with
damping profile with
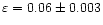 and
and
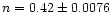 .
Following a similar procedure for the 21 March 2001 event, a least-square fit to the straight section of the double logarithm of the wavelet transform (Fig. 6b) suggests that this oscillation decays as e
.
Following a similar procedure for the 21 March 2001 event, a least-square fit to the straight section of the double logarithm of the wavelet transform (Fig. 6b) suggests that this oscillation decays as e
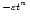 ,
with
,
with
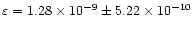 and
and
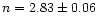 .
However, one has to keep in mind that the 21 March 2001 event is a complicated event and from a difference image of this region (Fig. 10 in Aschwanden et al. 2001) it is clear that it is impossible to trace any single loops individually. Therefore, the oscillation plotted in Fig. 6a is some kind of "average'' displacement of a whole bundle of loops.
.
However, one has to keep in mind that the 21 March 2001 event is a complicated event and from a difference image of this region (Fig. 10 in Aschwanden et al. 2001) it is clear that it is impossible to trace any single loops individually. Therefore, the oscillation plotted in Fig. 6a is some kind of "average'' displacement of a whole bundle of loops.
So far, we have analysed three different examples of coronal loop displacements and have obtained estimates of the decay exponent and power. This limited number of examples, added to the fact that several factors, such as noise in the original time series, have not been included in this analysis only allows for very tentative conclusions about the physical mechanisms involved in these events. Aschwanden et al. (2001) suggested that the observed, transversal loop oscillations conform to some extent to the evolution of impulsively generated MHD waves, where the rapid decay time could be explained by a realistic treatment of the leakage of wave energy at the footpoints of the loops (De Pontieu et al. 2001). However the authors also point out that the uncertainty in the measurements of most of the parameters is still too large to allow a definite selection between several possible models. From the examples analysed in this paper, we found a range of damping times,
 13-23 min, which is in agreement with the range of damping times calculated by Aschwanden et al. (2001). Several physical effects could lead to the range of estimated exponents. For example, the presence of small scale density inhomogeneities could lead to phase mixing, which could explain the
13-23 min, which is in agreement with the range of damping times calculated by Aschwanden et al. (2001). Several physical effects could lead to the range of estimated exponents. For example, the presence of small scale density inhomogeneities could lead to phase mixing, which could explain the
 exponent we found for the 21 March 2001 event. However, as was pointed out before, this is a complicated event and it is likely that the analysed oscillation is an average displacement of a bundle of loops. Coupling between different wave modes (Mann et al. 1997) could be a possible explanation for the
exponent we found for the 21 March 2001 event. However, as was pointed out before, this is a complicated event and it is likely that the analysed oscillation is an average displacement of a bundle of loops. Coupling between different wave modes (Mann et al. 1997) could be a possible explanation for the
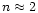 power that was found for the 14 July 1998 event. There is no obvious physical mechanism that could explain the
power that was found for the 14 July 1998 event. There is no obvious physical mechanism that could explain the
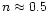 power that was found for the 25 October 1999 event. A more detailed and rigorous statistical analysis (Ireland & De Moortel 2001), taking into account all possible sources of error, is needed to determine not only a decay exponent N but also an associated error
power that was found for the 25 October 1999 event. A more detailed and rigorous statistical analysis (Ireland & De Moortel 2001), taking into account all possible sources of error, is needed to determine not only a decay exponent N but also an associated error 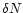 ,
before one can make a definite selection between the various possible physical mechanisms.
,
before one can make a definite selection between the various possible physical mechanisms.
The data that was analysed above is very different from the simple harmonic oscillations that were used in Paper I to demonstrate the method. The most important differences being that there are few clear oscillations present in the observational time series and that the temporal resolution is low. Again using simple harmonic oscillations, we investigate the effect of the number of oscillations and the temporal resolution on the wavelet transform in the next section.
As we want to concentrate on how wavelet analysis can provide diagnostic information we will only give a very brief overview of the definition and of some basic properties that we will refer to later on. For further details, we refer the reader to Paper I and references therein.
The continuous wavelet transform of a function f(t) is defined as the convolution of f(t) with a wavelet function
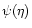 .
The wavelet function must be localised both in time and frequency space and should be admissible, which for an integrable function implies that its average is zero. We also assume that
.
The wavelet function must be localised both in time and frequency space and should be admissible, which for an integrable function implies that its average is zero. We also assume that 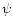 is normalised, i.e.
is normalised, i.e.
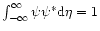 ,
where * denotes the complex conjugate. For
,
where * denotes the complex conjugate. For
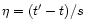 we have
we have
![$\displaystyle W(t,s) = \int_{-\infty}^{\infty}f(t'){1 \over \sqrt{s}}\quad\psi^* \left[{(t'-t) \over s} \right] {\rm d}t',$](/articles/aa/full/2002/01/aa1907/img47.gif) |
|
|
(1) |
where t is time and s is the wavelet scale. The factor
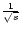 ensures that the normalisation condition is satisfied. However, when analysing observed oscillations, we will generally not be dealing with continuous functions but with discrete time series. For such a discrete time series of N observations xn,
ensures that the normalisation condition is satisfied. However, when analysing observed oscillations, we will generally not be dealing with continuous functions but with discrete time series. For such a discrete time series of N observations xn,
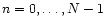 ,
with sample interval
,
with sample interval 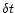 ,
the continuous wavelet transform is given by
,
the continuous wavelet transform is given by
![\begin{displaymath}W_n(s) = \sum_{n'=0}^{N-1}x_{n'}\sqrt{{\delta t \over s}}\psi^* \left[{(n'-n)\delta t \over s} \right],
\end{displaymath}](/articles/aa/full/2002/01/aa1907/img50.gif) |
(2) |
where s is again the wavelet scale and n allows us to translate the analysing wavelet in time. The normalisation condition is satisfied through the factor
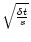 .
The wavelet power spectrum is defined as
|Wn(s)|2 and ranging through s and n will build up a 2D time-frequency transform of the original time series.
.
The wavelet power spectrum is defined as
|Wn(s)|2 and ranging through s and n will build up a 2D time-frequency transform of the original time series.
We will use the same basic wavelet function as in Paper I, namely the (complex-valued) Morlet wavelet,
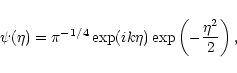 |
(3) |
consisting of a plane wave modulated by a Gaussian. We will also use the same set of scales s in the wavelet transform as in Paper I. It was demonstrated in Paper I that a larger value of k results in a more accurate resolution of the period whereas a smaller value improves the time resolution. However, the Morlet wavelet is only marginally admissible, meaning that its average is never exactly zero, although, for k > 6, the average is smaller than 10-16. Therefore, as a compromise between getting the best time resolution, which is what we are mainly interested in, and satisfying the admissibility condition, we choose the smallest value for the parameter k in Eq. (3) that still makes the function admissible and thus set k=6. Because the time series we generally work with are finite, the wavelet transform suffers from edge effects at both ends of the time series. Following Torrence & Compo (1998), we will use a cone of influence as a measure of where the edge of the finite sample data has affected the analysis. In the following section, we will demonstrate that the COI is an important indicator as to where the wavelet approach to coronal seismology can be applied confidently.
3.2 An e
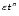 damping profile
damping profile
In Paper I, the analysis concentrated entirely on phase mixing of Alfvén waves and thus, on a e
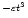 damping profile. To extend this initial analysis, we will use simple exponential damping profiles of the form e
damping profile. To extend this initial analysis, we will use simple exponential damping profiles of the form e
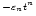 ,
without relating them to actual physical processes such as phase mixing. Given the outcome of the analysis of the observational time series in Sect. 2, we will work out the wavelet power spectrum |W|2 of
,
without relating them to actual physical processes such as phase mixing. Given the outcome of the analysis of the observational time series in Sect. 2, we will work out the wavelet power spectrum |W|2 of
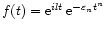 ,
,
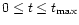 ,
in more detail for n=2.
,
in more detail for n=2.
Using the definition given in Eq. (1), with the Morlet wavelet (Eq. (3)) as mother wavelet, the wavelet transform is given by
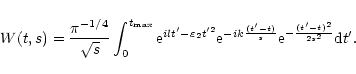 |
(4) |
Setting
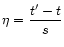 ,
we find
,
we find
and, completing the square in 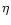 in the integrand we obtain
in the integrand we obtain
where
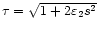 depends on the damping coefficient
depends on the damping coefficient
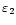 and the wavelet scale s. The wavelet power is thus given by
and the wavelet scale s. The wavelet power is thus given by
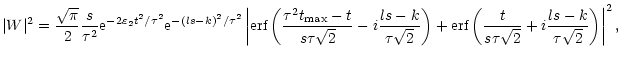 |
|
|
(5) |
where
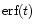 is the Error function (Abramowitz & Stegun 1965). These Error functions approximate the edge effects in the transform, and thus, away from the edges, where the Error functions are basically constant, the wavelet power can be approximated by
is the Error function (Abramowitz & Stegun 1965). These Error functions approximate the edge effects in the transform, and thus, away from the edges, where the Error functions are basically constant, the wavelet power can be approximated by
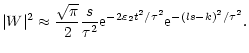 |
|
|
(6) |
At a given time t, the wavelet power given by this expression will reach its maximum at some complicated scale 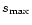 ,
that depends on the value of
,
that depends on the value of
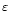 ,
k and l. However, to relate this scale
,
k and l. However, to relate this scale 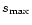 to a physically relevant quantity such as the frequency l or the period P, it will have to be multiplied by a specific factor F. For the case of no damping,
to a physically relevant quantity such as the frequency l or the period P, it will have to be multiplied by a specific factor F. For the case of no damping,
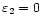 ,
the wavelet power will reach a maximum at
,
the wavelet power will reach a maximum at
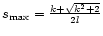 and the period will then by given by
and the period will then by given by
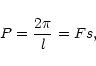 |
(7) |
with
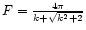 .
Thus, to relate the scales s used in the wavelet transform to the period P, we have to multiply by this factor F.
.
Thus, to relate the scales s used in the wavelet transform to the period P, we have to multiply by this factor F.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1907f7.ps}\end{figure}](/articles/aa/full/2002/01/aa1907/Timg74.gif) |
Figure 7:
The Error function part of Eq. (11) for P=5 (solid line) and P=20 (dashed line), with
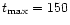 and k=6.
and k=6. |
| Open with DEXTER |
However, the appearance of an exponential decay in the time series will change this relation between period and wavelet scale, since
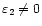 and thus
and thus
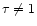 .
To be able to determine the appropriate factor F in this case, it is necessary to isolate
.
To be able to determine the appropriate factor F in this case, it is necessary to isolate 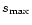 from Eq. (8) at a given time t, and relate it to the frequency l as was done in Eq. (9). In the case
from Eq. (8) at a given time t, and relate it to the frequency l as was done in Eq. (9). In the case
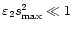 ,
we recover the original Fourier factor
,
we recover the original Fourier factor
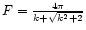 .
For
.
For
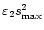 large, this F is not a good approximation any more and in this case it will not be straightforward to relate the wavelet scales to a frequency or period. Taking
large, this F is not a good approximation any more and in this case it will not be straightforward to relate the wavelet scales to a frequency or period. Taking
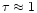 ,
,
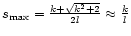 for k=6 and in this case the expression for the wavelet power can be reduced to
for k=6 and in this case the expression for the wavelet power can be reduced to
![$\displaystyle \vert W\vert^2 \approx {k \over l}{\sqrt{\pi} \over 2}{\rm e}^{-2...
...\sqrt{2}k}\right) + \mbox{erf}\left(\frac{t l}{\sqrt{2}k}\right) \right]^2\cdot$](/articles/aa/full/2002/01/aa1907/img81.gif) |
|
|
(8) |
In general, given that
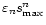 is sufficiently small, the wavelet power for
is sufficiently small, the wavelet power for
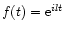 e
e
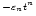 reaches its maximum at
reaches its maximum at
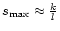 and is approximately given by
and is approximately given by
![$\displaystyle \vert W\vert^2 \approx {k \over l}{\sqrt{\pi} \over 2}{\rm e}^{-2...
...\sqrt{2}k}\right) + \mbox{erf}\left(\frac{t l}{\sqrt{2}k}\right) \right]^2\cdot$](/articles/aa/full/2002/01/aa1907/img84.gif) |
|
|
(9) |
This expression is identical to the one that was derived for n=3 in Paper I but note that the factor
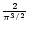 in Eq. (14) in Paper I is incorrect and should be replaced by
in Eq. (14) in Paper I is incorrect and should be replaced by
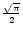 .
The condition that
.
The condition that
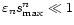 ,
ensures that we can use the original Fourier factor
,
ensures that we can use the original Fourier factor
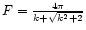 to relate the scales s to the frequency or period, as was demonstrated for n=2. The key point is that the e
to relate the scales s to the frequency or period, as was demonstrated for n=2. The key point is that the e
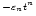 damping profile and thus both the damping coefficient
damping profile and thus both the damping coefficient
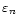 and the power n of the decay are present in Eq. (11). This implies that the original exponential damping profile survives the wavelet transform and that the values of the damping coefficient and the power of the decay can be extracted from the wavelet power given in Eq. (11) by taking a double logarithm of the normalised wavelet power. The following brief argument explains why it is necessary to consider the normalised wavelet power. Assume the square-root of the wavelet power
and the power n of the decay are present in Eq. (11). This implies that the original exponential damping profile survives the wavelet transform and that the values of the damping coefficient and the power of the decay can be extracted from the wavelet power given in Eq. (11) by taking a double logarithm of the normalised wavelet power. The following brief argument explains why it is necessary to consider the normalised wavelet power. Assume the square-root of the wavelet power
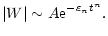 |
|
|
(10) |
Then
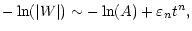 |
|
|
(11) |
and thus,
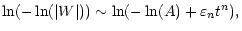 |
|
|
(12) |
from which it is only possible to extract the gradient of the damping profile if A=1. Thus the logarithm of this normalised wavelet power,
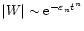 ,
plotted against
,
plotted against 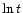 will be linear with gradient n.
will be linear with gradient n.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1907f8a.ps}\hspace*{4mm}\inc...
...1907f8c.ps}\hspace*{4mm}\includegraphics[width=8cm,clip]{1907f8d.ps}\end{figure}](/articles/aa/full/2002/01/aa1907/Timg95.gif) |
Figure 8:
a) The damped harmonic oscillation
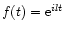 e e
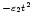 with
with
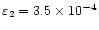 and the period P=5. b) Corresponding wavelet transform. The dashed line indicates the COI. c) Cross-section of the (normalised) wavelet power at maximum wavelet power, i.e. at P = 5.0. The dot-dashed line corresponds to the analytical approximation given in Eq. (11) with n=2. d) Logarithmic plot of the cross-section of the wavelet power at maximum wavelet power. The dot-dashed line corresponds to
and the period P=5. b) Corresponding wavelet transform. The dashed line indicates the COI. c) Cross-section of the (normalised) wavelet power at maximum wavelet power, i.e. at P = 5.0. The dot-dashed line corresponds to the analytical approximation given in Eq. (11) with n=2. d) Logarithmic plot of the cross-section of the wavelet power at maximum wavelet power. The dot-dashed line corresponds to
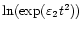 . . |
| Open with DEXTER |
However, the approximation given in Eq. (14) is only valid under the assumptions that, firstly,
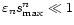 and secondly, that the Error functions in Eq. (11) can be treated as constant. We will now briefly discuss the implications of each of these assumptions.
and secondly, that the Error functions in Eq. (11) can be treated as constant. We will now briefly discuss the implications of each of these assumptions.
As
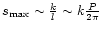 ,
where P is the period, the condition that
,
where P is the period, the condition that
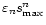 has to be sufficiently small implies that either
has to be sufficiently small implies that either
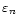 or the period of the analysed time series has to be sufficiently small. Imposing that the damping coefficient or the period is small, can be understood intuitively as the need for a sufficient number of oscillations in the time series. If the damping is very strong or the period large compared to the length of the time series, only a few oscillations will be present and it will not be straightforward to relate the scale s used in the wavelet analysis to a physically "interesting'' quantity such as the period of the original time series. If
or the period of the analysed time series has to be sufficiently small. Imposing that the damping coefficient or the period is small, can be understood intuitively as the need for a sufficient number of oscillations in the time series. If the damping is very strong or the period large compared to the length of the time series, only a few oscillations will be present and it will not be straightforward to relate the scale s used in the wavelet analysis to a physically "interesting'' quantity such as the period of the original time series. If
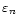 or P is sufficiently small,
or P is sufficiently small,
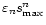 will be small, in which case the period of the signal can be extracted from the wavelet analysis by multiplying the scales s with
will be small, in which case the period of the signal can be extracted from the wavelet analysis by multiplying the scales s with
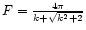 .
.
It was pointed out before that one of the important limitations of wavelet analysis is that it suffers from edge effects due to the finite lifetime of the analysed signal. As in Torrence & Compo (1998), we defined the COI as the point where the wavelet power has been reduced by a factor e-2 due to these edge effects, thus supplying a measure of where the edge of the finite sample data has affected the analysis. In the analytical expression for the wavelet power (Eq. (11)), the Error functions approximate the edge effects, and thus, where the Error functions are basically constant, the edge effects are negligible. By definition, this will be the case for that part of the wavelet transform that falls insided the COI.
In Fig. 7, we have plotted the Error function part of Eq. (11),
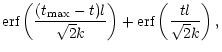 |
|
|
(13) |
for different values of the period P, where 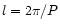 .
We assumed
.
We assumed
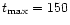 and k=6. We see that for P=5 (solid line), i.e. a period that is small compared to the length of the time series, a large portion of the Error functions is constant. However, for P=20 (dashed line), i.e. when there will only be a few oscillations present in the analysed time series, the Error functions only reach a constant value for a very small portion of the time interval. It is easy to see from Eq. (11) that in this case, the wavelet power will be dominated by the Error functions rather than the exponential decay. This implies that it will be much harder, if not impossible, to extract the correct exponential damping profile from the wavelet transform. As we will demonstrate in Sect. 3.3, only limiting estimates for the damping coefficient or the decay exponent can be determined from the wavelet analysis when the period is large, i.e. when large parts of the wavelet transform fall outside the COI.
and k=6. We see that for P=5 (solid line), i.e. a period that is small compared to the length of the time series, a large portion of the Error functions is constant. However, for P=20 (dashed line), i.e. when there will only be a few oscillations present in the analysed time series, the Error functions only reach a constant value for a very small portion of the time interval. It is easy to see from Eq. (11) that in this case, the wavelet power will be dominated by the Error functions rather than the exponential decay. This implies that it will be much harder, if not impossible, to extract the correct exponential damping profile from the wavelet transform. As we will demonstrate in Sect. 3.3, only limiting estimates for the damping coefficient or the decay exponent can be determined from the wavelet analysis when the period is large, i.e. when large parts of the wavelet transform fall outside the COI.
Overall, to obtain correct values for the period of the time series from the wavelet analysis and for the exponential behaviour of the analysed time series to be clearly present in the wavelet transform, there has to be a sufficient number of oscillations present in the time series, or in other words, a substantial part of the wavelet power has to be situated inside the cone of influence.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1907f9a.ps}\hspace*{4mm}\inc...
...1907f9c.ps}\hspace*{4mm}\includegraphics[width=8cm,clip]{1907f9d.ps}\end{figure}](/articles/aa/full/2002/01/aa1907/Timg99.gif) |
Figure 9:
a) The damped harmonic oscillation
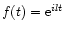 e e
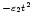 with
with
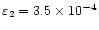 and the period P=20. b) Corresponding wavelet transform. The dashed line indicates the COI. c) Cross-section of the (normalised) wavelet power at maximum wavelet power, i.e. at P = 20. The dot-dashed line and dot-dot-dashed line correspond to the analytical approximation given in Eq. (11) with
and the period P=20. b) Corresponding wavelet transform. The dashed line indicates the COI. c) Cross-section of the (normalised) wavelet power at maximum wavelet power, i.e. at P = 20. The dot-dashed line and dot-dot-dashed line correspond to the analytical approximation given in Eq. (11) with
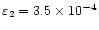 and
and
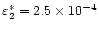 respectively. d) Logarithmic plot of the cross-section of the wavelet power. The dot-dashed line and dot-dot-dashed line correspond to
respectively. d) Logarithmic plot of the cross-section of the wavelet power. The dot-dashed line and dot-dot-dashed line correspond to
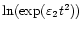 with
with
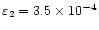 and
and
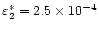 respectively.
respectively. |
| Open with DEXTER |
Finally, we point out that Eq. (11) can be generalised for any damping profile, provided the decay is sufficiently slow. Indeed, assume that a function g(t) consists of a plane wave, modulated by a decay that depends only weakly on the time t. The above calculation can then easily be adapted so that the wavelet power at
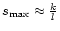 is given by
is given by
![$\displaystyle \vert W\vert^2 \approx {k \over l}{\sqrt{\pi} \over 2} g(t)\left[...
...\sqrt{2}k}\right) + \mbox{erf}\left(\frac{t l}{\sqrt{2}k}\right) \right]^2\cdot$](/articles/aa/full/2002/01/aa1907/img100.gif) |
|
|
(14) |
If the time series is sufficiently long, the weak decay condition will ensure that there are enough oscillations present and thus, that the same Fourier factor F can be used to relate the wavelet scales to periods and that for a substantial part of the time interval, the Error functions are constant. The original damping profile will then again be present in the wavelet transform of the signal, but obviously, it is only for an exponential decay that the logarithm of the normalised wavelet power will appear linear in a logarithmic plot.
The damped harmonic oscillation in Fig. 8a is obtained by setting
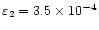 and
and 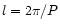 ,
P=5, in
,
P=5, in
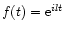 e
e
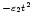 .
The period of this oscillation stays constant for all t, but the amplitude decays as e
.
The period of this oscillation stays constant for all t, but the amplitude decays as e
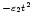 for increasing values of t. From Fig. 8b, we see that the wavelet power is indeed concentrated at P=5 and that the amplitude of the wavelet power decreases for increasing t. As the period of this oscillation is relatively small, most of the wavelet power lies inside the COI. Following the approach outlined in Paper I, Fig. 8c shows a normalised cross-section of the wavelet power at P=5. The only slight disagreement between the numerical solution for the wavelet power (solid line) and the analytical approximation (dot-dashed line) given in Eq. (11) occurs outside the COI (dashed lines) and is therefore of little importance. However it is clear that the e
for increasing values of t. From Fig. 8b, we see that the wavelet power is indeed concentrated at P=5 and that the amplitude of the wavelet power decreases for increasing t. As the period of this oscillation is relatively small, most of the wavelet power lies inside the COI. Following the approach outlined in Paper I, Fig. 8c shows a normalised cross-section of the wavelet power at P=5. The only slight disagreement between the numerical solution for the wavelet power (solid line) and the analytical approximation (dot-dashed line) given in Eq. (11) occurs outside the COI (dashed lines) and is therefore of little importance. However it is clear that the e
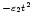 damping profile of the original signal is still present in its wavelet transform. Finally in Fig. 8d, we plotted the logarithm of the square-root of the normalised wavelet power on a logarithmic scale, as e
damping profile of the original signal is still present in its wavelet transform. Finally in Fig. 8d, we plotted the logarithm of the square-root of the normalised wavelet power on a logarithmic scale, as e
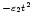 should appear to be linear with gradient 2 in such a graph. At larger times, i.e. where the edge effects are no longer important, Fig. 8d shows a good agreement between the logarithm of the wavelet power and
should appear to be linear with gradient 2 in such a graph. At larger times, i.e. where the edge effects are no longer important, Fig. 8d shows a good agreement between the logarithm of the wavelet power and
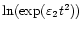 (dot-dashed line) inside the COI, thus confirming the analytical calculations and the results of Paper I for a time series with an adequate number of oscillations.
(dot-dashed line) inside the COI, thus confirming the analytical calculations and the results of Paper I for a time series with an adequate number of oscillations.
3.3 Effect of a large period and low temporal resolution on the WT
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1907f10a.ps}\hspace*{4mm}\includegraphics[width=8cm,clip]{1907f10b.ps}\end{figure}](/articles/aa/full/2002/01/aa1907/Timg101.gif) |
Figure 10:
a-d) The equivalent of Fig. 9 a) & d) for
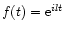 e e
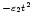 with
with
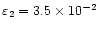 ,
P=20 but ,
P=20 but 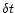 reduced to 5.0.
reduced to 5.0. |
| Open with DEXTER |
So far, we have a very promising agreement between the wavelet transforms and the original damping profiles. However, in all considered cases, the period of the oscillation was taken relatively small in comparison with the length of the time series, thus providing an adequate number of oscillations to base the wavelet analysis on. From the calculations done in Sect. 3.2, it is clear that we need plenty of oscillations to be able to, firstly, determine the Fourier factor F, that is needed to relate the scales s to the period of the time series and, secondly, to extract the damping profile from the wavelet transform. Additionally, if
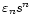 is large, Eq. (14) will have an extra (negative) term, in which case it will not be possible to obtain the original decay profile from the double logarithm of the normalised wavelet power. So to determine both the period and the damping profile of the analysed time series, there has to be a sufficient number of oscillations present in the time series, which can be achieved if the period P is relatively small compared to the length of the time series.
is large, Eq. (14) will have an extra (negative) term, in which case it will not be possible to obtain the original decay profile from the double logarithm of the normalised wavelet power. So to determine both the period and the damping profile of the analysed time series, there has to be a sufficient number of oscillations present in the time series, which can be achieved if the period P is relatively small compared to the length of the time series.
We now analyse
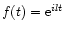 e
e
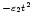 again, keeping the same value for the damping coefficient
again, keeping the same value for the damping coefficient
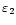 as above but reducing the number of oscillations by increasing the period to P=20. Decreasing the length of the time series, but keeping the same value for P would have produced the same effect, i.e. reduced the number of oscillations in the time series. Figure 9a shows that there are indeed only about 5 clear oscillations before the signal is damped. The wavelet power in Fig. 9b is concentrated around P=20 as expected but this figure also indicates that when there is only a small number of oscillations in the time series, a relatively large portion of its wavelet transform falls outside the COI. Indeed, comparing Figs. 8b and 9b, we see that in the latter, a much larger portion falls outside the COI, which will obviously affect the results of the analysis. Figure 9c clearly indicates the poor agreement between the cross-section of the wavelet power (solid line) and the analytical approximation given in Eq. (9) (dot-dashed line). The dot-dot-dashed line in this figure was obtained by shifting
as above but reducing the number of oscillations by increasing the period to P=20. Decreasing the length of the time series, but keeping the same value for P would have produced the same effect, i.e. reduced the number of oscillations in the time series. Figure 9a shows that there are indeed only about 5 clear oscillations before the signal is damped. The wavelet power in Fig. 9b is concentrated around P=20 as expected but this figure also indicates that when there is only a small number of oscillations in the time series, a relatively large portion of its wavelet transform falls outside the COI. Indeed, comparing Figs. 8b and 9b, we see that in the latter, a much larger portion falls outside the COI, which will obviously affect the results of the analysis. Figure 9c clearly indicates the poor agreement between the cross-section of the wavelet power (solid line) and the analytical approximation given in Eq. (9) (dot-dashed line). The dot-dot-dashed line in this figure was obtained by shifting
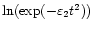 in the logarithmic plot (Fig. 9d) until it touched the logarithm of the wavelet power, giving a coefficient
in the logarithmic plot (Fig. 9d) until it touched the logarithm of the wavelet power, giving a coefficient
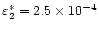 .
The dot-dot-dashed line in Fig. 9c is the approximation given in Eq. (11), using this
.
The dot-dot-dashed line in Fig. 9c is the approximation given in Eq. (11), using this
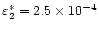 rather than the original damping coefficient
rather than the original damping coefficient
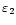 .
However, it is obvious that this is still a poor (and rather complicated) attempt to fit the original wavelet power and that neither of the approximations gives as good a result as obtained for P=5. Although the dot-dot-dashed line is a better fit to the wavelet power than the dot-dashed line, it gives us an incorrect value for the damping coefficient as
.
However, it is obvious that this is still a poor (and rather complicated) attempt to fit the original wavelet power and that neither of the approximations gives as good a result as obtained for P=5. Although the dot-dot-dashed line is a better fit to the wavelet power than the dot-dashed line, it gives us an incorrect value for the damping coefficient as
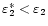 ,
where
,
where
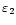 is the damping coefficient of the original time series and thus is the value we should have obtained. The combination of the strong edge effects in the transform and the fact that the additional term in Eq. (14) is negative implies that the fitted value
is the damping coefficient of the original time series and thus is the value we should have obtained. The combination of the strong edge effects in the transform and the fact that the additional term in Eq. (14) is negative implies that the fitted value
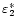 will be a lower limit for the true value
will be a lower limit for the true value
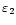 of the damping coefficient.
of the damping coefficient.
Figure 9d also suggests that when fitting a linear approximation to the logarithm of the wavelet power, one would probably have chosen a slightly steeper gradient than 2 as a best fit. This implies that the gradient obtained from the wavelet analysis will be an upper limit for the true value of the decay exponent. Keeping in mind that we are looking for a best fit to the wavelet transform at large times, i.e. where the transform is linear, the error on the gradient could be as much as 10-15% in this particular case. Therefore, when attempting to fit the logarithm of the wavelet power without any pre-existing knowledge of the actual damping profile of the time series, it is likely that one would only have found limiting values for both the damping coefficient and the gradient of the damping profile. Overall, this example demonstrates that a sufficient number of oscillations is needed to determine the correct damping profile from the wavelet analysis. For an oscillation with a relatively long period, limiting values for the decay coefficient and exponent can be obtained. Obviously, when analysing observations, it will not always be possible to ensure that there are plenty of oscillations in the time series and this will have to be taken into account in the interpretation of the results of the wavelet analysis.
We investigate the effect of a low temporal resolution on the wavelet analysis by again analysing
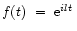 e
e
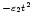 ,
with P=20, but reducing the cadence from
,
with P=20, but reducing the cadence from
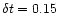 to
to
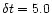 .
Having a relatively long period and low cadence, this example roughly simulates the observational time series that was analysed in Sect. 2 and will therefore give an indication of the relevance of the information that was obtained from the wavelet analysis. Figure 10a shows the time series, where the diamonds are the actual data points we have used in this analysis. The amplitude of the oscillation still roughly decays as e
.
Having a relatively long period and low cadence, this example roughly simulates the observational time series that was analysed in Sect. 2 and will therefore give an indication of the relevance of the information that was obtained from the wavelet analysis. Figure 10a shows the time series, where the diamonds are the actual data points we have used in this analysis. The amplitude of the oscillation still roughly decays as e
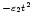 but there are now only about 5 data points present per oscillation. Figure 10d was obtained using exactly the same values for the coefficients
but there are now only about 5 data points present per oscillation. Figure 10d was obtained using exactly the same values for the coefficients
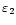 and
and
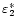 as in Fig. 9d and when we compare both figures, we see that there is no significant difference between the quality of the fits in both cases. When fitting a linear approximation to the data points in Fig. 10d, one would again have been inclined to use a steeper gradient.
as in Fig. 9d and when we compare both figures, we see that there is no significant difference between the quality of the fits in both cases. When fitting a linear approximation to the data points in Fig. 10d, one would again have been inclined to use a steeper gradient.
Overall the low temporal resolution of the time series does not greatly affect the wavelet analysis and it will be mainly the number of oscillations that has to be taken into account when evaluating the accuracy of the information obtained from the wavelet analysis. This implies that the information obtained from the wavelet analysis of the transverse loop oscillations in Sect. 2 has to be interpreted carefully; the value for the decay coefficient
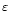 will be a lower limit, whereas the power n that was estimated for the decay exponent is an upper limit, with an associated error of about 15%.
will be a lower limit, whereas the power n that was estimated for the decay exponent is an upper limit, with an associated error of about 15%.
Finally, we briefly look into the effect of the wavelet parameter k (Eq. (3)) on the proposed method. Table 1 gives an overview of different values of the estimated damping coefficient
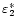 for different values of k (Eq. (3)). In Paper I, it was shown that for smaller values of k, the time resolution of the wavelet transform improves. As a direct consequence, the estimated value
for different values of k (Eq. (3)). In Paper I, it was shown that for smaller values of k, the time resolution of the wavelet transform improves. As a direct consequence, the estimated value
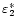 comes closer and closer to the true value
comes closer and closer to the true value
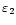 for increasingly small values of k. However, one has to keep in mind that for k<6 in the Morlet wavelet, the admissibility condition is not satisfied. Additionally, when the temporal resolution is poor, it will not always be possible to reduce the value of k. Remember that wavelet scales have to be multiplied with the Fourier factor F to be related to a period, and that the smallest scale that can be resolved is twice the cadence. With
for increasingly small values of k. However, one has to keep in mind that for k<6 in the Morlet wavelet, the admissibility condition is not satisfied. Additionally, when the temporal resolution is poor, it will not always be possible to reduce the value of k. Remember that wavelet scales have to be multiplied with the Fourier factor F to be related to a period, and that the smallest scale that can be resolved is twice the cadence. With
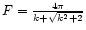 and
and
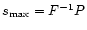 ,
it is clear that for the same P,
,
it is clear that for the same P, 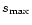 will decrease as k decreases. For example, assume that, as in Sect. 2, the period
will decrease as k decreases. For example, assume that, as in Sect. 2, the period
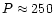 s and the cadence roughly 75 s. With k=3, the wavelet power would reach its maximum at
s and the cadence roughly 75 s. With k=3, the wavelet power would reach its maximum at
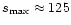 but, the smallest scale that could be resolved in this case would be
but, the smallest scale that could be resolved in this case would be
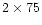 and thus it would not be possible to use k=3. So when the original time series has a low cadence, it might not be possible to reduce the value of k substantially. For larger k, the resolution of the period will be more accurate, but only a poor estimate of the damping coefficient will be obtained.
and thus it would not be possible to use k=3. So when the original time series has a low cadence, it might not be possible to reduce the value of k substantially. For larger k, the resolution of the period will be more accurate, but only a poor estimate of the damping coefficient will be obtained.
In this paper we developed the idea of coronal seismology through wavelet analysis introduced by De Moortel & Hood (2000) further, and applied the proposed method to TRACE data. We choose to mainly concentrate on the analysis of observations of a flare-induced, transversal loop displacement (Nakariakov et al. 1999) as this data is a very clear example of a damped coronal oscillation. The period of the oscillation was found to slowly decrease from about 260 s at the start of the time series to about 200 s, which corresponds to the values suggested by Nakariakov et al. (1999). An e
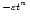 damping profile, with
damping profile, with
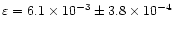 and
and
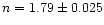 ,
was found to be the closest fit to the double logarithm of the normalised wavelet power. We applied the method to two additional flare-induced, damped, transversal loop oscillations, observed by TRACE on 25 October 1999 and 21 March 2001. For the 25 October 1999 event, we find a damping coefficient
,
was found to be the closest fit to the double logarithm of the normalised wavelet power. We applied the method to two additional flare-induced, damped, transversal loop oscillations, observed by TRACE on 25 October 1999 and 21 March 2001. For the 25 October 1999 event, we find a damping coefficient
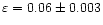 and a power
and a power
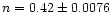 ,
whereas for the 21 March 2001 event, we find
,
whereas for the 21 March 2001 event, we find
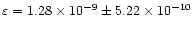 and
and
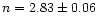 .
However, it was noted that the 21 March 2001 event is complicated and that the analysed oscillation is probably an average displacement of a bundle of loops. The limited number of examples that was analysed and the large uncertainty in the obtained parameters does not allow us to make a definite selection between the various possible physical mechanisms that could cause the rapid damping of these transversal loop oscillations.
.
However, it was noted that the 21 March 2001 event is complicated and that the analysed oscillation is probably an average displacement of a bundle of loops. The limited number of examples that was analysed and the large uncertainty in the obtained parameters does not allow us to make a definite selection between the various possible physical mechanisms that could cause the rapid damping of these transversal loop oscillations.
The data that was analysed have much longer periods and lower temporal resolution that the harmonic oscillations that were used in Paper I to develop the method. Therefore, in the second part of this paper, we investigated the effect of the number of oscillations and the temporal resolution on the wavelet transform by applying a wavelet analysis to harmonic oscillations with simple exponential damping profiles. The wavelet power spectrum was calculated analytically for an e-t2 damping profile and the error function approximation calculated in Paper I was generalised for any damping profile, provided the decay is sufficiently slow. It was demonstrated that when there is a sufficiently large number of oscillations present, the value of both the damping coefficient and the power of the exponential damping profile can be determined from the double logarithm of the normalised wavelet power. However, the analytical calculation revealed the important effect of the number of oscillations present in the analysed time series on its wavelet transform. Additionally, it was demonstrated that when strong damping is present, it will not always be straightforward to determine the factor F that is necessary to relate the scales s used in the wavelet analysis to the period or frequency of the analysed time series. So although the wavelet power might show a clear maximum at a certain scale 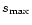 ,
there will be no easy way to determine exactly the period or frequency that this scale
,
there will be no easy way to determine exactly the period or frequency that this scale 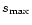 corresponds to. From the analysis of a time series in which there are only a few clear oscillations present, it was demonstrated that one can obtain an estimate of a lower limit for the value of the damping coefficient and an upper limit for the decay exponent from the wavelet analysis. It was shown that decreasing the temporal resolution does not greatly affect the wavelet analysis and that it is mainly the number of oscillations that has to be taken into account when evaluating the accuracy of the information obtained from the wavelet analysis.
corresponds to. From the analysis of a time series in which there are only a few clear oscillations present, it was demonstrated that one can obtain an estimate of a lower limit for the value of the damping coefficient and an upper limit for the decay exponent from the wavelet analysis. It was shown that decreasing the temporal resolution does not greatly affect the wavelet analysis and that it is mainly the number of oscillations that has to be taken into account when evaluating the accuracy of the information obtained from the wavelet analysis.
The main aim of this paper was to demonstrate the potential of wavelet analysis when making a detailed study of the transform. When one is presented with an observational time series to analyse, it will not always be possible to ensure that there is a sufficient number of oscillations in the time series. The effect of this on the obtained values of a decay coefficient and exponent will have to be taken into account. Also, there are several more aspects that have not been taken into account in the analysis of the decaying oscillations of the coronal loops in this paper. For example, we limited ourselves to simple, exponential damping profiles. Additionally, the determination of the loop oscillation itself is extremely sensitive to the exact location of the slit or box across the loop. A more detailed and rigorous statistical analysis (Ireland & De Moortel 2001), taking into account the errors of the original oscillating time series and the additional errors introduced by the wavelet analysis is needed to determine not only a decay exponent N but also an associated error 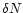 .
Wavelet analysis is a valuable diagnostic tool and a detailed analysis of the wavelet transform can provide information about the medium through which wave-like oscillations are propagating through coronal seismology. However, one has to be aware of the necessity of a careful interpretation of the results and take into consideration the various possible factors that could affect the obtained information. The high spatial and temporal resolution of TRACE provides an excellent opportunity to investigate both transversal and longitudinal, wave-like oscillations in the solar corona and, through a wavelet analysis, provide estimates for local coronal plasma properties.
.
Wavelet analysis is a valuable diagnostic tool and a detailed analysis of the wavelet transform can provide information about the medium through which wave-like oscillations are propagating through coronal seismology. However, one has to be aware of the necessity of a careful interpretation of the results and take into consideration the various possible factors that could affect the obtained information. The high spatial and temporal resolution of TRACE provides an excellent opportunity to investigate both transversal and longitudinal, wave-like oscillations in the solar corona and, through a wavelet analysis, provide estimates for local coronal plasma properties.
Acknowledgements
Wavelet software was provided by C. Torrence and G. Compo, and is available at URL: http:// paos.colorado.edu/research/wavelets. The authors are grateful to Markus Aschwanden and Karel Schrijver for allowing them to use the data of the 25 October 1999 and 21 March 2001 events.
- Abramowitz, M., & Stegun, I. A. 1965, Handbook of mathematical functions (Dover)
In the text
-
Aschwanden, M. J. 1987, Solar Phys., 111, 113
In the text
NASA ADS
-
Aschwanden, M. J., Fletcher, L., Schrijver, C. J., & Alexander, D. 1999, ApJ, 520, 880
In the text
NASA ADS
-
Aschwanden, M. J., De Pontieu, B., Schrijver, C. J., & Title, A. 2001, Solar Phys., 2001, submitted
In the text
-
Banerjee, D., O'Shea, E., & Doyle, J. G. 2000, A&A, 355, 1152
In the text
NASA ADS
-
Berghmans, D., & Clette, F. 1999, Solar Phys., 186, 207
In the text
NASA ADS
-
DeForest, C. E., & Gurman, J. B. 1998, ApJ, 501, L217
In the text
NASA ADS
-
De Moortel, I., Ireland, J., & Walsh, R. W. 2000, A&A, 355, L23
In the text
NASA ADS
-
De Moortel, I., & Hood, A. W. 2000, A&A, 363, 269
NASA ADS
-
De Pontieu, B., Martens, P. C. H., & Hudson, H. S. 2001, ApJ, 558, 859
In the text
NASA ADS
-
Giménez de Castro, C. G., Raulin, J.-P., Mandrini, C. H., Kaufmann, P., & Magun, A. 2001, A&A, 366, 317
In the text
NASA ADS
-
Ireland, J., & De Moortel, I. 2001, in preparation
In the text
-
Mann, I. R., Wright, A. N., & Hood, A. W. 1997, J. Geophys. Res., 102, 2381
In the text
NASA ADS
-
Nakariakov, V. M., Ofman, L., DeLuca, E. E., Roberts, B., & Davila, J. M. 1999, Science, 285, 862
In the text
-
Nakariakov, V. M., & Ofman, L. 2001, A&A, 372, L53
In the text
NASA ADS
-
Ofman, L., Romoli, M., Poletto, G., Noci, C., & Kohl, J. L. 1997, ApJ, 491, L111
In the text
NASA ADS
-
Ofman, L., Nakariakov, V. M., & DeForest, C. E. 1999, ApJ, 514, 441
In the text
NASA ADS
-
Ofman, L., Romoli, M., Poletto, G., Noci, C., & Kohl, J. L. 2000, ApJ, 529, 592
In the text
NASA ADS
-
O'Shea, E., Banerjee, D., Doyle, J. G., Fleck, B., & Murtagh, F. 2001, A&A, 368, 1095
In the text
NASA ADS
-
Robbrecht, E., Verwichte, E., Berghmans, D., et al.
2001, A&A, 370, 591
In the text
NASA ADS
-
Roberts, B. 2000, Solar Phys., 193, 139
In the text
NASA ADS
-
Schrijver, C. J., Title, A. M., Berger, T. E., et al. 1999, Solar Phys., 187, 261
In the text
NASA ADS
-
Schrijver, C. J., & Brown, D. S. 2000, ApJ, 537, L69
In the text
NASA ADS
-
Schrijver, C. J., Aschwanden, M. J., & Title, A. 2001, Solar Phys., 2001, submitted
In the text
-
Torrence, C., & Compo, G. P. 1998, Bull. Amer. Meteor. Soc., 79, 61
In the text
-
Tsubaki, T. 1988, in Solar and Stellar Coronal Structures and Dynamics, ed. R. C. Altrock (NSO, Sunspot NM)
In the text
Copyright ESO 2001
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1907f1.ps}\end{figure}](/articles/aa/full/2002/01/aa1907/Timg30.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1907f2a.ps}\hspace*{4mm}\includegraphics[width=8cm,clip]{1907f2b.ps}\end{figure}](/articles/aa/full/2002/01/aa1907/Timg33.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1907f3a.ps}\hspace*{4mm}\includegraphics[width=8cm,clip]{1907f3b.ps}\end{figure}](/articles/aa/full/2002/01/aa1907/Timg34.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1907f4a.ps}\hspace*{4mm}\includegraphics[width=8cm,clip]{1907f4b.ps}\end{figure}](/articles/aa/full/2002/01/aa1907/Timg35.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1907f5a.ps}\hspace*{4mm}\includegraphics[width=8cm,clip]{1907f5b.ps}\end{figure}](/articles/aa/full/2002/01/aa1907/Timg39.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1907f6a.ps}\hspace*{4mm}\includegraphics[width=8cm,clip]{1907f6b.ps}\end{figure}](/articles/aa/full/2002/01/aa1907/Timg40.gif)
![$\displaystyle W(t,s) = \int_{-\infty}^{\infty}f(t'){1 \over \sqrt{s}}\quad\psi^* \left[{(t'-t) \over s} \right] {\rm d}t',$](/articles/aa/full/2002/01/aa1907/img47.gif)
![\begin{displaymath}W_n(s) = \sum_{n'=0}^{N-1}x_{n'}\sqrt{{\delta t \over s}}\psi^* \left[{(n'-n)\delta t \over s} \right],
\end{displaymath}](/articles/aa/full/2002/01/aa1907/img50.gif)
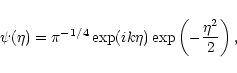
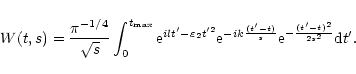
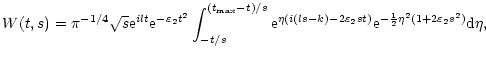
![$\displaystyle W(t,s) = {\pi^{1/4} \over \sqrt{2}} {\sqrt{s} \over \tau} {\rm e}...
...erf}\left({t \over s \tau\sqrt{2}} +i{ls-k \over \tau\sqrt{2}} \right) \right],$](/articles/aa/full/2002/01/aa1907/img62.gif)
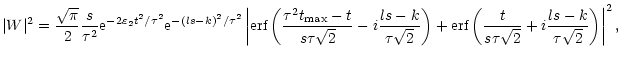
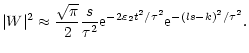
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1907f7.ps}\end{figure}](/articles/aa/full/2002/01/aa1907/Timg74.gif)
![$\displaystyle \vert W\vert^2 \approx {k \over l}{\sqrt{\pi} \over 2}{\rm e}^{-2...
...\sqrt{2}k}\right) + \mbox{erf}\left(\frac{t l}{\sqrt{2}k}\right) \right]^2\cdot$](/articles/aa/full/2002/01/aa1907/img81.gif)
![$\displaystyle \vert W\vert^2 \approx {k \over l}{\sqrt{\pi} \over 2}{\rm e}^{-2...
...\sqrt{2}k}\right) + \mbox{erf}\left(\frac{t l}{\sqrt{2}k}\right) \right]^2\cdot$](/articles/aa/full/2002/01/aa1907/img84.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1907f8a.ps}\hspace*{4mm}\inc...
...1907f8c.ps}\hspace*{4mm}\includegraphics[width=8cm,clip]{1907f8d.ps}\end{figure}](/articles/aa/full/2002/01/aa1907/Timg95.gif)
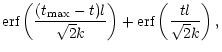
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1907f9a.ps}\hspace*{4mm}\inc...
...1907f9c.ps}\hspace*{4mm}\includegraphics[width=8cm,clip]{1907f9d.ps}\end{figure}](/articles/aa/full/2002/01/aa1907/Timg99.gif)
![$\displaystyle \vert W\vert^2 \approx {k \over l}{\sqrt{\pi} \over 2} g(t)\left[...
...\sqrt{2}k}\right) + \mbox{erf}\left(\frac{t l}{\sqrt{2}k}\right) \right]^2\cdot$](/articles/aa/full/2002/01/aa1907/img100.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1907f10a.ps}\hspace*{4mm}\includegraphics[width=8cm,clip]{1907f10b.ps}\end{figure}](/articles/aa/full/2002/01/aa1907/Timg101.gif)