For the mode identification, we proceed by iteration as follows.
We assume that all the modes seen in RXJ 2117+3412 have the same value of ![]() .
This assumption relies on the equidistant period spacing, discussed above
(Sect. 4.1), and on the similar rotational splitting found in the multiplets.
It is not possible to give an absolute identification for the k order
of the modes. Only differential k can be asserted. The reference mode
is chosen at 945.156
.
This assumption relies on the equidistant period spacing, discussed above
(Sect. 4.1), and on the similar rotational splitting found in the multiplets.
It is not possible to give an absolute identification for the k order
of the modes. Only differential k can be asserted. The reference mode
is chosen at 945.156 ![]() Hz, the central m=0 component
of a triplet, whose korder is some unknown k0. We will attempt now to identify the
relative order
Hz, the central m=0 component
of a triplet, whose korder is some unknown k0. We will attempt now to identify the
relative order
![]() ,
as well as the azimuthal number m for as many modes as possible.
Note that the
convention chosen for the sign of
m is different from the one used in classical textbooks: here
m=-1 is associated with the low frequency component of a triplet
(retrograde mode) while m=+1 corresponds to the high frequency component (prograde
mode). This sign convention is the same as in Unno et al. (1989) and Winget et al.
(1991, 1994).
The identification procedure starts by considering modes for which the
m=0 frequency is well determined, either from the two complete triplets,
(945
,
as well as the azimuthal number m for as many modes as possible.
Note that the
convention chosen for the sign of
m is different from the one used in classical textbooks: here
m=-1 is associated with the low frequency component of a triplet
(retrograde mode) while m=+1 corresponds to the high frequency component (prograde
mode). This sign convention is the same as in Unno et al. (1989) and Winget et al.
(1991, 1994).
The identification procedure starts by considering modes for which the
m=0 frequency is well determined, either from the two complete triplets,
(945 ![]() Hz, 1101
Hz, 1101 ![]() Hz),
or from the three doublets whose components are separated by twice the
rotational splitting (978/988
Hz),
or from the three doublets whose components are separated by twice the
rotational splitting (978/988 ![]() Hz, 1045/1055
Hz, 1045/1055 ![]() Hz and 1179/1190
Hz and 1179/1190 ![]() Hz).
In this latter case the m=0 frequency is
obtained by averaging the two components, assuming that the triplets are
symmetric. These five m=0 modes give a unique determination of the period spacing,
either by applying the inverse variance test (O'Donoghue 1994),
which yields a period spacing of
Hz).
In this latter case the m=0 frequency is
obtained by averaging the two components, assuming that the triplets are
symmetric. These five m=0 modes give a unique determination of the period spacing,
either by applying the inverse variance test (O'Donoghue 1994),
which yields a period spacing of
![]() s (HWHM),
or a linear unweighted least-squares fit which yields
s (HWHM),
or a linear unweighted least-squares fit which yields
![]() s.
The inverse variance procedure also yields the values of the relative radial order of the modes,
s.
The inverse variance procedure also yields the values of the relative radial order of the modes,
![]() ;
they are listed in the fourth column of Table 9.
We are not able to assign an absolute k value, because there are no models of
suitable quality at that high a luminosity in the literature.
;
they are listed in the fourth column of Table 9.
We are not able to assign an absolute k value, because there are no models of
suitable quality at that high a luminosity in the literature.
Starting from this point,
new m=0 modes are identified in a step by step procedure,
using linear
interpolation/extrapolation.
We allow for up to 2 s departures from the linear trend to
account for possible mode trapping effects. Later, we will show that this is
consistent with the actual trapping cycle, whose maximum amplitude
is ![]() 1.3 s.
An illustration of the mode identification procedure is given in Fig. 11 for the case
of the
1.3 s.
An illustration of the mode identification procedure is given in Fig. 11 for the case
of the
![]() and -4 modes.
From the straight line fit to the first five modes, we find that the m=0
mode for
and -4 modes.
From the straight line fit to the first five modes, we find that the m=0
mode for
![]() should appear at
should appear at
![]() s or in the
frequency interval
1003.8 to 1007.9
s or in the
frequency interval
1003.8 to 1007.9 ![]() Hz.
This estimate allows a unique identification of the m=0 component within the
doublet at 1005/1010
Hz.
This estimate allows a unique identification of the m=0 component within the
doublet at 1005/1010 ![]() Hz as the 1005.645
Hz as the 1005.645 ![]() Hz mode.
We can now include this mode into linear regression and
continue the procedure.
We then estimate the frequency range of the m=0 mode for
Hz mode.
We can now include this mode into linear regression and
continue the procedure.
We then estimate the frequency range of the m=0 mode for
![]() ,
which is 1025.9 to 1030.2
,
which is 1025.9 to 1030.2 ![]() Hz. It is clear that the mode
observed at 1023.594
Hz. It is clear that the mode
observed at 1023.594 ![]() Hz must be an m=-1 component of the triplet. The
m=0 component is not seen, but its frequency can be estimated from the
rotational splitting. We include the new m=0 frequency into the linear regression
and continue the procedure until we have determined the relative radial order (
Hz must be an m=-1 component of the triplet. The
m=0 component is not seen, but its frequency can be estimated from the
rotational splitting. We include the new m=0 frequency into the linear regression
and continue the procedure until we have determined the relative radial order (![]() )
and azimuthal order (m) for as many of the observed modes as is possible.
At each intermediate step, a linear fit
to m=0 modes is redetermined.
)
and azimuthal order (m) for as many of the observed modes as is possible.
At each intermediate step, a linear fit
to m=0 modes is redetermined.
We notice that the rotational splitting changes with period
(see Fig. 13), so we must interpolate the value for the
![]() ,
-8 modes. For
,
-8 modes. For
![]() smaller than
-11, the behaviour of rotational splitting is not known, and we assume a constant splitting
of
smaller than
-11, the behaviour of rotational splitting is not known, and we assume a constant splitting
of
![]()
![]() Hz for these modes.
While this is an arbitrary assumption, it has a negligible
effect on the trapping cycle parameters (Sect. 4.3) that we determine below.
We stop the mode identification at
frequencies lower than 780
Hz for these modes.
While this is an arbitrary assumption, it has a negligible
effect on the trapping cycle parameters (Sect. 4.3) that we determine below.
We stop the mode identification at
frequencies lower than 780 ![]() Hz, because below this limit the spacing between adjacent mmodes and between different overtone modes become comparable and we can no longer tell them apart.
Also, we refrained from
determining periods of unobserved m=0 modes
for
Hz, because below this limit the spacing between adjacent mmodes and between different overtone modes become comparable and we can no longer tell them apart.
Also, we refrained from
determining periods of unobserved m=0 modes
for ![]() larger than 0,
because the variation of rotational frequency splitting
with
larger than 0,
because the variation of rotational frequency splitting
with ![]() is not well established here because there are not enough multiplets detected at these
low frequencies.
In addition, at low frequencies,
any error in the interpolated/extrapolated value of
is not well established here because there are not enough multiplets detected at these
low frequencies.
In addition, at low frequencies,
any error in the interpolated/extrapolated value of
![]() would translate in relatively large error of the
mode's period and affect our mode trapping results.
Our procedure shows that some modes which could have been interpreted
as multiplets by considering only their frequency difference in Table 6 cannot be so.
That is the case for the modes at 789
would translate in relatively large error of the
mode's period and affect our mode trapping results.
Our procedure shows that some modes which could have been interpreted
as multiplets by considering only their frequency difference in Table 6 cannot be so.
That is the case for the modes at 789 ![]() Hz and 793
Hz and 793 ![]() Hz, which cannot
correspond to the same
Hz, which cannot
correspond to the same ![]() value, and for the modes at
830, 836 and 840
value, and for the modes at
830, 836 and 840 ![]() Hz, which must be a combination of a single mode and
a doublet of the successive k mode. Our proposed mode identification is
summarized in Table 9.
Hz, which must be a combination of a single mode and
a doublet of the successive k mode. Our proposed mode identification is
summarized in Table 9.
|
Frequency ( |
m | |
|
789.042 | +1 | +10 |
|
793.783 | -1 | +9 |
|
830.708 | +1 | +7 |
|
836.067 | -1 | |
| 1189.956 | 840.367: | 0 | +6 |
|
851.483 | -1 | +5 |
|
872.337 | 0 | +4 |
|
889.587 | 0 | +3 |
| 1117.568 | 894.800 | +1 | |
|
906.378 | 0 | +2 |
|
921.721 | -1 | +1 |
|
940.563 | -1 | |
| 1058.026 | 945.156 | 0 | 0 |
| 1052.732 | 949.909 | +1 | |
|
958.533 | -1 | |
| 1038.118 | 963.282 | 0 | -1 |
|
978.874 | -1 | |
| (1016.467) | (983.800) | 0 | -2 |
| 1011.403 | 988.726: | +1 | |
|
1005.645 | 0 | -3 |
| 989.569 | 1010.541 | +1 | |
|
1023.594 | -1 | |
| (972.247) | (1028.545) | 0 | -4 |
|
1045.690 | -1 | |
| (951.750) | (1050.697) | 0 | -5 |
| 947.236 | 1055.703 | +1 | |
|
1096.712 | -1 | |
| 907.489 | 1101.942 | 0 | -7 |
| 903.160 | 1107.224 | +1 |
|
Frequency ( |
m | |
|
1123.747: | -1 | |
| (885.736) | (1129.004) | 0 | -8 |
|
1179.955 | -1 | |
| (843.692) | (1185.267) | 0 | -10 |
| 839.928 | 1190.578: | +1 | |
|
1212.490 | -1 | |
| 821.145 | 1217.812 | 0 | -11 |
|
1245.457 | -1 | |
| (799.495) | (1250.789) | 0 | -12 |
|
(1283.828) | 0 | -13 |
| 775.699 | 1289.160 | +1 | |
|
1315.055 | -1 | |
| (757.354) | (1320.387) | 0 | -14 |
|
1362.495 | 0 | -15 |
|
1397.242 | -1 | |
| (712.975) | (1402.574) | 0 | -16 |
|
1439.198 | -1 | |
| (692.267) | (1444.530) | 0 | -17 |
Note that there is no correlation between mode trapping and mode amplitude,
where trapped modes are those defining the minima in Fig. 12. There
are 6 such minima. The corresponding modes have periods (![]() )
of
733.97 s (-15), 799.49 s (-12) and/or 821.15 s (-11), 885.74 s (-8)
and/or 907.49 s
(-7), 972.25 s (-4), 1058.03 s (0) and 1124.11 s (+3). Looking at
the trapped mode amplitudes during different runs (Table 6),
we see that trapped modes can have either low or high amplitudes.
Mode trapping and amplitude were also found to be uncorrelated in
PG 1159-035 (Winget et al. 1991) and in the DBV GD 358
(Winget et al. 1994).
Clearly, the amplitude
of a mode is not
simply governed by its linear growth rate.
The period spacing found here for RXJ 2117+3412 is remarkably similar to
the ones found in other PNNV and GW Vir stars:
)
of
733.97 s (-15), 799.49 s (-12) and/or 821.15 s (-11), 885.74 s (-8)
and/or 907.49 s
(-7), 972.25 s (-4), 1058.03 s (0) and 1124.11 s (+3). Looking at
the trapped mode amplitudes during different runs (Table 6),
we see that trapped modes can have either low or high amplitudes.
Mode trapping and amplitude were also found to be uncorrelated in
PG 1159-035 (Winget et al. 1991) and in the DBV GD 358
(Winget et al. 1994).
Clearly, the amplitude
of a mode is not
simply governed by its linear growth rate.
The period spacing found here for RXJ 2117+3412 is remarkably similar to
the ones found in other PNNV and GW Vir stars:
![]() s in
NGC 1501 (Bond et al. 1996), 21.5 s in PG 1159-035 (Winget et al.
1991),
21.6 s in PG 2131+066 (Kawaler et al. 1995) and 21.1 s in
PG 0122+200,
(Vauclair et al. 2001).
We do not understand what mechanism is forcing these pulsators - that have
different masses and luminosities - to display the same
period spacing. O'Brien (2000) suggests that an interplay between the
driving zone depth and the maximum allowed pulsation period, as a
function of
s in
NGC 1501 (Bond et al. 1996), 21.5 s in PG 1159-035 (Winget et al.
1991),
21.6 s in PG 2131+066 (Kawaler et al. 1995) and 21.1 s in
PG 0122+200,
(Vauclair et al. 2001).
We do not understand what mechanism is forcing these pulsators - that have
different masses and luminosities - to display the same
period spacing. O'Brien (2000) suggests that an interplay between the
driving zone depth and the maximum allowed pulsation period, as a
function of
![]() and the total mass, can explain the tendency for
higher mass pre-white dwarfs to pulsate at cooler
and the total mass, can explain the tendency for
higher mass pre-white dwarfs to pulsate at cooler
![]() than lower mass
ones. If higher mass GW Vir stars pulsate at cooler temperature than low mass ones,
then the average period spacings could be similar for all of the GW Vir stars.
However, it is still unclear how this preserves the almost constant
than lower mass
ones. If higher mass GW Vir stars pulsate at cooler temperature than low mass ones,
then the average period spacings could be similar for all of the GW Vir stars.
However, it is still unclear how this preserves the almost constant ![]() observed over a factor of almost 1000 in luminosity.
Clearly, the "numerology'' is telling us something about the nature of
the GW Vir and PNNV stars, but we do not yet understand it.
observed over a factor of almost 1000 in luminosity.
Clearly, the "numerology'' is telling us something about the nature of
the GW Vir and PNNV stars, but we do not yet understand it.
where
![]() takes a simple form in the asymptotic limit of high
order gravity modes, which applies to pre-white dwarfs, as discussed by
Winget et al. (1991). In that case
takes a simple form in the asymptotic limit of high
order gravity modes, which applies to pre-white dwarfs, as discussed by
Winget et al. (1991). In that case
![]() as shown by Brickhill (1975).
In the above expression for the frequencies, solid body rotation is
assumed. Any differential rotation present in the star would result in
an additional term
as shown by Brickhill (1975).
In the above expression for the frequencies, solid body rotation is
assumed. Any differential rotation present in the star would result in
an additional term
![]() to
to
![]() which depends on k, and so is different for different modes.
Assuming all the modes to be
which depends on k, and so is different for different modes.
Assuming all the modes to be ![]() modes, we derive an average rotation
period for RXJ 2117+3412, using the relation
modes, we derive an average rotation
period for RXJ 2117+3412, using the relation
One should keep in mind that the frequency
separation within multiplets may deviate from uniformity for different reasons.
There are at least four physical processes that could affect the
frequencies: i) non-linearities resulting from resonant coupling between
components of multiplets, ii) mode trapping, iii) structural changes
in the wave propagation cavities, and iv) magnetic field.
In case i), slight changes in the frequency of multiplets components are expected
even in
the case of modest non-linearity in the pulsations. The non-linearities result
in both amplitude and frequency variations for selected modes as described in
Goupil et al. (1998). In their application to the case of the DBV GD358,
however, they find that the frequency splitting is changed by the non-linear effects
by no more than 2%.
In case ii),
mode
trapping also introduces small variations in the frequency shift due to
rotational splitting (Kawaler et al. 1999).
Since the radial structure of the mode
is affected by trapping, so is the rotational kernel. If rotation is non-uniform,
it will affect the splitting constant.
In their discussion of the rotational
splitting in PG 1159-035, Kawaler et al. (1999) show that the
effect of mode trapping may change the frequency separation of the rotationally
split components by 2.5% in the period range 400
![]() s.
They also show that the rotation rate inside PG 1159-035 decreases with increasing radius.
The variations could be much larger would the gradient of the rotation curve be
steeper.
s.
They also show that the rotation rate inside PG 1159-035 decreases with increasing radius.
The variations could be much larger would the gradient of the rotation curve be
steeper.
As a consequence, any variations in the frequency splitting measured between
multiplets may be due to a combination of at least
these four effects and deriving any information on a potential
differential rotation profile is a speculative task.
Figure 13 shows the
variation of the rotational splitting as a function of
period for all multiplets observed in RXJ 2117+3412. Only secure detections are considered
(marginal detections are rejected). Rotational splittings derived from
1994 WET data are preferred because these data have the best window function. For data
from either the 1992 WET or the 1993 data set, splittings showing the smallest
formal error were preferred.
Figure 13 shows a clear trend of decreasing rotational splitting
with increasing period. Only one mode does not fit the trend: it is the
1124.117 s mode, seen only during the 1992 WET.
Several explanations can account for this discrepancy. We note from Table 6 that
for the few cases where we have frequency splitting information for the
same mode in different years, that the 1992 WET data have the largest splitting
for unknown reasons. We suspect that the systematically larger frequency splittings
in the 1992 data affect
the 1124.117 s mode, although we cannot rule out the possibility that there is an
incompletely corrected 2d alias present.
The observed
rotational splitting changes by a factor of 1.14 in the period
interval 821 s to 1058 s, covering 11 k orders. The factor is 1.24 if the longest
period mode (at 1189 s) is included, covering 17 k orders.
This variation of ![]() is 13-14 times greater than the
non-differentially rotating case considered by Kawaler et al.
(1999) who find
is 13-14 times greater than the
non-differentially rotating case considered by Kawaler et al.
(1999) who find
![]() % change in the rotational
splitting between 400 s and 800 s, covering 20 k orders, in their model
of PG 1159-035.
The conservative conclusion is that the rotational
splitting in RXJ 2117+3412 is inconsistent with solid-body rotation.
Kawaler et al. (1999) show
that a rotation law that decreases or increases outwards may have
similar signatures in a
% change in the rotational
splitting between 400 s and 800 s, covering 20 k orders, in their model
of PG 1159-035.
The conservative conclusion is that the rotational
splitting in RXJ 2117+3412 is inconsistent with solid-body rotation.
Kawaler et al. (1999) show
that a rotation law that decreases or increases outwards may have
similar signatures in a ![]() -Period diagram. They also show that mode
trapping affects the rotational splitting and that it is the phase shift
between the trapping seen in the period spacing (
-Period diagram. They also show that mode
trapping affects the rotational splitting and that it is the phase shift
between the trapping seen in the period spacing (![]() -Period
diagram) and the one seen in the rotational splitting (
-Period
diagram) and the one seen in the rotational splitting (![]() -Period
diagram) which contains the pertinent information on the rotation velocity
law. We do not see any such trapping cycle in the
-Period
diagram) which contains the pertinent information on the rotation velocity
law. We do not see any such trapping cycle in the ![]() -Period
diagram
of RXJ 2117+3412, which is in agreement with the weak trapping indicated by the small
amplitude of the trapping cycle, and this precludes any further statement on
the internal rotation profile of RXJ 2117+3412.
The observed trend of the rotational splitting in RXJ 2117+3412 is
surprisingly smooth. One would have expected a rather complex
internal rotation law,
if one considers that the star is i) still contracting towards the white
dwarf cooling sequence with a short time scale (
-Period
diagram
of RXJ 2117+3412, which is in agreement with the weak trapping indicated by the small
amplitude of the trapping cycle, and this precludes any further statement on
the internal rotation profile of RXJ 2117+3412.
The observed trend of the rotational splitting in RXJ 2117+3412 is
surprisingly smooth. One would have expected a rather complex
internal rotation law,
if one considers that the star is i) still contracting towards the white
dwarf cooling sequence with a short time scale (![]()
![]() )
and ii) is loosing mass at a rate of a
)
and ii) is loosing mass at a rate of a ![]()
![]() (Koesterke et al. 1998;
Koesterke & Werner 1998).
(Koesterke et al. 1998;
Koesterke & Werner 1998).
In the absence of any consistent physical interpretation of the
rotational splitting variation, we can only conclude that the
average rotation period is ![]() 1.1 d, and that the frequency splitting
is not consistent with solid body rotation.
The average rotation period for RXJ 2117+3412 is within the range of values
derived from asteroseismology for other pre-white
dwarfs. The PNNV NGC 1501 has a rotation period of 1.17 d (Bond et al.
1996).
Among other pulsating PG 1159 stars having rotation periods derived from
rotational splitting
PG 1159-035 has a period of 1.38 d (Winget et al. 1991),
PG 2131+066: 5.07 h (Kawaler et al. 1995) and PG 0122+200: 1.61 d
(O'Brien et al.
1996,
1998; Vauclair et al. 2001).
This trend persists with the cooler DBV and DAV white dwarfs, which have rotation
periods ranging from 9 to 58 hours (Bradley 2001).
Spruit (1998) argues that such rotation periods around one day for white dwarfs
can be expected if some small non-axisymmetries occur in the mass loss process
along the AGB evolutionary phase. In the case of RXJ 2117+3412, which is still losing
mass in its present pre-white dwarf phase (Werner et al. 1996;
Koesterke et al.
1998; Koesterke & Werner 1998), the complex structure
of its low surface brightness planetary nebula suggests such a
non-axisymmetrical mass loss.
1.1 d, and that the frequency splitting
is not consistent with solid body rotation.
The average rotation period for RXJ 2117+3412 is within the range of values
derived from asteroseismology for other pre-white
dwarfs. The PNNV NGC 1501 has a rotation period of 1.17 d (Bond et al.
1996).
Among other pulsating PG 1159 stars having rotation periods derived from
rotational splitting
PG 1159-035 has a period of 1.38 d (Winget et al. 1991),
PG 2131+066: 5.07 h (Kawaler et al. 1995) and PG 0122+200: 1.61 d
(O'Brien et al.
1996,
1998; Vauclair et al. 2001).
This trend persists with the cooler DBV and DAV white dwarfs, which have rotation
periods ranging from 9 to 58 hours (Bradley 2001).
Spruit (1998) argues that such rotation periods around one day for white dwarfs
can be expected if some small non-axisymmetries occur in the mass loss process
along the AGB evolutionary phase. In the case of RXJ 2117+3412, which is still losing
mass in its present pre-white dwarf phase (Werner et al. 1996;
Koesterke et al.
1998; Koesterke & Werner 1998), the complex structure
of its low surface brightness planetary nebula suggests such a
non-axisymmetrical mass loss.
The existence of a magnetic field would also lift the degeneracy of the
modes by splitting a mode of degree ![]() into
into ![]() +1 components. Since the
cumulative power spectrum of RXJ 2117+3412 does show some triplets,
the fine structure must at least be dominated by rotational splitting as
the magnetic field alone would only produce doublets for
+1 components. Since the
cumulative power spectrum of RXJ 2117+3412 does show some triplets,
the fine structure must at least be dominated by rotational splitting as
the magnetic field alone would only produce doublets for ![]() modes.
However, if a weak magnetic field is superimposed on the rotation, its
effect would be to shift each component relative to its non magnetic
frequency, with the shift in frequency proportional to
m2B2,
where B is the strength of the magnetic field. Both the
modes.
However, if a weak magnetic field is superimposed on the rotation, its
effect would be to shift each component relative to its non magnetic
frequency, with the shift in frequency proportional to
m2B2,
where B is the strength of the magnetic field. Both the ![]() components are equally shifted by the magnetic field to higher
frequencies. The m=0 component is also shifted to higher frequency by
a smaller amount (see Unno et al. 1989; Jones et al.
1989). As a result, a frequency asymmetry in the triplets
could be the signature of such magnetic field.
Unfortunately, there are only two true triplets
in the power spectrum of
RXJ 2117+3412 to search for such an asymmetry.
Considering these two triplets, one does find that the differences between
their prograde and
retrograde mode frequency splitting is within the formal uncertainties in
the frequency measurement with
components are equally shifted by the magnetic field to higher
frequencies. The m=0 component is also shifted to higher frequency by
a smaller amount (see Unno et al. 1989; Jones et al.
1989). As a result, a frequency asymmetry in the triplets
could be the signature of such magnetic field.
Unfortunately, there are only two true triplets
in the power spectrum of
RXJ 2117+3412 to search for such an asymmetry.
Considering these two triplets, one does find that the differences between
their prograde and
retrograde mode frequency splitting is within the formal uncertainties in
the frequency measurement with
![]()
![]() Hz. The corresponding
upper limit of the magnetic field, obtained by scaling the results of
Jones et al. (1989) for
Hz. The corresponding
upper limit of the magnetic field, obtained by scaling the results of
Jones et al. (1989) for ![]() modes (their Fig. 1) is of the
order of
modes (their Fig. 1) is of the
order of ![]() G. As this is taken from the calculations for a pure
carbon white dwarf model by Jones et al. (1989), it can only be an approximate
value when scaled to RXJ 2117+3412.
G. As this is taken from the calculations for a pure
carbon white dwarf model by Jones et al. (1989), it can only be an approximate
value when scaled to RXJ 2117+3412.
Mode trapping is interpreted as the signature of chemical
stratification in the star. Such a stratification is induced by the
previous history of nucleosynthesis within the star and the
gravitational settling combined with diffusion acting in a strong gravitational field.
The effect of mode trapping on the frequency of the pulsation modes has been
studied in detail for the pre-white dwarf pulsators (Kawaler & Bradley
1994), although for luminosities lower than that of RXJ 2117+3412.
The trapping cycle observed in RXJ 21117+3412,
folded by the
trapping phase, is shown in Fig. 14. It does not show evidence of a
double peaked structure; this absence suggests that we detect probably only one
chemical composition transition zone between the He-rich outer layers
and the C/O core. The amplitude of the trapping cycle (A)
depends on the gradient of the mean molecular weight through the
transition zone and on the thickness of the He-rich layer,
while the period of the trapping cycle depends mainly on the thickness of the
He-rich outer layer.
The thickness of the He-rich outer layer in
RXJ 2117+3412 could be precisely determined only
through the calculation of realistic
models, which are not yet available. The best we can do now is to
use the results published by Kawaler & Bradley (1994)
and extrapolate them to the range of
parameters of RXJ 2117+3412. The extrapolation may not be too bad, since at least
the average period spacing is only weakly dependent on luminosity.
The trapping period depends on the thickness
of the He-rich envelope at fixed
![]() ,
as shown in Fig. 3 of Kawaler & Bradley.
As can be inferred from this figure, the logarithm of the outer layer
fractional mass
is related to the trapping period through
a very tight linear relation. Similarly,
at fixed mass of the He-rich outer layer, the trapping period depends
on log (
,
as shown in Fig. 3 of Kawaler & Bradley.
As can be inferred from this figure, the logarithm of the outer layer
fractional mass
is related to the trapping period through
a very tight linear relation. Similarly,
at fixed mass of the He-rich outer layer, the trapping period depends
on log (
![]() ),
as shown in their Fig. 4. Again, the trapping period as a
function of log (
),
as shown in their Fig. 4. Again, the trapping period as a
function of log (
![]() )
is accurately fitted by a linear relation.
We combine these two relations to construct an
interpolation formula representing the models of Kawaler & Bradley:
)
is accurately fitted by a linear relation.
We combine these two relations to construct an
interpolation formula representing the models of Kawaler & Bradley:
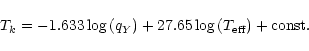
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS1689fig14.eps} \end{figure}](/articles/aa/full/2002/01/aa1689/Timg109.gif) |
Figure 14:
Folded trapping cycle. The residuals of the period distribution (same as in Fig. 12)
but plotted vs. trapping cycle phase. The mode
|
The above equation can be now rewritten as
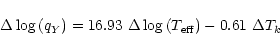
Despite similar trapping periods, we derive vastly different envelope thickness.
This is entirely due to the difference in
![]() between RXJ 2117+3412
and PG 1159-035. A comparison of the trapping amplitudes of PG 1159-035
and RXJ 2117+3412 shows that the
amplitude of RXJ 2117+3412 is only half that of PG 1159-035.
The smaller trapping amplitude of RXJ 2117+3412 could arise from two effects (see Kawaler & Bradley
1994, their Fig. 3). First, the trapping amplitude decreases with increasing
He-rich layer mass fraction and second, it also decreases towards longer
periods. Both effects are the result of the peak amplitude portion of the eigenfunction moving away
from the composition gradient, which decreases the resonance effect of mode trapping.
The observed periods of PG 1159-035 are in the range of
430 s to 840 s, while in RXJ 2117+3412 they are in the range of 690 s to 1190 s.
between RXJ 2117+3412
and PG 1159-035. A comparison of the trapping amplitudes of PG 1159-035
and RXJ 2117+3412 shows that the
amplitude of RXJ 2117+3412 is only half that of PG 1159-035.
The smaller trapping amplitude of RXJ 2117+3412 could arise from two effects (see Kawaler & Bradley
1994, their Fig. 3). First, the trapping amplitude decreases with increasing
He-rich layer mass fraction and second, it also decreases towards longer
periods. Both effects are the result of the peak amplitude portion of the eigenfunction moving away
from the composition gradient, which decreases the resonance effect of mode trapping.
The observed periods of PG 1159-035 are in the range of
430 s to 840 s, while in RXJ 2117+3412 they are in the range of 690 s to 1190 s.
The presently available evolutionary models for the transition between
the planetary nebulae nuclei and the white dwarfs are not
suitable for interpreting
RXJ 2117+3412. While the 0.7 ![]() evolutionary
sequence of Wood & Faulkner (1986) fits the location of
RXJ 2117+3412 in the
evolutionary
sequence of Wood & Faulkner (1986) fits the location of
RXJ 2117+3412 in the ![]() -
-
![]() diagram, the pure He surface
composition of their models does not adequatly represent the observed
abundances of RXJ 2117+3412. The more recent calculations by
Gautschy(1997), while using a composition more compatible
with the surface abundances of PG 1159 stars, do not fit the high
luminosity and temperature of RXJ 2117+3412, except by considering
stellar models with masses in excess of 0.7
diagram, the pure He surface
composition of their models does not adequatly represent the observed
abundances of RXJ 2117+3412. The more recent calculations by
Gautschy(1997), while using a composition more compatible
with the surface abundances of PG 1159 stars, do not fit the high
luminosity and temperature of RXJ 2117+3412, except by considering
stellar models with masses in excess of 0.7 ![]() ,
which
disagrees with the mass derived from asteroseismology (see below). None
of these models takes into account the chemical stratification induced
by diffusion in the presence of mass loss. As a consequence, one can hardly
use them to calculate
theoretical period spacings which one could use for asteroseismological mass
determination.
,
which
disagrees with the mass derived from asteroseismology (see below). None
of these models takes into account the chemical stratification induced
by diffusion in the presence of mass loss. As a consequence, one can hardly
use them to calculate
theoretical period spacings which one could use for asteroseismological mass
determination.
In Vauclair et al. (1993), the mass estimate
was based on an interpolation formula which did
not take into account the luminosity dependence of the period spacing
(Winget et al. 1991). This formula, used to estimate the mass of PG 1159-035
is probably not appropriate for RXJ 2117+3412, which is two orders of
magnitude more luminous than PG 1159-035. Kawaler & Bradley (1994)
calculated the period spacings,
![]() ,
for a grid of pre-white dwarf models of
various masses,
including the luminosity dependence (their Fig. 2). They derive an
interpolation formula that is valid for luminosities
between
,
for a grid of pre-white dwarf models of
various masses,
including the luminosity dependence (their Fig. 2). They derive an
interpolation formula that is valid for luminosities
between
![]() .
Extrapolating this formula to the luminosity of RXJ 2117+3412
log(
.
Extrapolating this formula to the luminosity of RXJ 2117+3412
log(
![]() is risky. Rather
than using their interpolation formula, we extrapolate
is risky. Rather
than using their interpolation formula, we extrapolate ![]() directly from their Fig. 2 by spline functions.
Using the period spacing derived
in Sect. 4.3,
directly from their Fig. 2 by spline functions.
Using the period spacing derived
in Sect. 4.3,
![]()
![]() s, and assuming that this period spacing is
valid for
asymptotic
s, and assuming that this period spacing is
valid for
asymptotic ![]() modes, we obtain
modes, we obtain
![]() s.
At the luminosity of RXJ 2117+3412 (see next section),
such a period spacing corresponds to a model of
s.
At the luminosity of RXJ 2117+3412 (see next section),
such a period spacing corresponds to a model of ![]() 0.56
0.56 ![]() .
The formula of Winget et al.
(1991) gives a mass of 0.58
.
The formula of Winget et al.
(1991) gives a mass of 0.58 ![]() .
The
value obtained from Kawaler & Bradley's interpolation formula would be
0.52
.
The
value obtained from Kawaler & Bradley's interpolation formula would be
0.52 ![]() ,
and the range
,
and the range
![]() is a rough
estimate of the uncertainty for this preliminary mass determination.
We should stress that the uncertainty we quote is entirely due to the fact that we
have to extrapolate the existing theoretical calculations
and does not include any observational uncertainty in
is a rough
estimate of the uncertainty for this preliminary mass determination.
We should stress that the uncertainty we quote is entirely due to the fact that we
have to extrapolate the existing theoretical calculations
and does not include any observational uncertainty in ![]() or
or
![]() .
A much more precise
mass estimate (as good as for PG 1159-035) must await models
covering the parameter range of RXJ 2117+3412.
For now, our best value for the mass of RXJ 2117+3412 is
.
A much more precise
mass estimate (as good as for PG 1159-035) must await models
covering the parameter range of RXJ 2117+3412.
For now, our best value for the mass of RXJ 2117+3412 is
![]() .
.
If we interpret the observed period spacing as corresponding to ![]() modes, the derived
mass would be
modes, the derived
mass would be ![]() 0.32
0.32 ![]() .
Such a low mass would be in conflict with the spectroscopically determined log g= 6.0.
It would imply that the progenitor of RXJ 2117+3412 was in a binary system, for which we do
not see evidence, and that the star would have a helium core as a result of previous mass
transfer in the binary system.
Higher
.
Such a low mass would be in conflict with the spectroscopically determined log g= 6.0.
It would imply that the progenitor of RXJ 2117+3412 was in a binary system, for which we do
not see evidence, and that the star would have a helium core as a result of previous mass
transfer in the binary system.
Higher ![]() values would imply even lower mass estimates for RXJ 2117+3412,
which would make the conflict even more severe.
On these grounds, we
conclude that the modes observed in RXJ 2117+3412 must be
values would imply even lower mass estimates for RXJ 2117+3412,
which would make the conflict even more severe.
On these grounds, we
conclude that the modes observed in RXJ 2117+3412 must be ![]() modes. This is
in agreement with the
modes. This is
in agreement with the ![]() value implied by the fine structure found in the power spectrum.
value implied by the fine structure found in the power spectrum.
Knowing the total mass of the star from asteroseismology on one hand and the surface gravity and effective temperature from spectroscopy on the other hand, it is straightforward to derive the luminosity and the distance of the star.
The best fit model atmosphere for RXJ 2117+3412 indicates a surface gravity
log g=6.0
+0.3-0.2 (Rauch & Werner 1997)
and an effective temperature
![]() (Werner et al. 1996).
The radius derived from the mass (
(Werner et al. 1996).
The radius derived from the mass (
![]() )
and gravity is:
)
and gravity is:
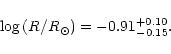
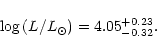
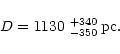
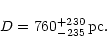
Adopting this new distance estimate, and its associated uncertainty, the linear
extent of the planetary nebula is:
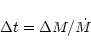
This estimate of the evolutionary time scale would imply a rate of
period change of the order of
![]() (
(
![]() )
for the
low He-rich envelope mass case (high He-rich envelope mass)
for periods around 1000 s. This is comparable to the
)
for the
low He-rich envelope mass case (high He-rich envelope mass)
for periods around 1000 s. This is comparable to the
![]() measured
for the 516 s mode in PG 1159-035 (Costa et al. 1999).
Such a high rate of period change would probably be detectable in
RXJ 2117+3412 if one could find an isolated mode with a stable
amplitude.
As shown in Fig. 12, mode trapping in RXJ 2117+3412 offers the
potential to measure
measured
for the 516 s mode in PG 1159-035 (Costa et al. 1999).
Such a high rate of period change would probably be detectable in
RXJ 2117+3412 if one could find an isolated mode with a stable
amplitude.
As shown in Fig. 12, mode trapping in RXJ 2117+3412 offers the
potential to measure ![]() for both trapped and nontrapped modes.
In the case of the trapped modes the resultant
for both trapped and nontrapped modes.
In the case of the trapped modes the resultant ![]() would be dominated
by the evolutionary time scale of the outer layers, where the structure reflects the
competition between contraction and mass loss. The
would be dominated
by the evolutionary time scale of the outer layers, where the structure reflects the
competition between contraction and mass loss. The ![]() of the nontrapped
modes would be dominated by the core cooling time scale.
Unfortunatly, it will be difficult to get an unambiguous
of the nontrapped
modes would be dominated by the core cooling time scale.
Unfortunatly, it will be difficult to get an unambiguous
![]() measurement for any mode of RXJ 2117+3412,
because of the rich pulsation spectrum (which requires multisite data)
and because of the large amplitude variations of the modes.
measurement for any mode of RXJ 2117+3412,
because of the rich pulsation spectrum (which requires multisite data)
and because of the large amplitude variations of the modes.
The mode at 1315.05 ![]() Hz, whose amplitude remained almost constant in
the data sets presented here, unfortunately takes part in a
linear combination
with the 653.987
Hz, whose amplitude remained almost constant in
the data sets presented here, unfortunately takes part in a
linear combination
with the 653.987 ![]() Hz to form the 1968.952
Hz to form the 1968.952 ![]() Hz
(plus some other higher order combinations). So it can not be
used as a clean mode to measure
Hz
(plus some other higher order combinations). So it can not be
used as a clean mode to measure ![]() .
As this mode may be suspected to
take part in a mode coupling, its frequency variation may
not reflect global stellar evolution, but would rather reflect some
properties of the mode coupling. It is worth mentioning however that,
while both the 653
.
As this mode may be suspected to
take part in a mode coupling, its frequency variation may
not reflect global stellar evolution, but would rather reflect some
properties of the mode coupling. It is worth mentioning however that,
while both the 653 ![]() Hz and 1968
Hz and 1968 ![]() Hz peaks
suffered large
amplitude variations in the period covered by the data, as seen in Table 6,
the 1315
Hz peaks
suffered large
amplitude variations in the period covered by the data, as seen in Table 6,
the 1315 ![]() Hz amplitude varies by only 20% during the same time. If those
three modes were coupled, it is difficult to understand how the
amplitude of two
components could vary so much while the third remains almost constant.
So long as we cannot determine whether the 1315
Hz amplitude varies by only 20% during the same time. If those
three modes were coupled, it is difficult to understand how the
amplitude of two
components could vary so much while the third remains almost constant.
So long as we cannot determine whether the 1315 ![]() Hz mode is an eigenmode or coupled
to other modes, it would be hazardous to infer any
physical meaning from a
Hz mode is an eigenmode or coupled
to other modes, it would be hazardous to infer any
physical meaning from a ![]() measurement for that particular mode. One must
conservatively conclude that
with the data presently available, there is no stable enough mode
in a clean enough part of the power spectrum which we could
identify as a potential
candidate for a
measurement for that particular mode. One must
conservatively conclude that
with the data presently available, there is no stable enough mode
in a clean enough part of the power spectrum which we could
identify as a potential
candidate for a ![]() measurement.
But given the presently poor physical constraints on evolution in this part of the H-R
diagram, attempting to measure a rate of period change is a worthy challenge.
measurement.
But given the presently poor physical constraints on evolution in this part of the H-R
diagram, attempting to measure a rate of period change is a worthy challenge.
The rapid evolution of RXJ 2117+3412 shows up in the mass loss.
RXJ 2117+3412 has a measured mass loss rate of
![]() ,
which has interesting implications for
the region where pulsation driving takes place.
The excitation mechanism (
,
which has interesting implications for
the region where pulsation driving takes place.
The excitation mechanism (![]() mechanism due to carbon
and oxygen partial ionization) operates at the depth of
mechanism due to carbon
and oxygen partial ionization) operates at the depth of
![]() K, which
lies in the outer
K, which
lies in the outer ![]() 10-8 M* mass fraction of the star
(Bradley & Dziembowski 1996).
The observed mass loss rate implies that the material in the driving region is renewed
on a time scale considerably shorter than the evolutionary time scale
(
10-8 M* mass fraction of the star
(Bradley & Dziembowski 1996).
The observed mass loss rate implies that the material in the driving region is renewed
on a time scale considerably shorter than the evolutionary time scale
(![]() 50 days!). As a consequence, the chemical composition
of the driving region could change on this time scale if there is compositional
stratification of the outer layers. This outflow of mass through the driving region
may affect the efficiency of the excitation mechanism, especially if the
mass loss rate is time dependent. The amplitude variations observed in
the star, including variations on time scale as short as that
exhibited by the mode at 717
50 days!). As a consequence, the chemical composition
of the driving region could change on this time scale if there is compositional
stratification of the outer layers. This outflow of mass through the driving region
may affect the efficiency of the excitation mechanism, especially if the
mass loss rate is time dependent. The amplitude variations observed in
the star, including variations on time scale as short as that
exhibited by the mode at 717 ![]() Hz during the 1994 WET campaign,
could be related to the effect of the mass loss on the
effectiveness of the driving in this region.
Hz during the 1994 WET campaign,
could be related to the effect of the mass loss on the
effectiveness of the driving in this region.
The non-radial g-mode instability in pre-white dwarf stars is triggered
by the
![]() and
and ![]() mechanism induced by the partial ionization of carbon and
oxygen at
mechanism induced by the partial ionization of carbon and
oxygen at
![]() K, as first suggested by Starrfield et al.
(1983, 1984) and confirmed by the subsequent analysis
of Stanghellini et al. (1991). More recently, instability
studies using models computed with the new He/C/O OPAL opacities (Iglesias &
Rogers 1993) show a better agreement with the observed
blue edge of the instability strip and put some constraints
on the composition of the
driving region (Bradley & Dziembowski 1996; Saio 1996;
Gautschy 1997). However, Kawaler et al. (1986)
had also anticipated that during the PN and pre-white dwarf evolutionary
phases, the possibility of a remnant He-burning shell that could drive g-modes by
the
K, as first suggested by Starrfield et al.
(1983, 1984) and confirmed by the subsequent analysis
of Stanghellini et al. (1991). More recently, instability
studies using models computed with the new He/C/O OPAL opacities (Iglesias &
Rogers 1993) show a better agreement with the observed
blue edge of the instability strip and put some constraints
on the composition of the
driving region (Bradley & Dziembowski 1996; Saio 1996;
Gautschy 1997). However, Kawaler et al. (1986)
had also anticipated that during the PN and pre-white dwarf evolutionary
phases, the possibility of a remnant He-burning shell that could drive g-modes by
the ![]() -mechanism. As the He burning necessarily occurs at the
bottom of the He-rich outer layers,
the periods of these unstable g-modes are in
the range of 70 s-200 s, corresponding to low k orders for
-mechanism. As the He burning necessarily occurs at the
bottom of the He-rich outer layers,
the periods of these unstable g-modes are in
the range of 70 s-200 s, corresponding to low k orders for ![]() modes.
Saio (1996) and Gautschy (1997) also find
g-modes triggered by the
modes.
Saio (1996) and Gautschy (1997) also find
g-modes triggered by the ![]() -mechanism in some of their models,
with typical periods between
-mechanism in some of their models,
with typical periods between ![]() 110 s and
110 s and ![]() 150 s. However,
such short period g-modes excited by
150 s. However,
such short period g-modes excited by ![]() -mechanism have not
been found in the surveys of PNN conducted by Grauer et al.
(1987) and by Hine & Nather (1987).
-mechanism have not
been found in the surveys of PNN conducted by Grauer et al.
(1987) and by Hine & Nather (1987).
At the high frequency end of the list given in Table 6, one finds some peaks
which could be candidates for such ![]() -mechanism driven modes, since
their periods are in the range 230-290 s. But, as discussed in Sect. 3.2,
all the peaks with frequency above 2180
-mechanism driven modes, since
their periods are in the range 230-290 s. But, as discussed in Sect. 3.2,
all the peaks with frequency above 2180 ![]() Hz (
Hz (
![]() s) are
the result of
linear combinations of lower frequency modes; they are not independent
modes. The highest frequency independent mode has a frequency of 2174.884
s) are
the result of
linear combinations of lower frequency modes; they are not independent
modes. The highest frequency independent mode has a frequency of 2174.884
![]() Hz (period of 459.8 s). A careful scrutiny of the power spectrum at
even higher frequencies (up to 12000
Hz (period of 459.8 s). A careful scrutiny of the power spectrum at
even higher frequencies (up to 12000 ![]() Hz), where the highest
noise peaks are at a 0.20 mma level, does not reveal any significant peak. We
conclude that our data show no evidence for low-k order mode driven
by the
Hz), where the highest
noise peaks are at a 0.20 mma level, does not reveal any significant peak. We
conclude that our data show no evidence for low-k order mode driven
by the ![]() -mechanism.
-mechanism.
Copyright ESO 2001