A&A 381, 122-150 (2002)
DOI: 10.1051/0004-6361:20011483

Asteroseismology of RXJ 2117+3412, the hottest pulsating PG 1159 star

G. Vauclair¹ - P. Moskalik² - B. Pfeiffer¹ - M. Chevreton³ - N. Dolez¹ - B. Serre¹ - S. J. Kleinman^4,18 - M. Barstow⁵ - A. E. Sansom⁵ - J.-E. Solheim²¹ - J. A. Belmonte⁶ - S. D. Kawaler²³ - S. O. Kepler⁷ - A. Kanaan^7,22 - O. Giovannini⁷ - D. E. Winget⁴ - T. K. Watson⁴ - R. E. Nather⁴ - J. C. Clemens^4,19 -
J. Provencal^4,20 - J. S. Dixson⁴ - K. Yanagida⁴ - A. Nitta Kleinman⁴ - M. Montgomery⁴ - E. W. Klumpe⁴ - A. Bruvold²¹ - M. S. O'Brien^23,24 - C. J. Hansen²⁵ - A. D. Grauer⁸ - P. A. Bradley^4,9,27 - M. A. Wood^26,27 - N. Achilleos¹⁰ - S. Y. Jiang¹¹ - J. N. Fu^1,11 - T. M. K. Marar¹² - B. N. Ashoka¹² - E. G. Mei $\breve{\rm s}$ tas¹³ - A. V. Chernyshev¹⁴ - T. Mazeh¹⁵ - E. Leibowitz¹⁵ - S. Hemar¹⁵ - J. Krzesinski¹⁶ -
G. Pajdosz¹⁶ - S. Zo $\l$ a^16,17

1 - Université Paul Sabatier, Observatoire Midi-Pyrénées, CNRS/UMR5572, 14 Av. É. Belin, 31400 Toulouse, France
2 - Copernicus Astronomical Center, Ul. Bartycka 18, 00-716 Warsaw, Poland
3 - Observatoire de Paris-Meudon, DAEC, 92195 Meudon, France
4 - Department of Astronomy and McDonald Observatory, Texas University at Austin, Austin, TX 78712, USA
5 - Department of Physics and Astronomy, University of Leicester, University Road, Leicester, LE1 7RH, UK
6 - Instituto de Astrofisica de Canarias, 38200 La Laguna, Tenerife, Spain
7 - Instituto de Física-UFRGS, Av. B. Goncalves 9500, 91501-900 Porto-Alegre, RS, Brazil
8 - Department of Physics and Astronomy, University of Arkansas at Little Rock, Little Rock, AR 72204, USA
9 - Los Alamos National Laboratory, X-2, MS B-220, Los Alamos, NM 87545, USA
10 - Siding Spring Observatory, and Department of Mathematics, Australian National University, Canberra, Australia
11 - Beijing Astronomical Observatory, Chinese Academy of Sciences, 20A, Datun Road, Beijing 100012, PR China
12 - Indian Space Research Organization, Airport Road, Vimanapura PO, Bangalore 560017, India
13 - Institute of Theoretical Physics and Astronomy, Gostauto 12, Vilnius 2600, Lithuania
14 - Astronomical Institute, Astronomicheskaya 33, Tashkent 700052, Uzbekistan
15 - Wise Observatory, Tel Aviv University, Tel Aviv 69978, Israel
16 - Mt. Suhora Observatory, Cracow Pedagogical University, Ul. Podchorazych 2, 30-084 Cracow, Poland
17 - Astronomical Observatory, Jagiellonian University, ul. Orla 171, 30-244 Cracow, Poland
18 - Sloan Digital Sky Survey, Apache Pt. Observatory, PO Box 59, Sunspot, NM 88349, USA
19 - Department of Physics, University of North Carolina, Chapel Hill, NC 27599-3255, USA
20 - Department of Physics and Astronomy, University of Delaware, Newark, DE 19716, USA
21 - Department of Physics, University of Tromso, 9037 Tromso, Norway
22 - Departamento de Física, Universidade Federal de Santa Catarina, CP 476, CEP 88040-900, Florianópolis, Brazil
23 - Department of Physics and Astronomy, Iowa State University, Ames, IA 50011, USA
24 - Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
25 - Joint Institute for Laboratory Astrophysics, University of Colorado, Box 440, Boulder, CO 80309, USA
26 - Department of Physics and Space Sciences and SARA Observatory, Florida Institute of Technology, Melbourne, FL 32901, USA
27 - Guest Observer, Institute for Astronomy, Honolulu, HI, USA

Received 17 July 2001 / Accepted 15 October 2001

Abstract
The pulsating PG 1159 planetary nebula central star RXJ&nb sp;2117+3412 has been observed over three successive seasons of a multisite photometric campaign. The asteroseismological analysis of the data, based on the 37 identified $\ell=1$ modes among the 48 independent pulsation frequencies detected in the power spectrum, leads to the derivation of the rotational splitting, the period spacing and the mode trapping cycle and amplitude, from which a number of fundamental parameters can be deduced. The average rotation period is $1.16\pm 0.05$ days. The trend for the rotational splitting to decrease with increasing periods is incompatible with a solid body rotation. The total mass is 0.56 ^+0.02_-0.04 $M_{\odot}$ and the He-rich envelope mass fraction is in the range 0.013-0.078 M_*. The luminosity derived from asteroseismology is log( $L/L_{\odot})= 4.05$ ^+0.23_-0.32 and the distance 760 ⁺²³⁰_-235 pc. At such a distance, the linear size of the planetary nebulae is $2.9\pm 0.9$ pc. The role of mass loss on the excitation mechanism and its consequence on the amplitude variations is discussed.

Key words: stars: fundamental parameters -- stars: individual (RXJ 2117+3412) -- stars: oscillations

1 Introduction

Asteroseismology is a powerful tool to explore the internal structure of stars and test the predictions of stellar evolution. Its application to the late stages of medium mass stellar evolution, i.e., to planetary nebulae nuclei and white dwarfs, has been particularly fruitful owing to the short period oscillations observed in these compact stars, allowing the accumulation of a large number of pulsation cycles over relatively short observation times. The organization of coordinated multisite observing campaigns was a breakthrough in the study of compact multiperiodic pulsators. In this respect, the Whole Earth Telescope network (WET, Nather et al. 1990), performing coordinated photometric campaigns, successfully contributed to this effort.

In these late stages of stellar evolution, stars have several opportunities to become pulsationally unstable. The first instability region is encountered during the high luminosity planetary nebula phase, and nine variable planetary nebulae nuclei (PNNV) are presently known (Ciardullo & Bond 1996). The second instability region is found among the pre-white dwarf stars of the PG 1159 spectral type, which are direct descendants of a significant fraction of PNN. These stars have passed the turning point in the H-R diagram, where planetary nebulae nuclei reach their highest effective temperature and start cooling towards lower temperatures and luminosities, as they begin contracting towards the white dwarf cooling sequence. Six such pulsating PG 1159 stars, also known as GW Vir variable stars, are presently known. Five are plain PG 1159 type stars that show no hydrogen in their spectra: PG 1159-035 (McGraw et al. 1979; Winget et al. 1991), PG 2131+066 (Bond et al. 1984; Kawaler et al. 1995), PG 1707+427 (Bond et al. 1984; Fontaine et al. 1991; Grauer et al. 1992), PG 0122+200 (Bond & Grauer 1987; Vauclair et al. 1995; O'Brien et al. 1996, 1998; Vauclair et al. 2001) and RXJ 2117+3412, the subject of this paper. The sixth object, HS 2324+3944 (Silvotti 1996; Silvotti et al. 1999), is a "hybrid'' PG 1159 type star, which has hydrogen in its spectrum. Both the PNNV and the PG 1159 instability strips are not "pure'' instability strips, i.e., both non-variable and variable stars are present in the same temperature and luminosity range. We still do not understand why stars of the same effective temperature and surface gravity, have some that pulsate, while others do not. In the case of the PG 1159 type stars, the only known distinction comes from spectroscopy: pulsating PG 1159 stars show nitrogen in their spectra while non-pulsating PG 1159 stars do not (Dreizler 1998; Dreizler & Heber 1998). However, there is the noticeable and puzzling exception of PG 1144+005, which shows N in its spectrum at the same level as the pulsating PG 1159 stars, but was not found to pulsate (Grauer et al. 1987).

**Table 1:** Participating sites.
Observatory	Location	Telescopes		(m)
		1992	1993	1994
OMP	Pic du Midi, France			2.0
Teide	Tenerife, Canary Islands		1.5	0.8
Roque de los Muchachos	La Palma, Canary Islands	2.5		1.0
LNA	Itajuba, Brazil	1.6
McDonald	Mount Locke, Texas	2.0	0.9	2.0, 2.6
Steward Observatory	Mount Bigelow, Arizona		1.5
Steward Observatory	Mount Lemmon, Arizona		1.5
U. of Hawaii	Mauna Kea, Hawaii	0.6		0.6
Siding Spring	Siding Spring Mt., Australia	1.0
Beijing Observatory	Xinglong, China			2.1
Vainu Bappu	Kavalur, India		2.2	1.0
Maidanak	Maidanak, Uzbekistan	1.0		1.0
Wise	Mount Ramon, Israel			1.0
Suhora	Mount Suhora, Poland	0.6	0.6	0.6

For completeness, we note that there are two more white dwarf instability strips. They are the pulsating helium atmosphere white dwarfs (8 DBVs known) and the pulsating hydrogen atmosphere white dwarfs (31 DAVs or ZZ Cetis known). The DBV instability strip is not a "pure'' instability strip either. The fraction of non-variable stars found within the instability strip varies between $\approx$ 25% and $\approx$ 50% depending whether their atmospheric parameters are derived from pure He model atmospheres or from model atmospheres allowing for a small admixture of undetectable hydrogen (Beauchamp et al. 1999). In contrast with the PNNV, PG 1159 and DBV instability strips, the DAVs form a "pure'' instability strip, i.e., no stable stars are found within the domain of the HR diagram (or equivalently in the $\log g$ - $\log T_{{\rm eff}}$ diagram) where the DAVs are located, once the mass dependence of the blue edge of the instability strip is properly accounted for (Kepler et al. 2000). The list and the properties of the variable planetary nebulae nuclei, variable PG 1159 type stars, DBVs and DAVs are summarized in Bradley (2000).

The variable stars in the pre-white dwarf evolutionary stage and on the white dwarf cooling sequence are non-radial gravity mode pulsators. This is unambiguously demonstrated for the two ZZ Cetis, R 548 (Robinson et al. 1982) and G 117-B15A (Kepler 1984). In the framework of the linear pulsation theory, it has been possible to extract fundamental stellar parameters for most of the pulsators in the PG 1159 instability strip: the total mass from the period spacing, the rotational period from the frequency splitting, the depth of the chemical composition transition zone between the helium-rich outer layer and the carbon-oxygen core etc. As a by-product of the asteroseismological analysis, the luminosity and distance can be derived for each star (Winget et al. 1994). In the case of the PNNV, few have been studied with the same scrutiny, because observing them requires CCD photometry campaigns to remove the surrounding nebula. In addition, the PNNV mode amplitudes vary on short time scales (days to weeks), making the mode identification difficult. However, the best studied case, NGC 1501 (Bond et al. 1996) shows many similarities with the GW Vir stars. The evolutionary link between the PNN and the PG 1159 stars is now well established and the stellar parameters deduced from asteroseismology of PNNV and GW Vir stars provide further confirmation.

The discovery that RXJ 2117+3412, an X-ray source detected in the ROSAT sky survey, is a member of the PG 1159 spectral class (Motch et al. 1993) is an additional evidence of an evolutionary link between the PNN and the white dwarfs. The low surface brightness planetary nebula surrounding RXJ 2117+3412 was discovered to be the largest planetary nebula known (Appleton et al. 1993). The nebula has an angular diameter of 13 arcmin, and at an estimated distance of 1.4 kpc (Motch et al. 1993), its linear extent should be about 5.3 pc. Furthermore, the complex structure of the nebula, which shows many thin filaments, is reminiscent of the structure predicted for the shock produced when a "superwind'' generated by the hot central star collides with the material ejected at the end of the previous AGB phase (Appleton et al. 1993).

**Table 2:** Journal of observations: 1992 WET (XCOV8).
Run Name	Telescope	Date	Start Time	Run Length
		(UT)	(UTC)	(s)
x-8006	Suhora 60 cm	22 September 92	01:07:15	4155
jesem-05	Maidanak 1 m	22 September 92	16:00:00	19930
x-8008	Suhora 60 cm	22 September 92	23:32:30	9550
int-0014	Isaak Newton 2.5 m	24 September 92	01:05:40	5920
ro-021	Itajuba 1.6 m	24 September 92	01:23:40	5825
pab-0147	McDonald 82 $^{\prime\prime}$	24 September 92	07:15:30	7620
jesem-06	Maidanak 1 m	24 September 92	14:49:50	22765
x-8011	Suhora 60 cm	25 September 92	01:05:10	4685
int-0017	Isaak Newton 2.5 m	25 September 92	20:50:10	18695
x-8013	Suhora 60 cm	25 September 92	23:53:20	6670
pab-0156	McDonald 82 $^{\prime\prime}$	26 September 92	01:46:00	14135
jesem-10	Maidanak 1 m	26 September 92	15:22:30	17945
x-8016	Suhora 60 cm	27 September 92	00:38:00	7480
int-0019	Isaak Newton 2.5 m	27 September 92	02:00:30	6025
pab-0160	McDonald 82 $^{\prime\prime}$	27 September 92	08:10:30	5260
maw-0107	Mauna Kea 24 $^{\prime\prime}$	27 September 92	10:35:20	5845
x-8018	Suhora 60 cm	27 September 92	21:26:45	17025
int-0022	Isaak Newton 2.5 m	28 September 92	01:27:40	7765
pab-0163	McDonald 82 $^{\prime\prime}$	28 September 92	06:54:30	9915
x-8019	Suhora 60 cm	28 September 92	18:27:35	2095
pab-0166	McDonald 82 $^{\prime\prime}$	29 September 92	07:39:00	6975
ro-023	Itajuba 1.6 m	29 September 92	22:15:50	16245
pab-0168	McDonald 82 $^{\prime\prime}$	30 September 92	01:40:30	28170
maw-0111	Mauna Kea 24 $^{\prime\prime}$	30 September 92	05:30:00	24085
sjk-0208	Siding Spring 40 $^{\prime\prime}$	30 September 92	12:02:00	8240
ro-025	Itajuba 1.6 m	30 September 92	23:51:40	8410
pab-0171	McDonald 82 $^{\prime\prime}$	1 October 92	01:50:00	27345
maw-0114	Mauna Kea 24 $^{\prime\prime}$	1 October 92	08:36:20	14360
x-8020	Suhora 60 cm	1 October 92	20:29:00	9780
pab-0173	McDonald 82 $^{\prime\prime}$	2 October 92	01:50:00	26910
maw-0118	Mauna Kea 24 $^{\prime\prime}$	3 October 92	06:02:20	15230

Table 3: Journal of observations (1993).

Run Name
Telescope Date Start Time Run Length

(UT) (UTC) (s)

rx-0914
TCS 1.5 m 14 September 93 21:26:00 15420

rx-0915 TCS 1.5 m 15 September 93 20:46:00 20670

suh-0001 Suhora 60 cm 15 September 93 21:19:40 5260

a-402 Mt. Bigelow 61 $^{\prime\prime}$ 16 September 93 03:51:00 19310

k93-0214 Kavalur 90 $^{\prime\prime}$ 16 September 93 18:14:00 8325

rx-0916 TCS 1.5 m 16 September 93 21:29:00 14660

rx-0917 TCS 1.5 m 17 September 93 20:13:00 21690

a-404 Mt. Bigelow 61 $^{\prime\prime}$ 18 September 93 02:36:00 21430

k93-0215 Kavalur 90 $^{\prime\prime}$ 18 September 93 14:16:10 18390

suh-0002 Suhora 60 cm 18 September 93 18:47:00 5890

rx-0918 TCS 1.5 m 18 September 93 20:19:00 21910

a-405 Mt. Bigelow 61 $^{\prime\prime}$ 19 September 93 02:46:00 22500

suh-0003 Suhora 60 cm 19 September 93 18:16:00 30210

rx-0919 TCS 1.5 m 19 September 93 20:48:00 19100

a-407 Mt. Bigelow 61 $^{\prime\prime}$ 20 September 93 02:39:00 28930

ra-288 McDonald 36 $^{\prime\prime}$ 20 September 93 03:34:40 18120

suh-0004 Suhora 60 cm 20 September 93 19:17:30 23685

rx-0920 TCS 1.5 m 20 September 93 20:27:00 20390

a-408 Mt. Bigelow 61 $^{\prime\prime}$ 21 September 93 02:29:00 28460

a-409 Mt. Lemmon 60 $^{\prime\prime}$ 22 September 93 02:43:00 27070

suh-0005 Suhora 60 cm 22 September 93 19:16:00 21825

rx-0922 TCS 1.5 m 22 September 93 20:37:00 19530

a-410 Mt. Lemmon 60 $^{\prime\prime}$ 23 September 93 02:37:00 27300

suh-0006 Suhora 60 cm 23 September 93 18:33:00 20515

rx-0923a TCS 1.5 m 23 September 93 20:21:00 4620

rx-0923b TCS 1.5 m 23 September 93 22:51:00 4720

The subsequent analysis of a HST high resolution spectrum of RXJ 2117+3412, using NLTE model atmosphere, indicates that it is the hottest known PG 1159 type star with $T_{{\rm eff}}= 170\,000$ K, $\log g= 6.0$ ^+0.3_-0.2, and abundance ratios typical of other PG 1159 stars: $\rm He/C/O=47.5$ /23.8/6.2 (by numbers) (Werner et al. 1996; Rauch & Werner 1997). The HST spectrum also shows evidence of ongoing mass loss from the central star. The mass loss is confirmed by more recent observations; it is estimated to be of the order of $\dot{M}$ = $10^{-7}~M_{\odot}\,{{\rm yr}}^{-1}$ from C IV line (Koesterke et al. 1998), or $\dot{M}= 4\times 10^{-8}~M_{\odot} \,{{\rm yr}}^{-1}$ from O VI line (Koesterke & Werner 1998), with a terminal velocity of 3500 km s^-1. Because of the association of a planetary nebula with a PG 1159-type central star, and because it is close to the point in the HR diagram where high luminosity PNN turn to lower effective temperature and luminosity to join the white dwarf cooling sequence (Dreizler & Heber 1998, see their Fig. 8), RXJ 2117+3412 is presently the best example of a PNN on its way to the white dwarf sequence.

Shortly after RXJ 2117+3412 was announced as a new PG 1159 type star, photometric observations were performed to determine whether it is a pulsator. Watson (1992) and Vauclair et al. (1993) independently discovered that RXJ 2117+3412 is pulsating. This opened the opportunity to investigate the internal structure and evolutionary status of this unique object.

This paper presents the results of an asteroseismological study of RXJ 2117+3412. The observational campaigns, which cover the 1992, 1993 and 1994 seasons are described in Sect. 2. Section 3 gives the analysis of the power spectra. The various stellar parameters derived for RXJ 2117+3412 from this analysis are discussed in Sect. 4. Section 5 summarizes the results and suggests some ideas for future work.

2 Observations and data reduction

2.1 The observations

The observations described in this paper result from multisite rapid photometry campaigns organized on three consecutive seasons in 1992, 1993 and 1994. The participating sites are listed in Table 1.

The data have been obtained with 2-channel or 3-channel photometers all equipped with blue sensitive photomultipliers (Hamamatsu R647-04 or similar) and used without a filter (white light). These instruments fulfill the specifications and requirements as prescribed by Kleinman et al. (1996). The sampling time was either 5 s or 10 s. In the former case, the data were coadded to 10 s afterwards. For 2-channel photometers, the observing procedure consists of simultaneously monitoring the target star in one channel and a comparison star in the second channel. The sky background is measured at random time intervals in both channels. For 3-channel photometers, the sky background is continuously monitored by the third channel, with the target and comparison stars placed in the other two channels.

2.2 Summary of the discovery data

After the announcement that RXJ 2117+3412 was a PG 1159 type star (Werner 1993; Motch et al. 1993), the star was immediately tested for photometric variability. It was found to be variable by Watson (1992) and Vauclair et al. (1993) independently. The data set obtained at the 2.5 m NOT is described in Vauclair et al. (1993). It was obtained with the Chevreton three-channel photometer - a short description is given in Vauclair et al. (1989). The data consist of 28 hr of time-series photometry accumulated during 4 consecutive nights, and allowed to extract 27 peaks in the power spectrum. The largest amplitude mode was found at 1217.8 $\mu$ Hz (821 s period) with a 4.6 mma amplitude, after re-reduction of the data. The frequency resolution of these single-site discovery data was only 2.7 $\mu$ Hz. Figure 1 shows the power spectrum of the light curve, re-reduced for the present paper.

$\begin{figure} \par\includegraphics[width=16cm,clip]{MS1689fig1.eps} \end{figure}$

Figure 1: Power spectrum of the discovery data re-reduced for the present paper. The corresponding window function is shown at the same frequency scale in the insert. Power is plotted in units of micro-modulation power ( $\mu$ mp) as a function of frequency (in $\mu$ Hz) between 0 and 4000 $\mu$ Hz.

$\begin{figure} \par\includegraphics[width=16cm,clip]{MS1689fig2.eps} \end{figure}$

Figure 2: Normalized light curve of RX J2117+3412 during the 1992 WET (XCOV8) campaign. The modulation intensity is plotted as a function of time (UT). Each panel corresponds to one day.

2.3 1992 WET campaign

A WET campaign had been planned for September 1992, shortly after the discovery of the variability of RXJ 2117+3412. The star was its third priority target. This campaign obtained 78 hr of non-redundant data. This WET campaign will be referred to as 1992 WET (or also XCOV8) in the following discussion. The observing sites involved are listed in Table 1. The total duration of the campaign was 10.7 days, with a corresponding frequency resolution in the Fourier transform of 1.1 $\mu$ Hz. The coverage of the 1992 WET for RXJ 2117+3412 was 35%, a rather satisfactory coverage for a third priority target. The observation log is given in Table 2, and Fig. 2 shows the normalized light curve of the 1992 WET data.

2.4 1993 multisite campaign

A multisite campaign was organized, independently of the WET network, one year after the 1992 WET campaign. 105 hr of fast photometry were obtained during 9.1 days. The coverage was 48% and the frequency resolution achieved 1.3 $\mu$ Hz. The sites involved are listed in Table 1 and the observation log is given in Table 3.

Surprisingly, the average amplitude of the pulsations observed during this campaign was much smaller than one year earlier. The normalized light curve of this campaign is shown in Fig. 3. Note that the vertical scale of Fig. 3 is the same as in Fig. 2.

$\begin{figure} \par\includegraphics[width=15.5cm,clip]{MS1689fig3.eps} \end{figure}$

Figure 3: Normalized light curve of RXJ 2117+3412 during the September 1993 campaign. The modulation intensity is plotted as a function of time (UT). Each panel corresponds to one day.

$\begin{figure} \par\includegraphics[width=15.5cm,clip]{MS1689fig4.eps} \end{figure}$

Figure 4: Normalized light curve of RXJ 2117+3412 during the 1994 WET (XCOV 11) campaign. The modulation intensity is plotted as a function of time (UT). Each panel corresponds to one day.

2.5 1994 WET campaign

RXJ 2117+3412 was the first priority target of the 1994 WET campaign. The observing sites involved are listed in Table 1 and the observation log is given in Table 4.

The campaign had a total duration of 15.0 days, of which only 13.8 days are used in the forthcoming reduction, implying a frequency resolution of 0.8 $\mu$ Hz in the power spectrum. 175 hr of non-redundant data were obtained, leading to a coverage of 49%. The light curve, shown in Fig. 4, looks quite different from those of the two previous campaigns. Here, the largest amplitude mode is at a frequency of 958.5 $\mu$ Hz (1043 s period). This campaign is referred to as 1994 WET (or also XCOV11) in the following text.

In addition to the data listed in Table 4, which were obtained with photomultiplier-based photometers, some CCD photometry data have been acquired at the Teide Observatory IAC 0.80 m telescope during part on the 1994 WET on three consecutive nights: 1994 August 9-11. Images of the RXJ 2117+3412 field were taken every 250 s, on average, with an exposure time of 150 s. Because of the different sampling time, the CCD data are reduced separately and are not included in the calculation of the power spectrum. They are useful for a comparison of the CCD photometry with photomultiplier photometry. Table 5 is the log of the CCD photometry observations.

Table 4: Journal of observations: 1994 WET (XCOV11).

Run Name
Telescope Date Start Time Run Length

(UT) (UTC) (s)

emcav-03
Maidanak 1 m 31 July 94 18:34:40 9750

emcav-04 Maidanak 1 m 1 August 94 16:56:40 10170

suh-0015 Suhora 60 cm 1 August 94 23:36:50 6010

gv-0414 TBL 2 m 2 August 94 00:54:00 8530

emcav-05 Maidanak 1 m 2 August 94 16:18:20 25010

suh-0016 Suhora 60 cm 2 August 94 22:20:30 12600

gv-0416 TBL 2 m 2 August 94 22:36:00 16300

sjk-0374 JKT 1 m 3 August 94 01:49:30 2990

sjk-0375 JKT 1 m 3 August 94 03:03:30 10310

emcav-06 Maidanak 1 m 3 August 94 16:14:00 24240

sjk-0376 JKT 1 m 3 August 94 21:11:30 22900

gv-0418 TBL 2 m 3 August 94 22:34:00 17340

sjk-0377 JKT 1 m 4 August 94 03:37:00 7640

pab-0179 Mauna Kea 24 $^{\prime\prime}$ 4 August 94 09:29:10 19260

emcav-07 Maidanak 1 m 4 August 94 16:39:40 23820

suh-0017 Suhora 60 cm 4 August 94 20:16:30 18690

sjk-0378 JKT 1 m 4 August 94 21:33:00 17700

gv-0420 TBL 2 m 5 August 94 00:10:00 11570

sjk-0379 JKT 1 m 5 August 94 02:30:30 12290

pab-0182 Mauna Kea 24 $^{\prime\prime}$ 5 August 94 07:12:00 27060

emcav-08 Maidanak 1 m 5 August 94 17:35:30 3530

emcav-10 Maidanak 1 m 5 August 94 18:38:30 5700

gv-0422 TBL 2 m 5 August 94 20:55:00 22930

suh-0018 Suhora 60 cm 5 August 94 21:07:00 16250

pab-0183 Mauna Kea 24 $^{\prime\prime}$ 6 August 94 06:22:30 24330

pab-0184 Mauna Kea 24 $^{\prime\prime}$ 6 August 94 13:15:30 5730

sjk-0380 JKT 1 m 6 August 94 21:07:30 6730

gv-0424 TBL 2 m 6 August 94 22:47:00 7400

sjk-0381 JKT 1 m 6 August 94 23:00:30 5060

**Table 4:** continued.
Run Name	Telescope	Date	Start Time	Run Length
		(UT)	(UTC)	(s)
pab-0185	Mauna Kea 24 $^{\prime\prime}$	7 August 94	06:15:00	30920
k44-0259	Kavalur 40 $^{\prime\prime}$	7 August 94	14:08:00	3220
k44-0260	Kavalur 40 $^{\prime\prime}$	7 August 94	15:17:40	23390
emcav-11	Maidanak 1 m	7 August 94	16:04:10	25870
sjk-0382	JKT 1 m	7 August 94	21:36:30	23050
gv-0445	TBL 2 m	7 August 94	22:40:00	16700
ra-340	McDonald 82 $^{\prime\prime}$	8 August 94	06:01:30	15200
pab-0186	Mauna Kea 24 $^{\prime\prime}$	8 August 94	06:30:10	23930
pab-0187	Mauna Kea 24 $^{\prime\prime}$	8 August 94	13:42:00	1770
emcav-12	Maidanak 1 m	8 August 94	16:01:40	26060
suh-0019	Suhora 60 cm	8 August 94	19:45:30	1940
sjk-0383	JKT 1 m	8 August 94	21:03:30	32000
gv-0426	TBL 2 m	8 August 94	22:07:00	18500
ra-341	McDonald 82 $^{\prime\prime}$	9 August 94	02:53:10	21410
pab-0188	Mauna Kea 24 $^{\prime\prime}$	9 August 94	06:38:10	29840
sh-0000	Wise 40 $^{\prime\prime}$	9 August 94	18:40:40	14690
suh-0020	Suhora 60 cm	9 August 94	23:26:00	9810
ra-342	McDonald 82 $^{\prime\prime}$	10 August 94	02:54:50	30450
pab-0189	Mauna Kea 24 $^{\prime\prime}$	10 August 94	06:16:30	31140
sh-0003	Wise 40 $^{\prime\prime}$	10 August 94	18:34:10	3650
sh-0004	Wise 40 $^{\prime\prime}$	10 August 94	20:02:00	2240
sh-0006	Wise 40 $^{\prime\prime}$	10 August 94	21:48:20	14860
ra-343	McDonald 82 $^{\prime\prime}$	11 August 94	05:30:20	21010
pab-0190	Mauna Kea 24 $^{\prime\prime}$	11 August 94	06:14:30	31300
sh-0007	Wise 40 $^{\prime\prime}$	11 August 94	18:13:30	24950
ra-344	McDonald 82 $^{\prime\prime}$	12 August 94	02:48:40	30740
ra-345	McDonald 107 $^{\prime\prime}$	13 August 94	05:05:50	6310
pab-0191	Mauna Kea 24 $^{\prime\prime}$	13 August 94	07:18:00	13490
ra-346	McDonald 107 $^{\prime\prime}$	13 August 94	09:00:50	8160
ra-347	McDonald 107 $^{\prime\prime}$	14 August 94	03:43:30	11760
ra-348	McDonald 107 $^{\prime\prime}$	14 August 94	07:04:10	2330
ra-349	McDonald 107 $^{\prime\prime}$	14 August 94	08:12:30	11620
gv-0472	Xinglong 2.16 m	14 August 94	12:31:00	25850
gv-0474	Xinglong 2.16 m	15 August 94	12:44:10	25890

2.6 Data reduction

The photomultiplier photometer data have been reduced in a now standard way (Nather et al. 1990; Kepler 1993). In both 2- and 3-channel photometers, the sky background is measured at the beginning and at the end of each run in all channels. This is used to determine the sensitivity ratios of the channels. In 3-channel photometric data, the sky background is monitored continuously in one channel, allowing for point by point subtraction of the sky background from the target and comparison star channels, after application of the proper sensitivity ratios. For 2-channel data, the sky background is normally measured at irregular intervals in both channels. The sky background is then constructed by polynomial interpolation. Each star channel is then corrected for extinction and normalized. When conditions show evidence for transparency variations, the normalized target star channel counts are divided by the smoothed comparison star channel counts. Subtracting unity from the resulting time series gives the time series on which the barycentric correction to the time base is applied.

Each of the observing campaigns has been reduced shortly after the observations. For the purpose of the present paper however, all the data have been re-reduced in an homogeneous way. A few runs have been rejected where the noise level was too high, which was usually due to clouds or instrumental problems. In case of overlapping data, we kept the best signal/noise ratio run in our analysis. The power spectrum of each time series is obtained by a Fourier Transform. A non-linear least-squares fitting routine (which fits the frequencies, amplitudes and phases of sine waves to the time series), followed by prewhitening, is used to extract the significant modes from the power spectra. The discovery data obtained in August 1992 at the NOT, were also re-reduced for comparison with the original reduction, although these data were not used in the present paper because they are single site data with too poor a frequency resolution. The power spectrum of these data is shown in Fig. 1. The power spectra of the time series obtained during the 1992 WET, the 1993 multisite campaign and the 1994 WET runs are shown in Figs. 5-7 respectively. Figure 8 illustrates the prewhitening sequence on a portion of the 1994 WET power spectrum.

Table 5: Journal of the CCD photometry obtained at the IAC 80 cm telescope.

Date
Start time Run length^*

(UT) (UTC) (s)

August 9, 1994
22:33:42 22250

August 10, 1994 22:57:12 24500

August 11, 1994 23:09:39 24750

Note. ^* The run lengths are the total lengths of the runs which consist in series of 150 s exposure time on RXJ 2117+3412 field taken every 250 s in average.

**Table 5:** Journal of the CCD photometry obtained at the IAC 80 cm telescope.
Date	Start time	Run length^*
(UT)	(UTC)	(s)
August 9, 1994	22:33:42	22250
August 10, 1994	22:57:12	24500
August 11, 1994	23:09:39	24750

Power is seen without ambiguity in the range 650 $\mu$ Hz-4340 $\mu$ Hz. Most of the peaks with significant power are found in the restricted range 650 $\mu$ Hz-1600 $\mu$ Hz. For each observing season, Table 6 lists the frequencies f, with their uncertainties $\delta$ f (in $\mu$ Hz) and the amplitudes A (in mma) of the peaks considered significant in the power spectra. These values are derived by the non-linear least squares fit. To decide whether a peak in a power spectrum is significant on an objective basis, the following rules were applied: a False Alarm Probability (FAP) (Kepler 1993) was estimated on the 1000 $\mu$ Hz frequency range embedding most of the significant power. All peaks with a $FAP \leq$ 10^-3 were considered as significant. Several peaks with FAP >10^-3were also included in the list (marked with colons in Table 6), but only if: i) they fit the pattern of rotationally split multiplets, or ii) they fit the period spacing ( $\Delta P$ ) distribution, or iii) they have frequency equal to, or close enough to, the frequency of a significant peak observed in other seasons.

CCD photometry obtained at the IAC 0.80 m telescope has been reduced independently. The images were taken without a filter. The basic reductions (bias subtraction and flatfield corrections) were made by use of the IRAF package. The photometric reductions were done using the MOMF package (Kjeldsen & Frandsen 1992). The resulting time series was analyzed by a non-linear least-squares fit. Frequencies extracted from this data set are listed in Table 7.

$\begin{figure} \par\includegraphics[width=16cm,clip]{MS1689fig5.eps} \end{figure}$

Figure 5: Power spectrum of the 1992 WET (XCOV 8) light curve. The units are the same as in Fig. 1. Note the different vertical scale on each panel. The window function is shown at the same frequency scale in the insert. The prominent sidelobes in the window function correspond to the 1 and 2 day aliases.

$\begin{figure} \par\includegraphics[width=16cm,clip]{MS1689fig6.eps} \end{figure}$

Figure 6: Power spectrum of the 1993 light curve. The units are the same as in Fig. 1. Note the different vertical scale on each panel. The window function is shown at the same frequency scale in the insert. The prominent sidelobes in the window function correspond to the 1 day alias.

$\begin{figure} \par\includegraphics[width=16cm,clip]{MS1689fig7.eps} \end{figure}$

Figure 7: Power spectrum of the 1994 WET (XCOV 11) light curve. The units are the same as in Fig. 1. Note the different vertical scale on each panel. The window function is shown at the same frequency scale in the insert. Note the small amplitude of the 1 day alias sidelobes.

$\begin{figure} \par\includegraphics[width=16cm,clip]{MS1689fig8.eps} \end{figure}$

Figure 8: Illustration of the prewhitening sequence. This figure is an enlarged part of the power spectrum of the 1994 WET shown in Fig. 7, restricted to the frequency range 750-1250 $\mu$ Hz, where most of the weak peaks appear. The five panels illustrate (from top to bottom) the successive steps by which the largest amplitude peaks are removed from the data. Those frequencies removed at each step are marked with thick arrows. Note in panel 3 the peaks at 1023.684 $\mu$ Hz and at 1045.944 $\mu$ Hz that are not significant in this run taken alone, according to our False Alarm Probability (FAP) criterion. However, since these two peaks are unambiguously present in the 1992 data, they are considered as real peaks and kept in the prewhitening procedure. Panel 5 shows what is left after removing of all the significant power. Three peaks are marked with arrows: 840.367 $\mu$ Hz, 988.726 $\mu$ Hz and 1123.747 $\mu$ Hz. These peaks are not significant on their own, according to our adopted FAP criterion. However, they fit the known rotational frequency splitting or period spacing (1123.747 $\mu$ Hz) pattern. We include them in Table 6, but denote them with a colon to indicate their lesser certainty.

**Table 6:** Combined list of the frequencies identified in RXJ2117+3412.
	1994			1993			1992
	WET						WET
f	$\delta f$	A	f	$\delta f$	A	f	$\delta f$	A
653.987	0.018	0.90				653.811	0.029	1.46
						655.556	0.031	1.33
666.938	0.028	0.57:
						706.260	0.039	0.98:
717.714	0.008	1.96
789.042	0.022	0.71
793.783	0.019	0.84
830.708	0.006	2.68				831.412	0.022	1.78
836.067	0.022	0.74	835.000	0.040	0.66
840.367	0.040	0.43:
			851.483	0.041	0.64
872.337	0.029	0.55
						889.587	0.033	1.23
						894.800	0.019	2.16
906.378	0.016	1.03
921.721	0.031	0.53
940.563	0.020	0.82	939.838	0.063	0.43:	939.948	0.051	0.89
						945.156	0.040	1.05
949.909	0.022	0.83				950.445	0.022	2.07
958.533	0.005	3.64	957.959	0.042	0.65
963.282	0.025	0.67	963.416	0.031	0.86
978.874	0.032	0.52
988.726	0.038	0.44:
1005.645	0.033	0.49
1010.541	0.032	0.52
1023.684	0.037	0.45	1023.292	0.029	0.90	1023.594	0.020	2.03
1045.944	0.050	0.35:	1044.904	0.072	0.36:	1045.690	0.045	0.90
1055.703	0.042	0.41
1096.712	0.016	1.05	1096.060	0.055	0.52
1101.942	0.039	0.41				1101.203	0.065	0.67:
			1107.300	0.063	0.46	1107.224	0.027	1.61
1123.747	0.049	0.32:
1179.955	0.007	2.16	1179.761	0.061	0.43	1179.893	0.029	1.43
						1190.578	0.054	0.79:

Table 6: continued.

1994 1993 1992

WET WET

f $\delta f$ A f $\delta f$ A f $\delta f$ A

1212.490
0.016 0.95 1212.419 0.047 0.58

1217.812
0.012 1.38 1217.886 0.022 1.21 1217.865 0.010 4.07

1245.457 0.059 0.46

1289.129
0.035 0.45 1289.136 0.060 0.45 1289.160 0.015 2.63

1315.055
0.012 1.24 1315.032 0.021 1.26 1315.181 0.026 1.55

1362.734
0.056 0.29: 1362.495 0.074 0.36

1397.385
0.057 0.28: 1397.242 0.061 0.45

1439.198
0.025 0.62

1539.991
0.055 0.29:

1548.653
0.043 0.37

1549.959 0.050 0.75

1572.012 0.094 0.27

1947.334
0.068 0.26:

1956.008
0.027 0.58 1956.785 0.103 0.29

1968.952
0.023 0.67 1968.222 0.085 0.35 1968.915 0.047 0.84

2109.129 0.049 0.76

2133.259
0.064 0.25: 2133.122 0.055 0.47

2143.374 0.124 0.21:

2153.980 0.079 0.33

2164.116 0.122 0.21:

2174.884 0.076 0.35

2184.777 0.110 0.23:

2402.113 0.098 0.26

3408.257 0.046 0.35

3517.490
0.049 0.30

3924.971 0.062 0.27

4077.942 0.100 0.41

4308.046 0.074 0.35

4339.147 0.132 0.20:

3 Analysis of the power spectra

3.1 Time variations

A comparison of power spectra from the campaigns covering 3 seasons shows that the amplitude varies dramatically for most of the observed modes. This is well illustrated by examining the amplitude evolution of the dominant modes in Table 6. In the discovery data and in the succeeding 1992 WET run, the dominant mode was at 1217 $\mu$ Hz, but its amplitude decreased by a factor 3 on a one year timescale. During the 1993 campaign, most of the modes observed one year before had decreased their amplitude by a comparable factor of 3, while a few modes increased their amplitude. Only one mode - at 1315 $\mu$ Hz - maintained an almost constant amplitude over the two year period covered by our observations. This mode may be useful for determining $\dot{P}$ , which will be discussed in Sect. 4.9. This mode was the dominant mode during the 1993 low amplitude phase of RXJ 2117+3412. In contrast, the power spectrum of the 1994 WET campaign was dominated by a mode at 958 $\mu$ Hz, which was below the detection limit during the 1992 WET run and barely present during the 1993 campaign. The amplitude of this mode increased by a factor 6 in one year interval. Such large amplitude variations are a common property of the PNNV and the pulsating PG 1159 stars (Bond et al. 1996; Kawaler 1998). The amplitude variations observed in RXJ 2117+3412 are reminiscent of what has been described for the PNNV NGC 1501 (Bond et al. 1996). In that case, amplitude variations, up to a factor of 2, are sometimes also associated with frequency variations. Some frequency variations are also observed for a few modes in RXJ 2117+3412. Amplitude variations are not uncommon in some cooler DBVs (Vuille et al. 2000) and ZZ Ceti stars (Kleinman et al. 1998).

3.2 Fine structure, multiplets

While the amplitude of the modes changed within the two years interval of the observing campaigns, most of the modes observed more than once were at the same frequencies, within the observational uncertainties. Some interesting exceptions will be discussed below. In the following, we will assume that any non-linear effects that are present only affect the mode amplitudes and have a negligible effect on the mode frequencies. Therefore, we can still rely on linear pulsation theory to compute the frequencies of the observed pulsation modes. Asteroseismology depends on having the maximum number of pulsation modes available for an accurate inference of the internal structure of a star. Given the large amplitude changes present in RXJ 2117+3412 from one season to the next, we had to observe the star with three multisite campaigns in order to detect enough modes to decipher the structure of RXJ 2117+3412. Combining the sets of frequencies derived from these observing campaigns, allows us to significantly increase the number of modes usable for asteroseismological analysis. The 1994 WET data set has the best frequency resolution and coverage. The superior coverage makes the window function the most useful for deciphering the power spectrum. This is seen in Fig. 9 where the window functions from the three multisite campaigns are compared. We start the process of mode identification with the best power spectrum (1994 WET) and then proceed to the other two campaigns. For this reason, Table 6 lists the frequencies identified in the data in the order of worsening spectral window, i.e., 1994 WET, 1993, 1992 WET, which is also the inverse chronological order.

$\begin{figure} \par\includegraphics[width=13.6cm,clip]{MS1689fig9.eps} \end{figure}$

Figure 9: A comparison of the window functions obtained during the three multisite photometric campaigns used in the present paper: from top to bottom, they correspond to the September 1992 WET run, the September 1993 run, and the August 1994 WET run.

A quick look at the frequency list derived from the 1994 WET campaign alone (Table 6, Col. 1), shows a total of 42 significant peaks. A number of them are separated in frequency by about 5 $\mu$ Hz. This is uncomfortably close to one half of the one day alias (5.8 $\mu$ Hz). If we examine the window function in 1994, there are no peaks present in the range of 5 to 6 $\mu$ Hz (as shown in Fig. 9), so we conclude that this frequency separation must be real. We interpret this splitting as due to slow rotation, implying that the star is rotating with a period of about one day, assuming these are $\ell =1$ modes. We follow this guideline to "read'' the frequency distribution and propose a mode identification. However, the 1994 WET frequency list by itself shows only doublets separated by about 5 $\mu$ Hz, and no triplets or quintuplets, which would be the clear signatures of $\ell =1$ or $\ell =2$ modes split by rotation. One only sees several cases of two modes separated by about 5 $\mu$ Hz. Considering the 1994 WET frequencies together with those derived in the previous campaigns, some of the missing multiplet members show up, which greatly aids our effort to decipher the power spectrum. This game can be difficult as the previous campaigns did not realize as good a coverage as the 1994 WET campaign; this is reflected in their poorer window function (see Fig. 9). The deconvolution of the power spectrum in some rich frequency domains could not be done unambiguously with the 1992 WET or 1993 data alone, and we relied on the 1994 WET data to help resolve ambiguities between the true frequencies and their aliases. In the following discussion, we discuss the features of the combined frequency list, which will be the basis for describing the fine structure used later to determine the rotational splitting and the period spacing.

The lowest frequency significant peak lies at 653.987 $\mu$ Hz. This peak is seen in both the 1992 and the 1994 WET runs, but was below the detection limit in 1993. Note that the tentative detection of modes at frequency below 650 $\mu$ Hz (Vauclair et al. 1993) is not confirmed by any of the multisite campaigns or by a re-reduction of the discovery data (see Fig. 1). We believe that they were probably the result of inadequate extinction and/or transparency corrections.

Table 7: Frequency list from the IAC CCD photometry.

$f~(\mu$ Hz)
$\delta$ $f~(\mu$ Hz) A (mma)

717.65
0.25 2.78

830.93 0.28 2.55

958.45 0.19 3.62

1179.60 0.32 2.23

1217.40 0.31 1.14

1315.61 0.58 1.23

**Table 7:** Frequency list from the IAC CCD photometry.
$f~(\mu$ Hz)	$\delta$ $f~(\mu$ Hz)	A (mma)
717.65	0.25	2.78
830.93	0.28	2.55
958.45	0.19	3.62
1179.60	0.32	2.23
1217.40	0.31	1.14
1315.61	0.58	1.23

The next few modes appear as single peaks. The feature seen at 717.714 $\mu$ Hz in the 1994 WET data is also present in the power spectrum of the CCD photometry obtained during the 3 consecutive nights subset, but with an amplitude of 2.78 mma, as compared to 1.96 mma for the whole 1994 WET. As the amplitude of the other modes found in both the photomultiplier and the CCD photometry are in quite good agreement (see the discussion below), so we interpret the amplitude discrepancy as the signature of an amplitude change of this mode on a time scale shorter than the WET campaign (15 days). To check this hypothesis further, we break the 1994 WET data set into two parts and recalculate the amplitudes of the modes by a non-linear least-squares fit to each half of the data. We find that during the second half of the WET run, which encompasses the three nights where we acquired the CCD simultaneous photometry, the amplitude of the 717.714 $\mu$ Hz exceeds by 44% its value during the first half of the run. This confirms the short time scale variability of that particular mode.

The first apparent fine structure feature is formed by the next two peaks at 789.042 and 793.783 $\mu$ Hz present only in the 1994 WET data. They seem to form a doublet with a frequency separation of 4.741 $\mu$ Hz, possibly due to rotational splitting. If this were the case, they would be $\ell =1$ modes with $\delta$ m=1. However, as we will discuss later, this is not a single, rotationally split mode.

The next mode at 830.708 $\mu$ Hz is also present in the CCD data with an amplitude in agreement with that of the whole 1994 WET run. However, this mode is also present in 1992 WET at a frequency shifted by 0.7 $\mu$ Hz and with a smaller amplitude. The neighboring two modes at 836.067 and 840.367 $\mu$ Hz, seen in the 1994 WET data, form the first true doublet. As will be shown later, they do not form a triplet with the 830.708 $\mu$ Hz mode. The 836.067 $\mu$ Hz mode is also present in the 1993 data, but with the frequency shifted to 835.000 $\mu$ Hz; the frequency shift is significant when compared to the least-squares fit errors. Either we are seeing different modes in the 1994 WET and 1993 campaigns, or the same mode is exhibiting an unexplained (non-secular) frequency shift. The frequency separation, $\Delta f= 4.3$ $\mu$ Hz measured in the 1994 WET spectrum suggests that these two peaks are two components of a $\ell =1$ triplet, with $\delta$ m=1. As we have no explanation for the observed frequency shift of the 830 and 836 $\mu$ Hz peaks, we will use the best determined frequency, i.e., the 1994 WET values which have the smaller least-squares fit errors, in the following analysis.

The next two peaks at 851.483 $\mu$ Hz (seen only in the 1993 run) and at 872.337 $\mu$ Hz (seen only in the 1994 WET data) are single peaks. More interestingly, the next two peaks seen in the 1992 WET data at 889.587 $\mu$ Hz and 894.800 $\mu$ Hz form another doublet. This doublet is also seen in the discovery data (Fig. 1), although strong aliasing made unambiguous frequency identification impossible. The frequency separation is 5.213 $\mu$ Hz. We interpret this doublet as two components of an $\ell =1$ mode split by slow rotation, with the third component missing.

The two next peaks at 906.378 $\mu$ Hz and 921.721 $\mu$ Hz, seen only in 1994 WET data, are single peaks. The next three peaks at 940.563, 945.156, and 949.909 $\mu$ Hz form the first identified triplet, suggesting an $\ell =1$ mode split by rotation. The WET 1994 data show only the m=+1 and -1 components of the triplet, while the all three components were detected in the 1992 WET run. By contrast, only the 940 $\mu$ Hz mode was marginally visible in the 1993 data. Taking the best determined frequency for the m=-1 and m=+1 modes from 1994 WET data and the central m=0 mode frequency from the 1992 WET data, one finds a frequency separation of 4.593 $\mu$ Hz from m=-1 to m=0 and 4.753 $\mu$ Hz from m=0 to m=+1. Also, the frequency separation between the extreme components of this triplet differs between the two WET data sets by as much as 1.15 $\mu$ Hz, which is significant compared to the frequency resolution of the data sets. The triplet was wider during the 1992 WET run. Given that the fine structure splitting of this and other modes changes from season to season, we try wherever possible to base our frequency splittings on the 1994 WET data, since this data set has the best window function.

The next two peaks at 958.533 $\mu$ Hz and 963.282 $\mu$ Hz form a doublet separated by 4.749 $\mu$ Hz. The 958 $\mu$ Hz peak also happens to be the largest amplitude mode in the 1994 WET data. While neither peak was detected in the 1992 WET data, they were both present in the 1993 data. The frequency separation suggests that these two peaks are also two adjacent components of a $\ell =1$ triplet. The CCD data also show a mode at 958.45 $\mu$ Hz with an amplitude of 3.6 mma both values in excellent agreement with the values in Table 6.

The next two small amplitude peaks at 978.874 $\mu$ Hz and 988.726 $\mu$ Hz, form a doublet separated by 9.852 $\mu$ Hz or 2 $\times$ 4.926 $\mu$ Hz. We interpret these peaks as the m=-1, +1 components of a triplet ( $\ell =1$ ) whose missing central (m=0) component should be near 983.8 $\mu$ Hz.

The next two peaks at 1005.645 and 1010.541 $\mu$ Hz, form another doublet seen only in the 1994 WET data. The frequency separation is 4.896 $\mu$ Hz. The doublet is interpreted as two adjacent components ( $\delta$ m = 1) of an $\ell =1$ mode split by rotation.

The next peak at 1023.594 $\mu$ Hz is seen in the three runs, with its largest amplitude occurring in the 1992 WET run. The next two peaks at 1045.690 $\mu$ Hz and 1055.703 $\mu$ Hz, separated by 10.013 $\mu$ Hz or 2 $\times$ 5.006 $\mu$ Hz are interpreted as the m=-1 and m=+1 components of a triplet whose m=0 mode is not seen, but should be near 1050.7 $\mu$ Hz. The 1046 $\mu$ Hz component is seen in all three runs, though only marginally in 1993, while the 1056 $\mu$ Hz component was seen only in the 1994 WET data.

There is a final triplet formed by the peaks at 1096.712, 1101.942 and 1107.224 $\mu$ Hz. The 1097 $\mu$ Hz component is seen in the 1994 WET and the 1993 data (though significantly displaced by 0.65 $\mu$ Hz to 1096.060 $\mu$ Hz in 1993). The central component at 1101.942 $\mu$ Hz is seen in the 1994 WET data, as well as in the 1992 WET data (where it is displaced by 0.73 $\mu$ Hz), but it is absent in 1993. The third component at 1107.223 $\mu$ Hz is seen in the 1992 WET and in 1993 data, but it is absent in the 1994 WET data. The components of this triplet are nearly symmetrically separated from their central m=0 mode by 5.230 $\mu$ Hz and 5.282 $\mu$ Hz respectively. We supplement the two 1994 modes with the 1992 WET m=+1 mode, although choosing the 1993 frequency would only change the splitting from 5.282 to 5.358 $\mu$ Hz. We note that the data suggest a decreasing frequency splitting for the modes of this triplet from 1992 to 1994. In 1992, the m=0 to +1 splitting is 6.021 $\mu$ Hz, while the average splitting in 1993 is 5.620 $\mu$ Hz, and it decreases further to 5.230 $\mu$ Hz in 1994.

The following mode at 1123.747 $\mu$ Hz is a single peak while the next two peaks at 1179.955 and at 1190.578 $\mu$ Hz form a doublet with a 10.623 or 2 $\times$ 5.311 $\mu$ Hz frequency separation. Only the 1179 $\mu$ Hz mode was present in all three data sets. We interpret this doublet as two components of a triplet whose missing m=0 component should be near 1185.3 $\mu$ Hz. The 1179 $\mu$ Hz mode is present in the CCD data at 1179.60 $\mu$ Hz and an amplitude of 2.23 mma; the frequency and amplitude are in good agreement with the values listed in Table 6. Next, one finds a doublet formed by the 1212.490 and the 1217.865 $\mu$ Hz modes. The 1217 $\mu$ Hz is present in all the data sets and was the largest amplitude mode in the 1992 WET data and the second largest mode in the 1993 data set. This peak is also seen in the CCD data at a frequency of 1217.40 $\mu$ Hz, in good agreement with the 1994 WET data, but with an amplitude (1.14 mma) which differs significantly from the amplitude of the whole WET run (1.38 mma). However, in contrast with the case of the 717 $\mu$ Hz discussed above, the frequency resolution of the CCD data is not sufficient to separate the two modes at 1212 and 1217 $\mu$ Hz. In this case, the amplitude discrepancy reflects the fact that these two modes interfere in the power spectrum of the CCD light curve, while they are resolved in the power spectrum of the whole WET data. With a separation of 5.375 $\mu$ Hz, this doublet is two adjacent components of an $\ell =1$ triplet.

Careful scrutiny of the combined frequency list does not reveal any other multiplets. The rest of the modes have single peaks of very low amplitude sparsely distributed in frequency up to 4340 $\mu$ Hz.

Looking at the possible linear combinations and harmonics, one finds only a few cases. We searched for all possible quadratic (f₁+ f₂=f₃) and cubic ( $f_{1}+f_{2}\pm f_{3}=f_{4}$ ) linear combination peaks. A selection of such linear combinations is listed in Table 8. Considering that both quadratic and cubic combination peaks are not very abundant in the power spectrum, and that the largest amplitude modes do not necessarily generate them, we expect peaks from 4th order or higher linear combinations are unlikely. Therefore, all peaks which cannot be explained as 2nd or 3rd order linear combination are most likely true pulsation modes. Among those, the peaks with frequency 1572 $\mu$ Hz, 2109 $\mu$ Hz, 2133 $\mu$ Hz, 2154 $\mu$ Hz, 2164 $\mu$ Hz and 2174 $\mu$ Hz must be true pulsation modes. All remaining peaks above 1550 $\mu$ Hz can be explained as 2nd and 3rd order combination peaks and are not independent modes.

**Table 8:** Linear combinations of frequencies in RXJ 2117+3412.
		1994 WET
f1	f2	f3	f4	$\delta f$
( $\mu$ Hz)	( $\mu$ Hz)	( $\mu$ Hz)	( $\mu$ Hz)	( $\mu$ Hz)
958.533	988.726		1947.334	0.075	a
666.938	1289.129		1956.008	0.059	b
789.042	1179.955		1968.952	0.045	b
963.282	1005.645		1968.952	0.025	a
1010.541	1179.955	1217.812	3408.257	0.051	a
921.721	1123.747	1362.734	3408.257	0.055	a
653.987	1315.055	1439.198	3408.257	0.017	a
789.042	1179.955	1439.198	3408.257	0.062	b
872.337	1096.712	1439.198	3408.257	0.010	a
958.533	1010.541	1439.198	3408.257	0.015	a
963.282	1005.645	1439.198	3408.257	0.132	b
836.067	1023.684	1548.653	3408.257	0.147	b
1010.541	1217.812	1289.129	3517.490	0.008	a
789.042	1289.129	1439.198	3517.490	0.121	b
921.721	1055.703	1539.991	3517.490	0.075	a
988.726	988.726	1539.991	3517.490	0.047	a
963.282	1005.645	1548.653	3517.490	0.090	b
1212.490	1315.055	1397.385	3924.971	0.041	a
978.874	1397.385	1548.653	3924.971	0.059	a
1055.703	1315.055	830.708	1539.991	0.059	a
1023.684	1397.385	872.337	1548.653	0.079	a
1212.490	1315.055	978.874	1548.653	0.018	a

Table 8: continued.
1993

f1
f2 f3 f4 $\delta f$

( $\mu$ Hz) ( $\mu$ Hz) ( $\mu$ Hz) ( $\mu$ Hz) ( $\mu$ Hz)

963.416 1179.761 2143.374 0.197 b

2133.122
2174.884 4308.046 0.040 a

2153.980 2153.980 4308.046 0.086 a

939.838
1245.457 2153.980 4339.147 0.128 a

1179.761
1968.222 963.416 2184.777 0.210 b

1397.242
1968.222 963.416 2402.113 0.065 a

1992 WET

f1 f2 f3 f4 $\delta f$

( $\mu$ Hz) ( $\mu$ Hz) ( $\mu$ Hz) ( $\mu$ Hz) ( $\mu$ Hz)

653.811 1315.181 1968.915 0.077 b

653.811
1315.181 2109.129 4077.942 0.179 b

945.156 1023.594 2109.129 4077.942 0.063 a

1179.893
1315.181 945.156 1549.959 0.041 a

**Table 8:** continued.
		1993
f1	f2	f3	f4	$\delta f$
( $\mu$ Hz)	( $\mu$ Hz)	( $\mu$ Hz)	( $\mu$ Hz)	( $\mu$ Hz)
963.416	1179.761		2143.374	0.197	b
2133.122	2174.884		4308.046	0.040	a
2153.980	2153.980		4308.046	0.086	a
939.838	1245.457	2153.980	4339.147	0.128	a
1179.761	1968.222	963.416	2184.777	0.210	b
1397.242	1968.222	963.416	2402.113	0.065	a

Notes: The table lists selected linear quadratic ( f1 + f2 = f3) and cubic ( $f1 + f2 \pm f3 = f4$ ) combinations. The difference between the frequency resulting from the combination and the frequency of the observed peak is listed in Col. 5 as $\delta f$ . The quality of the agreement is given in Col. 6 as: a) if the frequency mismatch is consistent with zero within formal errors, or b) if consistent with zero within twice formal errors.

Among the modes involved in linear combinations is the mode at 1315 $\mu$ Hz, which showed a nearly constant amplitude. Otherwise it would have been a good candidate for a $\dot{P}$ measurement. It appears in one quadratic combination and in at least four higher order combinations.

3.3 Frequency table summary

Among the 63 frequencies listed in Table 6, we find 15 linear combinations, which leaves 48 independent pulsation modes. Among them, we find two complete triplets and eight doublets. We interpret the doublets as triplets with one missing component. Among these doublets, three are interpreted as triplets with the central m=0 component missing.

As no multiplet structures more complex than triplets are found, we conclude that the multiplets recognized in RXJ 2117+3412 are probably $\ell =1$ modes split by rotation. The rotational splitting averaged between all multiplets is $\approx$ 5 $\mu$ Hz. If $\ell =2$ modes were present, and if RXJ 2117+3412 is in an asymptotic pulsation regime, we would expect to detect all or part of quintuplets with components separated in frequency by about 8.3 $\mu$ Hz. The only peaks listed in Table 6 which could potentially be identified as components of rotationally split $\ell =2$ modes are the 1539.991 $\mu$ Hz-1548.653 $\mu$ Hz ( $\Delta f=8.662$ $\mu$ Hz) and the 1947.334 $\mu$ Hz-1956.008 $\mu$ Hz ( $\Delta f=8.674$ $\mu$ Hz) doublets. However, these peaks can be explained as previously mentioned by quadratic and cubic combinations (Table 8) and we do not consider them to be real modes. We conclude that there is no evidence for $\ell =2$ modes split by rotation in the power spectrum.

Significant amplitude variations are seen in RXJ 2117+3412 as in most of the PNNV and GW Vir stars. They are accompanied by significant frequency variations for the two modes at 830 $\mu$ Hz and 836 $\mu$ Hz and the two triplets centered on 945 $\mu$ Hz and 1101 $\mu$ Hz. One can think of at least two explanations for these amplitude variations and frequency shifts: i) changes in the UV flux, as reported by Feibelman (1999), may reflect modifications in the chemical composition and in the structure of the outer layers which, in turn, affect the oscillatory properties of the modes having substantial amplitudes in those regions; ii) non linearities result in both amplitude and frequency variations for selected modes as described by Goupil et al. (1998).

4 Asteroseismology of RXJ 2117+3412

4.1 Period spacing

In the asymptotic limit, non-radial g-modes are equally spaced in period. Two main methods can be used for detecting regularly spaced periods: the Kolmogorov-Smirnov (K-S: Kawaler 1988) and inverse variance (IV: O'Donoghue 1994) significance tests. In principle, these methods should be applied to the periods of the central (m=0) modes, as they are not affected by rotation (to first order), unlike the $m=\pm 1$ modes. Among the 48 significant modes detected in RXJ 2117+3412, one finds only two triplets and eight doublets. Before performing the mode identification, one does not know which component of the doublets is the central m=0 one, nor the m value of the remaining single modes. Neither of the proposed tests will distinguish between the period interval between adjacent modes and the rotational splitting. To minimize this effect and get a clearer test, one first selects a limited range in the period distribution. Considering that all multiplets are found at frequency lower than 1500 $\mu$ Hz, and that the modes at higher frequency are sparsely distributed up to 4340 $\mu$ Hz, are all of low amplitude, and that most of them result from linear combinations of lower frequency modes, the tests were performed in a frequency domain restricted to the interval 600 $\mu$ Hz-1500 $\mu$ Hz ( $\approx$ 1600 s- 700 s periods). This interval contains 42 modes. For the triplets, the tests use the central mode period. For the doublets we can proceed in two different ways: either we use both observed modes or we use only the average of the two periods for each doublet. In the latter case, the K-S test shows a double minimum - typical for a K-S test - with the first minimum at 21.0 s and the second minimum at 22.1 s. The inverse variance test shows a single, obvious maximum at 21.9 s. Figure 10 shows both the K-S and the inverse variance tests. The agreement between the two methods is quite good, but the inverse variance test does not suffer the ambiguous double peak seen in the K-S test. However, if those tests are useful to detect the expected equidistant pattern in the period distribution, they do not provide a good enough estimate of the period spacing since they assign equal weights to all the periods. The determination of the period spacing, $\Delta P$ , can be refined by the weighted linear least-squares fit. The weight assigned to each period is inversely proportional to the square of its uncertainty. The uncertainties are defined in the following way: for single mode, the frequency uncertainty equals to the average frequency splitting found in the triplets (this is the real uncertainty of the frequency of the m=0 mode). For the doublets, we take the average frequency of the two components affected by an uncertainty equal to half their frequency difference. For the triplets, the m=0 mode is identified and the uncertainty is the formal error given by the non-linear least-squares fit to the time series data. Our best linear weighted fit gives a preliminary period spacing $\Delta P = 21.540$ $\rm s \pm 0.030$ s. The period spacing derived here is slightly larger than the 20.5 s derived in the discovery paper (Vauclair et al. 1993). Close inspection of the K-S test shown in their paper reveals the double minimum, with the other much shallower minimum at 22 s. Considering the much cleaner determination of the period spacing deduced from the weighted least-squares fit in this paper, it is not worth discussing that particular point any further. The main difference between the 1992 discovery analysis and the present one is that we do not find any evidence of the $\ell =2$ modes in the present data from the period spacing tests. If a substantial number of $\ell =2$ modes were present in the power spectrum, their signature in the period spacing tests would be a secondary minimum (maximum) at 21.540 s/ $\sqrt{3}$ $\approx$ 12.43 s in the K-S (IV) tests. Inspection of Fig. 10 does not show any evidence for such a $\ell =2$ modes signature.

$\begin{figure} \par\includegraphics[width=13.5cm,clip]{MS1689fig10.eps}\end{figure}$

Figure 10: The results of tests for period spacings. Upper panel: Kolmogorov-Smirnov (K-S) test; lower panel: Inverse Variance (IV) test. The K-S test shows a double minimum for period spacings $\Delta P \approx$ 21 s and $\Delta P \approx 22$ s. The IV test shows a single maximum for a period spacing $\Delta P \approx 22$ s. The single peak points to a single $\ell$ value being present, which we show to be $\ell =1$ . We see no evidence of $\ell =2$ modes, which should have a peak near 12.4 s.

4.2 Mode identification

For the mode identification, we proceed by iteration as follows. We assume that all the modes seen in RXJ 2117+3412 have the same value of $\ell$ . This assumption relies on the equidistant period spacing, discussed above (Sect. 4.1), and on the similar rotational splitting found in the multiplets. It is not possible to give an absolute identification for the k order of the modes. Only differential k can be asserted. The reference mode is chosen at 945.156 $\mu$ Hz, the central m=0 component of a triplet, whose korder is some unknown k₀. We will attempt now to identify the relative order $\Delta k= k-k_{0}$ , as well as the azimuthal number m for as many modes as possible. Note that the convention chosen for the sign of m is different from the one used in classical textbooks: here m=-1 is associated with the low frequency component of a triplet (retrograde mode) while m=+1 corresponds to the high frequency component (prograde mode). This sign convention is the same as in Unno et al. (1989) and Winget et al. (1991, 1994). The identification procedure starts by considering modes for which the m=0 frequency is well determined, either from the two complete triplets, (945 $\mu$ Hz, 1101 $\mu$ Hz), or from the three doublets whose components are separated by twice the rotational splitting (978/988 $\mu$ Hz, 1045/1055 $\mu$ Hz and 1179/1190 $\mu$ Hz). In this latter case the m=0 frequency is obtained by averaging the two components, assuming that the triplets are symmetric. These five m=0 modes give a unique determination of the period spacing, either by applying the inverse variance test (O'Donoghue 1994), which yields a period spacing of $\Delta P= 21.508~\rm s \pm 0.173$ s (HWHM), or a linear unweighted least-squares fit which yields $\Delta P=21.506~\rm s\pm 0.099$ s. The inverse variance procedure also yields the values of the relative radial order of the modes, $\Delta k$ ; they are listed in the fourth column of Table 9. We are not able to assign an absolute k value, because there are no models of suitable quality at that high a luminosity in the literature.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{MS1689fig11.eps} \end{figure}$

Figure 11: Illustration of the mode identification procedure. The figure shows how the observed modes are identified for the cases $\Delta k= -3$ and -4. The two large dots represent known periods of m=0 modes. The two straight lines are at $\pm$ 2 s from the linear least-squares fit to the m=0 modes identified so far. We assume all the m=0 modes to lie within this range. This generously allows for mode trapping which proves to be much smaller ( $\leq$ 1.3 s). The small dots represent the observed modes which need identification. At $\Delta k= -3$ , there is a doublet with periods of 994.387 s and 989.569 s. The mode with 994.387 s period must be the m=0 component, since it is the one whose period lies between the two lines, with the other mode being the prograde m=+1 component. For $\Delta k=-4$ , we see only one mode, which must be the retrograde (m=-1) mode, since its period falls outside and above the $\pm$ 2 s band. The calculated period of the unobserved m=0 mode is 972.247 s.

Starting from this point, new m=0 modes are identified in a step by step procedure, using linear interpolation/extrapolation. We allow for up to 2 s departures from the linear trend to account for possible mode trapping effects. Later, we will show that this is consistent with the actual trapping cycle, whose maximum amplitude is $\sim$ 1.3 s. An illustration of the mode identification procedure is given in Fig. 11 for the case of the $\Delta k= -3$ and -4 modes. From the straight line fit to the first five modes, we find that the m=0 mode for $\Delta k= -3$ should appear at $994.2\pm 2$ s or in the frequency interval 1003.8 to 1007.9 $\mu$ Hz. This estimate allows a unique identification of the m=0 component within the doublet at 1005/1010 $\mu$ Hz as the 1005.645 $\mu$ Hz mode. We can now include this mode into linear regression and continue the procedure. We then estimate the frequency range of the m=0 mode for $\Delta k=-4$ , which is 1025.9 to 1030.2 $\mu$ Hz. It is clear that the mode observed at 1023.594 $\mu$ Hz must be an m=-1 component of the triplet. The m=0 component is not seen, but its frequency can be estimated from the rotational splitting. We include the new m=0 frequency into the linear regression and continue the procedure until we have determined the relative radial order ( $\Delta k$ ) and azimuthal order (m) for as many of the observed modes as is possible. At each intermediate step, a linear fit to m=0 modes is redetermined.

We notice that the rotational splitting changes with period (see Fig. 13), so we must interpolate the value for the $\Delta k=-4$ , -8 modes. For $\Delta k$ smaller than -11, the behaviour of rotational splitting is not known, and we assume a constant splitting of $\Delta f= 5.332$ $\mu$ Hz for these modes. While this is an arbitrary assumption, it has a negligible effect on the trapping cycle parameters (Sect. 4.3) that we determine below. We stop the mode identification at frequencies lower than 780 $\mu$ Hz, because below this limit the spacing between adjacent mmodes and between different overtone modes become comparable and we can no longer tell them apart. Also, we refrained from determining periods of unobserved m=0 modes for $\Delta k$ larger than 0, because the variation of rotational frequency splitting with $\Delta k$ is not well established here because there are not enough multiplets detected at these low frequencies. In addition, at low frequencies, any error in the interpolated/extrapolated value of $\Delta f$ would translate in relatively large error of the mode's period and affect our mode trapping results. Our procedure shows that some modes which could have been interpreted as multiplets by considering only their frequency difference in Table 6 cannot be so. That is the case for the modes at 789 $\mu$ Hz and 793 $\mu$ Hz, which cannot correspond to the same $\Delta k$ value, and for the modes at 830, 836 and 840 $\mu$ Hz, which must be a combination of a single mode and a doublet of the successive k mode. Our proposed mode identification is summarized in Table 9.

4.3 Mode trapping

A linear least-squares fit to the 20 m=0 identified or inferred modes, leads to an average period spacing $\Delta P=21.639$ $\rm s \pm 0.021$ s. Figure 12 shows the residuals of this linear fit. They prove to be significantly different from zero and vary quasiperiodically, which previous experience (cf. Winget et al. 1991) indicates is due to mode trapping. Knowing that there is a signature of mode trapping superimposed on the asymptotic equidistant period distribution, one can repeat the fitting procedure to get the trapping cycle parameters by adding a sine function to the linear fit with a function of the form:

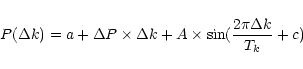
$\begin{displaymath}P(\Delta k)= a + \Delta P \times \Delta k + A \times \sin( \frac{2\pi \Delta k}{T_{k}} + c) \end{displaymath}$

where $\Delta P$ is the refined value of the period spacing (in s), A is the semiamplitude of the trapping cycle (in s) and T_k is the length of the trapping cycle (trapping period) expressed in number of modes. This new fitting yields $\Delta P$ , A and T_k simultaneously. One derives $\Delta P= 21.640$ $\rm s\pm 0.012$ s, A= 0.71 $\rm s\pm 0.11$ s and $T_{k}= 3.799 \pm 0.042$ (which translates in a period of the trapping cycle $P_{\rm tc}=82.21~\rm s\pm 0.91$ s). The mode $\Delta k=4$ (period 1146 s) does not satisfactorily fit the trapping cycle. Repeating the fitting procedure with this mode excluded leads to: $\Delta P= 21.618~\rm s \pm 0.008$ s, $A= 0.823~\rm s\pm 0.078$ s and $T_{k}= 3.880 \pm 0.026$ ( $P_{\rm tc}= 83.88~\rm s\pm 0.57$ s). These latter values will be used in the following discussion but either solution would lead to very similar results. The semi-amplitude of the mode trapping is comfortably smaller than the 2 s allowance accepted in the mode identification procedure (Sect. 4.2). Our implicit assumption that the trapping cycle is strictly periodic, i.e., can be fitted with a single sine function, is satisfied closely enough, as witnessed by the small errors of both the semiamplitude and the trapping period. This implies that either there is only one chemical composition interface, presumably between the He-rich envelope and the C/O core, or the beating between the trappings induced by this interface and those induced by another potential C/O interface is too small to be detected (see also Fig. 14).

**Table 9:** Period list and mode identification in RXJ 2117+3412.
Period (s)	Frequency ( $\mu$ Hz)	m	$\Delta k$
1267.360	789.042	+1	+10
1259.790	793.783	-1	+9
1203.792	830.708	+1	+7
1196.076	836.067	-1
1189.956	840.367:	0	+6
1174.422	851.483	-1	+5
1146.346	872.337	0	+4
1124.117	889.587	0	+3
1117.568	894.800	+1
1103.292	906.378	0	+2
1084.927	921.721	-1	+1
1063.193	940.563	-1
1058.026	945.156	0	0
1052.732	949.909	+1
1043.261	958.533	-1
1038.118	963.282	0	-1
1021.582	978.874	-1
(1016.467)	(983.800)	0	-2
1011.403	988.726:	+1
994.387	1005.645	0	-3
989.569	1010.541	+1
976.950	1023.594	-1
(972.247)	(1028.545)	0	-4
956.306	1045.690	-1
(951.750)	(1050.697)	0	-5
947.236	1055.703	+1
911.816	1096.712	-1
907.489	1101.942	0	-7
903.160	1107.224	+1

Table 9: continued.

Period (s)
Frequency ( $\mu$ Hz) m $\Delta k$

889.880
1123.747: -1

(885.736) (1129.004) 0 -8

847.490
1179.955 -1

(843.692) (1185.267) 0 -10

839.928 1190.578: +1

824.749
1212.490 -1

821.145 1217.812 0 -11

802.918
1245.457 -1

(799.495) (1250.789) 0 -12

(778.921)
(1283.828) 0 -13

775.699 1289.160 +1

760.424
1315.055 -1

(757.354) (1320.387) 0 -14

733.948
1362.495 0 -15

715.696
1397.242 -1

(712.975) (1402.574) 0 -16

694.831
1439.198 -1

(692.267) (1444.530) 0 -17

Notes. Periods and frequencies in parenthesis are for the m=0 components which are not observed and whose values are calculated on the basis of the known rotational splitting (see text for details). The chosen convention for m is: m=-1 for retrograde modes and m=+1 for prograde modes.

Note that there is no correlation between mode trapping and mode amplitude, where trapped modes are those defining the minima in Fig. 12. There are 6 such minima. The corresponding modes have periods ( $\Delta k$ ) of 733.97 s (-15), 799.49 s (-12) and/or 821.15 s (-11), 885.74 s (-8) and/or 907.49 s (-7), 972.25 s (-4), 1058.03 s (0) and 1124.11 s (+3). Looking at the trapped mode amplitudes during different runs (Table 6), we see that trapped modes can have either low or high amplitudes. Mode trapping and amplitude were also found to be uncorrelated in PG 1159-035 (Winget et al. 1991) and in the DBV GD 358 (Winget et al. 1994). Clearly, the amplitude of a mode is not simply governed by its linear growth rate. The period spacing found here for RXJ 2117+3412 is remarkably similar to the ones found in other PNNV and GW Vir stars: $\Delta P= 22.3$ s in NGC 1501 (Bond et al. 1996), 21.5 s in PG 1159-035 (Winget et al. 1991), 21.6 s in PG 2131+066 (Kawaler et al. 1995) and 21.1 s in PG 0122+200, (Vauclair et al. 2001). We do not understand what mechanism is forcing these pulsators - that have different masses and luminosities - to display the same period spacing. O'Brien (2000) suggests that an interplay between the driving zone depth and the maximum allowed pulsation period, as a function of $T_{{\rm eff}}$ and the total mass, can explain the tendency for higher mass pre-white dwarfs to pulsate at cooler $T_{{\rm eff}}$ than lower mass ones. If higher mass GW Vir stars pulsate at cooler temperature than low mass ones, then the average period spacings could be similar for all of the GW Vir stars. However, it is still unclear how this preserves the almost constant $\Delta P$ observed over a factor of almost 1000 in luminosity. Clearly, the "numerology'' is telling us something about the nature of the GW Vir and PNNV stars, but we do not yet understand it.

4.4 Rotation rate

Since the multiplets in the combined list of frequencies are $\ell =1$ modes split by rotation, one may derive the corresponding rotation rate of RXJ 2117+3412. In the slow, solid body rotation limit we have $\Omega\ll\sigma_{\ell,k}$ , where $\Omega$ is the angular rotation frequency and $\sigma_{\ell,k}$ is the non-rotating angular pulsation frequency for a mode of degree $\ell$ and of order k. In this limit, the frequencies for a rotating star are given by

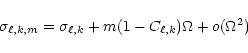
$\begin{displaymath}\sigma_{\ell,k,m}= \sigma_{\ell,k} + m(1- C_{\ell,k})\Omega + o(\Omega^{2})\end{displaymath}$

where $C_{\ell,k}$ takes a simple form in the asymptotic limit of high order gravity modes, which applies to pre-white dwarfs, as discussed by Winget et al. (1991). In that case $C_{\ell,k} \simeq 1/\ell(\ell+1)$ as shown by Brickhill (1975). In the above expression for the frequencies, solid body rotation is assumed. Any differential rotation present in the star would result in an additional term $C^{'}_{\ell,k,m}$ to $C_{\ell,k}$ which depends on k, and so is different for different modes. Assuming all the modes to be $\ell =1$ modes, we derive an average rotation period for RXJ 2117+3412, using the relation

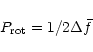
$\begin{displaymath}P_{\rm rot}= 1/2\Delta\bar{f} \end{displaymath}$

where $\Delta$ $\bar{f}$ is the mean rotational splitting. From the observed triplets and doublets (10 cases), one finds an average rotational splitting of $\Delta \bar{f}= 4.998 \pm0.23~\mu$ Hz, from which one derives a mean rotational period of 1.16 $\rm d\pm 0.05$ d, where the uncertainty is derived from the average deviation of the rotational splitting to the mean value. This is a conservative overestimate of the uncertainty since it does not take into account the variation of the rotational splitting with period discussed below.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{MS1689fig12.eps} \end{figure}$

Figure 12: A plot showing observational evidence of mode trapping. The residuals of the period distribution relative to the average period spacing ( $\Delta P= 21.618$ s) for the 20 m=0 modes are plotted as a function of the period. The best fit with a sine wave gives a trapping cycle of $3.88 \pm 0.026$ mode (i.e. 83.88 $\rm s \pm 0.57$ s) with a semi-amplitude $A= 0.823~\rm s\pm 0.078$ s. The modes defining the minima on this plot are trapped modes, while those defining the maxima are nontrapped modes. Filled circles represent the m=0 modes, which are either observed or whose frequencies are determined by interpolation between the observed m=-1 and m=+1 components of the triplets. Open circles represent the m=0 modes whose frequencies have been inferred from the observed singlets and the known rotational splitting.

One should keep in mind that the frequency separation within multiplets may deviate from uniformity for different reasons. There are at least four physical processes that could affect the frequencies: i) non-linearities resulting from resonant coupling between components of multiplets, ii) mode trapping, iii) structural changes in the wave propagation cavities, and iv) magnetic field. In case i), slight changes in the frequency of multiplets components are expected even in the case of modest non-linearity in the pulsations. The non-linearities result in both amplitude and frequency variations for selected modes as described in Goupil et al. (1998). In their application to the case of the DBV GD358, however, they find that the frequency splitting is changed by the non-linear effects by no more than 2%. In case ii), mode trapping also introduces small variations in the frequency shift due to rotational splitting (Kawaler et al. 1999). Since the radial structure of the mode is affected by trapping, so is the rotational kernel. If rotation is non-uniform, it will affect the splitting constant. In their discussion of the rotational splitting in PG 1159-035, Kawaler et al. (1999) show that the effect of mode trapping may change the frequency separation of the rotationally split components by 2.5% in the period range 400 ${\rm s}\leq P \leq 800$ s. They also show that the rotation rate inside PG 1159-035 decreases with increasing radius. The variations could be much larger would the gradient of the rotation curve be steeper.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{MS1689fig13.eps} \end{figure}$

Figure 13: Rotational splitting as a function of periods. The frequency splitting of the 10 multiplets (2 triplets and 8 doublets) is plotted as a function of the m=0 mode period. With the exception of the mode at 1124 s (open circle), a clear trend is present for the other modes (filled circles): the rotational splitting decreases with increasing period.

In case iii), changes in the structure of the outer layers modify the properties of the propagation regions. These changes would modify the trapping cycle and indirectly affect the rotational splitting in case of non-uniform rotation as discussed in case ii). There are evidences for spectroscopic and photometric variations in RXJ 2117+3412 (Feibelman 1999) as mentioned above which are not unexpected in a mass losing star. However, there is not enough data to determine whether 1) the mass loss rate could also be time dependent and whether 2) there is a correlation between spectroscopic and photometric variations. Qualitatively, one may expect that any variation in the mass loss rate should affect the chemical composition of the outer He-rich layer, where both the excitation and the propagation of the modes takes place. This should result in variations for both the frequencies and the amplitudes of the modes. Such effects need to be quantitatively estimated. Finally, in case iv), a magnetic field would produce an asymmetry in the frequency shifts of the m=+1 and -1 components relative to the m=0 component, since the additional frequency shift induced by the magnetic field is proportional to m².

As a consequence, any variations in the frequency splitting measured between multiplets may be due to a combination of at least these four effects and deriving any information on a potential differential rotation profile is a speculative task. Figure 13 shows the variation of the rotational splitting as a function of period for all multiplets observed in RXJ 2117+3412. Only secure detections are considered (marginal detections are rejected). Rotational splittings derived from 1994 WET data are preferred because these data have the best window function. For data from either the 1992 WET or the 1993 data set, splittings showing the smallest formal error were preferred. Figure 13 shows a clear trend of decreasing rotational splitting with increasing period. Only one mode does not fit the trend: it is the 1124.117 s mode, seen only during the 1992 WET. Several explanations can account for this discrepancy. We note from Table 6 that for the few cases where we have frequency splitting information for the same mode in different years, that the 1992 WET data have the largest splitting for unknown reasons. We suspect that the systematically larger frequency splittings in the 1992 data affect the 1124.117 s mode, although we cannot rule out the possibility that there is an incompletely corrected 2d alias present. The observed rotational splitting changes by a factor of 1.14 in the period interval 821 s to 1058 s, covering 11 k orders. The factor is 1.24 if the longest period mode (at 1189 s) is included, covering 17 k orders. This variation of $\Delta f$ is 13-14 times greater than the non-differentially rotating case considered by Kawaler et al. (1999) who find $a \approx 2$ % change in the rotational splitting between 400 s and 800 s, covering 20 k orders, in their model of PG 1159-035. The conservative conclusion is that the rotational splitting in RXJ 2117+3412 is inconsistent with solid-body rotation. Kawaler et al. (1999) show that a rotation law that decreases or increases outwards may have similar signatures in a $\Delta f$ -Period diagram. They also show that mode trapping affects the rotational splitting and that it is the phase shift between the trapping seen in the period spacing ( $\Delta P$ -Period diagram) and the one seen in the rotational splitting ( $\Delta f$ -Period diagram) which contains the pertinent information on the rotation velocity law. We do not see any such trapping cycle in the $\Delta f$ -Period diagram of RXJ 2117+3412, which is in agreement with the weak trapping indicated by the small amplitude of the trapping cycle, and this precludes any further statement on the internal rotation profile of RXJ 2117+3412. The observed trend of the rotational splitting in RXJ 2117+3412 is surprisingly smooth. One would have expected a rather complex internal rotation law, if one considers that the star is i) still contracting towards the white dwarf cooling sequence with a short time scale ( $\approx$ $10^{4}{-}10^{5}\,{{\rm yr}}$ ) and ii) is loosing mass at a rate of a $\approx$ $10^{-7}~M_\odot~{{\rm yr}}^{-1}$ (Koesterke et al. 1998; Koesterke & Werner 1998).

In the absence of any consistent physical interpretation of the rotational splitting variation, we can only conclude that the average rotation period is $\approx$ 1.1 d, and that the frequency splitting is not consistent with solid body rotation. The average rotation period for RXJ 2117+3412 is within the range of values derived from asteroseismology for other pre-white dwarfs. The PNNV NGC 1501 has a rotation period of 1.17 d (Bond et al. 1996). Among other pulsating PG 1159 stars having rotation periods derived from rotational splitting PG 1159-035 has a period of 1.38 d (Winget et al. 1991), PG 2131+066: 5.07 h (Kawaler et al. 1995) and PG 0122+200: 1.61 d (O'Brien et al. 1996, 1998; Vauclair et al. 2001). This trend persists with the cooler DBV and DAV white dwarfs, which have rotation periods ranging from 9 to 58 hours (Bradley 2001). Spruit (1998) argues that such rotation periods around one day for white dwarfs can be expected if some small non-axisymmetries occur in the mass loss process along the AGB evolutionary phase. In the case of RXJ 2117+3412, which is still losing mass in its present pre-white dwarf phase (Werner et al. 1996; Koesterke et al. 1998; Koesterke & Werner 1998), the complex structure of its low surface brightness planetary nebula suggests such a non-axisymmetrical mass loss.

4.5 Magnetic field

The existence of a magnetic field would also lift the degeneracy of the modes by splitting a mode of degree $\ell$ into $\ell$ +1 components. Since the cumulative power spectrum of RXJ 2117+3412 does show some triplets, the fine structure must at least be dominated by rotational splitting as the magnetic field alone would only produce doublets for $\ell =1$ modes. However, if a weak magnetic field is superimposed on the rotation, its effect would be to shift each component relative to its non magnetic frequency, with the shift in frequency proportional to m²B², where B is the strength of the magnetic field. Both the $m=\pm 1$ components are equally shifted by the magnetic field to higher frequencies. The m=0 component is also shifted to higher frequency by a smaller amount (see Unno et al. 1989; Jones et al. 1989). As a result, a frequency asymmetry in the triplets could be the signature of such magnetic field. Unfortunately, there are only two true triplets in the power spectrum of RXJ 2117+3412 to search for such an asymmetry. Considering these two triplets, one does find that the differences between their prograde and retrograde mode frequency splitting is within the formal uncertainties in the frequency measurement with $\sigma= 0.2$ $\mu$ Hz. The corresponding upper limit of the magnetic field, obtained by scaling the results of Jones et al. (1989) for $\ell =1$ modes (their Fig. 1) is of the order of $B\leq500$ G. As this is taken from the calculations for a pure carbon white dwarf model by Jones et al. (1989), it can only be an approximate value when scaled to RXJ 2117+3412.

4.6 Mass of the He-rich outer layers

Mode trapping is interpreted as the signature of chemical stratification in the star. Such a stratification is induced by the previous history of nucleosynthesis within the star and the gravitational settling combined with diffusion acting in a strong gravitational field. The effect of mode trapping on the frequency of the pulsation modes has been studied in detail for the pre-white dwarf pulsators (Kawaler & Bradley 1994), although for luminosities lower than that of RXJ 2117+3412. The trapping cycle observed in RXJ 21117+3412, folded by the trapping phase, is shown in Fig. 14. It does not show evidence of a double peaked structure; this absence suggests that we detect probably only one chemical composition transition zone between the He-rich outer layers and the C/O core. The amplitude of the trapping cycle (A) depends on the gradient of the mean molecular weight through the transition zone and on the thickness of the He-rich layer, while the period of the trapping cycle depends mainly on the thickness of the He-rich outer layer. The thickness of the He-rich outer layer in RXJ 2117+3412 could be precisely determined only through the calculation of realistic models, which are not yet available. The best we can do now is to use the results published by Kawaler & Bradley (1994) and extrapolate them to the range of parameters of RXJ 2117+3412. The extrapolation may not be too bad, since at least the average period spacing is only weakly dependent on luminosity. The trapping period depends on the thickness of the He-rich envelope at fixed $T_{{\rm eff}}$ , as shown in Fig. 3 of Kawaler & Bradley. As can be inferred from this figure, the logarithm of the outer layer fractional mass is related to the trapping period through a very tight linear relation. Similarly, at fixed mass of the He-rich outer layer, the trapping period depends on log ( $T_{{\rm eff}}$ ), as shown in their Fig. 4. Again, the trapping period as a function of log ( $T_{{\rm eff}}$ ) is accurately fitted by a linear relation. We combine these two relations to construct an interpolation formula representing the models of Kawaler & Bradley:

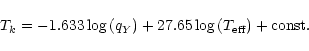
$\begin{displaymath}T_{k}= -1.633 \log\left(q_{Y}\right) + 27.65 \log\left(T_{{\rm eff}}\right)+ \rm const.\end{displaymath}$

where q_Y is the fractional mass of the He-rich envelope. Using this formula, we can now estimate the thickness of the He-rich outer layer in RXJ 2117+3412 relative to PG 1159-035. To do this, we first redetermine the trapping cycle in PG 1159-035 in the same way as we have done here for RXJ 2117+3412, because our method differs slightly from the way it is done for PG 1159-035 by Winget et al. (1991). Here, the mode trapping is derived from the residuals of the period distribution relative to the average period spacing, while Winget et al. (1991) derive the mode trapping from the forward difference [i.e. $P(k+1)-P(k)~{\rm vs.}~P(k)$ ] diagram. With the definition adopted here, the redetermined trapping cycle in PG 1159-035 is $T_{k}=3.752 \pm 0.039$ , which translates to a trapping period of $P_{\rm tc}= 80.60~{\rm s} \pm 0.84$ s through a period spacing of $\Delta P= 21.483~{\rm s} \pm 0.040$ s, with a semiamplitude of A= 1.59 $\rm s \pm 0.32$ s.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{MS1689fig14.eps} \end{figure}$

Figure 14: Folded trapping cycle. The residuals of the period distribution (same as in Fig. 12) but plotted vs. trapping cycle phase. The mode $\Delta k=+4$ does not fit the trapping cycle satistactorily and has been omitted. The cycle is repeated twice for a better visibility. The plot shows a single well defined maximum and minimum, indicating that we see only one trapping interface in the star, presumably between the He-rich outer layer and the C/O core.

The above equation can be now rewritten as

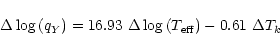
$\begin{displaymath}\Delta \log\left(q_{Y}\right)= 16.93~\Delta \log\left(T_{{\rm eff}}\right) - 0.61~\Delta T_{k} \end{displaymath}$

where the symbol $\Delta$ represents the difference of a given parameter between RXJ 2117+3412 and PG 1159-035. For RXJ 2117+3412, we adopt $T_{{\rm eff}}$ = 170000 K (Werner et al. 1996; Rauch & Werner 1997) and for PG 1159-035 $T_{{\rm eff}}$ = 140000 K (Dreizler & Heber 1998) and q_Y=0.0035 M_* (average of the two estimates of Kawaler & Bradley 1994). We find the thickness of the He-rich envelope in RXJ 2117+3412 to be 0.078 M_*. This result must be treated with caution, however, because it is based on an extrapolation. We recall here, that the temperature and luminosity of RXJ 2117+3412 are outside the range covered by the models of Kawaler & Bradley (1994). We can obtain a more conservative estimate as follows: 1) we assume that the increase of q_Y with $T_{{\rm eff}}$ continues outside the range covered by the models, 2) instead of a true temperature of RXJ 2117+3412, we use the highest $T_{{\rm eff}}$ for which models exist log ( $T_{{\rm eff}})= 5.184$ in our interpolation formula. This approach avoids extrapolation and yields a lower limit for the He-rich envelope mass of RXJ 2117+3412, which is q_Y=0.013 M_*. We conclude that the He-rich outer layer of RXJ 2117+3412 is at least 3.7 times more massive than that of PG 1159-035, and possibly more than 20 times more massive.

Despite similar trapping periods, we derive vastly different envelope thickness. This is entirely due to the difference in $T_{{\rm eff}}$ between RXJ 2117+3412 and PG 1159-035. A comparison of the trapping amplitudes of PG 1159-035 and RXJ 2117+3412 shows that the amplitude of RXJ 2117+3412 is only half that of PG 1159-035. The smaller trapping amplitude of RXJ 2117+3412 could arise from two effects (see Kawaler & Bradley 1994, their Fig. 3). First, the trapping amplitude decreases with increasing He-rich layer mass fraction and second, it also decreases towards longer periods. Both effects are the result of the peak amplitude portion of the eigenfunction moving away from the composition gradient, which decreases the resonance effect of mode trapping. The observed periods of PG 1159-035 are in the range of 430 s to 840 s, while in RXJ 2117+3412 they are in the range of 690 s to 1190 s.

4.7 Mass of RXJ 2117+3412

The presently available evolutionary models for the transition between the planetary nebulae nuclei and the white dwarfs are not suitable for interpreting RXJ 2117+3412. While the 0.7 $M_{\odot}$ evolutionary sequence of Wood & Faulkner (1986) fits the location of RXJ 2117+3412 in the $\log g$ - $\log T_{{\rm eff}}$ diagram, the pure He surface composition of their models does not adequatly represent the observed abundances of RXJ 2117+3412. The more recent calculations by Gautschy(1997), while using a composition more compatible with the surface abundances of PG 1159 stars, do not fit the high luminosity and temperature of RXJ 2117+3412, except by considering stellar models with masses in excess of 0.7 $M_{\odot}$ , which disagrees with the mass derived from asteroseismology (see below). None of these models takes into account the chemical stratification induced by diffusion in the presence of mass loss. As a consequence, one can hardly use them to calculate theoretical period spacings which one could use for asteroseismological mass determination.

In Vauclair et al. (1993), the mass estimate was based on an interpolation formula which did not take into account the luminosity dependence of the period spacing (Winget et al. 1991). This formula, used to estimate the mass of PG 1159-035 is probably not appropriate for RXJ 2117+3412, which is two orders of magnitude more luminous than PG 1159-035. Kawaler & Bradley (1994) calculated the period spacings, $\Pi_{0}=\sqrt{\ell(\ell+1)}\Delta P$ , for a grid of pre-white dwarf models of various masses, including the luminosity dependence (their Fig. 2). They derive an interpolation formula that is valid for luminosities between $1.6 \leq \log(L/L_{\odot})\leq 2.8$ . Extrapolating this formula to the luminosity of RXJ 2117+3412 log( $L/L_{\odot})\approx 4.0$ is risky. Rather than using their interpolation formula, we extrapolate $\Pi_{0}$ directly from their Fig. 2 by spline functions. Using the period spacing derived in Sect. 4.3, $\Delta P= 21.618$ ${\rm s}\pm 0.008$ s, and assuming that this period spacing is valid for asymptotic $\ell =1$ modes, we obtain $\Pi_{0}=30.573~{\rm s}\pm 0.011$ s. At the luminosity of RXJ 2117+3412 (see next section), such a period spacing corresponds to a model of $\approx$ 0.56 $M_{\odot}$ . The formula of Winget et al. (1991) gives a mass of 0.58 $M_{\odot}$ . The value obtained from Kawaler & Bradley's interpolation formula would be 0.52 $M_{\odot}$ , and the range $0.06~M_{\odot}$ is a rough estimate of the uncertainty for this preliminary mass determination. We should stress that the uncertainty we quote is entirely due to the fact that we have to extrapolate the existing theoretical calculations and does not include any observational uncertainty in $\log g$ or $T_{{\rm eff}}$ . A much more precise mass estimate (as good as for PG 1159-035) must await models covering the parameter range of RXJ 2117+3412. For now, our best value for the mass of RXJ 2117+3412 is $0.56^{+0.02}_{-0.04}~M_{\odot}$ .

If we interpret the observed period spacing as corresponding to $\ell =2$ modes, the derived mass would be $\approx$ 0.32 $M_{\odot}$ . Such a low mass would be in conflict with the spectroscopically determined log g= 6.0. It would imply that the progenitor of RXJ 2117+3412 was in a binary system, for which we do not see evidence, and that the star would have a helium core as a result of previous mass transfer in the binary system. Higher $\ell$ values would imply even lower mass estimates for RXJ 2117+3412, which would make the conflict even more severe. On these grounds, we conclude that the modes observed in RXJ 2117+3412 must be $\ell =1$ modes. This is in agreement with the $\ell$ value implied by the fine structure found in the power spectrum.

4.8 Luminosity and distance

Knowing the total mass of the star from asteroseismology on one hand and the surface gravity and effective temperature from spectroscopy on the other hand, it is straightforward to derive the luminosity and the distance of the star.

The best fit model atmosphere for RXJ 2117+3412 indicates a surface gravity log g=6.0 ^+0.3_-0.2 (Rauch & Werner 1997) and an effective temperature $T_{{\rm eff}}= 170\,000~{\rm K} \pm 10\,000~{\rm K}$ (Werner et al. 1996). The radius derived from the mass ( $0.56^{+0.02}_{-0.04}~M_{\odot}$ ) and gravity is:

$\begin{displaymath}\log\left(R/R_{\odot}\right) = -0.91^{+0.10}_{-0.15}.\end{displaymath}$

From the radius and $T_{{\rm eff}}$ , one derives a luminosity (assuming a spectral energy distribution similar to a blackbody):

$\begin{displaymath}\log\left(L/L_{\odot}\right) = 4.05^{+0.23}_{-0.32}.\end{displaymath}$

The distance can be derived from the ratio of the flux in the V band as observed on Earth to the flux emitted at the stellar surface, as given by the best fit model atmosphere (Werner et al. 1996 and Werner, personal communication). For this estimate, one uses a magnitude m_V= 13.16 (Motch et al. 1993) for RXJ 2117+3412 and the flux predicted by the model integrated through the spectral response of the V filter. One obtains a distance:

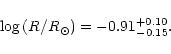
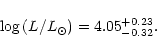
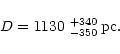
$\begin{displaymath}D= 1130~^{+340}_{-350}\,{{\rm pc.}}\end{displaymath}$

In estimating the error of the distance, one takes into account the uncertainty of the radius and the luminosity due to the uncertainty of the surface gravity and of $T_{{\rm eff}}$ . But the uncertainty of the model flux due to the uncertainty of $T_{{\rm eff}}$ was not taken into account as only the best fit model ( $T_{{\rm eff}}= 170\,000$ K, $\log g= 6.0$ ) was used. The derived distance is in good agreement with the distance determined by Motch et al. (1993), D=1400 ⁺⁷⁰⁰_-500 pc. The uncertainty of our result is smaller because of the better determination of the mass and atmospheric parameters. The remaining uncertainty is dominated by the relatively large error of log g. However, one still has to account for the interstellar absorption because of the proximity of RXJ 2117+3412 to the galactic plane. In Motch et al. (1993), the interstellar absorption was neglected on the argument that four stars in the direction of RXJ 2117+3412 do not show reddening significant enough to affect the distance estimate of RXJ 2117+3412. Three of these stars have good Hipparcos parallaxes (Perryman 1997): HD 202904 (HR 8146) with $\pi=3.62~{\rm mas}\pm 0.56$ mas is at $\approx$ 275 pc, HD 204403 (HR 8215) with $\pi= 1.84$ ${\rm mas}\pm 0.56$ mas is at $\approx$ 540 pc, and HD 207516 (HR 8338) with $\pi= 6.61$ ${\rm mas}\pm 0.61$ mas is at $\approx$ 150 pc. The fourth star (HD 203921) is not really useful since its parallax is not good enough ( $\pi=1.46~{\rm mas}\pm 1.13$ mas). The three stars are significantly closer than RXJ 2117+3412 and therefore cannot yield a reliable extinction estimate out to the distance of RXJ 2117+3412 itself. Therefore, we estimate the interstellar extinction towards RXJ 2117+3412 according to the model of Chen et al. (1998). Their interstellar extinction model improves the model of Arenou et al. (1992) by using a large sample of open clusters in the galactic plane. However, the interstellar extinction at low galactic latitude is patchy and its small scale structure still needs to be determined. The extinction derived by Chen et al. (1998) depends on the galactic longitude and varies non linearly with the distance. As distance and interstellar absorption are related, we must iterate to get the distance of RXJ 2117+3412. We stop the iterations as soon as the last two consecutive distance determinations differ by only $\approx$ 0.5 $\%$ , which is comparable to the precision of m_V ( $m_V=13.16\pm 0.01$ ). This puts RXJ 2117+3412 at a closer distance:

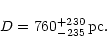
$\begin{displaymath}D= 760 ^{+230}_{- 235}\,{{\rm pc.}}\end{displaymath}$

The interstellar absorption at the average distance of RXJ 2117+3412 is: $A_{{\rm v}}=0.86$ mag. We predict the parallax of RXJ 2117+3412 to be 1.32 mas ^-0.30_+0.59 mas.

Adopting this new distance estimate, and its associated uncertainty, the linear extent of the planetary nebula is:

$\begin{displaymath}L_{\rm PN}= 2.9\pm~0.9\,{{\rm pc.}}\end{displaymath}$

The planetary nebula surrounding RXJ 2117+3412 is still the largest one known.

4.9 Secular evolution

We showed in Sect. 4.6 that the He-rich outer envelope in RXJ 2117+3412 could be at least 3.7 times more massive than in PG 1159-035, and could possibly be greater than 20 times more massive. Knowing the mass loss rate of RXJ 2117+3412, we can estimate how long it would take to RXJ 2117+3412 to loose most of its He-rich envelope so that it would become similar to PG 1159-035. This would give an order of magnitude estimate for the evolutionary time scale. Koesterke et al. (1998) derive a mass loss rate of $\log \dot{M}=-7.0 \left(M_{\odot}~{{\rm yr}}^{-1}\right)$ , from the C IV line profiles. More recently, Koesterke & Werner (1998) obtained a more precise mass loss rate of $\log \dot{M}= -7.4 \left(M_{\odot}~{{\rm yr}}^{-1}\right)$ from O VI line profiles, which we will use here. If we assume that RXJ 2117+3412 is a progenitor of PG 1159-035, and also assume that PG 1159-035 had the same internal structure as RXJ 2117+3412 at the same luminosity, then we can derive the age difference between the two stars, assuming a constant mass loss rate, as:

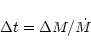
$\begin{displaymath}\Delta t= \Delta M/\dot{M}\end{displaymath}$

where $\Delta M$ is the difference in the He-rich envelope mass between RXJ 2117+3412 and PG 1159-035. It would take $\approx$ 1.3 $\times$ 10⁵ yr (or $\approx$ 1.1 $\times$ 10⁶ yr) for RXJ 2117+3412 to loose enough mass to become similar to PG 1159-035 if the He-rich envelope is 3.7 times (or 22.3 times) more massive than the envelope of PG 1159-035. This is only a lower limit to the evolutionary time scale, since it is expected that the mass loss rate decreases with decreasing luminosity.

This estimate of the evolutionary time scale would imply a rate of period change of the order of $\dot{P} \leq 2.4 \times 10^{-10}\,{{\rm s\,s}}^{-1}$ ( $2.9 \times 10^{-11}\,{{\rm s\,s}}^{-1}$ ) for the low He-rich envelope mass case (high He-rich envelope mass) for periods around 1000 s. This is comparable to the $\dot{P} = (+13.0 \pm 2.6) \times 10^{-11}\,{{\rm s\,s}}^{-1}$ measured for the 516 s mode in PG 1159-035 (Costa et al. 1999). Such a high rate of period change would probably be detectable in RXJ 2117+3412 if one could find an isolated mode with a stable amplitude. As shown in Fig. 12, mode trapping in RXJ 2117+3412 offers the potential to measure $\dot{P}$ for both trapped and nontrapped modes. In the case of the trapped modes the resultant $\dot{P}$ would be dominated by the evolutionary time scale of the outer layers, where the structure reflects the competition between contraction and mass loss. The $\dot{P}$ of the nontrapped modes would be dominated by the core cooling time scale. Unfortunatly, it will be difficult to get an unambiguous $\dot{P}$ measurement for any mode of RXJ 2117+3412, because of the rich pulsation spectrum (which requires multisite data) and because of the large amplitude variations of the modes.

The mode at 1315.05 $\mu$ Hz, whose amplitude remained almost constant in the data sets presented here, unfortunately takes part in a linear combination with the 653.987 $\mu$ Hz to form the 1968.952 $\mu$ Hz (plus some other higher order combinations). So it can not be used as a clean mode to measure $\dot{P}$ . As this mode may be suspected to take part in a mode coupling, its frequency variation may not reflect global stellar evolution, but would rather reflect some properties of the mode coupling. It is worth mentioning however that, while both the 653 $\mu$ Hz and 1968 $\mu$ Hz peaks suffered large amplitude variations in the period covered by the data, as seen in Table 6, the 1315 $\mu$ Hz amplitude varies by only 20% during the same time. If those three modes were coupled, it is difficult to understand how the amplitude of two components could vary so much while the third remains almost constant. So long as we cannot determine whether the 1315 $\mu$ Hz mode is an eigenmode or coupled to other modes, it would be hazardous to infer any physical meaning from a $\dot{P}$ measurement for that particular mode. One must conservatively conclude that with the data presently available, there is no stable enough mode in a clean enough part of the power spectrum which we could identify as a potential candidate for a $\dot{P}$ measurement. But given the presently poor physical constraints on evolution in this part of the H-R diagram, attempting to measure a rate of period change is a worthy challenge.

The rapid evolution of RXJ 2117+3412 shows up in the mass loss. RXJ 2117+3412 has a measured mass loss rate of $\log \dot{M}= -7.4 \left(M_{\odot}~{{\rm yr}}^{-1}\right)$ , which has interesting implications for the region where pulsation driving takes place. The excitation mechanism ( $\kappa$ mechanism due to carbon and oxygen partial ionization) operates at the depth of $T\approx10^{6}~$ K, which lies in the outer $\approx$ 10^-8 M_* mass fraction of the star (Bradley & Dziembowski 1996). The observed mass loss rate implies that the material in the driving region is renewed on a time scale considerably shorter than the evolutionary time scale ( $\approx$ 50 days!). As a consequence, the chemical composition of the driving region could change on this time scale if there is compositional stratification of the outer layers. This outflow of mass through the driving region may affect the efficiency of the excitation mechanism, especially if the mass loss rate is time dependent. The amplitude variations observed in the star, including variations on time scale as short as that exhibited by the mode at 717 $\mu$ Hz during the 1994 WET campaign, could be related to the effect of the mass loss on the effectiveness of the driving in this region.

4.10 Is there evidence for $\epsilon$ mechanism in RXJ 2117+3412?

The non-radial g-mode instability in pre-white dwarf stars is triggered by the $\kappa$ and $\gamma$ mechanism induced by the partial ionization of carbon and oxygen at $T\approx 10^{6}$ K, as first suggested by Starrfield et al. (1983, 1984) and confirmed by the subsequent analysis of Stanghellini et al. (1991). More recently, instability studies using models computed with the new He/C/O OPAL opacities (Iglesias & Rogers 1993) show a better agreement with the observed blue edge of the instability strip and put some constraints on the composition of the driving region (Bradley & Dziembowski 1996; Saio 1996; Gautschy 1997). However, Kawaler et al. (1986) had also anticipated that during the PN and pre-white dwarf evolutionary phases, the possibility of a remnant He-burning shell that could drive g-modes by the $\epsilon$ -mechanism. As the He burning necessarily occurs at the bottom of the He-rich outer layers, the periods of these unstable g-modes are in the range of 70 s-200 s, corresponding to low k orders for $\ell =1$ modes. Saio (1996) and Gautschy (1997) also find g-modes triggered by the $\epsilon$ -mechanism in some of their models, with typical periods between $\approx$ 110 s and $\approx$ 150 s. However, such short period g-modes excited by $\epsilon$ -mechanism have not been found in the surveys of PNN conducted by Grauer et al. (1987) and by Hine & Nather (1987).

At the high frequency end of the list given in Table 6, one finds some peaks which could be candidates for such $\epsilon$ -mechanism driven modes, since their periods are in the range 230-290 s. But, as discussed in Sect. 3.2, all the peaks with frequency above 2180 $\mu$ Hz ( $\rm Periods \leq 460$ s) are the result of linear combinations of lower frequency modes; they are not independent modes. The highest frequency independent mode has a frequency of 2174.884 $\mu$ Hz (period of 459.8 s). A careful scrutiny of the power spectrum at even higher frequencies (up to 12000 $\mu$ Hz), where the highest noise peaks are at a 0.20 mma level, does not reveal any significant peak. We conclude that our data show no evidence for low-k order mode driven by the $\epsilon$ -mechanism.

5 Conclusions, speculations and remarks on future work

We performed an asteroseismological analysis of the pulsating PG 1159-type planetary nebula central star/pre-white dwarf RXJ 2117+3412 based on three multisite campaigns. Because of its observed amplitude variations, a property shared with most of the variable planetary nebulae nuclei and pre-white dwarf stars, three campaigns were necessary for us to decipher the complex light curve and identify the pulsation modes. The cumulative power spectrum leads to the detection of 48 independent modes. Among them, we detected two triplets and eight doublets, which have an average frequency splitting of $\approx$ 5 $\mu$ Hz. We identify these modes as $\ell =1$ g-modes split by rotation.

From the analysis of the period distribution, we assign relative overtone numbers and m values to all the modes observed between 780 $\mu$ Hz and 1450 $\mu$ Hz. The mean rotational splitting of $\Delta \bar{f}= 4.998 \pm0.23~\mu$ Hz gives an average rotation period of $1.16\pm 0.05$ d. The rotational frequency splitting decreases with increasing period, but there is no signature of mode trapping on the rotational splitting, so we cannot infer the internal rotation law. We can only conclude that the observed trend is not compatible with a solid body rotation law. The lack of significant asymmetry between the prograde and retrograde components in the triplets indicates that the magnetic field strength is probably small, with $B\leq500$ Gauss.

From the period spacing ( $\Delta P= 21.618~\rm s \pm 0.008$ s) we derive a total mass of $M= 0.56^{+0.02}_{-0.04}~M_{\odot}$ . The mode trapping indicates that the He-rich outer layer mass should be at least 0.013 M_* and could be as large as 0.078 M_*. The asteroseismological mass and the spectroscopic atmospheric parameters (log g, $T_{{\rm eff}}$ ) allow us to derive a luminosity of $\log\left(L/L_{\odot}\right)=4.05 ^{+0.23}_{-0.32}$ . The distance of RXJ 2117+3412, taking into account the interstellar absorption on the line of sight, is 760 ⁺²³⁰_-235 pc. At this distance, the linear size of the surrounding planetary nebula is $2.9~\pm 0.9$ pc, confirming its status as the largest known planetary nebula.

Speculating on the probable evolutionary link between a star like RXJ 2117+3412 and PG 1159-035, we infer that it should take at least $\approx$ $1.3 \times 10^{5}$ yr (or $\approx$ $1.1 \times 10^{6}$ yr) to RXJ 2117+3412 to shed its excess He-rich envelope through mass loss, if its He-rich envelope mass fraction is 0.013 M_*(if 0.078 M_*). This rapid evolutionary time scale leads to a predicted $\dot{P}$ between $3 \times 10^{-11}\,{{\rm s\,s}}^{-1}$ and $2 \times 10^{-10}\,{{\rm s\,s}}^{-1}$ for periods of about 1000 s. Unfortunately, interpreting any measurement of $\dot{P}$ for the modes identified in RXJ 2117+3412 presents a severe challenge: most of the modes suffer amplitude variability, the frequency spectrum will likely require multisite data to properly resolve the modes, and the rapid evolution means that we may require several observing runs each season to maintain an accurate cycle count.

Through its pulsations, however, RXJ 2117+3412 may provide a clue to understanding the complex physical processes that compete during this rapid evolutionary phase. Considering the asteroseismological data presented here together with the evidence from spectroscopy and photometry presented elsewhere, it is tempting to speculate that time dependent mass-loss plays a dominant role in what we see in RXJ 2117+3412. For example, the present chemical composition of the He-rich outer layers should be the product of the interplay between diffusion and mass loss (see the recent calculations by Unglaub & Bues 1998, 2000). Changes in the mass-loss rate should translate into a change in the heavy elements distribution within the envelope and the photosphere. These changes could in turn affect the opacity and the efficiency of the driving mechanism. The structure of the outer layers should be modified accordingly, producing changes in the spectrum and in the UV flux, since most of the UV opacity is due to the heavy elements. As the abundances in the excitation region and the whole structure of the mode propagation cavities are affected by such variations, one would expect both the frequencies and amplitudes of the g-modes to vary. The presently available data provide some support for such a scenario, since a high UV flux was observed in 1993 (Feibelman 1999), while the star showed low amplitude oscillations. The subsequent decrease in the UV flux would then be explained by the restoration of the appropriate heavy element abundance producing the opacity in the UV and the associated $\kappa$ -mechanism efficiency. The missing piece of evidence is whether the mass-loss rate was really varying simultaneously. A fully consistent study of this complex problem would be to carry out: long-term observations of the spectroscopic and photometric variations in the UV; search for a time dependence in the mass-loss rate; and obtain simultaneous asteroseismological observations to determine how the g-mode frequencies and amplitudes respond to mass-loss and UV flux variations.

Acknowledgements

The WET gratefully acknowledges support from the National Science Foundation (US) through Grant AST-9876655 to Iowa State University. GV and PM acknowledge support from the French/Polish "Jumelage'' programme. GV and MC acknowledge support from the CNRS(France)/CSIC(Spain) exchange programme and from the CNRS(France)/Chinese Academy of Sciences "PICS'' programme. MAB was supported by PPARC, UK through an Advanced Research Fellowship. XCOV8 WET run was partly supported by the EU-HCM grant CHRX-CT94-0434. During the XCOV11 WET run, EGM was attacked and badly injuried as he was observing at the Maidanak Observatory. Despite his bad experience, EGM thanks the local astronomers for a 6km mountain-running to the military base, the pilots of the military helicopter for the quick delivery to the hospital, and the doctors of the Kitab hospital who rescued him. ADG thanks the Director and Staff of the Steward Observatory for telescope time and technical support with the telescopes on Mt. Bigelow and Mt. Lemmon. JNF thanks the K.C. Wong Education Foundation, Hong-Kong, China and the French Ministery for National Education for financial support. Astronomical research at the Wise Observatory is supported by the Basic Research Foundation of the Israeli Academy of Sciences. PM, JK, GP and SZ are supported in part by KBN grants No 2-P03D-015-08 and 2-P03D-014-14 in Poland.

References

Appleton, P. N., Kawaler, S. D., & Eitter, J. J. 1993, AJ, 106, 1973 In the text NASA ADS
Arenou, F., Grenon, M., & Gómez, A. E. 1992, A&A, 258, 104 In the text NASA ADS
Beauchamp, A., Wesemael, F., Bergeron, P., et al. 1999, ApJ, 516, 887 In the text NASA ADS
Bond, H. E., Kawaler, S. D., Ciardullo, R., et al. 1996, AJ, 112, 2699 In the text NASA ADS
Bond, H. E., & Grauer, A. D. 1987, ApJ, 321, L123 In the text NASA ADS
Bond, H. E., Grauer, A. D., Green, R. F., & Liebert, J. 1984, ApJ, 279, 751 In the text NASA ADS
Bradley, P. A. 2000, in Proc. of The Fifth WET Workshop, ed. E. G. Mei $\breve{\rm s}$ tas, & G. Vauclair (Baltic Astronomy), 9, 485 In the text
Bradley, P. A. 2001, ApJ, 552, 326 In the text NASA ADS
Bradley, P. A., & Dziembowski, W. 1996, ApJ, 468, 350 In the text NASA ADS
Brickhill, A. J. 1975, MNRAS, 170, 404 In the text
Ciardullo, R., & Bond, H. E. 1996, AJ, 111, 2332 In the text NASA ADS
Chen, B., Vergely, J. L., Valette, B., & Carraro, G. 1998, A&A, 336, 137 In the text NASA ADS
Costa, J. E. S., Kepler, S. O., & Winget, D. E. 1999, ApJ, 522, 973 In the text NASA ADS
Dreizler, S. 1998, in Proc. of the Fourth WET Workshop, ed. E. G. Mei $\breve{\rm s}$ tas, & P. Moskalik (Baltic Astronomy), 7, 71 In the text
Dreizler, S., & Heber, U. 1998, A&A, 334, 618 In the text NASA ADS
Feibelman, W. 1999, ApJ, 513, 947 In the text NASA ADS
Fontaine, G., Bergeron, P., Vauclair, G., et al. 1991, ApJ, 378, L49 In the text NASA ADS
Gautschy, A. 1997, A&A, 320, 811 In the text NASA ADS
Goupil, M. J., Dziembowski, W. A., & Fontaine, G. 1998, in Proc. of the Fourth WET workshop, ed. E. G. Mei $\breve{\rm s}$ tas, & P. Moskalik (Baltic Astronomy), 7, 21 In the text
Grauer, A. D., Bond, H. E., Liebert, J., Fleming, T. A., & Green, R. F. 1987, ApJ, 323, 271 In the text NASA ADS
Grauer, A. D., Green, R. F., & Liebert, J. 1992, ApJ, 399, 686 In the text NASA ADS
Hine, B. P., & Nather, R. E. 1987, in The Second Conference on Faint Blue Stars, IAU Colloq. 95, ed. A. G. D. Philip, D. S. Haayes, & J. Liebert (Schenectady, NY: L. Davis Press), 619 In the text
Iglesias, C. A., & Rogers, F. J. 1993, ApJ, 412, 752 In the text NASA ADS
Jones, P. W., Pesnell, W. D., Hansen, C. H., & Kawaler, S. D. 1989, ApJ, 336, 403 In the text NASA ADS
Kawaler, S. D. 1988, in Advances of Helio- and Asteroseismology, ed. J. Christensen-Dalsgaard, & S. Frandsen (Dordrecht: Reidel), 329 In the text
Kawaler, S. D. 1998, in Proc. of the Fourth WET workshop, ed. E. G. Mei $\breve{\rm s}$ tas, & P. Moskalik (Baltic Astronomy), 7, 11 In the text
Kawaler S. D., & Bradley, P. A. 1994, ApJ, 427, 415 In the text NASA ADS
Kawaler, S. D., Sekii, T., & Gough, D. 1999, ApJ, 516, 349 In the text NASA ADS
Kawaler, S. D., Winget, D. E., Hansen, C. J., & Iben, I. Jr. 1986, ApJ, 306, L41 In the text NASA ADS
Kawaler, S. D., O'Brien, M. S., Clemens, J. C., et al. 1995, ApJ, 450, 350 In the text NASA ADS
Kepler, S. O. 1993, in Proc. of the Third WET Workshop, ed. E. G. Mei $\breve{\rm s}$ tas, & J.-E. Solheim (Baltic Astronomy), 2, 515 In the text
Kepler, S. O. 1984, ApJ, 286, 314 In the text NASA ADS
Kepler, S.O., da Costa, A. F. M., Giovannini, O., & Koester, D. 2000, in Proc. of the Fifth WET Workshop, ed. E. G. Mei $\breve{\rm s}$ tas, & G. Vauclair (Baltic Astronomy), 9, 125 In the text
Kjeldsen, H., & Frandsen, S. 1992, PASP, 104, 413 In the text NASA ADS
Kleinman, S. J., Nather, R. E., & Phillips, T. 1996, PASP, 108, 356 In the text NASA ADS
Kleinman, S. J., Nather, R. E., Winget, D. E., et al. 1998, ApJ, 495, 424 In the text NASA ADS
Koesterke, L., Dreizler, S., & Rauch, T. 1998, A&A, 330, 1041 In the text NASA ADS
Koesterke, L., & Werner, K. 1998, ApJ, 500, L55 In the text NASA ADS
McGraw, J. T., Starrfield, S. G., Liebert, J., & Green, R. F. 1979, in White Dwarfs and Variable Degenerate Stars, IAU Colloq. 53, ed. H. M. Van Horn, & V. Weidemann (Univ. Rochester Press), 377 In the text
Motch, C., Werner, K., & Pakull, M. W. 1993, A&A, 268, 561 In the text NASA ADS
Nather, R. E., Winget, D. E., Clemens, J. C., Hansen, C. J., & Hine, B. P. 1990, ApJ, 361, 309 In the text NASA ADS
O'Brien, M. S., Clemens, C., Kawaler, & S. D., Dehner, 1996, ApJ, 467, 397 In the text NASA ADS
O'Brien, M. S., Vauclair, G., Kawaler, S. D., et al. 1998, ApJ, 495, 458 In the text NASA ADS
O'Brien, M. S. 2000, ApJ, 532, 1078 In the text NASA ADS
O'Donoghue, D. 1994, MNRAS, 270, 222 In the text NASA ADS
Perryman, M. A. C. 1997, The Hipparcos and Tycho Catalogues, ESA SP-1200 (ESA Publications Division, ESTEC, Noordwijk, The Netherlands) In the text
Rauch, T., & Werner, K. 1997, in The Third Conference on Faint Blue Stars, ed. A. G. D.Philip, J. Liebert, & R. A. Saffer (L. Davis Press, Schenectady, NY), 217 In the text
Robinson, E. L., Kepler, S. O., & Nather, R. E. 1982, ApJ, 259, 219 In the text NASA ADS
Saio, H. 1996, in Hydrogen-Deficient Stars, ed. C. S. Jeffery, & U. Heber, ASP Conf. Ser., 96, 361 In the text
Silvotti, R. 1996, A&A, 309, L23 In the text NASA ADS
Silvotti, R., Dreizler, S., Handler, G., & Jiang, X. J. 1999, A&A, 342, 74 In the text
Spruit, H. C. 1998, A&A, 333, 603 In the text NASA ADS
Stanghellini, L., Cox, A. N., & Starrfield, S. G. 1991, ApJ, 383, 766 In the text NASA ADS
Starrfield, S. G., Cox, A. N., Hodson, S. W., & Pesnell, W. D. 1983, ApJ, 268, L27 In the text NASA ADS
Starrfield, S. G., Cox, A. N., Kidman, R. B., & Pesnell, W. D. 1984, ApJ, 281, 800 In the text NASA ADS
Unglaub, K., & Bues, I. 1998, A&A, 338, 75 In the text NASA ADS
Unglaub, K., & Bues, I. 2000, A&A, 359, 1042 In the text NASA ADS
Unno, W., Osaki, Y., Ando, H., Saio, H., & Shibahashi, H. 1989, Nonradial Oscillations of Stars (University of Tokyo Press) In the text
Vauclair, G., Goupil, M.-J., Baglin, A., Auvergne, M., & Chevreton, M. 1989, A&A, 215, L17 In the text NASA ADS
Vauclair, G., Belmonte, J. A., Pfeiffer, B., et al. 1993, A&A, 267, L35 In the text NASA ADS
Vauclair, G., Pfeiffer, B., Grauer, A. D., et al. 1995, A&A, 299, 707 In the text NASA ADS
Vauclair, G., O'Brien, M. S., Fu, J. N., et al. 2001, in Twelfth European Workshop on White Dwarfs, ed. J. L. Provencal, H. L. Shipman, J. MacDonald, & S. Goodchild, ASP Conf. Ser., 226, 293 In the text
Vuille, F., O'Donoghue, D., Buckley, D. A. H., et al. 2000, MNRAS, 314, 689 In the text NASA ADS
Watson, T. K. 1992, IAU Circ., 5603 In the text
Werner, K. 1993, in White Dwarfs: Advances in Observation and Theory, ed. M. A. Barstow (Kluwer Academic Publishers), 67 In the text
Werner, K., Dreizler, S., Heber, U., et al. 1996, A&A, 307, 860 In the text NASA ADS
Winget, D. E., Nather, R. E., Clemens, J. C., et al. 1991, ApJ, 378, 326 In the text NASA ADS
Winget, D. E., Nather, R. E., Clemens, J. C., et al. 1994, ApJ, 430, 839 In the text NASA ADS
Wood, P. R., & Faulkner, D. J. 1986, ApJ, 307, 659 In the text NASA ADS

		1992 WET
f1	f2	f3	f4	$\delta f$
( $\mu$ Hz)	( $\mu$ Hz)	( $\mu$ Hz)	( $\mu$ Hz)	( $\mu$ Hz)
653.811	1315.181		1968.915	0.077	b
653.811	1315.181	2109.129	4077.942	0.179	b
945.156	1023.594	2109.129	4077.942	0.063	a
1179.893	1315.181	945.156	1549.959	0.041	a