A&A 381, 65-76 (2002)
DOI: 10.1051/0004-6361:20011492

A comprehensive study of the rich open star cluster NGC 2099 based on deep $\vec{BVI}$ CCD observations[*]

Nilakshi 1 - R. Sagar1,2


1 - State Observatory, Manora Peak, Nainital 263129, India
2 - Indian Institute of Astrophysics, Bangalore 560034, India

Received 12 July 2001 / Accepted 15 October 2001

Abstract
The CCD observations of the rich open star cluster NGC 2099 and its surrounding field region have been carried out up to a limiting magnitude of $V \sim 22$ mag in B, V and I passbands for the first time. A total of $\sim$12000 stars have been observed in the area of about $24\hbox{$^\prime$ }\times 34\hbox{$^\prime$ }$ in the cluster region, as well as $\sim$2180 stars in the $\sim$ $12\hbox{$^\prime$ }\times 12\hbox{$^\prime$ }$ area of the field region located $\sim$ $45\hbox{$^\prime$ }$ away from the cluster center. The cluster parameters determined by fitting the convective core overshoot isochrones in the V, (B-V) and V, (V-I) diagrams are $E(B-V) = 0.30\pm0.04$ mag, distance = $1360\pm 100$ pc, age = 400 Myr and metallicity Z = 0.008. A well-defined cluster main sequence spread over about 8 mag in range is observed for the first time. Its intrinsic spread amounting to $\sim$0.06 mag in colour is almost the same over the entire brightness and can be understood in terms of the presence of physical/optical binaries. The core and cluster radii determined from the radial stellar density profiles are 185 $^{\prime\prime}$ and 1000 $^{\prime\prime}$ respectively. Only about 22% of cluster members are present in the core region. The effects of mass segregation, most probably due to dynamical evolution, have been observed in the cluster. The mass function slope of the entire cluster is $\sim$ $-0.67\pm0.12$. It becomes closer to the Salpeter value of -1.35, if flattening in the cluster mass function due to presence of both binaries and a much more extended corona is considered.

Key words: open clusters and associations: individual: NGC 2099 - stars: HR diagram - evolution - formation


1 Introduction

A preliminary study of the spatial structure of 38 rich open clusters carried out by Nilakshi et al. (2002) indicates that, in addition to the nucleus, a large fraction of them have an extended corona consisting of significant low mass ( $M\le 1~\mbox{$M_{\odot}$ }$) members which are very important for studies like cluster dynamics and mass function (MF). We therefore plan to carry out extensive study of clusters showing the presence of a corona using wide field deep CCD photometric observations. The present paper is the second in that series, the first paper under this programme being a CCD photometric study of the cluster NGC 7654 (Pandey et al. 2001).

The northern rich galactic open star cluster NGC 2099 (M 37) is located in the Galactic anti-center direction in Auriga ( $\alpha_{2000} = 5^{\rm h}52^{\rm m}17\,\hbox{$.\!\!^{\rm s}$ }6$, $\delta_{2000} = 32\hbox{$^\circ$ }33\hbox{$^\prime$ }40\hbox{$^{\prime\prime}$ }, l = 177\hbox{$.\!\!^\circ$ }65, b = 3\hbox{$.\!\!^\circ$ }09$). Melotte (1915) describe it as a loose cluster having a regular well-defined outline. The cluster has been studied photometrically and kinematically (both proper motion and radial velocity) many times (see Table 1). Zhao et al. (1985) use the proper motion data given by Joy (1916), Jefferys (1962) and Upgren (1966) to determine the cluster membership of stars using improved methods of maximum-likelihood developed by Sanders (1972). However, accuracy of the proper motion data is not good enough to provide a clear separation of cluster members from the field stars and also they are only for $V \le$ 15 mag stars. Photoelectric and photographic UBV magnitudes are available mainly within about a 10$^\prime$ radius from the cluster center for $V \le$ 18 mag stars (see Table 1). The color-magnitude diagrams (CMDs), mostly based on photographic data which are not accurate, show a rather broad MS but a well populated clump of red giants. The colour excess E(B-V), apparent distance modulus (m-M) and log (age) values determined by various investigators (see Table 1) for the cluster range from 0.27 to 0.31; 11.5 to 11.8 and 8.3 to 8.7 respectively. In the cluster region, Robin (1982) provides UBV electronographic magnitudes of mostly uncrowded stars up to a limiting magnitude in $V \sim 20$ with an accuracy of 0.055 mag in V, 0.075 mag in B and 0.10 mag in U. The first variable star survey of M 37 carried out by Kiss et al. (2001) using CCD observations discovered 7 new variables in the cluster region. Mermilliod et al. (1996) presented radial velocity measurements for 55 red giants while Glushkova & Rastorguev (1991) published such measurements for 9 red giants. CCD photometric observations of the NGC 2099 are required for accurate determination of cluster parameters and to study the spatial structure and mass segregation effect of this populous cluster. The details of the present CCD observations are given in the next section while results etc. are given in the remaining part of the paper.

 
Table 1: Existing kinematical and photometric studies of the NGC 2099. N is the number of stars observed and $V_{\rm L}$ is the limiting magnitude of observations.
Proper motion studies
N Accuracy $V_{\rm L}$ Base line and Source
  ( $^{\prime\prime}$/century)    

243		 0.13   50 yr, Jefferys (1962)
292 0.3  13.5 11 yr, Joy (1916)
489 0.09 14.0 60 yr, Upgren (1966)
223 0.3  13.0 35 yr, White (1933)
Radial velocity studies
N Accuracy $V_{\rm L}$ Source
  (km/s-1)    
9   12 Glushkova & Rastorguev (1991)
55 0.17 12 Mermilliod et al. (1996)
Broad band Photometric studies
N filter $V_{\rm L}$ Source
Photoelectric
27 UBV 15.0 Hoag et al. (1961)
46 UBV 18.8 Brosterhus (1963)
39 UBV 17.7 West (1967)
1 VRI   Lee (1970)
9 UBV 11.7 Jennens & Helfer (1975)
5 DDO   Janes (1979)
18 VRI 11.7 Coleman (1982)
20 UBV 11.7 Mermilliod et al. (1996)
Photographic
2116 V 15.7 van Zeipel & Lindgren (1921)
141 UBV 15.4 Hoag et.al. (1961)
2089 BV 17.3 Brosterhus (1963)
1797 UBV 17.7 West (1967)
Electronographic
295 UBV 20.0 Robin (1982)
Cluster parameters
Age distance E(B-V) Source
(Myr) (pc) (mag)  
200 1450 0.27 West (1967)
200 1360 0.31 Lyngå (1987)
500 1320 0.29 Mermilliod et al. (1996)
450 1300 0.29 Kiss et al. (2001)


2 Observations and data reduction

We carried out B, V Johnson and I Cousins broad band photometric observations between November and December 1999. A CCD camera of size $2048\times2048$ pixels2 attached to f/13 Cassegrain focus of 104-cm Sampurnanand telescope of the State Observatory, Nainital was used. To increase the S/N ratio, we observed all the frames in a $2\times 2$ binning mode. In order to cover a wide field, we observed the cluster in 6 different parts and constructed the mosaic (see Fig. 1) which is equivalent to an area of $\sim$ $24\hbox{$^\prime$ }\times 34\hbox{$^\prime$ }$. The FWHMs of the star images were $\sim$ $ 2\hbox{$.\!\!^{\prime\prime}$ }5$. A field region $\sim$ $45\hbox{$^\prime$ }$ away from the cluster center was also observed in the BVI filters to correct for field star contamination. The identification map of the field region is also shown in Fig. 1. A number of bias and dawn or dusk flat frames were also taken. To calibrate the observations, eight Landolt (1992) standard stars covering a range in brightness ( 12.5 < V < 15.6) as well as in colour ( 0.6 < (V-I) < 1.4) were observed. The log of observations is given in Table 2. In order to provide accurate photometric measurements for faint stars, several deep exposure frames in each filter were taken.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms1673f1.eps}\end{figure} Figure 1: Identification maps for NGC 2099 cluster and field regions. In the cluster region, the six overlapping areas imaged with CCD (see Table 2) are marked. The (X,Y) co-ordinates are in pixel units and one pixel corresponds to 0 $\hbox{$.\!\!^{\prime\prime}$ }74$ on the sky. South and east directions are marked. The size of a star depends upon its brightness with largest and smallest sizes correspond to V = 10 and 17 mag respectively.
Open with DEXTER


 

 
Table 2: Log of CCD observations for the cluster NGC 2099, Landolt (1992) standard and surrounding field regions.

Date		 Filter Exposure time (s)

Cluster area 1
4/5 Nov. 1999 B 30, 100, $300\times6$
  V 20, 30, $300\times 3$
  I 20, 50, $180\times 2$
Cluster area 2
5/6 Nov. 1999 B 30, 100, $300\times6$
  V 30, $300\times 3$
  I 20, $180\times 3$
Cluster area 3
4/5 Nov. 1999 B 30, 100, $300\times6$
  V 30, 60, $300\times 3$
  I 30, 50, $180\times 3$
Cluster area 4
5/6 Nov. 1999 B 30, 100, $300\times6$
  V 30, 100, $300\times 3$
  I 30, 50, $180\times 3$
Cluster area 5
30/31 Nov. 1999 B 30, 100, $300\times6$
  V 30, 100, $300\times 3$
  I 20, 60, $180\times 3$
Cluster area 6
30/31 Nov. 1999 B 30, 100, $300\times6$
  V 30, 100, $300\times 3$
  I 20, 60, $180\times 3$
Standard field SA 92
30/31 Nov. 1999 B $180\times 2$
  V $120\times 3$
  I $30\times 2$
Field region
3/4 Dec. 1999 B 40, $300\times4$
  V 40, $300\times 3$
  I 30, $180\times 3$


Images were processed with the help of ESO MIDAS software packages using the standard procedures. Although the observed cluster and field regions are not exceptionally crowded, the magnitude estimation has been carried out using DAOPHOT profile-fitting software, as described by Stetson (1987, 1992), so that it can be determined reliably to faint levels. The stellar PSF used by DAOPHOT is evaluated from the sum of several uncontaminated stars present in each frame. Further processing and conversion of these raw instrumental magnitudes into the standard photometric system has been done using the procedure outlined by Stetson (1992). The ALLSTAR image parameter $\chi > 2.5$ and errors > 0.2 mag were used to reject poor measurements. In those cases where brighter stars are saturated in the deep exposure frames, their magnitudes have only been taken from the short exposure frames. Most of the stars brighter than $V \sim 11$ mag could not be measured because they are generally saturated even on the shortest exposure frames. Wherever more than one measurement is available in a passband for a star, the final magnitude is an average of the individual measurements weighted by the ALLSTAR output errors and its error is the error of the average. When only one measurement is available, the error is taken to be the output of ALLSTAR.

The photometric calibration equations are:

  \begin{displaymath} V = v_{0} + (0.029 \pm 0.008) \times (V-I) - (3.88 \pm 0.02) \end{displaymath} (1)


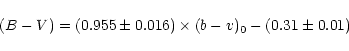\begin{displaymath}(B-V) = (0.955 \pm 0.016) \times (b-v)_{0} - (0.31 \pm 0.01) \end{displaymath} (2)


 \begin{displaymath}(V-I) = (0.992 \pm 0.013) \times (v-i)_{0} + (0.56 \pm 0.03) \end{displaymath} (3)

where B, V, I are standard magnitudes taken from Landolt (1992) and b0, v0, i0 are atmospheric extinction-corrected instrumental CCD aperture magnitudes. The values of atmospheric extinction coefficients used in the photometric calibration are 0.06, 0.15 and 0.25 mag/airmass in the I, V and B passbands respectively. The values are for 30/31 November 1999. The Eqs. (1) to (3) are used to standarize the CCD instrumental magnitudes of both cluster and field regions. To establish the local standards, we selected several isolated stars in all the observed regions and used the DAOGROW programme for the construction of an aperture growth curve required for determining the difference between aperture and profile-fitting magnitudes. These differences and differences in exposure times and atmospheric extinctions are used in evaluating zero-points for the reference frames. The zero-points are uncertain by $\sim$0.02 mag in B, V and I. Other factors contributing to the photometric uncertainty are described by Moitinho (2001). Amongst them, the internal errors estimated from the scatter in the individual measures of different exposures in a region mainly affect the photometric precision. They are given in Table 3 as a function of brightness for the cluster region. The errors become large ($\ge$0.1 mag) for stars fainter than V = 20 mag, so the measurements should be considered unreliable below this magnitude.
 

 
Table 3: Internal photometric errors as a function of brightness in the cluster region. The standard deviation ($\sigma $) is per observation in magnitudes.

Magnitude range		 $\sigma _B$ $\sigma _V$ $\sigma _I$
$\le$14 0.007 0.011 0.021
14-15 0.010 0.015 0.024
15-16 0.014 0.020 0.040
16-17 0.021 0.035 0.046
17-18 0.032 0.053 0.060
18-19 0.046 0.070 0.101
19-20 0.080 0.112 0.168


The (X, Y) pixel coordinates as well as the V, (B-V) and (V-I) magnitudes of a sample of stars observed in NGC 2099 and field regions are listed in Table 4 along with the errors. The format of the Table 4 is presented here while the entire data is available only in electronic form at the CDS in Strasbourg and the WEBDA open cluster database website at http://obswww.unige.ch/webda/ (Mermilliod 1995). It can also be obtained from the authors. In order to avoid introducing a new numbering system, we adopt the numbers from the database given by van Zeipel & Lindgren (1921). Stars not observed earlier have a number starting with 10001. There are about 11200 such stars in the cluster region and about 2180 stars in the field region.

 

 
Table 4: Sample of BVI photometric data of the stars in the NGC 2099 cluster and surrounding field regions. Stars observed earlier have numbering from the cluster database given by van Zeipel & Lindgren (1921) while those observed for the first time have a new number starting with 10001. X, Y are the CCD pixel coordinates shown in Fig. 1 for the cluster and field regions. $\sigma _B$, $\sigma _V$ and $\sigma _I$ are the errors in the B, V and I bands respectively. Proper motion and photometric cluster memberships are denoted by KM and PM respectively in the last column.

Star		 X Y V (B-V) (V-I) $\sigma _I$ $\sigma _V$ $\sigma _B$ Membership
  (pixel) (pixel) (mag) (mag) (mag) (mag) (mag) (mag)  
Cluster region
6 1058.29 959.64 13.64 0.43 0.60 0.01 0.01 0.01 PM
13 1003.89 996.83 13.68 0.59 0.84 0.03 0.02 0.01 KM
122 1051.44 1150.22 13.06 0.29 0.52 0.01 0.01 0.01 PM
126 1049.70 1213.59 14.13 0.48 0.69 0.01 0.01 0.01 PM
577 1618.83 848.67 13.34 1.23 1.41 0.01 0.01 0.01 KM
10001 1978.27 2686.89 21.74   2.15 0.10 0.12    
Field region
1 52.92 0.63 17.38 0.68 1.23 0.06 0.03 0.06  
2 172.02 1.46 21.51   1.62 0.21 0.12    



  \begin{figure} \par\includegraphics[width=15cm,clip]{ms1673f2.eps}\end{figure} Figure 2: The V, (B-V) and V, (V-I) diagrams for all stars observed in the cluster and field regions with $\sigma_{(B-V)}, \sigma_{(V-I)}~<~0.05$ mag. The regions delimiting the MS stars of the cluster and field populations are marked.
Open with DEXTER


 

 
Table 5: Comparison of the present CCD data with the existing photometries in the cluster database. The difference $\Delta $ (present - literature) is in magnitude. Mean and $\sigma $ are based on N stars in a V magnitude bin.
V range $\Delta V$ $\Delta (B-V)$
  $ \rm Mean\pm\sigma$ N $ \rm Mean\pm\sigma$ N
Hoag et al. (1961) photoelectric data
10-12 $-0.03\pm0.04$ 5 $ -0.03\pm0.03$ 4
12-13 $-0.01\pm0.02$ 4 $ -0.06\pm0.05$ 4
13-14 $-0.02\pm0.02$ 6 $ -0.05\pm0.01$ 6
14-15 $-0.05\pm0.04$ 7 $ -0.06\pm0.07$ 8
Brosterhus (1963) photoelectric data
10-12 $-0.05\pm0.03$ 4 $-0.08\pm0.03$ 4
12-14 $ -0.06\pm0.07$ 6 $-0.02\pm0.04$ 6
14-17 $-0.07\pm0.07$ 10 $ -0.04\pm0.05$ 9
West (1967) photoelectric data
11-12 $-0.04\pm0.01$ 3 $-0.01\pm0.05$ 2
12-13 $ -0.06\pm0.07$ 5 $-0.04\pm0.02$ 5
13-14 $-0.01\pm0.08$ 5 $-0.07\pm0.04$ 6
14-15 $-0.02\pm0.05$ 6 $-0.02\pm0.03$ 6
15-16 $-0.00\pm0.01$ 3 $-0.04\pm0.03$ 4
16-18 $-0.09\pm0.01$ 2 $-0.04\pm0.00$ 2
Jennens & Helfer (1975) photoelectric data
11-12 $-0.08\pm0.01$ 2 $-0.05\pm0.00$ 2
Coleman (1982) photoelectric data
11-12 $-0.04\pm0.01$ 4 $-0.05\pm0.03$ 4
Mermilliod (1996) photoelectric data
10-12 $-0.01\pm0.06$ 9 $-0.06\pm0.06$ 9
Hoag et al. (1961) photographic data
11-12 $~0.10\pm0.14$ 13 $ -0.05\pm0.08$ 13
12-13 $~0.10\pm0.09$ 15 $ -0.10\pm0.09$ 17
13-14 $~0.04\pm0.10$ 33 $-0.07\pm0.07$ 33
14-15 $-0.05\pm0.09$ 28 $ -0.04\pm0.04$ 26
15-16 $-0.07\pm0.06$ 15 $ -0.06\pm0.04$ 15
Brosterhus (1963) photographic data
10-12 $-0.03\pm0.04$ 55 $ -0.03\pm0.05$ 45
12-13 $-0.03\pm0.04$ 99 $ -0.07\pm0.05$ 99
13-14 $-0.03\pm0.04$ 197 $ -0.05\pm0.05$ 193
14-15 $ -0.03\pm0.05$ 252 $ -0.05\pm0.05$ 248
15-16 $ -0.05\pm0.05$ 373 $-0.05\pm0.04$ 364
16-17 $-0.07\pm0.00$ 569 $ -0.05\pm0.05$ 543
West (1967) photographic data
11-12 $ -0.06\pm0.07$ 36 $-0.06\pm0.08$ 34
12-13 $~0.06\pm0.06$ 68 $-0.06\pm0.06$ 75
13-14 $~0.05\pm0.07$ 123 $-0.04\pm0.07$ 133
14-15 $~0.03\pm0.07$ 157 $-0.01\pm0.09$ 164
15-16 $~0.01\pm0.08$ 193 $-0.05\pm0.09$ 200
16-18 $-0.06\pm0.10$ 360 $-0.03\pm0.11$ 269
Robin (1982) electronographic data
13-15 $~0.13\pm0.13$ 27 $~0.01\pm0.16$ 27
15-16 $~0.12\pm0.08$ 27 $ -0.16\pm0.15$ 26
16-17 $~0.05\pm0.08$ 24 $ -0.25\pm0.14$ 27
17-18 $-0.11\pm0.10$ 30 $ -0.01\pm0.16 $ 25
18-19 $-0.14\pm0.12$ 42 $ 0.17\pm0.23$ 40



  \begin{figure} \par\includegraphics[width=8.8cm, height=11.1cm,clip]{ms1673f3.eps}\end{figure} Figure 3: Comparison of the present CCD data with the photographic (Brosterhus 1963 - $\circ $, Hoag et al. 1961 - $\times $, West 1967 - triangle); photoelectric (Brosterhus 1963 - $\circ $, Hoag et al. 1961 - $\times $, West 1967 - filled triangles, Coleman 1982 - $\bullet $, Jennens & Helfer 1975 square, Mermilliod et al. 1996 - $\ast $) and Robin (1982) - $\times $electronographic data.
Open with DEXTER

2.1 CMDs based on the present observations

The apparent V, (B-V) and V, (V-I) diagrams of NGC 2099 cluster and field regions generated from the present data are displayed in Fig. 2. These include all stars with $\sigma_{B-V}, \sigma_{V-I} < 0.05$ mag. The deep CMDs extend down to V = 21 mag in both the cluster and field regions. A well-defined cluster main-sequence (MS) clearly separated from the bulk of field stars is visible in both CMDs of the cluster region. The cluster sequences fainter than V = 20 mag have a large scatter and perhaps are not clearly defined. The field population dominates the fainter as well as the bluer part of the CMDs (see Fig. 2).

   
2.2 Comparison with the earlier photometries

The present photometry is compared with available BV electronographic, photographic and photoelectric photometries. The differences $\Delta $ (present - literature) as a function of present V magnitude are shown in Fig. 3 and statistical results are given in Table 5. They indicate that in comparison to the present CCD data the photoelectric measurements are generally fainter and redder while both electronographic and photographic data systematically show varying differences with brightness. As expected, the scatter increases with decreasing brightness. The errors are most likely to lie in photographic and electronographic observations since a CCD is an intrinsically linear and better detector.

 

 
Table 6: The completeness factor (CF) of the present VI photometric data in the core and coronal regions of the NGC 2099. The $N_{\rm f}, N_{\rm a}$ and $N_{\rm r}$ are number of CCD frames generated, stars added and stars recovered respectively.
Range $N_{\rm f}$ Core Corona 1 Corona 2
in   $N_{\rm a}$ $N_{\rm r}$ CF $N_{\rm a}$ $N_{\rm r}$ CF $N_{\rm a}$ $N_{\rm r}$ CF
V mag
12-16 6 15 13 0.87 174 174 1.00 583 583 1.00
16-17 8 16 14 0.88 125 125 1.00 446 445 1.00
17-18 10 28 24 0.86 192 191 1.00 660 660 1.00
18-19 12 54 45 0.83 272 262 0.96 925 888 0.96
19-20 14 101 76 0.75 527 480 0.91 1425 1318 0.93
I mag
12-16 6 8 8 1.00 86 85 1.00 284 282 1.00
16-17 8 7 7 1.00 88 87 1.00 299 298 1.00
17-18 10 16 15 0.94 125 121 0.97 446 436 0.98
18-19 12 28 26 0.93 192 180 0.94 660 632 0.96
19-20 14 54 48 0.89 272 241 0.89 925 857 0.93


2.3 Completeness of the CCD data

The completeness factor (CF) of the photometric data is determined in V and I frames using the add-star routine of DAOPHOT. We randomly added only $\sim$15% of actually detected stars as artificial stars of known magnitudes and positions into the original V and I deep frames (see Table 6). The frames we re-reduced by applying the same procedure as used for the original frames. The values of CF as a function of both brightness and radius are given in Table 6. We found that the data completeness is almost 100% in the field region.
  \begin{figure} \par\includegraphics[width=7.8cm, height=11.7cm,clip]{ms1673f4.eps}\end{figure} Figure 4: The radial variation of the projected stellar density of proper motion members as well as for different magnitude levels of MS and all stars of the cluster region. Dotted horizontal line indicates the level of field star contamination.
Open with DEXTER

   
3 Radius and spatial structure of the cluster

To study the spatial structure and determine the cluster radius, we plot the radial variation of the stellar surface density ($\rho$). For this, the cluster center is determined first. Its (X,Y) pixel coordinates (1030, 1060) are derived iteratively by calculating average X and Y positions of stars located within 150 pixels of an eye-estimated center, until the values converged. This corresponds to $\alpha_{2000} = 05^{\rm h}52^{\rm m}17\hbox{$.\!\!^{\rm s}$ }6, \delta_{2000} = +32\hbox{$^\circ$ }32\hbox{$^\prime$ }40\hbox{$^{\prime\prime}$ }$. An error of a few tens of arcsec is expected in locating the cluster center. The cluster region is divided into a number of concentric circles with respect to the cluster center. The number density of stars in the ith annulus is given by $\rho_i = \frac{N_i} {A_i}$; where Ni is the number of stars (generally >50) in area Ai of the ith annulus. In the outer regions, the area correction for the portion of the annulus not observed by us is applied. The radial density profiles (RDPs) thus obtained for proper motion cluster members and different magnitude intervals of MS and all stars are shown in Fig. 4. The error bars are derived assuming that the number of stars in a zone follows Poisson statistics. All curves show almost the similar behaviour. We find a core radius =185 $^{\prime\prime}$ and cluster radius =1000 $^{\prime\prime}$ for NGC 2099 which match well with the values derived by Nilakshi et al. (2002). However, the value of $10\hbox{$^\prime$ }$ determined by White (1933) as a cluster radius is less than the present cluster radius but larger than the core radius. Based on the structure of $\rho(r)$, we divide the cluster region into three parts (i) core (radius = 185 $^{\prime\prime}$), (ii) corona 1 ( $185\hbox{$^{\prime\prime}$ }< \rm radius \leq 480\hbox{$^{\prime\prime}$ }$) and (iii) corona 2 ( $480\hbox{$^{\prime\prime}$ }< \rm radius \leq 1000\hbox{$^{\prime\prime}$ }$) for further study. Stars lying at radius >1000 $^{\prime\prime}$ from the cluster center are considered field stars.

4 Cluster members and field stars

We determine the density of the field sequence stars (see Fig. 2) in the V, (V-I) digrams as a function of brightness after applying the correction for data incompleteness for both cluster and field regions and list them in the lower part of the Table 7. This indicates that the distribution of the field stars around the cluster is uniform and it can be used for reliable statistical cluster membership determination. Using this field star density, the members in the core, corona 1 and 2 regions of the cluster are found to be 23, 46 and 31% respectively. Thus a large fraction (>75%) of members are located in the coronal region of the cluster. Considering the importance of these members for the studies like cluster MF, we use both the kinematical and photometric data, described below, for separating the cluster members from the field stars.

4.1 Proper motion and radial velocity data

The frequency distribution of the probabilty (p) of proper motion cluster membership determined by Zhao et al. (1985) for individual stars shows that there are two groups of stars separated clearly from each other. One group peaks around a low value of p while other around a high value of p. A total of 418 stars having $p \geq 50$% are considered as cluster members. Of these, ten stars found to be non-member on the basis of radial velocity measurements by Mermilliod et al. (1996) are excluded. In the remaining, BVI CCD observations exist for 322 stars. For another 21 stars photoelectric UBV data are present. As these stars are very important for the stellar evolutionary study, we include them in our further study by transferring various observations on the present BV photometric system using the results of photometric comparisons carried out in Sect. 2.2. However, the photographic BV measurements available for the remaining 65 proper motion cluster members are excluded, as they have large errors.

Van Zeipel & Lindgren (1921) star 9, the brightest in the cluster, with V = 9.208, (B-V) = 1.626 and (U-B) = 1.350, is located in the cluster center. Its cluster membership has been debated in the past. Based on its spectral types, F8 assigned by Lindblad (1954) and M1 by Blanco & Nassan (1957), West (1967) considered it as a field star. However, Upgren (1966) classified the star as a binary of spectral type A5V + K0III. Proper motion data obtained by Upgren (1966) indicates a high value of p for the star. Radial velocity measurements by Mermilliod et al. (1996) also confirm its cluster membership. We have therefore considered this star as a cluster member.

4.2 Photometric membership

Stars not falling on the cluster sequence are classified as non-members by the photometric criterion, as the probability of their cluster membership is small. We therefore draw the boundaries around the MS in the V, (B-V) and V, (V-I) diagrams (see Fig. 2) taking into account brightening due to unresolved physical/optical binary stars and scatter due to photometric errors and stellar peculiarities etc. A star is considered as a probable cluster member if it lies within the envelopes around the MS of both CMDs. Such stars are identified in Table 4. The amount of field-star contamination still present in the sample is quantified below.

4.3 Field-star contamination

Frequency distribution of stars in different parts of the V, (V-I) diagram in the cluster and field regions normalized for the difference in their areas is listed in the upper part of Table 7. The number of MS stars in the cluster region is generally greater than that in the adjacent field region and that the differences are statistically significant. However, the differences in the numbers of stars located blueward and redward of the MS in the two regions are generally not statistically significant.
 

 
Table 7: The frequency distribution of stars in the V, (V-I) diagrams of NGC 2099 and field regions are compared. The number of stars in cluster and field regions are normalised to the cluster area. $N_{\rm BC}$, $N_{\rm MC}$ and $N_{\rm RC}$ denote number of stars in the cluster region located blueward, near and redward of MS respectively. The corresponding numbers for the field region are $N_{\rm BF}$, $N_{\rm MF}$ and $N_{\rm RF}$ respectively. The star density in three subregions of NGC 2099 and field region under the field sequence envelope shown in Fig. 2 are also listed.
V $N_{\rm BC}$ $N_{\rm BF}$ $N_{\rm MC}$ $N_{\rm MF}$ $N_{\rm RC}$ $N_{\rm RF}$
12-13 3 11 139 0 34 5
13-14 28 21 192 21 78 63
14-15 41 53 233 95 96 84
15-16 121 116 381 185 97 121
16-17 400 380 456 227 107 111
17-18 887 923 407 179 114 95
18-19 1272 1276 332 200 118 121
19-20 1630 1856 312 158 157 127
20-21 1779 1951 423 279 160 142

  Density of field stars/arcmin2
V Core Corona 1 Corona 2 Field region
16-17 $0.42\pm0.12$ $0.39\pm0.05$ $0.35\pm0.03$ $0.33\pm0.05$
17-18 $1.28\pm0.21$ $1.06\pm0.08$ $0.98\pm0.05$ $0.96\pm0.08$
18-19 $1.00\pm0.18$ $1.52\pm0.09$ $1.49\pm0.06$ $1.35\pm0.09$
19-20 $1.96\pm0.26$ $1.91\pm0.11$ $1.92\pm0.06$ $2.01\pm0.11$


5 Cluster parameters

In order to define the morphological features of the cluster in CMDs accurately and also for reliable determination of cluster parameters, stars located in the central region (radius $\leq$480 $^{\prime\prime}$) of the cluster are considered in the following subsections, as it enhances the ratio of cluster to field stars in the sample.

5.1 Morphological features in the CMDs

The V, (B-V) and V, (V-I) diagrams for the cluster members are plotted in Fig. 5. As expected, cluster sequences are better defined in comparison with the photographic CMDs (see West 1967; Mermilliod et al. 1996). The CMDs show morphologies typical of intermediate age open star clusters. Evolutionary effects like the presence of a red giant branch and MS turn-off point are clearly visible in the upper part of the cluster MS. In CMDs, about 25 proper motion cluster members are located well away from the cluster sequence. The possibility that they are field stars cannot be ruled out as the median p value of 343 proper motion cluster members is 92%. This indicates that about 27 field stars can exist in the sample. However, precise kinematical data are required for confirmation.

Both cluster MS and red giant clumps are well defined in both CMDs. The BVI CCD measurements of most of the bright red giants could not be obtained as they are saturated even on our shortest exposures. However, we have used their available photoelectric values from the database. The number of red giants present in the V, (V-I) diagram are therefore fewer in comparison to the V, (B-V) diagram. However, the cluster red giant branch is well defined by proper motion members. Study of these stars provides valuable information to understand the advanced stages of stellar evolution in stars of masses 1 to 3 $M_{\odot}$. It is therefore essential to study them using high resolution spectroscopic measurements. A well-populated cluster MS down to V = 21 mag is clearly seen for the first time. The stars seem to be distributed uniformly along the MS. In both CMDs, a proper motion member (van Zeipel & Lindgren 1921, star 180) of spectral type A0 and V = 10.70, (U-B) = -0.22, (B-V) = 0.12 and (V-I) = 0.28 mag is brighter as well as bluer than the MS turn-off point, indicating that it can be a blue straggler. It lies just 2 $.\mkern-4mu^\prime$8 away from the cluster center and has been classified as a blue straggler in the cluster database. Its further photometric and spectroscopic studies can help in understanding the stellar evolutionary status of the blue stragglers.

5.2 Fitting of isochrones to the CMDs

For the determination of cluster parameters, we fit the theoretical stellar evolutionary isochrones given by Girardi et al. (2000) for (Z=0.008 and Z=0.02) in the CMDs, as the metallicity value for the cluster is not known spectroscopically and slightly less than solar metallicity has been indicated by Mermilliod et al. (1996) from the colours of red giants. We fit the isochrones by eye to the MS turn-off point and red giant clumps in both the V, (B-V) and V, (V-I) diagrams for the same age and distance. We found that isochrones of Z = 0.008 fit better rather than those of solar metallicity and yield values of colour excesses as E(B-V) = 0.30 mag and E(V-I) = 0.43 mag. For the study of interstellar extinction in the direction of the cluster, we also use spectral types available for 120 proper motion members in the cluster database and the solar metallicity calibration given by Schmidt-Kaler (1982). A large fraction (over 80%) of them are A type MS stars. Most of the remaining members are F and G red giants. To calculate E(U-B), E(B-V) and E(V-I) values, we use BVI CCD/photoelectric data along with the photoelectric/photographic U data and Walker's (1985) calibration between (B-V)0 and (V-I)0. The mean values derived in this way are $E(B-V) = 0.27\pm0.04$ mag, $\frac{E(U-B)} {E(B-V)} = 1.05\pm0.3$ and $\frac {E(V-I)}{E(B-V)} = 1.5\pm0.2$. The values of colour excess ratios seem to be not too different from the corresponding normal values of 0.72 and 1.3 (cf. Mathis 1990) indicating that the law of interstellar extinction in the direction of the cluster is normal. A study of spatial variation of E(B-V) indicates that the interstellar extinction across the cluster face is uniform. Considering the non-solar metallicity of the cluster, we adopt the value of $E(B-V) = 0.30\pm0.04$ mag for NGC 2099. This value agrees within errors with the earlier determinations (see Table 1).

The best fit isochrone (see Fig. 5) gives log(age) = 8.6 (400 Myr) and apparent distance modulus $(V-M_v) = 11.6\pm 0.15$ mag. The uncertainty in the value is estimated from the errors in total to selective absorption ratio $R [\equiv \frac{A_v}{E(B-V)}], E(B-V)$ and in fitting the ZAMS. The distance modulus yields a distance of $1360\pm 100$ pc to NGC 2099 by adopting a normal value of R = 3.1. The present value should be considered reliable because the theoretical isochrones have been fit over a wide range ($\sim$7 mag) of the cluster sequence. It agrees well with earlier determinations by Mermilliod et al. (1996) and West (1967). The value is also consistent with the cluster parallax of $1.19\pm2.18$ milliarcsec determined from the Hipparcos catalogue by Baumgardt et al. (2000) based on only one star. Present age determination of the cluster is in very good agreement with the value obtained by Mermilliod et al. (1996) but is older than the 220 Myr age estimated by West (1967). The relatively older but similar ages determined by us and by Mermilliod et al. (1996) are a result of using theoretical isochrones which include the effects of mass loss and convective core overshooting.

  \begin{figure} \par\includegraphics[angle=-90,width=15cm,clip]{ms1673f5.eps}\end{figure} Figure 5: The V, (B-V) and V, (V-I) diagrams for the kinematic ($\times $) and photometric ($\bullet $) members of the cluster NGC 2099. The kinematic members with photoelectric BV data taken from the literature are shown by open circles. Theoretical isochrones by Girardi et al. (2000) for age = 400 Myr and Z = 0.008 metallicity fitted to the turn-off point and the red giants for the marked values of apparent distance modulus and colour excess are shown. The dotted curve shows the extent that binaries of equal mass can brighten the isochrones. The fitting of the dotted curve indicates that most probably, scatter in the cluster MS is caused by the presence of unresolved physical/optical binaries.
Open with DEXTER


 

 
Table 8: The MFs of different regions of the cluster NGC 2099. The number of probable cluster members (Ni) in a magnitude bin have been obtained after correcting for both data incompleteness and field star contamination. The values of MF slopes are given in the last row. The Salpeter (1955) MF slope on this scale is -1.35.

Range		 Mass Mean Core Corona 1 Corona 2 Whole cluster
V mag ($M_{\odot}$) $\log(M/\mbox{$M_{\odot}$ })$ Ni $ \log \phi$ Ni $ \log \phi$ Ni $ \log \phi$ Ni $ \log \phi$
12-13 2.48-2.00 0.350 56.32 2.780 42.00 2.653 35.00 2.574 133.32 3.154
13-14 2.00-1.58 0.253 62.46 2.785 79.65 2.891 39.87 2.590 181.98 3.250
14-15 1.58-1.28 0.155 41.43 2.656 75.44 2.916 33.41 2.563 150.28 3.216
15-16 1.28-1.08 0.072 37.08 2.701 101.97 3.140 64.85 2.944 203.90 3.441
16-17 1.08-0.90 -0.004 28.26 2.553 95.28 3.080 101.60 3.108 225.14 3.454
17-18 0.90-0.77 -0.078 38.94 2.759 96.04 3.152 94.85 3.146 229.83 3.530
18-19 0.77-0.68 -0.140 27.77 2.711 71.48 3.122 63.34 3.021 155.89 3.461
19-20 0.68-0.60 -0.194 22.34 2.614 86.50 3.202 74.61 3.138 183.45 3.528
MF slope $0.22\pm0.15$ $-0.89\pm0.16$ $-1.24\pm0.25$ $-0.67\pm0.12$


5.3 Intrinsic colour width of the cluster MS

The cluster has a broad but well-defined MS in a magnitude range of $12 \leq V \leq 20$. To quantify broadening, the observed dispersion ($\sigma_0$) present in Fig. 5 is determined as a function of brightness by binning MS cluster members in 1 mag intervals of V. Although, the total photometric error present in our measurements is at least a combination of (a) the measuring error (internal error), (b) the intrinsic error involved in the standard stars used for calibration, and (c) the uncertainties in the transformations to the standard system; the scatter, $\sigma_{\rm E}$, expected in (B-V) and (V-I) at any given V, will arise purely from (a) which is listed in Table 3 as a function of brightness. Assuming a Gaussian distribution for $\sigma _{O}$ and $\sigma _{E}$, intrinsic widths $\sigma _I$ of the MS in (B-V) and (V-I) are estimated as $\sigma _{\rm I}^{2} = \sigma _{\rm O}^{2} - \sigma _{\rm E}^{2}$. It is observed that the intrinsic colour dispersion in cluster MS is $\sim$0.06 mag in both (B-V) and (V-I) colours and is also independent of brightness. As the extinction is uniform across the cluster face and the bulk of field stars are well separated from the cluster stars, we consider the presence of unresolved binaries, intrinsic variables and peculiar stars etc. in CMDs responsible for the intrinsic scatter in the MS, though it is not possible from this study to assess their relative contributions to such a spread. Radial velocity measurements by Mermilliod et al. (1996) indicate about 30% binaries in the cluster. The isochorone fitting shown in Fig. 5 also indicates that most probably the presence of physical/optical binaries is the main factor causing MS broadening in the cluster NGC 2099.

   
6 Luminosity function and mass function


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms1673f6.eps}\end{figure} Figure 6: A plot of the mass function for the entire cluster region i.e., $r\leq 1000\hbox {$^{\prime \prime }$ }$ (uppermost panel). Other three panels show the mass functions in three subregions of the cluster. The bars represent $1/\sqrt {N}$ Poisson errors.
Open with DEXTER

As we know that one of the fundamental and most important properties that provides a link between the easily-observable population of luminous stars in a stellar system and the fainter, but dynamically more important low mass stars is the MF. For NGC 2099, the MF can be obtained reliably because our deep observations cover coronal regions of the cluster also where presence of low mass stars is expected. The first step in MF determination is finding the luminosity function (LF) from the observed CMD corrected for both data incompleteness given in Table 6 and field star contamination listed in Table 7 using the following relation for determining number of cluster members (Ni) in a cluster region: $N_i=\frac{N_0}{CFBC}-NF$; where N0 and NF are the number of observed stars in the cluster and field regions respectively and CFBC is the completeness factor for the considered MS brightness in the V, (V-I) diagram. We prefer this diagram over other observed CMD, as it is deeper. Following the discussions by Sagar & Richtler (1991), Banks et al. (1995) and Sagar & Griffiths (1998) on the procedures used for the determination of the CF value in a CMD at a given brightness level, the minimum of CF values in V and I is taken as CFBC. To convert true LF into MF, the cluster reddening, metallicity and age along with the appropriate theoretical stellar evolutionary model are taken from the present work. Uncertainties in these parameters and in data incompleteness and field star contamination correction affect the slope of MF (Sagar 2000, 2001). We plot the MF in Fig. 6. For different cluster regions, the MFs and their slope are given in Table 8. The slope of the whole cluster region ( $r=1000\hbox{$^{\prime\prime}$ }$) is $-0.67\pm0.12$, which does not match with the Salpeter (1955) value, rather, it shows a flat slope. On the other hand, West (1967) states that the cluster MS LF agrees with the Salpeter LF up to Mv = 6 mag. This seems to be due to not accounting for the data incompleteness and field star contamination by West (1967), as the value of the cluster MF slope derived from the present data without applying these corrections turns out to be $-1.14\pm0.19$. This, in agreement with our earlier findings (cf. Sagar & Richtler 1991; Sagar & Griffiths 1998), again shows the importance of data incompleteness and field star contamination corrections in the determination of cluster MF. As it is an intermediate age (400 Myr) cluster, the flatness of the MF's slope is not a surprise and it may be due to dynamical evolution rather than the intrinsic difference in the initial MF (Sagar 2000, 2001). However, from Fig. 6 and Table 8, we notice that the slope becomes steeper as we move from core to corona 1 and corona 2.

7 Dynamical state of the cluster

The spatial stellar mass distribution changes as a cluster evolves dynamically if the cluster has a uniform spatial stellar mass distribution at the time of formation. As a consequence, massive stars concentrated towards the cluster center and low-mass stars attain a high random velocity and move away towards the outer region of the cluster. Both theory and simulations show that significant mass segregation among heaviest stars in the cluster core occurs in the local relaxation time, but affecting a large fraction of the mass of the cluster requires a time comparable to the average relaxation time averaged over the inner half of the mass (cf. Inagaki & Saslaw 1985; Chernoff & Weinberg 1990; Meylan & Heggie 1997). The dynamical relaxation time, $T_{\rm e}$, is the time in which the individual stars exchange energies and their velocity distribution approaches a Maxwellian equilibrium. It is given by Spitzer & Hart (1971) as

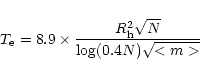
\begin{displaymath}T_{\rm e} = 8.9\times \frac{R^2_{\rm h} \sqrt{N}} {\log(0.4 N) \sqrt{<m>} } \end{displaymath}

where N is the number of cluster members, $R_{\rm h}$ is the radius containing half of the cluster mass and <m> is the average mass of the cluster stars. To determine $T_{\rm e}$, we estimate the total number of cluster stars in the mass range $2.48\ge M/\mbox{$M_{\odot}$ }\ge$ 0.6 as 1475 which yields a total cluster mass of $\sim$ $1750~\mbox{$M_{\odot}$ }$. The value of 531 $M_{\odot}$ indicated by Bruch & Sanders (1983) as the total cluster mass is thus underestimated at least by a factor of 3. For the half-mass radius, we used half of the cluster extent i.e., $R_{\rm h}$ = 3.1 pc due to inability to estimate $R_{\rm h}$ from the present data. Using these numbers $T_{\rm e}$ comes out to be $\sim$70 Myr. However, it can be remarked that the data considered here is limited up to a certain brightness. Inclusion of cluster members fainter than the limiting V magnitude will decrease the value of <m>and increase the value of N. This will result in higher values of $T_{\rm e}$. Hence the value $T_{\rm e} = 70$ Myr may be considered as the lower limit. As $T_{\rm e}$is significantly less than the age of cluster, we conclude that the cluster is dynamically evolved and consequently, we expect concentration of higher mass stars towards the cluster center. The spatial distribution of MS and evolved stars studied below, in fact, provides support for this.

7.1 Radial distribution of MS stars

To study the radial distribution of MS stars in NGC 2099, we divide the MS stars into three mass groups ( $2.48 > M/\mbox{$M_{\odot}$ }\ge 1.28; 1.28 > M/\mbox{$M_{\odot}$ }\ge 0.77$and $ 0.77 > M/\mbox{$M_{\odot}$ }\ge 0.60$). The cumulative radial distribution of cluster members in these mass bins is outlined in Fig. 7. This shows that massive stars tend to lie near the cluster center. The Kolomogorov-Smirnov test also substantiates our conclusion in the sense that the cumulative distribution of the most massive stars ( $2.48 > M/\mbox{$M_{\odot}$ }\ge 1.28$) is different at the confidence level better than 99% from the cumulative distribution of relatively low mass stars ( $ 0.77 > M/\mbox{$M_{\odot}$ }\ge 0.60$).

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms1673f7.eps}\end{figure} Figure 7: Cumulative distribution function for different MS mass intervals in NGC 2099.
Open with DEXTER

7.2 Radial distribution of evolved stars

The stars located in the 9 < V < 12 and 0.4 < (B-V) < 1.7 part of the CMD (see Fig. 5) have been considered as evolved stars and mostly are red giants, as they fall on the red giant branch of the theoretical isochrone of Girardi et al. (2000). The spatial distribution of these stars is shown in Fig. 8. It can be seen that a large number of them accumulate in the core of the cluster, although they have also extended in corona 1. In corona 2 only a negligible fraction of them are present. This may be due to dynamical state of the cluster.
  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms1673f8.eps}\end{figure} Figure 8: Spatial distribution of evolved stars in NGC 2099. The (X,Y) are the CCD pixel co-ordinates of the cluster region as shown in Fig. 1.
Open with DEXTER

8 Discussion and conclusion

The BVI CCD photometric observations are presented for a sample of $\sim$12000 stars in the cluster region and $\sim$2180 stars in the field region up to a limiting magnitude of $V \sim 22$ mag. The data form the basis for a study of spatial structure and radial variation of MF in the cluster region. Field star contaminations are estimated from a region located $\sim$45$^\prime$ away from the cluster center. The data completeness is empirically determined as a function of brightness and stellar crowding. The cluster parameters are determined by fitting the theoretical isochrones given by Girardi et al. (2000) in the V, (B-V) and V, (V-I) diagrams of the cluster. The Main conclusions of the present work are:

1.
The MF of the entire cluster appears to be one of the flattest with a value of $-0.67\pm0.12$ in the mass range 0.6 $< M/\mbox{$M_{\odot}$ }< 2.5 $. The radial velocity measurements by Mermilliod et al. (1996) indicate that the binary frequency in NGC 2099 can be $\sim$30%. The effect of such optical/physical binaries is to flatten the intrinsic MF slope. We use Table 10 of Sagar & Richtler (1991) to evaluate the amount of flattening for 30% of binary contents and derive a value of $\sim$-0.9 for the initial MF slope of NGC 2099. This value moves closer to the Salpeter (1955) value of -1.35, if the extent of the cluster is beyond 1000 $^{\prime\prime}$, as a relatively large number of low-mass cluster members are expected to be located there due to the dynamically relaxed state of the NGC 2099.

2.
The value of the core radius is about 185 $^{\prime\prime}$ while the extent of the cluster is about 5 times larger with a value of $\sim$1000 $^{\prime\prime}$.

3.
A well-defined cluster MS along with a red giant clump is clearly visible in the CMDs. The MS has an intrinsic colour spread of $\sim$0.06 mag over the entire range of observed brightness. As the interstellar extinction is uniform across the cluster face and field stars are not severely contaminating the cluster MS, we consider the presence of optical/physical binaries in the cluster mainly responsible for the intrinsic colour spread in the MS.

4.
The cluster distance estimated from a wide range ($\sim$7 mag) of cluster sequences is $1360\pm 100$ pc. It agrees well with earlier determinations. Fitting of the theoretical isochrones given by Girardi et al. (2000) for Z = 0.008 to the CMDs yield an age of 400 Myr for the cluster and a reddening value of $E(B-V) = 0.30\pm0.04$ mag.

5.
The cluster appears to be dynamically relaxed as the relaxation time (70 Myr) is much shorter than the cluster age (400 Myr). The observed mass segregation in the cluster can therefore be a result of the dynamical evolution of the system.

6.
The distinct separation of cluster MS from the bulk of field stars in the CMDs provides a unique opportunity to confirm the uniformity of distribution of field stars at least up to 45$^\prime$ away from the cluster center.

Acknowledgements
The valuable comments/suggestions provided by the referee Dr. A. Moitinho improved the presentation of the paper significantly. We are grateful to Drs. A. K. Pandey and T. Richtler for useful discussions. The present research has used the WEBDA open cluster database Website at http://obswww.unige.ch/webda/ maintained by Dr. J.-C. Mermilliod.

References

 
Copyright ESO 2001