A&A 381, 290-299 (2002)
DOI: 10.1051/0004-6361:20011495

Vertical structure of sunspots from THEMIS observations

M. T. Eibe^1, - G. Aulanier¹ - M. Faurobert² - P. Mein¹ - J. M. Malherbe¹

1 - DASOP, Observatoire de Paris, Section de Meudon, 92195 Meudon, France
2 - Observatoire de la Côte d'Azur, BP 4229, 06304 Nice Cedex 04, France

Received 22 June 2001 / Accepted 25 October 2001

Abstract
We have analysed two-dimensional spectro-polarimetric data taken with the MSDP observing mode of THEMIS in the NaID₁ line to investigate the height variation of the magnetic field in sunspot umbrae. From the Zeeman-induced circular polarization measured at individual MSDP channels within the line profile, maps of the longitudinal magnetic field have been computed. A method based on Response Functions has been developed to estimate the depth in the atmosphere at which the Zeeman measurements are originated, thus providing the line-of-sight field at different altitudes in the photosphere. The magnetogram corresponding to the deepest level has served as a boundary condition to perform the potential field extrapolation into the corona. We have found that the spatial distribution of vertical field gradient contours predicted from extrapolation is in qualitatively good agreement with that inferred from observations. Quantitatively, however, the longitudinal field gradients obtained with both methods differ about one order of magnitude, being larger for observations. The origin of this discrepancy has been discussed with respect to possible observation biases, as well as to idealizations used for field extrapolation. This is a crucial problem to be addressed in future work, and may have important implications for the physics of how the magnetic field evolves through sunspots and how the flux is distributed in the corona.

Key words: sunspots - Sun: magnetic fields

   
1 Introduction

In the last years great progress has been made in the study of sunspots, mainly in terms of observational information. This is in part due to the recent development of more advanced instrumentation. New solar telescopes provide more accurate spectro-polarimetric data, which constitute the main tool to investigate the physical conditions within the atmosphere of sunspots.

The inference of the atmospheric structure from the observed polarimetric profiles is a complicated problem that requires the inversion of the radiative transfer equation for polarized light. This is further complicated if non-LTE effects must be taken into account as it is the case for lines that are formed in the chromosphere and upper photosphere. A large effort has been made in recent years to develop inversion techniques of Stokes profiles, which allow to obtain an approximation of the model atmosphere where the observed profiles are originated. The strategy adopted by first works consisted in fitting selected parameters by minimization of the square differences between observed and synthetic Stokes profiles. Auer et al. (1977) derived an analytical solution of the radiative transfer equation by using the Milne-Eddington model atmosphere. Skumanich & Lites (1987) extended this method to include the presence of a uniform magnetic field by means of the Rachkovsky solution of the polarized radiative transfer (1962, 1967). This approach assumes that the magnetic field, the velocity and various spectral line parameters are constant along the line of sight. Such simplifications reduce considerably the computing time and allow for fast inversion of a large number of profiles. On the other hand, the estimates of parameters provided by these codes represent averages over the line of sight. The implementation of fast numerical methods to solve the multilevel transfer problem (Carlsson 1986; Rybicki & Hummer 1991, 1992) has given place to more sophisticated inversion methods of Stokes profiles. In the SIR code developed by Ruiz Cobo & del Toro Iniesta (1992) the radiative transfer equation is solved through linearization assuming LTE. As a result, the code provides the variation with depth of several atmospheric parameters simultaneously. An extension of the SIR technique to non-LTE has been recently presented by Socas Navarro et al. (2000). This technique ensures faster inversion of Stokes profiles, mainly because the minimization of the squared differences between observed and synthetic profiles is done by means of so-called Response Functions (hereafter, RF). In a first order approximation, RF represent the sensitivity of the emergent profiles to small perturbations of a given parameter. They were first defined and calculated for spectral line profiles (Mein 1971; Beckers & Milkey 1975; Canfield 1976; Caccin et al. 1977). RF for the Stokes parameters were introduced by Landi Degl'Innocenti & Landi Degl'Innocenti (1977).

A few trial-and-error techniques have also been developed by constraining in different manners the fits of free model parameters to reproduce observations. Keller et al. (1990) used selected observables derived from Stokes V spectra instead of fitting the full profile to derive empirical fluxtube models for the temperature and magnetic field stratification by means of a nonlinear least-squares algorithm. Solanki et al. (1992) used the same least-squares algorithm to find the best model that reproduce the observed I and V full profiles among a discrete set of five fixed models. Recent works based on the inversion of spectro-polarimetric data have revealed a complex structure of the magnetic field (see del Toro Iniesta 2001 for a review). Both the strength and the inclination of the field are found to be maximum in the spot umbra, decreasing progressively outwards through the penumbra. This picture is complicated by the presence of non-zero fields beyond the visible limits of the spot, suggesting that the field extends itself continuously outside the penumbra in the form of canopies (Giovanelli 1980; Giovanelli & Jones 1982; Solanki et al. 1992). In addition, the penumbral field seems to be structured into fine-scale components with different inclination (Degenhardt & Wiehr 1991; Lites et al. 1993).

The variation with depth of the magnetic field has been investigated by several authors and remains one of the most controversial issues. The magnetic field strength is generally seen to decrease with height in the umbra and the inner penumbra whereas in the outer penumbra it increases with height. However, the values obtained by different authors for the vertical gradient of the field differ by an order of magnitude, even for the spot umbra, where the magnetic field is believed to be more uniform (see for example Balthasar et al. 1993, and references therein).

The diagnostic values of the sodium D lines ( $\lambda = 5890$, 5896 Å) for the study of the solar atmosphere has long been recognized (Caccin et al. 1977; Bruls et al. 1992). The relatively lower temperature of sunspots with respect to the adjacent quiet-Sun atmosphere leads to increased neutral sodium densities and, consequently, enhanced NaID lines. In addition, these lines are Zeeman sensitive and, therefore, well suited to investigate the vertical structure of the magnetic field.

In this paper we concentrate on the depth dependence of the magnetic field in the sunspot umbra. In Sect. 2 we present the spectro-polarimetric observations from the MSDP instrument mounted on the THEMIS telescope which we use throughout the paper, and we briefly describe how the longitudinal field was derived from the Stokes parameters (I, V). In Sect. 3 we explain the method that we have developed to estimate the different height levels from which light is emitted in different spectral domains of the observed Zeeman polarization of the NaID₁ line. In Sect. 4, by applying this method to THEMIS/MSDP observations of a sunspot region, we have quantified the vertical gradient of the field. In Sect. 5, the value obtained for the longitudinal field at the low photosphere was used as a boundary condition to calculate the extrapolation of the field at larger heights in the potential approximation. Results obtained with the two methods are compared and discussed in Sect. 6. Finally, we summarize our results in Sect. 7.

   
2 Spectro-polarimetric observations with THEMIS/MSDP

2.1 Data acquisition

Spectro-polarimetric observations of an active region near disk centre (E18 N21) in the NaID₁ line were carried out on May 9, 2000 with the THEMIS telescope, operating in the MSDP. The Stokes parameters $I \pm V$ of the NaID₁ line were simultaneously recorded in 16 MSDP channels. Further details about the specific instrumental set up of THEMIS in the MSDP observing mode can be found in Mein (2002).

2.2 Line-of-sight magnetic field measurements

The line-of-sight magnetic field may be estimated from the observed I and V Stokes profiles of NaID₁ by using the centre-of-gravity method (Semel 1967), which is based on the Zeeman effect. According to this technique, the relative shift, , between the respective centres of (I + V) and (I - V) is directly related to the longitudinal component of the field, B_||:

$$\displaystyle\frac{\Delta\lambda_{B}}{2} = 4.67 \times 10^{-13} g_{\rm eff} \lambda_{\rm c}^{2} B_{\vert\vert},$$ (1)

for wavelengths given in Å. In this expression $g_{\rm eff}$ is the effective Landé factor and $\lambda_{\rm c}$ the line centre wavelength.

Intensity and computed longitudinal magnetic field maps are shown in Fig. 1.

	Figure 1: THEMIS/DPSM intensity and longitudinal magnetic field maps in Na D1 at 80 and 240 mÅ from line centre. The field of view is $138^{\prime \prime } \times 121^{\prime \prime }$, i.e. 102 Mm $\times$ 89 Mm. The data has been collected on $924 \times 806$ pixels.
Open with DEXTER

It is noteworthy that the strong field regions (in particular in the three leading sunspots and in the trailing pores) are more horizontally extended in the map at 80 mÅ than in the map at 240 mÅ. This qualitatively suggests that in most areas, the flux tubes expand from lower to higher altitudes, filling more space.

At this stage, it is necessary to estimate the physical height difference between both maps, so that the vertical field gradient can be obtained. In the following, we describe the method developed to this aim.

   
3 Description of the RF method

$\Delta \lambda_{B}$ for a given position in the profile is the result of the contribution of several atmospheric layers which are involved in the formation of the line. We use RF to evaluate the sensitivity of the line to the Zeeman effect caused by the magnetic field at different heights in the atmosphere.

We consider only the effect of a longitudinal magnetic field. The transversal component of the field would manifest itself through the Stokes parameters Q and U but it may be neglected if $\Delta \lambda_{B}$is small by comparison to the Doppler width of the original line profile, i.e. in the weak-field approximation, which is often valid for strong lines as D₁. A simple test was done by allowing for different inclinations of the field in order to confirm that the resulting $\Delta \lambda_{B}$ is independent of both parameters, Q and U.

The longitudinal magnetic field is treated as a small perturbation in the starting non-magnetized model atmosphere. We have checked that if instead of a zero magnetic field we assume a constant non-zero field in the starting model atmospheres, the final results are not significantly affected.

Under these assumptions the magnetic shift $\Delta \lambda_{B}$ would equal the Doppler shift caused by a macroscopic velocity , where c is the velocity of light. RF of the line to the magnetic field, RF_B, should then be equivalent to RF for velocity, RF_v. Through a linearization analysis of the radiative transfer equation, $\Delta \lambda_{B}$ may be approximated as:

  $$\begin{eqnarray*}\Delta \lambda_{B} &=& \displaystyle \int_{0}^{+\infty} RF_{B}(... ...yle\int_{0}^{+\infty} RF_{v}(\lambda, s)\,\Delta v(s)\,{\rm d}s. \end{eqnarray*}$$

Here s is the depth variable, which in our calculations corresponds to the logarithm of column mass, i.e. .

In order to calculate RF_v, one must be able to reproduce the expected for a particular model of perturbations, $\Delta v(s)$. The numerical calculation of the D₁ line profiles for given model atmospheres is done by using the version 2.2 of the non-LTE radiative transfer code MULTI (Carlsson 1986). As a reference model atmosphere (i.e. in the absence of velocity perturbations) we use the umbral core model M of Maltby et al. (1986), sampled from $\log m = 0.9$ to -2.0 with a total number of 80 grid points. The procedure followed to simulate the effect of velocity perturbations in the reference atmosphere is analogous to that used before by Eibe et al. (2001), taking the quiet-Sun model atmosphere (Vernazza et al. 1981) as reference atmosphere. The amplitude of the macroscopic velocity perturbations considered here is v = 0.02 kms^-1, corresponding to B = 20 G in Eq. (1). As in Eibe et al. (2001), the models of velocity perturbations, v_i(s), are defined as:

$$v_{i}(s) = \left\{ \begin{array}{ll} 0.02~{\rm km\,s}^{-1} &... ...\\ 0 & \mbox{if $s_{i}>s \geq s_{N}$ ,} \end{array} \right.$$

where s₀ and s_N are, respectively, the deepest and highest levels in the reference atmosphere. The limit s_i varies progressively from s₀ to s_N. The Zeeman shifts, , as measured in the synthetic profiles computed for each model v_i(s), are then used to calculate RF_v (i.e. RF_B) by means of the following expression:

$$RF_{v}(\lambda,s_{i}) = \displaystyle \frac{(\Delta \lambda_{... ...elta \lambda_{B})_{i-1}}{\displaystyle v (s_{i}-s_{i-1})}\cdot$$ (2)

The barycenters of the calculated RF_v give an indication of the height at which the measured B is mainly originated. Under the assumption that the vertical gradient of B is constant, the barycenters provide the depth at which $B = B_{\rm obs}$ for each of the observed wavelengths in the line profile. Barycenters, $G_{\lambda}$, were calculated as:

$$G_{\lambda}=\displaystyle{\frac{\displaystyle \int_{0}^{+\inf... ...splaystyle \int_{0}^{+\infty} RF(\lambda, s)\,{\rm d}s}} \cdot$$ (3)

   
4 Analysis of the MSDP spectrograms with RF

4.1 RF calculation

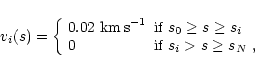
The radiative transfer calculations yield synthetic profiles for infinite spectral resolution. In order to simulate the observations we must account for the finite spectral resolution of the MSDP instrument. The main factors determining the effective spectral resolution of the spectrograph are the local bandpass (40 mÅ) and the interpolation which needs to be done to reconstruct the profiles from the 16 positions (MSDP channels) recorded in the observations. We constructed a smoothing filter that mimics both effects and we applied it to the synthetic profiles prior to the calculation of RF with Eq. (2).

The calculated RF_B for the observed wavelengths are shown in Fig. 2.

	Figure 2: RFB of D1 for the observed wavelengths.
Open with DEXTER

RF_B for the line wings differ considerably from those obtained near the core of the line. On the one hand, they cover a smaller range of heights, showing a well-defined peak in depth. On the other hand, they are seen to shift towards deeper layers.

The choice of the model atmosphere may be crucial for the reliability of this method. Unfortunately there is a lack of sunspot atmospheric models in the literature. In particular, a good knowledge of the upper photosphere and low chromosphere for our calculations is required since it is at these layers where the D₁ line is formed. We have considered the empirical models of sunspot umbrae obtained recently by Collados et al. (1994) but since they are limited to the photosphere, the resulting RF of D₁ are incomplete for line core positions. New models as the one obtained by Socas-Navarro et al. (2000) for the sunspot chromosphere will also be considered in future work.

We have carried out the same calculations for the VAL C mean quiet-sun model atmosphere (Vernazza et al. 1981). Comparison of barycenters obtained for both Maltby M and VAL C model for the observed wavelengths is shown in Fig. 3 and Table 1.

	Figure 3: Barycenters (Eq. (3)) obtained for VAL C model (crosses) and Maltby M umbra model (black filled circles) at the observed wavelengths.
Open with DEXTER

 

 

Table 1: RF_v barycenters in $\log m$ and height (km) coordinates for Maltby M and VAL C models at the observed wavelengths.

$\Delta\lambda$ (Å)	Maltby M		VAL C
	$\log m$	height	$\log m$	height
0.080	-1.07	481	-1.08	431
0.160	-0.82	408	-0.62	332
0.240	-0.38	280	0.00	183

The height difference between extreme barycenters (i.e. at $\Delta\lambda = 80$ and 240 mÅ away from line centre) is 200 km for the Maltby M model and 250 km for the VAL C model.

   
4.2 Vertical field gradient derived with RF

Although the reference model atmosphere is strictly valid for the dark umbra, the similarity of results for both Maltby M and VAL C models suggests that we may use an average of the corresponding barycenter heights for both models to obtain a qualitative view of the field gradient at all points in the entire field of view. This is also justified because we are dealing with relatively small spots and the observed magnetic field strength (with no stray-light correction) in the region is not larger than 1000 G. A map of the line-of-sight magnetic field in the observed field of view is shown in Fig. 1.

Figure 4 shows the D₁ intensity map of the area at 240 mÅ from line centre.

	Figure 4: Intensity map of the observed spot region. The gradient of B|| along the line of sight ($\Delta B$) isocontours indicate the spatial distribution of regions of increasing (pink) and decreasing (blue) longitudinal field as derived from observations of Na D1 at 80 and 240 mÅ from line centre. The marks A, B and C correspond to the dimmest pixel for each of the leading sunspots.
Open with DEXTER

Superimposed on the image are the contours of the longitudinal field strength difference, $\Delta B$, between the image taken at 80 and 240 mÅ with respect to line centre. Contours of increasing and decreasing field with height are plotted in pink and blue, respectively. The magnetic field is seen to decrease with height in the spot umbrae. An estimate of the field gradient along the line of sight may be obtained by using the barycenter heights calculated for the Maltby M umbra model (Table 1). In what follows, we will use L^-1to refer to the absolute gradient of the longitudinal field along the line of sight, l, as relative to the longitudinal field strength value in the low photosphere (measured at 80 mÅ away from line centre), B_||(l=0), i.e., In order to quantify the decrease of the field in the umbra, L^-1 has been obtained at the centre of three different spots. The spot centres, defined as the location of minimum brightness, are labeled as A, B and C in Figs. 4 and 5. Table 2 shows the individual values of L^-1. The average L^-1 over the three spot centres is around 1 $\times$ 10^-3 km^-1. It must be borne in mind that, due to projection effects, a given point in the field of view observed at different wavelengths (i.e. geometrical heights) does not correspond strictly to the same point in heliographic coordinates. This introduces a bias in the derived gradient which is small by comparison to errors from limited spatial resolution and height uncertainties.

In order to quantify the error in the determination of the field gradient with the RF method, we have carried out some numerical tests with known models of perturbations. We considered velocity perturbations that vary as linear functions of height with constant vertical gradient. Four different models were used for gradients in the range between 0.05 and 0.3 s^-1. The corresponding vertical gradient of the longitudinal magnetic field in the weak-field approximation (see Sect. 3) would vary between -0.2 and -1 Gkm^-1.

	Figure 5: As Fig. 4 but for the longitudinal field derived from extrapolation of the photospheric field in the potential approximation. The gradient of B|| along the line of sight $\Delta B$ is calculated between the same height level as covered by the observations. The field lines originating from A, B and C are drawn in dark blue.
Open with DEXTER

 

 

Table 2: Comparison of the field gradient along the line-of-sight, (L^-1 (as defined in Sect. 4.2), obtained with RF and with the potential extrapolation.

Sunspot	L-1 (km-1)		ratio
	RF	extrapol	RF/extrapol
A	$1.1 \times 10^{-3}$	$1.9 \times 10^{-5}$	58.0
B	$3.9 \times 10^{-4}$	$1.1 \times 10^{-4}$	3.5
C	$1.2 \times 10^{-3}$	$1.4 \times 10^{-4}$	8.6

Synthetic Na D₁ profiles were obtained for such models by using the MULTI code as described in Sect. 3. The errors in the relative vertical field gradient that was recovered from the computed profiles with the RF method are no larger than 8%.

   
5 Magnetic field extrapolation

   
5.1 Description of the method

Using the force-free extrapolation code developed by Démoulin et al. (1997), the magnetic field was extrapolated in the potential field approximation: $\vec{\nabla} \times \vec{B} = \vec{0}$. A discussion of the choice for this approximation is provided in Sect. 6.1. The lower boundary condition was taken as the longitudinal magnetogram B_|| observed in the wing (240 mÅ) of the Na D₁ line.

The code uses a cartesian geometry, and it calculates the field with Fourier harmonics, so the numerical box is periodic in (x,y), and the amplitude of the field tends to zero at infinite altitude z. The boundary condition at (x,y,z=0) was defined as follows: in order to reduce the periodicity effects, the observed longitudinal magnetogram (located at E18N21) was placed in a large region ( $Lx = Ly = 200^{\prime\prime}$) where B_z=0, taking into account the projection effects, and B_x,y,z(x,y,z=0) was calculated such as to satisfy the potential field condition and to maintain the observed longitudinal field.

The extrapolation was performed from B_x,y,z(x,y, z = 0) on a numerical mesh of 512² uniformly distributed points in (x,y), and 30 non-uniformly distributed points in z for $0 < z < 50\,000$ km, so with  km and  km.

5.2 Vertical fields gradients derived with extrapolation

Taking properly into account the projection effects, the variation of the longitudinal (as well as the vertical) component of the magnetic field (as well as its norm) along the line-of-sight (as well as along the heliographic altitude) can be calculated from the results of the extrapolation. The spatial distribution of regions of increasing/decreasing longitudinal field is shown in Fig. 5, for a distance above the z=0 plane equal to 220 km along the line-of-sight, which corresponds to 195 km along the vertical height.

We found several regions where . Analysis of the calculated fields permits to show that these regions are systematically located on the edges of strong vertical field regions, where the horizontal gradient of $\vec{B}$ is high, and where B_z is low compared to the neighbouring strong fields. More specifically, these correspond (i) to the edge of sunspots, pores and plages and (ii) to the boundary between two sunspots. Plots of the vertical gradient of the vertical field component basically show the same areas. These regions of increasing field with height are readily explained by the expansion of the flux tubes: the strong fields expand horizontally for z > 0, and even though their magnitude decreases with height, they remain much stronger than the underlying weak field regions, up to the top of the chromosphere ( $z \simeq 2000$ km). So above weak field regions, the vertical field gradient is positive. This only holds at low heights, as long as the magnitude of the flux tube does not fall below the one of the background at z=0. This property is maintained when the line of sight is not vertical, although the distribution of the regions of positive gradients are slightly modified.

The relative quantity L^-1 averaged over the same spot centres A, B and C as defined in Sect. 4.2, varies between $2.0 \times 10^{-5}$ and $1.4 \times 10^{-4}$ km^-1, with an average of $1.0 \times 10^{-4}$ km^-1.

5.3 Comparison RF vs. extrapolation

Comparison of Figs. 4 and 5 shows that for the whole field of view, the contours of the field gradient are qualitatively similar. This suggests that the general tendencies of the field expansion with height are the same in RF and extrapolation models. Note in particular the narrow regions of positive field gradient between and on the edges of the sunspots, as well as in the weak field regions. However we get the interesting result that the magnitudes of the gradients obtained with the extrapolation are systematically much weaker than observed and calculated with the RF for the same height difference.

As the RF calculations are most relevant in sunspots umbrae, in the following we emphasize the discussion on these regions. Figure 6 shows the longitudinal field variation with height at A, B and C as obtained directly from observations,

	Figure 6: Field strength relative to its value at the deepest level and for the sunspot centres A, B and C. Results from observations ( $B_{\rm obs}$) are compared to those obtained by extrapolation ( $B_{\rm cal}$) of the photospheric field.
Open with DEXTER

along with that resulting from potential field extrapolation, and the numbers are reported on Table 2.

We find that the rate of decrease of the field with height from the extrapolation is in average one order of magnitude lower than observed and calculated with the RF!

We find a large dispersion in the ratio L^-1(RF)/ L^-1(extrapol), as shown in Table 2, mainly caused by a very high value of this ratio for the spot A. The latter is mainly due to a weaker decrease of the extrapolated B_|| between the two considered heights. A careful look at Fig. 6 shows that in fact, B_|| slightly increases with height between 270 and 350 km, then it decreases for large heights with the same rate as spot B. Analysis of the calculated 3D magnetic field permits to explain this local increase by projection effects, since B_z monotonically decreases with z in A. This effect, apparently not present in the observations, is certainly due to the choice of the observed B_|| as boundary conditions (see Sect. 5.1), instead of assuming that the observed field is vertical, as done in Démoulin et al. (1997). Thus, the derived value of L^-1 for spot A may not be correct. With the extrapolation, the spot A has which is much closer to L^-1 of spot B. If one considers that this value is more significant for A, it substantially reduces the dispersion of our values.

The quantitative disagreement found between the two methods is too large to be explained by uncertainties in the analysis. Indeed, it is hardly possible to imagine that the NaID₁ emission in line core happens more than a few 100's of km above where the emission in the wings is done. Such a discrepancy may have critical consequences in terms of the structuring of the magnetic field in the corona, so it must be understood.

   
6 Discussion

In this section we discuss possible biases which might be brought by the observations themselves, as well as the ones brought by the over-simplification of the model based on a potential extrapolation.

   
6.1 Field-aligned currents and photospheric plasma

In order to investigate the effects of field-aligned currents, we have performed a linear force free field extrapolation, solving $\vec{\nabla} \times \vec{B} = \alpha \vec{B}$ with a value for $\alpha=4.2 \times 10^{-2}$ Mm^-1, which is very close to the resonant value for our periodic box for which $Lx = Ly = 200^{\prime\prime} = 147$ Mm. We have then included very strong field-aligned currents. We have shown that for the small heights considered in our study, the map of the gradient of the longitudinal (as well as vertical) field component was nearly indistinguishable from the one obtained with a potential field model shown in Fig. 5. This is quite natural, since in the linear force free field approximation, the magnetic field is mostly deformed by the electric currents at large heights, of the order of the horizontal size of the photospheric bipole (see Aulanier & Démoulin 1998). Also, we believe that non linear force free fields would not yield to a different result, though this remains to be tested properly.

The force free approximation is highly disputable in dense layers such as the photosphere, where the plasma $\beta$ is of the order of 1. We tested the effect of plasma pressure and gravity in the low atmosphere by performing a magneto-hydrostatic extrapolation (see Aulanier et al. 1998 for the method). This method assumes that relative over-densities for the plasma are present in relatively weaker field regions, as observed. We found that the gradients of the magnetic field were of the same of order than those derived with the potential field, though systematically smaller by 10-20%. This shows that the inclusion of dense plasma in the extrapolation does not lead to a better comparison with RF calculations. On the contrary, the lateral pressure gradients of the plasma lead to a weaker expansion of the field with height. This can simply be understood from the magnetic and plasma pressure balance: in the photosphere the strong lateral pressure gradients of the plasma lead to a lateral confinement of the flux tube. The opposite effect could be achieved if over-densities were present above strong field regions, however those are not observed.

6.2 Effect of stray light

The major source of uncertainty in the observed magnetic field is the presence of stray light, which leads to an underestimation of the field values. In order to evaluate the influence of this effect in the present THEMIS/MSDP observations, we have carried out some tests by representing the stray-light contamination in sunspot centers A, B and C as a fraction of the continuum intensity of the neighbouring quiet Sun.

We found that the ratio between the field values measured at different wavelengths is hardly affected. Therefore, we assume that the stray-light effect can be neglected if relative values of the field are considered instead of absolute measurements, which justifies the use of the quantity L^-1.

6.3 RF calculations and previous results

Although the heights determined through RF are dependent on the reference model, the difference found between the heights obtained for both Maltby M and VAL C models is relatively small. The computed gradients, in particular, do not change significantly if we use the VAL C model instead of the Maltby M model. Also, the gradient values that we obtained with the RF method are in agreement with those obtained in previous works by using photospheric lines of different formation heights (Wittmann 1974; Pahlke & Wiehr 1990; Bruls et al. 1995; Westendorp Plaza et al. 2001). This suggests that either the method we applied is relevant, or it suffers from the same systematic errors than previous works.

Note that our RF results are not in contradiction with the analysis done with photospheric and transition region (TR) lines by Hagyard et al. (1983) which results in lower gradients ( $L^{-1} \sim 1.7 \times 10^{-4}$ km^-1). In this work, the derived gradient has a slope which is an average between the height of the photosphere and of the TR, so that it is possible that at low heights, the slope is much steeper. Interestingly, if one assumes the height of the TR to be at z = 2000 km (right above the chromosphere) the gradient obtained from the potential configuration is in good agreement with the result of Hagyard et al. (1983). Unfortunately, this does not mean that this agreement is maintained in the corona.

It is worth noticing that other studies, based on measurements of the transverse field combined with the condition (Hagyard et al. 1983; Hofmann & Rendtel 1989; Liu et al. 1996), provide relative gradients of the same order as those obtained in Sect. 5 through potential field extrapolation, so nearly 10 times lower than estimated from the analysis with the RF.

6.4 Unresolved issues

The disparity of results published so far may, to some extent, be related to the different methods of analysis used for the gradient determination which can arise at different levels in both observations and extrapolations. In the following, we discuss several unresolved issues which will have to be investigated in the future.

Techniques based on transverse field measurements and/or field extrapolation must adopt some assumptions regarding the field configuration. Transverse field measurements strongly depend on the method used to solve the $180^\circ$ ambiguity, but to our knowledge, no consensus have been reached so far for one good reliable method.

We have shown that potential and linear force free fields are equivalent as far as the photospheric layer is concerned. It is also interesting that the inclusion of the photospheric dense plasma to produce non force free extrapolations not only does not help, but also leads to bigger discrepancies than with the observations. Non linear (non) force free field might give different results, but the latter depend on the observed spatial distribution of $\alpha$, which is itself derived from the transverse fields.

An effect which is not treated in any extrapolations is the dynamics of the photosphere. In particular, Evershed flows diverging from the sunspots may have sufficient kinetic energy to locally bend the field lines towards the photosphere. This could lead to a larger flux tube expansion with height than calculated from potential, linear force free and magneto-hydrostatic extrapolations.

Gradients derived with spectral lines that are sensitive to different depths in the atmosphere represent an average over certain layers. Therefore, the derived gradients may strongly depend on diagnostic properties of the selected lines, as well as on the approximation made in choosing the barycenter of the RF (as we did in this study). More comprehensive models covering wider ranges of heights will be needed in order to extend this work to other spectral lines, as well as to explore the dependence of the calculated gradients on the model atmosphere used as reference.

It is noteworthy that some disagreement is to be expected between gradients obtained for different spots. From the inversion of Stokes I and V profiles, Collados et al. (1994) found that the average field strength gradient between large and small sunspots may be up to an order of magnitude different.

Finally, the conversion of spectro-polarimetric observations into maps of the magnetic field does not necessarily reveal small scale magnetic structures in the vicinity of sunspots. This could be due to an incomplete analysis of small asymmetries in the Stokes profiles (del Toro Iniesta, private communication), or to a lack of emission in strong fields regions because their density is lower (Sánchez Almeida 2000). The existence of such small polarities is justified not only by the theory of flux tube fragmentation in the convection zone (e.g. Emonet & Moreno Insertis 1998), but also by the latest observation of Evershed flows which extend radially from umbrae and which fall back to the photosphere in the penumbrae (del Toro Iniesta et al. 2001). If these small scale magnetic concentrations are numerous and strong enough, if they are close enough to the sunspot umbra and if they have the opposite polarity than the one which dominates in the sunspot, then a non negligible fraction of the sunspot flux may close down to the photosphere in the close vicinity of the sunspot. This effect can substantially decrease the amount of magnetic flux which reaches higher altitudes. As a consequence the field decrease with height could be much higher when derived from any extrapolation method.

   
7 Summary

We have studied the height dependence of the longitudinal magnetic field in sunspot umbrae using THEMIS/MSDP spectro-polarimetric data in the NaID₁ line. By using the NaID₁ line, we have been able to explore a wide range of heights in the entire photosphere and lower chromosphere. As opposed to previous works on this subject, results presented here cover also the temperature minimum region in the photosphere.

We have developed a method based on Response Functions in order to estimate the height levels in the atmosphere at which the magnetic field measurements are originated. By applying this method to the THEMIS/MSDP magnetograms we have estimated the average line-of-sight field gradient in sunspot umbrae. The result, $\sim$- $1 \times 10^{-3}$ km^-1 (relative to the longitudinal field strength observed in the low photosphere), is in agreement with previous measurements made with photospheric lines.

The longitudinal field measured in the wing of the NaID₁ line was used as a boundary condition for the extrapolation of the field into the corona, assuming a potential field. The height variation of the extrapolated field within the entire active region is in qualitative agreement with that observed at corresponding heights in the atmosphere. Areas of increasing longitudinal field are found to be conspicuously located near the boundaries of strong concentrations of the field. This has been interpreted as a result of the expansion of magnetic flux tubes. In quantitative terms, however, the field gradient predicted from extrapolation of the photospheric field in sunspot umbrae is in average one order of magnitude (between 4 and 60, although we have shown the latter value may be unreliable) lower than that calculated with the RF method.

After comparison with previous works, we conclude that the longitudinal field gradient obtained here with the RF of the NaID₁ line is in agreement with what has been found so far by using other photospheric lines. On the other hand, earlier works based on transverse field measurement and the condition have led to much lower gradients, comparable to those obtained here from extrapolation of the potential field.

Several possibilities have been discussed (Sect. 6) in order to understand the disparity between the field gradient values that are derived with different techniques. Some of the explicit assumptions used in the extrapolation have been carefully addressed. Other possibilities raised to explain the large field gradients that are directly observed involve the presence of unresolved field inhomogeneities. Future observations may help to reinforce or invalidate this suggestion.

Finally, given that the extrapolation of the field into the corona is highly conditioned by photospheric field measurements, it is also important in this respect to solve the present controversy related to the evolution of the field through sunspots. Reliable estimation of the magnetic field in the corona is of great importance since the magnetic field cannot be measured in this region, where it is responsible of coronal heating as well as of much of the solar active phenomena.

Acknowledgements

We would like to thank all the people involved in the development of the THEMIS telescope, as well as the technical staff for their support during the observations. We also thank P. Démoulin for discussions. M.T.E. acknowledges financial support from IAC/INSU through a post-doctoral grant. The work of G.A. was funded by the CNES.

References

 

• Athay, C., & Canfield, R. C. 1969, ApJ, 156, 695 NASA ADS  
• Auer, L. H., Heasley, J. N., & House, L. L. 1977, Sol. Phys., 55, 47 In the text NASA ADS  
• Aulanier, G., & Démoulin, P. 1998, A&A, 329, 1125 In the text NASA ADS  
• Aulanier, G., Démoulin, P., Schmieder, B., Fang, C., & Tang, Y. H. 1998, Sol. Phys., 183, 369 In the text NASA ADS  
• Balthasar, H., & Schmidt, W. 1993, A&A, 279, 243 In the text NASA ADS  
• Beckers, J. M., & Milkey, R. W. 1975, Sol. Phys., 43, 289 In the text NASA ADS  
• Bruls, J. H. M. J., Rutten, R. J., & Shchukina, N. G. 1992, A&A, 265, 237 In the text NASA ADS  
• Bruls, J. H. M. J., Solanki, S. K., Rutten, R. J., & Carlsson, M. 1995, A&A, 293, 225 In the text NASA ADS  
• Caccin, B., Gomez, M. T., Marmolino, C., & Severino, G. 1977, A&A, 54, 227 In the text NASA ADS  
• Canfield, R. C. 1976, Sol. Phys., 50, 239 In the text NASA ADS  
• Carlsson, M. 1986, A Computer Program for Solving Multi-Level Non-LTE Radiative Transfer Problems in Moving or Static Atmospheres, Report No. 33, Upsalla Astronomical Observatory In the text  
• Collados, M., Martínez Pillet, V., Ruiz Cobo, B., del Toro Iniesta, J. C., & Vázquez, M. 1994, A&A, 291, 622 In the text NASA ADS  
• Emonet, T., & Moreno-Insertis, F. 1998, ApJ, 492, 804 In the text NASA ADS  
• Démoulin, P., Bagala, L. G., Mandrini, C. H., Henoux, J. C., & Rovira, M. G. 1997, A&A, 325, 305 In the text NASA ADS  
• Eibe, M. T., Mein, P., Roudier, Th., & Faurobert, M. 2001, A&A, 371, 1128 In the text NASA ADS  
• Giovanelli, R. G. 1980, Sol. Phys., 68, 49 In the text NASA ADS  
• Giovanelli, R. G., & Jones, H. P. 1982, Sol. Phys., 79, 267 In the text NASA ADS  
• Hagyard, M. J., Teuber, D., West, E. A., et al. 1983, Sol. Phys., 84, 13 In the text NASA ADS  
• Hofmann, A., & Rendtel, J. 1989, Astron. Nachr., 310, 61 In the text NASA ADS  
• Keller, C. U., Solanki, S. K., Steiner, O., & Stenflo, J. O. 1990, A&A, 233, 583 In the text NASA ADS  
• Landi Degl'Innocenti, E., & Landi Degl'Innocenti, M. 1977, A&A, 56, 111 In the text NASA ADS  
• Liu, Y., Wang, J., Yan, Y., & Guoxiang, A. 1996, Sol. Phys., 169, 79 In the text NASA ADS  
• Maltby, P., Avrett, E. H., Carlsson, M., et al. 1986, ApJ, 306, 284 In the text NASA ADS  
• Mein, P. 1971, Sol. Phys., 20, 3 In the text NASA ADS  
• Mein, P. 2002, A&A, 381, 271 In the text  
• Pahlke, K. D., & Wiehr, E. 1990, A&A, 238, 246 In the text  
• Rachkovsky, D. N. 1962, Izv. Krymsk. Astrofiz. Obs., 27, 148 In the text  
• Rachkovsky, D. N. 1967, Izv. Krymsk. Astrofiz. Obs., 37, 56 In the text  
• Ruiz Cobo, B., & del Toro Iniesta, J. C. 1992, ApJ, 398, 375 In the text NASA ADS  
• Rybicki, G. B., & Hummer, D. G. 1991, A&A, 245, 171 In the text NASA ADS  
• Rybicki, G. B., & Hummer, D. G. 1992, A&A, 262, 209 In the text NASA ADS  
• Sánchez Almeida, J. 2000, ApJ, 544, 1135 In the text NASA ADS  
• Skumanich, A., & Lites, B. W. 1987, ApJ, 322, 473 In the text NASA ADS  
• Socas-Navarro, H., Trujillo Bueno, J., & Ruiz Cobo, B. 2000, ApJ, 530, 977 In the text NASA ADS  
• Solanki, S. K., Rüedi, I., & Livingston, W. 1992, A&A, 263, 339 In the text NASA ADS  
• del Toro Iniesta, J. C. 1997, The Science with THEMIS, in Forum THEMIS, ed. N. Mein, & S. Sahal-Bréchot (Paris: Obs. de Paris), 93  
• del Toro Iniesta, J. C. 2001, in Magnetic Fields across the Hertzsprung-Russell diagram, ed. G. Mathys, & S. K. Solanki, ASP Conf. Ser., in press In the text  
• del Toro Iniesta, J. C., & Ruiz Cobo, B. 1996, Sol. Phys., 164, 169  
• del Toro Iniesta, J. C., Ruiz Cobo, B., & Collados M. 2001, ApJ, 549, L139 In the text NASA ADS  
• Westendorp Plaza, C., del Toro Iniesta, J. C., Ruiz Cobo, B., et al. 2001, ApJ, 547, 1130 In the text NASA ADS  
• Wittmann, A. 1974, Sol. Phys., 36, 29 In the text NASA ADS  
• Vernazza, J. E., Avrett, E. H., & Loeser, R. 1981, ApJ, 45, 635 In the text