A&A 381, 105-121 (2002)
DOI: 10.1051/0004-6361:20011422
F. Royer1,2 - M. Gerbaldi3,4 - R. Faraggiana5 - A. E. Gómez2
1 - Observatoire de Genève, 51 chemin des Maillettes, 1290 Sauverny, Switzerland
2 - DASGAL/CNRS UMR 8633, Observatoire de Paris, 5 place Janssen, 92195 Meudon Cedex, France
3 - CNRS, Institut d'Astrophysique de Paris, 98bis boulevard Arago, 75014 Paris, France
4 - Université de Paris-Sud XI, 91405 Orsay Cedex, France
5 - Dipartimento di Astronomia, Università degli Studi di Trieste, via Tiepolo 11, 34131 Trieste, Italy
Received 24 April 2001 / Accepted 11 October 2001
Abstract
Within the scope of a Key Programme determining fundamental
parameters of stars observed by HIPPARCOS, spectra of 525 B8 to
F2-type stars brighter than V=8 have been collected at
ESO. Fourier transforms of several line profiles in the range
4200-4500Å are used to derive
![]() from the frequency of
the first zero. Statistical analysis of the sample indicates that
measurement error is a function of
from the frequency of
the first zero. Statistical analysis of the sample indicates that
measurement error is a function of
![]() and this relative error of the rotational velocity is found to be about 6% on average.
The results obtained are compared with data from the literature. There
is a systematic shift from standard values from Slettebak et al. (#!Slk_75!#), which
are 10 to 12% lower than our findings. Comparisons with other
independent
and this relative error of the rotational velocity is found to be about 6% on average.
The results obtained are compared with data from the literature. There
is a systematic shift from standard values from Slettebak et al. (#!Slk_75!#), which
are 10 to 12% lower than our findings. Comparisons with other
independent
![]() values tend to prove that those from Slettebak et
al. are underestimated. This effect is attributed to the presence of
binaries in the standard sample of Slettebak et al., and
to the model atmosphere they used.
values tend to prove that those from Slettebak et
al. are underestimated. This effect is attributed to the presence of
binaries in the standard sample of Slettebak et al., and
to the model atmosphere they used.
Key words: techniques: spectroscopic - stars: early-type - stars: rotation
Since work began on the subject (Struve & Elvey 1931), it has been observed that stellar rotation rate is directly linked to the spectral type, and A-type stars are known to be mean high rotators.
The Doppler effect allows measurement of the broadening parameter
![]() ,
the projection of the equatorial velocity v along the line of sight. From a statistically significant sample of measured
,
the projection of the equatorial velocity v along the line of sight. From a statistically significant sample of measured
![]() ,
it is possible to derive the distribution of v assuming that the rotation axes are randomly distributed and the sample is not biased.
,
it is possible to derive the distribution of v assuming that the rotation axes are randomly distributed and the sample is not biased.
Projected rotational velocities can be derived in many ways. Although large surveys of
![]() already exist, great care must be
taken when combining their data, as various calibrations were used.
already exist, great care must be
taken when combining their data, as various calibrations were used.
The most accurate method of computing
![]() would be the time-consuming computation of line profiles, starting from a model
atmosphere (with the introduction of other broadening mechanisms), and
their comparison with the observed lines
(see Dravins et al. 1990, for their study of Sirius). Such high precision is not justified, however, in a statistical study of high rotators like the non-peculiar A-type stars where other mechanisms (macroturbulence, instrumental) are negligible compared to rotation.
would be the time-consuming computation of line profiles, starting from a model
atmosphere (with the introduction of other broadening mechanisms), and
their comparison with the observed lines
(see Dravins et al. 1990, for their study of Sirius). Such high precision is not justified, however, in a statistical study of high rotators like the non-peculiar A-type stars where other mechanisms (macroturbulence, instrumental) are negligible compared to rotation.
Line widths appear to be the natural indicator for measuring stellar
rotation, and most
![]() are derived in this way, as a function of
the full-width at half-maximum (FWHM). The largest catalogue of
are derived in this way, as a function of
the full-width at half-maximum (FWHM). The largest catalogue of
![]() is by Uesugi & Fukuda (1982). It is an extremely heterogeneous
compilation of observational data mainly based on the old Slettebak
system (Slettebak 1949, 1954, 1955, 1956; Slettebak & Howard 1955). Several years ago,
Abt & Morrell (1995) measured
is by Uesugi & Fukuda (1982). It is an extremely heterogeneous
compilation of observational data mainly based on the old Slettebak
system (Slettebak 1949, 1954, 1955, 1956; Slettebak & Howard 1955). Several years ago,
Abt & Morrell (1995) measured
![]() for 1700 A-type stars in the
northern hemisphere, calibrated with the new system from
Slettebak et al. (1975, hereafter SCBWP). More recently, Wolff & Simon (1997) measured the
for 1700 A-type stars in the
northern hemisphere, calibrated with the new system from
Slettebak et al. (1975, hereafter SCBWP). More recently, Wolff & Simon (1997) measured the
![]() of 250 stars, most of which were cooler than those in our
sample, by cross-correlation with the spectra of standard stars of similar temperature.
They found a small systematic difference with Abt & Morrell's results
(the former are larger by
of 250 stars, most of which were cooler than those in our
sample, by cross-correlation with the spectra of standard stars of similar temperature.
They found a small systematic difference with Abt & Morrell's results
(the former are larger by ![]() 5%), and with those of Danziger & Faber (1972) (smaller by
8%). This can be explained by the difference between the "old'' and "new'' Slettebak systems.
Brown & Verschueren (1997) derived
5%), and with those of Danziger & Faber (1972) (smaller by
8%). This can be explained by the difference between the "old'' and "new'' Slettebak systems.
Brown & Verschueren (1997) derived
![]() for a sample of early-type stars in
Sco OB2 association from spectra taken with the same instrument we
used. They adopted three different techniques according to the
expected
for a sample of early-type stars in
Sco OB2 association from spectra taken with the same instrument we
used. They adopted three different techniques according to the
expected
![]() values, which they show to be generally consistent
with each other. The
values, which they show to be generally consistent
with each other. The
![]() values so obtained correspond to those
defining the SCBWP scale, except for stars with
values so obtained correspond to those
defining the SCBWP scale, except for stars with
![]() below 60
below 60
![]() ,
for which the SCBWP values are systematically lower.
,
for which the SCBWP values are systematically lower.
The use of the Fourier technique in the determination of
![]() remains occasional, mainly because using a calibration FWHM-
remains occasional, mainly because using a calibration FWHM-
![]() is
much easier and fitting theoretical profiles to observed ones in
wavelength space allows one to derive more parameters than simply the rotational broadening. Nevertheless, Fourier techniques are a valuable tool for investigating stellar rotation, as described by Smith & Gray (1976).
Gray (1980) compared the
is
much easier and fitting theoretical profiles to observed ones in
wavelength space allows one to derive more parameters than simply the rotational broadening. Nevertheless, Fourier techniques are a valuable tool for investigating stellar rotation, as described by Smith & Gray (1976).
Gray (1980) compared the
![]() obtained from Fourier transform of the Mg II 4481 line profile with the
obtained from Fourier transform of the Mg II 4481 line profile with the
![]() values from Uesugi & Fukuda and SCBWP and found a reasonable agreement (deviations of
values from Uesugi & Fukuda and SCBWP and found a reasonable agreement (deviations of ![]() 10% with SCBWP), but his sample is quite small.
10% with SCBWP), but his sample is quite small.
Suspecting that the small differences found with respect to standard
values could be due to an underestimation in the SCBWP calibration of
the
![]() values, we decided to undertake a measure of
values, we decided to undertake a measure of
![]() independent of any pre-existing calibration. We adopted the method described in Ramella et al. (1989).
independent of any pre-existing calibration. We adopted the method described in Ramella et al. (1989).
The largest scatter in the average
![]() distribution is
found for late B and early A stars (Gray 1992, Fig. 17.16 p. 386),
and we want to test whether this is due only to errors in measurement or if it is related to some physical effect.
Brown & Verschueren (1997), in their study of the Sco OB2 association, found
that B7-B9 stars of the Upper Scorpius subgroup rotate faster than the
B0-B6 stars. This result corresponds to Gray's result, suggesting that
the apparent scatter may disguise a physical effect. This effect has already been detected by Mouschovias (1983).
distribution is
found for late B and early A stars (Gray 1992, Fig. 17.16 p. 386),
and we want to test whether this is due only to errors in measurement or if it is related to some physical effect.
Brown & Verschueren (1997), in their study of the Sco OB2 association, found
that B7-B9 stars of the Upper Scorpius subgroup rotate faster than the
B0-B6 stars. This result corresponds to Gray's result, suggesting that
the apparent scatter may disguise a physical effect. This effect has already been detected by Mouschovias (1983).
The possibility of a change on average
![]() with evolution from zero-age to terminal-age main sequence has been studied for several decades, and the absence of any evolutionary effect for stars with a mass higher than
with evolution from zero-age to terminal-age main sequence has been studied for several decades, and the absence of any evolutionary effect for stars with a mass higher than
![]() is confirmed by the recent study of Wolff & Simon (1997).
The fact that the colors of stars are affected by rotation was
observed for the first time by Brown & Verschueren, but only for
stars belonging to young groups, not field stars. They conclude,
moreover, that the determination of ages and mass distributions is not affected by rotation.
is confirmed by the recent study of Wolff & Simon (1997).
The fact that the colors of stars are affected by rotation was
observed for the first time by Brown & Verschueren, but only for
stars belonging to young groups, not field stars. They conclude,
moreover, that the determination of ages and mass distributions is not affected by rotation.
As a matter of fact, the effect of rotation on stellar parameters is
also known: a rapidly rotating star simulates a star with lower
![]() and
and ![]() .
However, in this case, all quantities (line strength,
photometric colors, for example) change in the same way so that the effect is practically undetectable
(this point was already discussed by Wolff 1983, p. 159), especially when field stars are studied.
.
However, in this case, all quantities (line strength,
photometric colors, for example) change in the same way so that the effect is practically undetectable
(this point was already discussed by Wolff 1983, p. 159), especially when field stars are studied.
In this paper, newly determined
![]() data, obtained with Fourier transforms, for 525 southern early-type stars are presented. The observations and the sample are described in Sect. 2. In Sect. 3 the technique used to derive
data, obtained with Fourier transforms, for 525 southern early-type stars are presented. The observations and the sample are described in Sect. 2. In Sect. 3 the technique used to derive
![]() from the spectra is detailed and discussed. In Sect. 4 the results are presented and compared to data from the literature. In Sect. 5 our conclusions are summarized.
This paper is the first of a series pertaining to rotational velocities of A-type stars; data collected in the northern hemisphere and measured
from the spectra is detailed and discussed. In Sect. 4 the results are presented and compared to data from the literature. In Sect. 5 our conclusions are summarized.
This paper is the first of a series pertaining to rotational velocities of A-type stars; data collected in the northern hemisphere and measured
![]() will be presented in a forthcoming paper.
will be presented in a forthcoming paper.
It is worth noticing that the spectra which are the subject of the present paper
were also studied by Grenier et al. (1999) to derive radial velocities, and that
the 71 A0 dwarf stars observed were investigated by
Gerbaldi et al. (1999). Basically, this sample includes objects with no
radial velocity or only for one epoch. Some stars with no
![]() determination were added from the Bright Star Catalogue (Hoffleit & Jaschek 1982).
The observational programme is more detailed by Grenier et al. (1999).
determination were added from the Bright Star Catalogue (Hoffleit & Jaschek 1982).
The observational programme is more detailed by Grenier et al. (1999).
| |
Figure 1: Distribution of the spectral type for the 525 programme stars. |
| Open with DEXTER | |
| |
Figure 2:
Normalized spectrum of Sirius, covering the 4210-4500 Å range, around H |
| Open with DEXTER | |
The complete reduction of the spectra using MIDAS![]() package, from CCD frame to linear spectrum, is detailed by Burnage & Gerbaldi (1990, 1992).
package, from CCD frame to linear spectrum, is detailed by Burnage & Gerbaldi (1990, 1992).
As pointed out by Gray & Garrison (1987), there is no "standard'' technique for measuring projected rotational velocity.
The first application of Fourier analysis in the determination of stellar rotational velocities was undertaken by Carroll (1933).
Gray (1992) uses the whole profile of Fourier transform of spectral lines to derive the
![]() ,
instead of only the zeroes as suggested by Carroll.
The
,
instead of only the zeroes as suggested by Carroll.
The
![]() measurement method we adopted is based on the position of
the first zero of the Fourier transform (FT) of the line profiles
(Carroll 1933). The shape of the first lobe of the FT allows us to
better and more easily identify rotation as the main broadening agent of a line compared to the line profile in the wavelength domain. FT of the spectral line is computed using a Fast Fourier Transform algorithm. The
measurement method we adopted is based on the position of
the first zero of the Fourier transform (FT) of the line profiles
(Carroll 1933). The shape of the first lobe of the FT allows us to
better and more easily identify rotation as the main broadening agent of a line compared to the line profile in the wavelength domain. FT of the spectral line is computed using a Fast Fourier Transform algorithm. The
![]() value is derived from the position of the first zero of the FT of the observed line using a theoretical rotation profile for a line at 4350Å and
value is derived from the position of the first zero of the FT of the observed line using a theoretical rotation profile for a line at 4350Å and
![]() equal to 1
equal to 1
![]() (Ramella et al. 1989). The whole profile in the Fourier domain is then compared with a theoretical rotational profile for the corresponding velocity to check if the first lobes correspond (Fig. 3).
(Ramella et al. 1989). The whole profile in the Fourier domain is then compared with a theoretical rotational profile for the corresponding velocity to check if the first lobes correspond (Fig. 3).
 |
Figure 3:
Profile of the Fourier transform of the Mg II 4481Å line (solid line) for the star HIP 95965 and theoretical rotational profile (dashed line) with
|
| Open with DEXTER | |
If ![]() is the position of the first zero of the line profile (at
is the position of the first zero of the line profile (at ![]() )
in the Fourier space, the projected rotational velocity is derived as follows:
)
in the Fourier space, the projected rotational velocity is derived as follows:
It should be noted that we did not take into account the gravity darkening, effect that can play a role in rapidly rotating stars when velocity is close to break-up, as this is not relevant for most of our targets.
Determination of the projected rotational velocity requires normalized spectra.
As far as the continuum is concerned, it has been determined visually, passing through noise fluctuations. The MIDAS procedure for continuum determination of 1D-spectra has been used, fitting a spline over the points chosen in the graphs.
Uncertainty related to this determination rises because the continuum observed on the spectrum is a pseudo-continuum. Actually, the true continuum is, in this spectral domain, not really reached for this type of stars.
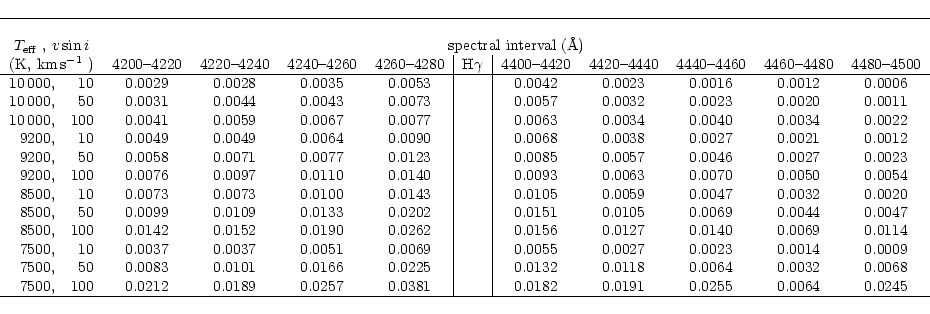
In order to quantify this effect, a grid of synthetic spectra of different effective temperatures (10000, 9200, 8500 and 7500K) and different rotational broadenings has been computed from Kurucz' model atmosphere (Kurucz 1993), and Table 1 lists the differences between the true continuum and the pseudo-continuum represented as the highest points in the spectra.
|
|
Continuum is then tilted to origin and the spectral windows corresponding to lines of interest are extracted from the spectrum in order to compute their FT.
The essential step in this analysis is the search for suitable spectral lines to measure the
![]() .
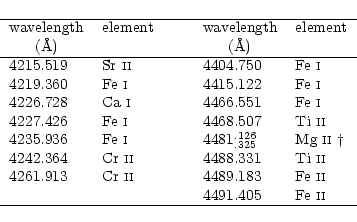
The lines which are candidates for use in the determination of rotation (Table 2) have been identified in the Sirius atlas (Furenlid et al. 1992) and retained according to the following criteria:
.
The lines which are candidates for use in the determination of rotation (Table 2) have been identified in the Sirius atlas (Furenlid et al. 1992) and retained according to the following criteria:
|
|
The lines selected in the Sirius spectrum are valid for early A-type
stars. When moving to stars cooler than about A3-type stars, the effects of
the increasing incidence of blends and the presence of stronger
metallic lines must be taken into account. The effects are: (1) an
increasing departure of the true continuum flux (to which the spectrum
must be normalized) from the curve that joins the highest points in
the observed spectrum, as mentioned in the previous subsection, and (2)
an increased incidence of blending that reduces the number of
lines suitable for
![]() measurements. The former effect will be
estimated in Sect. 3.4. The latter can be derived from the symmetry
of the spectral lines.
Considering a line, continuum tilted to zero, as a distribution, moments of kth order can be defined as:
measurements. The former effect will be
estimated in Sect. 3.4. The latter can be derived from the symmetry
of the spectral lines.
Considering a line, continuum tilted to zero, as a distribution, moments of kth order can be defined as:
The most noticeable finding in this table is that
![]() usually
increases with decreasing
usually
increases with decreasing
![]() and increasing
and increasing
![]() .
This is a typical effect of blends. Nevertheless, high rotational broadening can lower the skewness of a blended line by making the blend smoother.
.
This is a typical effect of blends. Nevertheless, high rotational broadening can lower the skewness of a blended line by making the blend smoother.
Skewness ![]() for the synthetic spectrum close to Sirius' parameters (
for the synthetic spectrum close to Sirius' parameters (
![]() K,
K,
![]()
![]() )
is contained between -0.09 and +0.10. The threshold, beyond which blends are regarded as affecting the profile significantly, is taken as equal to 0.15. If
)
is contained between -0.09 and +0.10. The threshold, beyond which blends are regarded as affecting the profile significantly, is taken as equal to 0.15. If
![]() the line is not taken into account in the derivation of the
the line is not taken into account in the derivation of the
![]() for a star with corresponding spectral type and rotational broadening. This threshold is a compromise between the unacceptable distortion of the line and the number of retained lines, and it ensures that the differences between centroid and theoretical wavelength of the lines have a standard deviation of about 0.02 Å.
for a star with corresponding spectral type and rotational broadening. This threshold is a compromise between the unacceptable distortion of the line and the number of retained lines, and it ensures that the differences between centroid and theoretical wavelength of the lines have a standard deviation of about 0.02 Å.
As can be expected, moving from B8 to F2-type stars increases the blending of lines. Among the lines listed in Table 2, the strongest ones in Sirius spectrum (Sr II 4216, Fe I 4219, Cr II 4242, Fe I 4405 and Mg II 4481) correspond to those which remain less contaminated by the presence of other lines. Only Fe I 4405 retains a symmetric profile not being heavily blended at the resolution of our spectra and thus measurable all across the grid of the synthetic spectra.
The Mg II doublet at 4481Å is usually chosen to measure
the
![]() :
it is not very sensitive to stellar effective temperature
and gravity and its relative strength in late B through mid-A-type
star spectra makes it almost the only measurable line in this
:
it is not very sensitive to stellar effective temperature
and gravity and its relative strength in late B through mid-A-type
star spectra makes it almost the only measurable line in this
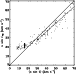 |
Figure 4:
|
| Open with DEXTER | |
Among the list of candidate lines chosen according to the spectral type and rotational broadening of the star, some can be discarded on the basis of the spectrum quality itself. The main reason for discarding a line, first supposed to be reliable for
![]() determination, lies in its profile in Fourier space. One retains the results given by lines whose profile correspond to a rotational profile.
determination, lies in its profile in Fourier space. One retains the results given by lines whose profile correspond to a rotational profile.
In logarithmic frequency space, such as in Figs. 3 and 5, the rotational profile has a unique shape, and the effect of
![]() simply acts as a translation in frequency. Matching between the theoretical profile, shifted at the ad hoc velocity, and the observed profile, is used as confirmation of the value of the first zero as a
simply acts as a translation in frequency. Matching between the theoretical profile, shifted at the ad hoc velocity, and the observed profile, is used as confirmation of the value of the first zero as a
![]() .
.
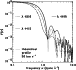 |
Figure 5:
Example of line profiles in the Fourier space for HD 75063 (A1III type star) whose
|
| Open with DEXTER | |
A discarded Fourier profile is sometimes associated with a distorted profile in wavelength space, but this is not always the case. For low rotational broadening, i.e.
![]()
![]() ,
the Fourier profile deviates from the theoretical rotational profile. This is due to the fact that rotation does not completely dominate the line profile and the underlying instrumental profile is no longer negligible. It may also occur that an SB2 system, where lines of both components are merged, appears as a single star, but the blend due to multiplicity makes the line profile diverge from a rotational profile.
,
the Fourier profile deviates from the theoretical rotational profile. This is due to the fact that rotation does not completely dominate the line profile and the underlying instrumental profile is no longer negligible. It may also occur that an SB2 system, where lines of both components are merged, appears as a single star, but the blend due to multiplicity makes the line profile diverge from a rotational profile.
To conclude, the number of measurable lines among the 15 listed in Table 2 also varies from one spectrum to another according to the rotational broadening and the signal-to-noise ratio and ranges from 1 to 15 lines.
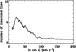 |
Figure 6:
Average number of measured lines (running average over 30 points) is plotted as a function of the mean
|
| Open with DEXTER | |
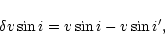 |
(5) |
 |
Figure 7:
Systematic shift
|
| Open with DEXTER | |
This estimation of the effect of the continuum is only carried out on synthetic spectra because the way our observed spectra have been normalized offers no way to recover the true continuum. The resulting shift is given here for information only.
Two types of uncertainties are present: those internal to the method and those related to the line profile.
The internal error comes from the uncertainty in the real position of the first zero due to the sampling in the Fourier space. The Fourier transforms are computed over 1024 points equally spaced with the step ![]() .
This step is inversely proportional to the step in wavelength space
.
This step is inversely proportional to the step in wavelength space
![]() ,
and the spectra are sampled with
,
and the spectra are sampled with
![]() Å. The uncertainty of
Å. The uncertainty of
![]() due to the sampling is
due to the sampling is
The best way to estimate the precision of our measurements is to study the dispersion of the individual
![]() .
For each star,
.
For each star,
![]() is an average of the individual values derived from selected lines.
is an average of the individual values derived from selected lines.
 |
Figure 8:
Differences between individual
|
| Open with DEXTER | |
 |
Figure 9:
Mean of differences between individual
|
| Open with DEXTER | |
Residual around this formal error can be expected to depend on the
effective temperature of the star. Figure 9 displays
the variations of the residuals as a function of the spectral
type. Although contents of each bin of spectral type are not constant
all across the sample (the error bar is roughly proportional to the
logarithm of the inverse of the number of points), there does not seem to be
any trend, which suggests that our choice of lines according to the
spectral type eliminates any systematic effect due to the stellar temperature from the measurement
of the
![]() .
.
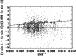 |
Figure 10:
Differences between individual
|
| Open with DEXTER | |
The differences
![]() ,
normalized by the
formal error
,
normalized by the
formal error
![]() ,
are plotted versus the
noise level (SNR-1) in Fig. 10 in order to
estimate the effect of SNR. Noise is derived for each spectrum using a
piecewise-linear high-pass filter in Fourier space with a transition
band chosen between 0.3 and 0.4 times the Nyquist frequency;
standard deviation of this high frequency signal is computed as the
noise level and then divided by the signal level. The trend in
Fig. 10 is computed as for Fig. 8,
using a robust estimation and GaussFit.
The linear adjustment gives:
,
are plotted versus the
noise level (SNR-1) in Fig. 10 in order to
estimate the effect of SNR. Noise is derived for each spectrum using a
piecewise-linear high-pass filter in Fourier space with a transition
band chosen between 0.3 and 0.4 times the Nyquist frequency;
standard deviation of this high frequency signal is computed as the
noise level and then divided by the signal level. The trend in
Fig. 10 is computed as for Fig. 8,
using a robust estimation and GaussFit.
The linear adjustment gives:
Distribution of observational errors, in the case of rotational velocities, is of particular interest during a deconvolution process in order to get rid of statistical errors in a significant sample.
To have an idea of the shape of the error law associated with the
![]() ,
it is necessary to have a great number of spectra for the same star.
Sirius has been observed on several occasions during the runs and its spectrum has been collected 48 times. Sirius spectra typically exhibit high signal-to-noise ratio (
,
it is necessary to have a great number of spectra for the same star.
Sirius has been observed on several occasions during the runs and its spectrum has been collected 48 times. Sirius spectra typically exhibit high signal-to-noise ratio (
![]() ). The 48 values derived from each set of lines, displayed in Fig. 11, give us an insight into the errors distribution. The mean
). The 48 values derived from each set of lines, displayed in Fig. 11, give us an insight into the errors distribution. The mean
![]() is
is
![]()
![]() and its associated standard deviation
and its associated standard deviation
![]()
![]() ;
data are approximatively distributed following a Gaussian around the mean
;
data are approximatively distributed following a Gaussian around the mean
![]() .
.
 |
Figure 11:
The
|
| Open with DEXTER | |
Moreover, for higher broadening, the impact of the sampling effect of
the FT (Eq. (6)) is foreseen, resulting in a distribution with a box-shaped profile. This effect becomes noticeable for
![]()
![]() .
.
In all, projected rotational velocities were derived for 525 B8 to F2-type stars. Among them, 286 have no rotational velocities either in the compilation of Uesugi & Fukuda (1982) or in Abt & Morrell (1995).
The results of the
![]() determinations are presented in
Table 4 which contains the following data: Col. 1
gives the HD number, Col. 2 gives the HIP number, Col. 3
displays the spectral type as given in the HIPPARCOS catalogue
(ESA 1997), Cols. 4, 5, 6 give respectively the derived value of
determinations are presented in
Table 4 which contains the following data: Col. 1
gives the HD number, Col. 2 gives the HIP number, Col. 3
displays the spectral type as given in the HIPPARCOS catalogue
(ESA 1997), Cols. 4, 5, 6 give respectively the derived value of
![]() ,
the associated standard deviation and the corresponding number
of measured lines (uncertain
,
the associated standard deviation and the corresponding number
of measured lines (uncertain
![]() are indicated by a colon), Col. 7 presents possible remarks about the spectra: SB2 ("SB'') and
shell ("SH'') natures are indicated for stars detailed in the
subsections which follow, as
well as the reason why
are indicated by a colon), Col. 7 presents possible remarks about the spectra: SB2 ("SB'') and
shell ("SH'') natures are indicated for stars detailed in the
subsections which follow, as
well as the reason why
![]() is uncertain - "NO'' for no selected
lines, "SS'' for variation from spectrum to spectrum and "LL'' for
variation from line to line, as detailed in the Appendix A.
is uncertain - "NO'' for no selected
lines, "SS'' for variation from spectrum to spectrum and "LL'' for
variation from line to line, as detailed in the Appendix A.
Grenier et al. (1999) studied the same stars with the same spectra and derived radial velocities using cross-correlation techniques. On the basis of the shape of the cross-correlation function (CCF) they find that less than half of the sample has a symmetric and Gaussian CCF and they classify stars with distorted CCF as, among other things, "certain'' "probable'' or "suspected'' doubles.
Uncertainties in
![]() are induced by peculiarities in the spectra
due for example to binarity or to the presence of a shell. The results for these objects are detailed below. These objects were either known as binaries or newly detected by Grenier et al. (1999).
are induced by peculiarities in the spectra
due for example to binarity or to the presence of a shell. The results for these objects are detailed below. These objects were either known as binaries or newly detected by Grenier et al. (1999).
Moreover, the difference in radial velocity
![]() has
to be large enough for the spectrum to show well separated
lines. Considering a Gaussian line profile, 98% of the distribution
is contained between
has
to be large enough for the spectrum to show well separated
lines. Considering a Gaussian line profile, 98% of the distribution
is contained between
![]() (
(![]() being the standard
deviation of the Gaussian) which is nearly equal to
being the standard
deviation of the Gaussian) which is nearly equal to
![]() FWHM. It follows that a double line resulting from the contribution of the components of a binary system should be spaced of
FWHM. It follows that a double line resulting from the contribution of the components of a binary system should be spaced of
![]() (where
(where
![]() and
and
![]() are the respective Doppler shifts) to overlap as little as possible and be measurable in terms of
are the respective Doppler shifts) to overlap as little as possible and be measurable in terms of
![]() determination. Taking the calibration relation from SCBWP as a rule of thumb (
determination. Taking the calibration relation from SCBWP as a rule of thumb (
![]() ), the difference of radial velocity in an SB2 system should be higher than:
), the difference of radial velocity in an SB2 system should be higher than:
Table 5 displays the results for the stars in our sample which
exhibit an SB2 nature. We focus only on stars in which the spectral lines
of both component are separated. Spectral lines are identified by comparing the SB2 spectrum with a single star spectrum. Projected rotational velocities are given for each component when measurable, as well as the difference in radial velocity
![]() computed from the velocities given by Grenier et al. (1999).
computed from the velocities given by Grenier et al. (1999).
| HD | HIP | Spect. type |
|
|
Fig. | |
| (
|
(
|
|||||
| A | B | |||||
| 10167 | 7649 | F0V | 17 | 14 | 80 | 12a |
| 11 | 13 | 62 | 12b | |||
| 18622 | 13847 | A4III+... | 71: | 74: | 154 | 13a |
| - | - | 109 | 13b | |||
| 83 | - | 13c | ||||
| 27346 | 19704 | A9IV | 35 | 35 | 135 | 14a |
| 36: | - | 14b | ||||
| 87330 | 49319 | B9III/IV | 11 | 9 | 67 | 15a |
| 10 | 10 | 45 | 15b | |||
| 90972 | 51376 | B9/B9.5V | 23: | 29: | 54 | 15c |
Less obvious SB2 lie in our sample, but individually analyzing line profiles one-by-one is not an appropriate method for detecting them. Results about binarity for these spectra are however indicated in Grenier et al.
The specific "shell'' feature in stars with a circumstellar envelope
is characterized by double emission and central absorption in hydrogen
lines. This characteristic is likely a perspective effect, as
suggested by (Slettebak 1979), and shell-type lines occur at high
inclination i when line of sight intersects with the disk-like
envelope. For our purpose,
![]() determination, critical effect is
due to metallic shell stars, where shell-type absorption not only
occurs in Balmer series but also in metallic lines. Our candidate
lines exhibit a broad profile, indicating rapid rotation of the
central star, a high inclination of the line of sight, and a
superimposed sharp absorption profile originating in the circumstellar
envelope (Fig. 16). Metallic shell-type lines arise when
perspective effect is more marked than for hydrogen shell stars
(Briot 1986). Measurement of
determination, critical effect is
due to metallic shell stars, where shell-type absorption not only
occurs in Balmer series but also in metallic lines. Our candidate
lines exhibit a broad profile, indicating rapid rotation of the
central star, a high inclination of the line of sight, and a
superimposed sharp absorption profile originating in the circumstellar
envelope (Fig. 16). Metallic shell-type lines arise when
perspective effect is more marked than for hydrogen shell stars
(Briot 1986). Measurement of
![]() requires a line profile from the
central star photosphere only, and not polluted by absorption caused by the circumstellar envelope which does not reflect the rotation motion.
requires a line profile from the
central star photosphere only, and not polluted by absorption caused by the circumstellar envelope which does not reflect the rotation motion.
| |
Figure 12:
The part of the spectrum of HD 10167, centered around
Mg II 4481 (4460-4500Å) is displayed for the two
observed spectra of the star. Both panels present the
binarity. Relative radial velocities are high enough compared to
rotational broadening to allow to measure
|
| Open with DEXTER | |
| |
Figure 13:
HD 18622 has been observed at three different times: a) HJD 2447790, b) 2448525 and c) 2448584. For each spectrum the region around Mg II 4481Å is displayed. Relative radial velocities vary from about indiscernible components in panel c) to nearly 150
|
| Open with DEXTER | |
| |
Figure 14: HD 27346 spectra have been collected at two different orbital phases separated in time by 981 days. Mg II line shows clearly the two components in panel a), whereas they are merged in b). |
| Open with DEXTER | |
| |
Figure 15:
a) and b) Observations of HD 87330 around Mg II, separated by almost three years. Low rotational broadening allows the measurement of
|
| Open with DEXTER | |
| |
Figure 16: Part of the spectrum of HD 225200 showing the rotationally broadened line Mg II 4481 (filled circle) and metallic lines exhibiting the signature of the shell as sharp core and extended wings (open triangle). |
| Open with DEXTER | |
Derived
![]() for the metallic shell stars present in our sample are listed in Table 6. These stars are already known as shell stars. HD 15004 (71 Cet) and HD 225200 are further detailed by Gerbaldi et al. In our spectral range, magnesium multiplet Mg II 4481 is the only measurable line.
for the metallic shell stars present in our sample are listed in Table 6. These stars are already known as shell stars. HD 15004 (71 Cet) and HD 225200 are further detailed by Gerbaldi et al. In our spectral range, magnesium multiplet Mg II 4481 is the only measurable line.
| HD | HIP | Spectral type |
|
| (
| |||
| 15004 | 11261 | A0III | 249 |
| 24863 | 18275 | A4V | 249 |
| 38090 | 26865 | A2/A3V | 204 |
| 88195 | 49812 | A1V | 236 |
| 99022 | 55581 | A4:p | 236 |
| 236 | |||
| 249 | |||
| 225200 | 345 | A1V | 345 |
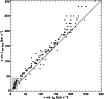 |
Figure 17:
Comparison between
|
| Open with DEXTER | |
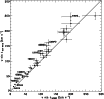 |
Figure 18:
Comparison between
|
| Open with DEXTER | |
The most homogeneous large data set of rotational velocities for
A-type stars which has been provided up to now is that of AM (1995),
who measured
![]() for about 1700 A-type stars in the northern
hemisphere.
The intersection with our southern sample includes 160 stars. The
comparison of the
for about 1700 A-type stars in the northern
hemisphere.
The intersection with our southern sample includes 160 stars. The
comparison of the
![]() (Fig. 17) shows that our determination is higher on average than
the velocities derived by Abt & Morrell (AM). The linear relation
given by GaussFit is:
(Fig. 17) shows that our determination is higher on average than
the velocities derived by Abt & Morrell (AM). The linear relation
given by GaussFit is:
There are 35 stars in common between our sample and the standard stars of SCBWP. It is worth emphasizing that among these 35 stars, only one third has a Gaussian CCF in the study of Grenier et al. Moreover there is an SB2 system (HD 18622) and almost one half of this group is composed of suspected or probable multiple stars, on the basis of their CCF.
Figure 18 displays the
![]() derived in this paper versus the
derived in this paper versus the
![]() from SCBWP for the 35 standard stars in common. The solid line represents the one-to-one relation. A clear trend is observed:
from SCBWP for the 35 standard stars in common. The solid line represents the one-to-one relation. A clear trend is observed:
![]() from SCBWP are on average 10 to 12% lower. A linear least squares fit carried out with GaussFit on these values makes the systematic effect explicit:
from SCBWP are on average 10 to 12% lower. A linear least squares fit carried out with GaussFit on these values makes the systematic effect explicit:
The difference between the two relations, Eq. (11) and
Eq. (12), concerns mainly the low
![]() region. When low
region. When low
![]() from Abt
& Morrell <25
from Abt
& Morrell <25
![]() ,
are not taken into account (grey box in
Fig. 17), the relation given by GaussFit between
,
are not taken into account (grey box in
Fig. 17), the relation given by GaussFit between
![]() from Abt & Morrell and this work becomes:
from Abt & Morrell and this work becomes:
| Name | HD | Sp. type |
|
HIPPARCOS | CFF | ||||||
| 47670 | B8III | 200 | 246 |
|
- | - | - | U | - | 5 | |
| 48915 | A0m... | 10 | 16 |
|
|
|
- | - | - | 0 | |
| 16.2(3) |
|
||||||||||
| QW Pup | 55892 | F0IV | 40 | 51 |
|
- | - | 50(8) | M | - | 4 |
| a Vel | 75063 | A1III | 20 | 30 |
|
- | - | - | - | - | 0 |
| 78045 | Am | 25 | 34 |
|
45(9) | - | - | C | - | 0 | |
| 97633 | A2V | 15 | 23 |
|
|
- | 23(10) | - | - | 0 | |
| A Cen | 100673 | B9V | 125 | 160 | - | - | - | - | C | - | 10 |
| 102249 | A7III | 50 | 60 |
|
- | - | 60(11) | C | O | 0 | |
| 125473 | A0IV | 100 | 124 |
|
132(9) | - | - | - | - | 5 | |
| 198001 | A1V | 85 | 102 | - |
|
- | - | - | - | 0 | |
| 222661 | B9V | 120 | 150 | - | - | - | - | C | - | 4 | |
| (1) Kurucz et al. (1977). | (5) Deeming (1977). | (9) Holweger et al. (1999). | |
| (2) Lemke (1989). | (6) Ramella et al. (1989). | (10) Fekel (1998). | |
| (3) Hill (1995). | (7) Dravins et al. (1990). | (11) Noci et al. (1984). | |
| (4) Smith (1976). | (8) Balachandran (1990). | (12) Dunkin et al. (1997). |
For slow rotational velocities, the discrepancy far exceeds the
estimate of observational errors. Figure 18 also shows
the stars which deviate the most from the one-to-one relation. These
twelve stars, for which the error box around the point does not
intersect with the one-to-one relation, are listed in
Table 7 with different rotational velocity
determinations gathered from the literature.
Their large differences together with comparison to other data
allow us to settle on which source carries the systematic effect.
Without exception, all data gathered from the literature and
listed in Table 7 are systematically higher than the
corresponding SCBWP's
![]() and for the majority of the listed stars, data from the literature are consistent with our
and for the majority of the listed stars, data from the literature are consistent with our
![]() determinations.
These stars are further detailed in the Appendix B.
determinations.
These stars are further detailed in the Appendix B.
The selection of several suitable spectral lines and the evaluation of
their reliability as a function of broadening and effective
temperature allows the computation of
![]() over the whole spectral range of
A-type stars and a robust estimate of the associated relative error.
over the whole spectral range of
A-type stars and a robust estimate of the associated relative error.
Up to 150
![]() ,
a statistical analysis indicates that the standard
deviation is about 6% of the
,
a statistical analysis indicates that the standard
deviation is about 6% of the
![]() .
It can be seen, in both Figs. 17 and 18,
that the dispersion increases beyond 180
.
It can be seen, in both Figs. 17 and 18,
that the dispersion increases beyond 180
![]() approximately, when
comparing rotational velocities to previous determination by Abt &
Morrell and SCBWP. SCBWP estimate a larger uncertainty for rotational velocities higher than
200
approximately, when
comparing rotational velocities to previous determination by Abt &
Morrell and SCBWP. SCBWP estimate a larger uncertainty for rotational velocities higher than
200
![]() ;
nevertheless our precision estimation for a 200
;
nevertheless our precision estimation for a 200
![]()
![]() is extrapolated from Fig. 8. Errors
may thus be larger, due to the sampling in Fourier space, which is proportional to
is extrapolated from Fig. 8. Errors
may thus be larger, due to the sampling in Fourier space, which is proportional to
![]() .
.
In addition, determination of continuum level induces a
systematic underestimation of
![]() that reaches about 5 to 10%
depending on the lines and broadening.
that reaches about 5 to 10%
depending on the lines and broadening.
Gravity darkening (von Zeipel effect, von Zeipel 1925) is not taken into account in
this work. Hardorp & Strittmatter (1968) quantify this effect, showing that
![]() could be 15 to 40% too small if gravity darkening is neglected for
stars near break-up velocity. Nevertheless, in a recent work (Shan 2000), this
effect is revised downwards and found to remain very small as long as
angular velocity is not close to critical velocity (
could be 15 to 40% too small if gravity darkening is neglected for
stars near break-up velocity. Nevertheless, in a recent work (Shan 2000), this
effect is revised downwards and found to remain very small as long as
angular velocity is not close to critical velocity (
![]() ): it induces an
underestimation
lower than 1% of the FWHM.
In our observed sample, 15 stars (with spectral type from B8V to
A1V) have
): it induces an
underestimation
lower than 1% of the FWHM.
In our observed sample, 15 stars (with spectral type from B8V to
A1V) have
![]()
![]() .
According to their radii and masses, derived from empirical
calibrations (Habets & Heintze 1981), their critical velocities
.
According to their radii and masses, derived from empirical
calibrations (Habets & Heintze 1981), their critical velocities ![]() are higher
than 405
are higher
than 405
![]() (Zorec, private communication).
Only seven stars have a high
(Zorec, private communication).
Only seven stars have a high
![]() ,
so that
,
so that
![]() .
The fraction of stars rotating near their break-up velocity remains
very small, probably lower than 2% of the sample size.
.
The fraction of stars rotating near their break-up velocity remains
very small, probably lower than 2% of the sample size.
A systematic shift is found between the values from the
catalogue of AM (1995). This difference arises from the use of the
calibration relation from SCBWP, for which a similar shift is
found. The discrepancy observed with standard
![]() values given by
SCBWP has already been mentioned in the literature.
Ramella et al. (1989) point out a similar shift with respect to the
values given by
SCBWP has already been mentioned in the literature.
Ramella et al. (1989) point out a similar shift with respect to the
![]() from SCBWP. They suppose that the discrepancy could come from the models SCBWP used to compute theoretical FWHM of the Mg II line.
Brown & Verschueren (1997) derived
from SCBWP. They suppose that the discrepancy could come from the models SCBWP used to compute theoretical FWHM of the Mg II line.
Brown & Verschueren (1997) derived
![]() for early-type stars. For low
for early-type stars. For low
![]() (up to
(up to ![]() 60
60
![]() ), their values are systematically higher than those of SCBWP. They attribute this effect to the use of the models from Collins & Sonneborn (1977) by SCBWP; they assert that using the modern models of Collins et al. (1991) to derive
), their values are systematically higher than those of SCBWP. They attribute this effect to the use of the models from Collins & Sonneborn (1977) by SCBWP; they assert that using the modern models of Collins et al. (1991) to derive
![]() from FWHM eliminates the discrepancy.
Fekel (private communication) also finds this systematic effect between values from AM (1995), which are directly derived from the SCBWP's calibration, and the
from FWHM eliminates the discrepancy.
Fekel (private communication) also finds this systematic effect between values from AM (1995), which are directly derived from the SCBWP's calibration, and the
![]() he measured using his own calibration (Fekel 1997).
he measured using his own calibration (Fekel 1997).
In addition, some stars used as
![]() standards turn out to be multiple
systems or to have spectral features such that their status as a
standard is no longer valid. The presence of these "faulty'' objects in the standard star sample may introduce biases in the
standards turn out to be multiple
systems or to have spectral features such that their status as a
standard is no longer valid. The presence of these "faulty'' objects in the standard star sample may introduce biases in the
![]() scale. There is no doubt that the list of standards established by SCBWP has to be revised.
scale. There is no doubt that the list of standards established by SCBWP has to be revised.
The above comparisons and remarks lead us to call into question the
![]() values of the standard stars from SCBWP.
values of the standard stars from SCBWP.
This paper is a first step, and a second part will complete these data with a northern sample of A-type stars.
Acknowledgements
We are very grateful to Dr M. Ramella for providing us the computer program used to derive the. We also thank the referee, Prof. J. R. de Medeiros, for his several helpful suggestions. Precious advice on statistical analysis was kindly given by Dr F. Arenou and was of great utility. We want to acknowledge Dr F. C. Fekel for his help in comparing
with data from the literature. Finally, we are thankful to B. Tilton for her careful reading of the manuscript. This work made use of the SIMBAD database, operated at CDS, Strasbourg, France.
Some of the stars whose spectrum has been collected several times show
different
![]() from one spectrum to another (flag "SS'' in
Table 4). These differences could be related to intrinsic
variations in the spectrum itself. Other stars present a high
dispersion in the measures from lines in a single spectrum (flag "LL'' in Table 4). These stars are detailed in Appendices A.2.1 and A.2.2 respectively.
from one spectrum to another (flag "SS'' in
Table 4). These differences could be related to intrinsic
variations in the spectrum itself. Other stars present a high
dispersion in the measures from lines in a single spectrum (flag "LL'' in Table 4). These stars are detailed in Appendices A.2.1 and A.2.2 respectively.