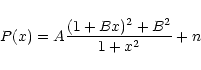A&A 380, 745-749 (2001)
DOI: 10.1051/0004-6361:20011450

Application of Fano profiles to asymmetric resonances in helioseismology

A. H. Gabriel1 - J.-P. Connerade 2 - S. Thiery1 - P. Boumier1

Institut d'Astrophysique Spatiale, Université Paris XI, 91405 Orsay, France - Imperial College of Science and Technology, London, UK

Received 27 October 2000 / Accepted 8 October 2001

Abstract
Parallels are drawn between the asymmetric resonance profiles observed in global helioseismology and the Fano theory for autoionisation profiles in atomic spectroscopy. We show that the underlying physics of the interaction of a discrete resonance with a correlated continuum is common to both systems. The approximate formula normally used for fitting to profiles in helioseismology is essentially similar to that developed for atomic spectroscopy by Fano. We propose that the two systems are in reality equivalent. This proposition enables us to understand better which resonances in helioseismology will be correlated with each other and with which solar background "continua". We also question whether the two interacting influences of excitation sources and correlated solar background, are really separate independent processes.

Key words: Sun: interior, helioseismology


1 Introduction

It is only in recent years that we have begun to understand the importance of asymmetry in the resonance profiles obtained in helioseismology (hereinafter referred to as HS). The possibility of such effects was predicted by M. Gabriel (1992) and soon confirmed through observations by Duvall et al. (1993). More recently, they have been studied in the high-degree resonances obtained from spatially-resolved HS (Kosovichev et al. 1997) and in global (integrated disk) solar resonances by Toutain et al. (1998) and Thiery et al. (2000).

In this paper, we take note of the similarity with another branch of physics, and examine what can be learned from this. We refer to the field of atomic spectroscopy (hereinafter referred to as AS), in which discrete atomic levels above the first ionisation limit are found to have similar asymmetric line profiles. These levels, first observed in absorption spectroscopy (Beutler 1935), were later interpreted theoretically by Fano (1961) as due to the interaction of the discrete state with continuum states of the same energy.

More important than the phenomenological resemblance is our perception that the underlying physics has many points in common. Both situations can be thought of as arising through the mixture of coincident stationary states, one arising from a discrete resonance, the other a "continuum" in the AS language, which is equivalent to "background noise" in the present-day terminology of HS. This mixing of states exists when they have the same energy (or frequency) and the same angular momentum (correlation in HS) and results in a new combined state of line and continuum, with the characteristic observed asymmetry.

The subject in HS is relatively new and it is clear from the diverse presentations at recent colloquia that a full understanding of the problem and its consequences is not yet attained. On the other hand, the problem in AS has been studied for over 40 years and has been developed into a well-understood field, capable of application to complex situations and showing detailed agreement between theory and observations.

2 Resonance profiles in helioseismology

After a long period of fitting Lorentzian profiles to the HS resonances, the analysts, motivated by theoretical predictions, have now moved towards fitting asymmetric profiles. Theoretical modelling for such profiles has followed the route of solving numerically the wave equations in a potential well, defined by the solar boundary conditions. Such modelling successfully reproduces many features of the observed profiles, especially for the "Rydberg" series observed in high-l spatially resolved HS. Rydberg series, having constant values of l and m, but a sequence of adjacent values of n are familiar in AS. In HS, they are produced in imaging resonance patterns by applying a spatial filter to isolate only one set of values of l and m.

Abrams & Kumar (1996) developed the theory of asymmetry in terms of the presence in the field of view of the exciting source for the oscillations, in addition to the standing waves themselves, this opening the possibility of using the asymmetry in order to identify the nature and depth of the exciting sources. A numerical solution does not give a convenient parametric form required by analysts to fit their measured resonances and to replace systematically the earlier Lorentzian fitting. With this in mind, Nigam & Kosovichev (1998) derived a simplified parametric formula on the basis of their more complete wave solutions. At the same time, Toutain et al. (1998), in analysing the resonances produced by the instruments MDI and VIRGO on the spacecraft SOHO, showed that the symmetry of the profiles was reversed in sign, as between observations made of the same resonances in velocity and in intensity. The Nigam & Kosovichev formulation is now adopted by the majority of observers as the basis of their fitting procedures. The formula is reproduced in the expression:

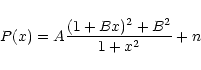\begin{displaymath}P(x) = A \frac{(1+Bx)^2 + B^2}{1+x^2} + n \end{displaymath} (1)

where $ x=2(\nu-\nu_0)/\Gamma $ and $A,\Gamma, \nu_0, n$ are the mode amplitude, linewidth, resonance frequency and uncorrelated background noise, respectively. B is a dimensionless asymmetry parameter, whose value is zero for a Lorentzian profile, increasing with the asymmetry, up to typical values around 0.05 for low-l resonances. In deriving this formula, the authors tried to take into account the reversal of symmetry observed by Toutain et al. and did this by introducing a new effect into the theory, which they termed the "correlated background". The principle was that some proportion of the background solar noise will be phase correlated with the resonances and that this will introduce an asymmetry in the opposite sense from that produced by the sources (B would be positive instead of negative). According to their ideas, the two effects produce asymmetry of the same functional form, but with different magnitude and of opposite sign.

The route for deriving Eq. (1) was such that a fully analytic form does not result easily and it proved necessary to simplify their expression through an expansion in small quantities and the neglect of higher order terms. Because of this, the authors caution that the expression is valid only in the immediate vicinity of the resonance. This reservation poses a number of questions for observers, which are not answered in the presentation. If the expression is only valid in the immediate vicinity of a single resonance, how do we fit multiplets? Also, how do we cope with the non-zero value of the expression at large distances from the resonance? Furthermore, is it possible to use this expression for a simultaneous fit to all of the observed resonances in the frequency range covered, as practised by some analysts? (cf. Lazrek et al. 2001).

If we examine the properties of the expression in Eq. (1) we see that the second term, represented by the B2 in the numerator represents an added Lorentzian component. However, for real cases encountered in global HS, where B is less than 0.05, the effect of this second term is very small and can be neglected. At large deviations from the resonant frequency, the expression tends to a constant value (equal to AB2 + n), a result that is not surprising, since it represent the combined effect of the resonance, the correlated and the uncorrelated backgrounds.

If we reflect on the ideal solution to the problem of excitation of proper modes by the random, non-linear turbulent field, we might conclude that a complete model requires the solution of the combined system in an integrated way. Since we are not today capable of modelling correctly the turbulence, we treat the components separately, using different methods, and combine the results. The danger inherent in this procedure is that of counting some effects twice. In this sense, we question here whether the presence of the source and the existence of correlated background are perhaps alternative representations of the same process.

3 Autoionisation profiles in atomic spectroscopy

The problem in AS can be represented in its simplest form by an energy level diagram, as shown in Fig. 1. An autoionising level, $\phi $, is in energy resonance with a band of continuum, indicated as E'. These two zero-order states do not truly exist separately. Their strong interaction results in a new combined state, shown diagrammatically on the right side of the figure. The interaction results in a characteristic asymmetric profile, representing the combined resonance and continuum, superposed upon a smoothly varying continuum. In a quantum situation, it is not possible to observe any energy state except through its transition to or from another level. In this case we examine the new combined level by looking at the absorption line from a lower ground level i. The transition to the combined asymmetric state is evaluated in terms of the hypothetical transitions to each of the two zero-order parent states.

  \begin{figure} \par {\psfig{figure=fig1d.ps,width=6cm,angle=0} } \end{figure} Figure 1: Showing the interaction between a discrete level $\phi $ and an adjacent continuum E'.
Open with DEXTER

The resultant profile, derived originally by Fano (1961) can be obtained using several alternative methods. These derivations can be found discussed in Connerade (1998). Fano's expression can be written

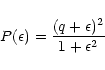\begin{displaymath}P(\epsilon) = \frac{(q+\epsilon)^2}{1+\epsilon^2} \end{displaymath} (2)

where

\begin{displaymath}q=\frac{<\phi\mid T\mid i>}{\sqrt{\Gamma/{2\pi}}<E'\mid T\mid i>}\cdot \end{displaymath}

Here $<\phi\mid T\mid i>$ is the transition matrix element between states i and $\phi $, etc., and $\Gamma$ is the damping width of the excited state. This is related to the spontaneous decay rate of the hypothetical zero-order state $\phi $ by radiationless transition to the continuum E'. $\epsilon$ is the displacement from the resonance frequency, expressed in units of $\Gamma/2$.

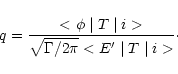
Examination of this expression shows it to have an identical form to that of Eq. (1), if we suppress the term B2 and the non-correlated background n in Eq. (1). The present asymmetry factor q is equivalent to 1/B and is infinity for the Lorentzian profile limit, decreasing with increasing asymmetry (see Fig. 2).

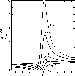  \begin{figure} \par {\psfig{figure=fig2.ps,width=6.8cm,angle=0} } \end{figure} Figure 2: The family of spectral profiles, resulting from Eq. (2) (Fano 1961).
Open with DEXTER

It should be emphasised that Eq. (2) has been obtained by diagonalising the zero-order matrix and is in this sense a complete expression, without any assumption regarding small quantities or perturbations. The sign of the asymmetry q depends on the relative signs of the two transition matrix elements in q. In AS, this depends on the symmetry of the wave-functions involved and has different values in different cases. It should be noted that in this quantum representation it is normal that this would depend on the third state, i. This implies that the asymmetry and sign of the combined state in question can depend upon the manner in which this state is observed. This suggests the possibility that this situation, common in quantum physics, has a useful parallel in the case of HS, where we observe a change in the sign of B between observations in intensity and velocity. On the other hand, in the atomic physics case, the damping width $\Gamma$ is a function only of the resonance and is unaffected by the method of observation.

Equation (2) in AS described here is only valid when we have one isolated resonance interacting with one continuum. The situation becomes more complex when we have more than one resonance interacting with the same continuum, or one or more resonances interacting with several continua. However, these more complex cases have been worked out in detail and many examples can be found in the literature cited above. In the AS situation we can predict which resonances will interact with which continua and with which other resonances. In general this depends only on the need to have the same angular quantum numbers. Here we speak of those that are "good" quantum numbers, depending on the situation. Thus in AS, for the case of LS coupling, we speak of L and S and parity. In the case of intermediate coupling, these are replaced by J and parity. By equivalence, it follows that for the HS case it is the numbers l and m that must be the same for the interacting states. Levels that satisfy these requirements, but have different order, n, interact with each other, as with also a common continuum (for which discrete values of n are not imposed). We recall here that levels can only interact if they have the same energy. In practice this means that the interaction is evaluated for each point on the frequency scale, treated point by point throughout the wings of the resonances.

A particular case arises when we consider a "Rydberg" series; that is a series of consecutive resonances having the same angular quantum numbers but with increasing values of order, n, interacting with a continuum having the same angular quantum numbers. Because of the tendency of these resonances to converge as n increases, the interaction between neighbouring resonances becomes important. In AS, this special case has a particular solution, illustrated by Connerade (1998) in which the far wings of the simple Fano profiles interact in phase with each other producing a characteristic profile for the series with zeros between each resonance. Analytic expressions exist for these profiles. Here we note that a very similar solution is derived in HS for the parallel case, which is commonly found in spatially filtered resonances of higher-degree observations (see Fig. 3).

  \begin{figure} \par {\psfig{figure=fig3b.ps,width=6.8cm,angle=0} } \end{figure} Figure 3: Showing Rydberg series of profiles: a) theory for autoionising lines in lead (Connerade & Lane 1998) and b) MDI observations for l=200 n-series of solar oscillation modes (Kosovichev et al. 1997).
Open with DEXTER

4 Important differences

The above sections discuss a number of parallels between the two situations compared. Here we draw attention to some important differences, which need to be further considered.

Firstly there is the fact that the AS situation falls in the quantum area, where the observables are always the result of a transition between two states. In the more classical HS situation, we have the impression that we observe directly one of the states. However, the Principle of Equivalence teaches us that these may in reality be only different limiting cases of a common situation.

The second difference lies in the shape of the potential well. In atomic physics this tends asymptotically to a coulomb potential and in this situation the solution of the wave equation predicts an infinite number of bound states below the first ionisation limit. In the case of the Sun, the potential well approximates to a rectangle and there are only a finite number of bound states. However, there will still be some bound states having the same energy as other free states, so that the analogy remains valid.

5 Connection with scattering theory

Further support for the assumptions made in the above comparison between the two disciplines can be found from the application to these questions of scattering theory.

Spherical resonators are not very common in classical (non-quantum) physics. Nor are situations in which resonances and free oscillations occupy the same frequency space. However, not only atomic (Beutler-Fano profiles), but also nuclear physics are familiar with such problems. In the latter case, these are the well-known Breit-Wigner resonances. Wigner (1946, 1948) introduced scattering matrices in order to treat this problem in the most general way. He made the important point that this step does not require one to solve the differential equation describing the system, but only to postulate its existence. He also points out that the method is applicable to any system described by a wave equation, of which the Schrödinger equation is only one particular example.

The scattering process is expressed in terms of phase shifts. The total phase shift $\Delta$ is expressed in terms of that due to the resonance $\Delta _0$ and the phase shift $\delta$ due to the background continuum:

\begin{displaymath}\Delta = \Delta_0 + \delta . \end{displaymath} (3)

The use of the K-matrix formulism then leads to the derivation of the Fano expression given in Eq. (2). Expressions for autoionization in terms of scattering phase shifts were already given in an Appendix to Fano's paper (1961). Later, Shore (1967) developed a scattering theory of absorption profiles and refractivity using Wigner's S-matrix formulation. This leads to a more general and symmetric version of the Fano formula:


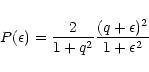\begin{displaymath}P(\epsilon) = \frac{2}{1+q^2} \frac{(q+\epsilon)^2}{1+\epsilon^2} \end{displaymath} (4)

where the normalisation factor ensures a value of $P(\epsilon)$ finite, even for $q \rightarrow \pm \infty$.

The development and the formulae are independent of $\hbar$. The only way quantum theory intrudes is that observations of a quantum system are usually performed by observing transitions to other bound states. For scattering transitions, which are the basis of Wigner's theory, these other states are not involved, so that the results are fully valid in the classical limit. The qparameter is then directly related to the phase shift $\delta$ of the continuum in the presence of the resonance.

6 What can we conclude from the comparisons?

To the extent that we may be convinced of a common physical basis underlying these comparisons, it is possible to draw a number of conclusions in the field of HS. These can be summarised:

1.
The Fano theory and its developed formalism can be applied in general to the field of HS, in particular the application of Eq. (2) to the profiles of isolated resonances.

2.
The additional term B2 in the Nigam fitting formula is unnecessary. It is an outcome of the simplification procedure used and has no significant reality. For HS, its effect on the profile is negligible, so that no error is introduced by its continued inclusion.

3.
The Nigam formula (with or without this term) has the correct asymptotic form at large frequency displacements, and can be safely applied up to distances where we begin to approach another interacting resonance. The caution expressed in this regard in the Nigam & Kosovichev paper is unnecessary.

4.
The formula used, Nigam or Fano, represents the combined profile of resonance and correlated background. When fitting a complete spectrum including many resonances, as do some workers, care must be exercised regarding the additive effects of such continua or backgrounds. One background will correlate with several resonances, which should then formally be treated together as a combined system. The correlated background for one resonance will be part of the non-correlated background for certain other resonances.

5.
Resonances and backgrounds that are correlated and therefore phase-interact with each other are those with the same energy (or frequency) and angular momentum. This implies the same angular "quantum numbers" l and m, whenever these are "good" quantum numbers. They can have different radial numbers, n and, of course, the backgrounds have no discrete radial numbers. It follows that there is no formal error in treating a multiplet, or even the combined multiplets l=0 and l=2, as a group of non-correlated components with their profiles added on a power scale.

In addition, we are tempted to question whether the opposite symmetries, observed for the same resonance viewed in velocity and intensity, are due to the same effect. The change in symmetry and in its sign could be due to the choice of the observing parameter chosen. To understand and predict this polarity will require a more complete development of the physical comparisons than can be performed in this paper. We note here that the theory of asymmetry reversals in AS is highly developed.

7 Discussion and conclusions

It is shown that there are strong parallels, both in the physics and in the formalism, between the two different systems compared here. This similarity enables us to use the more mature autoionisation theory in order to clarify a number of questions concerning asymmetries in helioseismology, in particular concerning how to treat a number of interacting resonances and backgrounds. Some doubt is expressed regarding the separate nature claimed for the source and correlated background effects in the HS formalism.

References

 

Copyright ESO 2001