A&A 380, 645-664 (2001)
DOI: 10.1051/0004-6361:20011479

Kinetic equilibrium of iron in the atmospheres of cool dwarf stars

II. Weak Fe I lines in the solar spectrum

T. Gehren1 - A. J. Korn1 - J. Shi1,2


1 - Institut für Astronomie und Astrophysik der Universität München, München, Germany
Universitäts-Sternwarte München (USM), Scheinerstr. 1, 81679 München, Germany
2 - National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100012, PR China

Received 22 August 2001 / Accepted 18 October 2001

Abstract
NLTE line formation calculations of Fe I in the solar atmosphere are extended to include weak lines in the visual spectrum of the Sun. Previously established atomic models are used to discriminate between different ways of treating collisional interaction processes. As indicated by the analysis of strong Fe I lines, the influence of deviations from LTE in the solar atmosphere on the Fe abundance is small for all lines. To derive a common solar Fe I abundance from both strong and weak lines fine-tuning of the microturbulence velocity parameter and the van der Waals damping constants is required. The solar Fe I abundances based on all available f-values are dominated by the large scatter already found for the stronger lines. In particular the bulk of the data from the work of May et al. and O'Brian et al. is not adequate for accurate abundance work. Based on f-values measured by the Hannover and Oxford groups alone, the Fe I LTE abundances are $\log\varepsilon_{\rm Fe{\sc i},\odot} = 7.57$ for the empirical and $\log\varepsilon_{\rm Fe{\sc i},\odot} = 7.48 \ldots 7.51$ for the line-blanketed solar model. The solar Fe ionization equilibrium obtained for different atomic and atmospheric models rules out NLTE atomic models with a low efficiency of hydrogen collisions. At variance with Paper I, it is now in better agreement with laboratory Fe II f-values for all types of line-blanketed models. Our final model assumptions consistent with a single unique solar Fe abundance $\log\varepsilon_{\rm Fe,\odot} \sim 7.48 \ldots 7.51$ calculated from NLTE line formation are (a) a line-blanketed solar model atmosphere, (b) an iron model atom with hydrogen collision rates $0.5 < S_{\rm H}< 5$ times the standard value to compensate for the large photoionization cross-sections, (c) a microturbulence velocity $\xi_{\rm t}= 1.0$ km s-1, (d) van der Waals damping parameters decreased by $\Delta\log C_6 = -0.10 \ldots -0.15$ as compared to Anstee & O'Mara's calculations, depending on $S_{\rm H}$, (e) Fe II f-values as published by Schnabel et al., and (f) Fe I f-values published by the Hannover and Oxford groups.

Key words: line: formation - line: profiles - Sun: photosphere - Sun: abundances


1 Introduction

Our previous attempt to understand the formation of the iron spectrum in cool dwarf stars (Gehren et al. 2001, Paper I) was successful in isolating some of the important interaction processes encountered in stellar atmospheres of spectral types F and G. The compensating influence of (a) strong collisional coupling of the highly excited (>7.3 eV) Fe I terms to the $a^{6}{\rm D}$ground state of Fe II, (b) hydrogen collision cross sections, and (c) photoionization from the low-excitation terms was shown to dominate the synthesis of line profiles and the abundances of solar lines.

The lines used for the analysis were selected for strength because it is planned to extend the investigation to extremely metal-poor stars where the NLTE effects are predicted to be much more important. In such stars only lines are detected that are strong in the Solar spectrum. The comparison of observed solar flux spectra with synthesized line profiles is thus hampered by all the problems usually occurring whenever line-broadening starts to play a role.

The treatment of van der Waals damping had been based on relatively simple approximations for a long time (Unsöld 1968; Kurucz 1992), often resulting in significant underestimates of the damping constant. For a treatment of NLTE effects this was completely inacceptable, thus in Paper I we applied the quantum mechanical calculations of Anstee & O'Mara (1991, 1995) without any corrections. Although the results show substantial improvements there were still multiplets for which corrections would seem adequate from profile fitting. This is not easily explained although the calculations refer to simple LS coupling schemes whereas some of the upper Fe I terms involved are affected by mixing from different configurations. It appears that the Anstee & O'Mara damping constants in some multiplets lead to line abundances that are slightly smaller than those obtained from weaker lines.

Granular hydrodynamics are a second item that affects our results (Asplund et al. 2000). Relying on horizontally homogeneous, plane-parallel atmospheric stratifications implies that dynamic movements are replaced by approximate velocity fields, usually termed micro- and macroturbulence. For obvious reasons such an artificial replacement could depend on atmospheric depth as found in the empirical solar model of Holweger & Müller (1974). Whereas such a stratification $\xi(\overline{\tau})$ can in principle also be constructed for other solar models, this is not always possible for other stars. Therefore, our fit to the solar Fe I line spectrum was based on a single microturbulence velocity $\overline{\xi}$. The values assumed for the strong lines of Paper I ( $\xi_{\rm t}= 1.00$ km s-1 for the empirical and $\xi_{\rm t}= 0.85$ km s-1 for the line-blanketed atmospheric model) were smaller than usually adopted for both types of model atmospheres. Thus, based on turbulence lines alone (lines whose equivalent widths are dominated by broadening due to microturbulence velocities), the abundances derived for both Fe II and Fe I would be slightly too high.

After having examined more than 100 strong Fe I lines arising from excitation energies between 0 and 5 eV including some of the stronger turbulence lines we have found that combinations of certain atomic model properties lead to acceptable solar flux profile fits if varying macroturbulence velocities $\Xi_{\rm rt}$ (Gray 1977) are applied. Due to the fact that a plane-parallel atmospheric model can not represent granular hydrodynamics with infinite accuracy, we have not tried to improve our NLTE profile fits beyond certain limits that are characterized by $\sim $1% rms deviation from the observed fluxes. Yet it became clear that atomic models with different strengths of collisional interaction led essentially to similarly good fits. This could be explained as a consequence of different Fe I abundances or uncertain f-values and van der Waals damping parameters. Unfortunately, the solar Fe II abundances are at least as uncertain due to significantly different sets of f-values. Thus the solar ionization equilibrium of iron could not be established because the absolute abundances were uncertain from both ends.

As explained above part of the uncertainty remaining after modelling the strong lines is due to line-broadening by microturbulence and damping. Our understanding of the kinetic equilibrium of Fe I could therefore be considerably improved by extending the NLTE line formation analysis to lines that are substantially weaker than those of Paper I. Such lines would not be detected in metal-poor stars, but they would help to select the atomic model producing the best fit to the solar spectrum. Our present investigation is thus extended to a large number of lines with equivalent widths smaller than $\sim $100 mÅ. This includes lines of all degrees of excitation, although recently identified Rydberg transitions in the infrared with excitation energies well above 7 eV (Johansson et al. 1994; Schoenfeld et al. 1999) were excluded because no f-values are available. The following section gives a short representation of the assumptions concerning both atomic and atmospheric models. Section 3 introduces the sample of Fe I lines with results of NLTE line formation and profile synthesis. The last section presents our conclusions and a comparison with those of Paper I. We note in advance that the present analysis is still not able to produce a unique atomic model that can be applied to all kinds of stars. Such an investigation is left to a forthcoming paper, in which we will extend the analysis to a number of (mostly metal-poor) reference stars.

2 Model assumptions

2.1 Atomic models

Basic atomic models are the same as those of Paper I. Because they are described there at considerable length we will not repeat the details here. The main differences between them are characterized by


  \begin{figure} \resizebox{\hsize}{!}{\includegraphics{plot/fig1.ps}}\end{figure} Figure 1: Photospheric solar temperature distributions of the HM empirical model (dashes) and the TH line-blanketed model (continuous curve).

2.2 Atmospheric models

The two plane-parallel horizontally homogeneous atmospheric models used in our analysis are the semi-empirical solar model of Holweger & Müller (HM, 1974) and our line-blanketed solar model (TH, see Paper I). Their most important difference with respect to line formation is the temperature stratification, with $T_{\rm HM}(\overline{\tau}) - T_{\rm TH}(\overline{\tau}) \sim 150$ K at optical depths between 0.1 and 1.0. The two stratifications are displayed in Fig. 1, and the most important result of the temperature difference is that typically the stronger lines are calculated with weaker line wings in the empirical solar model. Therefore a proper fit of Fe I line profiles using the HM empirical model always requires slightly higher damping parameters than for the TH model.

Other important parameters of the models are those determining non-thermal spectral line core broadening. In Paper I we have chosen $\xi = 1.00$ (HM) and 0.85 km s-1 (TH), $\Xi_{\rm rt} = 2.5$ (HM) and 3.2 km s-1 (TH), respectively. There is clear evidence that both micro- and macroturbulence vary with depth of line formation, however, only $\Xi_{\rm rt}$ was allowed to vary between $\sim $2.0 km s-1 for some of the most saturated Doppler profiles and $\sim $4.0 km s-1 for very weak lines. For a more realistic analysis of both weak and strong lines in this paper we have added a second value of $\xi = 1.00$ km s-1 for the TH model and recalculated the non-LTE populations and line profiles. No such alternative was examined for the HM model although this would probably reduce the solar Fe I abundances by similar amounts as for the TH model.

The empirical HM model is used here only as a comparison for abundance discussions. It had been established as a reference for LTE conditions in the solar photosphere, and therefore we have not attempted to calculate non-LTE populations for its temperature distribution. All the other level populations in this paper thus refer to the TH model for which we distinguish between the (sets of) model assumptions given in Table 1.

 

 
Table 1: TH models used in the present calculations.
  Type $\overline{\xi}$ $S_{\rm H}$ $E_{\rm min}$ $\Delta\log C_6$ Name

0		 LTE 0.85       LTE (0.85)
1 NLTE 0.85 0.0 7.3   0+ (0.85)
2 NLTE 0.85 5.0 7.3   5+ (0.85)
3 NLTE 0.85 5.0     5- (0.85)
5 LTE 1.00       LTE (1.00)
6 NLTE 1.00 5.0 7.3   5+ (1.00)
7 NLTE 1.00 1.0 7.3   1+ (1.00)
8 NLTE 1.00 1.0 7.3 -0.4 1+ (1.00)
9 NLTE 1.00 0.5 7.3 -0.4 0.5+ (1.00)


Here, $S_{\rm H}$ and $E_{\rm min}$ refer to the model atom interaction described in Sect. 2.1, whereas $\Delta\log C_6$ in the last two entries specifies a decrease of the damping constants with respect to the Anstee & O'Mara standard. This type of model leads to a substantially improved fit of turbulence lines and those broadened by van der Waals damping (see below). Note that for each model both NLTE populations and line profiles have been recalculated. When deriving solar Fe I abundances in Sect. 3, some of these models are used to interpolate between different damping parameters (models 7 and 8).

3 The solar weak line spectrum

Iron is the element with probably the greatest number of lines visible in the solar spectrum. This is the combined result of a relatively high element abundance and of a very complex atomic configuration. In particular for Fe I nearly 10000 lines have been identified in the laboratory (Nave et al. 1994), and possibly hundreds of thousands more are too weak to be detected. However, for only a small subset of these lines accurate f-values are known; most of them are laboratory data while only a subset has been derived from the solar spectrum itself. Our ability to identify the lines with laboratory f-values in the solar spectrum and calculate their solar Fe I abundances is therefore strongly influenced by the accuracy of the data, and it is this dependence that makes an analysis of the complete solar iron spectrum next to impossible as we will demonstrate below.

The term "weak line'' refers to all line strengths that had not been considered in Paper I, and it does not necessarily indicate a particularly small line strength. Thus, all lines in the list of Nave et al. have been examined if an f-value was available. Among them were only $\sim $500 lines with equivalent widths below 100 mÅ that were not too strongly blended by other lines. Some of the lines retained in our sample are still blended but are either well-resolved or at least permit the analysis of one line wing. From this list we had to exclude lines in spectral regions that in the solar spectrum were overly affected by weak line haze and continuum uncertainties. These lie in the blue-green ( $4400 \ldots 4800$ Å) and in the yellow ( $5500 \ldots 5900$ Å). The source of these spectral impurities is unknown although part of the blue could well be contaminated by a complicated pattern of Fe I autoionization transitions. Bautista's (1997) calculations show that they are there, but the accuracy of their wavelength positions is probably not very high. The total number of Fe I lines including weak and strong lines was therefore reduced to 410, and during subsequent NLTE analyses their number once again shrank to the final value of 391 lines.

One of the more surprising results of this evaluation of the solar Fe I spectrum is that the number of truly weak lines with both an acceptable spectral environment and laboratory f-value is so small. This is the case for lines in a range of solar equivalent widths from 3 to 30 mÅ. This has also been noticed among others by Rutten & van der Zalm (1984). If laboratory analyses were extended into the near infrared the line list could be greatly extended because of decreasing blend problems. The blue and near-ultraviolet spectral regions have been ignored here because of the problems localizing the continuum below 4200 Å.

3.1 Spectrum synthesis

The final set of lines is reproduced in Table 2 together with all relevant data. The sources of the f-values as well as the remarks in the second last column are noted at the end of the table. The damping constants are calculated according to Anstee & O'Mara's (1991, 1995) theory as in Paper I, and they are given here in terms of van der Waals damping constants. The equivalent widths in the last column are integrated on the basis of the best synthetic fit of the solar flux profile. We emphasize that they are not used for the line analysis which is solely based on profile fits. Rather, they are derived from the theoretical profile after the final profile fitting procedure. Their accuracy is low, which is uncritical since they are used for graphical purposes only.

3.1.1 Oscillator strengths

In order to determine abundance ratios in spectral lines of stars other than the Sun it is often sufficient to know the product $gf\varepsilon_\odot$, which can be obtained in the solar flux spectrum with no particular knowledge of the f-value. Were it not for consistency and identification checks and for the determination of the solar iron abundance itself, no oscillator strengths would be needed. Such consistency checks include the specification of broadening parameters such as microturbulence and damping constants, because both can to a certain degree replace abundances or oscillator strengths. Therefore a critical analysis of the f-values is necessary. As mentioned above, oscillator strengths available for Fe I lines come from essentially three different methods:

Of these three methods we have applied only the results of the last two methods to spectrum synthesis, and in solar abundance determinations we confine our sample to those lines for which laboratory f-values are available.

3.1.2 Line broadening
During the analysis of the strong Fe I lines we have discussed collision broadening at some length in Paper I, where it was documented that the results of the broadening theory of Anstee & O'Mara (1991, 1995) provided the necessary adjustment between weak and strong line abundances at least in a qualitative way. We have followed this approach in the present investigation, replaced the old van der Waals damping constants by the new collision parameters, however, staying aware of the dependence of abundance analyses upon atmospheric models. Thus, the empirical model of Holweger & Müller (1974) requires significantly higher damping constants than our theoretical model in order to fit solar strong line profiles with the same abundance as the weak lines. In fact, we have added to our sample of NLTE models two more items with reduced damping constants in order to explore their influence on the mean Fe I abundance. We come back to this point in Sect. 3.2.2.
  
Table 2: Fe I lines in the solar flux spectrum including lines of Paper I, which have been recalculated with current model settings and f-values eliminating some errors in the previous data set. Sources of f-values and remarks are noted at the end of the table. NLTE models are described in the text. Equivalent widths are in mÅ.

\begin{displaymath}{\tiny \begin{tabular}{rr@{--}lrrrlr\vert rrrr\vert rrrrrr\ve... ...6 & cd & $ 10.2$ \\ \noalign{\smallskip }\hline \end{tabular}}\end{displaymath}



Table 2.  continued.

\begin{displaymath}{\tiny \begin{tabular}{rr@{--}lrrrlrrrrrrrrrrrp{20pt}r} \hlin... ...3 & ac & $ 43.9$ \\ \noalign{\smallskip }\hline \end{tabular}}\end{displaymath}



Table 2.  continued.

\begin{displaymath}{\tiny \begin{tabular}{rr@{--}lrrrlrrrrrrrrrrrp{20pt}r} \hlin... ...61 & a & $ 16.8$ \\ \noalign{\smallskip }\hline \end{tabular}}\end{displaymath}



Table 2.    continued.

\begin{displaymath}{\tiny \begin{tabular}{rr@{--}lrrrlrrrrrrrrrrrp{20pt}r} \hlin... ...50 & a & $ 54.3$ \\ \noalign{\smallskip }\hline \end{tabular}}\end{displaymath}



Table 2.    continued.

\begin{displaymath}{\tiny \begin{tabular}{rr@{--}lrrrlrrrrrrrrrrrp{20pt}r} \hlin... ...3 & 7.45 & 7.50 & 7.51 & ac & $ 72.6$ \\ \hline \end{tabular}}\end{displaymath}

Sources of f-values: (a) O'Brian et al. (1991), (b) May et al. (1874), (c) Meylan et al. (1993), (e) Blackwell et al. (1979), (f) Blackwell et al. (1976), (g) Blackwell et al. (1982a), (h) Blackwell et al. (1982b), (i) Bridges & Kornblith (1974), (j) Garz & Kock (1969), (k) Wolnik et al. (1970), (l) Richter & Wulff (1970), (m) Gurtovenko & Kostik (1981), (n) Blackwell et al. (1979), (o) Blackwell et al. (1980), (p) Bard et al. (1991), (q) Bard & Kock (1994).
Line synthesis remarks: (a) no blend, no asymmetry, (b) resolved blend(s), (c) continuum adjusted, (d) unresolved blend(s), (e) core asymmetry, (f) blue and red wing deficit, (g) only red wing deficit, (h) core too wide, (i) core too narrow, (j) core too deep, (k) core too shallow, (l) all faint lines included.

The introduction of weak lines, among them many lines broadened by microturbulence, has considerably enhanced our possibility to judge the solar line spectrum and the necessary atomic data. So the present analysis required an extension of the parameter space covered by non-thermal motions to put both weak and turbulence lines on a common abundance level. In fact, irrespective of the source of f-values, lines between 50 and 120 mÅ tend to require systematically higher abundances than weak or very strong lines if the value of Paper I, $\xi = 0.85$ km s-1 was used. We introduced a second mean value of $\xi = 1.00$ km s-1 which seems more appropriate for our present investigation. Note that this value has only limited influence on the strong lines, so our former results stay essentially unchanged.

As will be shown in Sect. 3.1.3, the details of turbulent line broadening are still unsatisfactory for a number of medium-strong lines. Whereas all weak lines with equivalent widths below $W_\lambda \sim 70$ mÅ and most of the very strong lines are well represented by the synthetic line profiles, some lines around $W_\lambda \sim 70 \ldots 120$ mÅ are not reproduced by any choice of model parameters. This was noticed already in Paper I when trying to fit Fe II multiplet 42 or Fe I multiplets 1 or 36. The present selection of Fe I lines includes quite a lot of such lines that seem to document the ultimate difference between plane-parallel and hydrodynamical models. Following this difference it is interesting to compare the results of the two completely different model realizations of non-thermal motions. Therefore the results of Asplund et al. (2000) have been confronted with our data in Fig. 2.

  \begin{figure} \resizebox{\hsize}{!}{\includegraphics{plot/fig2.ps}}\end{figure} Figure 2: Abundance differences between lines synthesized in our plane-parallel LTE (TH) model and those obtained from a hydrodynamical solar model of Asplund et al. (2000). Lines that were synthesized in our plane-parallel model with continuum adjustment are drawn as open circles.

It is true that the mean abundance of the 49 lines in common is different by $\Delta\log\varepsilon \simeq 0.05$ (or even slightly more for turbulence lines), and this could be interpreted as the difference between plane-parallel and hydrodynamical models. But a closer view reveals that most of the weaker lines belong to a category that requires some continuum adjustment with respect to the solar flux atlas of Kurucz et al. (1984). There are some spectral regions that suffer from unknown continuum depressions, and whenever such an adjustment was used in our calculations, the abundance differences between our respective models shrank to a mean $\Delta\log\varepsilon \simeq 0.03$, more probably near the true difference between the models. It is interesting in this respect that the bulk of turbulence line abundances between 60 and 90 mÅ is systematically higher than those calculated from the hydrodynamical model. This is also found in our own data when strong lines and turbulence lines are compared, and it would mean that exactly this type of lines is not particularly well synthesized by plane-parallel models.

We emphasize, however, that a single value for the microturbulence velocity cannot be assumed to reproduce all types of core saturation found in turbulence lines. Our simple approximation is inconsistent in that it ignores the corresponding variations found and accepted for the macroturbulence velocity, and a free fit of the $\xi$ parameter for each line profile would have produced slightly improved results. Comparison with Asplund et al. (2000) finally shows that both weak and strong lines are not strongly affected by dynamic processes, which means that the conventional replacement of laminar flow patterns by a micro-/macroturbulence approach is still surprisingly valid.

  \begin{figure} \resizebox{\columnwidth}{!}{\includegraphics{plot/m1142.ps}} % \resizebox{\columnwidth}{!}{\includegraphics{plot/m1109.ps}} % \end{figure} Figure 3: Typical problems with the adjustment of the local solar flux atlas continuum. Top: weak line in Mult 1142 with no changes of the local continuum necessary. Bottom: Mult 1109 shown with and without continuum adjustment. The original atlas spectrum is reproduced with open circles and fitted by the grey curve with $\log\varepsilon_{\rm Fe} = 7.63$ and $\Xi = 4.0$ km s-1.


  \begin{figure} \par\hspace*{2mm}\hbox{\resizebox{\columnwidth}{!}{\includegraphi... ...\resizebox{\columnwidth}{!}{\includegraphics{plot/m1314_5650.ps}} } \end{figure} Figure 4: Profiles of weak lines ( $10 < W_\lambda < 60$ mÅ) of Fe I in the solar flux spectrum (filled circles). Synthetic profile fits are for LTE and HM ( ___ ) or TH ( .... ) atmospheres. Fit parameters are indicated.

   
3.1.3 Line profiles and equivalent widths

The overwhelming majority of publications is devoted to the investigation of equivalent widths which is mostly due to the easy access to such data in the literature. The critical examination of line profiles instead makes available an increased amount of information about line formation and stellar atmospheric conditions. Our present work on NLTE effects in Fe I lines is based on roughly 4000 line profiles, and their evaluation is coded in a very coarse set of remarks in Table 2. Such remarks combine the average profile properties of all models for a particular line, and the following description will show only typical properties.

Very weak lines ( $W_\lambda < 10$ mÅ):

Only 10% of the total sample consist of very weak lines. Most of them could be selected to be free from known blends, but only 10 of them were unaffected by problems with continuum adjustment. It is this latter quality that makes the analysis of very weak lines so ambiguous. This can be seen in Fig. 3 where the LTE profile fits for two lines are shown. Continuum adjustment is by far not always as small as 0.5% as it is for the line in Mult 1109, and ignoring it may lead to abundances higher by up to 0.15 dex in single cases.

It is no straightforward procedure to decide which lines to submit to continuum adjustment, because this requires a look at the whole spectral region. Consequently, we have adjusted the atlas continuum only if there is a continuum depression over at least 10 Å. In some cases we tried to synthesize faint background lines in order to estimate their influence on the continuum position. While weak lines should be least affected by broadening and therefore yield most reliable abundances, the continuum placement destroys a substantial part of this argumentation.

Weak lines ( $10 < W_\lambda < 60$ mÅ):

These lines constitute the majority of the sample with more than half in this range of equivalent widths. Up to 30 mÅ the lines do not depend significantly upon microturbulence, but their abundance change increases to -0.03 per 0.1 km s-1 at 60 mÅ. A number of weak lines that are fairly representative of our sample is reproduced in Fig. 4, together with LTE profile fits for both the HM and TH models. They are shown in particular to demonstrate the abundance differences between the two models. It should be mentioned here that this subsample of Fe I lines produces by far the best profile fits, followed by the strong lines, the very weak lines, and the turbulence lines, in order of decreasing fit quality. The profiles of the weak lines are not dictated by core saturation or line wing broadening but, nearly exclusively, by external line broadening due to solar rotation and macroturbulence. As is the case for some of the very weak lines, some weaker lines in Fig. 4 require a high macroturbulence of $\Xi > 4$ km s-1 in order to adjust the wings.

We note that the quality of the profile fit is the same for both atmospheric models, irrespective of the abundance differences. Thus most of the very weak and weak lines show a systematic abundance difference of $\Delta(\log\varepsilon_{\rm Fe,\odot})_{\rm HM-TH} = 0.06 \ldots 0.12$ (see below). As with the very weak lines, there is also no problem when fitting the profiles of the weak lines with different NLTE models (not shown in Fig. 4). However, the kinematic properties of all lines with equivalent widths below 100 mÅ are reproduced in a number of profiles that show systematic bisector curvature and a red line wing deficit. An even more critical inspection of some of the profiles reveals synthetic line cores that tend to be too broad even for $\xi = 0.85$ (TH) or 1.00 (HM) km s-1, respectively. This is evident in particular for lines that are formed further up in the atmosphere, and - together with the red wing asymmetries - it clearly documents the pitfalls of static atmospheric models. Some of the weak lines are also affected by a bad definition of the local continuum, which either lead to a removal of a significant number of lines originally selected or ended in a multi-line synthesis with a number of faint background lines included. Such results are not given too much weight in the abundance analysis.

  \begin{figure} \resizebox{\hsize}{!}{\includegraphics{plot/fig6.ps}}\end{figure} Figure 5: LTE profiles of Fe I 66, 5250.646 Å. Models are as in Figs. 4 and 6. Additionally, a TH LTE model with $\xi = 1.0$ km s-1 is plotted for comparison (dashes). The deep profiles are uncorrected for rotation and macroturbulence, the "v''-shaped profiles include external broadening.


  \begin{figure} \hspace*{2mm}\hbox{\resizebox{\columnwidth}{!}{\includegraphics{p... ...resizebox{\columnwidth}{!}{\includegraphics{plot/tm1260_5987.ps}} } \end{figure} Figure 6: Profiles of turbulence lines ( $60 < W_\lambda < 110$ mÅ) of Fe I in the solar flux spectrum (filled circles). Synthetic profile fits are again for LTE and HM ( ___ ) or TH ( .... ) atmospheres. Fit parameters are indicated.

Turbulence lines ( $60 < W_\lambda < 110$ mÅ):

Roughly 20% of our sample are strong enough for core saturation and are therefore shaped by the value of the microturbulence parameter. Naturally, a static model atmosphere reproduces such lines only in an approximative way. This is seen in Fig. 6 where a number of such lines and their synthetic fits are presented. Most of these fits require substantially smaller values of the macroturbulence velocity $\Xi$, but even then the synthetic core profiles are often too broad and too shallow.

In contrast to weaker lines for which the fit with synthetic profiles can be made nearly as accurate as desired, the fit of turbulence lines with a plane-parallel atmospheric model has its natural limitations which are explained by the velocity differences necessary to fit the innermost core and the wings simultaneously. Thus, in principle the saturated core seems to require relatively small velocity fields, whereas the opposite is required for the wings, a modulation that roughly represents the hydrodynamic equation of continuity. The microturbulence values used in the LTE models of Fig. 6 have in fact been chosen so as to fit the line core width. Using even larger values as would be indicated by comparison with weak and strong lines does not improve the profile fits although it may help to minimize the overall abundance scatter. Figure 5 emphasizes the difference in core saturation between the two model atmosphere types (HM and TH). Due to the temperature differences between the atmospheric models profiles synthesized from the HM model always require a smaller macroturbulence to fit the very line core than do the LTE or NLTE profiles based on the TH model.

We note that turbulence velocity gradients introduced within the scope of static plane-parallel models do not improve the profile fits either. The kinematic fine-tuning of the turbulence lines thus will stay the exclusive domain of granular hydrodynamics.

Again, as with the weaker lines, LTE and NLTE models both tend to produce similar profile fits for the turbulence lines provided that the abundances are correspondingly adjusted. This is a direct consequence of the source function thermalization inherent to our NLTE modelling. As can be seen in Table 2, lines with equivalent widths around 100 mÅ display an abundance spread of $\sim $0.2 dex among different LTE and/or NLTE models.

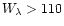The profiles of the stronger Fe I lines ( $W_\lambda > 110$ mÅ) have been discussed in Paper I. It is therefore sufficient to repeat here, that simultaneous fits of line cores and damping wings are only obtained outside the range of the inner wings ( $\pm 0.1 \ldots 0.4$ Å).

3.2 Abundances

Our investigation of NLTE excitation and ionization in the solar photosphere would not be complete without mentioning the solar Fe I abundance problem. Since there exists quite a number of publications on the "true'' solar Fe I abundance (e.g. Biémont et al. 1991; Blackwell et al. 1995a, 1995b; Holweger et al. 1995; Kostik et al. 1996; Grevesse & Sauval 1999), we will not enter into details but simply give our judgement according to the large number of lines of all strengths examined with reference to complete profile information (but ignoring their center-to-limb variation) and an exhaustive range of NLTE models.

Current analyses tend to put their results into perspective by denoting the differences between photospheric and meteoritic Fe I abundances. The latter has been known for many years now (Anders & Grevesse 1989), $\log\varepsilon_{\rm Fe{\sc i},\odot} = 7.51$. Photospheric abundance determinations, however, range from $\log\varepsilon_{\rm Fe{\sc i},\odot} = 7.42$ (Schnabel et al. 1999, Fe II) to 7.67 (Blackwell et al. 1995a, Fe I). As was pointed out by Kostik et al. (1996) and later iterated by Grevesse & Sauval (1999), the discrepancy between different groups of researchers depends on a number of different methods and data sets the influences of which are not always easily disentangled.


  \begin{figure} \resizebox{\hsize}{!}{\includegraphics{plot/fig7.ps}}\end{figure} Figure 7: LTE profiles of Fe I 1197, 6726.670 Å, computed with the HM model atmosphere displaying the sensitivity of turbulence lines with respect to abundance changes.

A few problems have already been discussed above, in particular the important influence of selecting a local spectral continuum. Other problems arise when determining abundances based on measurements of equivalent widths. Thus, Meylan et al. (1993) have used Voigt profile fits to reproduce their observed Fe I lines. Their results differ systematically from those of other methods produced either by planimeter measurements or - as in our case - from full line profile synthesis. This is an important source of systematic errors because anything but fitting synthesized profiles requires an estimate of the line wing extension that is often - and always systematically - neglecting a weak line haze. One of the more moderate examples is reproduced in Fig. 7. For this line Meylan et al. (1993) list an equivalent width of 53.6 mÅ, obtained from their Voigt profile fit. Our synthesis reproduces the observed solar flux spectrum with no continuum adjustment applying an Fe I abundance of $\log\varepsilon_{\rm Fe{\sc i},\odot} = 7.55$, whereas their equivalent width requires an abundance $\sim\!0.1$ dex higher than ours. More importantly, their equivalent width does not fit the observed profile. Other turbulence lines listed by Meylan et al. show even larger discrepancies up to 0.3 dex! Therefore it is not surprising that - using the f-values published in that paper - we derive a mean solar abundance of $\log\varepsilon_{\rm Fe{\sc i},\odot} = 7.25$. Altogether, at this stage of analyzing the solar Fe I abundance we ignore solar f-values because they would not add to abundance information, since their determination requires the input of a mean abundance value.
3.2.1 Sources of oscillator strengths

Except for the results of Meylan et al. (1993) and Gurtovenko & Kostik (1981) Table 2 contains only references to laboratory f-values that cover more than 80% of the lines. Among them we find essentially four different sets of data,

The rest of the sources is not very important for our investigation. The results listed in Table 2 refer to a broad selection of methods which have been repeatedly discussed (see Holweger et al. 1995; Kostik et al. 1996 or Grevesse & Sauval 1999). We start with a plain characterization of the abundance results obtained with the different sets of f-values.
  \begin{figure} \resizebox{\columnwidth}{!}{\includegraphics{plot/ab.ps}}\\ \resizebox{\columnwidth}{!}{\includegraphics{plot/efghnopq.ps}} \end{figure} Figure 8: Logarithmic solar abundances as a function of equivalent width in mÅ determined with the HM solar model in LTE and $\xi = 1.0$ km s-1. Top: oscillator strengths from May et al. (1974, filled circles) and from O'Brian et al. (1991, open circles). Bottom: f-values from the Hannover group (sources p, q of Table 2, filled circles) and from the Oxford group (sources e, f, g, h, n, o of Table 2, open circles). The range of $\pm 1\sigma $ rms scatter is indicated by the shading.

The top frame of Fig. 8 shows LTE abundance results obtained from the HM empirical model atmosphere using the data of O'Brian et al. (1991) and May et al. (1974), whereas the bottom frame of Fig. 8 displays the results for the oscillator strengths determined by the Oxford and Hannover groups. While the proper choice of models and parameters is discussed in the following subsection, it is already evident here that the two frames harbour sources of different quality. Thus, the f-values of O'Brian et al. or May et al. lead to approximately twice the rms scatter of the solar abundances as compared with the results derived from the f-values of the Oxford and Hannover groups. The May et al. abundances are also systematically higher than the mean.

The f-values of O'Brian et al. and those of Bard & Kock (1994) are on the same absolute scale since both have used very similar measurements and normalization procedures. In fact, Fig. 3 in Bard & Kock shows a negligible difference of the corresponding f-values for the lines in common, although the strong scatter is confirmed. What makes the O'Brian et al. sample so suspicious is the occurrence of abundance differences between lines in a common multiplet. An extreme case is Mult 66, where our results for $\lambda5145.099$ and $\lambda5250.646$ lead to $\log\varepsilon_{\rm Fe{\sc i}} = 7.34$ and 7.76, respectively. There are also other lines such as $\lambda4798.267$ and $\lambda4735.845$ of Mult 1042 with $\log\varepsilon_{\rm Fe{\sc i}} = 7.35$ and 7.81, respectively.

There is no simple explanation why the oscillator strengths of May et al. and those of Bard & Kock (1994) lead to different abundances. The data used in our analysis are those in Fuhr et al. (1988), which had been renormalized to the scale of the Oxford measurements. Most of the corrected May et al. f-values are therefore 0.1 dex smaller than the original data. Based on the original paper, the May et al. abundances thus would be 0.1 dex smaller. While this accounts for half of the difference between the two groups, there remains another 0.1 dex difference which is not seen in Fig. 2 of Bard & Kock. However, the rms scatter of both the original and the renormalized data set of May et al. is even slightly larger than that of O'Brian et al., and differences such as in $\lambda5395.250$ and $\lambda5487.160$ of Mult 1143 with $\log\varepsilon_{\rm Fe{\sc i}} = 8.01$ and 7.71, respectively, are also found in their sample.

Interestingly enough some of the more recent measurements of the Oxford and Hannover groups seem to produce substantially smaller scatter. Whereas $\sigma(\log\varepsilon_{\rm }) \sim 0.15$ for the O'Brian et al. and May et al. samples, $\sigma(\log\varepsilon_{\rm }) \sim 0.05 \ldots 0.07$ for the Oxford and Hannover lines. Figure 8 shows a marginal difference between the two groups, but that depends on a particular choice of our models with $(\Delta\log\varepsilon_{\rm Fe{\sc i}})_{\rm Oxf-Han} = 0.067$ for the HM LTE model and 0.026 for the TH LTE model. Let us mention here that line-by-line comparison of f-values of the two groups leads to a difference of $(\Delta\log gf_Fe{\sc i})_{\rm Oxf-Han} = -0.029 \pm 0.009$.

In order to evaluate the solar iron abundance we thus decided to disregard all but the Oxford and Hannover f-values. Unfortunately, this choice reduced our line sample from 391 to 97 lines. Figure 8 demonstrates that all of the weak lines in this combined sample are from Hannover sources whereas most of the strong lines were measured in Oxford. This correlates nicely with excitation energies, such that all low-excitation lines come from Oxford sources and all high-excitation lines are due to Hannover measurements.

3.2.2 The solar iron abundance


  \begin{figure} \par\hspace*{2mm}\hbox{\resizebox{85mm}{!}{\includegraphics{plot/... ...\hfill \resizebox{85mm}{!}{\includegraphics{plot/mod9e.ps}} } \par\end{figure} Figure 9: Solar Fe I abundances as a function of $W_\lambda $ (left) and lower-level excitation energy $E_{\rm low}$ (right), calculated for different models of line formation. Oscillator strengths are from the Oxford (open circles) and Hannover groups (filled circles). See text for further explanations.

Irrespective of the choice of the f-values the solar Fe I abundances as calculated from fitting the solar flux spectrum depend sensitively on the model assumptions. Blackwell et al. (1995a) and Grevesse & Sauval (1999) both have reported that the HM empirical solar model leads to Fe I abundances systematically higher than those obtained from theoretical models or other empirical models with a lower temperature in their upper layers. This is to be expected under the assumption of LTE since the source function then is always Planckian, and the emerging intensities in theoretical models will to first order follow the temperature stratification. It is, however, not evident for NLTE line formation, since there both the source function and the optical depth scale may deviate from their thermal behaviour.

In Paper I the level populations had been discussed for a number of LTE and NLTE population models. It was argued there that in most of the NLTE models - at least those with non-zero hydrogen collisions - the line source functions were very close to thermal, and the differences of line profiles with respect to LTE occurred essentially due to parametrization of (a) hydrogen collisions and (b) a cutoff energy above which all levels were thermalized with respect to the Fe II ground state. The latter operation had to be included to simulate the missing ionization/recombination channels. The different populations are shown in Fig. 6 of Paper I, and as yet we have not been able to choose a best case model on the basis of comparison with the strong lines only.


 

 
Table 3: Solar Fe I abundances based exclusively on the f-values of the Oxford and Hannover groups, calculated for different models of line formation. Note that $\Delta\log C_6$ refers to Anstee & O'Mara's damping constants. It was chosen so that the mean abundances did not depend on equivalent width (see left panels in Fig. 9). See text for further discussion.
  Model $\xi$ [km s-1] $\Delta\log C_6$ $\log\varepsilon_{\rm Fe{\sc i},\odot}$

0		 TH LTE 0.85 -0.12 7.508 $\pm$ 0.080
1 NLTE 0+ 0.85 -0.23 7.605 $\pm$ 0.087
2 NLTE 5+ 0.85 -0.10 7.521 $\pm$ 0.089
3 NLTE 5- 0.85 -0.15 7.629 $\pm$ 0.094
4 HM LTE 1.00 $\phantom{-}0.09$ 7.574 $\pm$ 0.074
5 TH LTE 1.00 -0.14 7.477 $\pm$ 0.070
6 NLTE 5+ 1.00 -0.12 7.488 $\pm$ 0.075
7 NLTE 1+ 1.00 -0.13 7.503 $\pm$ 0.077
8 NLTE 1+ 1.00 -0.16 7.499 $\pm$ 0.075
9 NLTE 1/2+ 1.00 -0.17 7.509 $\pm$ 0.077


Figure 9 therefore gives an impression of how the solar Fe I abundances obtained from line profile fits based on different LTE and NLTE models with different line-broadening parameters depend on the model assumptions. As mentioned above, only the Oxford and Hannover group f-values have been considered. With respect to Table 1 the models in Fig. 9 are modified using the original models 7 and 8 of Table 1 to interpolate corrections of the damping constant so that the resulting mean abundances are independent of line strength. As documented in Table 3 these additional corrections are always small. Comparing models 7 and 8 in Table 3 it is evident that the two interpolated results do not differ significantly.


  \begin{figure} \resizebox{\columnwidth}{!}{\includegraphics{plot/strongline.ps}}\end{figure} Figure 10: Solar flux spectrum of Fe I 41, $\lambda 4404.750$ Å, together with three nearly identical synthetic profile fits using the HM LTE, the TH LTE and the TH NLTE 1+ models. See text for a discussion of strong lines.

istic features are displayed in Fig. 9,
1.
There is still a systematic difference between abundances (oscillator strengths) of the Oxford and Hannover groups which is seen best in the domain of the turbulence lines around 80 to 100 mÅ. It is also found as a difference between lines of low and high excitation. This would be even easier to detect if the adjustment of the damping constants were applied to the individual sets of lines calculated from a common base of f-values. For our model (4) in Fig. 9 the Oxford data alone then would require a damping correction of $\Delta\log C_6 = -0.28$, and they would lead to the value of $\log\varepsilon_{\rm Fe{\sc i},\odot} = 7.693 \pm 0.052$, reasonably close to that of Blackwell et al. (1995a). Vice versa, LTE in the HM model (4) applied only to the Hannover f-values would require $\Delta\log C_6 = +0.13$, and result in $\log\varepsilon_{\rm Fe{\sc i},\odot} = 7.543 \pm 0.070$. Our compromise to fit the combined data set thus does not at all resolve the long-standing discrepancy. It is important to recognize that this problem does not seem to depend on the particular LTE or NLTE model chosen. The difference between the Oxford and Hannover line abundances is only slightly smaller (0.10 dex) for the TH LTE model. It is removed here only by adjustment of the damping constants for the individual models, the shortcomings of which are hidden in a slightly increased scatter.
2.
The turbulence lines deviate from both weak and strong lines in models (0) to (3), and perhaps in the HM LTE model (4) because the mean microturbulence is relatively low. This choice was made in Paper I mostly to model a number of the stronger turbulence lines with equivalent widths around 100 mÅ. After having examined a series of tests with different values we concluded that a value of $\xi = 1.0$ km s-1 produced profile fits of approximately the same quality. As is evident from comparing models (0) and (5) in Fig. 9 the higher value of $\xi$ tends to improve the uniformity of the abundances. A similar increase would also improve the results of the HM model.
3.
Even after having adjusted the strong lines to fit to a common mean abundance with the weaker lines it is surprising how they lead to systematically lower abundances than the sample mean. Part of this difference may be attributed to a relatively bad fit of the line wings. Figure 10 shows the discrepancy between inner and outer wing synthesis. Both parts of the profile are of photospheric origin. We note that a slightly better fit of the outer wings can be achieved with an increase of the iron abundance by $\simeq $0.03 dex which, however, would not remove the trend. Moreover, it would destroy the fit of the inner wing to an unacceptable degree.
4.
The run of abundances with excitation energies displays a decrease with $E_{\rm low}$ for most of the models. As was emphasized by Blackwell et al. (1995a) and Grevesse & Sauval (1999) this tendency is relaxed or even removed by introducing atmospheric models with lower temperatures in the upper photosphere. This trend is confirmed when comparing the HM and TH LTE models in our analysis. However, care must be taken not to confuse it with a similar one produced by the dependence upon microturbulence. The current sample of Fe I lines includes quite a number of low-excitation lines in the turbulence regime (Mults 1, 2, 3 and 13), which dominate the least-squares approach in Fig. 9. This becomes particularly evident by comparison of the LTE model (0) and (5), and by the NLTE models (2) and (6), where the increase of $\xi$ from 0.85 to 1.00 km s-1 removed most of the energy dependence.

The solar iron abundance determined by even the most careful spectral analysis thus depends on the proper choice of both the atmospheric model and the oscillator strengths. While Grevesse & Sauval (1999) claim to have solved the discrepancies of the long-standing debate on the solar iron abundance by introducing their special semi-empirical adjustment to the HM atmospheric model, it is only fair to notice that even their final data produce an abundance difference with mean values of $(\log\varepsilon_{\rm Fe{\sc i},\odot})_{\rm Han} = 7.476 \pm 0.053$, and $(\log\varepsilon_{\rm Fe{\sc i},\odot})_{\rm Oxf} = 7.514 \pm 0.036$. What makes this result less useful is the neglect of all strong lines. As was shown above it is the strong lines in the Oxford sample that - having been adjusted to the weaker lines by a corresponding decrease of the damping constants - confirm the high solar Fe I abundance claimed by Blackwell et al. (1995a). Different from the Kiel-Hannover group the Oxford group does not cover the full range of line strengths and excitation energies encountered in the solar spectrum. In particular the weak lines are missing, for which an analysis would allow a direct comparison of the f-value sources without reference to the uncertainties of line broadening processes.

There is no use ignoring the fact that either the oscillator strengths currently available are discrepant at a level that cannot be explained by laboratory measurement errors alone, or that the solar spectral line identifications are erroneous at an equally unacceptable level, or that atmospheric inhomogeneities are much more important for individual lines than expected. Let us discuss all three possibilities.

Much of the different absolute scales of f-values is due to the necessary normalization which can be improved; however, an individual scatter of lines in a common multiplet is obtained even for experimental methods thought to be very accurate. As an example let us consider the abundance scatter of lines in Mult 114. All lines have been measured by the Hannover group, and the abundances spread from 7.41 at $\lambda 5141.739$ to 7.65 at $\lambda 5049.819$ to a value as high as 7.78 for $\lambda 4924.769$ if the HM LTE model is applied. These are not faint lines for which high measurement errors could be accepted; the experimental error estimates range from 0.04 to 0.07 dex for these lines, which transforms to the fact that our abundances lead to results that are discrepant on much more than a $3\sigma$ level. Of course, the results may tell us that the hollow-cathode measurements of $\lambda 5141.739$ are not of the same quality as the other two lines which were measured by laser-induced fluorescence, but that would invalidate the experimental error estimates.

Comparison of such multiplet abundance scatter based on common source f-values with that already discussed above indicates that this does not depend very much on the experimental methods either, although there may exist still a number of problems that are connected with the control of experimental environment parameters as discussed by Holweger et al. (1995). Thus we conclude that agreement of mean abundance values between different sources of oscillator strengths (often claimed for the O'Brian et al. data) is not a significant measure of methodical accuracies. Taken at face value the rms scatter of abundances obtained from a single set of oscillator strengths such as that of O'Brian et al. is a measure of the accuracy of the mean solar Fe I abundance that can be reached with these data. In fact the accuracy is then even less due to blends and other problems referring to the profile fits, and to the ambiguities of atmospheric modelling.

There exists a number of lines in the iron spectrum that could be misidentified in that the spectral features could be blends that are not only unresolved but also fall within a few mÅ of the same center wavelength. As with other undetected blends such profiles will be fitted with too large abundances. This should produce abundance distributions that are systematically shifted to the high-abundance side, something that is not detected in the results. To reduce the dominating intrinsic abundance scatter to reasonable amounts it would mean that more than half of the lines would have to be corrected for such blend or identification problems, a situation that seems highly unlikely. We note that many blend problems of the kind producing too large fit abundances are avoided by our profile fitting method which allows an exchange of certain fit parameters such as abundance, microturbulence or damping parameters only within a narrow region. In such cases the profile fit procedure always tends to produce higher abundances.

Our discussion of line broadening in Sect. 3.1.2 and Fig. 2 has shown that the true abundance differences resulting from line formation in plane-parallel and in hydrodynamic atmospheres are quite small. They are even negligible taking into account the large abundance differences that appear between sets of different f-values. The mere change of atmospheric models affects the mean abundance but not the rms scatter as can be found in Table 3, and it is obvious that changing the microturbulence has a greater influence on such results. Thus it is doubtful if any other atmospheric model could significantly reduce the abundance scatter.

Our results then indicate that it is the atomic data, in particular the oscillator strengths, that presently do not allow the determination of the solar Fe I abundance with an accuracy better than $\sim $0.1 dex. Based on the most reliable sets of f-values (Oxford and Hannover data) and on the model producing the smallest overall dependence on excitation energy (TH NLTE 1/2+) we find a value of $\log\varepsilon_{\rm Fe{\sc i},\odot} = 7.509 \pm 0.075$ with no dependence on line strength but a small residual gradient with energy, $\Delta\log\varepsilon_{\rm }/\Delta E_{\rm low,{\rm eV}} = -0.005$. In view of the differences between the Oxford and Hannover f-values it is important to notice that this value is only 0.02 dex above that obtained from the Hannover data alone, while it is 0.09 dex below the pure Oxford value. This apparent contradiction is resolved by inspection of the corresponding energy dependence of the respective sources. Whereas the Hannover results show no energy gradient, the Oxford data - after having adjusted the damping constants to remove a line strength trend - keep a strong gradient with excitation energy for which $\Delta\log\varepsilon_{\rm }/\Delta E_{\rm low,{\rm eV}} = 0.034$. The last three models in Fig. 9 show only a small residual energy dependence of the Fe I abundances ranging from $\Delta\log\varepsilon_{\rm }/\Delta E_{\rm low,{\rm eV}} = -0.0094$ for the TH NLTE5+ model to $\Delta\log\varepsilon_{\rm }/\Delta E_{\rm low,{\rm eV}} = -0.0054$ for the TH NLTE1/2+ model.

The above results are to be understood as a clear report of our failure to solve the photospheric solar Fe I abundance problem if more than the Hannover data set were involved. Using this data set alone with the HM LTE model, a microturbulence of 1.05 km s-1 together with damping corrections $\Delta\log C_6 = 0.11$ (above the Anstee & O'Mara damping constants) yields $\log\varepsilon_{\rm Fe{\sc i},\odot} = 7.535 \pm 0.070$. The energy gradient for that result is $\Delta\log\varepsilon_{\rm }/\Delta E_{\rm low,{\rm eV}} = -0.008$. The overall best NLTE model (TH NLTE 1/2+) applied to the Hannover data alone leads to $\log\varepsilon_{\rm Fe{\sc i},\odot} = 7.480 \pm 0.072$ with no dependence on energy.

4 Conclusions

The choice of a particular model to determine the solar Fe I line formation with a valid parametrization of the atomic collisions is not possible even when including the weak solar lines. Arguments referring only to the solar abundance problem with or without inclusion of the Fe II lines are not conclusive since both sets of f-values (Fe I and Fe II) are far from producing homogeneous results. One marginal result is that the models of Paper I with their low microturbulence are no longer competitive because they all display a relatively strong gradient with excitation energy (see Fig. 9). This does no longer appear when increasing the microturbulence from $\xi = 0.85$ km s-1 to 1.00 km s-1 as in our present models 5 to 9. All the TH models are roughly compatible with meteoritic abundance. Small corrections for dynamic line formation such as suggested by comparison with hydrodynamic results of Asplund et al. (2000) in Sect. 3.1.2 are of the order of -0.03, which would bring the solar abundance to a value slightly below that of the carbonaceous chondrites.

The quality of individual line fits are significantly different for the HM and TH model atmospheres only for the cores of strong lines. In Paper I this was demonstrated for a number of lines of various excitation energies. The line center flux reflects essentially the different temperatures in the upper photosphere with a 150 ...200 K difference predicting $\Delta F \sim 4$% as observed. However, these differences vanish when a compromise is accepted for a profile fit of the inner wings (see Fig. 10) allowing the synthetic profile to fall below the observed flux by a small amount. The evaluation of profile fits thus has changed marginally as compared with Paper I. For the weaker lines Figs. 4 and 6 document the independence of fit quality from the model atmosphere if abundances and macroturbulence velocities are adjusted accordingly.

The selection of a particular atmospheric/atomic model on the grounds of profile synthesis of the solar Fe I flux spectrum is therefore still somewhat ambiguous. This would be different if the abundance determinations were of higher quality. For differential analyses of stellar spectra it is obvious that our atmospheric model can be only one of the TH models because only they allow a physically consistent change of parameters such as $T_{\rm eff}$, $\log g$ or [Fe/H]. Since strong lines in the solar spectrum reduce to weak or turbulence lines in stars of low metal abundance, it is most important to install a unique recipe for the determination of the damping parameter. This can be done with reference to Table 3 where a good mean value for the correction would be $\Delta\log C_6 = -0.15$. We should, however, bear in mind that this deviation from the Anstee & O'Mara results is essentially necessary to correct the strong lines with f-values from the Oxford group. The error introduced to differential abundance determinations in metal-poor stars thus will have to include a systematic uncertainty of $\sim $0.04 dex due to inconsistencies in the interpretation of the solar lines.

Current investigations of a small number of reference stars with different iron abundances will have to show how to select a common NLTE model that fits the Fe II/Fe I ionization equilibria of all stars.

Acknowledgements
Part of this work was funded by the Deutsche Forschungsgemeinschaft under grant Ge 490/12-2. AJK benefitted from a stipend of the Studienstiftung des Deutschen Volkes. JS is grateful for support from the National Natural Science Foundation of China.

References

 

Copyright ESO 2001