A&A 380, 590-598 (2001)
DOI: 10.1051/0004-6361:20011461
New neighbours: IV. 30 DENIS late-M dwarfs
between 15 and 30 parsecs
N. Phan-Bao
1,2 -
J. Guibert
1,2 -
F. Crifo
2 -
X. Delfosse
3 -
T. Forveille
3,4 -
J. Borsenberger
5 -
N. Epchtein
6 -
P. Fouqué
7,8 -
G. Simon
2
1 - Centre d'Analyse des Images, DASGAL, Observatoire de Paris, 61 avenue
de l'Observatoire, 75014 Paris, France
2 -
Observatoire de Paris (DASGAL/UMR-8633), 75014 Paris, France
3 -
Laboratoire d'Astrophysique de Grenoble, Université J.
Fourier, BP 53, 38041 Grenoble, France
4 -
Canada-France-Hawaii Telescope Corporation, 65-1238 Mamalahoa
Highway, Kamuela, HI 96743, USA
5 -
Institut d'Astrophysique de Paris, 98bis boulevard Arago,
75014 Paris
6 -
Observatoire de la Côte d'Azur, Département Fresnel, BP 4229, 06304 Nice Cedex 4, France
7 -
DESPA, Observatoire de Paris, 5 place J. Janssen, 92195
Meudon Cedex, France
8 -
European Southern Observatory, Casilla 19001, Santiago 19, Chile
Received 16 July 2001 / Accepted 15 October 2001
Erratum
Abstract
We present 30 new nearby (d< 30 pc) red dwarf candidates, with
estimated spectral types M 6 to M 8. 26 were directly selected from the
DENIS database, and another 4 were first extracted from the LHS catalogue
and cross-identified with a DENIS counterpart. Their proper motions were
measured on the MAMA measuring machine from plates spanning 13 to 48 years,
and are larger than 0.1 yr ,
ruling out the possibility that
they are giants. Their distances were estimated from
the DENIS colours and IR colour-magnitude relations and range
between 15 and 30 pc.
,
ruling out the possibility that
they are giants. Their distances were estimated from
the DENIS colours and IR colour-magnitude relations and range
between 15 and 30 pc.
Key words: astrometry - proper motions - low mass stars
Much of our understanding of stellar astronomy rests upon the nearest
stars. As individual objects they are the brightest and hence best
studied examples of their spectral type, and their trigonometric parallaxes
can be measured accurately, although with significant effort.
The solar neighbourhood sample also provides deep insight into the nature
of our Galaxy's components,
through studies of its stellar luminosity and mass functions, its
kinematics, chemical composition, and multiplicity statistics.
Perhaps surprisingly, this sample is still incomplete, even very close to
the Sun, as illustrated by the recent discoveries of three
new stars with d< 6 pc (Henry et al. 1997; Delfosse et al.
2001; Scholz et al. 2001).
From a comparison of the observed star densities within 5 and
10 parsecs, Henry et al. (1997) estimate that approximately
130 systems are missing from the 10 pc sample. Most of these missing stars
are red M dwarfs, with B-V> 1.70 (Gliese et al. 1986),
and the deficit is largest south of declination
 .
For the most part the known members of the solar neighbourhood have
been selected within the available catalogues of
trigonometric parallaxes, though some significant fraction is still included
on the basis of photometric or spectroscopic distances (Gliese 1956;
Gliese & Jahreiß 1979, 1991). However, for at least the
last fifty years, parallax programs have selected their targets for a good part
from proper motion catalogues,
such as the Cincinnati catalogues (Porter et al. 1918, 1930),
the Luyten catalogues (LFT 1955; LTT 1957, 1961;
LHS 1979; NLTT 1980)
or the Lowell catalogues (Giclas et al. 1971, 1978).
This leads to a proper motion bias of the
resulting sample, at least for the faint end.
To date even the smaller LHS catalogue has been incompletely
followed-up, and the Luyten catalogues therefore contain many unrecognized
nearby stars (e.g. Scholz et al. 2001, for an extreme example).
Several groups are working to identify them (Henry et al. 1997;
Gizis & Reid 1997; Jahreiß et al. 2001).
One limitation to these efforts is the much brighter
limiting magnitude of the proper motion catalogues south of declination
.
For the most part the known members of the solar neighbourhood have
been selected within the available catalogues of
trigonometric parallaxes, though some significant fraction is still included
on the basis of photometric or spectroscopic distances (Gliese 1956;
Gliese & Jahreiß 1979, 1991). However, for at least the
last fifty years, parallax programs have selected their targets for a good part
from proper motion catalogues,
such as the Cincinnati catalogues (Porter et al. 1918, 1930),
the Luyten catalogues (LFT 1955; LTT 1957, 1961;
LHS 1979; NLTT 1980)
or the Lowell catalogues (Giclas et al. 1971, 1978).
This leads to a proper motion bias of the
resulting sample, at least for the faint end.
To date even the smaller LHS catalogue has been incompletely
followed-up, and the Luyten catalogues therefore contain many unrecognized
nearby stars (e.g. Scholz et al. 2001, for an extreme example).
Several groups are working to identify them (Henry et al. 1997;
Gizis & Reid 1997; Jahreiß et al. 2001).
One limitation to these efforts is the much brighter
limiting magnitude of the proper motion catalogues south of declination
 (e.g. Scholz et al. 2001, for a
recent discussion), where a much larger fraction of the solar
neighbourhood stars is currently missing.
(e.g. Scholz et al. 2001, for a
recent discussion), where a much larger fraction of the solar
neighbourhood stars is currently missing.
The recent near-infrared sky surveys, DENIS and 2MASS, represent
a powerful alternative tool to identify these faint and cool nearby
stars. Candidates are first selected on simple colour and photometric
distance criteria, producing an initial list that also contains many giants,
and potentially some pre-main-sequence stars. At low galactic
latitudes it would also include many reddened distant stars.
In a second step these contaminating populations need to be
rejected, through either (1) a systematic spectroscopic follow up
(Gizis et al. 2000), or (2) proper motion selection (distant
giants have very small proper motions), or (3) more accurate multi-colour
photometry than
available from the surveys. Systematic spectroscopy is clearly
the cleanest approach, and does not reject the few nearby star that, like
Gl 710 for instance, have small proper motions. Proper motion selection
on the other hand is cheap and effective, but it obviously does nothing
to correct for the proper motion bias of the present nearby star catalogues.
We are using here the DENIS near infrared sky survey to identify
possible very-low-mass stars within 30 parsecs. We conservatively adopt
a distance cutoff slightly larger than the 25 pc limit of the Catalogue of
Nearby Stars of Gliese and Jahreiß (CNS3, 1991),
to avoid losing bona-fide d< 25 pc stars from imprecise photometric
distances.
One initial result of this effort was the discovery of an M 9 dwarf
at a spectroscopic distance of only 4 pc, DENIS-P J104814.7-395606.1
(Delfosse et al. 2001). In this paper we present 26 nearby
red dwarf candidates, selected with I-J> 2.0 (M6 or later) in the DENIS
database and with a proper motion larger than 0.1 yr .
13 of these are new, and another 13 were known as high-PM objects but
had not been characterized further. Four additional candidates were
first selected from the southern part of the LHS catalogue
and then identified with DENIS counterparts.
.
13 of these are new, and another 13 were known as high-PM objects but
had not been characterized further. Four additional candidates were
first selected from the southern part of the LHS catalogue
and then identified with DENIS counterparts.
Section 2 reviews the sample selection, and Sect. 3 presents the
photographic photometry and the proper motion measurements.
We discuss the results in Sect. 4 and summarize in Sect. 5.
Table 1:
Typical detection limiting distances (
 )
for M dwarfs with colour
)
for M dwarfs with colour
 in the DENIS survey. The spectral
types are from Leggett
(1992) and the absolute magnitude is taken from
Fig. 1.
in the DENIS survey. The spectral
types are from Leggett
(1992) and the absolute magnitude is taken from
Fig. 1.
|
I-J |
Spectral type |
MI |
 |
|
2.0 |
M 5.5-M 6 |
11.5 |
250 pc |
| 2.5 |
M 6.5-M 7 |
12.9 |
130 pc |
| 3.0 |
M 8 |
14.0 |
80 pc |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.6cm,clip]{H3000F1.ps}\end{figure}](/articles/aa/full/2001/47/aah3000/Timg14.gif) |
Figure 1:
MI: I-J HR diagram for M dwarfs with known distances (from
Leggett 1992 and Tinney et al. 1995). Our
empirical polynomial fit and the 3 Gyr model of Baraffe et al. (1998) for a solar
metalicity are overlaid. |
| Open with DEXTER |
The DEep Near-Infrared Survey (DENIS) is a southern sky
survey (Epchtein 1997), which will provide
full coverage of the southern hemisphere in two near-infrared bands (Jand  )
and one optical band (I).
DENIS observations are carried out on the ESO 1 m telescope at La Silla.
Dichroic beam splitters separate the three channels, and a
focal reducing optics provide scales of 3
)
and one optical band (I).
DENIS observations are carried out on the ESO 1 m telescope at La Silla.
Dichroic beam splitters separate the three channels, and a
focal reducing optics provide scales of 3
 per pixel on the
256
per pixel on the
256 256 NICMOS3 arrays used for the two infrared channels, and
1
256 NICMOS3 arrays used for the two infrared channels, and
1
 per pixel on the
per pixel on the
 Tektronix CCD detector of the Ichannel.
Tektronix CCD detector of the Ichannel.
The image data were processed with the
standard DENIS software pipeline (Borsenberger 1997;
Borsenberger et al., in preparation) at the
Paris Data Analysis Center (PDAC). The thermal background produced
by the instrument and the sky emission is derived from a local clipped
mean along the
strip. Flat-field corrections are derived from observation of the
sunrise sky.
Source extraction and photometry are performed at PDAC, using
a space-varying kernel algorithm (Alard 2000).
The astrometry of the individual DENIS frames is referenced to the
USNO-A2.0 catalogue, whose  1
1
 accuracy therefore determines
the absolute precision of the DENIS positions.
accuracy therefore determines
the absolute precision of the DENIS positions.
With a 100% completeness level at
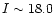 ,
,
 and
and
 ,
the DENIS survey is sensitive to M
dwarfs out to large distances (Table 1),
well beyond the 25 pc limit of the CNS3 (1991).
In this part of the HR diagram the I-J (or alternately I-K)
colour index is an excellent spectral type and luminosity estimator
(Leggett 1992). The DENIS data therefore provide
immediate identification of M dwarf candidates from I-J > 1.0, and,
under the assumption that they are indeed dwarfs, a good estimate of their
distance through colour-magnitude relations.
,
the DENIS survey is sensitive to M
dwarfs out to large distances (Table 1),
well beyond the 25 pc limit of the CNS3 (1991).
In this part of the HR diagram the I-J (or alternately I-K)
colour index is an excellent spectral type and luminosity estimator
(Leggett 1992). The DENIS data therefore provide
immediate identification of M dwarf candidates from I-J > 1.0, and,
under the assumption that they are indeed dwarfs, a good estimate of their
distance through colour-magnitude relations.
Table 2:
Position and observation information for the 30 new nearby
star candidates.
|
DENIS Name |
Other name |
 |
 |
DENIS |
Number of |
Time |
| |
|
|
|
Epoch |
observations |
baseline [yr] |
|
DENIS-P J0004575-170937 |
... |
00 04 57.54 |
-17 09 37.0 |
1999.521 |
4 |
47.834 |
| DENIS-P J0013466-045736 |
LHS 1042 |
00 13 46.60 |
-04 57 36.5 |
1999.846 |
4 |
45.173 |
| DENIS-P J0019275-362015 |
... |
00 19 27.53 |
-36 20 15.7 |
1999.877 |
3 |
21.064 |
| DENIS-P J0041353-562112 |
... |
00 41 35.39 |
-56 21 12.9 |
1999.803 |
3 |
20.984 |
| DENIS-P J0145434-372959 |
... |
01 45 43.49 |
-37 29 59.3 |
1999.877 |
3 |
22.165 |
| DENIS-P J0253444-795913 |
... |
02 53 44.41 |
-79 59 13.6 |
1999.699 |
3 |
21.921 |
| DENIS-P J0312251+002158 |
... |
03 12 25.11 |
+00 21 58.6 |
1999.704 |
3 |
48.020 |
| DENIS-P J0324268-772705 |
... |
03 24 26.88 |
-77 27 05.5 |
1999.855 |
3 |
22.077 |
| DENIS-P J0413398-270428 |
LP 890- 2 |
04 13 39.81 |
-27 04 28.9 |
1999.838 |
4 |
41.869 |
| DENIS-P J0602542-091503+ |
LHS 1810 |
06 02 54.26 |
-09 15 03.8 |
1999.929 |
3 |
17.040 |
| DENIS-P J0848189-201911+ |
LHS 2049 |
08 48 18.94 |
-20 19 11.4 |
1999.258 |
3 |
21.014 |
| DENIS-P J1003191-010507+ |
LHS 5165 |
10 03 19.18 |
-01 05 07.7 |
1999.030 |
3 |
13.011 |
| DENIS-P J1136409-075511 |
LP 673-63 |
11 36 40.99 |
-07 55 11.7 |
1999.373 |
4 |
45.195 |
| DENIS-P J1216101-112609 |
LP 734-87 |
12 16 10.16 |
-11 26 09.9 |
1999.203 |
4 |
44.948 |
| DENIS-P J1223562-275746 |
LHS 325a |
12 23 56.27 |
-27 57 46.7 |
1999.304 |
4 |
41.162 |
| DENIS-P J1236153-310646 |
LP 909-55 |
12 36 15.32 |
-31 06 46.0 |
1999.249 |
4 |
41.923 |
| DENIS-P J1357149-143852 |
... |
13 57 14.97 |
-14 38 52.6 |
1999.225 |
4 |
44.959 |
| DENIS-P J1406493-301828+ |
LHS 2859 |
14 06 49.33 |
-30 18 28.0 |
1999.395 |
3 |
24.927 |
| DENIS-P J1412069-041348 |
LP 679-32 |
14 12 06.98 |
-04 13 48.2 |
1999.444 |
4 |
42.118 |
| DENIS-P J1553251-044741 |
... |
15 53 25.13 |
-04 47 41.3 |
1999.581 |
4 |
45.170 |
| DENIS-P J1614252-025100 |
LP 624-54 |
16 14 25.20 |
-02 51 00.5 |
1999.280 |
4 |
45.763 |
| DENIS-P J2002134-542555 |
... |
20 02 13.42 |
-54 25 55.7 |
1999.581 |
4 |
23.077 |
| DENIS-P J2049527-171608 |
LP 816-10 |
20 49 52.72 |
-17 16 08.6 |
1999.518 |
3 |
44.946 |
| DENIS-P J2107247-335733 |
... |
21 07 24.73 |
-33 57 33.3 |
1999.581 |
4 |
19.812 |
| DENIS-P J2134222-431610 |
WT 792 |
21 34 22.27 |
-43 16 10.4 |
1999.767 |
3 |
21.189 |
| DENIS-P J2202112-110945* |
LP 759-17 |
22 02 11.28 |
-11 09 45.8 |
1999.419 |
4 |
45.672 |
| DENIS-P J2213504-634210 |
WT 887 |
22 13 50.47 |
-63 42 10.0 |
1999.537 |
3 |
22.976 |
| DENIS-P J2331217-274949 |
... |
23 31 21.73 |
-27 49 49.9 |
1999.869 |
5 |
45.119 |
| DENIS-P J2333405-213353 |
LHS 3970 |
23 33 40.59 |
-21 33 53.2 |
1999.770 |
4 |
45.176 |
| DENIS-P J2353594-083331 |
... |
23 53 59.44 |
-08 33 31.6 |
1999.693 |
3 |
46.077 |
+
Objects selected from LHS initially.
*
Already listed by Gizis et al. (2000).
Columns 1 & 2: object name in the DENIS data base and other
identification if available.
Columns 3, 4 & 5: DENIS Position with respect to equinox J2000 at DENIS epoch.
Columns 6 & 7: number of position observations and time baseline.
|
Column 1: object name.
Columns 2, 3 & 4: DENIS Position with respect to equinox J2000 at DENIS epoch.
Columns 5, 6 & 7: DENIS I-magnitude and colours.
|
Color-magnitude relations have yet to be established for the native
DENIS photometric system, and we therefore resort to a relation in the
standard Cousins-CIT system to derive distances for red stars in the
DENIS database. A preliminary comparison of the two photometric systems
for very late M dwarfs shows differences of  0.1 mag between the
K bands, of slightly less than 0.05 mag between the J bands, and below
0.05 mag between the two I bands (Delfosse 1997b).
We therefore choose to determine distances from the (I-J, MI)
relation, which is least affected by the neglected colour terms, and
note that systematic errors from adopting the Cousins-CIT relation are much
smaller than the intrinsic dispersion of that relation.
The two analytic (I-J, MI) relations in the literature, from Leggett
(1992) and Tinney (1993), respectively concentrate
on early and late M dwarfs.
For consistency across the M spectral class (and for convenience), we
therefore fitted a polynomial relation to the photometric
and trigonometric data of Leggett (1992), Tinney
(1993) and Tinney et al. (1995), adding some
photometry from Alonso et al. (1996) and Weis
(1993). Figure 1 shows the resulting relation,
0.1 mag between the
K bands, of slightly less than 0.05 mag between the J bands, and below
0.05 mag between the two I bands (Delfosse 1997b).
We therefore choose to determine distances from the (I-J, MI)
relation, which is least affected by the neglected colour terms, and
note that systematic errors from adopting the Cousins-CIT relation are much
smaller than the intrinsic dispersion of that relation.
The two analytic (I-J, MI) relations in the literature, from Leggett
(1992) and Tinney (1993), respectively concentrate
on early and late M dwarfs.
For consistency across the M spectral class (and for convenience), we
therefore fitted a polynomial relation to the photometric
and trigonometric data of Leggett (1992), Tinney
(1993) and Tinney et al. (1995), adding some
photometry from Alonso et al. (1996) and Weis
(1993). Figure 1 shows the resulting relation,
 |
|
|
(1) |
valid for
1.0< I-J < 3.0 and demonstrates its fair agreement with the theoretical track of Baraffe et al. (1998). The new polynomial fit complements the
(I-K, MK) relation derived by Tinney et al. (1995)
for the same spectral type range.
With the above Color-Magnitude relation as tool, we have searched the
first 2110 squares degrees processed
by PDAC (Fig. 2) for new members of the solar neighbourhood.
We select all DENIS sources with
 that have the
I-J colour of an M dwarf (
that have the
I-J colour of an M dwarf (
 ;
Leggett 1992).
We then compute their photometric distance (
;
Leggett 1992).
We then compute their photometric distance (
 )
from the
DENIS photometry and the above polynomial colour-magnitude relations,
and retain those with
)
from the
DENIS photometry and the above polynomial colour-magnitude relations,
and retain those with
 pc.
In the present paper we focus on the
2.0 < I-J < 3.0 range, or
spectral types of approximately M 6 to M 8. Bluer nearby M dwarfs are brighter and hence
less likely to have been overlooked. At present we therefore give them
a lower priority. Redder ones, like DENIS-P J104814.7-395606.1 (Delfosse et al. 2001), are addressed by the DENIS Brown Dwarf program (Delfosse et al., in preparation).
pc.
In the present paper we focus on the
2.0 < I-J < 3.0 range, or
spectral types of approximately M 6 to M 8. Bluer nearby M dwarfs are brighter and hence
less likely to have been overlooked. At present we therefore give them
a lower priority. Redder ones, like DENIS-P J104814.7-395606.1 (Delfosse et al. 2001), are addressed by the DENIS Brown Dwarf program (Delfosse et al., in preparation).
These criteria are met by 60 objects
(Tables 2, 3), 13 of which are listed in proper motion
catalogues but had no distance estimate (except WT 792, discussed below).
At that stage the sample is a mix of
distant giants and nearby dwarfs, which cannot be completely separated
using the DENIS photometry alone: the dwarf and giant sequences
are distinct in the DENIS I-J/J-K colour-colour diagram, but
not sufficiently separated to distinguish the two classes with 100%
completeness and reliability.
We additionally browsed the LHS catalogue (Luyten 1979) for
objects that match the colour and photometric distance criteria, but which
had been missed because of our galactic latitude cutoff, or whose DENIS
observations had not yet been entered in the database. To narrow down
that search, we looked for unambiguous DENIS identifications to southern
LHS stars matching
 > 16.0,
> 16.0,
 > 15.0, and
> 15.0, and
 > 1.5, and then applied the colour and
photometric distance cutoffs. This identified 4 additional candidates:
LHS 1810, 2049, 2859 and 5165, which are added in the Tables.
> 1.5, and then applied the colour and
photometric distance cutoffs. This identified 4 additional candidates:
LHS 1810, 2049, 2859 and 5165, which are added in the Tables.
*
Not previously known as a high proper motion star.
Columns 2, 3 & 4:
 , ,
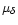 , ,
 our measurement, in arcsec yr
our measurement, in arcsec yr . .
Column 5: literature total proper motion, from Luyten (1979,
1980) or Wroblewski et al.
(1994) when available.
|
As an initial step towards rejecting
giants, we determine the proper motion of the candidates from a comparison
of the DENIS position with archival Schmidt plates digitized on the MAMA
microdensitometer. Objects fainter than R = 10 with a proper motion
 yr
yr must be dwarfs: a red giant with such
an apparent magnitude and proper motion would have a very large and improbable
space velocity (
must be dwarfs: a red giant with such
an apparent magnitude and proper motion would have a very large and improbable
space velocity ( 1000 km s-1), much larger than the Galactic escape speed
(Meillon 1999). Conversely, some small fraction of the
nearby dwarfs must have proper motions below our cutoff.
1000 km s-1), much larger than the Galactic escape speed
(Meillon 1999). Conversely, some small fraction of the
nearby dwarfs must have proper motions below our cutoff.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.4cm,clip]{H3000F2.ps}\end{figure}](/articles/aa/full/2001/47/aah3000/Timg40.gif) |
Figure 2:
All DENIS sources with the I-J colour of an M-dwarf
(1.0 < I-J < 3.0) detected in the first 2110 squares degrees
processed by PDAC, with a photometric distance  30 pc and a
galactic latitude 30 pc and a
galactic latitude
 .
The dots represent the early
M-stars (1.0 < I-J < 3.0). Amongst the 60 DENIS sources
in the 2.0-3.0 range (corresponding to a late-M spectral class)
the solid circles represent the objects with a proper motion .
The dots represent the early
M-stars (1.0 < I-J < 3.0). Amongst the 60 DENIS sources
in the 2.0-3.0 range (corresponding to a late-M spectral class)
the solid circles represent the objects with a proper motion
 > 0.1 yr > 0.1 yr ,
and the triangles those with a smaller proper
motion. The solid and dashed lines
respectively represent the dwarf and giant sequences of Bessell & Brett
(1988), for slightly different filters. The (indicative) spectral
type labels on the top axis are adopted from Leggett (1992). ,
and the triangles those with a smaller proper
motion. The solid and dashed lines
respectively represent the dwarf and giant sequences of Bessell & Brett
(1988), for slightly different filters. The (indicative) spectral
type labels on the top axis are adopted from Leggett (1992). |
| Open with DEXTER |
To estimate that proportion, we counted the fraction of the stars within
25 pc in both the CNS3 and the Hipparcos catalogue that have a proper
motion smaller than 0.1 yr .
In the CNS3, this fraction of "slow'' stars
is about 13% for limiting magnitudes of V < 7, 8 and 9. In the Hipparcos
catalogue and for the same limiting magnitudes it is much lower,
only 6.5%. The CNS3 is considered complete to V = 9. The Hipparcos
catalogue is complete up to V = 7.3, and nearly
complete up to at least 9 for nearby stars, as potential nearby
stars were systematically included in the Hipparcos Input catalogue.
Incompleteness therefore cannot explain the discrepancy between the
fractions of low proper-motion stars in the two catalogues.
A careful comparison between the two lists of "slow''
stars shows that half of the slow CNS3 objects have a Hipparcos
distance larger than 25 pc, and should therefore not be taken into
consideration. The fraction of nearby stars lost due to our proper motion
cut-off is therefore of the order of 6%. Our future
goal is to obtain spectra of
all candidates, independently of their proper motions, to assemble
a complete and unbiased inventory of the solar neighbourhood for the
high galactic latitude southern sky.
.
In the CNS3, this fraction of "slow'' stars
is about 13% for limiting magnitudes of V < 7, 8 and 9. In the Hipparcos
catalogue and for the same limiting magnitudes it is much lower,
only 6.5%. The CNS3 is considered complete to V = 9. The Hipparcos
catalogue is complete up to V = 7.3, and nearly
complete up to at least 9 for nearby stars, as potential nearby
stars were systematically included in the Hipparcos Input catalogue.
Incompleteness therefore cannot explain the discrepancy between the
fractions of low proper-motion stars in the two catalogues.
A careful comparison between the two lists of "slow''
stars shows that half of the slow CNS3 objects have a Hipparcos
distance larger than 25 pc, and should therefore not be taken into
consideration. The fraction of nearby stars lost due to our proper motion
cut-off is therefore of the order of 6%. Our future
goal is to obtain spectra of
all candidates, independently of their proper motions, to assemble
a complete and unbiased inventory of the solar neighbourhood for the
high galactic latitude southern sky.
To obtain B and R photometry of the candidates and determine their proper
motions, we identified all Survey plates in the CAI
(http://dsmama.obspm.fr/) plate vault that
contained images of the nearby star candidates. Depending on the
declination of the candidates, the following plates were available: POSS I for
 ,
SRC-J for
,
SRC-J for
 ,
SRC-R for
,
SRC-R for
 ,
and ESO-R for
,
and ESO-R for
 .
We used the MAMA microdensitometer (Berger et al. 1991) at
CAI to digitize the survey plates,
and analysed the resulting images with SExtractor (Bertin & Arnouts
1996).
.
We used the MAMA microdensitometer (Berger et al. 1991) at
CAI to digitize the survey plates,
and analysed the resulting images with SExtractor (Bertin & Arnouts
1996).
![\begin{figure}
\par\includegraphics[width=20.5cm,clip]{H3000F3.ps}\end{figure}](/articles/aa/full/2001/47/aah3000/Timg46.gif) |
Figure 3:
I-band finding charts for the objects listed in Table 2.
The size of each chart is  3.5 3.5
 .
North is up and east is to
the left. The 4 stars selected directly from the LHS are not included. .
North is up and east is to
the left. The 4 stars selected directly from the LHS are not included. |
| Open with DEXTER |
The SExtractor source parameters were calibrated using the
GSPC-2 (Postman et al. 1997; Bucciarelli et al.
2001) and ACT catalogues (Urban et al. 1998) as
photometric and astrometric references to produce B and R magnitudes
(Table 5),
and equatorial coordinates at the epoch of the plate. Absolute proper
motions were then determined through a least square fit to the positions
at the 2 to 4 Schmidt plate epochs and the DENIS survey epoch.
The proper motion errors range between 8 and 19 mas/year, depending on the
object magnitude and the available time baseline. The magnitude errors are
 mag for B and
mag for B and  mag for R.
mag for R.
Table 5:
MAMA and DENIS photometry, and estimated distances, for the
30 DENIS red dwarf candidates.
|
DENIS objects |
B |
R |
I |
I-J |
J-K |
MI |
MK |
DistI |
DistK |
 |
| |
|
|
|
|
|
|
|
[pc] |
[pc] |
[km s-1] |
|
J0004575-170937 |
18.2 |
15.6 |
13.00 |
2.03 |
0.93 |
11.59 |
8.78 |
19.1 |
17.8 |
13.2 |
| J0013466-045736 |
19.5 |
16.8 |
13.88 |
2.44 |
0.99 |
12.73 |
9.69 |
17.0 |
14.2 |
48.7 |
| J0019275-362015 |
18.2 |
17.0 |
14.30 |
2.14 |
0.89 |
11.95 |
8.95 |
29.6 |
29.1 |
25.3 |
| J0041353-562112 |
20.6 |
18.7 |
14.68 |
2.74 |
1.07 |
13.37 |
10.12 |
18.2 |
14.1 |
11.8 |
| J0145434-372959 |
20.2 |
17.7 |
15.05 |
2.56 |
0.94 |
13.00 |
9.79 |
25.7 |
22.5 |
53.6 |
| J0253444-795913 |
18.7 |
16.2 |
13.47 |
2.15 |
0.98 |
11.98 |
9.17 |
19.9 |
17.1 |
10.4 |
| J0312251+002158 |
20.4 |
17.0 |
14.30 |
2.17 |
0.93 |
12.03 |
9.11 |
28.4 |
26.2 |
23.7 |
| J0324268-772705 |
20.4 |
17.3 |
14.36 |
2.26 |
1.04 |
12.29 |
9.49 |
26.0 |
20.6 |
42.0 |
| J0413398-270428 |
22.0 |
17.7 |
14.45 |
2.26 |
0.99 |
12.29 |
9.40 |
27.1 |
22.9 |
30.2 |
| J0602542-091503 |
17.3 |
15.6 |
12.98 |
2.12 |
0.85 |
11.88 |
8.81 |
16.6 |
17.4 |
48.9 |
| J0848189-201911 |
19.7 |
17.2 |
14.51 |
2.21 |
0.98 |
12.15 |
9.29 |
29.7 |
25.4 |
88.3 |
| J1003191-010507 |
21.0 |
18.0 |
14.94 |
2.62 |
1.08 |
13.12 |
10.02 |
23.1 |
17.6 |
51.7 |
| J1136409-075511 |
17.8 |
16.5 |
14.31 |
2.20 |
0.90 |
12.12 |
9.11 |
27.4 |
26.3 |
29.1 |
| J1216101-112609 |
19.5 |
17.1 |
14.72 |
2.30 |
1.10 |
12.39 |
9.65 |
29.2 |
21.6 |
30.9 |
| J1223562-275746 |
19.6 |
16.4 |
14.19 |
2.30 |
0.88 |
12.39 |
9.27 |
22.9 |
22.3 |
138.9 |
| J1236153-310646 |
18.5 |
16.7 |
13.97 |
2.23 |
1.01 |
12.21 |
9.39 |
22.5 |
18.6 |
19.3 |
| J1357149-143852 |
21.1 |
18.5 |
15.55 |
2.69 |
1.14 |
13.27 |
10.13 |
28.5 |
20.8 |
48.1 |
| J1406493-301828 |
18.5 |
15.7 |
13.42 |
2.13 |
1.01 |
11.91 |
9.19 |
20.0 |
16.5 |
77.5 |
| J1412069-041348 |
19.1 |
16.3 |
13.66 |
2.04 |
0.98 |
11.63 |
8.93 |
25.5 |
22.0 |
39.8 |
| J1553251-044741 |
17.4 |
15.1 |
13.67 |
2.10 |
1.37 |
11.82 |
9.75 |
23.4 |
12.3 |
14.0 |
| J1614252-025100 |
19.3 |
17.3 |
13.63 |
2.29 |
1.04 |
12.37 |
9.54 |
17.9 |
14.2 |
31.1 |
| J2002134-542555 |
19.4 |
17.1 |
13.89 |
2.20 |
1.18 |
12.12 |
9.62 |
22.6 |
15.1 |
39.5 |
| J2049527-171608 |
18.9 |
16.8 |
14.16 |
2.32 |
1.08 |
12.44 |
9.65 |
22.0 |
16.7 |
33.4 |
| J2107247-335733 |
19.9 |
16.7 |
14.36 |
2.20 |
1.02 |
12.12 |
9.35 |
28.0 |
22.8 |
66.8 |
| J2134222-431610 |
17.6 |
15.3 |
12.78 |
2.02 |
1.06 |
11.56 |
9.07 |
17.5 |
13.4 |
66.7 |
| J2202112-110945 |
20.7 |
17.9 |
15.11 |
2.66 |
0.98 |
13.21 |
9.96 |
24.0 |
20.1 |
25.9 |
| J2213504-634210 |
18.7 |
16.3 |
13.05 |
2.16 |
1.04 |
12.01 |
9.31 |
16.2 |
12.8 |
16.7 |
| J2331217-274949 |
20.4 |
17.7 |
14.25 |
2.59 |
1.04 |
13.06 |
9.94 |
17.3 |
13.6 |
61.0 |
| J2333405-213353 |
19.3 |
16.5 |
13.89 |
2.06 |
0.90 |
11.69 |
8.78 |
27.5 |
26.9 |
98.2 |
| J2353594-083331 |
** |
18.6 |
15.93 |
2.97 |
1.13 |
13.92 |
10.32 |
25.3 |
20.0 |
44.3 |
**
Too faint for the plate.
Column 1: object name.
Columns 2, 3: B, R magnitudes determined from the plates using GSPC and GSPC-2 calibrations.
Columns 4, 5, 6: DENIS I-magnitude and colours.
Column 7: MI absolute I band magnitude, from the colour magnitude
relation
derived in the present paper.
Column 8: MK absolute K band magnitude, from the Tinney et al.
(1995) relation.
Columns 9, 10: DistI,
DistK distances estimated from
MI and MK respectively.
Column 11:  tangential velocity, computed from DistI and the
proper motion.
tangential velocity, computed from DistI and the
proper motion.
|
From the full sample of 60 objects, 34 have no proper motion above
the 0.1 yr level and are listed in Table 3. They are
not studied in this paper, and leave us with 26 high quality
nearby star candidates (Table 2) to which the 4 LHS stars are added
(finding charts in Fig. 3).
Of the 30 proper-motion objects, 13 were previously unknown.
2 of those have a proper motion,
level and are listed in Table 3. They are
not studied in this paper, and leave us with 26 high quality
nearby star candidates (Table 2) to which the 4 LHS stars are added
(finding charts in Fig. 3).
Of the 30 proper-motion objects, 13 were previously unknown.
2 of those have a proper motion,  yr
yr ,
that would have
qualified them
for inclusion in the LHS. An additional 5 have
,
that would have
qualified them
for inclusion in the LHS. An additional 5 have  yr
yr and could have been included in the NLTT. The 17 remaining objects
belong to the LHS, the NLTT, or the Catalogue of
New proper motion stars (Wroblewski & Torres 1994).
For those, the difference between our
proper motions and the literature values has a mean of 9 masyr
and could have been included in the NLTT. The 17 remaining objects
belong to the LHS, the NLTT, or the Catalogue of
New proper motion stars (Wroblewski & Torres 1994).
For those, the difference between our
proper motions and the literature values has a mean of 9 masyr and a dispersion
of 23 masyr
and a dispersion
of 23 masyr ,
of the order of the quoted LHS accuracy.
Table 4 lists our proper motion measurements, and the
literature proper motion when available.
Figure 2, which distinguishes the high and low proper motion
stars in
the I-J/J-K diagram, immediately shows that the high proper
motion stars belong to the dwarf sequence, with only one exception,
DENIS-P J1553251-044741.
On the other hand, some low proper motion stars do, as expected, seem
to belong to the dwarf sequence.
,
of the order of the quoted LHS accuracy.
Table 4 lists our proper motion measurements, and the
literature proper motion when available.
Figure 2, which distinguishes the high and low proper motion
stars in
the I-J/J-K diagram, immediately shows that the high proper
motion stars belong to the dwarf sequence, with only one exception,
DENIS-P J1553251-044741.
On the other hand, some low proper motion stars do, as expected, seem
to belong to the dwarf sequence.
In addition to the (I, I-J) distances computed from the relation derived
above, Table 5 contains (I, I-K) distances derived using
the (I-K, MK) colour-magnitude relation of Tinney et al.
(1995) for
1.2<I-K<5.4. The latter are systematically somewhat smaller,
most likely because of our use of DENIS  magnitudes and a
colour-magnitude relation established in the Cousins-CIT photometric
system. The (I, I-J) distances are therefore most likely more reliable.
Carpenter (2001) carefully derived relations for colour transformations
between 2MASS and other systems, including CIT and DENIS.
However the DENIS data he used is the part publicly released at CDS and reduced by
the Leiden Data Center (LDAC), and covers only a very small fraction of the DENIS data.
The data presented here was reduced by the Paris Data Center (PDAC) which uses
slightly different methods and relations. Therefore the Carpenter's equations
should not be used here.
We note that Patterson et al. (1998) estimate a distance
of 22 pc to WT 792 from VRI photometry that is compatible with our
Dist
magnitudes and a
colour-magnitude relation established in the Cousins-CIT photometric
system. The (I, I-J) distances are therefore most likely more reliable.
Carpenter (2001) carefully derived relations for colour transformations
between 2MASS and other systems, including CIT and DENIS.
However the DENIS data he used is the part publicly released at CDS and reduced by
the Leiden Data Center (LDAC), and covers only a very small fraction of the DENIS data.
The data presented here was reduced by the Paris Data Center (PDAC) which uses
slightly different methods and relations. Therefore the Carpenter's equations
should not be used here.
We note that Patterson et al. (1998) estimate a distance
of 22 pc to WT 792 from VRI photometry that is compatible with our
Dist within the errors.
within the errors.
It must be realized that the distances in Table 5 carry considerable
uncertainties, as any photometric parallaxes do. The intrinsic scatter
of the colour-luminosity relation (Fig. 1) is  1 mag,
which on a star by star basis translates into a 45% random distance
error. At a lower level, the poynomial relations most likely
have systematic errors at some colours: 0.3 magnitude local
errors (i.e. 14% distance errors) can quite easily creep in when
fitting a phenomenological model to such a dispersed diagram.
1 mag,
which on a star by star basis translates into a 45% random distance
error. At a lower level, the poynomial relations most likely
have systematic errors at some colours: 0.3 magnitude local
errors (i.e. 14% distance errors) can quite easily creep in when
fitting a phenomenological model to such a dispersed diagram.
Finally, some of the 30 objects must be multiple systems,
whose distances are underestimated by attributing their
luminosity to one single star.
Tangential velocities calculated from the proper motions and distances,
are listed in the last column of Table 5; 4 stars have tangential
velocities larger than 70 km s-1: LHS 2049; 325a; 2859; 3970. Of those
LHS 325a and LHS 2049 were previously recognized as late-M stars with
high reduced proper motion (H = m + 5 log  + 5) by Bessell
(1991). LHS 325a is photometrically classified as an old-disk
star by Leggett (1992).
+ 5) by Bessell
(1991). LHS 325a is photometrically classified as an old-disk
star by Leggett (1992).
The sample of low proper motion objects (Table 3) probably contains a few
nearby stars, that happen to have a low tangential velocity, and is presently
under study.
The I-J and I-K colours of the 30 nearby star candidates indicate
spectral types of M 6 to M 8, which we plan to ascertain through
low-resolution spectroscopy. Such objects have masses of 0.1
 (Delfosse et al. 2000) or lower.
(Delfosse et al. 2000) or lower.
The 2110 square degrees explored here contain 26 stars with
2.0 <I-J< 3.0,
 > 0.1 yr
> 0.1 yr ,
and a photometric distance d< 30 pc. The whole
celestial sphere therefore contains
,
and a photometric distance d< 30 pc. The whole
celestial sphere therefore contains  500 similar objects, of which
500 similar objects, of which
 60%,
or 300, will have a photometric distance below 25 pc. Malmquist bias from
our approximate photometric distances must bias this number up, and
the number of stars that are actually within 25 pc must be significantly
smaller, perhaps by as much as a factor of 2.
The (R-I)
60%,
or 300, will have a photometric distance below 25 pc. Malmquist bias from
our approximate photometric distances must bias this number up, and
the number of stars that are actually within 25 pc must be significantly
smaller, perhaps by as much as a factor of 2.
The (R-I)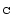 colour index that corresponds to our I-J = 2.0 cutoff is
(R-I)
colour index that corresponds to our I-J = 2.0 cutoff is
(R-I)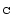 = 2.0 (Leggett 1992), or about 1.6 in the Kron system
used in the CNS3.
The whole CNS3 contains only 23 stars with (R-I)
= 2.0 (Leggett 1992), or about 1.6 in the Kron system
used in the CNS3.
The whole CNS3 contains only 23 stars with (R-I)
 > 1.6.
An effort similar to ours over the whole
celestial sphere would thus identify 150 to 250
new stars within 25 pc.
> 1.6.
An effort similar to ours over the whole
celestial sphere would thus identify 150 to 250
new stars within 25 pc.
Many new nearby stars have been recently identified thanks to
the near-IR sky surveys: DENIS and 2MASS have proved to be valuable
resources for the identification of new nearby stars. In the present
paper, we identify 60 photometric nearby star candidates in 2110 square
degrees, with distances that lie between 15 and 30 pc.
26 of those have large proper motions that exclude that they are distant
giants, 13 of which are new; 4 additional known LHS stars were
recognized as nearby star candidates outside the main search area.
A few stars have large tangential
velocities and may be subdwarfs, whose distances would then be
slightly overestimated.
We plan to obtain low-resolution spectra for all candidates in the near
future.
Acknowledgements
We are grateful to the DENIS consortium for providing the DENIS data, and
to René Chesnel for scanning and
pre-reducing the photographic plates. The long-term loan of POSS I plates
by the Leiden Observatory to Observatoire de Paris is gratefully acknowledged.
We thank the referee, Dr. Hartmut Jahreiß, for his prompt and very
constructive report.
- Alard, C. 2000, A&AS, 144, 363
In the text
NASA ADS
- Allard, F., Hauschildt, P. H., Baraffe, I., & Chabrier, G. 1996, ApJ, 465, L123
NASA ADS
- Alonso, A., Arribas, S., & Martinez-Roger, C. 1994, A&AS, 107, 365
In the text
NASA ADS
- Baraffe, I., Chabrier, G., Allard, F., & Hauschildt, P. H. 1995, ApJ, 446, L35
NASA ADS
- Baraffe, I., Chabrier, G., Allard, F., & Hauschildt, P. H. 1998, A&A, 337, 403
In the text
NASA ADS
- Berger, J., & Cordoni, J. -P., Fringant, A.-M., et al. 1991, A&AS, 87, 389 In the text
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393
In the text
- Bessell, M. S., & Brett, J. M. 1988, PASP, 100, 1134
NASA ADS
- Bessell, M. S. 1991, AJ, 101, 662
In the text
NASA ADS
- Borsenberger, J. 1997, in the 3rd DENIS Euroconference, The impact of large scale near-infrared surveys, ed. F. Garzon et al. (Kluwer Dordrecht), 121
In the text
- Bucciarelli, B., Garcia Yus, J., Casalegno, R., et al. 2001, A&A, 368, 335
In the text
NASA ADS
- Burrows, A., Hubbard, W. B., Saumon, D., & Lunine, J. I. 1993, ApJ, 406, 158
NASA ADS
- Carpenter, J. M. 2001, AJ, 121, 2851
In the text
NASA ADS
-
Chabrier, G., & Baraffe, I. 1997, A&A, 327, 1039
NASA ADS
- D'Antona, F., & Mazzitelli, I. 1994, ApJS, 90, 467
NASA ADS
- Delfosse, X., Tinney, C. G., Forveille, T., et al. 1997a, A&A, 327, L25
NASA ADS
- Delfosse, X. 1997b, Ph.D. Thesis, page 43 and Fig. 2.9, Grenoble University
In the text
- Delfosse, X., Forveille, T., Ségransan, D., et al. 2000, A&A, 364, 217
In the text
NASA ADS
- Delfosse, X., Forveille, T., Martin, E. L., et al. 2001, A&A, 366, L13
In the text
NASA ADS
- Epchtein, N. 1997, in the 2nd DENIS Euroconference, The impact of large scale near-infrared surveys, ed. F. Garzon et al. (Kluwer Dordrecht), 15
In the text
- Gizis, J. E., & Reid, I. N. 1997, PASP, 109, 849
In the text
NASA ADS
- Gizis, J. E., Monet, D. G., Reid, I. N., et al. 2000, AJ, 120, 1085
In the text
NASA ADS
- Giclas, H. L., Burnham, R. Jr., & Thomas, N. G. 1971, Lowell Northern Hemisphere Catalogue, The G Numbered Stars, Lowell Obs.
In the text
- Giclas, H. L., Burnham, R. Jr., & Thomas, N. G. 1978, Lowell Southern Hemisphere Catalogue, Lowell Obs. Bull., 164, 89
In the text
- Gliese, W. 1956, ZA, 39, 1
In the text
NASA ADS
- Gliese, W., & Jahreiß, H. 1979, A&AS, 38, 423
In the text
NASA ADS
- Gliese, W., Jahreiß, H., & Upgren, A.R. 1986, in The galaxy and the solar system, ed. R. Schmoluchowski et al. (The University of Arizona press), 13
In the text
- Gliese, W., & Jahreiß, H. 1991, Preliminary Version of the Third
Catalogue of Nearby Stars, as available at CDS Strasbourg
In the text
- Henry, T. J., Ianna, P. A., Kirkpatrick, J. D., & Jahreiß, H. 1997, AJ, 114, 388
In the text
NASA ADS
- Jahreiß, H., Scholz, R. D., Meusinger, H., & Lehmann, I. 2001, A&A, 370, 967
In the text
NASA ADS
- Leggett, S. K. 1992, ApJS, 82, 531
In the text
- Luyten, W. J. 1955, A Catalogue of 1849 stars with proper motions exceeding 0
 5 annually (LFT) (Lund Press, Minneapolis, Minn.)
In the text
5 annually (LFT) (Lund Press, Minneapolis, Minn.)
In the text
- Luyten, W. J. 1957, A Catalogue of 9867 stars in the southern hemisphere
with proper motions exceeding 0
 2 annually (LTT) (Lund Press, Minneapolis, Minn.)
In the text
2 annually (LTT) (Lund Press, Minneapolis, Minn.)
In the text
- Luyten, W. J. 1961, A Catalogue of 7127 stars in the northern hemisphere
with proper motions exceeding 0
 2 annually (LTT) (Lund Press, Minneapolis, Minn.)
In the text
2 annually (LTT) (Lund Press, Minneapolis, Minn.)
In the text
- Luyten, W. J. 1979, Catalogue of stars with proper motions exceeding
0
 5 annually (LHS) (Minneapolis, University of Minnesota)
In the text
5 annually (LHS) (Minneapolis, University of Minnesota)
In the text
- Luyten, W. J. 1980, New Luyten catalog of stars with proper motions
larger than Two Tenths of an arcsecond (NLTT) (Minneapolis, University of Minnesota)
In the text
- Martin, E. L., Basri, G., Delfosse, X., & Forveille, T. 1997, A&A, 327, L29
- Meillon, L. 1999, Ap&SS, 265, 179
In the text
- Patterson, R. J., Ianna, P. A., & Begam, M. C. 1998, AJ, 115, 1648
In the text
NASA ADS
- Porter, J. G., Yowell, E. J., & Smith, E. S. 1918, Publ. Cincinnati Obs., 18, No. 4
In the text
- Porter, J. G., Yowell, E. J., & Smith, E. S. 1930, Publ. Cincinnati Obs., 20, 1
In the text
NASA ADS
- Postman, M., Bucciarelli, B., Sturch C., et al. 1997, IAU Symp., 179,
379
In the text
- Scholz, R. D., Meusinger, H., Jahreiß, H. 2001, A&A, 374, L12
In the text
NASA ADS
- Tinney, C. G 1993, AJ, 105, 1169
In the text
NASA ADS
- Tinney, C. G, Reid, I. N., Gizis, J., & Mould, J. R. 1995, AJ, 110, 3014
In the text
NASA ADS
- Urban, S. E., Corbin, T. E., & Wycoff, G. L. 1998, AJ, 115, 2161
In the text
NASA ADS
- Weis, E. W. 1993, AJ, 105, 1962
In the text
NASA ADS
- Wroblewski, H., & Torres, C. 1994, A&AS, 105, 179
In the text
NASA ADS
Copyright ESO 2001
![\begin{figure}
\par\includegraphics[angle=-90,width=8.6cm,clip]{H3000F1.ps}\end{figure}](/articles/aa/full/2001/47/aah3000/Timg14.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.4cm,clip]{H3000F2.ps}\end{figure}](/articles/aa/full/2001/47/aah3000/Timg40.gif)
![\begin{figure}
\par\includegraphics[width=20.5cm,clip]{H3000F3.ps}\end{figure}](/articles/aa/full/2001/47/aah3000/Timg46.gif)